Groupwise Registration by Hierarchical Anatomical Correspondence Detection

Abstract

We present a novel feature-based groupwise registration method to simultaneously warp the subjects towards the common space. Due to the complexity of the groupwise registration, we resort to decoupling it into two easy-to-solve tasks, i.e., alternatively establishing the robust correspondences across different subjects and interpolating the dense deformation fields based on the detected sparse correspondences. Specifically, several novel strategies are proposed in the correspondence detection step. First, attribute vector, instead of intensity only, is used as a morphological signature to guide the anatomical correspondence detection among all subjects. Second, we detect correspondence only on the driving voxels with distinctive attribute vectors for avoiding the ambiguity in detecting correspondences for non-distinctive voxels. Third, soft correspondence assignment (allowing for adaptive detection of multiple correspondences in each subject) is also presented to help establish reliable correspondences across all subjects, which is particularly necessary in the beginning of groupwise registration. Based on the sparse correspondences detected on the driving voxels of each subject, thin-plate splines (TPS) are then used to propagate the correspondences on the driving voxels to the entire brain image for estimating the dense transformation for each subject. By iteratively repeating correspondence detection and dense transformation estimation, all the subjects will be aligned onto a common space simultaneously. Our groupwise registration algorithm has been extensively evaluated by 18 elderly brains, 16 NIREP, and 40 LONI data. In all experiments, our algorithm achieves more robust and accurate registration results, compared to a groupwise registration method and a pairwise registration method, respectively.

1 Introduction

Registration of a population data has received more and more attention in recent years due to its importance in population analysis [1-4]. Since groupwise registration method is able to register all images without explicitly selecting the template, it can avoid bias in template selection and thus becomes attractive to the precise analysis of population data, compared to the pairwise registration methods. However, it is complicated for groupwise registration of multiple images simultaneously.

Although groupwise registration can be achieved by exhausting pairwise registrations between all possible subject combinations in the population [4], this type of method suffers from very heavy computation. Recently, more favorable approaches were proposed to align all subjects simultaneously by following the groupwise concept explicitly. Specifically, Joshi et al. [1] proposed to perform groupwise registration by iteratively (1) registering all subjects to the group mean image, and (2) constructing the group mean image as the Fréchet mean of all registered images. Also, Learned-Miller [3] proposed a congealing method to jointly warp the subjects towards a hidden common space by minimizing the sum of stack entropies in the population. Balci et al. [2] further extended the congealing method to non-rigid image registration by modeling the transformations with B-Splines. However, as the method itself is intensity-based, it is intrinsically insufficient to establish good anatomical correspondences across images. Furthermore, although the groupwise registration can be solved through steepest descent optimization [2, 3], it is unfortunately sensitive to local minima. Also, since the cost function is estimated based on only ~1% randomly sampled voxels (regardless of their morphological importance), the registration performance could be seriously affected.

To the best of our knowledge, the issue of anatomical correspondence in groupwise registration, which is very critical to measure the inter-subject difference, has not been well addressed in the literature. In this paper, we propose a novel feature-based groupwise registration method for achieving robust anatomical correspondence detection. Specifically, we formulate our groupwise registration by alternatively (1) estimating the sparse correspondences across all subjects and (2) interpolating the dense transformation field based on the established sparse correspondences.

In Step (1), we use attribute vector, instead of intensity only, as a morphological signature to help guide correspondence detection. Furthermore, the robustness of correspondence detection based on attribute vectors is achieved in two ways. First, we only detect correspondences for the most distinctive voxels, called as driving voxels, in the brain images, and then use their detected correspondences to guide the transformations of the nearby non-driving voxels. Second, multiple correspondences are allowed to alleviate the ambiguities particularly in the beginning of registration, and these one-to-many correspondences are gradually restricted to one-to-one correspondence with progress of registration in order to achieve accuracy for the final registration results. It is worth noting that this soft assignment strategy is also applied to all subjects in the population, where the contributions from different subjects are dynamically controlled through the registration. In Step (2), TPS is utilized to interpolate the dense transformation fields based on the sparse correspondences.

We have compared the performance of our groupwise registration with the congealing method [2] and the pairwise HAMMER registration algorithm [5, 6] by evaluation on 18 elderly brains, 16 NIREP dataset with 32 manually delineated ROIs, and 40 LONI dataset with 54 manually labeled ROIs. Experimental results show that our method can achieve the best performance.

2 Methods

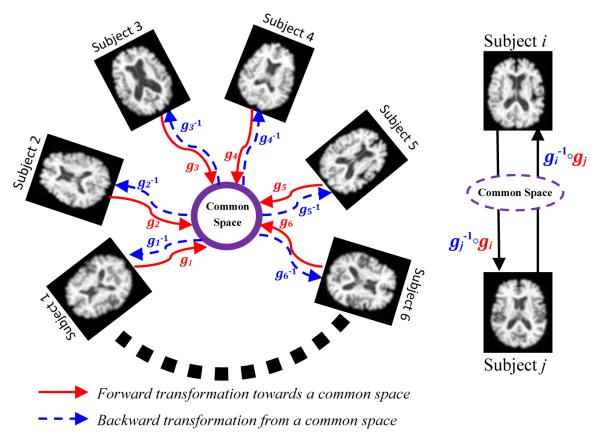
Given a group of subjects S = {S_i|i = 1 … N}, the goal of the groupwise registration is to find a set of transformations G = {g_i|g_i(x) = x + h_i(x), x = (x₁, x₂, x₃) ∈ ℜ³, i = 1, ⋯, N} that are able to transform each subject towards a hidden common space with its individual displacement h_i(x). Fig. 1 schematically illustrates the concept of our groupwise registration. To connect each pair of subjects through the common space, the inverse transformation fields $G^{-1}=\{g_i^{-1}\mid g_i^{-1}\left(x\right)=x+h_i^{-1}\left(x\right),x=(x_1,x_2,x_3)\in {ℛ}^3,i=1,\cdots ,N\}$ should be calculated as in Fig. 1. Thus the composite transformation $g_j^{-1}\circ g_i$ can be used to warp subject S_i to S_j, and also $g_i^{-1}\circ g_j$ can be used to warp subject S_j to S_i (as shown in the right panel of Fig. 1). In the following, we use i to index the subject under consideration and j for any other subject except S_i. Also, we call G the set of forward transformations and G⁻¹ the set of backward transformations, which enter and leave the common space, respectively. In the following, we will present the energy function in Section 2.1, and then provide a solution to groupwise registration in Section 2.2.

Fig. 1.

The schematic illustration of the proposed groupwise registration algorithm. All subjects in the group are connected by the forward transformations g_i (i.e., red solid arrows) to the common space (i.e., a purple circled region), and by the backward transformations $g_i^{-1}$ (i.e., blue dashed arrows) coming from the common space. The right panel shows the composite transformations bridging subjects S_i and S_j.

2.1 Energy Function in Groupwise Registration

As pointed in Fig. 1, all subjects will agglomerate to the hidden common space by following the simultaneously estimated transformation fields. To identify the anatomical correspondence among all subjects, we propose using attribute vector as a morphological signature of each voxel x for guiding the correspondence detection. Without loss of generality, the geometric moment invariants of white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) are calculated from a neighborhood of each voxel x for defining its attribute vector $\stackrel{\rightharpoonup }{a}\left(x\right)$ [5]. Further, we hierarchically select distinctive voxels (with distinctive attribute vectors) as driving voxels in the image [5], by adaptively setting thresholds on the attribute vectors. Here, the driving voxels are represented as {x_i,m|i = 1, …, N,m = 1, …, M_i}, where M_i is the number of the driving voxels in subject S_i. In our groupwise registration, we establish the sparse correspondences only on the driving voxels due to their distinctiveness, and let these driving voxels steer the dense transformation, by considering them as control points in TPS-based interpolation [7].

The overall energy function of groupwise registration can be defined to minimize the differences of attribute vectors on the corresponding locations across different subjects and also preserve the smoothness of estimated transformation fields:

$$E\left(G\right)=\underset{i=1}{\overset{N}{\Sigma }}\underset{x\in S_i}{\Sigma }\underset{j=1,j\ne i}{\overset{N}{\Sigma }}{\Vert {\stackrel{\rightharpoonup }{a}}_i\left(x\right)-{\stackrel{\rightharpoonup }{a}}_j\left(g_j^{-1}{}_{°}{g}_i\left(x\right)\right)\Vert }^2+\underset{i=1}{\overset{N}{\Sigma }}{\parallel {\mathit{Lg}}_i\parallel }^2,$$ (1)

where L is an operator to compute the bending energy of transformation field g_i.

However, directly optimizing E(G) is usually intractable. Thus, we introduce the sparse correspondence fields F = {f_i(x)|x ∈ ℜ³, i = 1, …, N} in our method. Here, each f_i is a set of correspondence vectors defined for subject S_i: for each driving voxel x_i,m in subject S_i, it gives the latest estimated corresponding location (pointing to the common space), while for each non-driving voxel, it keeps the previous estimated transformation. As the result, the energy function in Eq. 1 becomes:

$$E(F,G)=\underset{i=1}{\overset{N}{\Sigma }}\underset{x\in S_i}{\Sigma }\left\{\underset{j=1,j\ne i}{\overset{N}{\Sigma }}{\Vert {\stackrel{\rightharpoonup }{a}}_i\left(x\right)-{\stackrel{\rightharpoonup }{a}}_j\left(g_j^{-1}{}_{°}{f}_i\left(x\right)\right)\Vert }^2+{\parallel f_i\left(x\right)-g_i\left(x\right)\parallel }^2\right\}+\underset{i=1}{\overset{N}{\Sigma }}{\parallel {\mathit{Lg}}_i\parallel }^2,$$ (2)

The advantage of introducing F is that it decouples the complicated optimization problem into two simple-to-solve sub-problems, i.e., alternatively (SP₁): estimating the correspondence field f_i via correspondence detection; and (SP₂): interpolating the dense transformation g_i with regularization on G.

Estimating the Correspondence Field F (SP₁)

In this step, we take advantage of the driving voxels to establish the correspondence on each driving voxel x_i,m of subject S_i by inspecting each candidate in a neighborhood n₁, w.r.t. each of other subjects S_j one by one. For evaluating each candidate, several useful strategies are employed here to achieve robust correspondences. First, not only the voxelwise but also the regionwise difference on attribute vectors is proposed by computing the distance of each pair of corresponding attribute vectors within a neighborhood n₂. Second, multiple spatial correspondences are allowed on each driving voxel x_i,m by introducing a spatial assignment ${\pi }_{i,m}^{j,v}$ to indicate the likelihood of the true correspondence v w.r.t. subject S_j. Also, we use ${\tau }_{i,m}^j$ to describe the likelihood of subject S_j being selected as a reference image for correspondence detection of x_i,m of subject S_i, according to the similarity of local morphology between S_i and S_j.

Therefore, by fixing G in Eq. 2, the new energy function E₁ in this step can be defined as:

$$\begin{array}{cc}\hfill & E_1(\pi ,\tau ,F)=\underset{i=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{M_i}{\Sigma }}{E}_{\mathit{corr}}({\pi }_{i,m},{\tau }_{i,m},f_i)+\underset{i=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{M_i}{\Sigma }}{E}_{\mathit{fuzzy}}({\pi }_{i,m},{\tau }_{i,m})+\underset{i=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{M_i}{\Sigma }}{\parallel f_i\left(x_{i,m}\right)-g_i\left(x_{i,m}\right)\parallel }^2\hfill \\ \hfill & E_{\mathit{corr}}({\pi }_{i,m},{\tau }_{i,m},f_i)=\underset{j=1}{\overset{N}{\Sigma }}{\tau }_{i,m}^j\underset{v\in n_1\left(g_i\left(x_{i,m}\right)\right)}{\Sigma }{\pi }_{i,m}^{j,v}\cdot \left[{\parallel g_i\left(x_{i,m}\right)-v\parallel }^2+d({\stackrel{\rightharpoonup }{a}}_i\left(x_{i,m}\right),f_i,g_j^{-1})\right]\hfill \\ \hfill & E_{\mathit{fuzy}}({\pi }_{i,m},{\tau }_{i,m})=r_1\cdot {\pi }_{i,m}^{j,v}\cdot \mathit{log}{\pi }_{i,m}^{j,v}+r_2\cdot {\tau }_{i,m}^j\cdot \mathit{log}{\tau }_{i,m}^j\hfill \end{array}$$ (3)

where $d\left({\stackrel{\rightharpoonup }{a}}_i\left(x_{i,m}\right),f_i,g_j^{-1}\right)={\Sigma }_{z\in n_2\left(x_{i,m}\right)}{\Vert \stackrel{\rightharpoonup }{a}\left(z\right)-\stackrel{\rightharpoonup }{a}\left(g_j^{-1}\left(f_i\left(z\right)\right)\right)\Vert }^2$ measures the regionwise difference of attribute vector ${\stackrel{\rightharpoonup }{a}}_i\left(x_{i,m}\right)$ and its corresponding counterpart in S_j w.r.t. the current estimated correspondence f_i and the previous obtained inverse transformation field $g_j^{-1}$. There are totally three terms in the energy function E₁. The first term E_corr measures the matching discrepancy on each driving voxel x_i,m, where the criteria in evaluating the candidate v w.r.t. subject S_j are: 1) the spatial distance between g_i(x_i,m) and v in the common space should be as small as possible according to the ICP principle [8]; 2) not only the candidate location v but also its neighborhood should have the similar attribute vectors based on the measurement $d({\stackrel{\rightharpoonup }{a}}_i\left(x_{i,m}\right),f_i,g_j^{-1})$.

Soft assignment is very important for brain image registration to reduce the risk of mismatching, particularly in the beginning of registration. All voxels in the search neighborhood n₁ have the chance to become correspondence candidate, but their contributions to the true correspondence vary according to the matching criteria. To increase the registration accuracy and specificity, it is also necessary to evolve to oneto-one correspondence in the end of registration. Therefore, the second term E_fuzzy(π_i,m,τ_i,m) is used to dynamically control the soft assignment by requiring the entropy of π_i,m and τ_i,m gradually to decrease with progress of registration.

The third term in E₁ ensures that the correspondence field F be close to the previous estimated transformation field G, by minimizing the difference between each pairs of f_i and g_i.

Interpolating the Dense Transformation Field G (SP₂)

After updating the correspondence in each driving voxel, the energy function in this step is given as:

$$E_2\left(G\right)=\underset{i=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{M_i}{\Sigma }}\left\{{\Vert f_i\left(x_{i,m}\right)-g_i\left(x_{i,m}\right)\Vert }^2\right\}+\underset{i=1}{\overset{N}{\Sigma }}{\parallel {\mathit{Lg}}_i\parallel }^2.$$ (4)

By regarding the driving voxels as control points in each subject, TPS interpolation can be used to estimate the optimal g_i that fits the transformation on x_i,m to f_i(x_i,m) and reaches the minimal bending energy (the second term) [7,9].

2.2 Implementation for Groupwise Registration

In our method, we alternatively optimize SP₁ and SP₂ in each round of registration. In SP₁, the explicit solutions of ${\pi }_{i,m}^{j,v}$ and ${\tau }_{i,m}^j$ are obtained by letting $\partial E_1∕\partial {\pi }_{i,m}^{j,v}=0$ and $\partial E_1∕\partial {\tau }_{i,m}^j=0$:

$$\begin{array}{cc}\hfill \partial E_1∕\partial {\tau }_{i,m}^j& =0:\hfill \\ \hfill {\pi }_{i,m}^{j,v}& =c_1\cdot \mathit{exp}\left(-\frac{{\xi }_v}{r_1}\right),{\pi }_{i,m}^{j,v}\leftarrow {\pi }_{i,m}^{j,v}∕{\Sigma }_{v\in n_2\left(g_i\left(x_{i,m}\right)\right)}{\pi }_{i,m}^{j,v}\hfill \end{array}$$ (5)

$${\pi }_{i,m}^j=c_2\cdot \mathit{exp}\left(-\frac{{\Sigma }_{v\in n_2\left(g_i\left(x_{i,m}\right)\right)}{\pi }_{i,m}^{j,v}{\xi }_v}{r_2}\right),{\tau }_{i,m}^j{\leftarrow }^{{\tau }_{i,m}^j}{/}_{{\Sigma }_{j=1}^N{\tau }_{i,m}^j}$$ (6)

where ${\xi }_v=\left[{\Vert g_i\left(x_{i,m}\right)-v\Vert }^2+d\left({\stackrel{\rightharpoonup }{a}}_i\left(x_{i,m}\right),f_i,g_j^{-1}\right)\right]$ denotes the bracket part in E_corr(π_i,m, τ_i,m, f_i), and c₁ and c₂ are constants. After ${\pi }_{i,m}^{j,v}$ and ${\tau }_{i,m}^j$ are determined by Eqs. 5 and 6 on each x_i,m, the correspondence f_i(x_i,m) is updated by moving it to the mean location of all candidates under the guidance of ${\pi }_{i,m}^{j,v}\cdot {\tau }_{i,m}^j$:

$${\widehat{f}}_i\left(x_{i,m}\right)=\underset{j=1}{\overset{N}{\Sigma }}\underset{v\in n_2\left(g_i\left(x_{i,m}\right)\right)}{\Sigma }{\tau }_{i,m}^j\cdot {\pi }_{i,m}^{j,v}\cdot v.$$ (7)

It is worth noting that we introduce a multi-resolution strategy to implement our proposed groupwise registration method for fast and robust registration. Specifically, in each resolution, the size of the search neighborhood n₁ decreases gradually with the progress of registration, for achieving more specific detection of correspondences. Moreover, in the initial state of registration, only a small set of voxels with distinctive features, such as those locating at ventricular boundaries, sulcal roots and gyral crowns, are selected as driving voxels. After that, more and more driving voxels are added to drive the registration and eventually all voxels in the brains join the groupwise registration.

By taking the driving voxels as control points, TPS is used to interpolate the dense transformation field after we repeat the calculations of Eqs. 5~7 for each driving voxel x_i,m. To avoid the cumbersome inversion of large matrix in TPS (proportional to the number of control points), we perform TPS interpolation in overlapping blocks (32 × 32 × 32) and also down-sample the driving voxels in each block.

3 Experiments

In our experiments, we have extensively evaluated the performances of our groupwise registration method in atlas building and ROI labeling. For comparison, we use the congealing groupwise registration method [2] with its available codes, http://www.insight-journal.org/browse/publication/173. To demonstrate the advantage of groupwise registration over pairwise registration, the registration results by a pairwise registration method, namely HAMMER [5], are also provided.

To demonstrate the group overlap of labeled brain regions after registration, we specifically vote a reference by assigning each voxel with a tissue label that is the majority of all tissue labels at the same location from all aligned subjects. Then, the overlap ratio between each of the registered label images and the voted reference can be calculated. Here, we use the Jaccard Coefficient metric as the overlap ratio to measure the alignment of the two regions (A and B) with the same label, defined as:

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}.$$ (8)

18 Elderly Brain Images

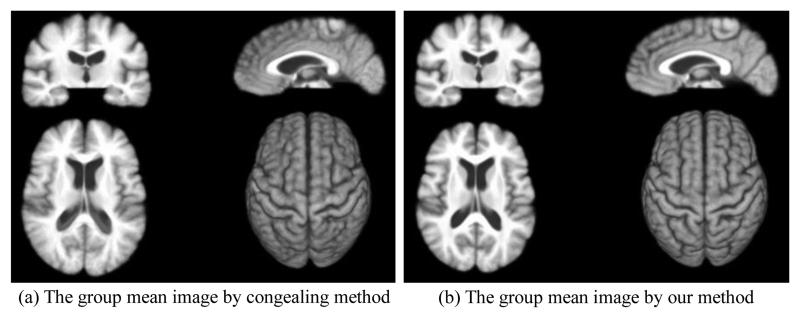
18 elderly brain images, each with 256 × 256 × 124 voxels and the resolution of 0.9375 × 0.9375 × 1.5mm³, are used in this experiment. The group mean images produced by the congealing method and our groupwise registration method are both displayed in Fig. 2. Through visual inspection, the group mean of our method is sharper and gains better contrast (especially around ventricles) than that of the congealing method, indicating better performance of our registration method. The overlap ratios on WM, GM, and VN, as well as the overall overlap ratio on the whole brain, by our method and the congealing method, are provided in Table 1. It can be observed that our method achieves better results than the congealing method in each tissue type. On the other hand, it is interesting to compare the performance between groupwise and pairwise registrations of these 18 brain images. In HAMMER-based pairwise registration, 5 out of 18 subjects are randomly selected as the templates to align all other 17 remaining subjects. The average overlap ratios produced by these five different templates, as well as the standard deviations, are shown in the first row of Table 1, which verify again the power of our groupwise registration in consistently registering the population data.

Fig. 2.

The groupwise registration results by the congealing method and our method. It can be observed that our group mean image is much sharper than that by the congealing method, indicating a more accurate and consistent registration by our method.

Table 1.

Overall overlap ratios of WM, GM, and VN by pairwise HAMMER algorithm, congealing method, and our groupwise registration method.

	WM	GM	VN	Overall
Pairwise HAMMER	63.86% (±3.87%)	57.25% (±2.18%)	76.51% (±3.70%)	65.64% (±3.15%)
Congealing Method	59.68%	51.09%	70.61%	59.43%
Our Method	75.81%	63.61%	81.16%	73.52%

NIREP Data and LONI Data

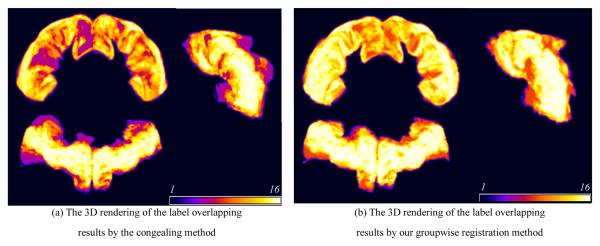
In this experiment, we employ pairwise HAMMER, congealing method, and our groupwise registration method to align 16 NIREP data (with 32 manual ROIs) and LONI40 dataset (with 54 manual ROIs). Table 2 shows the average overlap ratios on these two datasets by the three registration methods. Obviously, our groupwise registration method achieves the most accurate registration results among all three registration methods. In particular, Fig. 3 shows the performance of registration accuracy at the left and the right precentral gyri of 16 NIREP brains by the two groupwise methods. The average overlap ratio is 45.95% by congealing and 57.34% by our method. The brighter color indicates the higher consistency of registration across different subjects, while the darker color means the poor alignment. Again, our method achieves much better alignment.

Table 2.

Overall overlap ratios of the aligned ROIs in NIREP and LONI datasets by pairwise HAMMER algorithm, congealing method, and our groupwise registraion method.

	Pairwise HAMMER	Congealing Method	Our Method
NIREP (32 ROIs)	56.58%	52.07%	61.52%
LONI (54 ROIs)	54.12%	60.60%	67.02%

Fig. 3.

3D renderings of the aligned left and right precentral gyri by the congealing method and our groupwise registration method.

4 Conclusion

In this paper, we have presented a new feature-guided groupwise registration method and also demonstrated its applications in atlas building and population data analysis. Specifically, by taking advantage of the driving voxels (with distinctive features) automatically detected from all images, we develop a feature-based groupwise registration method by alternatively estimating the correspondences on the driving voxels and updating the dense transformation fields by TPS. Extensive experiments have been performed to compare the performance of our method with that of the congealing method and the pairwise HAMMER algorithm. All experimental results show that our method can achieve the best performance.