Abstract
Background
Most model analyses examining the role of primary HIV infection in the HIV epidemic ignore the fact that HIV is often transmitted through long-term, concurrent sexual partnerships. We sought to understand how duration and concurrency of sexual partnerships affect the role of transmissions during primary HIV infection.
Methods
We constructed a stochastic individual-based model of HIV transmission in a homogeneous population where partnerships form and dissolve. Using observed contagiousness by stage of HIV infection, the fraction of transmissions during primary HIV infection at equilibrium was examined across varying partnership durations and concurrencies.
Results
The fraction of transmissions during primary HIV infection has a U-shaped relationship with partnership duration. The fraction drops with increasing partnership duration for partnerships with shorter average duration but rises for partnerships with longer average duration. Partnership concurrency modifies this relationship. The fraction of transmissions during primary HIV infection increases with increasing partnership concurrency for partnerships with shorter average duration, but decreases for partnerships with longer average duration.
Conclusions
Partnership patterns strongly influence the transmission of HIV and do so differentially by stage of infection. Dynamic partnerships need to be taken into account to make a robust inference on the role of different stages of HIV infection.
Model analyses have produced varying estimates of infection transmission during sex between men during different stages of HIV infection—primary, asymptomatic, and late stages. Earlier studies showed that transmissions during primary HIV infection play a disproportionately large role during the initial period of an epidemic1 and also when HIV is endemic, under certain assumptions of population structure.2 On the other hand, model fitting to the San Francisco City Clinic Cohort data produced the highest transmission rate during the late stage.3
These inferences are all based on model analyses using simplifying assumptions, and might be changed by realistic relaxation of those assumptions. Various assumptions of concern in this regard are (1) that contacts are instantaneous events in thoroughly mixed populations rather than events during on-going and dynamically changing partnerships, (2) that risk behaviors are fixed across time rather than being subject to fluctuations and cohort effects, (3) that each individual plays both insertive and receptive roles, and (4) that high-risk sex acts and partnerships in which those sex acts occur are not clustered temporally or socially. We address the first issue here, using a simple model form with abstract parameterization to explore how the duration and concurrency of partnerships might affect inferences about transmissibility.
Analyses of transmissions during primary HIV infection as a function of partnership duration have been performed previously by Xiridou et al4 and Kretzschmar et al.5 They, however, did not consider the effects of long-term, concurrent partnerships on such transmissions. We examine how the endemic prevalence and the fraction of transmissions during primary HIV infection at equilibrium are influenced by the duration and the concurrency of sexual partnerships, using a discrete individual-based model.
METHODS
Compartmental Flows
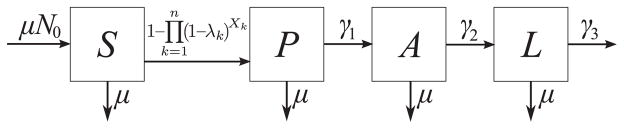
The natural history of HIV infection is modeled with 3 stages—primary (P), asymptomatic (A), and late (L) stages of infection. We will refer to both the asymptomatic and late stages as postprimary HIV infection stage. Compartmental flows are shown in Figure 1. The leftmost arrow indicates new susceptible men entering into the sexually active population. Vertical arrows indicate that men become sexually inactive at the same probability independent of infection category. There is a balance between these 2 flows in a way that the expected population size remains constant in the absence of HIV transmissions. The other horizontal arrows represent infection and stage progression, with the final arrow being death from AIDS. Men may have 0, 1, or multiple partners at any point in time. Parameters and their values explored appear in the Table.6,7
FIGURE 1.
Compartmental flows. The natural history of HIV infection is modeled with 3 stages—primary (P), asymptomatic (A), and late stages (L) of infection. The susceptible population is represented with S. The vertical arrows represent removal from the sexually active population. The leftmost horizontal arrow represents susceptible men? entering the sexually active population. The other horizontal arrows represent infection and stage progression with the final arrow being death from AIDS. Parameters are defined in Table 1. Probability of infection (in the arrow from S to P) is explained in Methods section.
TABLE.
Model Parameters
| Symbol | Values Explored | Description |
|---|---|---|
| N0 | 10,000 | Initial population size |
| c | 0.1, 0.1666, 0.3333, 0.5, 1.1111 | Mean no. sex acts per partnership per day |
| βa i | (β1, β2, β3) = (0.03604, 0.00084, 0.00421) | Transmission probability per act during stage i |
| γi | (γ1, γ2, γ3) = (1/49, 1/2570, 1/365) | Stage-progression probability from stage i to the next per day |
| σ | 0, 0.0001, 0.001, 0.01, 0.1, 1 | Partnership dissolution probability per day |
| ξ | 0, 0.3, 0.7, 1 | The ratio of partnership formation probabilities comparing a partnership between 2 individuals of whom at least one is not single to a partnership between 2 single individuals |
| μ | 1/9120 | Probability an individual leaves the sexually active population per day |
| N | 0.9, 1, 1.5, 3, 5 | Population-averaged no. partners per person |
β1 and β2 were based on new analyses6 of the Rakai study.7 To compute β3, we used the data about the last 2 follow-up periods of the “late-stage index partner” cohort from the Rakai study.7 There were total 66 discordant couples and transmissions occurred in 17 couples. Average no. sex acts was 70.7 per couple. Thus, β3 = 1 − (1 − NT/N)1/c for N = 66, NT = 17, c = 70.7.
Probability of Infection
If a susceptible man has n-infected partners on a certain day, then the probability the susceptible person becomes infected on that day is
Here, λk is the transmission probability per sex act for the kth infected partner and is determined by the stage of infection (ie, λk = β1, β2, β3). Xk is the frequency of sex acts per day in the partnership between the susceptible and the kth infected partner. This is a Poisson random variable with parameter c, which is the mean frequency of sex acts per partnership per day.
Model Simulation
A simulation starts with a susceptible population of size N0 of which 1% is randomly chosen as initially infected with primary HIV infection. Total run time was 100,000 days.
The following events occur at each day:
New partnerships are formed until the number of partnerships in the population reaches the target number, 0.5 nNt, where n is the target mean degree. Nt is the number of men at day t.
Susceptible men are infected with probability described previously.
Infected men progress from stage i to the next with probability γi for i = 1, 2.
Men with late HIV infection die with probability γ3. Partnerships involving dead persons dissolve.
Men leave the sexually active population with probability μ. Partnerships involving removed persons dissolve.
Partnerships dissolve with probability σ.
A susceptible man is recruited with probability μ. This is repeated for N0 times.
Partnership Formation
Partnerships are formed as follows:
Two men are chosen uniformly at random.
If 2 men are both single, then they will become partners.
If at least one of them is not single, then they will become partners with probability ξ.
The above procedure is repeated until the target number of partnerships is reached.
The distribution of the number of partners per person is controlled by parameter 0 ≤ ξ ≤ 1, which has previously been used by other researchers.8 If ξ = 1, the current partnership status does not affect the probability of gaining a new partner. Since partnership dissolution also occurs randomly, the distribution of the number of partners per person follows a Poisson distribution in the limit of large population size. If ξ = 0, no man may have more than 1 partner. That is, ξ provides a transition from serial monogamy to Poisson random partnerships.
Partnership Dissolution
Each partnership dissolves with probability σ per day. There are 2 other ways in which partnerships dissolve; when one’s partner dies from AIDS or the partner leaves the sexually active population. Ignoring deaths from AIDS gives roughly 1/(σ + 2 μ) days of partnerships for σ ≤ 0.1 (parameter values are given in the Table), which we use to indicate average partnership duration. Note we need a factor of 2 for μ to compute partnership duration because there are 2 persons in a partnership with each person leaving the population (and dissolving the partnership) at probability μ per day. If σ = 1, every partnership lasts only one day. Applying a fixed probability of dissolution per day leads that partnership duration is geometrically distributed, where partnerships with a very short duration always comprise a substantial fraction even when average duration is very long. Our inferences do not change qualitatively even when we apply gamma-distributed partnership duration (eFigure, http://links.lww.com/EDE/A403).
RESULTS
We first show the typical time series of a simulation run of our model. We then present 3 analyses to assess the effects of concurrency and duration of partnerships on the endemic prevalence and fraction of transmissions during primary HIV infection at equilibrium. In Analysis 1, we vary partnership duration at a given mean degree. In Analysis 2, we vary the mean degree as well as partnership duration. Finally, in Analysis 3, we vary partnership concurrency at a given mean degree, as well as partnership duration.
Figure 2A shows the typical time series of a simulation run for the mean degree of 1.5 and average partnership duration of about 820 days. As infections increase, population size decreases because of deaths from AIDS. Regardless of population size, the mean degree remains the same, which is reflected by the decrease in the number of partnerships. As seen in Figure 2B, men infected by an index case with primary HIV infection comprise more than half of all prevalent infections during the first 5 years or so. As the epidemic progresses, however, the proportion of individuals infected by an index case with primary HIV infection decreases because more and more infected men advance to later stages and generate secondary infections.
FIGURE 2.
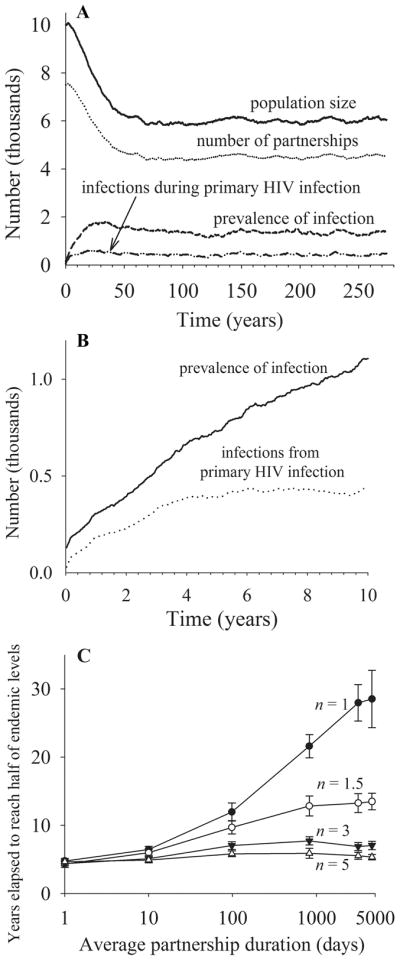
A, The typical time series of a simulation run for mean degree n = 1.5, partnership dissolution probability per day σ = 0.001, and mean frequency of sex acts per partnership per day c = 0.3333. B, Prevalence of infection and infections from primary HIV infection over the first 10 years. C, Years elapsed to reach half of endemic levels under varying average partnership duration and mean degree.
After 60 years or so, the system reaches a quasiequilibrium, and the variables shown in Figure 2A remain more or less constant over time. Dynamics of these variables are affected by partnership patterns. For example, as seen in Figure 2C, infection takes longer to reach endemic equilibrium with increasing partnership duration and with decreasing mean degree. Our analyses focus on endemic prevalence and the fraction of transmissions during primary HIV infection at endemic equilibrium. To compute endemic prevalence and the fraction of transmissions during primary HIV infection, we first calculated the time-averaged value over the last 40,000 days (from about 164 to 274 years) and then calculated averages and standard deviations of these time-averaged values from 10 simulation runs.
Analysis 1: Partnership Duration Varies at a Given Mean Degree
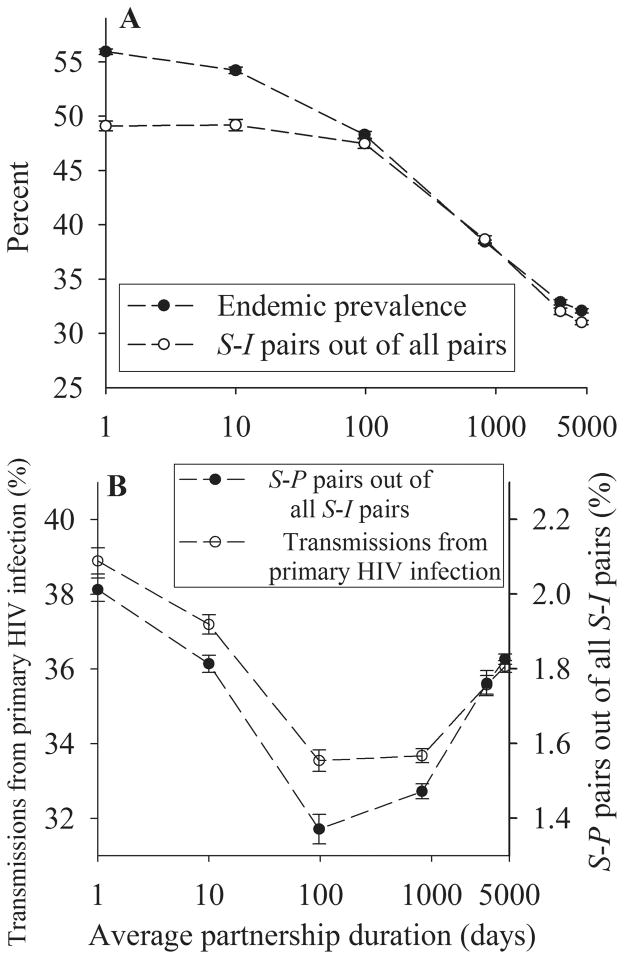
Figure 3A and B present results for a mean degree of 1.5 with a mean frequency of sex acts of 1/3 per partnership per day so that men engage in a sex act on average every other day. As seen in Figure 3A (filled circles), endemic prevalence of HIV infection monotonically decreases with increasing partnership duration.
FIGURE 3.
Simulation results when partnership duration is varied. The mean degree n = 1.5 and the mean frequency of sex acts per partnership per day c = 0.3333. S-I and S-P pairs denote a pair of a susceptible person and any infected person, and a pair of a susceptible person and a person infected with primary HIV infection, respectively. Each data point is the mean from 10 simulation runs, and error bars indicate one standard deviation. A, Endemic prevalence and the fraction of S-I pairs out of all pairs across partnership duration. B, Fraction of transmissions during primary HIV infection and the fraction of S-P pairs out of all S-I pairs across partnership duration.
The decrease in endemic prevalence with increasing partnership duration arises because in prolonged partnerships, once transmission occurs, infected persons are having sex with someone who is already infected. Thus, fewer sex acts of infected persons are with susceptibles. By contrast, for partnerships with shorter average duration, infected persons are freed from their infectors or their infectees more quickly and meet new partners more often, thereby having a higher chance of having sex with susceptible persons. Because transmissions occur only in discordant pairs (labeled S-I pairs), the decrease in endemic prevalence is associated with the decrease in S-I pairs out of all pairs (open circles in Fig. 3A).
Unlike the monotonic decrease in endemic prevalence, the fraction of transmissions during primary HIV infection first falls and then rises (open circles in Fig. 3B). This pattern is associated with the fraction of discordant pairs where the infected individual has primary HIV infection (labeled S-P pairs, filled circles in Fig. 3B).
One mechanism for the decrease in the fraction of transmissions during primary HIV infection with increasing partnership duration is that an increase in partnership duration reduces the probability that the partnership will dissolve just after transmission has occurred. From the infectee’s point of view, this means that newly infected men spend their early period of infection (ie, primary HIV infection) with their infector, which nullifies their infectious sex acts. In addition, from the infector’s point of view, men infected with primary HIV infection infect their susceptible partners faster because of the higher transmission rate during primary HIV infection. Consequently, compared with infected men with postprimary HIV infection, infected men with primary HIV infection use up more of their sex acts with their infectees.
The increasing fraction of transmissions during primary HIV infection for partnerships with long average duration (eg, >1000 days in Fig. 3B) is understood by considering an extreme case of fixed partnerships. In this case, the fraction of susceptible partners is always smaller for postprimary HIV infection than primary HIV infection. This is because some of initially susceptible partners are infected during the index case’s primary HIV infection, but are not replaced with susceptible men, as could happen if partnerships were dynamic. Thus, if all susceptible partners had been infected during the index case’s primary HIV infection, no susceptible partners are left to be infected after the index case has progressed to postprimary HIV infection. This causes the fraction of transmissions during primary HIV infection to be higher in fixed partnerships than in instantaneously changing partnerships, where infected men meet susceptible men randomly, independent of the stage of infection. Our particular case differs from this extreme of fixed partnerships even when partnership dissolution probability σ is zero (ie, right-most points in Fig. 3B) because men who die from? AIDS or who leave the population dissolve their partnerships and new susceptible men entering? into the population form new partnerships. Therefore, the fraction of transmissions during primary HIV infection does not increase quite as much as in fixed partnerships.
Analysis 2: Mean Degree and Partnership Duration Are Varied Simultaneously
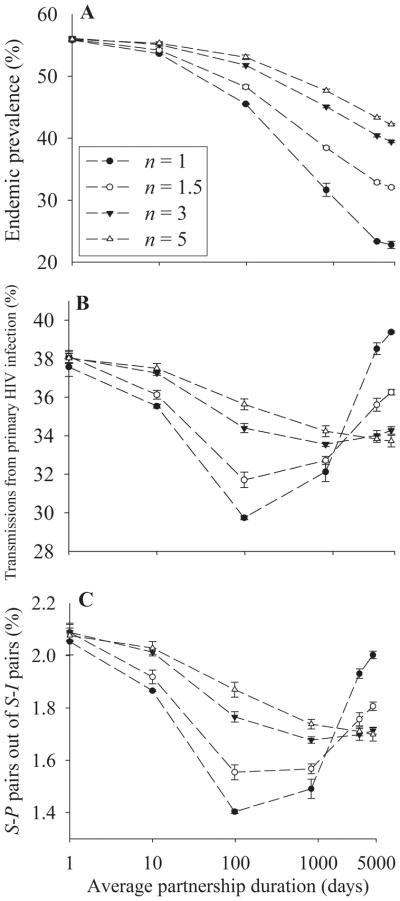
In this analysis, as the mean degree n is varied, mean frequency of sex acts per partnership per day c is also varied to keep constant the mean frequency of sex acts per person per day (n × c).
As seen in Figure 4A, endemic prevalence decreases with increasing partnership duration and is higher for higher mean degree at a given partnership duration. This can be explained from the perspectives of the infector and the infectee. First, note that the increasing mean degree reduces the frequency of sex acts per partnership per day c, and thus also the probability of transmission per partnership per day. Thus, for each S-I pair, the susceptible partner becomes infected more slowly with increasing mean degree and so fewer nontransmitting sex acts occur between the infector and the infectee. In addition, a newly infected individual has a higher chance to transmit infection to a concurrent partner with increasing mean degree.
FIGURE 4.
Simulation results when the mean degree n as well as partnership duration is varied. The mean frequency of sex acts per partnership per day c is varied in the way that c × n = 0.5. A, Endemic prevalence across partnership duration at 4 levels of n. B, Fraction of transmissions during primary HIV infection across partnership duration at 4 levels of n. C, Fraction of S-P pairs out of all S-I pairs across partnership duration at 4 levels of n.
As seen in Figure 4B, the general pattern of the fraction of transmissions during primary HIV infection—an initial decrease followed by a later increase—is similar for all levels of mean degree. As the mean degree increases, however, the rate of fall of the fraction of transmissions during primary HIV infection with increasing partnership duration is decreased and the inflection point where that fraction begins to rise again is pushed to longer partnership durations with a slower subsequent rise. The highest fraction of transmissions during primary HIV infection is seen when the mean degree is lowest, given partnerships with long average duration. As seen in Figure 4C, the fraction of S-P pairs out of all S-I pairs is associated with the fraction of transmissions during primary HIV infection.
The higher fraction of transmissions during primary HIV infection given a higher mean degree for partnerships with moderate average duration (eg, ≤1000 days) is explained as in the previous case of higher endemic prevalence given a higher mean degree. The reduced probability of transmission per partnership with increasing mean degree slows transmissions and thus reduces the nontransmitting sex acts between the infector and the infectee, which is especially likely during the infectee’s primary HIV infection. Also, increasing the mean degree increases the likelihood that a newly infected individual transmits infection to concurrent partners, which is also especially likely during primary HIV infection.
Why then is the fraction of transmissions during primary HIV infection lower for higher mean degree than lower mean degree for partnerships with long average duration (eg, >1000 days)? We have mentioned that the fraction of susceptible partners will be smaller for postprimary HIV infection than primary HIV infection in fixed partnerships. Note that increasing mean degree increases the frequency of new partnership formation at a given partnership duration. Increased frequency of new partnership formation will decrease the difference in the fraction of susceptible partners between primary HIV infection and postprimary HIV infection since new partners are distributed randomly over the stage of infection.
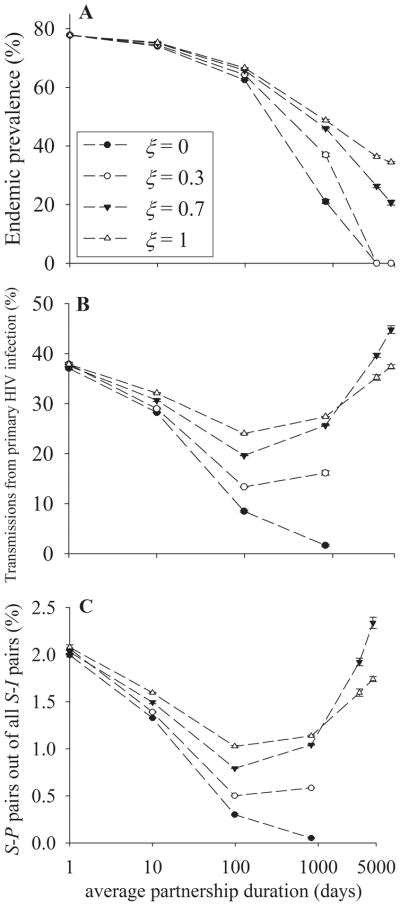
Analysis 3: Partnership Concurrency and Partnership Duration Are Varied Simultaneously
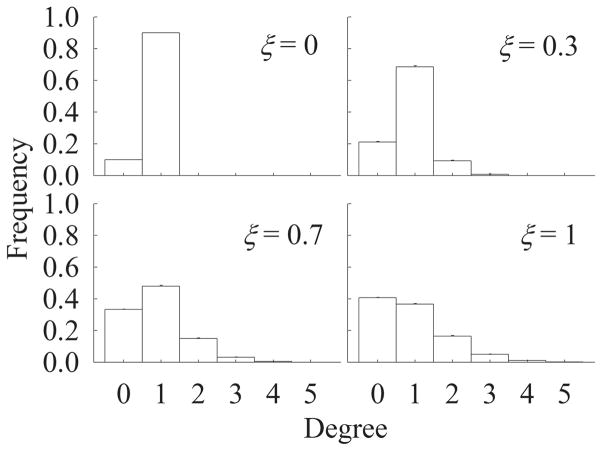
In this case, we vary partnership concurrency from monogamy at one extreme to Poisson random partnerships in the previous analyses at the other extreme, while keeping the mean degree constant. Because the maximum mean degree is 1 in monogamy, we set the mean degree at 0.9. Figure 5 shows the distribution of number of partners per person at 4 levels of ξ. If ξ = 0, then there are only 2 groups: single persons and those with 1 partner. As ξ is increased from 0 to 1, the fraction of men with concurrent partners increases. For this reason, partnership concurrency increases with increasing ξ at a given mean degree. Note that, unlike varying mean degree in Analysis 2, varying ξ does not alter the mean frequency of sex acts per partnership per day.
FIGURE 5.
Degree distribution at 4 levels of ξ. Mean degree n = 0.9.
As Figure 6A illustrates, the endemic prevalence at a given partnership duration is higher for higher ξ while decreasing with increasing partnership duration. A similar phenomenon has previously been described.8–10 This pattern arises primarily because the number of persons connected in the network at any point in time (ie, the size of the largest component) is higher for higher ξ. From the infectee’s point of view, increasing ξ (ie, the fraction of population with concurrent partners) increases the chance that infectees transmit infection while being connected to their infector, whereas infectees can not transmit infection until they form new partnerships when ξ = 0 (ie, serial monogamy).
FIGURE 6.
Simulation results when ξ as well as partnership duration is varied. Mean degree n = 0.9, mean frequency of sex acts per partnership per day c = 1.1111. A, Endemic prevalence across partnership duration at 4 levels of ξ. B, Fraction of transmissions during primary HIV infection across partnership duration at 4 levels of ξ. C, Fraction of S-P pairs out of all S-I pairs across partnership duration at 4 levels of ξ.
As seen in Figure 6B, the fraction of transmissions during primary HIV infection is higher for higher ξ for partnerships with moderate average duration (eg, ≤ 1000 days), whereas it has the opposite pattern for partnerships with longer average duration. The general pattern—an initial decrease followed by a later increase—is similar for all levels of ξ. The lines are truncated for ξ = 0 and 0.3 because infection dies out for partnerships that are longer than 1000 days. As seen in Figure 6C, the fraction of S-P pairs out of all S-I pairs is associated with the fraction of transmissions during primary HIV infection.
From the infectee’s point of view, increasing ξ increases the chance that an infectee transmits infection to concurrent partners. As was the case in Analysis 2, transmission of a newly acquired infection from an infected concurrent partner to a susceptible concurrent partner is especially likely during primary HIV infection. Accordingly, the fraction of transmissions during primary HIV infection is higher for higher ξ for partnerships with moderate average duration.
On the other hand, the fraction of transmissions during primary HIV infection is higher for ξ= 0.7 than for ξ = 1 for partnerships with long average duration (eg, >1000 days in Fig. 6B). This is similar to what is shown in Analysis 2; that is, the fraction of transmissions during primary HIV infection is higher for lower mean degree of partnerships than for higher mean degree for partnerships if average partnerships duration is long. A higher ξ means a higher frequency of partnership formation for men with partners. As was the case in Analysis 2, new partnership formation counteracts the lower fraction of susceptible partners for postprimary HIV infection than primary HIV infection for partnerships with long average duration because new partners are distributed randomly over the stage of infection.
DISCUSSION
We have shown how the endemic prevalence and the fraction of transmissions during primary HIV infection at equilibrium are influenced by the duration and concurrency of sexual partnerships. These influences are strong enough that any assessments of potential effects of control programs that affect primary HIV infection and postprimary HIV infection differentially should consider them. Thus, models assuming instantaneous partnerships2,3,11 are inadequate for estimating the fraction of transmissions by stage of infection.
The homogeneous population model generated fractions of transmissions during primary HIV infection that varied from around 2% to around 42%, depending on the duration and the concurrency of partnerships. The estimate of 42%, higher than other previous modeling studies,3,11–13 arises because per-act transmission probability during primary HIV infection in our model is higher and because other studies fail to capture the increase in the fraction of transmissions during primary HIV infection in long-term, concurrent partnerships. Similarly, those studies do not capture fractions as low as 2% in long-term, monogamous partnerships.
Numerous modeling studies have shown that infection levels are substantially affected by partnerships with nonzero duration regardless of whether partnerships are serially monogamous5,14 or concurrent.8 –10,15–24 Heterogeneity in methods of forming and dissolving partnerships, which varies the distribution of partnerships across the population, also affects the infection levels and the growth rate of an epidemic.8 –10,18,25 For infections with variable infectivity over the course of infection (eg, HIV), partnerships with non-zero duration reduce transmissions during the initial period of infection (eg, primary HIV infection). Here, we show again that the fraction of transmissions during primary HIV infection as well as the overall transmission decreases with increasing partnership duration. In addition, we show that for partnerships with very long duration, the fraction of transmissions during primary HIV infection increases again and can go above the fraction in instantaneous partnerships.
The range of partnership durations and mean degrees explored here can cover a wide variety of populations. For a typical population, it seems reasonable to assume that mean degree is around one, as was measured in African urban city populations.26 On the other hand, for a specific subpopulation, eg, gay men who go to the same bathhouse and repeatedly encounter the same partners, the mean degree may be quite high. Duration of partnerships can also vary considerably across different populations. Xiridou et al4,27 estimated that steady partnerships last 1.5 years on average based on the Amsterdam Cohort Study of young homosexual men in Amsterdam, The Netherlands. Partnerships with longer average durations appear in a population where heterosexual marriage is the norm and divorce is not common. Morris and Kretzschmar28 estimated that nonspousal and spousal partnerships last on average 2 and 20 years, respectively, based on 1994 Ugandan sexual network survey. Also, according to Zambia Domestic Health Survey,29 partnerships between men and women last a long time with the divorce rate of 0.015 per year.
Although we model only a one-sex population with one type of partnerships, our model analysis provides insights to transmissions under more complex situations. In the study of The Netherlands population of men who have sex with men,4 the fraction of transmissions during primary HIV infection was about 6% in steady partnerships and around 35% in casual ones. These findings are consistent with our inference that the fraction of transmission from primary HIV infection decreases as partnership duration increases from instantaneous to several hundred days. Another study on the Zambia epidemic29 shows that the fraction of transmissions during primary HIV infection increases up to 60% in spousal partnerships, compared with about 30% in nonspousal ones. Those results are also consistent with our inference that the fraction of PHI transmissions increases again as partnership duration increases from several hundred days to longer than 10 years, given the mean degree is around one.
For the sake of conceptual clarity, we have eliminated real-world population heterogeneities that may affect our inferences. One is population heterogeneity regarding the number of sexual partners.30–32 This heterogeneity will affect the fraction of transmissions during primary HIV infection through the partnership duration effects we have illustrated. High-risk behavior with casual partners is another. We have performed model analyses indicating that when high-risk behavior lasts for a relatively short time, the fraction of transmissions during primary HIV infection can rise considerably. The fraction of transmissions during a particular stage of HIV infection is still an open question. The analysis here is focused only on understanding the mechanisms through which the concurrency and duration of partnerships affect transmissions during primary HIV infection risk. Our results can help guide the choice of model details in the more thorough and realistic modeling needed to assess how much transmission occurs from primary HIV infection under different conditions.
It is important that models assessing the effects of control programs get the role of transmissions during primary HIV infection right, because programs that depend upon identifying HIV-positive persons and slowing transmission from them are likely to have little or no effect on transmissions during primary HIV infection. Our analysis shows that realistic assessment of potential interventions with transmission- system model analyses must employ models that capture the effects of concurrency in ongoing but dynamic partnerships. Models assuming instantaneous or fixed partnerships are likely to overestimate the role of transmissions during primary HIV infection if average partnership duration falls in between those 2 extremes and the concurrency of partnerships is low in the population.
Supplementary Material
Acknowledgments
Supported by NIH, University of Michigan, Blue Cross Blue Shield of Michigan Foundation, and Korea Science and Engineering Foundation (to J.H.K.); supported by NIH (to J.S.K.) and also supported by the Center for the Study of Complex Systems, University of Michigan (to R.L.R.).
We thank the Center for the Study of Complex Systems at the University of Michigan, Ann Arbor for allowing us to use their computing resources. We also thank 2 anonymous reviewers.
Footnotes
Supplemental digital content is available through direct URL citations in the HTML and PDF versions of this article (www.epidem.com).
References
- 1.Jacquez JA, Koopman JS, Simon CP, Longini IM., Jr Role of the primary infection in epidemics of HIV infection in gay cohorts. J Acquir Immune Defic Syndr. 1994;7:1169 –1184. [PubMed] [Google Scholar]
- 2.Koopman JS, Jacquez JA, Welch GW, et al. The role of early HIV infection in the spread of HIV through populations. J Acquir Immune Defic Syndr Hum Retrovirol. 1997;14:249 –258. doi: 10.1097/00042560-199703010-00009. [DOI] [PubMed] [Google Scholar]
- 3.Rapatski BL, Suppe FP, Yorke JA. HIV epidemics driven by late disease stage transmission. J Acquir Immune Defic Syndr. 2005;38:241–253. [PubMed] [Google Scholar]
- 4.Xiridou M, Geskus R, de Wit J, Coutinho R, Kretzschmar M. Primary HIV infection as source of HIV transmission within steady and casual partnerships among homosexual men. AIDS. 2004;18:1311–1320. doi: 10.1097/00002030-200406180-00010. [DOI] [PubMed] [Google Scholar]
- 5.Kretzschmar M, Dietz K. The effect of pair formation and variable infectivity on the spread of an infection without recovery. Math Biosci. 1998;148:83–113. doi: 10.1016/s0025-5564(97)10008-6. [DOI] [PubMed] [Google Scholar]
- 6.Pinkerton SD. Probability of HIV transmission during acute infection in Rakai, Uganda. AIDS Behav. 2008;12:677– 684. doi: 10.1007/s10461-007-9329-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wawer MJ, Gray RH, Sewankambo NK, et al. Rates of HIV-1 transmission per coital act by stage of HIV-1 infection, in Rakai, Uganda. J Infect Dis. 2005;191:1403–1409. doi: 10.1086/429411. [DOI] [PubMed] [Google Scholar]
- 8.Kretzschmar M, Morris M. Measures of concurrency in networks and the spread of infectious disease. Math Biosci. 1996;133:165–195. doi: 10.1016/0025-5564(95)00093-3. [DOI] [PubMed] [Google Scholar]
- 9.Morris M, Kretzschmar M. Concurrent partnerships and transmission dynamics in networks. Soc Net. 1995;17:299 –318. [Google Scholar]
- 10.Morris M, Kretzschmar M. Concurrent partnerships and the spread of HIV. AIDS. 1997;11:641– 648. doi: 10.1097/00002030-199705000-00012. [DOI] [PubMed] [Google Scholar]
- 11.Abu-Raddad LJ, Longini IM., Jr No HIV stage is dominant in driving the HIV epidemic in sub-Saharan Africa. AIDS. 2008;22:1055–1061. doi: 10.1097/QAD.0b013e3282f8af84. [DOI] [PubMed] [Google Scholar]
- 12.Pinkerton SD. How many sexually-acquired HIV infections in the USA are due to acute-phase HIV transmission? AIDS (London, England) 2007;21:1625–1629. doi: 10.1097/QAD.0b013e32826fb6a6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hollingsworth TD, Anderson RM, Fraser C. HIV-1 transmission, by stage of infection. J Infect Dis. 2008;198:687– 693. doi: 10.1086/590501. [DOI] [PubMed] [Google Scholar]
- 14.Dietz K, Hadeler KP. Epidemiological models for sexually transmitted diseases. J Math Biol. 1988;26:1–25. doi: 10.1007/BF00280169. [DOI] [PubMed] [Google Scholar]
- 15.Altmann M. Susceptible-infected-removed epidemic models with dynamic partnerships. J Math Biol. 1995;33:661– 675. doi: 10.1007/BF00298647. [DOI] [PubMed] [Google Scholar]
- 16.Altmann M. The deterministic limit of infectious disease models with dynamic partners. Math Biosci. 1998;150:153–175. doi: 10.1016/s0025-5564(98)00012-1. [DOI] [PubMed] [Google Scholar]
- 17.Watts CH, May RM. The influence of concurrent partnerships on the dynamics of HIV/AIDS. Math Biosci. 1992;108:89 –104. doi: 10.1016/0025-5564(92)90006-i. [DOI] [PubMed] [Google Scholar]
- 18.Chick SE, Adams AL, Koopman JS. Analysis and simulation of a stochastic, discrete-individual model of STD transmission with partnership concurrency. Math Biosci. 2000;166:45– 68. doi: 10.1016/s0025-5564(00)00028-6. [DOI] [PubMed] [Google Scholar]
- 19.Hudson CP. Concurrent partnerships could cause AIDS epidemics. Int J STD AIDS. 1993;4:249 –253. doi: 10.1177/095646249300400501. [DOI] [PubMed] [Google Scholar]
- 20.Keeling MJ, Eames KT. Networks and epidemic models. J R Soc Interface. 2005;2:295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Keeling MJ. The effects of local spatial structure on epidemiological invasions. Proc Biol Sci. 1999;266:859–867. doi: 10.1098/rspb.1999.0716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Keeling M. The implications of network structure for epidemic dynamics. Theor Popul Biol. 2005;67:1– 8. doi: 10.1016/j.tpb.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 23.Volz E, Meyers LA. Susceptible-infected-recovered epidemics in dynamic contact networks. Proc Biol Sci. 2007;274:2925–2933. doi: 10.1098/rspb.2007.1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ghani AC, Swinton J, Garnett GP. The role of sexual partnership networks in the epidemiology of gonorrhea. Sex Transm Dis. 1997;24:45–56. doi: 10.1097/00007435-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 25.Eames KT, Keeling MJ. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc Natl Acad Sci. 2002;99:13330 –13335. doi: 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lagarde E, Auvert B, Carael M, et al. Concurrent sexual partnerships and HIV prevalence in five urban communities of sub-Saharan Africa. AIDS. 2001;15:877– 884. doi: 10.1097/00002030-200105040-00008. [DOI] [PubMed] [Google Scholar]
- 27.Xiridou M, Geskus R, de Wit J, Coutinho R, Kretzschmar M. The contribution of steady and casual partnerships to the incidence of HIV infection among homosexual men in Amsterdam. AIDS. 2003;17:1029– 1038. doi: 10.1097/00002030-200305020-00012. [DOI] [PubMed] [Google Scholar]
- 28.Morris M, Kretzschmar M. A microsimulation study of the effect of concurrent partnerships on the spread of HIV in Uganda. Math Popul Stud. 2000;8:109 –133. [Google Scholar]
- 29.Leclerc PM, Matthews AP, Garenne ML. Fitting the HIV epidemic in Zambia: a two-sex micro-simulation model. PLoS One. 2009;4:e5439. doi: 10.1371/journal.pone.0005439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jones JH, Handcock MS. An assessment of preferential attachment as a mechanism for human sexual network formation. Proc Biol Sci. 2003;270:1123–1128. doi: 10.1098/rspb.2003.2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jones JH, Handcock MS. Social networks: sexual contacts and epidemic thresholds. Nature. 2003;423:605– 606. doi: 10.1038/423605a. [DOI] [PubMed] [Google Scholar]
- 32.Liljeros F, Edling CR, Amaral LA, Stanley HE, Aberg Y. The web of human sexual networks. Nature. 2001;411:907–908. doi: 10.1038/35082140. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.