Abstract
Motivation: Metagenomics is a recent field of biology that studies microbial communities by analyzing their genomic content directly sequenced from the environment. A metagenomic dataset consists of many short DNA or RNA fragments called reads. One interesting problem in metagenomic data analysis is the discovery of the taxonomic composition of a given dataset. A simple method for this task, called the Lowest Common Ancestor (LCA), is employed in state-of-the-art computational tools for metagenomic data analysis of very short reads (about 100 bp). However LCA has two main drawbacks: it possibly assigns many reads to high taxonomic ranks and it discards a high number of reads.
Results: We present MTR, a new method for tackling these drawbacks using clustering at Multiple Taxonomic Ranks. Unlike LCA, which processes the reads one-by-one, MTR exploits information shared by reads. Specifically, MTR consists of two main phases. First, for each taxonomic rank, a collection of potential clusters of reads is generated, and each potential cluster is associated to a taxon at that rank. Next, a small number of clusters is selected at each rank using a combinatorial optimization algorithm. The effectiveness of the resulting method is tested on a large number of simulated and real-life metagenomes. Results of experiments show that MTR improves on LCA by discarding a significantly smaller number of reads and by assigning much more reads at lower taxonomic ranks. Moreover, MTR provides a more faithful taxonomic characterization of the metagenome population distribution.
Availability: Matlab and C++ source codes of the method available at http://cs.ru.nl/˜gori/software/MTR.tar.gz.
Contact: gori@cs.ru.nl; elenam@cs.ru.nl
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
New-sequencing technologies and the dramatic reduction in the cost of sequencing have boosted the development of metagenomics, a new discipline that studies DNA and RNA sequences sampled from genomic material present in a microbial community (Yooseph et al., 2007). Metagenomics has gained popularity because it allows researchers to study (the large amount of) microbes that cannot be cultured (Amann et al., 1995) and their role in the environment, for instance in term of interaction with other organisms. Sequencing a sample produces a collection of DNA or RNA fragments, called reads, belonging to the different genomes present in the sample. A metagenomic dataset is a collection of these sampled reads.
Until recently shotgun Sanger sequencing was the main technology used in metagenomics (Sanger and Coulson, 1975; Sanger et al., 1977), producing reads of length ranging between 800 and 1000 bp). Nowadays, other less expensive technologies like Roche 454 (Margulies et al., 2005) and Illumina platforms1 generate reads of 100–400 bp and 75–100 bp, respectively. Such new-sequencing technologies produce very large datasets containing short reads. Computational analysis techniques are indispensable to extract knowledge from these datasets (Kunin et al., 2008; McHardy and Rigoutsos, 2007; Qin et al., 2010; Raes et al., 2007).
In this article, we focus on the taxonomic assignment of very short reads (about 100 bp) to putative taxa. Taxonomic assignment is a way to assess species diversity and to understand what the different populations are doing. It is also used for improving reads assembly (Delcher et al., 2007).
Computational approaches for taxonomic assignment can be divided into two main groups: composition based and similarity based. Composition-based annotation methods cluster the reads according to their GC content, codon usage and other oligonucleotide frequencies. These methods cannot be directly applied to short reads because of the local variation of nucleotides distribution across a genome (Bentley and Parkhill, 2004). Moreover, external environmental factors seem to influence the GC nucleotide composition of a community, suggesting that it may be even harder to distinguish the reads of different organisms relying on GC content (Foerstner et al., 2005). Similarity-based taxonomic annotation methods assign reads to organisms or taxa using similarities of reads to reference sequences of a given database. Similarity is usually measured by means of sequence alignment tools, like BLAST (Altschul et al., 1997). This approach is useful when most reads in the sample have significant similarities to reference sequences from known operational taxonomic units (Wooley et al., 2010). The incompleteness of the information contained in reference databases and the bias toward cultivable species constitute inherent limitations of the similarity-based approach. Nevertheless, similarity-based techniques have been shown to be effective for the taxonomic analysis of metagenomes (Dalevi et al., 2008; Huson et al., 2007). Furthermore, results of ongoing projects on sequencing reference genomes will likely produce many more reference data available in the near future (Turnbaugh et al., 2007).
A simple similarity-based algorithm for taxonomic assignment is the Lowest Common Ancestor (LCA; Liu et al., 2008; Wang et al., 2007). LCA is the core algorithm of MEGAN (Huson et al., 2007) and of the Galaxy (Blankenberg et al., 2007, 2010) web-based annotation tool2; also CARMA (Krause et al., 2008) is based on an algorithm somewhat similar to LCA. CARMA identifies protein family fragments among the reads and it assigns each fragment to the ancestor taxon shared by the phylogenetic subtree of reference proteins where the fragment is located. LCA assigns to each read one taxon computed by means of the least common taxonomic ancestor of a suitable set of sequences (hits). These hits are obtained by matching the read against a database of reference sequences, like the NCBI-NR protein database. In this way, LCA assigns reads to taxa at possibly different taxonomic ranks.
Two limitations of LCA rise from the way in which taxonomic information from matching reference sequences is combined. (i) LCA annotates a relatively small percentage of reads because a read is discarded if the least common taxon of its hits cannot be computed; (ii) LCA assigns many reads to taxa at high ranks, because it computes the lowest common ancestor of (possibly many) matching sequences (Kunin et al., 2008). The first limitation is addressed by methods that assign all reads. The simplest and most used of such methods assigns each read to its best matching reference sequence, called best hit (BH); as recently shown for instance in Brady and Salzberg (2009), this is still the best stand-alone assignment method for long reads (of length >800 bp). A more involved method assigning all reads is Phymm (Brady and Salzberg, 2009). In Phymm, a classifier is trained based on interpolated Markov models on a large amount of curated genomes. This classifier constructs probability distributions representing observed patterns of nucleotides that characterize each chromosome or plasmid. On metagenomic datasets with long reads (800 bp and 1000 bp), Phymm was shown to outperform BH at ranks Class and Phylum. The authors also showed that a suitable combination of BH and Phymm (called PhymmBL) significantly improved accuracy of both BH and Phymm. However, its accuracy for short reads (100 bp) remains rather low, ranging from 58.5% at rank Genus to 77.5% at rank Phylum. The second drawback of LCA, that is, the fact that it assigns many reads to taxa at high ranks, has been recently tackled in Clemente et al. (2010), where a method was proposed for assigning each read to a taxon at a rank lower (or equal) than the one selected by LCA. The choice of such taxon is based on the number of mismatches between the read and the organisms in that taxon.
To overcome both drawbacks of LCA , we introduce an algorithm for the taxonomic assignment of reads. Our approach is motivated by the following observations. LCA uses taxonomic information of matching reference sequences locally, that is, the taxonomic assignment of each read is performed independently of the other ones. However, reads of a metagenome are related among each other. In particular, groups of reads have common matching reference sequences. We propose to use this global type of information to design a new taxonomic assignment algorithm, called multiple taxonomic ranks (MTR-based clustering). MTR performs the following two steps at each taxonomic rank. First, taxonomic information shared by reads at that rank is used for characterizing clusters of reads having the same taxon. Next, a ‘best’ subset of the resulting clusters is selected. Such selection task is casted into a combinatorial optimization problem and solved using an existing efficient approximation algorithm. This global optimization method for grouping reads into clusters having a common taxa produces multiple taxonomic assignments, one for each rank. However, the taxons assigned to a read at different ranks may be inconsistent with each others. We solve such inconsistencies by assigning each read to a taxon at lowest rank such that the multiple taxonomic assignments of that read from the highest to the selected rank form a consistent taxonomic lineage.
We demonstrate the effectiveness of this approach on several metagenomic datasets, both simulated and real life. On all the considered datasets, MTR discards a significantly smaller number of reads than LCA and it assigns much more reads at lower taxonomic ranks. Furthermore, on simulated metagenomes M1, M2 and M3, MTR is shown to provide a more faithful taxonomic characterization of the population distribution than LCA. With respect to the correctness of the assignments, both LCA and MTR's accuracy appears to reflect the difference in taxonomic composition of the simulated datasets, with M1 composed of representatives of the less well-sampled phyla than M2 and M3 (Dalevi et al., 2008). Nevertheless, results indicate that MTR is capable to assign a read to a taxon close to the true one, when the true taxon does not occur among (the taxa of) its hits. In general, our experimental investigation indicates that MTR provides an effective method for performing taxonomic analysis of a metagenomic dataset with short reads.
2 METHODS
We propose a method for taxonomic assignment of short reads motivated and inspired by LCA (Huson et al., 2007). In LCA, a read is compared against a database of reference sequences, such as the NCBI-NR protein database, and the taxonomic information of significant matches, called hits, is extracted and mapped onto the leaves of the NCBI taxonomy. The leaves of the NCBI taxonomy represent different species and strains. LCA computes the lowest common ancestor of all these hits, which corresponds to some higher rank taxon, and will then assign the read to that taxon. In this way, species-specific sequences are assigned to the leaves, whereas sequences that are conserved among different species, or that are susceptible to horizontal gene transfer, are assigned to taxa of less-specific rank.
Observe that LCA processes each read independently: hence, it does not use taxonomic information shared by alignments of different reads. However, reads are related among each others since sets of reads are part of the same organism. Therefore, we propose to use information shared among reads for developing the following global taxonomic assignment method, called MTR.
2.1 Read assignment at MTR
Like in LCA, all reads are submitted as BLASTx queries against a protein sequence database and proteins of high-quality alignments are selected. This process generates one set of protein hits for each read. The taxonomic information of these proteins is used by MTR for clustering reads at each taxonomic rank, such that reads in the same group are assigned to the same taxon at that rank.
Specifically, let R be the set of reads having at least one high-quality alignment, and let r denote a read. For each taxonomic rank, from the highest to the lowest, each read r is either assigned to a taxon at that rank or is considered not assigned at that and lower taxonomic ranks. The latter case happens if the taxonomic assignment of r at that rank is not consistent with its assignments computed at higher ranks. In that case, r is removed from R. This consistency test is performed at each rank (see step 3 below).
Taxonomic assignment at a given taxonomic rank is performed using a clustering approach. Here, we view clustering as the problem of searching for a minimum family of possibly overlapping clusters of reads that together cover the considered set of reads. To this aim, we define an ad hoc search space and search strategy. The search space consists of clusters of reads directly characterized using the taxa of proteins of those high-quality alignments, which are obtained by submitting the reads as BLASTx queries. The search strategy is based on combinatorial optimization. The search space construction procedure, search strategy and consistency test are described in detail below.
Search space construction: generate clusters of reads using the taxa of their hits. MTR generates a collection of clusters of reads, where each cluster is associated to a taxon at the considered rank. A cluster Cj consists of those reads in R having a high-quality alignment with at least one protein having taxon j.
-
Search strategy: select an optimal family of clusters. The algorithm selects a minimum family of clusters that together contain all the considered reads. This selection task is casted into a combinatorial optimization problem, the set covering problem (SCP):
Here n is the total number of clusters generated at step 1. This approach is inspired by previous works for clustering reads using proxygenes (Dalevi et al., 2008; Folino et al., 2009). The program used by MTR for solving (heuristically) the SCP is an implementation of the greedy set covering algorithm (Chvatal, 1979). This is a very simple greedy algorithm that, at each stage, chooses the set that contains the largest number of uncovered elements (Algorithm 1). The greedy algorithm can be efficiently implemented in time that is linear in the size of the input (Bar-Yehuda and Even, 1981).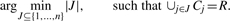
(SCP) 
The selection process is illustrated by means of the following toy example. Suppose we have 10 reads, R = {r1,…, r10}. For each read, the taxa of its hits at a given rank are shown in Table 1, left matrix. A bullet in entry (i, j) indicates that read ri belongs to cluster Cj; this means that if Cj is selected, ri will be assigned to taxon j. The problem is to select a minimum number of clusters (columns of that matrix) that together ‘cover’ all the 10 reads. A solution is shown in the figure on the right-hand side of Table 1, where the selected clusters are C1, C2 and C5. Therefore, the reads are assigned to taxa 1, 2 and 5.
Consistency test: for each read in R, MTR now checks that its taxonomic assignment at this rank is consistent with its taxonomic assignments computed at higher ranks. That is, if read r has been assigned to taxon j at the considered rank, we check that at higher ranks r was assigned to ancestors of taxon j. If this does not happen, then r is not assigned from that rank onwards and is removed from R.
Table 1.
Input covering matrix (left) and a solution of the SCP (Right)
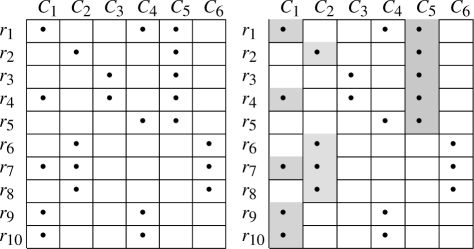 |
Observe that at a given rank, MTR can assign a read to more than one cluster. This is illustrated in our toy example where for instance read r2 is assigned to clusters C2 and C5. However, we want to assign a unique taxon to each read. Therefore, MTR assigns each read r to the largest cluster among those containing r (ties are broken randomly), while keeping the taxonomical consistency of the assignments of r at different ranks. For instance, read r2 will be assigned to C5. The final assignment computed by MTR associates of each read r in R to the taxon (cluster) containing r and having the lowest rank.
Both LCA and MTR process a set of hits computed using BLAST and output a read-taxon assignment, where reads are possibly assigned to taxa at different taxonomic ranks. MTR and LCA are also similar in that they output the same taxon for each read that is assigned by both methods at the same taxonomic rank. In fact, if a read r is assigned by both methods at the same rank it means that that rank contains the lowest common ancestor taxon of the hits of r. At that rank, r is covered by only one taxon, therefore MTR will be forced to assign r to that taxon.
The running time of both MTR and LCA is dominated by the alignment of reads with the reference protein sequences database using BLASTx. This is a computational bottleneck common to similarity-based methods for metagenomic analysis based on the alignment of reads with sequences of a large database of reference.
3 EXPERIMENTS
3.1 Data
We analyzed nine simulated and three real-life metagenomic datasets. The nine simulated datasets had been derived from three sets of organisms, here denoted by M1, M2 and M3; these datasets had been introduced in Dalevi et al. (2008). M1, M2 and M3 are composed by 9, 5 and 8 distinct genomes, respectively. These genomes had been sequenced at the Joint Genome Institute (JGI) using the 454 GS20 pyrosequencing platform that produces ∼100 bp reads. From each set of organisms, reads had been randomly sampled at three different levels of coverage (0.1×, 1× and 4×) resulting in a total of nine datasets. The coverage is the mean number of times a nucleotide is being sequenced (Wooley et al., 2010). Table 1 of Supplementary Material shows the names of the organisms and the number of reads generated for the datasets for coverage 0.1×. A detailed description of the simulated datasets can be found in Dalevi et al. (2008).
We retrieved from the metagenomics RAST server (Meyer et al., 2008) three real-life datasets (4440426.3, 4440319.3 and 4440283.3) containing short reads (average length of about 100 bp) and sampled using pyrosequencing on Roche 454 CS20. These datasets had been derived from a Saltern sample (Edwards et al., 2006), a Coral Holobiont sample (Rodriguez-Brito et al., 2007) and a Chicken Cecum sample, respectively. The Saltern metagenome dataset contains 34 296 fragments with an average fragment length of 100.69 bp; the Coral Holobiont metagenome dataset contains 316 279 fragments with an average fragment length of 102.07 bp; the Chicken Cecum metagenome dataset contains 294 682 fragments with an average length of 104.4 bp.
3.2 Aligning reads with protein sequences
All the reads were submitted as NCBI-BLASTx queries against the NCBI-NR3 (non-redundant) protein sequence database (downloaded on March 3, 2009). The default BLASTx parameters were used, adding a neighborhood word score threshold of 14 and an E-value cutoff of 10−6. We set the word score threshold to 14, higher than the default value 12, in order to increase the speed more than 2-fold while maintaining a high sensitiveness [see (Korf et al., 2003), Paragraph 9.3.1.1]. Low-quality alignments were removed from the BLASTx outputs, by discarding alignments with bit-score less than 30. For each query read (at most), the top 50 hits were selected. Before performing the alignment of reads in a simulated metagenome, we removed from NCBI-NR all the sequences belonging to the species present in that metagenome. This masking process is commonly applied in order to assess the performance of taxonomic annotation algorithms on datasets containing species that have never been observed before, because a real-life metagenome is likely to contain undiscovered organisms (Brady and Salzberg, 2009).
4 RESULTS
For all datasets, a small percentage of reads had at least one high-quality hit (Supplementary Table S3), an expected phenomenon related to the incompleteness of the information contained in the database of reference (Huson et al., 2007). These reads were selected for taxonomic assignment.
We assessed comparatively the performance of LCA and MTR with respect to the number of reads assigned and the taxa detected. Moreover, we compared MTR and LCA in term of their characterization of the taxonomic population distribution at ranks Order and Genus. For real-life datasets, the characterizations were performed also at ranks Phylum and Class. Finally, on simulated datasets, where the true taxonomic assignment is known by construction, we compared the quality of the assignments given by MTR and LCA using taxon accuracy (i.e. the percentage of taxa correctly detected), taxon sensitivity (i.e. the number of taxa correctly detected by the algorithm divided by the total number of true taxa) and accuracy (i.e. the percentage of reads correctly assigned).
4.1 Results on simulated datasets
Results on a total of 54 cases (three metagenomes, for each metagenome three datasets produced using different coverages, for each resulting dataset six ranks) are reported in Tables 2–4. They show the accuracy and number of reads assigned up to a given rank for datasets M1, M2 and M3, respectively.
Table 3.
Accuracy and number of assigned reads on M2 datasets
| M2 | 0.1× | 1× | 4× |
|---|---|---|---|
| MTR | |||
| Kingdom | 95.27 (9030) | 95.07 (88 537) | 91.41 (174 583) |
| Phylum | 93.83 (9030) | 93.21 (88 537) | 88.75 (174 583) |
| Class | 89.98 (9012) | 89.25 (87 635) | 86.32 (168 854) |
| Order | 90.44 (8822) | 89.24 (85 657) | 86.14 (167 222) |
| Family | 80.56 (7264) | 77.35 (81 366) | 73.01 (159 591) |
| Genus | 64.41 (6480) | 61.36 (77 307) | 55.91 (147 139) |
| LCA | |||
| Kingdom | 94.82 (7205) | 94.66 (73 176) | 90.76 (143 226) |
| Phylum | 93.21 (7205) | 92.57 (73 169) | 87.80 (143 206) |
| Class | 89.82 (5941) | 88.98 (60 294) | 83.59 (117 881) |
| Order | 89.90 (5615) | 88.44 (57 373) | 83.01 (113 168) |
| Family | 83.77 (4757) | 81.84 (48 760) | 77.61 (100 925) |
| Genus | 76.91 (3907) | 74.60 (40 823) | 69.68 (82 805) |
Table 2.
Accuracy and number of assigned reads on M1 datasets
| M1 | 0.1× | 1× | 4× |
|---|---|---|---|
| MTR | |||
| Kingdom | 100.00 (5669) | 99.93 (56 348) | 99.93 (173 541) |
| Phylum | 92.50 (5669) | 92.59 (56 325) | 93.39 (173 521) |
| Class | 84.04 (5556) | 85.44 (54 341) | 87.15 (167 546) |
| Order | 64.93 (5366) | 66.23 (53 395) | 66.69 (163 840) |
| Family | 64.87 (4904) | 63.67 (50 587) | 63.22 (154 134) |
| Genus | 63.66 (4628) | 62.58 (48 244) | 60.50 (144 475) |
| LCA | |||
| Kingdom | 100.00 (4145) | 99.92 (42 620) | 99.91 (132 130) |
| Phylum | 95.08 (4145) | 94.81 (42 593) | 95.02 (132 099) |
| Class | 94.46 (3739) | 93.24 (38 970) | 93.60 (121 980) |
| Order | 75.29 (3497) | 74.18 (36 857) | 72.43 (116 632) |
| Family | 71.94 (2961) | 69.94 (31 913) | 69.07 (102 239) |
| Genus | 71.03 (2686) | 68.39 (29 360) | 66.63 (94 346) |
Table 4.
Accuracy and number of assigned reads on M3 datasets
| M3 | 0.1× | 1× | 4× |
|---|---|---|---|
| MTR | |||
| Kingdom | 100.00 (11 792) | 99.97 (116 869) | 100.00 (166 948) |
| Phylum | 99.58 (11 792) | 99.47 (116 869) | 99.86 (166 948) |
| Class | 96.97 (11 763) | 97.07 (116 134) | 99.73 (166 936) |
| Order | 91.79 (11 606) | 91.70 (115 034) | 97.67 (166 148) |
| Family | 92.27 (11 117) | 91.25 (111 560) | 97.62 (165 231) |
| Genus | 94.06 (10 419) | 92.19 (101 533) | 97.42 (140 476) |
| LCA | |||
| Kingdom | 100.00 (10 333) | 99.96 (102 824) | 99.99 (155 263) |
| Phylum | 99.72 (10 333) | 99.69 (102 813) | 99.93 (155 258) |
| Class | 98.86 (9162) | 98.82 (91 445) | 99.81 (141 829) |
| Order | 96.74 (7788) | 96.62 (77 822) | 98.14 (115 732) |
| Family | 96.87 (7545) | 96.42 (75 616) | 98.04 (110 488) |
| Genus | 97.61 (6748) | 96.01 (68 573) | 98.35 (110 139) |
4.1.1 Number of reads assigned
on the average, MTR assigned 22.66% more reads than LCA, varying from a minimum of 7.53% for M3 with coverage 4× to a maximum of 36.77% for M1 with coverage 1×. Moreover, on each simulated dataset, MTR assigned much more reads than LCA up to each given rank, especially at low taxonomic ranks. For instance, at rank Genus differences between MTR and LCA range from 27.54% for dataset M3 coverage 4× to 89.37% for dataset M2, coverage 1×.
4.1.2 Taxa detected
MTR detected slightly more taxa than LCA. For instance, on dataset M1, coverage 1×, the number of taxa detected by MTR and LCA ranged from 20 and 19 at rank Phylum to 127 and 117 at rank Species, respectively. The two algorithms showed similar taxa sensitivity and accuracy (Supplementary Tables S4–S6). The differences in taxa detection accuracy seems mainly due to the fact that MTR detected more taxa than LCA, therefore affecting taxa specificity. Nevertheless, the erroneous detected taxa are taxonomically close to true taxa, as described in the below analysis of the population distribution.
4.1.3 Population distribution
we analyzed the population distributions generated by the methods in two ways. First, we compared the percentages of reads assigned by the methods to true taxa. Next, we measured quantitatively the similarity between the population distributions generated by a method and the true ones.
The percentages of reads assigned by the methods to taxa are shown in Supplementary Figures S1–S18. On the M1 metagenome, MTR gave a more faithful population characterization of the true detected taxa than LCA at rank Genus, in particular for coverages 0.1× (Supplementary Fig. S2). Specifically, the percentage of reads assigned by MTR to Clostridium (14.61%) was close to the true percentage (19.07%), while LCA assigned only 8.08% reads to that taxon. Moreover, LCA assigned more reads to Lactobacillus than Clostridium, in contrast with the trend in the real population distribution. Both methods did not detect four of the true taxa present in M1 (Herpetosiphon, Halothermothrix, Prochlorococcus, Caldicellulosiruptor) because these taxa did not occur in (the taxa of) the processed BLASTx hits. For instance, at coverage 0.1×, there were no hits from Halothermothrix and Herpetosiphon. Moreover, only 2 and 10 hits were from the geni Prochlorococcus and Caldicellulosiruptor, respectively. The absence of Halothermothrix was expected because this genus contains only the species present in M1, which were removed from the database of reference, as explained in Subsection 3.2. Geni Herpetosiphon and Caldicellulosiruptor were not detected probably because they had few sequences in the reference protein dataset used by BLASTx: these geni contain only 4 and 12 species, respectively. Among the predicted geni with more than 5% of the reads, only Anaerocellum was not present in M1. Reads assigned to Anaerocellum were mostly reads of Caldicellulosiruptor; these two geni belong to the same taxon at rank Class (Clostridia). For coverage 0.1×, 92.99 and 97.66% of the reads assigned to Anaerocellum by LCA and MTR, respectively, were Caldicellulosiruptor reads.
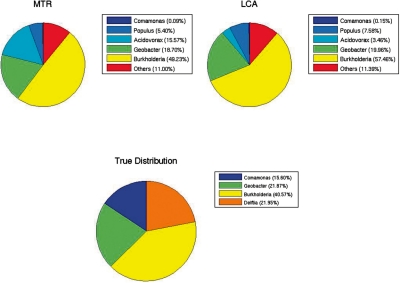
On the M2 metagenome, the population characterizations of true detected taxa generated by MTR were better than those of LCA for all the three datasets. In particular, LCA underestimated the presence of Burkholderiales at rank Order, and for coverage 0.1× and 1× it also overestimated the percentage of reads from Burkholderia at rank Genus. For coverage 0.1×, the true population distribution and the characterizations given by MTR and LCA at rank Order contained 78.13, 72.56 and 68.01% of reads of Burkholderiales, respectively (Supplementary Fig. S7). At rank Genus, the percentages of reads of Burkholderia were 40.57% in the true population, and 49.23 and 57.46% for MTR and LCA, respectively (Fig. 1). These results were in line with those obtained for coverage 1×. For all the coverages, both methods assigned a small number of reads to the true geni Delftia and Comamonas, due to the very few BLASTx hits having these taxa (for instance, at coverage 0.1×, only 27 and 57 hits, respectively). Nevertheless, both methods detected the related taxa Acidovorax at rank Genus, that together with the geni Delftia and Comamonas belongs to the taxon Comamonadaceae at rank Family. Specifically, for coverage 0.1×, MTR and LCA assigned 15.57 and 3.46% of reads to Acidovorax, respectively, so the result of MTR was closer to the true percentage of the union of the two true geni present in M2 (37.55%). Furthermore, MTR assigned a much greater percentage of Delftia's reads to Acidovorax than LCA for all the coverages: at rank Genus an average of 36.78% and 11.96%, respectively. MTR also assigned a higher percentage of Comamonas reads to Acidovorax for coverage 0.1× and 1× (53.24% for MTR and 27.37% for LCA, respectively).
Fig. 1.
Population distributions (rank Genus) of M2, coverage 0.1×, by MTR and LCA, and the true population distribution. Label ‘Others’ means taxa with less than 5% of the reads and not occurring in the true distribution.
The two algorithms gave population distributions of true detected taxa close to the true ones on the M3 metagenome, where MTR was slightly better than LCA. In particular, for coverage 0.1× and 1× at rank Order, LCA assigned more reads to Xanthomonadales than Pseudomonadales, in contrast with the trend in the real population distribution (Supplementary Fig. S13, S15 and S17). At rank Genus, the percentage of reads assigned to Bifidobacteria by MTR was closer to the real one. For instance, at coverage 0.1×, the true population distribution and the characterizations given by MTR and LCA contained 8.52, 8.86 and 11.75% of reads of Bifidobacteria (Supplementary Fig. S14).
In order to quantitatively measure how close a population distribution produced by a method was to the true one, we used a divergence measure based on Shannon entropy, called L-divergence (Lin , 1991). Let pA and pB be two probability distributions on X and let K be defined as follows:
The L-divergence of pA and pB is defined as
The L-divergence assumes values between 0 and 2.
In our setting, for a given method M and a selected taxonomic rank, a probability distribution pM of X is considered, where X is the set of all taxa of that rank. For a given taxon x ∈ X, we estimated pM(x) as the number of reads assigned by M to x divided by the total number of reads assigned by M to taxa at that rank. Furthermore, the probability distribution p of the true population is considered, where p(x) is estimated as the fraction of reads belonging to x. For instance, suppose that at a given rank X consists of taxa a, b, c, d, e and M assigned 30, 50 and 20% of the reads to taxon a, b and c, respectively. Suppose that the true population consists of 30, 40 and 30% of taxon a, d and e, respectively. Then pM = (0.3, 0.5, 0.2, 0, 0) and p = (0.3, 0, 0, 0.4, 0.3).
Results at ranks Family and Genus show that both MTR and LCA produced population distributions close to the true ones (Table 5). At rank Genus, MTR generated distributions closer to the true one on M1 datasets, while on the M2 datasets LCA's population distributions were closer to the true ones. On datasets M3, both algorithms generated distributions very close to the true ones. At rank Family, distributions generated by MTR were better than those of LCA on M1 and M2 datasets, while LCA's distributions were slightly closer to the true one on datasets M3. Since M1 is composed of representatives of less well-sampled phyla than M2 and M3 (Dalevi et al., 2008), results indicate that MTR is more effective than LCA on metagenomes containing less well-sampled phyla.
Table 5.
Divergence between true population distribution and the population distributions obtained by MTR and LCA at ranks Family and Genus
| Dataset | Family |
Genus |
||
|---|---|---|---|---|
| MTR | LCA | MTR | LCA | |
| M1 0.1× | 0.539 | 0.608 | 0.544 | 0.601 |
| M1 1× | 0.565 | 0.604 | 0.570 | 0.607 |
| M1 4× | 0.628 | 0.642 | 0.643 | 0.654 |
| M2 0.1× | 0.172 | 0.232 | 0.696 | 0.611 |
| M2 1× | 0.191 | 0.256 | 0.690 | 0.623 |
| M2 4× | 0.261 | 0.334 | 0.825 | 0.747 |
| M3 0.1× | 0.099 | 0.091 | 0.103 | 0.095 |
| M3 1× | 0.102 | 0.091 | 0.115 | 0.104 |
| M3 4× | 0.024 | 0.020 | 0.026 | 0.017 |
4.1.4 Accuracy
results are in accordance with the analysis conducted in Dalevi et al. (2008), and show that differences in accuracy for the three simulated metagenomes appear to reflect the difference in their taxonomic composition, with M1 composed of representatives of less well-sampled phyla than M2 and M3.
Comparison of accuracy results between the two algorithms should be interpreted with care, since they are computed on sets of reads of different sizes: the sets used to compute accuracy of MTR are much bigger than those of LCA. LCA achieved in general higher accuracy results. In particular, on M1 LCA was more accurate than MTR for all the coverages. For coverages 0.1× and 4×, the difference in accuracy peaked at rank Order. For instance, LCA and MTR accuracies were 75.29 and 64.93% for coverage 0.1×, respectively. The accuracy of both algorithms dropped dramatically from rank Class to Order, with the biggest gaps for the two lowest coverages. For coverage 1×, for instance, the accuracy decreased from 85.44% to 66.23% for MTR and from 93.24% to 74.18% for LCA. On M2, LCA was more accurate at rank Family and Genus. MTR outperformed slightly LCA until rank Order; from rank Order to Family, the accuracy of both algorithms decreased and LCA became more accurate than MTR. The difference in accuracy peaked at rank Genus for coverage 4×, where LCA and MTR accuracies were 69.68 and 55.91%, respectively. LCA was slightly more accurate on M3. The biggest difference was reached at rank Family for coverage 1×, where LCA and MTR accuracies were 96.42 and 91.25%, respectively.
4.2 Results on real-life datasets
4.2.1 Number of reads assigned
results on real-life datasets are shown in Table 6, and are in line with those obtained on the simulated datasets. Specifically, MTR assigned more reads than LCA (29.91, 15.20 and 19.52% for the dataset Saltern, Coral and Chicken, respectively), also up to each taxonomic rank. The difference peaked at rank Species for the datasets Saltern and Chicken (201.29 and 208.02% more, respectively). On the Coral dataset, the highest difference was 208.88% at rank Family, but also at rank Species the difference was neat (120.28%). On this dataset, MTR assigned at rank Order three times the number of reads assigned by LCA, whereas the difference dropped to 143.80% at rank Genus. Similarly, on dataset Saltern, the differences were 63.20 and 49.78% at rank Order and Family, respectively.
Table 6.
Real-life datasets: number of reads assigned up to a rank
| Saltern | Coral | Chicken | |
|---|---|---|---|
| MTR | |||
| Kingdom | 1581 | 24 522 | 111 655 |
| Phylum | 1576 | 23 027 | 111 650 |
| Class | 1530 | 21 920 | 109 986 |
| Order | 1317 | 21 019 | 108 100 |
| Family | 1035 | 15 583 | 100 676 |
| Genus | 979 | 11 422 | 94 507 |
| Species | 937 | 9560 | 89 818 |
| LCA | |||
| Kingdom | 1217 | 21 287 | 93 416 |
| Phylum | 1208 | 16 526 | 93 399 |
| Class | 1051 | 12 301 | 87 917 |
| Order | 807 | 6841 | 87 146 |
| Family | 691 | 5045 | 70 376 |
| Genus | 635 | 4685 | 69 636 |
| Species | 311 | 4340 | 29 160 |
MTR assigned more reads than LCA for each taxon detected by both the methods, at every rank (Supplementary Figs S19–S30). For instance, on the Saltern dataset, at rank Order, MTR assigned about 50% more reads than LCA to Rickettsiales. The reads assigned by MTR to Rhizobiales and Rhodobacterales were two times as many as those assigned by LCA to that taxa.
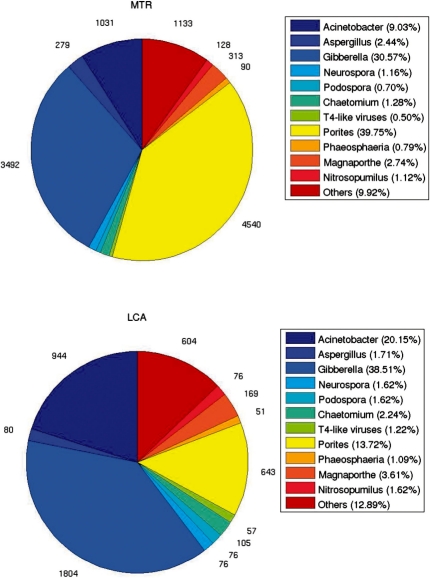
On the Coral dataset, at rank Genus, MTR assigned 4540 reads to Porites, seven times more that LCA (643); the number of reads assigned to Gibberella by MTR was 3492, whereas LCA assigned 1804 reads to that taxon.
On the Chicken dataset, at rank Genus, MTR assigned 6743 reads to Clostridium, three times as many as LCA did (2055); furthermore, 25.5% more reads of Bacteroides were detected by MTR, 15 603 reads more than LCA.
4.2.2 Taxa detected
MTR detected slightly more taxa than LCA (Supplementary Table S7). For instance, on the Coral dataset the number of taxa detected by MTR and LCA were 17 and 16 at rank Phylum, and 70 and 58 at rank Genus, respectively. On the Chicken dataset, at rank Species, the number of taxa detected by MTR and LCA were almost the same (133 and 135, respectively), whereas on the Coral dataset MTR detected 15 taxa and LCA only 8. Also on the Saltern dataset, MTR detected more taxa than LCA: the number of taxa detected by MTR and LCA were 6 and 4 at rank Phylum, and 15 and 8 at rank Genus, respectively.
4.2.3 Population distribution
results of the two algorithms show interesting differences, especially on the Coral dataset, where MTR assigned a higher percentage of reads to Porites and its ancestor taxa at all the ranks (Supplementary Figs S19–S30). Both algorithms identified Cnidaria and Ascomycota as the two largest Phylum populations. However, MTR and LCA considered Cnidaria and Ascomycota as the dominant phyla (47.67 and 50.02%, respectively). Results at rank Phylum show that MTR provided a population characterization of the Coral dataset very similar to the one given in Rodriguez-Brito et al. (2007), which was obtained by comparing the reads with the SEED non-redundant database (Overbeek et al., 2004) using BLASTx. The population characterization of the Coral dataset at rank Genus is shown in the pie charts of Figure 2. MTR labeled 39.75% of the reads as Porites, making it the biggest group, while LCA assigned just 13.72% of the reads to that taxon. Both algorithms generated also different taxonomic distributions of other groups of organisms. For instance, at rank Genus, MTR assigned only 9.03% of the reads to Acinectobacter, while LCA considered this taxon as the second biggest group (20.15%).
Fig. 2.
Population distributions (rank Genus) of Coral dataset by MTR (top) and LCA (bottom).
On the Saltern dataset, MTR and LCA produced similar population distributions, except at rank Genus. At that level, MTR assigned 1.23% of the reads to Clavibacter, a taxon not detected by LCA. Both methods identified Candidatus pelagibacter as the dominant taxon. However, MTR assigned 8.38% of the reads to Roseobacter, almost 10 times as many as LCA.
On the Chicken dataset, the population distributions given by the two algorithms presented many similarities, with MTR showing a slightly higher proportion of Clostridia and of its ancestor taxa. This difference was more apparent at rank Genus, where MTR and LCA assigned 7.13 and 2.95% of the reads to Clostridium, respectively. A predominant occurrence of Bacteroides was detected by both algorithms: 81.18 and 76.33% of the reads were assigned to this taxon by LCA and MTR, respectively.
5 DISCUSSION
Results of our study on simulated and real-life datasets indicate that MTR is better than LCA with respect to the number of assigned reads. The total number of reads assigned increases, as well as the number of reads assigned at lower ranks.
With respect to correctness of the assignment, results indicate higher accuracy of LCA. However, these results are computed on sets of different size, where much greater sets of reads are used for computing accuracy of MTR. Therefore, accuracy results should be interpreted with care. For instance, on the simulated metagenome M3, MTR assigns on the average 43.36% more reads than LCA at rank Genus, with a small loss of accuracy (2.77% on the average). Accuracy reduction of MTR on M1 at rank Genus is 6.44% but the method assigns 63.25% more reads than LCA. On M2 at rank Genus, MTR assigns 77.64% more reads than LCA with an accuracy reduction of 13.17%; nevertheless, at rank Order MTR is 1.76% more accurate than LCA.
Interestingly, these differences in accuracy are not reflected in differences in the quality of population characterization. On the contrary, on the simulated datasets the population characterizations of MTR are better than those of LCA, with neat differences at rank Genus. On the real-life datasets, MTR and LCA give rather different population characterizations at rank Phylum and lower. The difference is neat on the Coral dataset, where MTR assigns a much higher percentage of reads to Porites than LCA, especially at ranks Order and Genus and also at higher ranks (for instance, Phylum).
In conclusion, results indicate effectiveness of the proposed method for performing global taxonomic analysis of very short metagenomic reads using a protein database of reference.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to thank Mavrommatis Konstantinos for providing the metagenomes M1, M2 and M3.
Funding: This work was partially supported by Netherlands Organization for Scientific Research (NWO) within NWO project 600.065.120.09N213.
Conflict of Interest: none declared.
Footnotes
1See http://www.illumina.com/.
2LCA is present in Galaxy Metagenomic Analyses tools by the name ‘lowest diagnostic rank’.
3Publicly available at ftp://ftp.ncbi.nlm.nih.gov/blast/db.
REFERENCES
- Altschul S, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amann R, et al. Phylogenetic identification and in situ detection of individual microbial cells without cultivation. Microbiol. Rev. 1995;59:143–169. doi: 10.1128/mr.59.1.143-169.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Yehuda R, Even S. A linear-time approximation algorithm for the weighted vertex cover problem. J. Algorithms. 1981;2:198–203. [Google Scholar]
- Bentley S, Parkhill J. Comparative genomic structure of prokaryotes. Ann. Rev. Genet. 2004;38:771–791. doi: 10.1146/annurev.genet.38.072902.094318. [DOI] [PubMed] [Google Scholar]
- Blankenberg D, et al. A framework for collaborative analysis of ENCODE data: making large-scale analyses biologist-friendly. Genome Res. 2007;17:960–964. doi: 10.1101/gr.5578007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankenberg D, et al. Galaxy: a web-based genome analysis tool for experimentalists. Curr. Protoc. Mol. Biol. 2010 doi: 10.1002/0471142727.mb1910s89. Chapter 19Unit 19.10.1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady A, Salzberg S. Phymm and phymmbl: metagenomic phylogenetic classification with interpolated markov models. Nat. Methods. 2009;6:673–676. doi: 10.1038/nmeth.1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chvatal V. A greedy heuristic for the set-covering problem. Math. Operat. Res. 1979;4:233–235. [Google Scholar]
- Clemente J, et al. Accurate taxonomic assignment of short pyrosequencing reads. Pac. Symp. Biocomput. 2010;15:3–9. doi: 10.1142/9789814295291_0002. [DOI] [PubMed] [Google Scholar]
- Dalevi D, et al. Annotation of metagenome short reads using proxygenes. Bioinformatics. 2008;24:i7–i13. doi: 10.1093/bioinformatics/btn276. [DOI] [PubMed] [Google Scholar]
- Delcher A, et al. Identifying bacterial genes and endosymbiont DNA with Glimmer. Bioinformatics. 2007;23:673–679. doi: 10.1093/bioinformatics/btm009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards R, et al. Using pyrosequencing to shed light on deep mine microbial ecology. BMC Genomics. 2006;7:57. doi: 10.1186/1471-2164-7-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foerstner K, et al. Environments shape the nucleotide composition of genomes. EMBO Rep. 2005;6 doi: 10.1038/sj.embor.7400538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folino G, et al. EvoBIO. Vol. 5483. Springer; 2009. Clustering metagenome short reads using weighted proteins; pp. 152–163. of LNCS. [Google Scholar]
- Huson D, et al. Megan analysis of metagenomic data. Genome Res. 2007;17:377–386. doi: 10.1101/gr.5969107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korf I, et al. BLAST. Sebastopol, CA, USA: O'Reilly & Associates, Inc.; 2003. [Google Scholar]
- Krause L, et al. Phylogenetic classification of short environmental DNA fragments. Nucleic Acids Res. 2008;36:2230–2239. doi: 10.1093/nar/gkn038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunin V, et al. A bioinformatician's guide to metagenomics. Microbiol. Mol. Biol. Rev. 2008;72:557–578. doi: 10.1128/MMBR.00009-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin J. Divergence measures based on the Shannon Entropy. IEEE Trans. Inf. Theory. 1991;37:145–151. [Google Scholar]
- Liu Z, et al. Accurate taxonomy assignments from 16S rRNA sequences produced by highly parallel pyrosequencers. Nucleic Acids Res. 2008;36:e120. doi: 10.1093/nar/gkn491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies M, et al. Genome sequencing in microfabricated high-density picolitre reactors. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McHardy A, Rigoutsos I. What's in the mix: phylogenetic classification of metagenome sequence samples. Curr. Opin. Microbiol. 2007;10:499–503. doi: 10.1016/j.mib.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Meyer F, et al. The metagenomics rast server - a public resource for the automatic phylogenetic and functional analysis of metagenomes. BMC Bioinformatics. 2008;9:386. doi: 10.1186/1471-2105-9-386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overbeek R, et al. The SEED: a peer-to-peer environment for genome annotation. Comm. ACM. 2004;47:46–51. [Google Scholar]
- Qin J, et al. A human gut microbial gene catalogue established by metagenomic sequencing. Nature. 2010;464:59–65. doi: 10.1038/nature08821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raes J, et al. Get the most out of your metagenome: computational analysis of environmental sequence data. Curr. Opin. Microbiol. 2007;10:490–498. doi: 10.1016/j.mib.2007.09.001. [DOI] [PubMed] [Google Scholar]
- Rodriguez-Brito B, et al. Metagenomic analysis of the microbial community associated with the coral. Porites astreoides. Environ. Microbiol. 2007;9:2707–2719. doi: 10.1111/j.1462-2920.2007.01383.x. [DOI] [PubMed] [Google Scholar]
- Sanger F, Coulson AR. A rapid method for determining sequences in dna by primed synthesis with DNA polymerase. J. Mol. Biol. 1975;94:441–446. doi: 10.1016/0022-2836(75)90213-2. [DOI] [PubMed] [Google Scholar]
- Sanger F, et al. DNA sequencing with chain-terminating inhibitors. Proc. Natl Acad. Sci. USA. 1977;74:5463–5467. doi: 10.1073/pnas.74.12.5463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbaugh PJ, et al. The Human Microbiome Project. Nature. 2007;449:804–810. doi: 10.1038/nature06244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, et al. Naive Bayesian classifier for rapid assignment of rRNA sequences into the New Bacterial Taxonomy. Appl. Environ. Microbiol. 2007;73:5261–5267. doi: 10.1128/AEM.00062-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wooley J, et al. A primer on metagenomics. PLoS Comput. Biol. 2010;6:e1000667. doi: 10.1371/journal.pcbi.1000667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yooseph S, et al. The Sorcerer II global ocean sampling expedition: expanding the universe of protein families. PLoS Biol. 2007;5:e16. doi: 10.1371/journal.pbio.0050016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.