Hydrophilization of Magnetic Nanoparticles with Modified Alternating Copolymers. Part 2: Behavior in solution

Abstract

Aqueous solutions of iron oxide nanoparticles (NPs) stabilized by poly(maleic acid-alt-1-octadecene) (PMAcOD) modified with the 5,000 Da poly(ethylene glycol) (PEG) or the short ethylene glycol (EG) tails were analyzed by small-angle X-ray scattering (SAXS). Advanced SAXS data analysis methods were employed to systematically characterize the structure and interactions between the NPs. Depending on the type of the grafted tail and the grafting density all NPs can be separated into three groups. All the samples contain mixtures of individual nanoparticles, their dynamic clusters and aggregates, and the fractions of these species are different in the different groups. The first group consists of NPs coated with PMAcOD modified with the long PEG tails with the maximal grafting density, and the content of dynamic clusters and aggregates in the samples of this group does not exceed 4%. The samples from the second group with less dense coatings demonstrate a larger amount (5–7%) of the aggregates and dynamic clusters. The samples from the third group consisting of the NPs protected by EG modified PMAcOD contain mostly individual NPs and some amount of dumbbell dimers without noticeable aggregation. Importantly, the solution behavior of the NPs is independent on the iron oxide core size. Our results therefore provide means of predicting stabilization and avoiding aggregation of NPs based on the type of a protective shell.

Introduction

Small-angle X-ray scattering (SAXS) is a universal method to analyze the structure of various disperse systems at resolution from about 1 to 100 nm.¹ SAXS is useful due to its capability to comprehensively characterize complex systems, including e.g. polymer matrices and nanocomposites containing nanoparticles (NPs). The SAXS patterns provide structural information both about nanoscale inhomogeneities (particles or clusters) and about the internal ordering in the sample. One of the important benefits of SAXS is that specimens are studied in their natural media and aggregate states allowing nondestructive quantitative analysis of structural characteristics of the materials in native environment. Application of SAXS provides sizes and shapes of various NPs, their distributions and locations in NP-containing polymer matrices,^2–8 and structural information about internal organization of the entire system.^9–14 Development of novel SAXS data analysis methods including a new approach to model simulations allows one to build low resolution three-dimensional structural models of different kinds of polymer organizations. In particular, ab initio methods for low resolution shape reconstruction (e.g. program DAMMIN)¹⁵ along with rigid body modeling methods,¹⁶ although originally developed for biological systems, can be successfully employed to analyze various polymer systems including those containing metals and to build structural models of complex natural or artificial materials.^9,17–19

Various types of nanocomposites were actively studied using SAXS. This method was crucial for determining the morphology of NPs in thin films,²⁰ polymer networks,²¹ clays in polymers,^22,23 or NPs themselves.^24,25 SAXS has been used for characterizing arrays of NPs,^26–28 the self-assembly in nanocomposites including mesoscopic materials,^29–35 the deformation behavior of nanocomposites,³⁶ and for proving existence of oxo-metal domains in a nanocomposite.³⁷

It is noteworthy that for better characterization of material structure, the SAXS studies should be complemented by other methods such as atomic force microscopy, X-ray diffraction, transmission electron microscopy (TEM), dynamic light scattering, ζ-potential measurements, etc. The combination of the techniques allows for comprehensive structural and functional analyses of sophisticated nanocomposites, revealing fine changes occurring during NP formation or other processes.^{2,6,7,10,14,38,39}

In our recent work monodisperse iron oxide nanoparticles coated with phospholipids containing poly(ethylene glycol) (PEG) tails³⁹ and those protected by poly(maleic acid-alt-1-octadecene) (PMAcOD)³⁸ were studied by SAXS. It was shown that in both cases mainly individual functionalized magnetic NPs were formed, but these specimens also demonstrated different kinds of interactions in solution. The iron oxide NPs coated with PEGylated phospholipids formed dynamic nanoclusters exhibiting regular interparticle distances, while those coated with the alternating copolymer had a tendency to aggregation. For various applications of NPs it is of paramount importance to understand the influence of such properties of NP protective shells as their thickness, charge and density on the behavior of the NPs in solution to prevent them from aggregation or to control the aggregation behavior. In the present work using synchrotron SAXS and modern tools of SAXS data interpretation we studied solution interactions of iron oxide NPs coated with PMAcOD modified with grafted 5,000 Da poly(ethylene glycol) (PEG) or short ethylene glycol (EG) tails of different grafting density. The synthesis and characterization of these NPs is described in Part 1 of this work.⁴⁰ Comparing NPs of different sizes with the same shell, and different shells on the NPs of the same size, we were able to identify the most important factors influencing the behavior of NPs in solution. In particular, the NP aggregation (which is an undesirable phenomenon and needs to be minimized when magnetic NPs are hydrophilized) appeared to be linked to the properties of the shell, allowing one to control the aggregation by the appropriate selection of the coating.

1. Experimental

2.1 Materials

Hexanes (85%), ethanol (95%), and acetone (99.78%) were purchased from EMD and used as received. Chloroform (Mallinckrodt, 100%), FeCl₃·6H₂O (98%, Aldrich), docosane (99%, Aldrich), oleic acid (OA, 90%, Aldrich), oleic acid sodium salt (97%, TCI), and TBE buffer (1.3 M Tris, 450 mM boric acid, 25 mM EDTA·Na₂ in H₂O, Fluka) were used without purification. PMAOD (30 000 – 50 000 Da, Aldrich) was used as received. O-(2-aminoethyl)-o′-methyl polyethylene glycols (PEG) with MW5000 and (±)-3-amino-1,2-propanediol (98.0%) (EG) were purchased from Fluka and used as received. Water was purified with a Milli-Q (Millipore) water purification system (18 μS).

2.2. Synthetic procedures

2.2.1. Synthesis of Iron Oxide Nanoparticles

For the detailed procedure see our preceding paper.⁴¹ The synthesis of iron oleate was carried out according to the published procedure.⁴² Iron oleate was then purified and dried for 24 h at room temperature and 20 h at 70 °C in a vacuum oven. Spherical iron oxide nanoparticles of various sizes were then prepared through thermal decomposition of iron oleate in the presence of oleic acid in docosane as solvent. The details of NP precipitation and purification are described in Part 1 of this work. Three NP samples have been used with the sizes 21.6 nm (NP1), 26.5 nm (NP2), and 19.3 nm (NP3), as measured using the TEM images (Figure 1).

Figure 1.

TEM images of 21.6 (a), 26.5 (b), and 19.3 (c) nm NPs.

2.2. Encapsulation of Iron Oxide Nanoparticles with PMAOD-PEG(EG)

In order to encapsulate the iron oxide NPs in PMAOD-PEG(EG), first the modified PMAcOD polymers were synthesized. Notations “P” and “G” are reserved for PMAOD-PEG(5,000) and PMAOD-EG, respectively. Mole ratios of 1:20 (P1, G1), 1:30 (P2, G2), 1:60 (P3, G3), and 1:80 (P4) of PMAOD to PEG or EG were used. The details of the modified PMAcOD synthesis and NP coating are described in the Part 1 of the present work.⁴⁰

1.3. Characterization

Electron-transparent specimens for TEM were prepared by placing a drop of a dilute solution onto a carbon-coated Cu grid. Images were acquired at an accelerating voltage of 80 kV on a JEOL JEM1010 transmission electron microscope. Images were analyzed with ImageJ software package to estimate NP diameters. Normally 150 to 300 NPs were used for analysis.

The synchrotron radiation X-ray scattering measurements were carried out in the European Molecular Biology Laboratory (EMBL) on the storage ring DORIS III of the Deutsches Elektronen Synchrotron (DESY, Hamburg) on the X33 camera with a MAR Image plate detector.⁴³ The scattering was recorded in the range of the momentum transfer 0.07 < s < 5.0 nm⁻¹, where s = (4πsinθ)/λ, 2θ is the scattering angle, and λ = 0.15 nm is the X-ray wavelength. All measurements were carried out in a vacuum cuvette when exposure times of 2 minutes were used to diminish the parasitic scattering. The scattering profiles were corrected for the background scattering from distilled water and processed using standard procedures.⁴⁴ The distance distribution functions p(r) and radii of gyration R_g of the iron oxide cores of the nanoparticles were calculated using an indirect transform program GNOM.⁴⁵

The interaction of the iron oxide cores in solution was analyzed using several approaches. The low-resolution shapes and internal structures of the NP cores were reconstructed ab initio from the scattering patterns using the program DAMMIN.¹⁵ Higher angle portions of the scattering data corresponding to the scattering from the individual NPs were employed for the shape reconstruction. The scattering amplitudes from DAMMIN models of the individual cores were computed using CRYSOL.⁴⁶ A simulated annealing protocol was employed to build the models of the NP clusters by SASREF¹⁶ minimizing discrepancy between the experimental scattering data and the curves calculated from the model assemblies at smaller scattering angles responsible for interparticle interactions. Multiple SASREF runs starting from different initial configurations were performed by varying the number of individual particles in the cluster.

The fractions of aggregates in the samples were estimated using the scattering intensity at zero scattering angle I₀ as is shown below:

$$\begin{array}{c}{I}_{0\mathit{mono}}\sim N_{\mathit{mono}}{(V_{\mathit{mono}})}^2,\\ (\mathrm{\Delta })=I_{0\mathit{whole}}-I_{0\mathit{mono}}=I_{0\mathit{clust}}=N_{\mathit{clust}}{(k\ast V_{\mathit{mono}})}^2,\end{array}$$

where I_0mono, I_0whole and I_0clust - the intensities at zero angle for the monodisperse fraction, entire sample and clusters (aggregates), respectively, N denotes the number of the objects, and V their volumes. The number of monomers in the cluster k can be estimated as k =(R_g/R_single)³, where R_g and R_single are the radii of gyration of the cluster and of the individual NP, respectively. Given that

$$N_{\mathit{mono}}/N_{\mathit{clust}}=k^2(I_{0\mathit{mono}}/I_{0\mathit{clust}}),$$

one obtains the estimate of the volume fraction of monomers

$$v_m=k(I_{0\mathit{mono}}/I_{0\mathit{clust}})/(1+k(I_{0\mathit{mono}}/I_{0\mathit{clust}})),$$

or their number fraction

$$n_m=k^2(I_{0\mathit{mono}}/I_{0\mathit{clust}})/(1+k^2(I_{0\mathit{mono}}/I_{0\mathit{clust}})),$$

3. Results and Discussion

The samples characterized by SAXS are listed in Table 1 (see also notations in the Experimental part). The characteristics of most of the NPs coated with modified PMAcOD are described in Part 1 of the present work.⁴⁰ The sample NP2-P4 has a larger diameter of the iron oxide core (26.5 nm), than that of NP3-P4 (19.3 nm) but the same stabilizing polymer to detect the influence of the NP size on the interparticle interactions. The other samples based on NP1 have the same iron oxide core size (21.6 nm) but are coated with different shells to reveal the effect of the properties of the protective coatings on the NP aggregation. The concentrations of the samples were kept low (in the range 0.05–0.15 mg/mL) to minimize NP interactions caused by the excluded volume effect.

Table 1.

The NP radii, their maximum sizes from SAXS, and the diameters from TEM

Sample	R=4.49/s1 (nm)	R=1.29Rsingle (nm)	Dmax (nm)	DTEM (nm)
NP1-P1	10.8±0.2	11.1±0.2	22.0±1.0	21.6
NP1-P2	10.7±0.2	11.1±0.2	22.0±1.0	21.6
NP1-P3	10.7±0.2	11.1±0.2	22.0±1.0	21.6
NP1-G2	10.8±0.2	11.1±0.2	22.0±1.0	21.6
NP1-G3	10.7±0.2	11.0±0.2	22.0±1.0	21.6
NP1-PMAcOD	10.7±0.2	11.1±0.2	22.0±1.0	21.6
NP2-P4	12.2±0.3	12.6±0.3	26.0±1.0	26.5
NP3-P4	9.7±0.1	10.0±0.2	19.5±1.0	19.3

The experimental scattering profiles from the samples in solution, shown in Figure 2, display distinctive maxima characteristic for largely monodisperse systems of spherical particles.

Figure 2.

Experimental SAXS profiles from iron oxide NPs in solution for NP1-PMAcOD (1), NP1-P3 (2), NP2-P4 (3), and NP3-P4 (4). The scattering curves from samples with different core sizes are displaced down by two logarithmic units for better visualization.

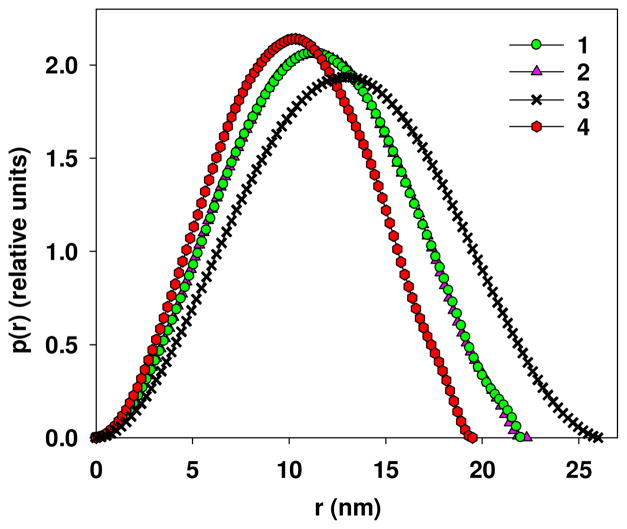
The scattering patterns from the group of samples NP1-PMAcOD, NP1-P1, NP1-P2, NP1-P3, NP1-G2 and NP1-G3 practically coincide with each other in the range of the maxima due to the spherical form factor. Only 2 out of 6 these scattering patterns are shown in Figure 2 as the most different. Experimental SAXS profiles from NP1-P1, NP1-P2, NP1-G2 and NP1-G3 are not shown being graphically indistinguishable in this region. However all curves of the group are slightly differ in the initial part of the experimental SAXS profile in the range of the momentum transfer 0.07 < s < 0.3 nm⁻¹ responsible for interparticle interactions. This observation indicates that the structures of the NPs are similar but their interactions in solution are different. The SAXS curves from NP2-P4 and NP3-P4 are significantly different from the others due to the difference of the iron oxide core sizes. The average particle radii R for all NPs were estimated from the position of the first minima s₁ as R= 4.49/s₁. Moreover, the distance distribution functions p(r) of the single NPs were evaluated using GNOM (Figure 3) from the higher angle portions of the data s > 0.3 nm⁻¹ to yield the maximum sizes of the NPs D_max and their radii of gyration R_single. The latter were employed to obtain an alternative estimate of the radii of the single NPs assuming that R_single² = 3/5 R² (Table 1).

Figure 3.

Distance distribution functions calculated by program GNOM from the experimental SAXS curves for NP1-PMAcOD (1), NP1-P3 (2), NP2-P4 (3), and NP3-P4 (4). Distance distribution functions for NP1-P1, NP1-P2, NP1-G2, and PN1-G3 are not shown because they coincide with the functions for NP1-PMAcOD (1) and NP1-P3 (2).

The obtained values correlate well with the TEM data. For the same size (samples based on NP1), they also agree well with each other within the experimental error. It should be noted that the SAXS derived sizes refer to the iron oxide cores only. These cores have much higher electron density contrast with respect to water than the protective shells, so that the latter remain practically invisible for the X-rays. Some differences in the radii of the iron oxide cores obtained from the first minima and those calculated from the radii of gyration occur due to possible presence of small amounts of some larger scattering objects because R_g is very sensitive to the presence of such objects.

Further analysis of the SAXS data was divided into two parts: (i) the determination of the structural characteristics of the individual NPs from the higher angle parts of the scattering data (s > 0.3 nm⁻¹), and (ii) the investigation of the particle interactions reflected by the initial portion of the scattering patterns. The structural models built at the first step were used to evaluate the NP behavior in solution at the second phase.

For this, the higher-angle portions of the scattering data corresponding to the particle form factor reflect the shape and the inner structure of the individual iron oxide cores, which can be reconstructed ab initio at low resolution. The distance distribution functions in Figure 3 were back transformed to extrapolate the form factor of the individual particle to zero angle scattering and the shape was further reconstructed by the program DAMMIN. The typical shapes of the iron oxide cores with different diameters represented by densely packed beads are shown in the inserts of Figure 4.

Figure 4.

Examples of the shape restoration for the cores with different diameters: (a) shape restoration for the cores with a diameter of 22.0 nm (NP1-PMAcOD, NP1-P1, NP1-P2, NP1-P3, NP1-G2, and NP1-G3); (b) shape restoration for the core with a diameter of 26.0 nm (NP3-P4); (c) shape restoration for the core with a diameter of 19.5 nm (NP3-P4). Curves: (1) the experimental data, (2) the GNOM curves extrapolated to zero angle, and (3) the scattering patterns computed from the bead model (all for the cores). Inserts: ab initio bead models reconstructed from the scattering data.

The scattering patterns computed from the bead models yield very good fits to the experimental data with discrepancy of about 2.0–3.0 for all the samples. All NPs display multilayered structure, reflecting the process of the formation of the iron oxide core from smaller nuclei as discussed in our preceding papers.^38,39 The ab initio models of the individual particles were further employed to determine the influence of the core sizes and the protective shell on the behavior of the magnetic NPs in solution. For this, the initial portions of the scattering patterns displayed in Figure 5a were analyzed, revealing information about the interparticle interactions.

Figure 5.

Comparison of the initial portion of the scattering profiles (a) and distance distribution functions calculated on the whole experimental curves: (b) for NP1-P3 (1), NP2-P4 (2), and NP3-P4 (3); (c) for NP1-PMAcOD (4), NP1-P1 (5), NP1-P2 (6), NP1-G2 (7), and NP1-G3 (8).

As one can see from Figure 5, the initial portions of the experimental scattering profiles in the range of the momentum transfer 0.07 < s < 0.3 nm⁻¹ can be divided into three groups. The first group (I), containing samples NP1-P3, NP2-P4, and NP3-P4, demonstrates distinct shoulders at about 0.10 – 0.20 nm⁻¹ reflecting interference between the particles and regularly spaced NPs (dynamic clusters) similar to those observed in our preceding papers.^38,39 The scattering curves from NP1-PMAcOD, NP1-P1 and NP1-P2 of the second group (II) display weak shoulders, whereas the scattering from the last group (III) of the samples NP1-G2 and NP1-G3 displays small interference effects. All these samples contain mixtures of individual nanoparticles, dynamic clusters and aggregates, but the fractions of these kinds of scattering objects are different in the different groups. To quantitatively assess the content of the three fractions we analyzed the behavior of the distance distribution functions p(r) calculated using the entire scattering curves (Figure 5b). These p(r) functions can be divided into the same three groups observed for the initial portion of the scattering patterns (Figure 5a). Considering the profiles of the p(r) functions, the largest contributions from the clusters or aggregates are present in the samples of the first group, while the samples of the third group contain mainly individual NPs with a small fractions of relatively small (presumably dimeric) aggregates. The amount of aggregates in each sample was quantitatively estimated using the scattering intensity at zero scattering angle I₀ as described in Experimental part and the results are presented in Table 2.

Table 2.

Contents of clusters (aggregates) in the samples

Samples	Group	Rg, (nm)	Dmax1 (nm)	k=(Rg/Rsingle)3a)	Vsingleb)	Nsinglec)
NP1-P3	I	16.5	50	7.1	0.83	0.97
NP2-P4		13.7	40	5.6	0.80	0.96
NP3-P4		17.3	55	5.2	0.82	0.96
NP1-P1	II	14.1	45	4.2	0.83	0.95
NP1-P2		13.4	45	3.5	0.84	0.95
NP1-PMAcOD	III	12.3	40	2.8	0.83	0.93
NP1-G2		9.9	35	1.5	0.83	0.88
NP1-G3		9.9	35	1.5	0.83	0.88

^a)R_g and R_single are the radii of the clusters and individual NPs, respectively, k is the number of individual nanoparticles in clusters or aggregates;

^b)volume fraction of individual NPs,

^c)number fraction of individual NPs. D_max1 is the maximum size of the clusters or aggregates in the system.

This table reveals the same separation of samples into three groups. The volume fractions of aggregates or clusters in all the samples are approximately the same, but their numerical fractions are different because of the different number of individual nanoparticles per cluster. Note that the employed estimate k=(R_clust/R_single)³ assumes shape similarity of the clusters and the individual NPs and gives only a rough (and usually somewhat overestimated) value, which is still sufficiently accurate for quantitative analysis. Although the value of k is the largest for the first group, the content of clusters and aggregates in the samples of the group still does not exceed 4%. This suggests that in this case the protective shell successfully prevents NPs from aggregation, and the shoulders at the small angles reflect mostly interference between the particles and an existence of the dynamic clusters. The samples of the second group demonstrate a larger amount (up to 5–7%) of aggregates and dynamic clusters. The last group (NP1-G2 and NP1-G3) contains a significant amount (12%) of relatively small structural formations consisting on average of two NPs (presumably, NP dimers) in addition to the individual nanoparticles. We believe the dimers can be considered as new structural formations (rather than aggregates) which have emerged due to specific interactions between their protective shells. Indeed, the distance distribution functions for these samples (Figure 5b) demonstrate a complete absence of larger aggregates, but the presence of some amount of double-sized nanoparticles (see the tails of the p(r) functions in the range of 25 – 35 nm) instead. It should be noted that concentrations of the samples were kept in the range 0.05–0.15 mg/mL, thus the effect of the excluded volume on the interparticle interactions can be completely neglected so the interactions in solution should be attributed solely to magnetic interaction of the iron oxide cores and to the properties of the protective shells.

The structures formed by the NPs due to the interparticle interactions were further characterized by rigid body modeling. The calculations were carried out in the range of scattering angles from 0.1 nm⁻¹ up to 0.4 nm⁻¹, i.e., at the very beginning of the experimental scattering curves containing the major information about the ensembles of individual NPs in solution. Figure 6 demonstrates the typical spatial models calculated by the program SASREF for the different groups of the specimens.

Figure 6.

Examples of structures of clusters and aggregates in different groups of specimens: I (NP1-P3, NP2-P4, and NP3-P4); II (NP1-PMAcOD, NP1-P1, and NP1-P2); III (NP1-G2 and NP1-G3).

The group I containing scattering from NP1-P3, NP2-P4, and NP3-P4 displays a regular structure of NPs with an equal distance between the nearest neighbors (dynamic clusters). The samples of the group have different core sizes, but practically equally dense and thick protective shells. These shells are formed by a comparatively dense brush of the 5,000 Da PEG tails on the PMAcOD chain (60–80% of all units are modified with a PEG tails). Therefore, the crucial factor determining the behavior of the NPs coated with the modified PMAcOD is the properties of the protective shells and not the size of the magnetic core, despite the fact that the larger the particles from the same material, the stronger the magnetic interactions. The thickness of the protective shell can be evaluated as half the distance between the NPs yielding about 1.4 – 1.5 nm. This value agrees with the minimal thickness of the NP shell determined by us in the preceding paper,³⁹ where a PEGylated phospholipid served as a stabilizing molecule. This thickness can account for strongly interdigitated hydrophobic tails but it does not take into consideration the PEG tails. The latter are apparently squeezed out of the interparticle space of the dynamic clusters.

The group II (NP1-P1, NP1-P2, and NP1-PMAcOD) demonstrates stronger interparticle attraction: in this case average distance between closely located NPs is about 1.0 – 1.2 nm, which demonstrates not only squeezing out of the PEG tails, but also distortion of the hydrophobic bilayer. Here the PEG brush is significantly less dense with 20% (NP1-P1) or 30% (NP1-P2) of maleic anhydride units containing a PEG tail. Besides dynamic clusters, there also exists apparently a significant amount of aggregates in solution. This is easily explained by the way of stabilization of these particles. Indeed, PMAcOD coated NPs are stabilized purely due to electrostatic interactions. This allows for a good stabilization due to electrostatic repulsion but the shell is so thin, that permanent aggregation is also possible (although the degree of the aggregation is low). NP1-P1 (20% PEG tails) and NP1-P2 (30% PEG tails) have a lower negative charge (see Part 1 of the present work,⁴⁰ Table 2) than NP1-PMAcOD, but higher steric stabilization, thus they may form both dynamic clusters and aggregates.

The rigid body analysis of all the scattering profiles was performed with the minimum amount of NPs sufficient to fit the scattering data. For the two preceding groups, three particles had to be taken into account. The data from the last group (NP1-G2 and NP1-G3) could be well fitted by dimeric dumb-bell structure (Figure 6, III) suggesting the presence of permanent dimeric structural formations, coexisting with individual nanoparticles. It is noteworthy that G2 and G3 copolymers have a smaller charge than that of PMAcOD, thus electrostatic stabilization decreases, but the grafted tails are very short, so the steric stabilization is not realized. On the other hand, the addition of two hydroxyl groups per each G tail allows for a higher hydrophilicity, but also additional hydrogen bonding between the adjacent shells. Apparently this combination leads to dumbbell structures. At the same time, the solutions of NP1-G2 and NP1-G3 demonstrate the lowest content of large conglomerates to compare with the groups I and II.

In general, the independent rigid body analysis fully confirmed the results obtained when considering the behavior of the distance distribution functions and the initial portions of the scattering profiles.

4. Conclusions

The structural analysis performed to understand the influence of the type of the magnetic NP shell on the solution behavior of NPs in water revealed a dependence of the NP aggregation on the type of the grafted tails and the grafting density of the modified PMAcOD. The negatively charged NPs protected by the modified copolymers of the P and G series showed only a small amount of real aggregates and high stability of individual NPs in aqueous solutions, the solution behavior which is important for practical applications of magnetic NPs. Nevertheless, there are differences between the NP specimens depending on the protective shell. The detailed analysis carried out by independent methods demonstrated that the NP coating by modified PMAcOD with a high degree (60–80%) of grafted 5,000 Da PEG tails leads to minimal aggregation in solution. Moreover, in this case, dynamic clusters prevail over the permanent aggregates. These properties along with the NP stability in buffers⁴⁰ make them good candidates for medical and biological applications.

Decreasing the shell density (and, accordingly, its thickness) with the same type of grafted tails (P series) leads to more aggregates and to a poorer stabilization. However, when the modification of PMAcOD is done using the short ethylene glycol tails (G series), the behavior of the NPs in solutions changes dramatically. We observed formation of dumbbell structures, which coexisted with individual iron oxide NPs, thus these solutions contained two kinds of practically monodisperse objects. As was shown in Part 1 of the present work,⁴⁰ for the G and PMAcOD coatings approximately 400 molecules need to be attached to a single NP to ensure its stability in water, while the P coatings are successful only with approximately 20 macromolecules, emphasizing the importance of PEG tails in NP hydrophilization. On the other hand, the thin G coating, with a balance of decreased negative charges, possible additional hydrogen bonding, and increased hydrophilicity due to two hydroxyl groups per each G tail allows one to produce solutions of magnetic NPs with the lowest content of large conglomerates.