Distance Matrix-Based Approach to Protein Structure Prediction

Abstract

Much structural information is encoded in the internal distances; a distance matrix-based approach can be used to predict protein structure and dynamics, and for structural refinement. Our approach is based on the square distance matrix D = [r_ij²] containing all square distances between residues in proteins. This distance matrix contains more information than the contact matrix C, that has elements of either 0 or 1 depending on whether the distance r_ij is greater or less than a cutoff value r_cutoff .We have performed spectral decomposition of the distance matrices $\mathbf{D}=\sum {\lambda }_k{\mathbf{V}}_k{\mathbf{V}}_k^T$ , in terms of eigenvalues λ_k and the corresponding eigenvectors v_k and found that it contains at most 5 nonzero terms. A dominant eigenvector is proportional to r² - the square distance of points from the center of mass, with the next three being the principal components of the system of points. By knowing r² we can approximate a distance matrix of a protein with an expected RMSD value of about 4.5Å. We can also explain the role of hydrophobic interactions for the protein structure, because r is highly correlated with the hydrophobic profile of the sequence. Moreover, r is highly correlated with several sequence profiles which are useful in protein structure prediction, such as contact number, the residue-wise contact order (RWCO) or mean square fluctuations (i.e. crystallographic temperature factors). We have also shown that the next three components are related to spatial directionality of the secondary structure elements, and they may be also predicted from the sequence, improving overall structure prediction. We have also shown that the large number of available HIV-1 protease structures provides a remarkable sampling of conformations, which can be viewed as direct structural information about the dynamics. After structure matching, we apply principal component analysis (PCA) to obtain the important apparent motions for both bound and unbound structures. There are significant similarities between the first few key motions and the first few low-frequency normal modes calculated from a static representative structure with an elastic network model (ENM) that is based on the contact matrix C (related to D), strongly suggesting that the variations among the observed structures and the corresponding conformational changes are facilitated by the low-frequency, global motions intrinsic to the structure. Similarities are also found when the approach is applied to an NMR ensemble, as well as to atomic molecular dynamics (MD) trajectories. Thus, a sufficiently large number of experimental structures can directly provide important information about protein dynamics, but ENM can also provide a similar sampling of conformations. Finally, we use distance constraints from databases of known protein structures for structure refinement. We use the distributions of distances of various types in known protein structures to obtain the most probable ranges or the mean-force potentials for the distances. We then impose these constraints on structures to be refined or include the mean-force potentials directly in the energy minimization so that more plausible structural models can be built. This approach has been successfully used by us in 2006 in the CASPR structure refinement (http://predictioncenter.org/caspR).

Introduction

Mathematical approach to studies of various protein properties by the analysis of the corresponding matrices has been quite popular in bioinformatics. In our earlier work we tried to approximate 20×20 dimensional matrices corresponding to contact potentials by 20-dimensional vectors of various physical properties of amino acids by using a simple linear c₀ + x_i + x_j and quadratic functions c₀ + x_ix_j + y_iy_j of two amino acid properties x and y.(Pokarowski et al., 2005) We analyzed 29 different matrices of contact potentials published in literature. We used AAindex database of over 500 amino acid indices collected by Kanehisa(Kawashima et al., 2000;Kawashima et al., 2008) http://www.genome.jp/aaindex/ and have found that all matrices of contact potentials can be approximated with correlation 0.9 by hydrophobicities and isoelectric points of amino acids. A dominant role of hydrophobicity in interactions among residues in proteins has been already well known, and our study have shown that isoelectric points, that measure electric charges of various amino acids are also important for contact potentials. We have found two classes of contact potentials. The first class of contact potentials can be approximated by a linear combination of hydrophobicities. Major contribution comes from the one body transfer energy of amino acids from water to protein environment. The second class of contact potentials can be approximated by a quadratic function of hydrophobicities and isoelectric points of amino acids. Potentials of this class represent energies of contact of amino acid pairs within an average protein environment.

In our later work we have extended our method to substitution matrices.(Pokarowski et al., 2007) We have analyzed 29 different substitution matrices known in the literature, plus 5 statistical contact potentials. We found that substitution matrices can be approximated with correlation 0.9 by a quadratic expression c₀ + x_ix_j + y_iy_j + z_iz_j with vectors x, y and z corresponding to hydrophobicity, molecular volume, and coil preferences of amino acids. We also found that some substitution matrices correlate well with contact potentials.

In our present work we apply a similar approach to matrices containing structural information for proteins. We try to express these original matrices in terms of their eigenvectors, try to connect these eigenvectors with physical properties of amino acids and predict them from the amino acid sequence. Our work was motivated by a recent work of Vendruscolo(Bastolla et al., 2005) who found that the eigenvector corresponding to the dominant eigenvalue of the contact matrix in proteins correlates well with the vector of hydrophobicities of the amino acid sequence. We show that the structural matrices relate to experimental B-factors (temperature factors) that measure thermal fluctuations of atoms around their mean positions in crystals (for X-ray determined structures) or in solution (for NMR-determined structures). We discuss elastic network models of proteins that mathematically relate contact matrices to mean square fluctuations of residues. We show that motions of amino acids in proteins computed from elastic network models better fit NMR-determined. Finally we discuss methods of refinement of protein structures based on libraries of interatomic distances in proteins, and propose a new optimization method of solving a generalized distance geometry problem for determination of NMR structures by using B-factors.

METHODS

Matrices containing structural information

There are several different matrices that contain structural information for proteins. The most common is the distance matrix

$$\mathbf{d}=\left({\text{d}}_{\text{ij}}\right)$$ (1)

where the ij-the element of the matrix is the distance d_ij between residues i and j. Usually the distance is measured between the C^α atoms of the residues, although other definitions of distances, such as: the distance between the centers of side chains of the amino acids, or the distance between the closest heavy atoms of the two residues, are also popular.

Distance matrices have been used for a long time in structural bioinformatics mostly for protein structure comparison and alignment and for inferring protein-protein interactions(Choi et al., 2004;Domingues et al., 2007;Godzik et al., 1993;Heger et al., 2004;Holm et al., 2000;Huang et al., 2006;Jaroszewski et al., 2002;Kolodny et al., 2004;Mooney et al., 2005;Pazos et al., 2008;Rodionov et al., 1992;Sato et al., 2005;Sato et al., 2006;Schneider, 2000;Snyder et al., 2005a;Snyder et al., 2005b;Szustakowski et al., 2000;Ye et al., 2004;Zhou et al., 2006). In particular Snyder and Montelione used this approach for identification of core atom sets and for the assessment of the precision in NMR-derived protein structure ensembles.(Snyder et al., 2005a)

From the mathematical point of view it is easier to deal instead of distances with their squares. Because of this we define the matrix of square distances

$$\mathbf{D}=\left({{\text{d}}_{\text{ij}}}^2\right)$$ (2)

containing information about square distances d_ij between amino acids i and j. All diagonal elements of the distance matrix d and the square distance matrix D are zeros.

Another matrix that is very popular in computational biology and contains significantly less information than the distance matrix is the contact matrix

$$\mathbf{C}=\left({\text{c}}_{\text{ij}}\right)$$ (3)

with elements c_ij defined as:

$$\begin{array}{cc}\hfill {\text{c}}_{\text{ij}}=1& \text{if}{\text{d}}_{\text{ij}}\le {\text{d}}_{\text{cutoff}}\hfill \\ \hfill {\text{c}}_{\text{ij}}=0& \text{otherwise}\hfill \end{array}$$ (4)

Here d_cutoff is the cutoff distance defining residues being in contact.

Laplacian of C that is frequently called the Kirchhoff matrix is defined

$${\mathbf{L}}_{\text{c}}=\mathbf{diag}\left(\Sigma {\text{c}}_{\text{ij}}\right)-\mathbf{C}$$ (5)

The diagonal elements of L_c are the sums of its off-diagonal elements taken with the negative sign. Because of such definition the sums of all elements in each row or column are zero and the determinant of L_c is zero, i.e. the matrix is singular and has no inverse. We may however, define a generalized inverse (pseudoinverse that might be right or left) L_c⁻¹ of the Laplacian matrix L_c. Such generalized inverse L_c⁻¹ of the Laplacian of the contact matrix is introduced in elastic network models of proteins (described in detail in the next section) and its elements represent covariances between instantaneous fluctuations of residues i and j.

Similarly we can define Laplacian of the matrix of square distances D:

$${\mathbf{L}}_{\text{D}}=\mathbf{diag}\left(\Sigma {{\text{d}}_{\text{ij}}}^2\right)-\mathbf{D}$$ (6)

and its generalized inverse L_D⁻¹.

Elastic Network Models of proteins

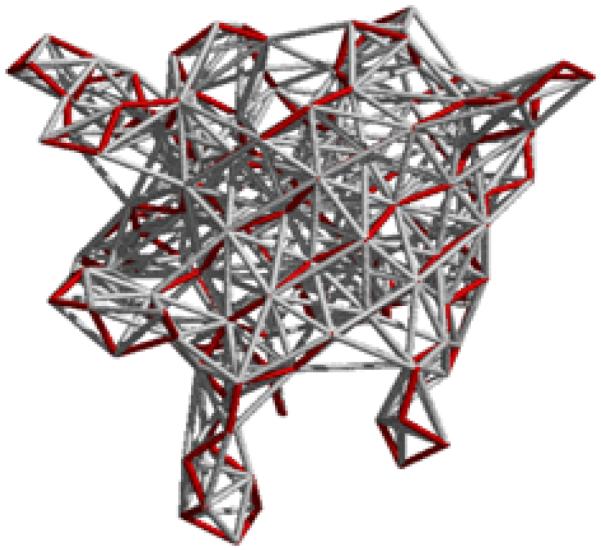
Elastic network models treat proteins as elastic bodies. A coarse-grained representation of proteins with a single site per residue is usually used. Positions of these sites are generally identified with the coordinates of the C^α atoms in proteins. Residues separated by a distance less than or equal to a certain cutoff value R_c (including neighbors along the sequence) are assumed to be in contact, and are connected with identical mass-less harmonic springs. This leads to an elastic network representation of a protein structure in the folded state that resembles a random polymer network. Fig. 1 illustrates the basic idea of this model.

Fig. 1.

Beads and springs representation of proteins in elastic network models. Protein backbone is shown in red.

The simplest of the elastic network models is Gaussian Network Model (GNM). This model was originally developed for the theory of rubber-like elasticity of random polymer networks (Flory, 1976;Kloczkowski et al., 1989) to calculate fluctuations of junctions and chains inside the network. The model was adapted to proteins by Bahar and Erman (Bahar et al., 1997;Haliloglu et al., 1997) using an earlier result of Tirion (Tirion, 1996) who used a single harmonic force parameter to analyze atomic motions in proteins.

The total potential energy for the network composed of N nodes is

$${\mathit{V}}_t=\frac{1}{°2}\gamma \sum _{i<j}^N{{(}_i\Delta R_j)}^2{H}_c(R_i-R_j)$$ (7)

where γ is a uniform universal spring constant, and H(x) is the Heaviside step function that equals 1 if x > 0, and is zero otherwise. Here $\Delta {\mathit{R}}_{ij}={\mathit{R}}_{ij}-{\mathit{R}}_{ij}^0$ is the instantaneous displacement of the distance vector R_ij between the ith and the jth sites from the mean value ${\mathit{R}}_{ij}^0$ observed in the native structure. Eq. 7 can be rewritten in the following form

$${\text{V}}_{\text{tot}}=(\gamma ∕2){\left\{\Delta \mathit{R}\right\}}^T\Gamma \left\{\Delta \mathit{R}\right\}$$ (8)

where Γ is the Kirchhoff matrix of size N×N, defined on the basis of the cutoff distance R_c , with off-diagonal elements ij being either -1 if nodes i and j are in contact or zero otherwise, and the diagonal elements are defined as the sum of the off-diagonal elements in the i-th row (or column) taken with a negative sign. Mathematical definition of the Kirchhoff matrix was given earlier by Eq. 5. Kirchhoff matrices were introduced first in physics to study electric currents in networks. Similarly as for electrical circuits where all currents at a given node sum up to zero, for a system of connected springs forming a network a sum of elastic forces at each node is zero. The matrix is equivalent to the Laplacian L_c of the contact matrix in Eq. 5. Here {ΔR} is the N-dimensional fluctuation vector ΔR = col (ΔR₁,ΔR₂,… ,ΔR_N) of ΔR_i for all N nodes, and the superscript T denotes the transpose. We should note that

$$\Delta {\mathit{R}}_i={\Delta }_j\mathit{R}{-}_i\Delta {\mathit{R}}_j$$ (9)

Then the average changes in positions, given either as the correlation < ΔR_i · ΔR_j > between the displacements of pairs of residues i and j or as the mean-square fluctuations < (ΔR_i)² > = < ΔR_i · ΔR_i > for a single residue i, are

$$<\Delta {\mathit{R}}_i\cdot \Delta {\mathit{R}}_j>=\frac{\int (\Delta {\mathit{R}}_i\cdot \Delta {\mathit{R}}_j)\text{exp}(-V_{tot}{k}_B∕T)d\left\{\Delta \mathit{R}\right\}}{\int \text{exp}(-V_{tot}∕k_{B}T)d\left\{\Delta \mathit{R}\right\}}\text{for all i,j}$$ (10)

This can be rewritten (Flory, 1976) in a simple form as

$$<\Delta {\mathit{R}}_i\cdot \Delta {\mathit{R}}_j>=\frac{3k_{B}T}{2\gamma }{\left({\Gamma }^{-1}\right)}_{ij}$$ (11)

where (Γ⁻¹)_ij is the ij-th element of the inverse of the Kirchhoff matrix Γ, k_B is the Boltzmann constant, T is the absolute temperature, and γ is a spring constant. Mean-square fluctuations < (ΔR_i)² > of the i-th residue in a protein are given by the i-th diagonal element of $\underset{\cdot }{\Gamma }{}^{-1}$. Since the Laplacian matrix Γ is singular because det( Γ) = 0 only the pseudoinverse of Γ can be computed through the use of the singular value decomposition method. The pseudoinverse of Γ may be written as Γ⁻¹ = U(Λ⁻¹)U^T where U is the matrix composed of eigenvectors u_i (1 ≤ i ≤ N) of Γ, and Λ is the diagonal matrix of the eigenvalues of Γ. Additionally, it can be proven that all eigenvalues λ_i of Γ are non-negative.

Mean-square fluctuations of the position of each C^α computed from Eq. 11 can be compared with the Debye-Waller thermal factors, which are measured by X-ray crystallography and deposited in the Protein Data Bank. The relationship between the B-factor and the mean square fluctuations for the i-th residue is given by

$$B_i=8{\pi }^2<{\left(\Delta R_i\right)}^2>∕3$$ (12)

The B-factors computed by GNM usually are in excellent agreement with experimental data (Kundu et al., 2002;Sen et al., 2006).

The Gaussian Network Model is based on the assumption that all instantaneous fluctuations are isotropic. A more sophisticated elastic network model of proteins is the Anisotropic Network Model (ANM).(Atilgan et al., 2001) Eq. 8 is then replaced by

$$V=(1∕2)\Delta {\mathbf{R}}^{\mathbf{T}}\mathbf{H}\Delta \mathbf{R}$$ (13)

where ΔR is the 3N-dimensional vector of fluctuations, ΔR^T its transpose and H is the (3N×3N) Hessian matrix, whose elements are the second derivatives of the total potential energy with respect to the Cartesian coordinates of the i^th and j^th nodes.

Spectral decomposition of structural matrices

Decomposition of matrices is a standard algebraic procedure to factorize them into a canonical form. There are various different methods of decomposition, such as for example LU decomposition where the original matrix is expressed a product of a lower triangular matrix L and an upper triangular matrix U. Decomposition based on eigenvalues of a square matrix A is called eigendecomposition or spectral decomposition. It allows us to express the original square matrix A of size in N×N terms of its eigenvalues λ_k and corresponding eigenvectors ν_k

$$A=\sum _k{\lambda }_k{\nu }_k{\nu }_k^T$$ (14)

The inverse matrix A⁻¹ is then expressed by the same Eq. 14 with eigenvalues λ_k replaced by their inverses λ_k⁻¹. In mathematical problems related to system dynamics the eigenvalues correspond to frequencies of motions that are called modes.

The matrix Γ⁻¹ for the Gaussian Network Model can be written as the sum of contributions from individual modes:

$${\Gamma }^{-1}=\sum _k{\gamma }_k^{-1}{\mathit{u}}_k{\mathit{u}}_k^T$$ (15)

where zero eigenvalues of the Kirchhoff matrix Γ (related to rigid body motions of the center of mass of the system) are excluded from the summation. The i-th component of the eigenvector u_k specifies the magnitude of fluctuations of the i-th residue in the protein in the k-th mode. If we order the eigenvalues according to their ascending values starting from zero, then the most important contributions to Γ⁻¹ in Eq. 15, and therefore (because of eqs 11-12) also to temperature factors are given by the smallest non-zero eigenvalues λ_k of Γ that correspond to the large-scale slow modes. The slowest modes play a dominant role in the fluctuational dynamics of protein structures, because their contributions to the mean-square fluctuations scale with λ_k⁻¹. It has been shown that the most important functional motions of proteins (Keskin et al., 2002a;Keskin et al., 2002b;Navizet et al., 2004) or large biological structures (such as the ribosome (Wang et al., 2004;Wang et al., 2005;Yan et al., 2008)) correspond only a few of the slowest modes derived from the GNM.

To calculate the normal modes for the Anisotropic Network Model, the Hessian matrix H is diagonalized to the canonical form S^THS=Λ , where Λ is a (3N×3N) diagonal matrix with diagonal elements corresponding to eigenvalues (λ₁,…, λ_3N) and S is an orthogonal (3N × 3N) matrix (i.e. S^TS = I) built from eigenvectors.

The mean-square fluctuations of the residue i can be expressed as a sum over all normal modes (except the first six zero modes that corresponds to translations and rotations of the system) as

$$\langle {\left(\Delta {\mathbf{R}}_i\right)}^2\rangle =(k_{B}T∕\gamma )\sum _{l=1}^{3N-6}\frac{{S_{il}}^2}{{\lambda }_1}$$ (16)

where $\langle {\left(\Delta {\mathbf{R}}_i\right)}^2\rangle$ are the mean-square fluctuations of residue i.

Structure Determination and Refinement Using Distances

We consider a problem of the determination of a structure or an ensemble of structures for a protein with a given set of inter-atomic distances or their ranges. This problem arises in modeling proteins using NMR distance data. Mathematically, it requires the solution for a nonlinear system of equations or inequalities. Let x_i = (x_i1,x_i2,x_i3)^T be the coordinate vector of atom i; (i = 1, …, n), with n being the total number of atoms in the protein. The problem can be formulated to find x_i, i = 1, …, n such that

$$\parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel =d_{i,j},(i,j)\in S\subset D=\{(i,j):i=1,\dots ,n,j>i\}$$ (17)

where d_i,j are the given distances between atoms i and j or

$$l_{i,j}\le \parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel \le u_{i,j},(i,j)\in S\subset D=\{(i,j):i=1,\dots ,n,j>i\}$$ (18)

Here l_i,j and u_i,j are the given lower and upper bounds on d_i,j, respectively.

The problem formulated in Eq. 17 has been studied in several fields and has many applications. It is called the distance geometry problem in mathematics, the multidimensional scaling problem in statistics, and the graph embedding problem in computer science. Distance geometry methodology for proteins has been developed 30 years ago by Havel and Crippen. (Crippen et al., 1978;Havel et al., 1979;Havel et al., 1983a;Havel et al., 1983b;Havel et al., 1983c)

The problem can be solved in polynomial time by using for example the well-known singular value decomposition algorithm if the distances for all the pairs of atoms in the protein are given, but it is NP-hard for an arbitrarily given subset of all the distances. The problem defined in eq. 18 has a particular application in NMR protein modeling, where only a lower and upper bound can be estimated for a distance. A set of solutions can be obtained for this problem, which corresponds to an ensemble of structures, all satisfying the given distance constraints. It is of great practical interest to obtain the whole ensemble of structures, since it shows how a structure may change dynamically given the possible ranges of their distances. However, the problem to obtain the whole solution set, even for a linear system of inequalities, is NP-hard.

Heuristic methods have been developed for the solution of the first problem (Eq. 17), and been extended to the solution of a generalized problem (Eq. 18). A common approach to the later (Eq. 18) is to generate repeatedly a set of distances within the given distance ranges, and solve Eq. 17 with the generated distances. In the end, a set of solutions is obtained that represents the whole solution set for the problem defined by Eq. 18. The obtained solutions form an ensemble of structures. They can be put together to show how they deviate from each other at different times. A long-standing issue with this approach is that the solution set for Eq. 18 is often underdetermined or not well represented by the obtained solutions, and therefore, the ensemble of structures cannot fully reflect the dynamic behavior of structures. Besides, solving Eq. 17 for each generated set of distances can be very costly.

RESULTS

Spectral decomposition of a square distance matrix

The eigenvalue spectrum of contact matrices or Laplacian (Kirchhoff) matrices is rather complex, with only one eigenvalue out of N being zero for GNM, and six out of 3N being zero for ANM. In the case of the square distance matrix D (Eq. 2) the eigenspectrum is much simpler. Spectral decomposition of a square distance matrix is a complete and simple description of a system of points and has at most 5 nonzero, interpretable terms: A dominant eigenvector associated with the dominant eigenvalue is proportional to r² - the square distance of points to the center of the mass, and the next three are principal components of the system of points. It can be shown that these principal components are related to the directionality of the secondary structure elements. This means that the square distance matrix D that contains almost complete information about protein structure (except impossibility to distinguish protein from its mirror image) can be completely reconstructed from the dominant r²-related eigenvector and three eigenvectors corresponding to the principal components.

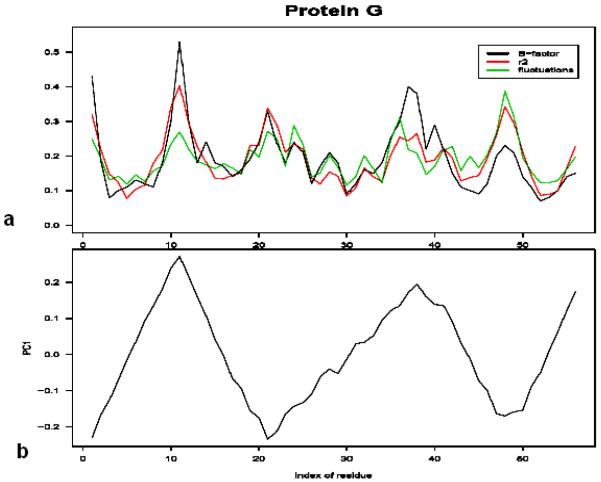
To illustrate relationships with the square distance of residues from the center of mass and the secondary structure let us consider protein G. Fig. 2a shows the plots of experimental B-factors of C^α atoms measured by the X-ray crystallography (shown in black), mean-square fluctuations computed from the Gaussian Network Model, and the values of the square distance of C^α atoms from the protein center of mass plotted vs. the residue index. We see that r² correlates with B-factors better than predictions provided by elastic network model. Fig. 2b shows the plot of the first principal component vs. the residue index for protein G. The relation with directionality of the secondary structure elements is obvious if we compare Fig. 2 with Fig. 3 that shows protein G oriented in the direction of the first principal component.

Fig. 2.

a) The plot experimental B-factors (black), fluctuations computed from Gaussian Network Model (green), and the square of the distance from the center of mass (red) vs. the residue index for protein G. b) The plot of the first principal component vs. residue index for protein G.

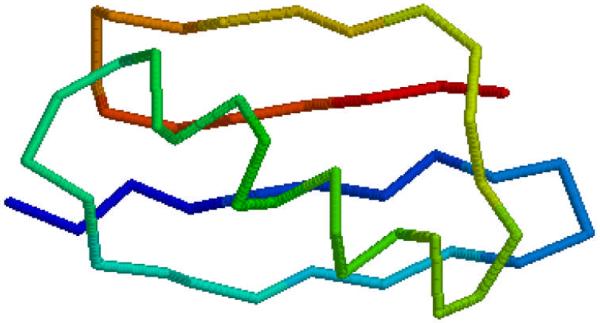
Fig. 3.

Structure of protein G in the direction of the first principal component

The first principal component (Fig. 2b) increases as the residue index follows the direction of the secondary structure in proteins (Fig. 3), when the secondary structure reverses its direction the principal components starts decreasing, etc. In the case of the second (or the third) principal component the relationship between the values of these components and orientation of the secondary structure in the direction of the principal component (Fig. 4) is much more difficult to visualize.

Fig. 4.

Structure of protein G in the direction of the second principal component

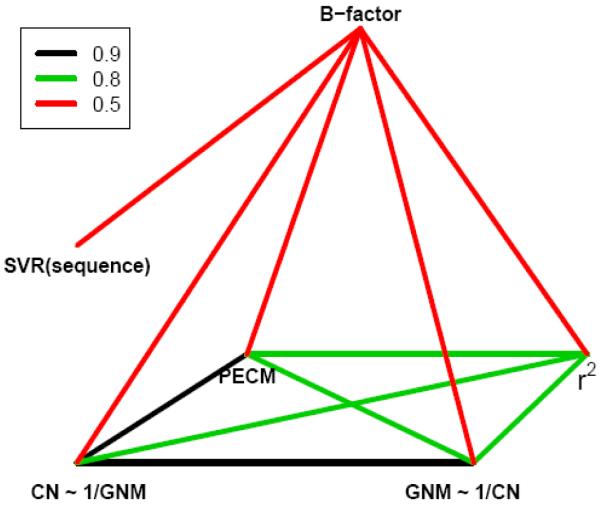
We used a nonredundant database of 680 structures derived from the ASTRAL database and computed average correlations between experimental B-factors and various theoretically computed quantities, as well as correlations among them. We analyzed the square distance of each residue from the center of mass (r²), principal eigenvector of the contact matrix (PECM), contact number (the number of residues being in contact) for each residue (CN), and mean-square fluctuations computed from the Gaussian Network Model (GNM). We tried also to predict B-factors from the sequence alone using Support Vector Regression (SVR) that is a variant of Support Vector Machines for continuous variables. The results of our computations are shown in Fig. 5. Highest correlations of the order 0.9 are shown in black, correlations 0.8 are shown in green, and correlations of order 0.5 are shown in red. We see that all four quantities (r², PECM, CN and GNM) are very well correlated with each other. Especially the correlations between the fluctuations predicted from GNM and the inverse of the contact number CN, or PECM are surprisingly high (0.9). Accuracy of predictions of experimental B-factors from the sequence alone using SVR is almost the same (~0.5) as for predictions based on structural information contained in the contact matrix. (for GNM, CN and PECM), or in the square distance matrix (for r²).

Fig. 5.

Correlations among experimental B-factors, contact numbers (CN), principal eigenvectors of the contact matrix PECM, square distances from the center of mass r², and predictions of GNM. Support Vector Regression (SVR) predictions of B-factors from the sequence alone are also shown. The extent of correlations is illustrated by colors.

Some of these observations have been already reported in literature. In 1980 Petsko found that crystallographic B-factors correlate with the distances of residues from the center of mass r² .(Petsko et al., 1980) Correlations between fluctuations of residues and the inverse of their contact numbers have been pointed out by Halle in 2002.(Halle, 2002) Prediction of B-factors from the sequence using SVM was recently reported.(Chen et al., 2007)

Approximation of distance matrices

We tried to reconstruct the original structure described by the square distance matrix by using eigenvalue decomposition (eq. 14). The inclusion of all four terms in the summation in Eq. 14 gives to the original square distance matrix. By using only the first term related to the dominant eigenvector, or the first two terms (the dominant eigenvector and the first principal component) we can assess the contribution of these terms to the reconstruction of the original square distance matrix from the eigenvalue decomposition. The computations were performed on our nonredundant database of 680 structures derived from the ASTRAL database. We found that the dominant eigenvector r² alone approximates protein structures with average RMSD 7.3 Å. However if we used two terms in eq. 14 by combining r² with the first principal component the original structures were approximated with much better RMSD 4.0 Å. Addition of the second principal component would of course additionally improve these approximations. Since both r² and the first principal component can be predicted from the sequence alone, that allows us to predict the tertiary structure of proteins with RMSD better than 4.0 Å from the sequence. Such predictions can be based only on the predicted distances of residues from the center of mass, and prediction of the secondary structure elements and their orientation in space. We are currently working on this problem by using Support Vector Regression.

Principal Component Analysis of Multiple HIV-1 Proteases Structures

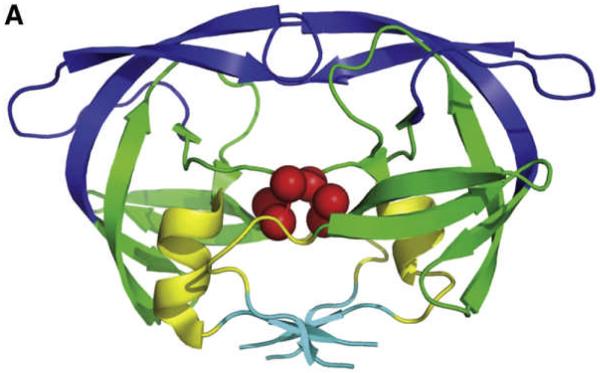
We used 164 X-ray-determined and 28 NMR-determined structures of HIV-1 proteases deposited in PDB structures.(Yang et al., 2008) Fig. 6 shows the structure of HIV-1 protease. We used also 10,000 structures (snapshots) obtained from the Molecular Dynamics simulations of HIV-1 protease. We performed the Principal Component Analysis of the structural matrices for all these three different datasets. Then we compared the results of Principal Component Analysis with normal modes computed from the Anisotropic Network Model. We computed the overlap (measured as the dot products of vectors) between directions of motions computed from ANM and principal components for X-ray determined structures and NMR-determined structures for first few slowest modes. The results are shown in Table 1.

Fig. 6.

The α-carbon trace of the HIV-1 structure

Table 1.

Overlap between ANM directions of motions and principal components

	X-Ray			NMR
	Mode 1	Mode 2	Mode 3	Mode 1	Mode 2	Mode 3
PC1	0.06	0.06	0.24	0.25	0.91	0.02
PC2	0.07	0.04	0.64	0.88	0.28	0.04
PC3	0.46	0.53	0.13	0.02	0.05	0.30

Table 1 suggests that MNR-determined structures fit predictions of elastic network models better than X-ray-determined structures. This idea was further evidenced after the computation of the cumulative overlap (a sum of overlaps for the first k-modes), shown in Table 2.

Table 2.

Cumulative overlap between directions of motions and principal components

	X-Ray			NMR
	PC1	PC2	PC3	PC1	PC2	PC3
3 modes	0.25	0.65	0.71	0.94	0.92	0.31
6 modes	0.25	0.65	0.74	0.95	0.94	0.35
20 modes	0.32	0.69	0.84	0.96	0.95	0.46

NMR-derived structures fit prediction of Anisotropic Network Model much better than X-Ray-derived structures. A possible explanation is that NMR experiments enable us to study single isolated molecules in solution, and elastic networks are basically also single molecule models, whereas in X-ray crystallography motions of protein residues are affected by interactions with the rest of the crystal lattice.

An Optimization Approach for Structure Determination and Refinement Using Distances

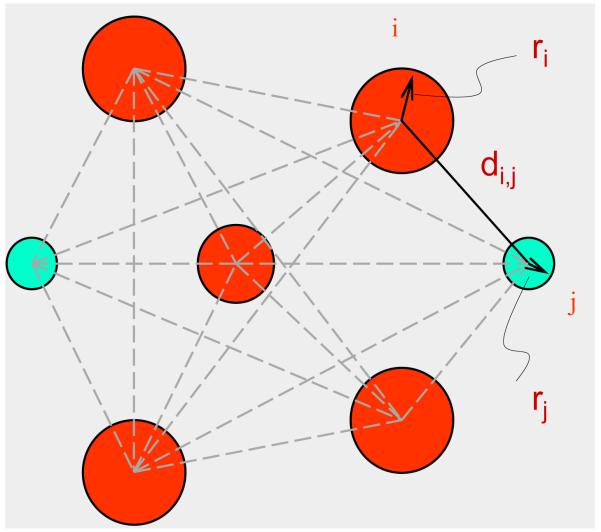
We propose a new model for the solution of the problem defined by Eq. 17 by making a similar assumption as in X-ray crystallography that a protein has an equilibrium structure and the atoms fluctuate around their equilibrium positions. These thermal fluctuations are represented by the B-factors in the X-ray crystal structure. With this model, we can then reformulate the problem for determining an ensemble of structures for a given set of distance ranges as an optimization problem, i.e., to find the equilibrium positions and maximal possible fluctuation radii for the atoms in the protein, subject to the condition that the fluctuations should be within the given distance ranges (see Fig. 7). Let r_i be the fluctuation radius of atom i.

Fig. 7. Protein Model.

A protein is assumed to have an equilibrium structure and the atoms fluctuate around their equilibrium positions (as represented by the B-factors in an X-ray crystal structure).

Then, the problem can be written as to find x_i and r_i, i = 1, …, n such that we maximize the total volume of spheres corresponding to fluctuations of atoms, subject to the lower and upper distance constraints imposed on interatomic distances:

$$\begin{array}{cc}\hfill \underset{x_i,r_i}{\text{max}}& {\Sigma }_{i=1}^n{r}_i^3\hfill \\ \hfill \text{subj.}& \parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel +r_i+r_j\le u_{i,j}\hfill \\ \hfill & \parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel -r_i-r_j\ge l_{i,j},(i,j)\in S\hfill \\ \hfill & r_i\ge 0,i=1,\dots ,n.\hfill \end{array}$$ (19)

We call this problem a generalized distance geometry problem. This problem is not exactly equivalent to Eq. 18, but the solution of the problem can provide a meaningful description for the structure to be determined and its dynamic behavior. Moreover, the formulation given by Eq. 19 has many advantages over Eq. 18. First, it is a much better defined problem, because it requires only a single solution rather than a solution set. Second, it is computationally more tractable because there are well-developed methods for solving optimization problems. Third, the solution of the problem can deliver an NMR structure in a similar form as an X-ray crystal structure, with a single structural file containing the coordinates and fluctuation radii (or B-factors) for the atoms. These advantages make it possible for us to develop an efficient algorithm for the determination of a structure using a set of distance data and improve the way to represent a structural ensemble in NMR modeling.

A Buildup Algorithm

In practice, there can be more than tens of thousands of variables and constraints for the problem in Eq. 19. A constrained optimization problem of such complexity can still be very difficult to solve. We therefore propose a novel so-called buildup algorithm for the solution of the problem. The idea of this algorithm is to determine the coordinate vectors and fluctuation radii of the atoms, one at a time, using the distance constraints from the determined atoms to the undetermined ones. Let x_j and r_j be the coordinate vector and fluctuation radius of an atom to be determined. Suppose that there are l determined atoms x_i, i = 1, …, l from which the lower and upper bounds on the distances to atom j are given. Then, a subproblem for determining atom j can be formulated as follows:

$$\begin{array}{cc}\hfill \underset{x_j,r_j}{\text{max}}{r}_j^3& \hfill \\ \hfill \text{subj.}& \parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel +r_i+r_j\le u_{i,j}\hfill \\ \hfill & \parallel {\mathbf{X}}_i-{\mathbf{X}}_j\parallel -r_i-r_j\ge l_{i,j}\hfill \\ \hfill & r_i\ge 0,i=1,\dots ,l.\hfill \end{array}$$ (20)

This subproblem has only four variables and 2l constraints, and can be solved easily. By repeatedly solving such subproblems for undetermined atoms, the coordinate vectors and fluctuation radii of the all atoms in the protein can all be determined eventually. We have implemented such a buildup algorithm in Matlab and applied it to a set of test problems. We demonstrate how the algorithm works in the following.

Let us consider the structure of protein 1AX8 as an example. In order to test the algorithm, we first used the PDB data for 1AX8 to compute all the distances less than or equal to 5 Å. We then computed the root-mean-square fluctuations for all the atoms based on their B-factors. Let y_i and b_i be the coordinate vectors and B-factors for atom i, respectively, i = 1, …, n. We then set a fluctuation radius for atom i to be

$$f_i=C\text{sqrt}(b_i∕D)$$ (21)

where constants C and D are the scaling factors that are evaluated by solving later the optimization problem defined by Eq. 19. Let d_i,j be the distance between atoms i and j. We then set

$$\begin{array}{cc}\hfill l_{i,j}=& d_{i,j}-f_i-f_j,\hfill \\ \hfill u_{i,j}=& d_{i,j}+f_i+f_j,\hfill \\ \hfill (i,j)& \in S=\{(i,j):d_{i,j}=\parallel {\mathbf{y}}_i-{\mathbf{y}}_j\parallel \le 5\mathrm{A}\}\hfill \end{array}$$ (22)

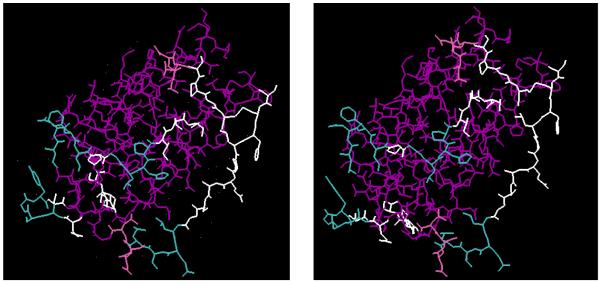
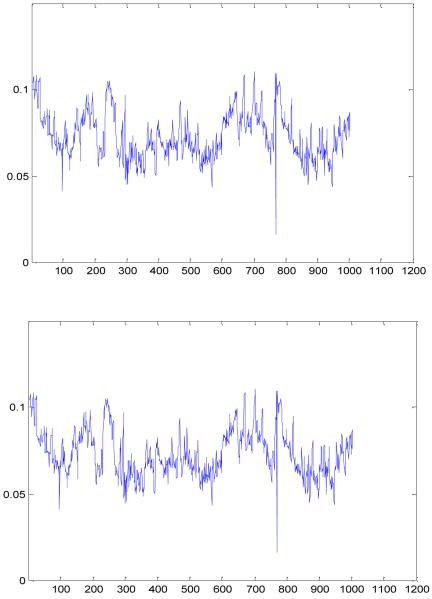
With such a set of distance intervals, we then solve an optimization problem (Eq. 19) by using a buildup procedure. Fig. 8 shows the X-ray crystal structure for 1AX8 and the equilibrium structure determined after solving Eq. 19 using the distance data given in Eq. 22. Let Y = {y_i, i = 1, …, n} and X = {x_i, i = 1, …, n} be two n×3 coordinate matrices for the two structures, respectively. Then, RMSD (X, Y) = 2.0e-04 Å, showing that the two structures are almost the same. After solving Eq. 19, we have also obtained the fluctuation radii for the atoms. Fig. 9 shows the computed radii r_i and the radii f_i derived from the B-factors of the crystal structure, i = 1, …, n. Clearly, the two sets of radii correlate very well

Fig. 8. Computational vs Experimental Structures.

The structure on the left is the crystal structure for protein 1AX8. The one on the right is the structure for 1AX8 obtained by solving a generalized distance geometry problem using a set of distance bounds.

Fig. 9. Atomic Fluctuation Radii.

The upper graph shows the fluctuation radii of the atoms extracted from the B-factors of the original crystal structure of protein 1AX8. The lower graph shows the fluctuation radii obtained by solving a generalized distance geometry problem.

Structure Refinement Using Statistical Distances

We propose a computational approach to refining an NMR structure (and possibly other types of structures as well) by statistically deriving additional distance data from a large set of known protein structures. General idea of our approach is based on earlier work of Sippl (Sippl, 1990;Sippl, 1992;Sippl, 1993;Sippl, 1995;Sippl et al., 1986;Sippl et al., 1985), Melo and Feytmans (Melo et al., 1997;Melo et al., 1998), Garbuzynskiy (Garbuzynskiy et al., 2005) among others.

By statistically deriving additional distance data, we mean that we can search for the distances between certain pairs of atoms, especially for those missing in the experimental data, in a database of known protein structures such as PDB, and then obtain a statistical distribution of each distance type, say the distance between the two C_β atoms in two neighboring residues, alanine (ALA) and tryptophan (TRP). Using these distributions, a probable range or a mean-force potential of each distance type can be defined, and applied to refining a structure.

Consider the distances between two atoms in two residues separated by some residues in sequence. Let A₁ and A₂ be the two atoms, R₁ and R₂ the two residues, and S₁, …, S_N the residues between R₁ and R₂. Let the distances between A₁ and A₂ in R₁ and R₂ separated by S₁, …, S_N be collected from a database of know protein structures and grouped into a set of uniformly divided distance intervals [D_i, D_i+1], where D_i = 0.1 * i Å, i = 0, 1, …, n-1. Then, the distribution of this particular type of distances can be defined by a function P[A₁,A₂,R₁,R₂,S₁,…,S_N](D) for any distance D, and

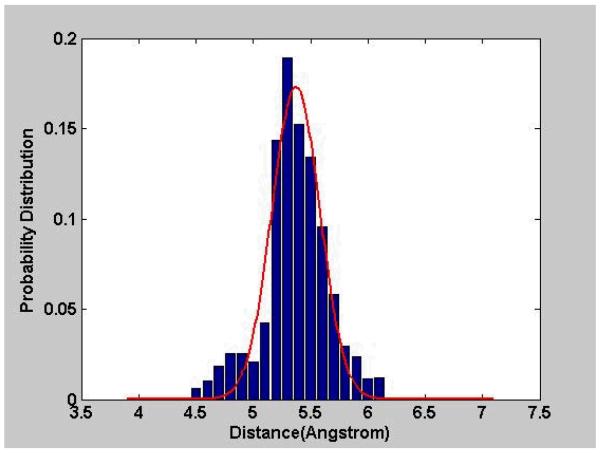
$$P[A_1,A_2,R_1,R_2,S_1,\dots ,S_N]\left(D\right)=\frac{\#\text{distances in}[D_i,D_{i+1}]}{\#\text{distances in}[D_0,D_n]},D\in [D_i,D_{i+1}].$$ (23)

The distribution graphs for most distance types should have non-uniform patterns if the two residues are not too far apart. This is primarily due to the fact that large portions of protein segments form regular secondary structures, i.e., α-helices or β-sheets, where short-range distances always have certain ranges (see Fig. 10). Based on the distribution of the distances of a given type, we can extract a probable range for the distances by using the mean minus and plus a few standard deviations of the distances. Let l and u be the lower and upper bounds of the distances between A₁ and A₂ in R₁ and R₂ separated by S₁, …, S_N. We can define l = μ - kσ and u = μ + kσ, where μ and σ are the mean and the standard deviation of P[A₁,A₂,R₁,R₂,S₁,…,S_N] and k is a constant. Alternatively, we can also use the distribution of the distances to define a mean-force potential.

Fig. 10. Statistical Distances.

The distances of a specific type have been collected from known protein structures and used to form a probability distribution function of the distances.

For example, for the distances between A₁ and A₂ in R₁ and R₂ separated by S₁, …, S_N, we can define a potential function E such that for any distance D of this type

$$E[A_1,A_2,R_1,R_2,S_1,\dots ,S_N]\left(D\right)=-kT\log P[A_1,A_2,R_1,R_2,S_1,\dots ,S_N]\left(D\right)$$ (24)

where k_B is the Boltzmann constant and T the temperature.

Once a set of distance bounds or mean-force potentials are obtained, we can impose the bounds on a structure to be refined or include the mean-force potentials in energy minimization so that a more plausible structural model may be built.

Results of structure refinement

We have downloaded around 2000 X-ray crystal structures with resolution of ≤ 2.0 Å and sequence similarity of ≤ 90% from PDB, and calculated a set of short-range distances and their distributions.(Wu et al., 2007a) The types of the distances calculated can be specified in terms of five parameters [A₁,A₂,R₁,R₂,S], where A₁ and A₂ are the atoms, R₁ and R₂ the residues, and S the residue separating R₁ and R₂. Also, only five different types of atoms were considered: the amide N, C_α, and the carbonyl C and O along the backbone and the carbon C_β in the side-chain. The residue types included all twenty different amino acid types. For convenience, we call them cross-residue distances. For each set of A₁, A₂, R₁, R₂, and S, all corresponding distances in the downloaded crystal structures were computed and collected into a set of uniformly divided distance intervals [D_i, D_i+1], where D_i = 0.1 i Å, i = 0, 1, …, 200. The distribution function P[A₁,A₂,R₁,R₂,S](D) for any D in [D_i, D_i+1] was defined as the number of distances in [D_i, D_i+1] normalized by the total occurrences of distances in all intervals.

The distribution functions for a subset of cross residue distances were used to generate a set of bound constraints for the corresponding distance types, with the lower and upper bounds equal to the mean values of the distances minus and plus twice the standard deviations, respectively. The generated distance bounds were then taken as additional distance constraints to refine a set of NMR structures, including five structures for 1EPH, 1GB1, 1IGL, 2IGG, 2SOB and five for 1CEY, 1CRP, 1E8L, 1ITL, 1PFL. The last five were selected because they have X-ray structures available. The original NMR experimental constraints for the structures were downloaded from NMR structure database BioMagResBank (Ulrich et al., 2008). The structures were refined using the default torsion angle dynamic simulated annealing protocol implemented in CNS (Brunger et al., 1998;Brunger, 2007). The results obtained with and without additional database distance constraints were examined on the deviations of all simple cross-residue distances from their average distributions, and compared and assessed in terms of several criteria used in NMR modeling, including the acceptance rates of the structures, the RMSD values of the ensembles of structures, and the RMSD values of the structures compared with their X-ray structures (for available ones).

The distribution functions for a set of cross residue distances were also used to define a set of mean force potentials.(Wu et al., 2007b) Let P be the distribution function for any distance of interest between two atoms. Then, the mean-force potential E for the distance was computed from Eq. 24. The potentials for all the cross residue distances were then summed up and inserted into the energy function in CNS software. The extended energy function was applied to refining a set of selected NMR structures. Again, the original NMR experimental constraints for the structures were downloaded from NMR structure database BioMagResBank. The embedding and energy minimization routines in CNS were used for the refinement. The results obtained with and without using the mean-force potentials were compared and assessed in terms of several standard measures, including the potential energy of the structures in various categories, the RMSD values of the ensembles of structures, and the RMSD values of the structures compared with their X-ray reference structures (for available ones), and the Ramachandran plots.

As shown in Table 3, the means and standard deviations of the RMSD values for the listed ensembles of NMR structures all became smaller after the structures were refined with the statistically derived distance constraints. Note that the RMSD values were calculated in terms of either just backbone atoms or all non-hydrogen atoms. The results were consistent in both calculations.

Table 3.

RMSD of the Ensembles of Refined NMR Structures

Protein	#Res	Data	Means ± Standard Deviations*
			Backbone†	Non-H‡
1EPH	53	NMR	2.04±0.61	2.94±0.70
		NMR+DB	1.78±0.40	2.76±0.54
1GB1	56	NMR	0.45±0.12	1.04±0.18
		NMR+DB	0.38±0.09	0.91±0.16
1IGL	67	NMR	4.50±1.52	5.49±1.55
		NMR+DB	3.81±1.24	4.70±1.43
2IGG	64	NMR	2.62±0.85	3.29±0.83
		NMR+DB	2.16±0.90	2.87±0.85
2SOB	103	NMR	7.25±1.60	8.06±1.67
		NMR+DB	5.54±1.77	6.41±1.77

^*The means and standard deviations of the RMSD values of the structure ensembles refined with and without database distance constraints

^†RMSD values in terms of backbone atoms

^‡RMSD values in terms of all non-hydrogen atoms.

The refined NMR structures for five proteins (1CEY, 1CRP, 1E8L, 1ITL, and 1PFL) were compared with their corresponding X-ray structures for the RMSD values of the pairs of NMR and X-ray structures. As shown in Table 4, both means and standard deviations of the RMSD values for the ensembles of structures refined with the derived distance constraints were clearly smaller than those refined without them, indicating strongly that the structures agreed more closely with their reference structures after being refined with the derived distance constraints.

Table 4.

Refined NMR Structures Compared to X-ray Structures

NMR ID	X-Ray ID	#Res	Means ± Standard Deviations*
			NMR†	NMR + DB‡
1CEY	3CHY	128	1.85±0.19	1.80±0.17
1CRP	1IAQ_A	166	1.77±0.29	1.60±0.26
1E8L	193L	129	2.05±0.22	2.02±0.19
1ITL	1RCB	129	2.88±0.76	2.79±0.21
1PFL	1FIK	139	1.66±0.07	1.65±0.07

^*The means and standard deviations of the RMSD values for the ensembles of NMR structures compared with their X-ray structures

^†Refined with only NMR distance constraints

^‡Refined with NMR and database distance constraints.

As a case study, we have also applied the derived distance constraints to refining the NMR structure of the human PrP^c E200K variant of the prion protein. Two biologically critical but under-determined loop regions (residues 167-171 and 195-199) were targeted particularly for improvement. The Ramachandran plots of the average and energy-minimized structure and the lowest energy structure of the refined structural ensemble showed a significantly higher percentage (89.6%) of residues in the most favorable regions of the plots than the 85.4% of such residues found in the regularly refined structures, which was a clear indication on the improvement of the structures due to the use of the statistically derived distance constraints. Table 5 shows the energy values for a list of refined structures in various categories and in particular, the means and standard deviations of the energy values in each structural ensemble. Note that for a fair comparison, the calculation of the overall energy did not count the contribution from the mean-force potentials although the latter were used in the CNS+PMF refinement. Note also that the energy due to electrostatic interactions was not listed because the corresponding potentials were not included in the default CNS refinement protocol. Table 3 shows that the means and standard deviations of the energy values of the ensembles of structures became smaller in almost all categories after the structures were refined with the addition of the mean force potentials. The results suggested that the refined structures, when using the mean-force potentials, were clearly more favorable energetically. Surprisingly, they also satisfied the experimental constraints better as the NOE and DIH energies were decreased in many cases as well. Overall, in terms of the means and standard deviations of the energy values in the structural ensembles, of the 70 selected NMR structures, about 80% had the overall energy significantly reduced, in average by 7.5%, and about 65% had the NOE energy decreased, in average by 5%, after refined with mean-force potentials. Here we have not calculated the statistics for the DIH energy because some structures did not have the DIH data and energy available.

Table 5.

Energy of Refined NMR Structures (KJ/MOL)^*

PDB	Method	Overall	Bond	Angle	Improper	Van der Waals	NOE	DIH
1AFI	CNS	160.9±72.0	6.2±3.3	63.6±18.8	8.4±7.2	54.2±21.7	27.6±20.1	0.9±0.9
	CNS+PMF	122.1±56.5	4.2±2.3	53.9±15.8	6.2±4.7	37.8±17.3	19.0±15.4	1.0±1.1
1BA4	CNS	93±60.8	4.0±3.0	34.3±21.8	4.4±5.9	26.0±14.3	24.3±15.9	NA
	CNS+PMF	57.8±14.7	2.1±0.7	24.1±3.7	2.1±1.2	17.1±4.0	12.4±5.2	NA
1DKC	CNS	155.7±90.1	7.4±4.1	40.1±10.6	4.7±2.5	48.9±48.6	54.6±24.3	NA
	CNS+PMF	118.6±40.4	5.2±2.0	31.4±8.1	3.2±2.1	34.6±12.4	44.3±15.8	NA
1DVV	CNS	85.6±19.6	3.1±0.9	40.7±5.8	4.0±1.1	23.7±7.8	14±5.2	0.05±0.06
	CNS+PMF	73.3±15.8	2.5±0.9	37.5±3.7	3.5±0.9	18.4±4.7	11.2±5.5	0.03±0.02
1I6F	CNS	190.0±73.2	1.4±2.1	24.4±8.8	1.3±1.9	113.8±47.3	48.9±12.9	0.16±0.47
	CNS+PMF	173.8±8.3	0.9±0.3	22.6±1.8	0.9±0.5	103.4±3.3	45.9±2.4	0.06±0.09

^*Listed are means and standard deviations of the energies of the structural ensembles in various categories: Overall – total energy; Bond – bond-length energy; Angle – bond-angle energy; Improper – improper angle energy; Van der Waals – Van der Waals interaction energy; NOE – energy for NOE distance constraint satisfaction; DIH – energy for dihedral angle constraints. CNS – refined with original NMR data and CNS built-in energy function. CNS+PMF – refined with original NMR data, CNS built-in energy function, and database derived mean-force potentials.

Refining Comparative Models

We have also participated in the CASPR 2006 structure refinement experiments. In these experiments eight structural models (predicted with comparative modeling) were provided for further refinement. The RMSD values of the models compared with PDB structures ranged from 2.0 Å to 5.0 Å. To illustrate our methodology we focus on a model of a protein with 70 residues and a 2.19 Å RMSD from its crystal structure (1WHZ, see Fig. 11). We have used the following procedure to refine the structure. First, 16 different structures were generated by randomly perturbing the residues of the target structure. Energy minimization was then carried out using CHARMM (Brooks et al., 1983)with the generated structures as starting points. Of the 16 obtained minima, 4 were selected randomly, and each was used to generate 16 more structures for further energy minimization. The process was repeated until the maximum number of structures was generated.

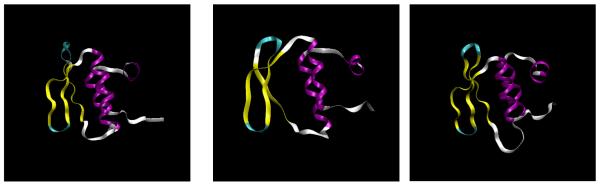
Fig. 11. Refining Comparative Models.

From left to right are the crystal structure, the given target, and the refined model. The RMSD of the given target is 2.19 Å against the crystal structure, while the refined model is 1.80 Å. The differences can be observed in both the helical (purple) and extended (yellow) regions.

In the end, total 100 minimum energy structures were selected from the structures obtained in the energy minimization stage. Based on the energy values and the Ramachandran plots of the structures, a small set of structures were selected and the one with both low energy and good residual distribution in the Ramachandran plot was used as an initial model. The RMSD value of the initial model against the experimental structure was 1.92 Å. From this initial model, a large set of distances between atoms contact distances was computed. A set of lower and upper bounds for the distances was then generated by subtracting 20% from or adding 20% to the distances. Then, the CNS NMR refinement protocols were used to further refine the model with the generated distance constraints.

The distributions of distances between certain pairs of atoms, especially the distances between heavy atoms in different residues separated by several residues in the primary sequence, were also computed. A set of mean-force potentials for the distances was constructed using the distribution functions, and was added to the CNS energy function.

The initial model was refined with the modified energy function. Total 50 structures were generated by CNS as an ensemble of models for the protein. The structures were analyzed based on their total energies and residual distributions in the Ramachandran plots. The one with both low energy and good Ramachandran plot was selected as the final model. This model had a 1.80 Å RMSD from the experimental 1WHZ structure. The improvement in this sense was significant compared to the RMSD value (2.19 Å) of the original model.

DISCUSSION

Conclusions

We show that mathematical approach based on distance matrices is very powerful and enable us to predict protein structure from the sequence. The information contained in the square distance of residues from the center of mass, and the first principal component allows us to reconstruct protein structure with RMSD 4.5 Å. We demonstrate that crystallographic B-factors can be predicted from the sequence using Support Vector Regression. We also prove that protein structures can be refined by using statistical interatomic distances, and that generalized distance geometry problem for solving NMR structures based on distances between atoms subject to upper and lower bounds can be reduced to an optimization problem that involves maximization of the volume of spheres with the radii equal to the range of corresponding thermal fluctuations of atoms. All methods presented are still being improved and may lead to a significant progress in prediction of protein structure and dynamics and to substantial refinement of protein models.

Summary

We have applied distance matrices and the related contact matrices to several different, although interconnected problems relevant to structural bioinformatics. We have performed eigenvalue decomposition of square distance matrices, and we have shown that a dominant eigenvector is proportional to r² - the square distance of points from the center of mass, while the next three eigenvectors are the principal components of the system of points. We have shown that both the dominant eigenvector and the first principal component can be predicted from the sequence alone that allows us to predict the tertiary structure of proteins from sequence with RMSD around 4.0 Å.

We have performed elastic network analysis (based on contact matrices) of the large number of available HIV-1 protease structures, and have shown that they provide a remarkable sampling of conformations, which can be viewed as direct structural information about the dynamics. Finally, we have used distance constraints from databases of known protein structures for structure refinement.