The behavior of the micro-mechanical cement-bone interface affects the cement failure in total hip replacement

Abstract

In the current study, the effects of different ways to implement the complex micro-mechanical behavior of the cement-bone interface on the fatigue failure of the cement mantle was investigated. In an FEA-model of a cemented hip reconstruction the cement-bone interface was modeled and numerically implemented in four different ways: (I) as infinitely stiff, (II) as infinitely strong with a constant stiffness, (III) a mixed-mode failure response with failure in tension and shear, and (IV) realistic mixed mode behavior obtained from micro FEA-models. Case II, III and IV were analyzed using data from a stiff and a compliant micro-FEA model and their effects on cement failure were analyzed. The data used for Case IV was derived from experimental specimens that were tested previously. Although the total number of cement cracks was low for all cases, the compliant Case II resulted in twice as many cracks as Case I. All cases caused similar stress distributions at the interface. In all cases, the interface did not display interfacial softening; all stayed the elastic zone. Fatigue failure of the cement mantle resulted in a more favorable stress distribution at the cement-bone interface in terms of less tension and lower shear tractions. We conclude that immediate cement-bone interface failure is not likely to occur, but its local compliancy does affect the formation of cement cracks. This means that at a macro-level the cement-bone interface should be modeled as a compliant layer. However, implementation of interfacial post-yield softening does seem to be necessary.

1. INTRODUCTION

Fatigue failure of the cement mantle in terms of cement cracking is one of the failure mechanisms that leads to aseptic loosening in cemented hip reconstructions (Jasty et al., 1991). Finite element analysis (FEA) has been proven successful in simulating the fatigue failure process of the cement mantle in complete hip reconstructions and is therefore a good tool to predict implant survival (Perez and Palacios, 2010; Jeffers et al., 2007; Stolk et al., 2007).

It has previously been demonstrated that the stem-cement interface is a debonded interface, which enables gapping and sliding between the stem and cement (Ramos and Simoes, 2009; Gravius et al., 2008). This has widely been implemented in FEA-models in which the stem-cement interface was invoked as a frictional contact layer (Perez et al., 2009; Hertzler et al., 2002; Verdonschot and Huiskes, 1997). Recently, however, experiments have demonstrated that the movements at the cement-bone interface are also substantial (Mann et al., 2010; Race et al., 2010). It can therefore be suggested that the compliance of the cement-bone interface may have substantial influence on the fatigue failure of the cement mantle and should therefore be incorporated into computational models of complete cemented hip reconstructions.

The cement-bone interface has previously been modeled in basically three different manners, as: (1) An infinitely stiff interface between the cement and bone (Jeffers et al., 2007; Stolk et al., 2007; Hung et al., 2004; Katoozian and Davy, 2000); (2) a layer of soft tissue elements with a constant stiffness (Waide et al., 2004; Colombi, 2002; Verdonschot and Huiskes, 1997), which represented osteolysis around the cement mantle (Bauer and Schils, 1999); and (3) a layer of cohesive elements in which the mixed-mode behavior of the cement-bone interface is implemented (Perez et al., 2009; Moreo et al., 2006; Mann and Damron, 2002). The experimental validation of these three aforementioned methods is, however, debatable. Experiments with laboratory prepared cement-bone interface specimens demonstrate a significant variation in compliance and strength (Mann et al., 2008) which does not match the infinitely stiff (1) or soft tissue layer (2) assumption. Input for the cohesive elements was experimental mixed-mode data: linear increase followed by softening, for the tension and shear direction (Mann et al., 2001). A considerable deviation in stiffness and strength was reported. Theoretical mixed-mode models (Alfano and Crisfield, 2001) were used to fit the stiffness and strength while accurate modeling of the softening phase was neglected.

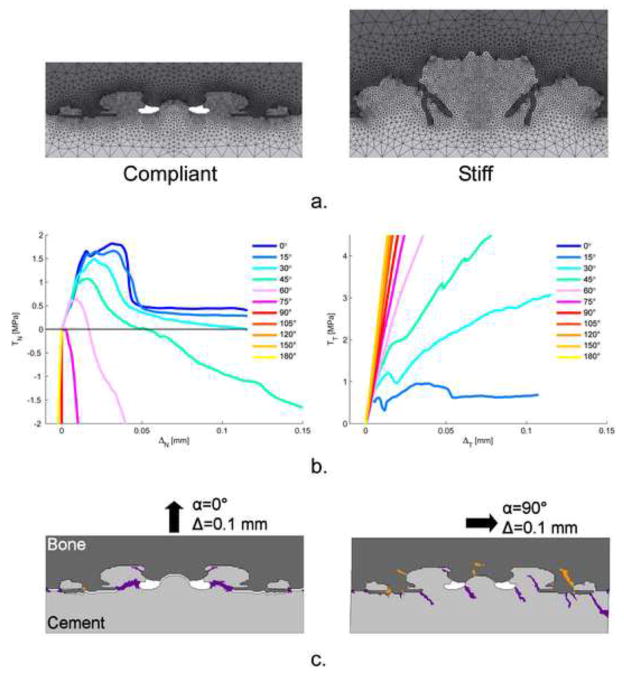
Recently, the mixed-mode behavior of the cement-bone interface has been studied utilizing four micro FEA-models (Figure 1a) (Waanders et al., 2010). These FEA-models included simulation of cement and bone cracking and were loaded in 11 different directions, while monitoring tractions (T_N and T_T) and displacements (Δ_N and Δ_T)in normal and tangential direction. Only frictional contact was assumed at the complex interdigitated interface between cement and bone. Because no bonding was assumed, failure (cracking) of the interface on an apparent level could only occur through failure of the bulk cement and bone; no failure could occur at the actual contact interface between cement and bone. Depending on the micro-structure of the interface, considerable different magnitudes in strength and stiffness were found (Table 1), which compared favorably with experiments (Mann et al., 2008). Innovative observations included (i) a considerable compression generated during the softening phase at mixed-mode angles larger than 45°; and (ii) lack of failure under pure shear loading (Figure 1b). This could be explained by the presence of crack patterns (Figure 1c) and applied the boundary conditions. This new information allows the implementation of the validated micro-mechanical behavior into macro-models of cemented hip reconstructions. However, implementation of this more realistic behavior of the cement-bone interface is rather complex and increases computational time. It is therefore worthwhile to assess whether it is truly necessary to represent the compliancy and post-yield mechanical behavior of the cement-bone interface.

Figure 1.

a. The compliant and stiff generated plain strain micro FEA-model of the cement-bone interface used to determine the mixed-mode behaviour of the cement-bone interface (Waanders et al., 2010). All models were mirrored to facilitate the application of periodic boundary conditions to both sides of the models. The bottom part of the cement was fixed for all degrees of freedom, while the top part of the bone was uniformly displaced under eleven different angles without allowing transverse motions. In each model, both the bone and cement had provision for element cracking.

b. Mechanical mixed-mode response of the compliant micro FEA-model: on the left, the normal traction versus normal displacement response, T_N-Δ_N, and on the right the tangential traction versus tangential displacement response, T_T-Δ_T, for the eleven different directions. For the mixed-mode responses in which tension was involved, compressive stresses were generated in the softening phase. Also, the mixed-mode responses showed a gradual decrease in ultimate T_N as the loading angle increased. The T_T-Δ_T-response showed no failure in pure shear (α=90°).

c. Crack patterns predicted in the bone and cement. Because of the mirroring of the models, symmetric crack patterns occurred in pure tension (α=0°). In pure shear, (α=90°), cracks progresses into the bulk material without breaking off cement or bone spurs. This could clarify the feature that was found of no failure in shear.

Table 1.

Interface properties of the most stiff and most compliant responses obtained from micro FEA-models (Waanders et al., 2010). The tensile strength and stiffness of the most stiff model differed approximately a factor 2 compared to the compliant model. The displacement at the tensile strength, δ_N, was much larger for the compliant model. The difference in shear stiffness was not comparable to the difference in tensile stiffness.

Response	Tensile strength, TN,max, [MPa]	Tensile stiffness, $\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N},\left[\frac{\mathit{MPa}}{mm}\right]$	Displacement at TN,max, δN, [mm]	Shear stiffness, $\frac{\partial T_T}{\partial {\mathrm{\Delta }}_T},\left[\frac{\mathit{MPa}}{mm}\right]$
Stiff	2.79	251	0.012	241
Compliant	1.82	123	0.030	217

We therefore assessed in this study the added value of the cement-bone interface mechanics in an increasingly complex fashion using four steps. Four different cement-bone interface behaviors were considered: (I) infinitely stiff interface; (II) compliant interface with infinite strength; (III) mixed-mode failure response according to experimental findings including post-yield softening under tensile and shear conditions; and (IV) mixed-mode behavior as obtained with the aforementioned micro FEA-models. Each case was analyzed with the most compliant and most stiff cement-bone interface as found in the aforementioned micro FEA-study (Table 1) (Waanders et al., 2010). An FEA-model of a complete cemented hip reconstruction utilizing a Lubinus SPII prosthesis, in which the cement-bone interface was macroscopically implemented using the micro FEA-data, was subjected to a loading configuration simulating normal walking. Crack formation in the cement mantle and load distribution at the cement-bone interface were monitored. We asked: (1) How do cement-bone interface variations of stiffness and strength influence number and distribution of cracks in the cement mantle? (2) Does failure of the cement-bone interface occur during cyclic loading of normal walking? (3) Does fatigue failure of the cement mantle influence the probability of failure of the cement-bone interface?

2. METHODS

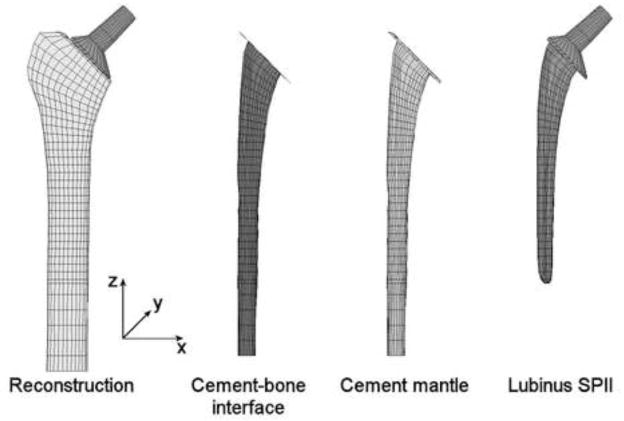
We used a complete 3D FEA-model of a cemented hip reconstruction utilizing a Lubinus LPII stem from a previous study (Figure 2) (Stolk et al., 2007). This model was based on a laboratory implantation of the stem in a composite femur whose stem orientation was based on radiographs and CT-data of the reconstruction. The complete reconstruction was meshed with eight-node isoparametric brick elements. The cortex was modeled as transversely isotropic, with a higher stiffness in axial direction of the femur (Table 2). Trabecular bone, cement mantle, and stem were modeled as isotropic (Table 2). For this study, an additional layer of cohesive elements was modeled between cement and bone, to represent the cement-bone interface (Figure 2). To maintain the initial mesh, the cohesive elements were physically modeled with zero thickness. The stem-cement interface was considered to be debonded and contact was modeled utilizing a node-to-surface algorithm with a friction coefficient of 0.25 (MSC.MARC 2007r1, MSC Software Corporation, Santa Ana, CA, USA).

Figure 2.

The complete cemented hip reconstruction implanted with a Lubinus SPII stem. Between the cement mantle and the bone, a layer of cohesive elements was modeled that represented the cement-bone interface.

Table 2.

Material properties of the hip reconstruction. Stem, cement and trabecular bone were modeled as isotropic materials, while cortical bone was modeled as transversely isotropic. All material properties were based on Stolk et al. (2007).

Part	Young’s Modulus, E, [MPa]	Poisson’s ratio, ν, [−]
Stem	210,000	0.3
Cement	2,400	0.3
Trabecular bone	400	0.3
Cortical bone	Ex = Ey = 7,000; Ez = 11,500 Gxy = 2,600; Gyz = Gzx = 3,500	νxy = νyz = νzx = 0.4

The models were subjected to a loading history of 20 million cycles of walking. The loading configuration included the hip contact force and two muscle forces (abductors and vastus lateralis (Stolk et al., 2002)), all based on 700N body weight. Fatigue failure of the bulk cement was calculated by means of a custom-written FEA-algorithm that simulated creep and damage accumulation (Stolk et al., 2004). This method calculated the element’s deformation as {ε}= [S]·{σ}+{ε^c}. The compliance matrix [S] incorporated the damage by reduction of stiffness to 0.1MPa perpendicular to corresponding maximum principal stress direction. Each component of the creep strain tensor {ε^c} was dependent on the scalar ε^c defined as ε^c = 7.985 · 10⁻⁷ · n^{0.4113−0.116·log(σ)}·σ^1.9063 (Verdonschot and Huiskes, 1995).

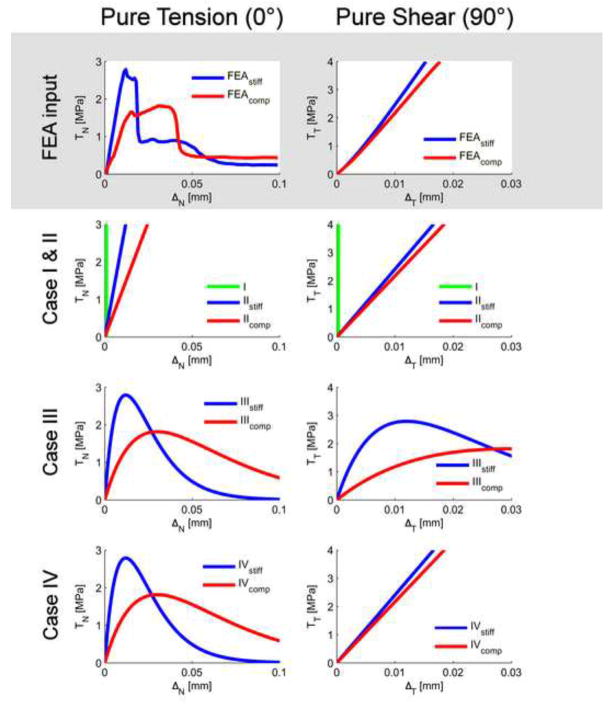
The cement-bone interface was numerically implemented with four different cases (Figure 3):

Figure 3.

The mechanical behaviors in pure tension (0°) and pure shear (90°) of the micro FEA-model (in grey) and the four different cases. Note that only the responses in pure tension and pure shear are presented and not the mixed mode responses. In pure tension, the micro FEA-models resulted in a linear increase of T_N followed by yielding and softening. In pure shear, a linear increase of T_T was found without any softening. Case I and II were modeled as a constant stiffness in tension and shear in which Case I was assumed to be infinitely stiff. Case III had a similar behavior as has been found in experiments: yielding and softening in tension and shear with a equal stiffness in tension as in shear (Mann et al., 2008; Mann et al., 1999). Case IV had the same mixed mode behavior as the micro FEA-models. For Case III and IV, the parameters of the cohesive model were set according to the interfacial strength (T_N and T_T) and its corresponding displacement (δ_N and δ_T) (Table 3).

1. An infinitely stiff interface with infinite strength

2. A compliant interface with infinite strength

3. A mixed-mode failure response according to experimental findings

4. A mixed-mode failure response according to micro-FEA mixed-mode models

The interface in Case I was assumed to be completely bonded without the possibility for deformations at the cement-bone interface. Case II represented a constant stiffness without interfacial failure and represented a soft tissue layer as implemented previously (Verdonschot and Huiskes, 1997; Colombi, 2002). Case III represented failure in tension and shear; a behavior widely observed experimentally: (Mann et al., 1999; Wang et al., 2010). Case IV represented the behavior obtained from a previous micro FEA-study (Waanders et al., 2010). Case II to IV were each analyzed at high and low stiffness and referred to as “stiff” and “compliant”. The magnitudes of stiffness and strength were based on the stiffest and most compliant response of the micro-FEA study (Table 1).

All cases were numerically implemented using a cohesive model which defined the normal and tangential traction (T_N and T_T) as a function of normal and tangential displacements (Δ_N and Δ_T) (Wei and Hutchinson, 2008):

$$\begin{array}{l}{T}_N=\frac{{\mathrm{\Gamma }}_0}{{\delta }_N}\left[\frac{{\mathrm{\Delta }}_N}{{\delta }_N}-\left((1+\beta )\frac{{\mathrm{\Delta }}_N}{{\delta }_N}-\beta \right)f({\mathrm{\Delta }}_T)\right]exp\left(-\frac{{\mathrm{\Delta }}_N}{{\delta }_N}\right)\\ T_T={\mathrm{\Gamma }}_0\frac{df({\mathrm{\Delta }}_T)}{d{\mathrm{\Delta }}_T}\left[1+(1+\beta )\frac{{\mathrm{\Delta }}_N}{{\delta }_N}\right]exp\left(-\frac{{\mathrm{\Delta }}_N}{{\delta }_N}\right)\end{array}$$

where Γ₀ denotes the total fracture energy in and δ_N the displacement at the tensile strength. The function f(Δ_T) was used to define the response in pure shear: $T_T(0,{\mathrm{\Delta }}_T)={\mathrm{\Gamma }}_0\frac{df({\mathrm{\Delta }}_T)}{d{\mathrm{\Delta }}_T}$. Case I, II and IV were assumed to have a constant stiffness in pure shear without interfacial failure (Figure 3). Hence: $\frac{df({\mathrm{\Delta }}_t)}{d{\mathrm{\Delta }}_t}=\frac{1}{{\mathrm{\Gamma }}_0}\frac{\partial T_t}{\partial {\mathrm{\Delta }}_t}·{\mathrm{\Delta }}_t$, where $\frac{\partial T_t}{\partial {\mathrm{\Delta }}_t}$ is the tangential stiffness in shear (Table 1). Case III assumed interfacial failure in shear (Figure 3) and was defined as: $\frac{df({\mathrm{\Delta }}_t)}{d{\mathrm{\Delta }}_t}=\frac{{\mathrm{\Delta }}_t}{{{\delta }_t}^2}exp\left(-\frac{{\mathrm{\Delta }}_t}{{\delta }_t}\right)$. The values of all parameters are listed in Table 3.

Table 3.

The values of all parameters used by the cohesive model (Wei and Hutchinson, 2008). Γ₀ was the total fracture energy and δ_N the displacement which corresponded to the displacement at the tensile strength. The function $\frac{df({\mathrm{\Delta }}_T)}{d{\mathrm{\Delta }}_T}$ was used to define the behaviour in pure shear. The parameter β was used to model the compressive normal tractions which occurred in the softening phase. A negative value of β resulted in compression in the softening phase. Finally, δ_T corresponded to the displacement at the shear strength and was therefore only used for Case III.

Case	Γ0	δN[mm]	$\frac{df({\mathrm{\Delta }}_T)}{d{\mathrm{\Delta }}_T}$	β	δT
I	400,000	2.0	$\frac{100,000}{{\mathrm{\Gamma }}_0}·{\mathrm{\Delta }}_t$	0.0	-
IIstiff	1,004	2.0	$\frac{241}{{\mathrm{\Gamma }}_0}·{\mathrm{\Delta }}_t$	0.0	-
IIcompliant	492	2.0	$\frac{217}{{\mathrm{\Gamma }}_0}·{\mathrm{\Delta }}_t$	0.0	-
IIIstiff	0.091	0.012	$\frac{{\mathrm{\Delta }}_t}{{{\delta }_t}^2}\mathbf{exp}\left(-\frac{{\mathrm{\Delta }}_t}{{\delta }_t}\right)$	0.0	0.012
IIIcompliant	0.148	0.030	$\frac{{\mathrm{\Delta }}_t}{{{\delta }_t}^2}\mathbf{exp}\left(-\frac{{\mathrm{\Delta }}_t}{{\delta }_t}\right)$	0.0	0.030
IVstiff	0.091	0.012	$\frac{241}{{\mathrm{\Gamma }}_0}·{\mathrm{\Delta }}_t$	−0.8	-
IVcompliant	0.148	0.030	$\frac{217}{{\mathrm{\Gamma }}_0}·{\mathrm{\Delta }}_t$	−0.8	-

To investigate how cement-bone interface variations influence cement cracking, we monitored the number of cracks formed in the cement and analyzed the distribution of the cracks. We monitored whether failure occurs during cyclic walking simulation by tracking whether cohesive elements at the interface entered the softening phase. Finally, we analyzed whether fatigue failure of the cement mantle influenced failure of the cement-bone interface by comparing interfacial failure directly after loading and after 20 million cycles of normal walking.

3. RESULTS

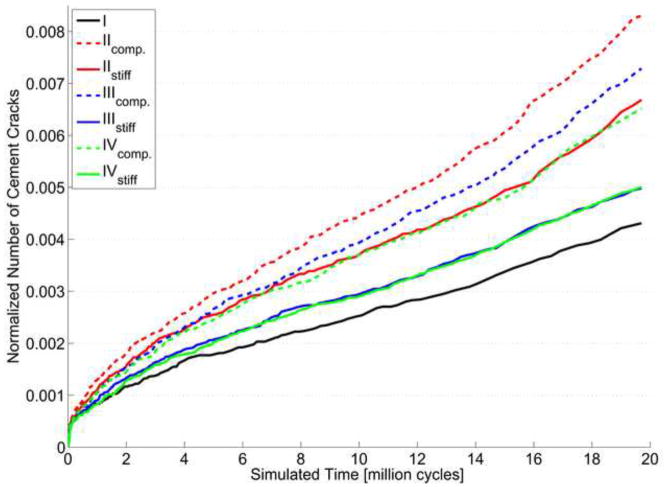
The number of bulk cement cracks that were predicted varied considerably over the seven different simulations, although the total number of cracks was always <1% of the complete cement mantle (Figure 4). After 20 million cycles, the compliant Case II showed a number of cracks twice as large as Case I. For each case, the compliant cement-bone interface resulted in more cracks than the stiff interface. Remarkable are the normalized number of cracks of the stiff Case III and the stiff Case IV, which hardly resulted in any differences. On the other hand, the compliant Case III and compliant Case IV do show some differences. Qualitatively, the differences between the crack patterns of all simulations were negligible.

Figure 4.

Normalized number of cement cracks in the cement mantle with respect to the number of loading cycles of the 7 different simulations. The cracks were normalized by dividing the predicted number of cracks by the maximum number of cracks possible, which was equal to three time the number of integration points of the cement mantle. Case I, the infinitely stiff interface, resulted in the smallest number of cement cracks. The compliant Case II resulted in almost double number of cement cracks compared to Case I.

In none of the simulations in which failure of the cement-bone interface could occur, interfacial failure was predicted. The normal and tangential tractions (T_N and T_T) stayed below the interfacial strength during the entire loading history. Furthermore, after 20 million cycles the maximum normal traction (T_N) at the cement-bone interface decreased for Case II, III and IV (Table 4).

Table 4.

The minimum and maximum tractions that occurred at the cement-bone interface at N=100 and N=20 million cycles. For all cases, the maximum normal compression traction, min TN, increased and the maximum normal tensile traction decreased, with respect to Case I. Surprisingly, the maximum tangential traction increased, while it was also shown that overall the tangential tractions decreased (Figure 6b).

Case	N=100			N=20 million
	min TN	max TN	max TT	min TN	max TN	max TT
I	−10.1	2.76	2.93	−10.5	3.15	3.19
IIstiff	−2.17	1.23	2.10	−3.27	0.67	2.53
IIcompliant	−3.16	1.62	1.94	−4.42	0.72	2.04
IIIstiff	−3.41	1.12	1.40	−5.08	0.65	1.55
IIIcompliant	−6.44	1.77	1.95	−8.48	1.00	2.12
IVstiff	−3.34	1.03	1.93	−5.21	0.64	2.27
IVcompliant	−6.70	1.66	1.66	−8.70	0.99	2.16

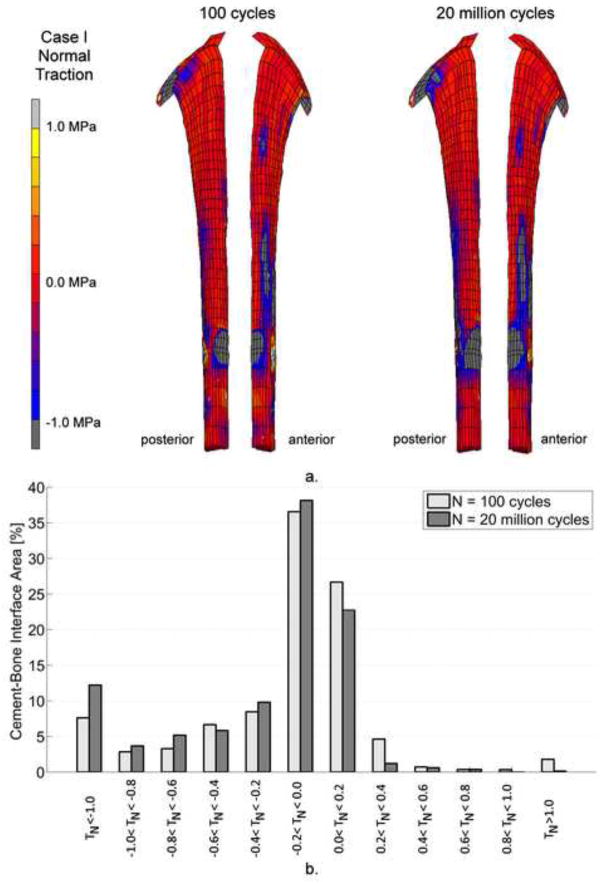
The distribution of normal tractions (T_N) at the cement-bone interface was qualitatively the same for all simulations. Initially, considerable normal compression (T_N < 0) was observed below the medial implant collar and lateral at tip level (Figure 5a). The stem tip also resulted in some areas with tension at the medial side of the cement-bone interface, which almost disappeared after 20 million cycles. At the end of the simulations, more areas with compression were visible as a result of stem subsidence. Overall, the total area with tensile tractions decreased as a result of cement failure (Figure 5b).

Figure 5.

a. Distribution of normal tractions, T_N, at the cement-bone interface for Case I. There were hardly any differences regarding T_N-distribution over the 7 different cases. As a result of stem subsidence, a larger area of the cement bone interface was loaded under compression.

b. The percentage cement-bone interface area under different ranges of normal traction, T_N. The amount of area of the cement-bone interface that was loaded under tension decreased considerably after 20 million cycles. On the other hand, more area was loaded under compression.

The initial distribution of tangential tractions (T_T ) revealed high tangential tractions at the medial side of the collar and at the stem tip level of the cement-bone interface (Figure 6a). After 20 million cycles the area with high tangential tractions at the stem tip level had moved from the posterior to the lateral side. Overall, the tangential tractions decreased in time (Figure 6b), although the maximum peak tangential traction at the cement-bone interface increased (Table 4).

Figure 6.

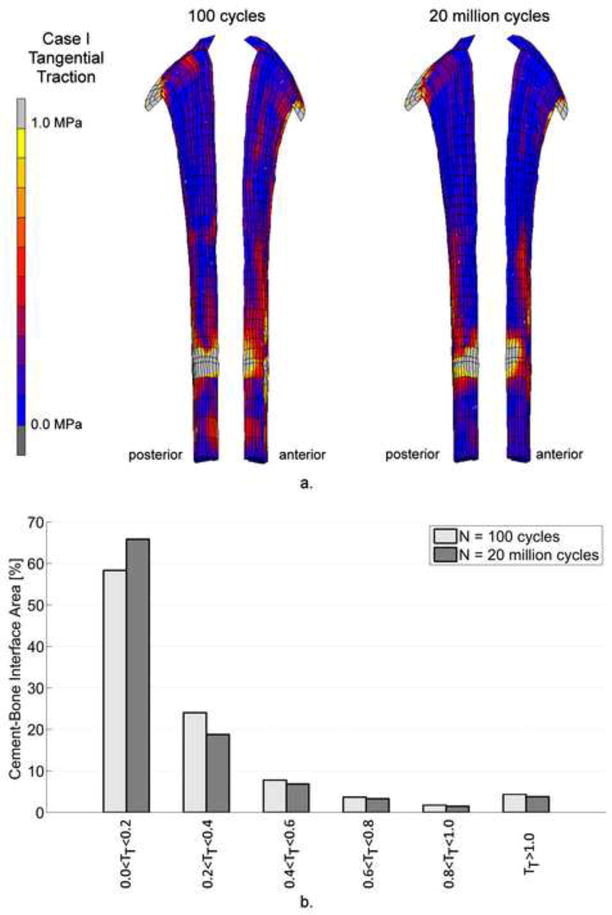
a. Distribution of tangential tractions, T_T, at the cement-bone interface. After 20 million loading cycles, the tangential tractions decreased. However, the maximum tangential peak traction increased (Table 4).

b. The percentage cement-bone interface area under different ranges of tangential traction, T_T. The magnitude of the tangential tractions, TT, decreased considerable after 20 million cycles.

4. DISCUSSION

We investigated the effect of various behaviors of the cement-bone interface on the fatigue failure of the cement mantle. We find that compliant cement-bone interfaces results in more cement cracking than a stiff interface. The investigated interfacial behaviors did not influence the distribution and magnitude of normal and tangential tractions at the cement-bone interface. Fatigue failure of the cement mantle resulted in increased compression at the cement-bone interface and in decreased tangential tractions. We find also that the tractions stayed in the elastic zone for the cases in which failure of the interface was allowed.

The finding that increased compression was found at the interface after fatigue crack formation of the interface may be attributed to the fact that the cement cracks may create room for the implant to subside or rotate, causing a redistribution of the load transfer. Although the shift from tangential to compression tractions at the cement-bone interface seems beneficial, the underlying mechanism may not be, as more room for implant motion would also entail increased micromotions at the implant-cement interface, possibly leading to the generation of wear debris and particle-induced osteolysis.

Our finding that failure did not occur at the cement-bone interface may be explained by the simulation of normal walking and by the well-functioning of the majority of the cemented hip reconstructions, without evidence of interface gapping or formation of fibrous tissue layers. The lack of failure, even in the compliant case, is consistent with analyses of post-mortem en-bloc specimens (Mann et al., 2010). Indeed, some en-bloc specimens displayed a compliant response despite the fact that the reconstructions were well-functioning.

The predicted amount of cracks in the cement mantle was less than 1% of the bulk. This is a low percentage in comparison to the ~6% and ~8% found for a Charnley and Exeter stem, respectively (Perez and Palacios, 2010). This difference could be attributed to the fact that in the current study only simulated walking was considered. However, it has previously also been shown that a Lubinus SPII stem results in the fewest number of cement cracks compared with three other stems (Stolk et al., 2007). Furthermore, from a clinical point of view, the clinical results of the Lubinus SPII stem are excellent (Malchau H et al., 2006).

One might expect that the reconstruction with the compliant interface at lower strength would fail earlier than the stiff case. However, in none of the simulated cases failure was predicted, in terms of interfacial softening. Hence, the entire cement-bone interface was only elastically stimulated for both compliant and stiff cases. This can be explained by the interfacial elastic energy in pure tension, which can be determined as: $W({\delta }_n,0)=\underset{0}{\overset{{\delta }_n}{\int }}{T}_N\partial {\mathrm{\Delta }}_N={\mathrm{\Gamma }}_0·[1-2exp(-1)]$ and is larger for the compliant than for the stiff interface (Table 3).

Although simulations referred to the elastic phase, differences were predicted in the number of cracks. A possible explanation for this difference can be related to the definition of the normal traction (T_N) in the utilized numerical model (Wei and Hutchinson, 2008). The input parameters of this model for Case II were set to match the constant normal stiffness $\left(\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}\right)$ to the normal stiffness of our previous micro FEA-study (Waanders et al., 2010). Instead, Case III and IV were fit to the tensile strength (T_N,max) and its corresponding displacement (δ_N). This resulted in a decreasing normal stiffness $\left(\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}\right)$ in the elastic phase for Case III and IV (Figure 3) and therefore a different T_N-Δ_N-response compared to the normal stiffness of Case II. For example, the normal stiffness at zero displacement (Δ_N = Δ_T = 0.0mm) matches $\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}=\frac{{\mathrm{\Gamma }}_0}{{{\delta }_N}^2}$. For Case II and Case III or IV, this results in a $\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}$ of $251\frac{\mathit{MPa}}{mm}$ and $631.9\frac{\mathit{MPa}}{mm}$, respectively. This considerable difference is also visible in the T_N-Δ_N-responses (Figure 3). The difference in $\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}$ has hardly any influence on the traction distribution at the cement-bone interface (Figure 5), but does result in differences of interfacial displacement, which are significantly higher for the compliant cases.

Apart from the fact that only one stem type in one bone was considered, one of the main limitations of this study was that fatigue failure of the cement-bone interface was not considered. It can be expected that, although all the deformations were elastic, fatigue failure is likely to occur and to affect the mechanical situation at the local level. Fatigue failure will result in a mechanical degradation of the cement-bone interface and a further increase of cement cracks in the cement mantle.

It was previously found that fatigue failure of the cement-bone interface includes a decay of the interfacial stiffness (Mann et al., 2009; Waanders et al., 2009; Kim et al., 2004a). Furthermore, the number of cycles to failure, N_f, was determined as: $N_f=12.581·{\left(\frac{\sigma }{{\sigma }_{\mathit{ult}}}\right)}^{-13.43}$ (Kim et al., 2004b). This finding can be related to a damage parameter, d, as ${\stackrel{.}{d}}^{\mathit{cyc}}=\frac{1}{N_f}$ which linearly influences the stiffness, K = (1 − d)K₀ (with 0 ≤ d ≤ 1) (Moreo et al., 2006). Also, the stiffness of the cement-bone interface can be defined as: K = 10^0.52δ_c^−0.46CA^0.63, in which CA is the interface contact area and δ_c the interface creep: ${\delta }_c={10}^{0.57}·{\left(\frac{{\tau }_{max}}{K}\right)}^{1.35}{n}^{0.24}{CA}^{-0.40}$ with n represents the number of loading cycles (Mann et al., 2009). Assuming that the interface always shows an elastic behavior, mixed-mode traction-displacement responses are not a necessary input and the initial stiffness in tension $\left(\frac{\partial T_N}{\partial {\mathrm{\Delta }}_N}\right)$ and shear $\left(\frac{\partial T_T}{\partial {\mathrm{\Delta }}_T}\right)$ would already be sufficient.

Only two micromechanical models were used as input for the cohesive models of Case IV. This is a limitation to our study considering the wide spread of micromechanical response that has been shown experimentally (Mann et al., 2008, 2009). Because the extraction of multi-axial data from micromechanical FEA models requires a substantial amount of computational power, the number of calculations that can be performed is limited. In order to still provide representative data for the cohesive models, we selected the two extremes (stiffest and most compliant) of the four experimental specimens with distinct differences in terms of interface morphology and mechanical response (Waanders et al., 2010a).

A homogenous distribution of the cement-bone interface characteristics around the cement mantle is assumed even though that the cement penetration of a cemented hip reconstruction is much higher proximally than elsewhere (Stone et al., 1996). This is because no reliable data exist on the distribution of the mechanical properties of the cement-bone interface affected by the non-homogenous distribution (Waanders et al., 2010b; Perez and Palacios, 2010).

Although the above mechanical descriptions of the cement-bone interface are rather sophisticated, they still lack the major influence of the biological component. Indeed, biological processes govern the micro-biomechanical behavior of the interface (Mann et al., 2010) in terms of considerable soft-tissue formation around the cement, which reduces strength and stiffness roughly by a factor of 10. Hence, this biological response (and its subsequent mechanical deterioration) should be taken into account in the implementation of long-term degradation of cement-bone properties on the survival of cemented total hip arthroplasty.

With reference to the research questions as posed in the introduction, we conclude that: (1) A compliant cement-bone interface results in more cracks in the cement mantle than a stiff interface. Therefore the compliancy of the cement-bone interface should be included in models that focus on the prediction of failure of the cement mantle. (2) The cement-bone interface does not show immediate failure under the loading conditions as utilized in this study. Hence, it does not seem to be necessary to implement complex softening of the cement-bone interface. (3) Fatigue failure of the cement mantle results in more compression at the cement-bone interface and a decrease in tangential tractions. Finally, we conclude that failure of the cement-bone interface relies on fatigue damage, which can be based on decay of the interfacial stiffness as has been found experimentally. Therefore, use of complex mixed-mode models are unnecessary. Finally, we conclude that failure of the cement-bone interface in the direct post-operative situation does not occur, in agreement with clinical data. However, the compliancy of the cement-bone interface does have an accelerating effect on the formation of cement cracks and should be considered, without the necessity of the implementation of post-yield softening. For a realistic description of the cement-bone interface behavior on the longer-term, the mechanical representation of soft-tissue interpositioning at the interface should be represented. In that circumstance, post-yield softening may acquire importance, and require more complex descriptions to represent the mechanical behavior of the cement-bone interface accurately.