Abstract
The risk of fracture increases with age due to the decline of bone mass and bone quality. One of the age-related changes in bone quality occurs through the formation and accumulation of advanced glycation end-products (AGEs) due to non-enzymatic glycation (NEG). However as a number of other changes including increased porosity occur with age and affect bone fragility, the relative contribution of AGEs on the fracture resistance of aging bone is unknown. Using a high-resolution nonlinear finite element model that incorporate cohesive elements and micro-computed tomography-based 3d meshes, we investigated the contribution of AGEs and cortical porosity on the fracture toughness of human bone. The results show that NEG caused a 52% reduction in propagation fracture toughness (R-curve slope). The combined effects of porosity and AGEs resulted in an 88% reduction in propagation toughness. These findings are consistent with previous experimental results. The model captured the age-related changes in the R-curve toughening by incorporating bone quantity and bone quality changes, and these simulations demonstrate the ability of the cohesive models to account for the irreversible dynamic crack growth processes affected by the changes in post-yield material behavior. By decoupling the matrix-level effects due to NEG and intracortical porosity, we are able to directly determine the effects of NEG on fracture toughness. The outcome of this study suggests that it may be important to include the age-related changes in the material level properties by using finite element analysis towards the prediction of fracture risk.
Keywords: Non-enzymatic glycation, fracture mechanics, microcrack-based toughening, finite element modeling, cortical bone
1. Introduction
Fracture mechanics allow for the mechanistic evaluation of material fracture resistance by experimentally localizing the fracture processes (Brown et al., 2000; Zioupos and Currey, 1998). When a flaw is propagated in a structure, the stress intensity factor and strain energy release rates can be determined as a function of the crack length, applied load, and the geometric function of the specimen in order to obtain the fracture toughness at the material level. The relationship between fracture toughness and the extension of a crack is known as the resistance curve (R-curve), it can quantify the ability of a material to resist propagation of fracture (Vashishth et al., 1997; Vashishth, 2004). Unlike classical brittle materials, bone derives its fracture resistance from the intrinsic and extrinsic mechanisms during the process of crack propagation (Nalla et al., 2004; Nalla et al., 2005; Vashishth et al., 1997), and bone demonstrates a toughening behavior characterized by increasing resistance with increasing crack length (Nalla et al., 2004; Vashishth, 2004). Aging human bone demonstrates a steady decline in this R-curve behavior (Nalla et al., 2005; Vashishth et al., 1997; Vashishth, 2004). The cause of this increase in fragility has been attributed to increased porosity (Norman et al., 1995; Yeni and Norman, 2000) and a decline in bone matrix quality (Hui et al., 1988; Riggs and Melton, 1995; Tang et al., 2008; Zioupos, 2001). However, the relative contributions of these factors toward the fragility of bone remain unclear.
The cohesive modeling of crack process zones has been experimentally validated and shown to be useful for describing a wide range of physical situations including human bone (Ural and Vashishth, 2006a; Ural and Vashishth, 2005; Ural and Vashishth, 2007). Cohesive models have been widely applied in simulating materials that exhibit microcracking failure mechanisms including the yielding of steel plates (Dugdale, 1960), crack propagation of concrete (Hillerborg et al., 1976), void nucleation in metallic materials (Needleman, 1987), plasticity effects in ductile materials, (Tvergaard and Hutchinson, 1992), dynamic fracture in brittle solids (Camacho and Ortiz, 1996; Ortiz and Pandolfi, 1999) and fatigue crack growth in metals (de Andres et al., 1999). The cohesive crack represents the physical processes occurring in the vicinity of a propagating crack in a material by a simplified traction–displacement relationship (Tvergaard and Hutchinson, 1992). This approach allows the inclusion of phenomenological observations in the predictions of fundamental failure mechanisms that can be defined independently from the continuum constitutive laws. Consequently, this technique allows the precise modeling of physical alterations such as the pore distribution and material-level changes including those caused by non-enzymatic glycation, and their relative roles in the fracture propagation in bone.
Non-enzymatic glycation (NEG) is a post-translational modification of proteins that has been shown to reduce bone quality (Tang et al., 2007; Vashishth et al., 2001; Wang et al., 2002). NEG occurs through the Maillard reaction where extra-cellular sugars spontaneously react with free amino groups on proteins to form molecular crosslinks, known as advanced glycation end-products (AGEs) (Knott and Bailey, 1998). The elevated concentrations of these crosslinks can adversely affect bone resorption (Valcourt et al., 2006), and the accumulation of AGEs in bone is known to increase with age, disease, and therapies (Odetti et al., 2005; Tang et al., 2007; Wang et al., 2002). Accumulated AGEs reduces bone fracture resistance (Tang et al., 2008; Vashishth et al., 2001; Wang, et al.) through modifying toughening mechanisms such as microdamage formation (Tang and Vashishth, 2010). However, as a number of changes including increasing porosity occur in the bone matrix that affect its fracture toughness (Norman et al., 1995; Yeni and Norman, 2000), the relevance of AGEs in bone’s propensity to fracture and the mechanistic contributions of AGEs on the fracture behavior of aging bone remain to be investigated.
Using a combination of a non-linear plasticity fracture mechanics cohesive model, high-resolution imaging, and experimental data, we seek to determine the contribution of NEG on the R-curve toughening behavior of bone and cortical porosity on the fracture toughness of human bone.
2. Methods
Finite element Mesh
The simulations for crack growth were performed for a compact tension specimen with dimensions in accordance with ASTM standards (ASTM, 2002). Three different previously generated finite element meshes (Ural and Vashishth, 2007) in the shape of compact tension specimens (E399-90) were used (Figure 1). The first case is a manually generated solid mesh containing no porosity; the other two cases were generated from a microCT scan conducted at 21 μm resolution (VivaCT 40; Scanco Medical, CH) on a 19 year-old donor bone specimen containing 1% intracortical porosity, and on an 81 year-old donor bone specimen containing 5% intracortical porosity. The crack propagation direction was parallel to the osteonal direction in these specimens. All three meshes were either created or scaled to have 210 μm voxels. Previous work has shown that the scaling of the microCT meshes has only a modest effect on the bone volume fraction and alters approximately 0.1% of the in-plane porosity values (Ural and Vashishth, 2006a). All simulations were conducted in displacement control in 1% linear increments at each step that were applied linearly from the top surface of the circular holes of the compact tension specimens (Ural and Vashishth, 2007). The load and crack growth data, generated in the simulations, were used to calculate the crack growth resistance KR at various crack lengths (Eq. 1, 2):
| (Equation 1) |
| (Equation 2) |
Where P is the load, a is the crack length, W is the width of the specimen from the load line, and B is the thickness. The energy required to initiate a crack, or the initiation toughness (KIC), is defined at the point at which max load occurs. For all simulations, KR is plotted as a function of the square root of the crack growth to determine the R-curve slope by linear regression, also known as the propagation toughness, for the various crack lengths ranging from 0.25 mm to 2.25 mm (Ural and Vashishth, 2006a; Vashishth et al., 1997; Vashishth, 2004). The crack plane was defined as the plane that coincides with the notch tip of the compact tension specimen, and the elements that lie on this plane are assigned cohesive properties.
Figure 1.
Three different finite element meshes of ASTM E399-90 compact tension specimens were used in this study: (A) a solid mesh containing no porosity; (B) a mesh containing 1% porosity; and (C) a mesh containing 5% porosity (Ural and Vashishth, 2007).
Elastic constants
The continuum material was modeled as a linear elastic orthotropic material, and the constants were obtained from literature (Saulgozis et al., 1973) (Table I). These values were maintained as constant through all the simulations since the objective of the study NEG has shown to have relatively little effects on the linear elastic behavior of bone.
Table I.
The values of orthotropic material constants assigned to the elastic elements in the simulations (Saulgozis et al., 1973).[I reduced the width of the table]
| Material properties of the human tibia | |
|---|---|
| E1 [GPa] | 6.9 |
| E2 [GPa] | 18.4 |
| E3 [GPa] | 8.5 |
| G12 [GPa] | 3.6 |
| G23 [GPa] | 4.9 |
| G13 [GPa] | 2.4 |
| ν 13 | 0.49 |
| ν 23 | 0.31 |
| ν 12 | 0.12 |
Cohesive modeling parameters
The cohesive model used here employs an ascending and descending branch with a coupled representation of normal and shear crack displacements (Ortiz and Pandolfi, 1999; Tvergaard and Hutchinson, 1992; Ural and Vashishth, 2006a; Ural and Vashishth, 2005; Ural and Vashishth, 2006b). In such a cohesive model, two parameters, namely the energy release rate (GC) and critical stress (σC), are sufficient to define the unique traction-displacement relationship in the cohesive zone, because δU can be defined as GC/σC. Since non-enzymatic glycation does not affect the ultimate stress of cortical bone (Tang et al., 2008; Vashishth et al., 2001), σC was set to an experimentally determined value (σC = 35.7 MPa) and kept constant in all simulations (Tang et al., 2008). The traction-displacement relationship was defined by the following relationship (Eq. 3):
| (Equation 3) |
Where traction T is a function that relates the displacement δ and the characteristic parameters of the material. Each cohesive element follows the traction-crack opening profile described above and is considered to be cracked when there is no transfer of traction between the opening interfaces. The values of characteristic effective crack opening displacement (δU) were calculated from GC and σC (Table II). δC was selected to be 0.00175 mm and is small compared to (δU). The cohesive elements are represented as surface elements with zero thickness and are compatible with solid elements (Ural and Vashishth, 2006b). A traction-crack profile is assigned to each cohesive element where there is no transfer of traction between the opening surfaces such that T = 0 and δ=δU.
Table II.
The cohesive parameters used in the simulations for this study
| % Increase of AGEs | % Loss in GC | GC (N/mm)1 | σC (MPa)2 | δU (mm)3 |
|---|---|---|---|---|
| 0 | 0 | 1.12 | 35.7 | 0.031 |
| 100% | 45.5% | 0.64 | 35.7 | 0.016 |
| 200% | 60.3% | 0.44 | 35.7 | 0.012 |
| 300% | 68.9% | 0.34 | 35.7 | 0.0097 |
| 400% | 75.0% | 0.27 | 35.7 | 0.0078 |
| 500% | 79.8% | 0.22 | 35.7 | 0.0063 |
| 600% | 83.7% | 0.18 | 35.7 | 0.0051 |
The baseline value for GC was selected based the published value (Brown et al., 2000).
Because glycation has previously been shown to not have a significant effect on ultimate stress, the average experimental values of ultimate stress from these samples were used for the simulations (Tang et al., 2008).
The values of characteristic effective crack opening displacement (δU) were calculated from GC and σC that are given in the third and fourth columns. δC is selected to be 0.00175 and is small compared to δU.
The determination of AGEs-dependent Energy release rate (GC)
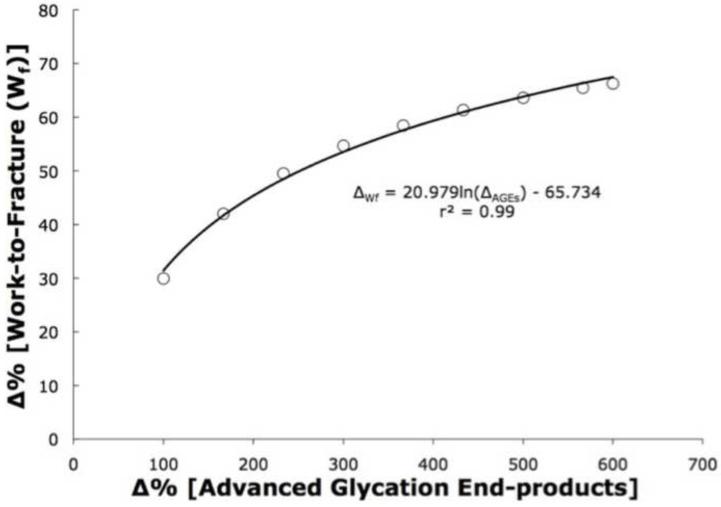
The determination of energy release rate (GC) was based on the previously published relationships between the bone matrix concentrations of advanced glycation end-products with experimentally measured work-to-fracture (Tang et al., 2008) to define a normalized relationship where Wf declines in a nonlinear manner with increasing AGEs (Figure 2) (Eq 4):
| Equation (4) |
Where ΔWf and ΔAGEs are percentage changes in work-to-fracture and AGEs concentration in the bone matrix. Work-to-fracture (Wf) is equivalent to the path-independent J-integral, defined as the amount of irrecoverable energy of the stress-strain relationship in three-point bending (DeLorenzi, 1982; Rice, 1974; Rice, 1968). In addition, since the J-integral approximates GC in a two-dimensional crack path (Jin and Sun, 2004), we are therefore able derive the following relationship between the changes in the percentages of Wf and percentage Gc (Eq 5):
| Equation (5) |
Values of ΔGc are subsequently computed for 100% - 600% increases in AGEs (Table II). These percentages are consistent with previous works that showed that a doubling of AGEs corresponds to approximately two to three decades of aging. Consequently, a 600% increase in AGEs corresponds to 60-70 years of aging (Odetti et al., 2005; Tang et al., 2007). In order to determine the numerical values of Gc, a baseline value of 1.12 N/mm, a value experimentally determined from a healthy 19-year-old individual (Brown et al., 2000), was used to determine the subsequent AGEs-dependent decreases in Gc.
Figure 2.
Based on a previous study (Tang et al., 2008), we established a relationship between the change of work-to-fracture and the changes in advanced glycation end-products. Because work-to-fracture is intrinsically related to the energy release rate (DeLorenzi, 1982; Jin and Sun, 2004; Rice, 1974; Rice, 1968), the resulting Gc is based on the changes in the AGEs to determine the contributions of increased AGEs on the loss of bone toughness.
Numerical simulations
The following simulations were conducted: 0% porosity mesh with 0, 100, 200, 300, 400, 500, and 600% AGEs; 1% porosity mesh with 0, 300, and 600% AGEs; and 5% porosity mesh with 0, 300, and 600% AGEs. All simulations were done using Abaqus 6.5.5 (Abaqus Inc, Providence, RI. USA), using a Windows XP (Microsoft Inc, Redmond, WA, USA) based dual-Xeon 3.0 Ghz processors (Intel Inc. Santa Clara, CA, USA) with 2 gigabytes of RAM.
Statistical analyses
Linear regressions were used to determine the R-curve values based on the crack propagation curves, and the respective coefficients of determination (r2) were calculated. Microsoft Excel (Microsoft Corp, Redmond, WA, USA) was used for these calculations.
3. Results
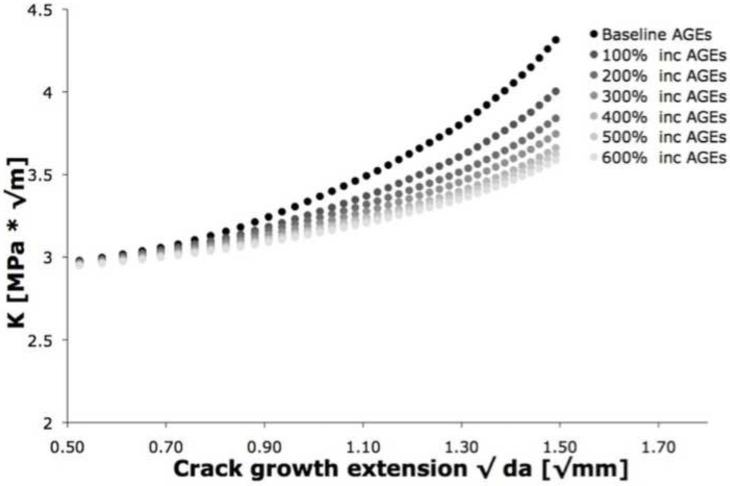
For the solid mesh case, the cohesive-based finite element modeling showed increasing load with crack propagation (Figure 3). Consistent with experimental observations of toughening in bone, these increasing trends reflect a rising crack growth resistance behavior (Brown et al., 2000; Vashishth et al., 1997; Vashishth, 2004). The coefficients of determination (r2) for the R-curve slope ranged from 0.97 to 0.99.
Figure 3.
The rising resistance curve (R-curve) behavior for the solid 0% porosity mesh showed that increasing the AGEs reduces the R-curve slope, confirming that NEG causes a loss of toughening mechanisms.
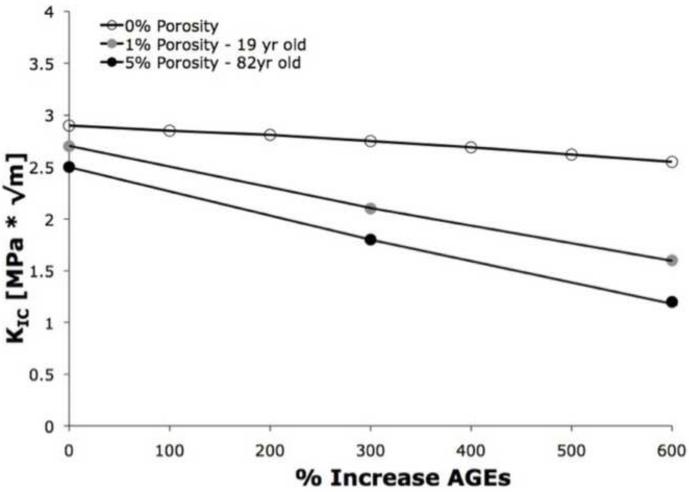
Effects of AGEs and porosity on initiation toughness
In the 0% porosity solid mesh, the increasing values of AGEs had a relatively small effect on initiation toughness (KIC). The increase of 100-600% in AGEs, resulted in only minor reductions of in KIC ranging from 1.7% to 12%, suggesting that KIC is relatively insensitive to changes in AGEs at 0% porosity (Table III; Figure 4). In contrast, when coupled with increasing porosity, the effects of AGEs on initiation toughness were more pronounced. For example, in the 1% porosity case, increasing AGEs to 300% of the baseline resulted in a 22% loss in KIC. Further increases of AGEs up to 600% of the baseline values resulted in 41% loss in KIC. Additionally, at the same levels of AGEs, the 1% porosity mesh resulted in greater decreases in KIC when compared with the 0% solid mesh, suggesting that the effects of porosity on KIC are more pronounced when coupled with NEG-induced material level changes. Likewise, in the 5% porosity case, increasing AGEs to 300% of the baseline values resulted in a 28% loss of KIC, and 600% AGEs results in 52% loss of KIC.
Table III.
The effects of increasing AGEs and cortical porosity on the reduction of initiation toughness (KIC). Values are expressed in terms of percentages increased when compared with the 0% AGEs cases
| Increases of advanced glycation end-products | ||||||
|---|---|---|---|---|---|---|
| Intracortical porosity |
100% | 200% | 300% | 400% | 500% | 600% |
| 0% | − 1.7% a | − 3.1% a | − 5.2% a | − 7.2% a | − 9.7% a | − 12% a |
| 1% | -- | -- | − 22% b | -- | -- | − 41% b |
| 5% | -- | -- | − 28% c | -- | -- | − 52% c |
When compared with the 0% AGEs, 0% porosity case.
When compared with the 0% AGEs, 1% porosity case.
When compared with the 0% AGEs, 5% porosity case.
Figure 4.
Despite increases in the AGEs in the solid mesh, initiation toughness (KIC) declined at most by 12%, suggesting that unlike propagation of fractures, the increased accumulation of AGEs alone has little effect on initiation of fractures. However, when coupled with increased porosity, increased AGEs reduced the initiation toughness by as much as 52% for the 5% porosity/600% AGEs case.
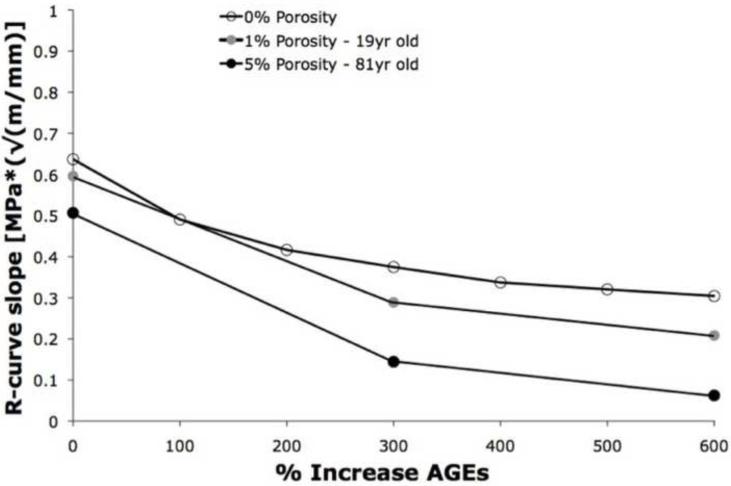
Effects of AGEs and porosity on R-curve toughening
Increasing the AGEs had a greater effect on the propagation toughness (R-curve slope) than the similar increases of AGEs on initiation toughness (Table IV; Figure 5). In the 0% porosity mesh, increases in AGEs resulted in 23%-52% decreases in R-curve toughening. When AGEs were increased to 300% along with 1% porosity, the propagation toughness increased up to 51%, and further increases in AGEs to 600% caused a reduction of 71% in propagation toughness (Figure 5). Similarly, in the 5% porosity mesh, an increase of 300% AGES resulted in a 65% reduction in propagation toughness, and a 600% increase in AGEs resulted in up to 88% loss of propagation toughness.
Table IV.
The effects of increasing AGEs and cortical porosity on the reduction of propagation toughness (R-curve slope). Values are expressed in terms of percentages increased when compared with the 0% AGEs cases
| Increases of advanced glycation end-products | ||||||
|---|---|---|---|---|---|---|
| Intracortical porosity |
100% | 200% | 300% | 400% | 500% | 600% |
| 0% | 23% a | 34% a | 41% a | 47% a | 49% a | 52% a |
| 1% | -- | -- | 51% b | -- | -- | 71% b |
| 5% | -- | -- | 65% c | -- | -- | 88% c |
When compared with the 0% AGEs, 0% porosity case.
When compared with the 0% AGEs, 1% porosity case.
When compared with the 0% AGEs, 5% porosity case.
Figure 5.
Propagation toughness (R-curve slope) decreased significantly with increasing AGEs for a given value of porosity (0%, 1%, and 5%). The combination of 5% porosity and 600% increase of AGEs resulted in an 88% reduction in propagation toughness.
4. Discussion
The model developed in this study captures the changes in bone fragility caused by changes in bone quantity (porosity) and bone quality (accumulation of advanced glycation end-products), and demonstrates our ability to decouple the material level and the microstructural changes associated with aging. The cohesive model has been previously validated experimentally to accurately capture the mechanistic fracture processes of bone given material level properties (Ural and Vashishth, 2006a; Ural and Vashishth, 2005; Ural and Vashishth, 2007). The computational findings obtained here confirm that non-enzymatic glycation has a greater effect on propagation toughness than on initiation toughness (Vashishth et al., 2003). The novel application of an experimentally derived relationship between the biochemistry of the organic matrix and a specific fracture mechanics parameter, namely the collagen crosslinking by non-enzymatic glycation and fracture toughness by energy release rate (Gc), captures the effects of AGEs on bone fragility.
The results of this study show that the combined effects of porosity and increased AGEs decrease fracture toughness greater than either factor alone. For example, at the baseline value of AGEs, increasing the mesh porosity from 0% to 5% only reduced the R-curve slope values by 16% (Figure 5). However, combining the 5% porosity structure with a 600% increase in AGEs at the material level resulted in a nearly 92% reduction in propagation toughness compared to the 0% porosity/100% AGEs case. When a 300% increase of AGEs is used, the simulations show a 10% reduction in R-curve slope between 0% to 1% porosity meshes and a 24% reduction in R-curve slope between 0% to 5% porosity meshes. Similarly, at a level corresponding to a 600% increase of AGEs, increasing the porosity from 0% to 1% reduces the R-curve slope by 19%; increasing the porosity from 0% to 5% reduces the R-curve slope by 36%. Taken together, these results suggest that the adverse effects of increased AGEs in bone are nonlinear and may be worsened by the increasing porosities of aging bone.
The percentage increases of AGEs used in this study were derived from published works that directly measured from the age-related increases in the in vivo levels of AGEs measured from a human cadaveric model. Previous studies have shown that AGEs can increase up to 600% from young to elderly individuals (Odetti et al., 2005; Tang et al., 2007; Wang et al., 2002). Disorders in glucose metabolism such as diabetes (Monnier et al., 1984; Reiser, 1998; Schwartz, 2003) and pharmacological treatments such as bisphosphonates (Allen et al., 2008; Saito et al., 2008; Tang et al., 2008) are known to further elevate the accumulation of AGEs in bone. Such increased levels may further increase the propensity to fracture even at relatively normal intracortical porosities.
Consistent with the simulation results provided here, NEG-mediated changes in bone have been shown to increase the production of crack-like morphologies (Tang and Vashishth, 2010). The higher incidence of cracks experimentally observed in highly glycated bone might be explained by the reduced R-curve toughening that subsequently allows the increased propagation of cracks. Experimental observations of microdamage formation in bone have found that age-related and pathological changes in bone quality can cause an increased formation of microcracks (Diab et al., 2005a; Diab et al., 2005b; Diab and Vashishth, 2005; Diab and Vashishth, 2006). The results of this study suggest that the loss in fracture toughness may be attributable to NEG. The increased accumulation of AGEs in bone causes a stiffening of the organic matrix (Tang et al., 2007; Vashishth et al., 2001) and may cause the premature debonding and delamination of the mineral-collagen interfaces to reduce tissue level toughness (Siegmund et al., 2008).
Although clinical fractures involve failure of both the cortical shell and cancellous bone (Eswaran et al., 2006), to date limited FEA approaches have been described to predict cortical bone failure. Our results show that the material properties and the porosity of bone are important determinants of fragility and should be incorporated in the clinical assessment of fracture risk. In particular, the prediction of radial fractures where the cancellous bone has a limited structural contribution (Black and Becker, 2009) may be improved by the approach described here. Recent advances have shown that material properties of bone can be minimally invasively measured in vivo (Hansma et al., 2006), and it may be valuable to incorporate material level information into finite element analyses to improve the assessment of fracture risk.
It is important to note several underlying assumptions of this study. This model does not incorporate local mineral heterogeneity that can change with age and may contribute to fracture (Riggs and Melton, 1995). The contributions of other matrix effects in this model have been suppressed by setting the critical or ultimate stress (σc) constant. However, the incorporation of mineralization information in a voxel-based finite element model has been shown to improve predictability by only 8% (Nagaraja et al., 2006). In addition, the model used here does not account for other microstructural features of the cortical bone including osteons, cement lines, and lamellae. Instead, the combined effects of these microstructural entities are introduced into the simulations through globally measured model parameters. Although it has been proposed that cement lines and osteonal orientation can affect crack growth and deflection (O’Brien et al., 2005; Nalla et al., 2005), little experimental data exists that quantify these effects. By using experimental data and material properties measured from the same length scale as the model, the simulations allow us to determine the effects of NEG on the mechanistic crack processes.
In conclusion, using a novel cohesive finite element model incorporating bone quality changes due to non-enzymatic glycation and bone quantity changes measured by intracortical porosity, we show that the increased accumulation of AGEs together with bone porosity can adversely affect both the initiation and propagation toughness of bone. The technique described may be useful clinically by improving prediction of fracture using structural and material level information about bone.
Acknowledgements
This work was funded through NIH grant AG20618 (DV) and AR059497 (ST). The authors acknowledge the Imaging Core Facility at the Centre of Biotechnology & Interdisciplinary Studies at Rensselaer Polytechnic Institute for the use the MicroCT.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
None declared.
References
- Allen MR, Gineyts E, Leeming DJ, Burr DB, Delmas PD. Bisphosphonates Alter Trabecular Bone Collagen Cross-Linking and Isomerization in Beagle Dog Vertebra. Osteoporosis international. 2008;19:329–337. doi: 10.1007/s00198-007-0533-7. [DOI] [PubMed] [Google Scholar]
- ASTM . Astm E-399: Standard Test Method for Plain-Strain Fracture Toughness of Metallic Materials. ASTM International; 2002. [Google Scholar]
- Black WS, Becker JA. Common Forearm Fractures in Adults. American Family Physician. 2009;80:1096–1102. [PubMed] [Google Scholar]
- Brown CU, Yeni YN, Norman TL. Fracture Toughness Is Dependent on Bone Location--a Study of the Femoral Neck, Femoral Shaft, and the Tibial Shaft. Journal of Biomedical Material Research. 2000;49:380–389. doi: 10.1002/(sici)1097-4636(20000305)49:3<380::aid-jbm11>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- Camacho GT, Ortiz M. Computational modeling of impact damage in brittle materials. International Journal of Solids and Structures. 1996;33:2899–2938. [Google Scholar]
- de Andres A, Perez JL, Ortiz M. Elastoplastic finite element analysis of three-dimensional fatigue crack growth in aluminum shafts subjected to axial loading. International Journal of Solids and Structures. 1999;36:2231–2258. [Google Scholar]
- DeLorenzi H. On the Energy Release Rate and the J-Integral for 3-D Crack Configurations. International Journal of Fracture. 1982;19:183–192. [Google Scholar]
- Diab T, Condon KW, Burr DB, Vashishth D. Age-Related Change in the Damage Morphology of Human Cortical Bone and Its Role in Bone Fragility. Bone. 2005;38:427–431. doi: 10.1016/j.bone.2005.09.002. [DOI] [PubMed] [Google Scholar]
- Diab T, Sit S, Kim D, Rho J, Vashishth D. Age-Dependent Fatigue Behaviour of Human Cortical Bone. European Journal of Morphology. 2005;42:53–59. doi: 10.1080/09243860500095539. [DOI] [PubMed] [Google Scholar]
- Diab T, Vashishth D. Effects of Damage Morphology on Cortical Bone Fragility. Bone. 2005;37:96–102. doi: 10.1016/j.bone.2005.03.014. [DOI] [PubMed] [Google Scholar]
- Diab T, Vashishth D. Morphology, Localization and Accumulation of in Vivo Microdamage in Human Cortical Bone. Bone. 2006;40:612–618. doi: 10.1016/j.bone.2006.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dugdale DS. Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids. 1960;8:100–104. [Google Scholar]
- Eswaran SK, Gupta A, Adams MF, Keaveny TM. Cortical and Trabecular Load Sharing in the Human Vertebral Body. Journal of Bone Mineral. Research. 2006;21:307–314. doi: 10.1359/jbmr.2006.21.2.307. [DOI] [PubMed] [Google Scholar]
- Hansma P, Turner P, Fantner G. Bone Diagnostic Instrument. Review of Scientific Instruments. 2006;77:1–6. doi: 10.1063/1.2937199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillerborg A, Modeer M, Petersson PE. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research. 1976;6:773–782. [Google Scholar]
- Hui SL, Slemenda CW, Johnston CC. Age and Bone Mass as Predictors of Fracture in a Prospective Study. Journal Clinical Investigation. 1988;81:1804–1809. doi: 10.1172/JCI113523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin Z, Sun C. On J-Integral and Potential Energy Variation. International Journal of Fracture. 2004;126:19–24. [Google Scholar]
- Knott L, Bailey AJ. Collagen Cross-Links in Mineralizing Tissues: A Review of Their Chemistry, Function, and Clinical Relevance. Bone. 1998;22:181–187. doi: 10.1016/s8756-3282(97)00279-2. [DOI] [PubMed] [Google Scholar]
- Monnier VM, Kohn RR, Cerami A. Accelerated Age-Related Browning of Human Collagen in Diabetes Mellitus. Proceedings of National Academy Science U.S.A. 1984;81:583–587. doi: 10.1073/pnas.81.2.583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagaraja S, Lin ASP, Guldberg RE. Age-Related Changes in Trabecular Bone Microdamage Initiation. Bone. 2006;40:973–980. doi: 10.1016/j.bone.2006.10.028. [DOI] [PubMed] [Google Scholar]
- Nalla RK, Kruzic JJ, Kinney JH, Ritchie RO. Effect of Aging on the Toughness of Human Cortical Bone: Evaluation by R-Curves. Bone. 2004;35:1240–1246. doi: 10.1016/j.bone.2004.07.016. [DOI] [PubMed] [Google Scholar]
- Nalla RK, Stölken JS, Kinney JH, Ritchie RO. Fracture in Human Cortical Bone: Local Fracture Criteria and Toughening Mechanisms. Journal of Biomechanics. 2005;38:1517–1525. doi: 10.1016/j.jbiomech.2004.07.010. [DOI] [PubMed] [Google Scholar]
- Needleman A. A Continuum Model for Void Nucleation by Inclusion Debonding. Journal of Applied Mechanics. 1987;54:525–531. [Google Scholar]
- Norman TL, Vashishth D, Burr DB. Fracture Toughness of Human Bone under Tension. Journal of Biomechanics. 1995;28:309–320. doi: 10.1016/0021-9290(94)00069-g. [DOI] [PubMed] [Google Scholar]
- Odetti P, Rossi S, Monacelli F, Poggi A, Cirnigliaro M, Federici M, Federici A. Advanced Glycation End Products and Bone Loss During Aging. Annals of the New York Academy of Sciences. 2005;1043:710–717. doi: 10.1196/annals.1333.082. [DOI] [PubMed] [Google Scholar]
- Ortiz M, Pandolfi A. Finite-Deformation Irreversible Cohesive Elements for Three-Dimensional. International Journal for Numerical Methods in Engineering. 1999;44:1267–1282. [Google Scholar]
- Reiser KM. Nonenzymatic Glycation of Collagen in Aging and Diabetes. Proceedings of Society Experimental Biology and Medicine. 1998;218:23–37. doi: 10.3181/00379727-218-44264. [DOI] [PubMed] [Google Scholar]
- Rice JR. Limitations to the Small Scale Yielding Approximation for Crack Tip Plasticity. Journal of the Mechanics and Physics of Solids. 1974;22:17–26. [Google Scholar]
- Rice JR. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. Journal of Applied Mechanics. 1968;35:379–386. [Google Scholar]
- Riggs BL, Melton LJ. The Worldwide Problem of Osteoporosis: Insights Afforded by Epidemiology. Bone. 1995;17:505S–11S. doi: 10.1016/8756-3282(95)00258-4. [DOI] [PubMed] [Google Scholar]
- Saito M, Mori S, Mashiba T, Komatsubara S, Marumo K. Collagen Maturity, Glycation Induced-Pentosidine, and Mineralization Are Increased Following 3-Year Treatment with Incadronate in Dogs. Osteoporosis international. 2008;19:1343–1354. doi: 10.1007/s00198-008-0585-3. [DOI] [PubMed] [Google Scholar]
- Saulgozis Y, Slutskii L, Knets I, Yanson K. Investigation of the Relationships between the Various Mechanical Properties and the Biochemical Composition of Human Bone Tissue. Mechanics of Composite Materials. 1973;1:138–145. [Google Scholar]
- Schwartz AV. Diabetes Mellitus: Does It Affect Bone? Calcified Tissue International. 2003;73:515–519. doi: 10.1007/s00223-003-0023-7. [DOI] [PubMed] [Google Scholar]
- Siegmund T, Allen MR, Burr DB. Failure of Mineralized Collagen Fibrils: Modeling the Role of Collagen Cross-Linking. Journal of Biomechanics. 2008;41:1427–1435. doi: 10.1016/j.jbiomech.2008.02.017. [DOI] [PubMed] [Google Scholar]
- Tang SY, Allen MR, Phipps R, Burr DB, Vashishth D. Changes in Non-Enzymatic Glycation and Its Association with Altered Mechanical Properties Following 1-Year Treatment with Risedronate or Alendronate. Osteoporosis international. 2008;20:887–894. doi: 10.1007/s00198-008-0754-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang SY, Vashishth D. Non-Enzymatic Glycation Alters Microdamage Formation in Human Cancellous Bone. Bone. 2010;46:148–154. doi: 10.1016/j.bone.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang SY, Zeenath U, Vashishth D. Effects of Non-Enzymatic Glycation on Cancellous Bone Fragility. Bone. 2007;40:1144–1151. doi: 10.1016/j.bone.2006.12.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tvergaard V, Hutchinson J. Resistance and Fracture Process Parameters in Elastic-Plastic Solids. Journal of Mechanics Physical Solids. 1992;40:1377–1397. [Google Scholar]
- Ural A, Vashishth D. Anisotropy of Age-Related Toughness Loss in Human Cortical Bone: A Finite Element Study. Journal of Biomechanics. 2006;40:1606–1614. doi: 10.1016/j.jbiomech.2006.07.023. [DOI] [PubMed] [Google Scholar]
- Ural A, Vashishth D. Cohesive Finite Element Modeling of Age-Related Toughness Loss in Human Cortical Bone. Journal of Biomechanics. 2005;39:2974–2982. doi: 10.1016/j.jbiomech.2005.10.018. [DOI] [PubMed] [Google Scholar]
- Ural A, Vashishth D. Interactions between Microstructural and Geometrical Adaptation in Human Cortical Bone. Journal of Orthopedic Research. 2006;24:1489–98. doi: 10.1002/jor.20159. [DOI] [PubMed] [Google Scholar]
- Ural A, Vashishth D. Effects of Intracortical Porosity on Fracture Toughness in Aging Human Bone: A MicroCT-Based Cohesive Finite Element Study. Journal of Biomechanical Engineering. 2007;129:625–631. doi: 10.1115/1.2768377. [DOI] [PubMed] [Google Scholar]
- Valcourt U, Merle B, Gineyts E, Viguet-Carrin S, Delmas PD, Garnero P. Non-Enzymatic Glycation of Bone Collagen Modifies Osteoclastic Activity and Differentiation. Journal Biological Chemistry. 2006;282:5691–5703. doi: 10.1074/jbc.M610536200. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Behiri JC, Bonfield W. Crack Growth Resistance in Cortical Bone: Concept of Microcrack Toughening. Journal of Biomechanics. 1997;30:763–769. doi: 10.1016/s0021-9290(97)00029-8. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Gibson GJ, Khoury JI, Schaffler MB, Kimura J, Fyhrie DP. Influence of Nonenzymatic Glycation on Biomechanical Properties of Cortical Bone. Bone. 2001;28:195–201. doi: 10.1016/s8756-3282(00)00434-8. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Wu P, Gibson GJ. Age-Related Loss in Bone Toughness Is Explained by Non-Enzymatic Glycation of Collagen. Transactions of Orthopedic Research Society. 2003;1:497. [Google Scholar]
- Vashishth D. Rising Crack-Growth-Resistance Behavior in Cortical Bone: Implications for Toughness Measurements. Journal of Biomechanics. 2004;37:943–946. doi: 10.1016/j.jbiomech.2003.11.003. [DOI] [PubMed] [Google Scholar]
- Wang X, Shen X, Li X, Agrawal CM. Age-Related Changes in the Collagen Network and Toughness of Bone. Bone. 2002;31:1–7. doi: 10.1016/s8756-3282(01)00697-4. [DOI] [PubMed] [Google Scholar]
- Yeni YN, Norman TL. Calculation of Porosity and Osteonal Cement Line Effects on the Effective Fracture Toughness of Cortical Bone in Longitudinal Crack Growth. Journal Biomedical Materials Research. 2000;51:504–509. doi: 10.1002/1097-4636(20000905)51:3<504::aid-jbm27>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Zioupos P, Currey JD. Changes in the Stiffness, Strength, and Toughness of Human Cortical Bone with Age. Bone. 1998;22:57–66. doi: 10.1016/s8756-3282(97)00228-7. [DOI] [PubMed] [Google Scholar]
- Zioupos P. Ageing Human Bone: Factors Affecting Its Biomechanical Properties and the Role of Collagen. Journal of Biomaterials Applications. 2001;15:187–229. doi: 10.1106/5JUJ-TFJ3-JVVA-3RJ0. [DOI] [PubMed] [Google Scholar]