Understanding Equivalence and Noninferiority Testing

Abstract

Increasingly, the goal of many studies is to determine if new therapies have equivalent or noninferior efficacies to the ones currently in use. These studies are called equivalence/noninferiority studies, and the statistical methods for their analysis require only simple modifications to the traditional hypotheses testing framework. Nevertheless, important and subtle issues arise with the application of such methods. This article describes the concepts and statistical methods involved in testing equivalence/noninferiority. The aim is to enable the clinician to understand and critically assess the growing number of articles utilizing such methods.

INTRODUCTION

Effective standards of care have been developed in many clinical settings, and it is increasingly more difficult to develop new therapies with higher efficacy than the standard of care. Nowadays, the goal of many studies is to determine if novel therapies have equivalent or noninferior efficacies to the ones currently in use. These therapies offer advantages such as fewer side effects, lower cost, easier application, or fewer drug interactions. In most respects, the design of such studies follows the same general principles (avoidance of bias, confounding, etc.) of traditional comparative studies in which the objective is to establish either a difference between the efficacies or the superiority of one of them. The objective in testing for equivalence/noninferiority is precisely the opposite, and it requires modifications to the traditional hypotheses testing methods.

In hypotheses testing, the research or alternative hypothesis represents what the study aims to show. The null hypothesis is the opposite of the research hypothesis and is what the investigator hopes to disprove. Traditionally, the error that is minimized is that of incorrectly establishing the research hypothesis (i.e., incorrectly rejecting the null hypothesis). This error is called the type I error, and the probability of it occurring is called the significance level of the test. This level is denoted by α, and its value is frequently set at 0.05 or lower. Therefore, the burden of proof is on the research hypothesis in the sense that it is established only if there is strong enough evidence in its favor. When this evidence is not realized, the null hypothesis cannot be rejected.

In traditional (two-sided) comparative studies, the burden of proof rests on the research hypothesis of difference between the efficacies (Table 1). If the evidence is not strong enough in favor of a difference, equality cannot be ruled out. In contrast, the goal of equivalence studies is to demonstrate equivalency, so that is where the burden of proof rests (Table 1). If the evidence in favor of equivalence is not strong enough, nonequivalence cannot be ruled out. In essence, the null and research hypotheses in testing equivalence are simply those of a traditional comparative study reversed. For noninferiority studies, the research hypothesis is that the new therapy is either equivalent or superior to the current therapy (Table 1).

Table 1.

Hypotheses Associated with the Different Types of Studies when Comparing a New Therapy Against a Current Therapy with Respect to Efficacy

Type of study	Null hypotheses	Research hypothesis
Traditional comparative	There is no difference between the therapies	There is a difference between the therapies
Equivalence	The therapies are not equivalent	The new therapy is equivalent to current therapy
Noninferiority	The new therapy is inferior to the current therapy	The new therapy is not inferior to the current therapy

The term equivalent is not used here in the strict sense, but rather to mean that the efficacies of the two therapies are close enough so that one cannot be considered superior or inferior to the other. This concept is formalized in the definition of a constant called the equivalence margin. The equivalence margin defines a range of values for which the efficacies are “close enough” to be considered equivalent. In practical terms, the margin is the maximum clinically acceptable difference that one is willing to accept in return for the secondary benefits of the new therapy. The equivalence margin, denoted by δ, is the most distinctive feature of equivalence/noninferiority testing. In summary, the equivalence of a new therapy is established when the data provide enough evidence to conclude that its efficacy is within δ units from that of the current therapy.

Staszewski et al.¹ reported the results of a clinical trial in 562 HIV patients designed to demonstrate equivalence between an abacavir-lamivudine-zidovudine therapy and an indinavir-lamivudine-zidovudine therapy. The primary endpoint was the proportion of patients having an HIV RNA level of 400 copies/ml or less at week 48. Based on discussions with researchers, clinicians, and the FDA, the equivalence margin for the difference in proportions was set at δ = 12 percentage points. That is to say that, if the data provide sufficient evidence that the true proportion of patients on abacavir who achieve the endpoint is within 12 percentage points of the true proportion of patients on indinavir who achieve the endpoint, equivalence would be established.

Similarly, noninferiority is established if the evidence suggests that the efficacy of the new therapy is no more than δ units less than that of the current therapy (assuming higher is better). When lower is better, noninferiority is established if the evidence suggests that the efficacy of the new therapy is no more than δ units more than that of the current therapy. Note that if the equivalence margin is set to zero, δ = 0, then the problem simplifies to a traditional one-sided superiority test.

PROCEDURE

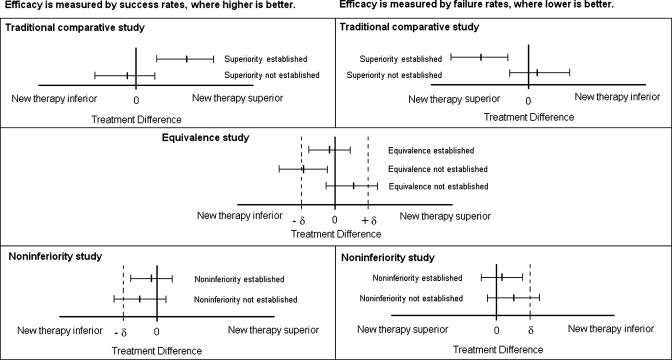
The simplest and most widely used approach to test equivalence is the two one-sided test (TOST) procedure². Using TOST, equivalence is established at the α significance level if a (1–2α) × 100% confidence interval for the difference in efficacies (new – current) is contained within the interval (-δ, δ) (Fig. 1). The reason the confidence interval is (1–2α) × 100% and not the usual (1- α) × 100% is because this method is tantamount to performing two one-sided tests. Thus, using a 90% confidence interval yields a 0.05 significance level for testing equivalence. The TOST procedure can be directly extended to testing equivalency in other parameters like means, odds ratios, hazard ratios, etc.

Figure 1.

Two one-sided test procedure (TOST) and the equivalence margin in equivalence/noninferiority testing.

Returning to the HIV example where the equivalence margin was set at δ = 12 percentage points, the response rates were 50.8% and 51.3% for abacavir and indinavir, respectively. The reported 95% confidence interval for the difference in the response rates was (-9, 8) and, since it is included in (-12, 12), the two therapies could be declared equivalent at the 0.025 significance level.

In noninferiority studies, the objective is to demonstrate that a therapy is not inferior (i.e., equivalent or possibly superior) than another. In terms of the equivalence margin, the research hypothesis is that the efficacy of the new therapy is no more than δ units lower than that of the current therapy (when higher is better). Noninferiority is established, at the α significance level, if the lower limit of a (1–2α) × 100% confidence interval for the difference (new – current) is above -δ (Fig. 1). When efficacy is measured by failure rates, where lower is better, noninferiority is established if the upper limit of a (1–2α) × 100% confidence interval is below δ.

The researchers of OASIS-5³ reported the results of a multicenter clinical trial designed to establish the noninferiority of fondoparinux against enoxaparin in patients with unstable angina or myocardial infarction without ST-segment elevation. The primary outcome was a composite of death, myocardial infarction or refractory ischemia at 9 days after acute coronary syndrome. The justification for testing noninferiority was the fact that fondoparinux was believed to be as effective as enoxaparin, but with a better safety profile. Based on a previously published meta-analysis, the noninferiority margin for the relative risk was set at 1.185. That is, noninferiority would be established if the data provided enough evidence that the true risk of the outcome for fondoparinux was, at most, 18.5% higher than the true risk of the outcome for enoxaparin. The observed risks for fondoparinux and enoxaparin were 5.8% and 5.7% [RR = 1.01, 95% confidence interval (0.90, 1.13)]. Since the upper limit of the confidence interval was less than 1.185, noninferiority could be established. Reassuringly, for the primary safety outcome of major bleeding, fondoparinux demonstrated strong superiority to enoxaparin [RR = 0.52, 95% confidence interval (0.44, 0.61)].

Confidence intervals are very informative, but when used to test equivalence have the disadvantage of not producing a p-value. The p-value is widely used as a measure of the strength of the evidence against the null hypothesis. Even though it is not standard practice, a p-value for equivalence can be calculated. Since an equivalence test is tantamount to applying two traditional one-sided tests⁴, a p-value can be reported as the larger of the two p-values of each of the one-sided tests. Like in traditional testing, if this p-value is less than alpha, then the research hypothesis (of equivalence) is established. The p-value for noninferiority is readily available since the test is just a slightly modified traditional one-sided test that can be carried out with any statistical software. Our recommendation is to report both a confidence interval and the p-value.

EQUIVALENCE MARGIN

The determination of the equivalence margin, δ, is the most critical step in equivalence/noninferiority testing. A small value of δ determines a narrower equivalence region, and makes it more difficult to establish equivalence/noninferiority. The equivalence margin not only determines the result of the test, but also gives scientific credibility to a study. The value and impact of a study depend on how well the equivalence margin can be justified in terms of relevant evidence and sound clinical considerations. Frequently, regulatory issues also have to be considered⁵.

An equivalence/noninferiority study should be designed to minimize the possibility that a new therapy that is found to be equivalent/noninferior to the current therapy can be nonsuperior to a placebo. One way to minimize this possibility is to choose a value of the equivalence margin based on the margin of superiority of the current therapy against the placebo. This margin of superiority can be estimated from previous studies. In noninferiority testing, a common practice is to set the value of δ to a fraction, f, of the lower limit of a confidence interval of the difference between the current therapy and the placebo obtained from a meta-analysis. The smaller the value of f, the more difficult the establishment of equivalence/noninferiority of the new therapy.

Kaul and Diamond⁶ present the way the value of f was determined for several cardiovascular trials. Kaul and Diamond⁶ state: “The choice of f is a matter of clinical judgment governed by the maximum loss of efficacy one is willing to accept in return for nonefficacy advantages of the new therapy.” Kaul and Diamond ⁶ mention the seriousness of the clinical outcome, the magnitude of effect of the current therapy, and the overall benefit-cost and benefit-risk assessment as factors that affect the determination of f. When the outcome is mortality, the FDA has suggested a value of f of 0.50.

It must be stressed that the value of the equivalence margin should be determined before the data is recorded. This is essential to maintain the type I error at the desired level.

NO DIFFERENCE DOES NOT IMPLY EQUIVALENCE

Using a traditional comparative test to establish equivalence/noninferiority leads frequently to incorrect conclusions. The reason is two-fold. First, the burden of the proof is on the wrong hypothesis, i.e., that of a difference. In this setting, a significant result establishes a difference, whereas a nonsignificant result implies only that equivalency (or equality) cannot be ruled out. Consequently, the risk of incorrectly concluding equivalence can be very high. The other reason is that the margin of equivalence is not considered, and thus the concept of equivalence is not well defined.

Barker et al.⁷ contrasted the results of the traditional two-sided test and the equivalence (TOST) test for the comparison of vaccination coverage in children. The objective was to determine if the coverages of different groups of children were equivalent to that of white children. Using data from the National Immunization Survey (NIS) Barker et al.⁷ applied the traditional and the TOST tests to compare the vaccination coverage of white children to each of three minority groups (Black, Hispanic, and Asian) for seven different vaccines. Using α = 0.05 and an equivalence margin of 5 percentage points for TOST, the two procedures yielded contradictory results in 9 out of 21 comparisons.

The inconsistencies can be explained using graphs. In traditional two-sided testing, the null hypothesis of no difference is rejected if a 95% confidence interval does not cover zero, whereas TOST establishes equivalence if a 90% confidence interval is included within the interval (−δ, δ). The results of the measles-mumps-rubella (MMR) vaccine appear in Figure 2. The left panel shows the traditional comparative approach. Illustrated is the 95% confidence interval for the difference in coverage for each minority group compared to white (the reference group). The right panel shows the TOST approach. Illustrated is the 90% confidence interval for the difference in coverage for each minority group compared to white (the reference group). The coverage of black children is declared differently than in white children by the traditional two-sided test because the 95% confidence interval of the difference does not cover 0. However, since the 90% confidence interval is included within (-0.05, 0.05), coverage of black children is declared equivalent to that of white children by the TOST procedure. The two tests agree in that the coverages for Hispanic and white children are not different/equivalent. However, the coverages of Asian and white children are declared no different by the traditional test, but TOST does not conclude equivalence.

Figure 2.

Results of traditional two-sided and two one-sided test (TOST) (δ = 5) procedures to compare MMR vaccination coverages between white and minority group children (adapted from Barker,⁷).

Barker et al.⁷ argue that equivalence is the appropriate test in many situations in public health policy for which the objective is to eliminate health disparities across different demographic groups. The problem with traditional tests is that they “…cannot prove that a state of no difference between groups exists.”

SAMPLE SIZE

Power is the probability of correctly establishing the research hypothesis. Power analysis, also called sample size determination, consists of calculating the number of observations needed to achieve a desired power. Not surprisingly, in equivalence/noninferiority testing, the sample size depends directly on the equivalence margin. For example, the sample of n = 562 gave the abacavir-indinavir trial a power of approximately 0.80 to establish equivalence for δ = 12 percentage points, whereas a sample of n = 1,300 would have been required to achieve the same power for δ = 8 percentage points.

The sample size software PASS⁸ was used to calculate the samples sizes for testing equivalence between a new drug and an active control in the following context. Assume that the true efficacies are 33% and 28% for the new drug and the active control, respectively. Table 2 displays the sample sizes required to achieve a 0.80 power with α = 0.05 to establish equivalency at different values of the equivalence margin. The results show how small changes in the equivalence margin can cause large changes in the required sample size to achieve the same power.

Table 2.

Sample Size to Achieve 0.80 Power to Test Equivalency at the α = 0.05 Significance Level for True Proportions of 0.28 and 0.33

Equivalence margin	Sample sizea (per group)
0.06	26,185
0.07	6,547
0.08	2,910
0.09	1,637
0.10	1,048
0.11	728
0.12	535

^aCalculations performed on PASS software are ⁸

MEASURE OF EFFECT

Outcomes are frequently measured as proportions that can be compared in an absolute or a relative way. In the former, the interest is in the difference between proportions. This is called the absolute risk difference (ARD) and is the measure used in the abacavir-indinavir trial¹. Often, however, the comparison is made in relative terms using the ratio of the proportions. Two common measures of relative difference are the relative risk (RR) and the odds ratio (OR). In the fondoparinux vs. enoxaparin trial³, equivalence was defined as a value of the RR less than 1.185 or the risk of the outcome for the fondoparinux group at most 18.5% larger than the risk of the outcome for the enoxaparin group.

Absolute measures are independent of the baseline rate, whereas relative measures describe a difference that is directly dependent on the denominator. It is critical to determine the measure to be used from the outset in order to choose an appropriate value of the equivalence margin. The reason is that there is no direct relationship between absolute and relative measures. That is, the same ARD can be associated with very different RRs or ORs, and consequently, it is possible for two proportions to be equivalent with respect to the RR or the OR but have very different ARDs.

ANALYSIS OF DATA

An important decision in any study is whether to perform an intention to treat (ITT) or per protocol (PP) data analysis. In ITT, the analysis is done on all patients who were originally randomized regardless of whether they actually received the treatment or followed the protocol. In PP, only patients that received the treatment and followed the protocol are included in the analysis. In most traditional comparison studies, ITT is the accepted method of analysis. Because ITT includes patients who did not receive the treatment or follow the protocol, the difference in efficacies are typically smaller, thus making it harder to reject the null hypothesis of no difference. Thus, ITT is considered a conservative approach. However, the smaller differences commonly observed in ITT have the opposite effect when testing equivalence/noninferiority. That is, ITT makes it easier to establish equivalency/noninferiority and is considered anticonservative. There is considerable controversy in the appropriate type of analysis for equivalence/noninferiority testing. Wiens and Zhao⁹ comment on the merits of each type of analysis, and Ebbutt and Frith¹⁰ discuss this and other issues from the pharmaceutical industry point of view. The FDA requires the reporting of both types of analyses¹¹.

Equivalence/noninferiority is clearly established when both ITT and PP analyses agree. Discrepancies in the results of the two analyses indicate the possibility of exclusion bias, suggesting that the reason that patients not included in the PP analysis is somehow related to the treatment. Unless these discrepancies can be explained, the conclusions of the study are weakened.

REPORTING OF RESULTS

There is specific information that is essential for the evaluation of the methodologic quality of equivalence/noninferiority studies:

• Justification for testing an equivalence/noninferiority hypothesis as opposed to a superiority criterion.

• Clear statement and justification of the equivalence margin.

• Detailed method (including software) used to calculate the sample size needed to achieve the desired power. The method should take into account the equivalence margin. All the elements necessary to reproduce the calculation, including the proportion of dropouts anticipated, should be reported.

• The analysis section should report clearly the sets of patients analyzed and report the results of both, the ITT and PP analyses.

• The statistical methods should state whether the confidence interval is one- or two-sided and match the significance level used in the sample size calculation to that of confidence interval. Recall that the correct procedure to test equivalence at significance level α is to use a (1–2α) × 100% confidence interval.

CONCLUSIONS

There has been a recent increase in the use of equivalence/noninferiority testing. One reason is that much research is devoted nowadays to finding new therapies with similar effectiveness to those currently used, but with better properties such as fewer side effects, convenience, or lower cost. Another reason is that in many instances the use of placebos is unethical. On the other hand, the use of current therapies (active controls) can also be controversial. The issues involved in this decision are discussed by Ellenberg and Temple¹² and Temple and Ellenberg¹³.

There is much confusion in the literature surrounding equivalence/noninferiority studies. Le Henanff¹⁴ identified 162 reports of equivalence/noninferiority trials published in 2003 and 2004. They found deficiencies in many aspects. For example, about 80% of the reports did not justify their choice of equivalence margin, and 28% did not take into consideration the margin in the sample size calculation. Le Henanff¹⁴ concludes: “…even for articles fulfilling these requirements, conclusions are sometimes misleading.”

An important cause of the confusion is the lack of uniformity and transparency in terminology¹⁵. This is not surprising and occurs often when new methods are introduced. It is to be expected that the state of affairs will improve as these methods become more widespread. An important step in the right direction was the publication of guidelines for reporting equivalence/noninferiority studies¹⁶.

Given the current trends in medical research, it is reasonable to expect that the use of equivalence/noninferiority studies will only increase, and the clinician needs be able to judge their value.