Application of Metamorphic Testing to Supervised Classifiers

Abstract

Many applications in the field of scientific computing - such as computational biology, computational linguistics, and others - depend on Machine Learning algorithms to provide important core functionality to support solutions in the particular problem domains. However, it is difficult to test such applications because often there is no “test oracle” to indicate what the correct output should be for arbitrary input. To help address the quality of such software, in this paper we present a technique for testing the implementations of supervised machine learning classification algorithms on which such scientific computing software depends. Our technique is based on an approach called “metamorphic testing”, which has been shown to be effective in such cases. More importantly, we demonstrate that our technique not only serves the purpose of verification, but also can be applied in validation. In addition to presenting our technique, we describe a case study we performed on a real-world machine learning application framework, and discuss how programmers implementing machine learning algorithms can avoid the common pitfalls discovered in our study. We also discuss how our findings can be of use to other areas outside scientific computing, as well.

1. Introduction

Many applications in the field of scientific computing - such as computational physics, bioinformatics, etc. - depend on supervised Machine Learning (ML) algorithms to provide important core functionality to support solutions in the particular problem domains. For instance, [1] lists over fifty different real-world computational science applications, ranging from facial recognition to computational biology, that use the Support Vector Machines [18] classification algorithm alone. As these types of applications become more and more prevalent in society [14], ensuring their quality becomes more and more crucial.

Quality assurance of such applications presents a challenge because conventional software testing processes do not always apply: in particular, it is difficult to detect subtle errors, faults, defects or anomalies in many applications in these domains because there is no reliable “test oracle” to indicate what the correct output should be for arbitrary input. The general class of software systems with no reliable test oracle available is sometimes known as “non-testable programs” [19]; the fact that such programs exist is often referred to as “the oracle problem”. Many of these applications fall into a category of software that Weyuker describes as “Programs which were written in order to determine the answer in the first place. There would be no need to write such programs, if the correct answer were known” [19].

The majority of the research effort in the domain of machine learning focuses on building more accurate models that can better achieve the goal of automated learning from the real world. However, to date very little work has been done on assuring the correctness of the software applications that perform machine learning. Formal proofs of an algorithm’s optimal quality do not guarantee that an application implements or uses the algorithm correctly, and thus software testing is necessary.

To help address the quality of scientific computing software, in this paper we present a technique for testing implementations of the supervised machine learning algorithms on which such software depends. Our technique is based on an approach called “metamorphic testing” [3], which uses properties of functions such that it is possible to predict expected changes to the output for particular changes to the input, based on so-called “metamorphic relations” between sets of inputs and their corresponding outputs. Although the correct output cannot be known in advance, if the change is not as expected, then either a defect in the implementation must exist, or there is a violation between the algorithm and the user’s expectation. In this way, we not only address the oracle problem so that it is possible to verify the implementation of the machine learning program, but we can also validate whether the chosen algorithm is an appropriate one to solve a given problem.

In our approach, we first enumerate the metamorphic relations based on the expected behaviors of a given machine learning problem, and then utilize these relations to conduct metamorphic testing on the applications of interest. Our approach can serve both the purposes of verification and validation, of which details are presented in Section 3.

In addition to presenting our technique, we describe a case study we performed on the real-world machine learning application framework Weka [20], which is used as the foundation for such computational science tools as BioWeka [9] in bioinformatics. We also discuss how our findings can be of use to other areas of computational science and engineering, such as computational linguistics.

The rest of this paper is organized as follows: Section 2 describes the background of our work, including an overview of machine learning and the particular algorithms we investigated. Section 3 discusses our testing approach and provides a further explanation of metamorphic testing. In Section 4, we present our findings in a case study of two machine learning algorithms, and analyze and discuss the results in Section 5 and Section 6. Section 7 identifies related work, and Section 8 concludes.

2. Background

This section describes some of the basics of machine learning and the two algorithms we investigated (k-Nearest Neighbors and Naïve Bayes Classifier) (we previously considered Support Vector Machines in [15]), as well as the terminology used. Readers familiar with machine learning may skip this section.

One complication in our work arose due to conflicting technical nomenclature: “testing”, “regression”, “validation”, “model” and other relevant terms have very different meanings to machine learning experts than they do to software engineers. Here we employ the terms “testing”, “regression testing”, and “validation” as appropriate for a software engineering audience, but we adopt the machine learning sense of “model”, as defined below.

2.1. Machine Learning Fundamentals

In general, input to a supervised machine learning application consists of a set of training data that can be represented by two vectors of size k. One vector is for the k training samples S = <s₀, s₁, …, s_k-1> and the other is for the corresponding class labels C = <c₀, c₁, …, c_k-1>. Each sample s ∈ S is a vector of size m, which represents m features from which to learn. Each label c_i in C is an element of a finite set of class labels, that is, c ∈ L = <l₀, l₁, …, l_n-1>, where n is the number of possible class labels.

Supervised ML applications execute in two phases. The first phase (called the training phase) analyzes the training data; the result of this analysis is a model that attempts to make generalizations about how the attributes relate to the label. In the second phase (called the testing phase), the model is applied to another, previously-unseen data set (the testing data) where the labels are unknown. In a classification algorithm, the system attempts to predict the label of each individual example. That is, the testing data input is an unlabeled test case t_s, and the aim is to predict its class label c_t based on the data-label relationship learned from the set of training samples S and the corresponding class labels C. The label c_t must be an element l_i ∈ L.

2.2. Algorithms Investigated

In this paper, we only focus on programs that perform supervised learning. Within the area of supervised learning, we particularly focus on programs that perform classification, since it is one of the central tasks in machine learning. The work presented here has focused on the k-Nearest Neighbors classifier and the Naïve Bayes Classifier, which were chosen because of their common use throughout the ML community. However, it should be noted that the problem description and techniques described below are not specific to any particular algorithm, and as shown in our previous work [4] [15], the results we obtain are applicable to the general case.

In k-Nearest Neighbors (kNN), for a training sample set S, suppose each sample has m attributes, <att₀, att₁, …, att_m-1>, and there are n classes in S, <l₀, l₁, …, l_n-1>. The value of the test case t_s is <a₀, a₁, …, a_m-1>. kNN computes the distance between each training sample and the test case. Generally kNN uses the Euclidean Distance: for a sample s_i ∈ S, the value of each attribute is <sa₀, sa₁, …, sa_m-1>, and the distance formula is as follows:

$$\mathit{dist}(s_i,t_S)=\sqrt{\sum _j^{m-1}{({\mathit{sa}}_j-a_j)}^2}.$$

After sorting all the distances, kNN selects the k nearest ones and these samples are considered the k nearest neighbors of the test case. Then kNN calculates the proportion of each label in the k nearest neighbors, and the label with the highest proportion is predicted as the label of the test case.

In the Naïve Bayes Classifier (NBC), for a training sample set S, suppose each sample has m attributes, <att₀, att₁, …, att_m-1>, and there are n classes in S, <l₀, l₁, …, l_n-1>. The value of the test case t_s is <a₀, a₁, …, a_m-1>. The label of ts is called l_ts, and is to be predicted by NBC.

NBC computes the probability of l_ts belonging to l_k, when each attribute value of t_s is <a₀, a₁, …, a_m>. In the Naïve Bayes method, we assume that attributes are conditionally independent with one another given the class label, therefore we have the equation:

$$P(l_{\mathit{ts}}=l_k\mid a_{\mathit{0}}{a}_{\mathit{1}}\dots a_{m­\mathit{1}})=\frac{P(l_k)\prod _{j}P(a_j\mid l_{\mathit{ts}}=l_k)}{{\sum }_{i}P(l_i){\prod }_{j}P(a_j\mid l_{\mathit{ts}}=l_i)}$$

After computing the probability for each l_i ∈ {l₀, l₁, …, l_n-1}, NBC chooses the label l_k with the highest probability, which is then predicted as the label of test case t_s.

Generally NBC uses a normal distribution to compute P(a_j ∣ l_ts = l_k). Thus NBC trains the training sample set to establish a distribution function for each att_j ∈ {att₀, att₁, …, att_m-1} in each l_i ∈ {l₀, l₁, …, l_n-1}, that is, for all samples with label l_i ∈ {l₀, l₁, …, l_n-1}, it calculates the mean value μ and mean square deviation σ of att_j in all samples with l_i. It then constructs the probability density function for a normal distribution with μ and σ.

For test case t_s with m attribute values <a₀, a₁, …, a_m-1>, NBC computes the probability of P(a_j ∣ l_ts = l_k) using a small interval δ to calculate the integral area. With the above formulae NBC can then compute the probability of l_ts belonging to each l_i and choose the label with the highest probability as the classification of t_s.

3. Approach

Our approach is based on the concept of metamorphic testing [3], summarized below. To facilitate that approach, we first identify the metamorphic relations that a supervised classification algorithm is expected to exhibit between sets of inputs and sets of outputs. We then utilize these relations to conduct our testing of the implementations of the algorithms under investigation.

3.1. Metamorphic Testing

One popular technique for testing programs without a test oracle is to use a “pseudo-oracle” [6], in which multiple implementations of an algorithm process the same input and the results are compared; if the results are not the same, then one or both of the implementations contains a defect. This is not always feasible, though, since multiple implementations may not exist, or they may have been created by the same developers, or by groups of developers who are prone to making the same types of mistakes [11].

However, even without multiple implementations, often these applications exhibit properties such that if the input were modified in a certain way, it should be possible to predict the new output, given the original output. This approach is what is known as metamorphic testing. Metamorphic testing can be implemented very easily in practice. The first step is to identify a set of properties (“metamorphic relations”, or MRs) that relate multiple pairs of inputs and outputs of the target program. Then, pairs of source test cases and their corresponding follow-up test cases are constructed based on these MRs. These test cases are then executed using the target program, and outputs of the source and follow-up test cases are checked to see whether they satisfy their corresponding MRs.

A simple example of a function to which metamorphic testing could be applied would be one that calculates the standard deviation of a set of numbers. Certain transformations of the set would be expected to produce the same result: for instance, permuting the order of the elements should not affect the calculation; nor would multiplying each value by -1, since the deviation from the mean would still be the same. Furthermore, there are other transformations that will alter the output, but in a predictable way: for instance, if each value in the set were multipled by 2, then the standard deviation should be twice as much as that of the original set, since the values on the number line are just “stretched out” and their deviation from the mean becomes twice as great. Thus, given one set of numbers (the source test cases), we can use these metamorphic relations to create three more sets of follow-up test cases (one with the elements permuted, one with each multiplied by -1, and another with each multiplied by 2); moreover, given the result of only the source test case, we can predict the expected result of the others.

It is not hard to see that metamorphic testing is simple to implement, effective, easily automatable, and independent of any particular programming language. Further, since the most crucial step in metamorphic testing is the identification of the MRs, we can harness the domain knowledge. This is a useful feature since in scientific computing the programmer may, in fact, also be the domain expert and will know what properties of the program will be used more heavily or are more critical. Perhaps more importantly, it is clear that metamorphic testing can be very useful in the absence of a test oracle, i.e., when the correct output cannot be known in advance: regardless of the input values, if the metamorphic relations are violated, then there is likely a defect in the implementation.

3.2. Identifying Metamorphic Relations

Previous work [15] broadly classified six types of metamorphic relations (MRs) that apply in general to many different types of machine learning applications, including both supervised and unsupervised ML. Roughly speaking, these properties include: adding a constant to numerical values; multiplying numerical values by a constant; permuting the order of the input data; reversing the order of the input data; removing part of the data; and, adding additional data.

In this work, however, our approach calls for focusing on the specific metamorphic relations of the application under test; we would expect that we could then create more follow-up test cases and conceivably reveal more defects than by using more general MRs. In particular, we define the MRs that we anticipate classification algorithms to exhibit, and define them more formally as follows.

MR-0: Consistence with affine transformation

The result should be the same if we apply the same arbitrary affine transformation function, f(x) = kx + b, (k ≠ 0) to every value x to any subset of features in the training data set S and the test case t_s.

MR-1.1: Permutation of class labels

Assume that we have a class-label permutation function Perm() to perform one-to-one mapping between a class label in the set of labels L to another label in L. If the source case result is l_i, applying the permutation function to the set of corresponding class labels C for the follow-up case, the result of the follow-up case should be Perm(l_i).

MR-1.2: Permutation of the attribute

If we permute the m attributes of all the samples and the test data, the result should not change.

MR-2.1: Addition of uninformative attributes

An uninformative attribute is one that is equally associated with each class label. For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we add an uninformative attribute to S and respectively a new attribute in s_t. The choice of the actual value to be added here is not important as this attribute is equally associated with the class labels. The output of the follow-up test case should still be l_i.

MR-2.2: Addition of informative attributes

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we add an informative attribute to S and t_s such that this attribute is strongly associated with class l_i and equally associated with all other classes. The output of the follow-up test case should still be l_i.

MR-3.1: Consistence with re-prediction

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we can append t_s and c_t to the end of S and C respectively. We call the new training dataset S’ and C’. We take S’, C’ and t_s as the input of the follow-up case, and the output should still be l_i.

MR-3.2: Additional training sample

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we duplicate all samples in S and L which have label l_i. The output of the follow-up test case should still be l_i.

MR-4.1: Addition of classes by duplicating samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we duplicate all samples in S and C that do not have label l_i and concatenate an arbitrary symbol “*” to the class labels of the duplicated samples. That is, if the original training set S is associated with class labels <A, B, C> and l_i is A, the set of classes in S in the follow-up input could be <A, B, C, B*, C*>. The output of the follow-up test case should still be l_i. Another derivative of this metamorphic relation is that duplicating all samples from any number of classes which do not have label l_i will not change the result of the output of the follow-up test case.

MR-4.2: Addition of classes by re-labeling samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we re-label some of the samples in S and C which do not have label l_i and concatenate an arbitrary symbol “*” to their class labels. That is, if the original training set S is associated with class labels <A, B, B, B, C, C, C> and c₀ is A, the set of classes in S in the follow-up input may become <A, B, B, B*, C, C*, C*>. The output of the follow-up test case should still be l_i.

MR-5.1: Removal of classes

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we remove one entire class of samples in S of which the label is not l_i. That is, if the original training set S is associated with class labels <A, A, B, B, C, C> and l_i is A, the set of classes in S in the follow-up input may become <A, A, B, B>. The output of the follow-up test case should still be l_i.

MR-5.2: Removal of samples

For the source input, suppose we get the result c_t = l_i for the test case t_s. In the follow-up input, we remove part of some of the samples in S and C of which the label is not l_i. That is, if the original training set S is associated with class labels <A, A, B, B, C, C> and l_i is A, the set of classes in S in the follow-up input may become <A, A, B, C>. The output of the follow-up test case should still be l_i.

3.3. Analysis of Applying MT for Classifiers

Normally in the development of software, there are three parts: the problem to be solved, a particular algorithm chosen to solve this problem, and an implementation of the chosen algorithm.

Usually a problem has some expected behaviors. For example, in the classification problem, one expected behavior is that the ordering of the training data set should not affect the outcomes of a classifier.

In previous related studies on metamorphic testing, such as [3] and [5], the scope and the expected behaviors of the problem were always well-defined. Hence the algorithm chosen or designed to solve the problem always fulfilled all the expected behaviors of the problem. Therefore, MRs derived from such expected behaviors of the problem can be considered the necessary properties of the algorithm, which can be used for the purpose of verifying the correctness of the implementation of the algorithm.

However, in machine learning, the situation is much more complicated. Generally speaking, a problem that involves machine learning is less well defined and may even have varying scope of definition from person to person. Usually there exist various algorithms for dealing with a given machine learning problem. Since these algorithms are developed according to different intuitions, a particular expected behavior of the machine learning problem may not be satisfied by all of the algorithms. Consequently, even though we can still derive MRs from the expected behaviors of a machine learning problem in general, they may not be necessary properties of the chosen machine learning algorithm.

Therefore engineers actually face two tasks when they try to test the machine learning programs: validation and verification. Validation considers whether the chosen algorithm is appropriate for solving the problem, that is, whether the algorithm will satisfy all the expected behaviors. Verification, on the other hand, considers whether the implementation of the chosen algorithm is correct. Both of them are equally important.

To the best of our knowledge, current software testing methods have never taken validation into consideration; that is, testing methods only address the purpose of verification, and are therefore not obliged to serve the purpose of validation. Fortunately our technique serves for both validation and verification.

In our technique, we derive a series of MRs based on the generally expected behaviors of the machine learning problem. Before we use these MRs to drive metamorphic testing of the applications we are investigating, we carry out a quick inspection and filtering process. If an MR can be easily demonstrated as not being a necessary property of the chosen algorithm, it is apparent that this algorithm will not fulfil all of our expected behaviors. In this situation, we exclude this MR in further metamorphic testing. Otherwise, when the MRs are deemed to be necessary properties of the algorithm, we use them to conduct metamorphic testing of the implementation. If we cannot find any violation, we have no further information to draw any conclusion; we cannot say that the implementation is defect-free, of course, but neither have we discovered any defects. However, if violations occur, we then need to determine whether the violations are due to defects in the implementation, or they just follow from the fact that the violation-revealing MR is not actually a necessary property of the algorithm. Hence we conduct both validation (is the algorithm appropriate for the problem?) and verification (is the implementation of the algorithm correct?) in our method.

4. Experimental Study

To demonstrate the effectiveness of metamorphic testing in verifying and validating machine learning applications, we applied the approach to the k-Nearest Neighbors (kNN) classifier and Naïve Bayes Classifier (NBC) implementations in Weka 3.5.7 [20]. Weka is a popular open-source machine learning package that implements many common algorithms for data preprocessing, classification, clustering, association rule mining, feature selection and visualization. Due to its large range of functionality, it is typically used as a “workbench” for applying various machine learning algorithms. Furthermore, Weka is widely used as the back-end machine learning engine for various applications in computational science, such as BioWeka [9] for machine learning tasks in bioinformatics.

4.1. Experimental Setup

The data model in our experiments is as follows. In one source suite, there are k inputs. Each input_i consists of two parts: tr_i and t_i, in which tr_i represents the training sample set, and t_i represents the test case. In each training sample set tr_i and test case t_i, there are four attributes: <A₀, A₁, A₂, A₃>, and a label L. In our experiments, there are three labels in all, that is, <L₀, L₁, L₂>. The value for each attribute is within [1, 20]. We generate the tr_i and t_i values randomly, both in the value of the attribute and the label. Additionally, the number of samples in tr_i is also randomly generated with a maximum of n.

This randomly generated data model does not encapsulate any domain knowledge, that is, we do not use any meaningful, existing training data for testing: even though those data sets are more predictable, they may not be sensitive to detecting faults. Random data may, in fact, be more useful at revealing defects [8].

For the source suite of k inputs, we perform a transformation according to the MRs and get k follow-up inputs for each MR-j. From running the k follow-up inputs and comparing the results between the source and the follow-up cases for the each MR-j, we try to detect faults in Weka or find a violation between the classifier under test and the anticipated behaviors of the classifier.

For each MR-j, we conducted several batches of experiments, and in each batch of experiments we changed the value of k (size of source suite) and n (max number of training samples). Intuitively the more inputs we tried (the higher is k), the more likely we are to find violations. Also, we would expect that with fewer samples in the training data set (the less is n), the less predictable the data are, thus the more likely we are to find faults. In our experiments, k ranges from 20 to 300 and n ranges from 20 to 50.

4.2. Results

In our experimental study, the original MRs were derived from the commonly expected behaviors of a machine learning classifier, which are described above in Section 3.2. In the first inspection and filtering process, we did not identify any MR that is clearly not a necessary property of the algorithms under investigation, kNN and NBC. Thus we used all the MRs in metamorphic testing of the implementations of the two algorithms.

The experimental results reveal violations in some MRs for both kNN and NBC. With the information we acquired from these violations, we conducted a much deeper inspection of the two algorithms, and found that only some, but not all, of the MRs were actually necessary properties of the corresponding algorithm. Table 1 summarizes the results of testing kNN and NBC with all these MRs. In the table, NP indicates whether the given MR is a necessary property of the corresponding algorithm, and VP indicates the percentage of violations in our experiments (that is, the number of test cases in which a violation of the property was revealed).

Table 1.

Result of testing kNN and NBC

MR	kNN		NBC
	NP	VP	NP	VP
0	Y	0	Y	7.4%
1.1		15.9%	Y	0.3%
1.2	Y	0	Y	0
2.1	Y	0	Y	0.6%
2.2		4.1%	Y	0
3.1	Y	0		0
3.2	Y	0	Y	0
4.1		25.3%	Y	0
4.2	Y	0		3.9%
5.1		5.9%	Y	5.6%
5.2		2.8%		2.8%

Violations in those MRs that are necessary properties imply defects in the implementation of the related algorithm, which serves the purpose of verification. On the other hand, violations in MRs that are not necessary properties do not reveal defects in the implementation, but rather provide us information to support validation, which could not be demonstrated in the first quick inspection process.

Due to space limitations, we do not formally prove these necessary properties in Table 1 for the k-Nearest Neighbors and Naïve Bayes Classifiers. Rather, we demonstrate here that the rest of the MRs are not necessary properties of the corresponding algorithms of interest, and how they serve the purpose of validation.

For kNN, five of the metamorphic relations (MR-1.1, MR-2.2, MR4.1, MR5.1 and MR-5.2) are not necessary properties but can instead be used for validation purposes. MR-1.1 (Permutation of class labels) may not hold because of tiebreaking between two labels for prediction that are equally likely: permuting their order may change which one is chosen by the tiebreaker, and hence affect the output.

Another one is MR-4.1 (Addition of classes by duplicating samples). Suppose the label of test case is l_i. MR-4.1 duplicates all the samples without label l_i. Thus the number of samples without l_i in the k nearest neighbors will increase or remain the same. Therefore the number and the proportion of samples with l_i in the k nearest neighbors will decrease or remain the same. Therefore the follow-up prediction may be different to the source prediction.

Additionally, MR-5.1 (Removal of classes) is also not a necessary property. Suppose the predicted label of the test case is l_i. MR-5.1 removes a whole class of samples without label l_i. Consequently this will remove the same samples in the set of k nearest neighbors, and thus some other samples will be included in the set of k nearest neighbors. These samples may have any labels except the removed one, and so the likelihood of any label (except the removed one) may increase. Therefore there are two situations: (1) If in the k nearest neighbors of the source case, the proportion of l_i is not only the highest, but also higher than 50%, then in the follow-up prediction, no matter how the k nearest neighbors change, the prediction will remain the same, because no matter which labels increase, the proportion of l_i will still be higher than 50% as well. Thus the prediction remains l_i. Now consider situation (2), in which in the k nearest neighbors of the source case, the proportion of l_i is the highest but lower or equal to 50%. Since the number of each survived label may increase, and the original proportion of l_i is lower or equal to 50%, it is possible that the proportion of some other label increases and becomes higher than l_i: thus, the prediction changes.

Similar logic can be used to show that MR-2.2 (Addition of informative attributes) and MR-5.2 (Removal of samples) also may not hold if the predicted label has a likelihood of less than 50%.

For the Naïve Bayes Classifier, three of the metamorphic relations are not considered necessary properties, which can be used for validation: MR-3.1 (Consistence with re-prediction), MR-4.2 (Addition of classes by re-labeling samples), and MR-5.2 (Removal of samples). The first of the three could not be proven as a necessary property, and thus is considered not necessary; the other two introduce noise to the data set, which could affect the result.

5. Findings and Analysis

Our investigation into the kNN and Naïve Bayes implementations in Weka demonstrated violations in some MRs that are not necessary properties of kNN or NBC, which serves the purpose of validation. Additionally we also found violations in some MRs that are necessary properties of NBC, thus revealing defects in the implementation.

5.1. k-Nearest Neighbors

In our experiments, none of the MRs that are necessary properties of kNN were violated, which indicates that no defect in the implementation of kNN in Weka has been found by our testing.

On the other hand, we did uncover violations in some of the MRs that are not necessary properties and can be used for validation. Although these are not necessarily indicative of defects per se, they do demonstrate a deviation from what would normally be considered the expected behavior, and indicate that the algorithm may not be appropriate for a given ML problem.

1. Calculating distribution

In the Weka implementation of kNN, a vector distance[numOfSamples] is used to record the distance between each sample from the training data and the test case to be classified. After determining the values in distance[], Weka sorts it in ascending order, to find the nearest k samples from the training data, and then puts their corresponding labels into another vector k-Neighbor[k].

Weka traverses k-Neighbor[], computes the proportion of each label in it and records the proportions into a vector distribution[numOfClasses] as follows: For each i, distribution[i] is initialized as 1/numberOfSamples. It then traverses the array k-Neighbor[], and for each label in k-Neighbor[], it adds the weight of its distribution value (in our experiments, the weight is 1), that is, for each j, distribution[k-Neighbor[j].label] + 1. Finally, Weka normalizes the whole distribution[] array.

Figure 1 shows two data sets, with the training data on the left, and the test case to be classified on the right. For the test case to be classified, the (unsorted) values in the array distance[] are {11.40, 7.35, 12.77, 10.63, 13, 4.24}, and the values in k-Neighbor are {1, 2, 0}, assuming k = 3. The array distribution[] is initialized as {1/6, 1/6, 1/6, 1/6, 1/6, 1/6}. After traversing the array k-Neighbor[], we get distribution[] = {1+1/6, 1+1/6, 1+1/6, 1/6, 1/6, 1/6} = {1.167, 1.167, 1.167, 0.167, 0.167, 0.167}. After the normalization, distribution[] = {0.292, 0.292, 0.292, 0.042, 0.042, 0.042}.

Figure 1.

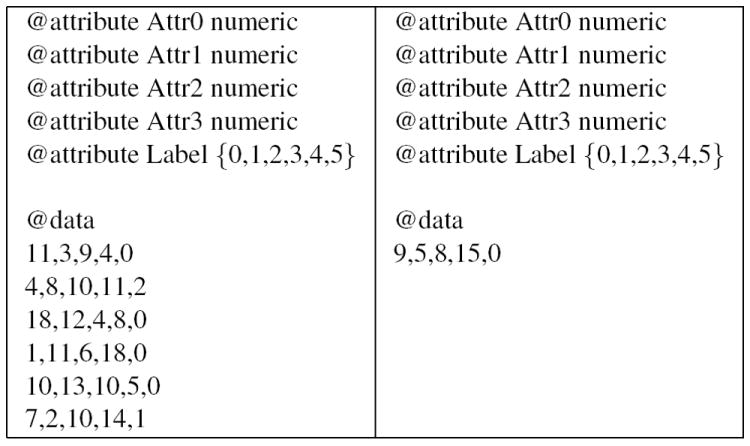
Sample data sets

The issue here, as revealed by MR-5.1 (Removal of classes), is that labels that were non-existent in the training data samples have non-zero probability of being chosen in the array distribution[]. Ordinarily one might expect that if a label did not occur in the training data, there would be no reason to classify a test case with that label. However, by initializing the distribution[] array so that all labels are equally likely, even non-existent ones become possible. Although this is not necessarily an incorrect implementation, it does deviate from what one would normally expect.

2. Choosing labels with equal likelihood

Another issue comes about regarding how the label is chosen when there are multiple classifications with the same probability. Our testing indicated that in some cases, this method may lead to the violation in some MR transformations, e.g. MR-1.1 (Permutation of class labels).

Consider the example in Figure 1 above. To perform the classification, Weka chooses the first highest value in distribution[], and assigns its label to the test case. For the above example, l₀, l₁, and l₂ all have the same highest proportion in distribution[], so based on the order of the labels, the final prediction is l₀, since it is first.

However, if the labels are permuted (as in MR-1.1, for instance), then one of the other labels with equal probability might be chosen if it happens to be first. This is not a defect per se (after all, if there are three equally-likely classifications and the function needs to return only one, it must choose somehow) but rather it represents a deviation from expected behavior (that is, the order of the data set shall not affect the computed outputs), one that could have an effect on an application using this functionality.

3. Choosing labels with the highest proportion

This operation seems very reasonable for a classifier, however it does lead to an unexpected result after some metamorphic transformation. The first situation is that the selected label only has the highest proportion in the k nearest neighbors, rather than the proportion higher than 50%. In this case, a violation may be found in some MRs, particularly MR-2.2 (Addition of informative attributes), MR-5.1 (Removal of classes) and MR-5.2 (Removal of samples). The reason is that even though these transformations do not actually decrease the proportion of the selected label, they may increase the proportion of other labels. If the proportion of the selected label is less than 50%, proportions of other labels may increase until becoming the new highest proportion.

However, as for metamorphic relations like MR-4.1 (Addition of classes by duplicating samples), even if the highest proportion is higher than 50%, the transformation may also lead to an unexpected result. In this situation, the proportion of the selected label may decrease while others may increase, which could result in a new highest proportion in the k nearest neighbors.

5.2. Naïve Bayes

Our investigation into the Naïve Bayes algorithm revealed a number of violations in MRs that are its necessary properties, which indicate defects in the implementation.

1. Loss of precision

Precision can be lost due to the treatment of continuous values. In a pure mathematical model, a normal distribution is used for continuous values. However, it is impossible to realize true continuity in a digital computer. To implement the integral function, for instance, it is necessary to define a small interval δ to calculate the area. In Weka, a variable called precision is used as the interval. The precision for att_j is defined as the average interval of all the values. For example, suppose there are 5 samples in the training sample set, and the values of att_j in the five samples are 2, 7, 7, 5, and 10 respectively. After sorting the values we have {2, 5, 7, 7, 10}. Thus precision = [(5-2) + (7-5) + (10-7)] / (1 + 1 + 1) = 2.67.

However, Weka rounds all the values x in both the training samples and test case with precision pr by using round(x / pr) * pr. These rounded values are used for the computation of the mean value μ, mean square deviation σ, and the probability P(l_ts = l_k ∣ a₀a₁…a_m-1). This manipulation means that Weka treats all the values within ((2k-1)* pr/2, (2k+1)* pr/2] as k*pr, in which k is any integer.

This may lead to a loss of precision and our tests resulted in the violation of some MR transformations, particularly MR-0 (Consistence with affine transformation) and 5.1 (Removal of classes). Since both of these are necessary properties, they demonstrate defects in the implementation.

There are also related problems of calculating integrals in Weka. A particular calculation determines the integral of a certain function from negative infinity to t = x - μ / σ. When t > 0, a replacement is made so that the calculation becomes 1 minus the integral from t to positive infinity. However, this may raise an issue because in Weka, all these values are of the Java datatype “double”, which only has a maximum of 16 bits for the decimal fraction. It is very common that the value of the integral is very small, thus after the subtraction by 1.0, there may be a loss of precision. For example, if the integral I is evaluated to 0.0000000000000001, then 1.0 - I =0.9999999999999999. Since there are 16 bits of the number 9, in Java the double value is treated as 1.0. This also contributed to the violation of MR-0 (Consistence with affine transformation).

2. Calculating proportions of each label

In NBC, to compute the value of P(l_ts = l_k ∣ a₀a₁…a_m-1), we need to calculate P(l_k). Generally when the samples are equally weighted, P(l_k) = {number of samples with l_k} / {number of all the samples}. However, Weka uses Laplace Accuracy by default, that is, P(l_k) = {number of samples with l_k + 1} / {number of all the samples + number of classes}.

For example, consider a training sample with six classes and eight labels as follows: { l₀, l₀, l₁, l₁, l₁, l₂, l₃, l₃ }. In the general way of calculating the probability, the proportion of each label is {2/8, 3/8, 1/8, 2/8, 0/8, 0/8} = {0.25, 0.375, 0.125, 0.25, 0, 0}. However in Weka, using Laplace Accuracy, the proportion of each label is {(2+1)/(8+6), (3+1)/(8+6), (1+1)/(8+6), (2+1)/(8+6), (0+1)/(8+6), (0+1)/(8+6)} = {0.214, 0.286, 0.143, 0.214, 0.071, 0.071}. This difference caused a violation of MR-2.1 (Addition of uninformative attributes), which was also considered a necessary property.

3. Choosing labels

Last, there are problems in the principle of “choosing the first label with the highest possibility”, as seen above for kNN. Usually the probabilities are different among different labels. However in Weka, since the non-existent labels in the training set have non-zero probability, those non-existent labels may conceivably share the same highest probability. This caused a violation of MR-1.1 (Permutation of class labels), which was considered a necessary property.

On the other hand, our experiments also found violations in MRs that are not necessary properties, which demonstrate a deviation from what would normally be considered the expected behavior of a classifier. Investigation into these violations reveals that after these metamorphic transformations, e.g. MR-3.1 (Consistence with re-prediction) and MR-5.2 (Removal of samples), we may accidentally remove noise from or bring noise into the original training data, which could lead to an unexpected result.

6. Discussion

6.1. Addressing Violations in MRs

Our testing discovered the violation of four MRs for kNN; however, none of these were its necessary properties and are mostly related to the fact that the algorithm must return one result when there is more than one “correct” answer. However, in NBC, we uncovered violations in some MRs that are its necessary properties, which indicate defects; the lessons learned here serve as a warning to others who are developing similar applications.

To address the issues in NBC related to the precision of floating point numbers, we suggest using the BigDecimal class in Java rather than the “double” datatype. A BigDecimal represents immutable arbitrary precision decimal numbers, and consists of an arbitrary precision integer unscaled value and a 32-bit integer scale. If zero or positive, the scale is the number of digits to the right of the decimal point. If negative, the unscaled value of the number is multiplied by ten to the power of the negation of the scale. The value of the number represented by the BigDecimal is therefore (un-scaledValue * 10^-scale). Thus, it can help to avoid the loss of precision when calcuating “1.0 - x”.

The use of Laplace Accuracy also led to some of the violations in the NBC implementation. Laplace Accuracy is used for the nominal attributes in the training data set, but Weka also treats the label as a normal attribute, because it is nominal. However, the label should be treated differently: as noted, the side effect of using Laplace Accuracy is that the labels that never appear in the training set also have some probability of being selected as the classification; thus, they may interfere with the prediction, especially when the size of the training sample set is quite small. In some cases the predicted results are the non-existent labels. We suggest that the use of Laplace Accuracy should be set as an option, and the label should be treated as a special-case nominal attribute, with the use of Laplace Accuracy disabled.

6.2. More General Application

Our technique has been shown to be effective for these two particular algorithms, but the MRs listed above hold for all classification algorithms, and [15] shows that other types of machine learning (ranking, unsupervised learning, etc.) exhibit the same behaviors classification algorithms do; thus, the approach is feasible for other areas of ML beyond just kNN and NBC.

More importantly, the approach can be used to validate any application that relies on machine learning techniques. For instance, computational biology tools such as Medusa [13] use classification algorithms, and some entire scientific computing fields (such as computational linguistics [12]) rely on machine learning; if the underlying ML algorithms are not correctly implemented, or do not behave as the user expects, then the overall application likewise will not perform as anticipated. As long as the user of the software knows the expected metamorphic relations, then the approach is simple and powerful to validate the implementation.

Last, the approach can also be used outside the field of machine learning as well. Applications that fall into the category of “non-testable programs” can be tested using the technique as long as they exhibit metamorphic properties. For instance, discrete event simulation systems can be tested using properties like “if all timings are doubled, overall resource usage should stay the same” since everything just takes twice as long. Similar properties can be used in optimization problems, too. Thus, the approach extends beyond scientific computing and machine learning into other domains.

7. Related Work

Although there has been much work that applies machine learning techniques to software engineering in general and software testing in particular (e.g., [2]), we are not currently aware of any other work in the reverse sense: applying software testing and validation techniques to machine learning applications. ML frameworks such as Orange [7] provide testing functionality but it is focused on comparing the quality of the results, and not evaluating the “correctness” of the implementations. Repositories of “reusable” data sets have been collected (e.g., [17]) for the purpose of comparing result quality, i.e., how accurately the algorithms predict, but not for the software engineering sense of testing (to reveal defects).

Applying metamorphic testing to situations in which there is no test oracle was first suggested in [3] and is further discussed in [5]. Metamorphic testing has previously been shown to be effective in testing different types of machine learning applications [16], and has recently been applied to testing specific scientific computation applications, such as in bioinformatics [4]. The work we present here seeks to extend the previous techniques to scientific computation domains that rely on machine learning, and into the realm of software validation.

8. Conclusion

As noted in [10], “scientists want to do science” and do not want to spend time addressing the challenges of software development. Thus, it falls upon those of us in the software engineering community to develop simple yet powerful methods to perform testing and validation. Our contribution is a set of metamorphic relations for classification algorithms, as well as a technique that uses these relations to enable scientists to easily test and validate the machine learning components of their software; this technique is also applicable to problem-specific domains as well. We hope that our work helps to increase the quality of the software being developed in the fields of computational science and engineering.