Higher Level of Replication Efficiency of 2009 (H1N1) Pandemic Influenza Virus than Those of Seasonal and Avian Strains: Kinetics from Epithelial Cell Culture and Computational Modeling

Abstract

The pathogenicity and transmission of influenza A viruses are likely determined in part by replication efficiency in human cells, which is the net effect of complex virus-host interactions. H5N1 avian, H1N1 seasonal, and H1N1 2009 pandemic influenza virus strains were compared by infecting human differentiated bronchial epithelial cells in air-liquid interface cultures at relatively low virus particle/cell ratios. Differential equation and computational models were used to characterize the in vitro kinetic behaviors of the three strains. The models were calibrated by fitting experimental data in order to estimate difficult-to-measure parameters. Both models found marked differences in the relative values of p, the virion production rate per cell, and R₀, an index of the spread of infection through the monolayer, with the values for the strains in the following rank order (from greatest to least): pandemic strain, followed by seasonal strain, followed by avian strain, as expected. In the differential equation model, which treats virus and cell populations as well mixed, R₀ and p varied proportionately for all 3 strains, consistent with a primary role for productivity. In the spatially explicit computational model, R₀ and p also varied proportionately except that R₀ derived for the pandemic strain was reduced, consistent with constrained viral spread imposed by multiple host defenses, including mucus and paracrine antiviral effects. This synergistic experimental-computational strategy provides relevant parameters for identifying and phenotyping potential pandemic strains.

Influenza viruses cause annual epidemics and occasional pandemics, and the recent pandemic due to the swine-origin 2009 (H1N1) virus provides a fresh opportunity to explore in vitro and in vivo measures of pathogenicity and transmission among different strains (12, 23, 31). Comparative analysis of virulence and transmission in animal models has been informative (21, 24, 30), although the sensitivity of this approach in identifying a pandemic strain is not yet clear. The ultimate goal of linking detailed phenotype with detailed genotype is impeded by a limited repertoire of tools to characterize the strain phenotype.

Pathogenicity and transmission are in part functions of virus replication, but the complex kinetics of replication are not necessarily reflected in simple counts of virus particles harvested from infected mucosa in vivo or from cell monolayers in vitro. Strains differ dramatically in their entry and replication efficiencies within specific cell types, and they display various potencies in suppressing cell defenses (43). Strains also differ in their efficiencies of person-to-person transmission as measured in closed populations and expressed as the basic reproductive number R₀ (12). The kinetics of viral replication in respiratory mucosal epithelial cells may reflect critical determinants in person-to-person transmission.

Using a seasonal strain as a reference point, we compared its replication kinetics to that of an avian strain (as a group, avian strains display inefficient person-to-person transmission) and to that of the 2009 pandemic strain (which is highly transmissible). With the goal of extracting more information from simple experimental measurement of virus secretion, we used two modeling strategies. Both differential equations (2, 7, 16-18, 22, 28, 33) and spatial models, such as cellular automata (6), have been used to quantify the kinetic behavior of influenza viruses in mucosal epithelia, but they are rarely used in a head-to-head model comparison. From detailed monitoring of viral replication in primary normal human bronchial epithelial (NHBE) cells in air-liquid interface (ALI) cultures, we used the computational power of these two quantitative modeling approaches to derive multiple parameters of viral replication. A differential equation model was fit to the experimental data, and the resulting parameters were used to calibrate components of two spatial models. The two modeling strategies are employed to take advantage of the strengths of each and to compare results from the same experimental data.

We used the models to derive two difficult-to-measure parameters, virus productivity per cell and the basic reproductive number (R₀), a surrogate for viral spread through the monolayer. These outputs have yielded consistent and dramatic differences in kinetics between the seasonal, avian, and pandemic strains and have suggested that constraints on viral spread in the mucosa may contribute significantly to the kinetic characteristics of different influenza virus strains.

MATERIALS AND METHODS

Air-liquid interface culture cells.

Differentiated human bronchial epithelial cells (13) were obtained from two sources. For experiments with avian and seasonal strains, differentiated pseudostratified tracheal bronchial cells in established air-liquid interface culture were purchased (EpiAirway Tissue, MatTek Corp., Ashland, MA) and used within 24 to 30 h of delivery. The cultures had been established under air for 27 days with the maintenance of transepithelial resistance (TER) of >200 Ω/cm². Upon receipt, beating cilia and mucus production were confirmed by videomicroscopy. In experiments with seasonal and pandemic strains, the cultures were established at Lovelace Respiratory Research Institute (LRRI) from cryopreserved undifferentiated single-cell suspensions obtained from the University of Miami Health Science Center Lung Transplant Program. NHBE cell pellets obtained from the University of Miami were plated on T125 tissue culture flasks in a density of 500 cells/cm² for cell proliferation. Bronchial epithelial basal medium (BEBM) (Lonza Inc., Walkersville, MD) was supplemented with growth factors and hormones as described previously (13). After expansion for two rounds of subculture, cells were plated to a density of 2 × 10⁵ cells/cm² on human collagen IV (BD Science)-coated Transwell inserts (Corning, Inc.). BEBM was supplemented with 10⁻⁷ M retinoic acid. Medium was changed every 48 h until cell confluence after 7 days, when air-liquid interface cultures were established by removing the medium from the apical compartment. Basolateral medium was changed every 48 h for 21 days. Transepithelial resistance exceeded 600 Mohm, measured by a volt/ohm meter (EVOM; World Precision Instruments, Sarasota, FL), and beating cilia were observed.

Virus.

Stock strains were obtained from the Centers for Disease Control and Prevention (Atlanta, GA), stored at −80°C, and thawed immediately before use. Influenza A/Hong Kong/483/97 (H5N1) virus isolated from a fatal case was a low-passage stock passaged twice more at LRRI in 10-day embryonated eggs. Influenza A/New Caledonia/20/99 (H1N1) virus, a seasonal strain circulating worldwide from 1999 to 2006, was a low-passage stock and was further passaged twice in embryonated eggs. The swine origin 2009 H1N1 strain A/California/04/09 stock was passaged twice in embryonated eggs and twice in Madin-Darby canine kidney (MDCK) cells.

Cell infection.

For each harvest-time group, 4 to 6 Transwells were inoculated with 100 μl of stock virus diluted in phosphate-buffered saline (PBS) to achieve an estimated ratio of virus particles to cells (multiplicity of infection [MOI]) of 0.01 in all experiments unless otherwise noted. The calculated MOI was subsequently derived from enumeration of surface epithelial cells and subtraction of nonadherent virus removed after 1 h of incubation at 37°C in a 5% CO₂ atmosphere. Transwells were harvested for secreted virus enumeration by a two-step process described below. The monolayer was then fixed in methanol for histology and immunohistochemistry.

Apical fluid collection.

Apical fluid was harvested by a two-step process because in early experiments with avian strains, we discovered that a large percentage of the virus capable of plaque formation remained on the cell surface after repeated washes with PBS, and incubation with pronase released more viable virus without diminishing virus plaque-forming ability or cell integrity. At the end of the culture interval designated for each well, in the first step, 500 μl PBS was added to the apical surface, slowly rinsed three times by trituration, and removed. The wash was repeated with an additional volume of 500 μl PBS, pooled for a total apical wash fraction of 1.0 ml. A 200-μl aliquot was added to 800 μl RNABee for RNA analysis, and the remainder was stored at −80°C for subsequent viral culture. In the second step, 500 μl of 0.05 M protease (Pronase, Sigma) was added to the monolayer for 10 min at 37°C to remove mucus remaining after the PBS wash without disrupting the monolayer adherent to the membrane. The Pronase wash was gently removed, an additional 500 μl of PBS was added to wash the monolayer, and both washes were pooled, for a total of 1.0 ml pronase incubation fraction. Histologic sections of the monolayer were stained with bromophenol blue dye, identifying no adherent mucus. Viral culture supernatants are presented as the apical wash and pronase incubation fractions combined (see Fig. 1) or as the two fractions separately (see Fig. 2). In two experiments after pronase incubation and wash removal, the cell layer was removed from the Transwell membrane by gentle scraping with a rubber policeman and cell suspensions were directly plaqued on MDCK cells.

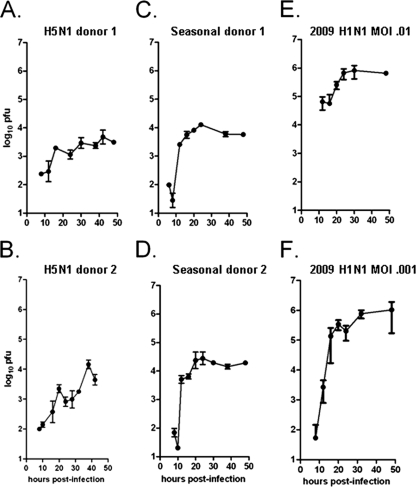
FIG. 1.

Plaque assay data for three influenza virus strains. Viral output for the A/HK/483/97 (avian) (A and B), A/NewCaledonia/20/99 (seasonal) (C and D), or A/California/04/2009 (pandemic) (E and F) influenza virus strain was assessed in normal human differentiated bronchial epithelial cells. Two separate experiments were performed for each strain, each from a separate lung tissue donor, such that each of the six experiments shown represents data from a distinct human donor. Cell layers with approximately 10⁶ surface-exposed cells were exposed to either 10⁴ (A to E) or 10³ (F) PFU for 1 h, residual virus was removed, and monolayer was harvested for apical fluids and cells at the times indicated. Total extracellular viral particles were collected by combining apical wash and pronase-released samples. Samples were taken from wells dedicated for each time point. Harvested virions were assessed by standard plaque assay; values shown are the means of four to five replicates ± standard deviations.

FIG. 2.

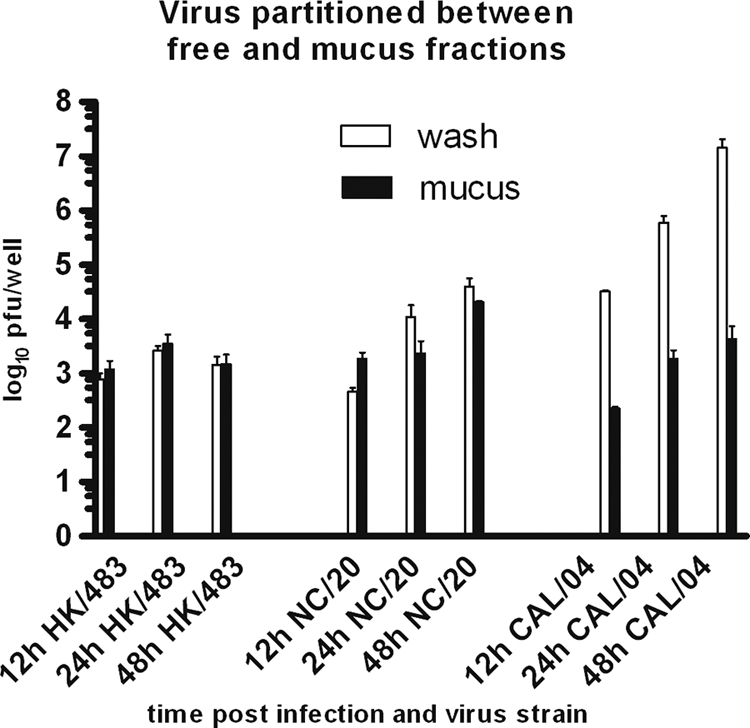
Fraction of viral particles collected from apical washes and pronase-released washes. Viral particles (PFU/well) were collected in apical washes (open bars) or pronase-released mucus-associated washes from the same culture (adjacent closed bars) at three intervals (12 h, 24 h, and 48 h) after viral inoculation. The mean for each experiment included 4 replicates; bars represent means ± SD of data from 5 experiments at each interval for the avian strain and from 4 experiments for each of the 2009 H1N1 and seasonal strains. For each strain, differences in mucus-associated virus between the 12-h, 24-h, and 48-h levels were not significant (two-sided Student t test at P < 0.05), except for the 12-h group for 2009 H1N1, which was not tested because n = 2 experiments at 12 h.

Quantitative viral culture.

The plaque assay on MDCK cells was a modified protocol based on the method described in reference 20. Assays were performed in 6-well plates in triplicate for at least 3 dilutions. MDCK cells were plated in 6-well plates in 10% fetal bovine serum (FBS) Eagle's minimal essential medium (EMEM). Medium was aspirated, cells were washed to remove FBS, and 200 μl of serial 10-fold dilutions of influenza virus samples were added to each well. Plates were rocked for 10 min at 37°C and then allowed to sit for 1 h at 37°C undisturbed. Medium was then aspirated off, and overlay medium (1× EMEM, 3 μg/ml tosylsulfonyl phenylalanyl chloromethyl ketone [TPCK] trypsin, and 0.6% Avicel) was gently applied. Plates were kept in a 37°C incubator undisturbed for 3 days. Plates were then washed, fixed, and stained with 0.05% Neutral Red. Plaques were enumerated, and verification of typical plaque morphology was performed under 10× inverted scope objection. The limit of detection is 50 virions per 1.0 ml of apical fluid.

Decay of virus.

To assess the effect of extracellular mucus on the decay of virus in the pronase fraction, mucus was collected from well-differentiated NHBE cells and diluted 1:25 in PBS. Influenza A/California/04/2009 virus was added at a concentration of 80,000 PFU/ml. Four hundred microliters of virus-mucus mix was placed in empty 24-well plates and incubated for 0 h, 1 h, 3 h, 6 h, 22 h, 30 h, or 46 h. Samples were subjected to microplaque assay as described previously (25). Samples were serially diluted and plated on monolayers of MDCK cells in 96-well microtiter plates with an Avicel (FMC Biopolymer) overlay. After 24 h, the cells were fixed, permeabilized, and stained with an antibody to influenza virus nucleoprotein (MAB8251; Millipore). After labeling with peroxidase-conjugated secondary antibody, plaques were visualized by staining with 3-amino-9-ethylcarbazole.

Immunohistochemistry.

Cell monolayers were fixed in acetone-methanol for 20 min immediately after apical fluid harvest and stored at 4°C for several days in PBS until mounting in paraffin. Sections (5 μm thick) were stained with hematoxylin-eosin for morphology. To label influenza virus nucleoprotein, H₂O₂-treated monolayer sections were incubated overnight at 4°C with rabbit antinucleoprotein antibody (MAB5281 [Chemicon] or IMG-5187 [ImGenex]) followed by peroxidase-labeled goat anti-rabbit IgG (Pierce) for 1 h. Cilia were labeled with antiacetylated α-tubulin antibody. To label cells in apoptosis, monolayer sections were incubated with anti-caspase-3 mouse monoclonal antibody (Pierce) followed by rabbit anti-mouse IgG.

Differential equations.

The following system of differential equations was used to model the viral infection dynamics:

As illustrated in Fig. 4, T is the number of susceptible target cells, V is the number of free virions, I₁ is the number of infected cells not yet producing virus, I₂ is the number of infected cells secreting virus, and F is a unitless quantity of antiviral factor produced by infected cells. The parameter β determines the rate at which virus infects target cells, t is time, τ₁ is the length of the virion release delay period (sometimes called the eclipse phase), i.e., the length of time before an infected cell starts producing virus, τ₂ is the length of time before infected cells start producing antiviral factor, δ is the death rate of virus-secreting cells, p is the rate at which a virus-producing cell secretes new virus, and e is the effectiveness of the antiviral factor at inhibiting viral production. This system of equations is a variant of the systems defined by Baccam et al. (2) and Beauchemin et al. (7) and refined for an analytic approximation in reference 38.

The model was initialized with 10⁶ target cells and 10⁴ virions for all experiments except the lower MOI experiment with the 2009 H1N1 strain, which had an initial virion inoculation of 10³ virions. The time until viral production begins, τ₁, was fixed at 10 h based on our observations of the time when the viral titer is first elevated above levels of unabsorbed virions. Sensitivity analysis of τ₁ (±50%) shows that the model is robust only for variations of ±10% for the free parameters to remain well within the original confidence intervals. Virus is not lost in the culture except through cell entry, and thus, c represents a loss of viral infectivity (7). The loss of virion infectivity was studied experimentally in the context of mucus (see Fig. 6) and showed no appreciable decay in the time frame of our experiments. Thus, c was chosen as c = 0. Further, the antiviral factor decay term (−d_F) had a negligible impact on the behavior of the model under all parameter fits for the 48-h time period of the model because d_F covaried with the parameter e. To simplify the model and limit the number of unknown parameters, d_F was also chosen as d_F = 0.

The equations were solved numerically using the odeiv Runge-Kutta package of the GNU Scientific Library (http://www.gnu.org/software/gsl/), which was modified to handle delay equations.

The formula for R₀ (7) was calculated by taking the number of new virions an infected cell can produce over its lifetime (p/δ) multiplied by the fraction of those virions that infect a cell, i.e., [βT₀/(c + βT₀)], where T₀ is the initial population of susceptible target cells.

(2)

R₀ calculations apply to the 10-h-to-24-h interval after cell inoculation, where the virion population increased rapidly. Although included in the formula, the term δ does not contribute to the differences in R₀ because its value is set identically in all runs of the model (see Discussion).

CA modeling.

The cellular automaton (CA) software program “ma_virions” (5) uses a virtual plate of cells on a hexagonal grid to approximate the two-dimensional configuration of real cells. We used version 0.10 of ma_virions, to which we made minor modifications (available on request). Each modeled cell consists of a unique grid location and infection state, which can be one of the following: uninfected, infected, secreting, or inactive. Each cell tracks the virion and antiviral factor concentration in its immediate environment, and each cell is assigned a life span. The infected cell life span, virion release delay period, and antiviral release delay period for each cell were selected randomly from a Gaussian distribution whose mean, μ, is an input parameter of the simulation and whose variance, σ, is μ/10. The cellular antiviral response was implemented as a single diffusible antiviral factor secreted by infected cells. The model has several input parameters, which were held constant during all runs (see Table 2).

Each site in the CA's lattice represents one epithelial cell. For simplicity, there is no cell division or differentiation over the course of the infection. Each location also keeps track of the amount of virus local to the site. Epithelial cells are initialized to the uninfected state, i.e., they do not contain any influenza virus. Virus either is introduced at the outset of the simulation (at random locations in the grid, with probability determined by the MOI) or secreted by actively infected cells. Once virus enters a cell, the cell state becomes infected (but not secreting) until the end of the eclipse phase (virion release delay). After the eclipse phase, the cell enters the secreting state and secretes virus according to the production rate (virion production rate). Each cell has an infected cell life span, which is sampled from the exponential distribution, and at the end of its life span, the cell becomes inactive, no longer absorbing or secreting virus. Virus diffuses across the grid according to a discretized version of the diffusion equation. References 5 and 6 give a detailed description of the model, and the software is publicly available at (http://adaptive.cs.unm.edu/mitchell/CA.tar). Free parameters derived from comparing simulation runs to the experimental data include the following: (i) life span of an infected cell, (ii) delay in release of the antiviral factor, (iii) virion production rate, and (iv) antiviral factor production rate.

In the in vitro experiment, virus was incubated for 1 h before the supernatant was removed. Thus, some virus included in the initial MOI is removed before it can enter a cell. We modeled this by setting the virus concentration in all cell locations to zero after 1 h of simulated time. The probability of infection was selected to allow reasonable fits to the experimental data and once determined was held constant during all runs. On each time step for each cell, its probability of becoming infected is calculated by multiplying the local virion concentration by the infection probability value.

To compute R₀ and for this case only, a single randomly selected cell was infected, and only that cell was allowed to secrete virions. In this way, infections resulting from virions produced by secondarily infected cells would not distort results. R₀ was calculated as the mean of 500 independent simulations, where each simulation ran for the secretion phase of the infected cell.

Model parameters that describe characteristics of individual cells, such as the viral secretion rate p, the secretion delay τ₁, and the reproduction number R₀, can be directly compared between the two models. However, other parameters, such as the antiviral potency e and the infection rate coefficient, are inherently different in that they are for the entire population of target cells in the case of the ordinary differential equation (ODE) system but pertain only to individual cells in the CA model. Values for these parameters from the two models cannot therefore be compared. Instead, values of this second type of parameter can be compared only within the same model.

CyCells.

To rule out implementation errors and other model dependencies, we corroborated the ma_virions model using an independently designed and implemented simulation called CyCells (41). CyCells was defined on a grid 360 by 360 by 10 μm³ in size. The grid was filled with 1,448 cells in a hexagonal arrangement (using the CyCells cell_hexmix property). Thirteen of the cells (approximating an MOI of 0.01) chosen randomly were infected at the start of the simulation. Free parameters included the incubation period (τ₁), cell decay rate (δ), viral infectivity (β), viral secretion rate (p), viral diffusion rate, and viral decay rate (c). These parameters were set without any model calibration using values that matched as closely as possible those obtained by modeling the first avian experiment using the ma_virions model. The CyCells model was simulated for 48 h in 10-s time steps.

Parameter fitting.

Best-fit values for unknown parameters in both models were found using a stochastic optimization method known as the genetic algorithm (GA). The GA maintains a population of individuals, where each individual represents one set of parameter values for the model. Each individual in the population can be thought of as a guess by the algorithm about a potentially good set of parameters. The guess is tested by the fitness function, which runs the model (either the ODE or CA model) with the parameter values set to match those specified by the individual. The quality of the guess is evaluated by comparing the model behavior with the experimental data, using the inverse of least-squares fits on a logarithmic scale. The GA was used instead of more standard nonlinear regression or exhaustive search due to the size and complexity of the search space, and in most cases the GA found better fits than those found using regression techniques. Algorithm details were tailored to meet the needs of each model.

Parameters in the ODE model (β, p, δ, e, and τ₂) were fit using the GAlib software package (http://lancet.mit.edu/ga/) with a population size of 100 individuals, 250 generations per run, tournament selection, and mutation and crossover rates of 0.01 and 0.5 respectively. The search procedure was restricted to parameter values within biologically plausible ranges. In all cases the ranges spanned several orders of magnitude, so parameters were represented in logarithmic units except for delay terms, which were represented in minutes. Fitness was evaluated by calculating the least-squares fit of the model to the experimental data in a four-phase process. Each phase consisted of 50 independent runs of the GA, where a standard run consisted of 100 individuals and 250 generations. Results with scores more than 2 standard deviations below the mean were removed. The search bounds were narrowed based on the remaining population, and these bounds were used to constrain the next phase. At the end of the fourth phase, the best individual of the 200 runs was retained. We also tried fitting parameters with the Berkeley Madonna (BM) regression software package (http://www.berkeleymadonna.com). Of the six data sets, fits to the data were better in five out of six data sets when using the GA. In each case, however, the fits from the two methods were similar, and only the GA results are reported.

Confidence intervals were calculated by the resampling residuals bootstrapping method (42), which reshuffles the residuals (error terms) of the primary fit onto the values predicted by the primary fits at time points when the experimental data were measured. This creates a new set of data points, to which the model is refit. This process was repeated a minimum of 1,000 times for each data set, producing new parameter values for each new fit. These values were sorted, and cutoffs for the inner 95% of the values are listed as the confidence interval.

In the CA model, free parameters were fit using a GA implemented by our group (http://adaptive.cs.unm.edu/mitchell/CA.tar). For each fitness evaluation of the GA, candidate parameter values selected by the GA were used to parameterize ma_virions, and the simulation was run for 1,440 time steps of 2 min each. The behavior of the simulation was compared to the experimental data at corresponding time points, and the error, computed identically to the computation for the ODEs, was interpreted as the fitness.

For all experiments except the high-MOI 2009 H1N1 experiment, a radius of 45 cells (7,333 total cells) was used to find candidate best-fit parameters. For the low-MOI 2009 H1N1 study, a radius of 60 cells (13,057 total cells) was used and candidate parameter sets were tested 10 times to account for stochastic variations in model behavior. The low-MOI study was treated differently because there is greater variation among runs when infecting with fewer viruses; more cells and more runs compensated for the higher variability. For each run of the GA, the output values from the simulation were scaled up to reflect a full-size plate, so that the output of the simulation could be properly compared to the experimental results. After best-fit parameters were found with the GA, the winning parameter sets were simulated on a plate size representative of the actual plate size used in the experiments, which was a radius of 525 cells (999,853 total cells), to confirm that the error calculations of the simulation on a small scale were close to the score on a large scale.

RESULTS

Experimental kinetics in ALI cultures.

NHBE monolayers were inoculated with virus, unabsorbed virus was removed after 1 h, and secreted virus was harvested by a two-step process beginning 8 to 10 h postinoculation (p.i.); each well was harvested only once. Virus was harvested at 4- to 8-h intervals in order to reveal patterns that might not be detectable with less-frequent harvesting. At each time point, the reported amount of secreted virus is the sum of the apical wash and pronase-released fractions, expressed as log₁₀ virus particles in a culture with 1 million NHBE cells (Fig. 1).

Virus was not detected in the apical wash or pronase-released fractions after 6 h postinoculation (p.i.). Low levels of virus were first detected at 8 to 10 h p.i., and virus retrieved in both fractions rapidly increased until approximately 24 h p.i., when subsequent harvests found a modest or no further increase in virus titers. In infection with the 2009 H1N1 strain, the peak level was 10⁵ to 10⁶ PFU at 24 h p.i. (Fig. 1E and F); with the seasonal strain, the peak level was 10⁴ to 10⁵ PFU at 24 h p.i. (Fig. 1C and D); and with the avian strain, the peak levels were 10³ to 10⁴ PFU at 24 h p.i. These interstrain peak-level differences were significant (t test, P < 0.001). Although a pattern of apparent oscillation in the virus levels was evident in all avian experiments (Fig. 1 A and B), the difference between the high and low virus levels at 20 h and 25 to 30 h p.i. was statistically significant only for avian donor 2 experiments (t test, P < 0.02) (Fig. 1B). With the exception of this experiment, differences between the virus levels at 24 h and 48 h p.i. were not statistically significant (analysis of variance [ANOVA] of repeated measures, P > 0.5), consistent with a balance between the virus secreted and the extracellular virus absorbed into susceptible cells or inactivated in the extracellular environment after 24 h p.i. (Fig. 1).

After removal of the apical wash, incubation of the cells with pronase enzyme yielded additional secreted virus particles (Fig. 2). Infections of NHBE cells with the avian strain produced viral particles equally divided between the apical wash and pronase-released fractions. For each time point p.i., the levels of virus in the pronase-released fractions were approximately the same for all three strains (Fig. 2). Although not quantified, mucus secretion increased during each infection and was collected primarily in the pronase-released fraction, except for the avian strain, which decreased at 48 h. This observation suggests that the mucus became saturated with viral particles to the same level regardless of the infecting strain.

Cell life span and apoptosis.

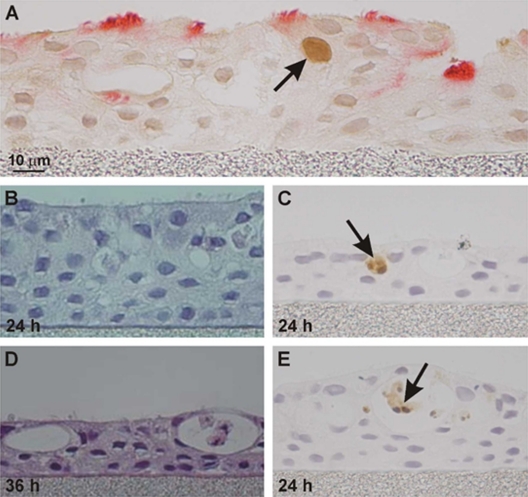
Relative estimates of cell apoptosis were sought by immunohistochemical (IHC) labeling of caspase-3-positive cells. The percentage of caspase-3⁺ cells varied from a background of 0.2 to 0.5% to a maximum of 7% of surface epithelial cells at 24 h in the H5N1-infected cultures and 3% in seasonal H1N1 virus-infected cells. During the preparation of cell monolayers for labeling, we noted that surface cells with clumped chromatin were washed from the monolayer. Loss of surface apoptotic cells occurs by an active extruding process, preserving the integrity of the monolayer (37). Most caspase-3⁺ cells visualized by IHC were located in the lumens of surface invaginations (Fig. 3), apparently protected from removal during the apical fluid collections. Because most apoptotic cells appeared to be lost during the wash and pronase treatment steps, enumeration of apoptotic cells was considered too imprecise to experimentally validate subsequent values of infected cell life span derived from the mathematical modeling.

FIG. 3.

Immunohistochemical microscopy of NHBE cells 24 h after infection with H5N1 strain A/HK/483/97. (A) Immunohistochemical localization of influenza virus NP antigen in the surface epithelial cell nucleus (arrow) in NHBE cells obtained from MatTek Corp. Cilia stained red with anti-alpha-acetylated tubulin, including infected cell. At right is invagination of the surface epithelial cell layer. (B and D) Hematoxylin-eosin staining of NHBE monolayer 24 h and 36 h after infection, showing loss of monolayer depth and desquamated cells in invagination lumen. (C and E) Immunohistochemical staining for caspase-3 apoptotic enzyme in surface epithelium (C) or in desquamated cells in invagination lumen (E).

Differential equation modeling.

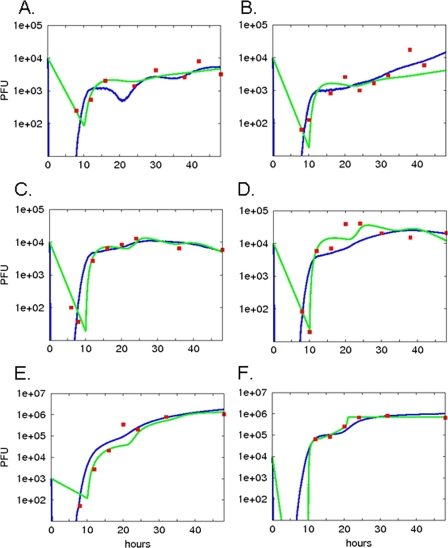
Our quantitative models were designed to identify the contribution of key steps in the viral replication process (Fig. 4). Our objective was to determine unmeasurable parameters of strain-specific replication capacity by calculating the basic reproductive number R₀ (the number of infected cells that results from one initially infected cell) and virion production rate per cell, p. The ODE model results (Fig. 5, green lines) closely replicate the data points for each influenza virus strain, although the oscillatory pattern suggested by the data for the avian strain (Fig. 1) is less apparent in the model output. For both experiments, R₀ values were 2.9 and 3.3 for the avian strain, 12.0 and 23.0 for the seasonal strain, and 305 and 316 for the 2009 H1N1 strain (Table 1). The rates of virion production per infected cell, p, were 0.18 and 0.20 PFU/h for the avian strain, 0.71 and 1.36 PFU/h for the seasonal strain, and 18 and 19 PFU/h for the 2009 H1N1 strain (Table 1). Thus, for each strain there was close interexperimental agreement, and there were marked differences between the strains for the estimated values of both R₀ and p. There were no significant differences in the infection rate, β, between the strains, in marked contrast to the differences in p and R₀, consistent with the hypothesis that strain differences in productivity are a function of intracellular replication efficiency, not cell entry efficiency or selectivity. The model accounted for the effectiveness of the antiviral cell defense (F) with the coefficient e. e varies markedly among the strains (P < 0.001, F test for each strain comparison): in rank order from highest to lowest values, the pandemic strain is followed by the seasonal strain, which is followed by avian strain (Table 1), suggesting different abilities to inhibit or avoid the host antiviral response.

FIG. 4.

Illustration of ODE model parameters. (A) Viruses enter the susceptible cell population according to the infection rate coefficient (β). (B) Cell-mediated inhibition of viral replication is initiated after interval τ₂. The inhibition is governed by parameter e. (C) Infected cells begin secreting virus after incubation delay τ₁, fixed at 10 h based on experimental data. (D) Virus is released at virion production rate p. (E) Virus secretion by a single cell is limited by 1/δ (production window). (F) Free virus is cleared from the secreted virus pool by the decay rate (c) plus the absorption rate (β). (G) Free virus is available to infect susceptible cells with rate constant β.

FIG. 5.

Best-fit results for differential equation and cellular automaton models. Both the differential equation and the cellular automaton models were run repeatedly with free parameters selected by a genetic algorithm as input. Simulated viral secretion output from the models was compared to the actual experimentally determined output at each time point, and a score was assigned to each candidate set of input parameters based on the sum of the squares of the residuals. The parameter set resulting in the best score for each experiment was chosen as the winning set. Simulation output from the winning parameter set for each experiment (A to F, corresponding to panel labels in Fig. 1) is shown for the differential equation model (green lines) and the cellular automaton model (blue lines). Experimental data are indicated with red squares.

TABLE 1.

Best-fit free parameter values for differential equation model^a

Strain	Expt	τ2 (h)	p (PFU/h)	e	B (PFU·h)-1	R0	MOI
Avian	1	3.3 (2.0-24)	0.18 (0.10-0.41)	1.0E-8 (1.0E-8-4.3E-7)	4.8E-7 (3.7E-7-7.8E-7)	2.9	0.01
	2	21.5 (2.1-24)	0.20 (0.16-1.33)	1.0E-8 (1.0E-8-7.0E-7)	5.3E-7 (4.4E-7-6.3E-7)	3.3	0.01
Seasonal	1	23.9 (6.7-23.9)	0.71 (0.60-1.69)	9.4E-7 (2.7E-7-1.1E-6)	6.3E-7 (6.3E-7-6.9E-7)	11.7	0.01
	2	23.6 (5.9-24)	1.4 (0.99-5.4)	1.6E-6 (1.3E-7-3.0E-6)	6.1E-7 (5.0E-7-6.6E-7)	22.7	0.01
2009 H1N1	1	22.8 (2.1-23.6)	19.0 (13.6-19.0)	2.1E-5 (3.5E-8-3.4E−5)	2.1E-7 (7.7E-8-3.7E-7)	316	0.001
	2	21.0 (20.8-24.0)	18.3 (10.1-19.0)	3.4E-3 (2.6E-5-1.0E-1)	2.7E-6 (4.8E-8-3.0E-6)	305	0.01

^aτ₂, antiviral molecule release delay; p, virion release rate; e, antiviral factor effectiveness; b, infection rate; R₀, viral reproduction number. Ninety-five percent confidence intervals for each of the free parameter values are shown in parentheses.

CA modeling.

In the cellular automaton (CA) model, fixed parameter values were taken either from the literature or laboratory results (Table 2; Fig. 6), and the unknown parameters were determined using a GA (Table 3). Model estimates closely approximated experimental values at all time points (Fig. 5, blue lines) and resembled the ODE model estimates. However, the CA model mimics the oscillatory secretion behavior seen in the avian strain data (Fig. 5A). Rather than calculating R₀ from the rate parameters (see equation 2) as in the ODE model, we measured R₀ directly in the CA simulation (Table 3). These values showed a pattern similar to that of the ODE model, namely, that the avian strain had the lowest R₀ value (3.0 to 4.0), the R₀ value for the seasonal strain was significantly higher (12 to 15), and the R₀ value for 2009 H1N1 was the highest (34 to 64). Infected cell virion production rates (p) were 0.28 and 0.22 PFU/h for the avian strain, 3.8 and 1.4 for the seasonal strain, and 20.0 and 7.9 for the 2009 H1N1 strain. The rank orders of p and R₀ are the same for the three strains: the order from least to greatest is avian, seasonal, and then pandemic. Variation of each free parameter by 10% above and below the reported value resulted in negligible changes in the simulation results (results not shown).

TABLE 2.

Input parameters for cellular automaton model

Input	Default value(s)	Value determined by:	Source and/or reference
Cell diameter (mM)	11	Measurement	This study; 5
Time step size (min)	2	Selection	This study; 5
Virtual plate radius (cells)	45, 60, 525	Measurement	This study
Virion diffusion rate (m2/s)	3.18 × 10−15	Estimation	5
Diffusion rate of antiviral factor (m2/s)	3.18 × 10−13	Selection	This study
MOI	0.001, 0.01	Selection	This study
Virion release delay (h)	10	Observation	Fig. 1, this study
Antiviral factor decay rate	0.0	Selection	This study
Infection rate coefficienta	35.0	Selection	This study
Viral decay rate	0.0	Measurement	Fig. 6, this study

^aThis unitless value was selected to be high enough to ensure that cells are infected as soon as there is virus present. Any value greater than 15 is sufficient for this purpose.

FIG. 6.

Effect of conditions present during ALI cell incubation on viral decay. Viral particles of the 2009 H1N1 strain were incubated in empty wells at 37°C for the indicated times with mucus removed from ALI cultures. Means ± SD of viable virus remaining after incubation were determined using a microplaque plaque assay (solid line). An exponential decay curve was fit to the resulting data (dashed line), with a decay constant of 1.76 × 10⁻¹⁶ h⁻¹; half-life, 3.95 × 10¹⁵ h.

TABLE 3.

Best-fit free parameter values for cellular automaton model^a

Strain	Expt	Life span (h)	τ2 (h)	p (PFU/h)	e	R0	MOI
Avian	1	18.8	11.4	0.28	0.16	3.0 ± 0.1	0.01
	2	24.5	6.9	0.22	0.01	4.0 ± 0.2	0.01
Seasonal	1	29.9	8.1	3.8	8.1	15.0 ± 1.3	0.01
	2	25.4	7.9	1.4	1.7	12.2 ± 0.7	0.01
2009 H1N1	1	24.5	8.6	20.0	2.4	63.5 ± 5.2	0.001
	2	22.5	11.8	7.9	6.2	33.8 ± 2.8	0.01

^aLife span, infected cell life span; τ₂, antiviral molecule release delay; p, virion release rate; e, antiviral factor effectiveness; R₀ viral reproduction number; MOI, multiplicity of infection. R₀ intervals represent means ± SD for 500 independent trials.

To confirm that our CA results did not depend on subtle implementation details, we compared our simulation results using CyCells, which has been previously used for modeling tuberculosis infection (41). By initializing CyCells similarly to that of the ma_virions software program, we demonstrated a similar kinetic profile between the two models (model comparison at http://adaptive.cs.unm.edu/mitchell/cycells/.html). For the avian strain infection, the oscillatory pattern of infection was replicated by both models, although CyCells did not approximate the data points as well as the CA.

DISCUSSION

Mathematical and computational models were used to derive numerical values for the replication kinetics of different influenza virus strains in human bronchial epithelial cells. The relative values for each free parameter, particularly p and R₀, among the three influenza virus strains studied are highly informative for comparison of strain-specific pathogenicities. The absolute values reported here for these parameters and cell types are considered to be robust since they were derived by an unbiased process, but since the values may be model specific, they await confirmation in other models.

In vitro human bronchial epithelial cells in air-liquid interface cultures allowed us to sample virus more frequently and completely than in the in vivo study (2), and it avoided possible effects of antibody or cell-mediated immune responses, which may provide more variability in an in vivo model (17, 18). NHBE cell cultures are likely more relevant than cell lines for studying kinetics of influenza virus replication, although no attempt was made here to compare primary to immortalized cells. NHBE cells support the replication of 2009 H1N1 and seasonal strains (21, 39), but there is disagreement on whether replication of avian strains is supported in well-differentiated NHBE cells (8, 39). We have found replication of two highly pathogenic H5N1 avian influenza virus strains, HK/483 (Fig. 1) and A/Vietnam/1203/2004 (data not shown), in 7 independent experiments performed using both sources of NHBE cells. Documenting of replication may depend on the timing of sampling (Fig. 1B), enumeration of all secreted viral particles (Fig. 2), and temperature of the cell culture (36). Replication of human seasonal strains has been shown to be consistently greater than that of avian strains in NHBE cells (8, 39).

Cell tropism of different influenza virus strains is determined largely by preferential binding of hemagglutinin proteins to specific sialic acid-decorated glycan receptors. NHBE cultures reproduce the receptor-type distributions found in human respiratory mucosal tissues (39). In addition, except for in vivo immigrant humoral and cellular innate immune elements, the in vitro NHBE cells present in-life barriers to viral entry and spread in mucosal tissue. Avian strains preferentially bind the α-2,3-linked sialic acid receptors in the first cycle of infection (26). In spite of the loss of cilia during influenza virus infection, we identified by immunohistochemistry early nuclear staining of the avian virus N protein in ciliated cells (Fig. 3). Human-adapted strains preferentially bind α-2,6-linked sialic acid on nonciliated secretory cells, although receptor preferences may shift during adaptation to different hosts (26). Human mucin proteins predominantly display the α-2,3-linked sialic acid receptors (11). This would appear to favor the binding of avian strains to mucus-associated fractions, but no evidence for this preference was found when comparing the avian, seasonal, and 2009 H1N1 strains (Fig. 2). Thus, rather than serving exclusively as a binding decoy for H5N1 strains, mucus and mucin proteins may serve other trapping functions beyond specific receptor binding and deserve further investigation.

We used the ODE model to describe aggregate infection kinetics. ODEs are valuable for studying viral dynamics in a well-mixed system, particularly for blood-borne pathogens, such as HIV and hepatitis viruses (4, 9, 33, 34). However, spatial effects are not represented, yet they are likely important in the experimental system where influenza virus infection spreads though a monolayer of epithelial cells. Thus, a model that accounts for the spread of infection to nearby susceptible cells may better represent influenza dynamics (4). In addition, resistance to infection has been shown to pass directly from infected cells to adjacent neighbors (32), further justifying a spatially explicit model. CA modeling corroborated the results of the ODE model, but in the 2009 H1N1 infection, R₀ values in the CA model were lower than those in the ODE model, possibly reflecting the constraints on lateral spread of virus in the in vitro system more effectively. In contrast, the wide orders-of-magnitude variation in the absolute values of e between the two models is explained by the different way each model treated e, making comparison between the models not relevant. In the ODE model, e refers to the inhibitory effect among all cells at once, whereas the CA model considers each cell at a given instant in time.

Oscillations in the experimentally derived virus output from avian virus-infected cells were consistently seen but were statistically significant only for donor 2 (Fig. 1). Mild oscillations were also noted in both models of all three viruses studied (Fig. 5). This observation suggests overlapping cycles of replication that occur due to the delay in production between the cycles. The CA model predicted an infected cell life span (eclipse plus secreting phase) of 20 to 24 h in almost every simulation, and the eclipse phase, τ₁, estimated from the experimental data was approximately 10 h. Absorption of secreted virus into cells infected during the next cycle would produce a temporary decrease in viral levels and apparent oscillatory behavior.

We observed experimentally that 2009 H1N1 produced more virus after 24 h in culture than the other strains, and the models calculated a higher R₀ for the 2009 H1N1 strain than for the avian and seasonal strains. Productivity varies among strains of the same hemagglutinin subtype, and some seasonal strains may even approximate the replication efficiency of 2009 H1N1 strains (21). The amount of secreted virus at any given time is determined by the balance of virus production and virus decay (Fig. 4), and variable decay among different strains has not been rigorously tested. Greater levels of secreted virus on the respiratory mucosa may be a key determinant of the contagiousness of the infected host. Productivity of virus secretion on the respiratory mucosa, however, may not be the only determinant of transmission by exhaled aerosol. In controlled exposure chamber experiments in which susceptible ferrets were exposed to exhaled aerosols from infected ferrets, 2009 H1N1 transmission was more efficient than seasonal virus transmission (F. Koster et al., unpublished data). The exhaled aerosols contained the same levels of viral RNA for the two strains, suggesting that transmission was primarily dependent on more-efficient viral replication in the susceptible host.

In the human study (2), nasal washes were collected only once daily following intranasal inoculation with an unknown MOI, measuring the productivity in nasal turbinate and respiratory airway cells. Interestingly, in spite of differences in the frequency of collection, MOI, and cells infected, our seasonal strain R₀ calculations in the ODE model (range, 11 to 22) and CA model (range, 12 to 15) are comparable to the seasonal strain R₀ calculation (∼22) for human nasal cells (2). Bronchial epithelial cells from the airway portion of the lower respiratory tract and nasal turbinate cells may support the replication of influenza virus strains equally; 2009 H1N1 virus infection of epithelial cells from ferret bronchi and turbinates displayed identical kinetics (J. Tipper et al., unpublished data).

The infected cell life span was treated differently in the ODE and CA modeling approaches, with different results. In the ODE model, virus-producing cells (I₂) were assumed to die at a constant rate, δ, implying an exponential distribution of cell lifetimes. The rate δ was constrained to correspond to a biologically plausible range for infected cell half-life (ln 2/δ) between 6 h and 24 h. The value for δ in each independent fit resulted in the lower boundary of that range. Because the infected cell death rate (δ) and viral production rate (p) covary in the model, differences between the abilities of strains to produce virus are best seen by examining the values of p (Table 1). For the CA model, best-fit values of the infected cell life span ranged from a mean of 21.7 h for the avian strain to a mean of 27.6 h for the seasonal virus. Recent modeling of influenza virus kinetics has used a fixed life span at 24 h based on experimental data (35), and experimental data in the murine model of a mouse-adapted seasonal strain were used to calculate an epithelial cell life span of 29 h (28).

The infected cell life span has not been measured experimentally in influenza virus-infected epithelial cells in vitro to our knowledge. Influenza virus infection induces cell apoptosis (19), and viral strains vary in their ability to retard apoptosis (44). Attempts to measure relative levels of apoptosis here were inaccurate due to the loss of infected cells from the surface. We noted thinning of the monolayer during the culture, which was more pronounced with the avian strain than with the H1N1 strains (Fig. 3B and D). A large number of variables affect the measurement of infected cell life span, including the monolayer integrity, the interval between apoptosis induction and cell dissolution, and the surface cell replacement rate from basal cell differentiation. Epithelial barrier function is preserved after surface cell loss by a process of apoptotic cell extrusion in which dying cells are squeezed out of the epithelium (37).

Both models predicted e to be smaller in the avian strain than in either the 2009 H1N1 strain or the seasonal strain (see Tables 1 and 3). This is consistent with published experimental observations finding greater suppression of interferon-mediated defense by virulent avian strains (3, 14, 40, 43). The ODE model predicted a higher e value in the 2009 H1N1 strain than in the seasonal strain, while the CA model predicted that these two strains would have similar e values. The differences in how the two models handle diffusion and spatial distribution of infected cells may account for these differences, but experimental validation is needed to resolve this discrepancy.

Uninfected cell susceptibility to infection, and thus the number of target cells, is determined by the cell phenotype, differentiation state, and activation of antiviral defense mechanisms. Avian (H5N1) and seasonal (H1N1 and H3N2) influenza virus strains have distinct preferences for cell type infection (27). We observed that the monolayers used in this study contained 25 to 40% ciliated cells and that of the remaining nonciliated cells, 10 to 20% were goblet cells, distributions observed by other investigators (27, 39). During injury, lung progenitor cells located below the surface are activated, undergo robust clonal expansion, and replace lost infected surface epithelial cells (15). However, the rate of differentiation at the surface and subsequent susceptibility to influenza virus infection are unknown for our in vitro experimental system and have been considered to be a relatively minimal contribution to the target cell population in vivo (35). Finally, the susceptibility of cells adjacent to an infected cell is altered in a paracrine fashion by local signaling through gap junctions for interferon-mediated defenses (32). Our observations are consistent with paracrine defense activation, since infected cells identified by immunohistochemistry early in infection occurred in isolation (Fig. 3), and we rarely found adjacent infected cells. Modeling of in vivo data has also found a major role for a paracrine-distributed innate defense, leaving most respiratory epithelial cells uninfected (35). In view of the multiple unknowns in our experimental system, our models make the assumption that each monolayer had the same number of susceptible cells and that the phenotype of susceptible cells did not change during the course of infection.

Taken together, our results show that in vitro infection of human well-differentiated bronchial epithelial cell monolayers can be used to derive relative numerical estimates for replication of three influenza virus strains. Mathematical and computational models can provide reproducible results for R₀ and p. Whether these derived parameters are useful as phenotypic characteristics of each strain will require further replications that account for differences in host cell donor characteristics and study of multiple strains to incorporate strain-specific modulations of the host response (43). These phenotypic indices can then be compared to the transmissibility and virulence of each strain, since transmissibility to humans cannot be quantified experimentally (1). The higher R₀ value of the 2009 H1N1 strain derived here may be one of several parameters predicting the higher epidemiological R₀ value derived from field studies in human populations (10). Likewise, the low R₀ value calculated here for an avian strain may predict the rare human-to-human transmission of H5N1 strains (29). The caveats applicable to this in vitro experimental model and the computational models include restriction to one tissue source of epithelial cells, the absence of immigrant innate and acquired immune response operating in the intact host, a simplistic representation of the innate host cellular response, and insufficient information about the actual life span of infected cells. Nonetheless, the ability to study and compute kinetics of virus replication in human epithelial cells provides a step in the direction of deriving accurate phenotypes of the pandemic potential of any influenza virus strain.