Identifying a Transcription Factor’s Regulatory Targets from its Binding Targets

Abstract

ChIP-chip data, which shows binding of transcription factors (TFs) to promoter regions in vivo, are widely used by biologists to identify the regulatory targets of TFs. However, the binding of a TF to a gene does not necessarily imply regulation. Thus, it is important to develop computational methods which can extract a TF’s regulatory targets from its binding targets. We developed a method, called REgulatory Targets Extraction Algorithm (RETEA), which uses partial correlation analysis on gene expression data to extract a TF’s regulatory targets from its binding targets inferred from ChIP-chip data. We applied RETEA to yeast cell cycle microarray data and identified the plausible regulatory targets of eleven known cell cycle TFs. We validated our predictions by checking the enrichments for cell cycle-regulated genes, common cellular processes and common molecular functions. Finally, we showed that RETEA performs better than three published methods (MA-Network, TRIA and Garten et al’s method).

Introduction

A cell responds to environmental and physiological changes through reorganization of genomic expression. This kind of regulation is realized by transcriptional regulatory networks (TRNs), which are mainly controlled by transcription factors (TFs). Therefore, identifying the sophisticated architecture of TRNs would reveal the fundamental aspects of the mechanisms involved in the maintenance of life and adaptation to new environments.^1–5

The first step toward reconstructing TRNs is to identify the target genes of known TFs.^6–10 Genome-wide transcription factor binding analysis, also called ChIP-chip analysis, was developed to fulfill this goal.^11,12 ChIP-chip analysis can be used to identify physical interactions between TFs and the promoter regions which they bind to. Simon et al¹³ performed ChIP-chip experiments to find out the binding targets of nine major cell cycle TFs. Lee et al¹⁴ performed ChIP-chip experiments to investigate how the yeast 106 TFs bind to promoter sequences across genome. Harbison et al¹⁵ conducted genome-wide transcription factor binding assays for 203 TFs in yeast to construct an initial map of the yeast’s transcriptional regulatory code. All these three studies are experiment-based approaches. They provided direct evidence of TF-promoter binding relationships. However, TF-promoter binding relationships are not equal to TF-gene regulatory relationships. A TF may bind to the promoter of a gene but has no regulatory effect on that gene’s expression. Hence, additional information is required to solve this ambiguity inherent in ChIP-chip data.

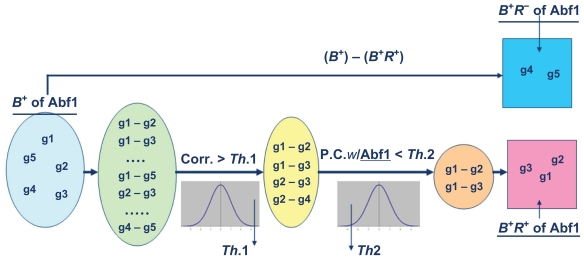
Gene expression data were widely used to solve this problem. Exploiting the additional information provided by gene expression data, several algorithms have been developed to identify a TF’s regulatory targets from its binding targets (inferred from the ChIP-chip analysis). For instance, Garten et al’s method⁶ used co-expression analysis, MA-Network⁹ used multivariate regression analysis, and TRIA⁷ used time-lagged correlation analysis on gene expression data to classify a TF’s binding targets (inferred from the ChIP-chip analysis) into regulatory and non-regulatory targets. In this paper, we develop a new method, called REgulatory Targets Extraction Algorithm (RETEA), which applies partial correlation analysis between a TF and all those pairs of its binding targets which are highly co-expressed. Partial correlation analysis has been widely used to determine whether the association between two variables is due to the effect of the third variable.^16,17 Here partial correlation is used to measure the residual correlation between two co-expressed binding targets of a TF after removing the TF’s regulatory effect. Low partial correlation means that the co-expression between the two binding targets of the TF is mainly due to that TF’s regulatory effect. That is, this co-expressed binding target pair of the TF can be regarded as the co-regulation pair of the TF. Therefore, RETEA assigns a pair of the TF’s binding targets as the TF’s regulatory targets if these two binding targets have high correlation but low partial correlation. The flowchart of RETEA could be seen in Figure 1.

Figure 1.

The flowchart of RETEA.

Note: In the figure, g1 to g5 represent the five binding targets of Abf1. Among them, only g1, g2 and g3 are identified by RETEA as the regulatory targets of Abf1.

Methods

Datasets

Four data sources were used in this study. First, the ChIP-chip data of the cell cycle TFs in the rich media growth condition were downloaded from Harbison et al’s paper.¹⁵ Second, the gene expression data of the yeast cell cycle process were downloaded from Paramila et al’s paper.¹⁸ Samples for all genes in the yeast genome are collected every 5 minutes for 25 time points, which cover two cell cycles. Third, the mutant data of the TFs under study are downloaded from Hu et al’s paper.⁸ They grew each of 263 TF knockout strains as replicates and compared mRNA expression of each of these strains with a wild-type strain using microarrays to identify the target genes whose expression profiles are affected when a TF has been knocked out. Fourth, the genome-wide distribution of the high-confidence TFBSs of many TFs in yeast was downloaded from MacIsaac et al’s paper.¹⁹ The high-confidence TFBSs were derived by using six motif discovery methods, with the requirement for conservation across at least two of four related yeast species.

REgulatory Targets Extraction Algorithm (RETEA)

We first define B⁺ as the set of genes that are significantly bound by a TF. Three previous papers^13–15 used a statistical error model to assign a P-value to the binding relationship of a TF-promoter pair. They found that if P-value ≤0.001, the binding relationship of a TF-promoter pair is of high confidence and can usually be confirmed by promoter-specific PCR. Therefore, we include a gene in the set B⁺ if the P-value indicating that a TF would bind to the promoter of the gene is ≤0.001. Then RETEA is used to classify B⁺ (binding targets of a TF) into B⁺R⁺ (regulatory targets of a TF) and B⁺R⁻ (non-regulatory targets of a TF). Two genes in B⁺ are assigned into B⁺R⁺ if they have high expression correlation but low partial expression correlation (ie, low residual expression correlation after removing the regulatory effect of the TF). Those genes in B⁺ that are not belong to B⁺R⁺ are assigned into B⁺R⁻.

The details of RETEA are as follows. Let ⟶ = (x₁,..., x_N) and &yrarr; = (y₁,..., y_N) be the gene expression time profiles of two genes x and y retrieved from the cell cycle microarray data.¹⁸ Let &zrarr; = (z₁,..., z_N) be the protein activity time profile of TF z. Since the protein activity profiles of TFs are not available in the public domain, they need to be estimated by computational methods. In this study, we combine the mutant and gene expression data to do this task. The protein activity time profile of TF z is estimated by using the average of the gene expression time profiles of all the genes whose expressions are affected by the deletion of the TF z (inferred from the mutant data).⁸

Assume that the genes x and y are in the set B⁺ of TF z. Compute the Pearson correlation r_xy between genes x and y and the partial correlation r_xy|Z between the genes x and y given the TF z as follows

$$\begin{array}{l}{r}_{xy}=\frac{{\displaystyle \sum _{i=1}^N}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\displaystyle \sum _{i=1}^N}{(x_i-\overline{x})}^2}\sqrt{{\displaystyle \sum _{i=1}^N}{(y_i-\overline{y})}^2}},\\ r_{xy|z}=\frac{r_{xy}-r_{xz}{r}_{yz}}{\sqrt{1-r_{xz}^2}\sqrt{1-r_{yz}^2}},\end{array}$$

where $\overline{x}={\displaystyle \sum _{i=1}^N}{x}_i/N,\overline{y}={\displaystyle \sum _{i=1}^N}{y}_i/N$, r_xz (or r_yz) is the Pearson correlation between the gene expression time profile of gene x (or y) and the protein activity time profile of TF z. Then the genes x and y are assign to B⁺R⁺ of TF z if r_xy > Th₁ & r_xy|z < Th₂, where Th₁ and Th₂ are the given thresholds. That is, the genes x and y are regarded as the regulatory targets of TF z if they have high expression correlation but low residual expression correlation after removing the regulatory effect of the TF z. Those genes in B⁺ that are not belong to B⁺R⁺ are assigned into B⁺R⁻. We claim that the genes in B⁺R⁺ are more likely to be the TF’s regulatory targets than are the genes in B⁺R⁻.

Results

Only a subset of a TF’s binding targets are identified as its regulatory targets

Since cell cycle process is one of the most well-investigated cellular processes in yeast, we applied our method to identify the plausible regulatory targets of known cell cycle TFs (according to MIPS database).²⁰ Eleven cell cycle TFs whose sizes of B⁺ greater than 65 are considered in this study. The number of genes in B⁺R⁺ and B⁺R⁻ is listed in Table 1. On average, 60% of a TF’s binding targets are identified as its regulatory targets, which is similar to the results of MA-Network⁹ (58%) and TRIA⁷ (55%). The following two analyses were performed to validate our results.

Table 1.

The numbers of genes in B⁺, B⁺R⁺ and B⁺R⁻ for each of the eleven cell cycle TFs under study.

TF	B+	B+R+	B+R−
Abf1	213	129	84
Swi4	134	84	50
Swi6	134	88	46
Cin5	127	55	72
Rap1	125	87	38
Fkh1	116	83	33
Mbp1	114	88	26
Fkh2	107	66	41
Ume6	100	39	61
Swi5	90	45	45
Mcm1	67	35	32

First validation: Enrichment for cell cycle-regulated genes in B+R+ and B+R⁻

Since the function of a cell cycle TF is to regulate the expression of the cell cycle-regulated genes, the regulatory targets of a cell cycle TF should be enriched in cell cycle-regulated genes. Therefore, our predictions are validated if the cell cycle-regulated genes are more enriched in B⁺R⁺ than in B⁺R⁻. We first compute the proportions of genes of B⁺R⁺ and B⁺R⁻ that belong to the 666 cell cycle-regulated genes identified by Pramila et al.¹⁸ We then test whether the enrichment of the cell cycle-regulated genes in B⁺R⁺ is statistically higher than that in B⁺R⁻. The cumulative hypergeometric distribution is used to assign a P-value for determining the statistical significance (see Appendix for details). In most cases (9/11), except for Rap1 and Ume6, the cell cycle-regulated genes are more enriched in B⁺R⁺ than in B⁺R⁻ with P-value <0.005 (see Table 2). This result suggests that our criterion for distinguishing regulatory from non-regulatory targets of a cell cycle TF is reliable.

Table 2.

The enrichment of the cell cycle-regulated genes in B⁺R⁺ and B⁺R⁻.

TF	B+R+	B+R−	P-value
Abf1	23/129	4/84	3.37E-03
Swi4	55/84	6/50	5.73E-10
Swi6	61/88	7/46	1.32E-09
Cin5	16/55	3/72	1.05E-04
Rap1	12/87	4/38	4.28E-01
Fkh1	41/83	5/33	4.63E-04
Mbp1	56/88	1/26	1.70E-08
Fkh2	49/66	6/41	1.00E-09
Ume6	8/39	9/61	3.14E-01
Swi5	22/45	8/45	1.65E-03
Mcm1	26/35	7/32	1.83E-05

Second validation: Enrichment for the common cellular processes and common molecular functions in B+R+ and B+R⁻

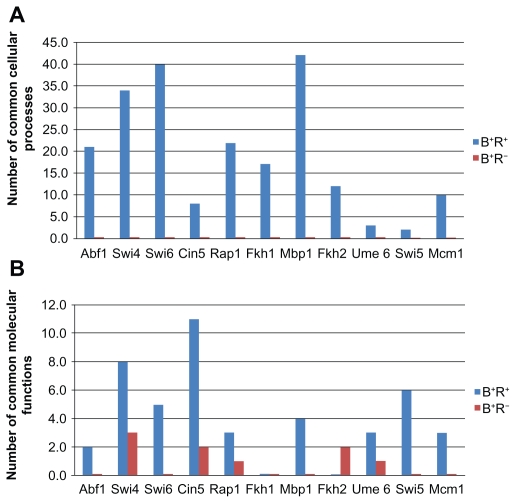
Because genes in B⁺R⁺ are regulated by the same TF, they are likely to be involved in the same cellular process or even have the same molecular function. Therefore, our predictions are validated if B⁺R⁺ is more enriched than B⁺R⁻ for the common cellular processes and common molecular functions. Using GO term finder in SGD²¹ with FDR <0.05, we found that in all cases (11/11), the number of enriched common cellular processes in B⁺R⁺ is larger than that in B⁺R⁻ (see Fig. 2A). Besides, using GO term finder in SGD with FDR <0.05, we found that in most cases (9/11), except for Fkh1 and Fkh2, the number of enriched common molecular functions in B⁺R⁺ is larger than that in B⁺R⁻ (see Fig. 2B). This result suggests that our criterion for distinguishing a TF’s regulatory from non-regulatory targets is reliable because co-regulated genes should have a greater probability to have the common cellular processes and common molecular functions than non-co-regulated genes.

Figure 2.

Testing for the enrichment for the common cellular processes and common molecular functions in B⁺R⁺ and B⁺R⁻ for eleven cell cycle TFs.

Taken together, the two validations mentioned above convincingly demonstrate that RETEA is capable of extracting a TF’s regulatory targets from its binding targets.

Discussions

Performance comparison with three published methods

To identify the regulatory targets of a TF, Gao et al⁹ developed MA-Network that used multivariate regression analysis on gene expression data and Wu et al⁷ developed TRIA that identified a temporal relationship between a TF and its target genes. Besides, Garten et al⁶ developed a method to identify a TF’s regulatory targets by integrating the ChIP-chip, promoter sequence, and gene expression data. In their approach, gene i is said to be regulated by TF j if it is a binding target of the TF j (inferred from the ChIP-chip data) and it also has the following four kinds of evidence strengthening this assignment: 1) significant expression coherence in at least one condition, 2) TFBS-containment in the promoter of gene i, 3) significant colocalization of the TF j with another TF where gene i is the binding target of both TFs, and 4) synergy of TF j with another TF where gene i is the binding target of both TFs.

Since our method and the three published methods mentioned above are developed to do the same task, a performance comparison of these methods should be done. Since a TF has to bind to its regulatory targets in order to regulate their expressions, enrichment of the high-confidence TFBS among the identified regulatory targets of that TF can be used as a criterion for performance comparison. The high-confidence TFBS were downloaded from the MacIsaac et al’s paper,¹⁹ which were derived using six binding motif discovery methods, also including the requirement for conservation across at least two of the four related yeast species.

The details of the performance comparison are as follows. Let S₁ (S₂, S₃) be the set of regulatory targets of a TF that are identified by RETEA but not by MA-Network (TRIA, Garten et al’s method) and T₁ (T₂, T₃) be the set of regulatory targets of a TF that are identified by MA-Network (TRIA, Garten et al’s method) but not by RETEA. We tested overrepresentation of the high-confidence TFBS in S_j and T_j for j = 1,2,3. The cumulative hypergeometric distribution is used to assign a P-value to the TFBS enrichment (see Appendix for details). Since only five TFs (Abf1, Fkh2, Mbp1, Mcm1 and Swi4) were investigated in both RETEA and MA-Network, we used these five TFs for performance comparison. We found that in all of the five (5/5) cases the high-confidence TFBS are enriched in S₁ with P-value <0.001 but only three of the five (3/5) cases are enriched in T₁ (see Table 3). This result shows that RETEA has a much better ability to identify the regulatory targets of a TF than does MA-Network. Similarly, as shown in Tables 4 and 5, RETEA is demonstrated to be better than TRIA (5/8 vs. 4/8) and Garten et al’s method (7/8 vs. 6/8) in extracting regulatory targets from the binding targets of a TF.

Table 3.

Performance comparison of RETEA with MA-Networker using TFBS data.

TF	Expected	Observed S1	P-value	Observed T1	P-value
Abf1	870/6229	42/53	<1.00E-12	56/62	<1.00E-12
Fkh2	916/6229	13/24	7.13E-06	13/19	1.59E-07
Mbp1	792/6229	16/40	1.29E-05	7/17	3.20E-03
Mcm1	148/6229	6/15	6.82E-07	13/22	1.71E-11
Swi4	1731/6229	27/33	1.51E-10	11/24	4.46E-02

Table 4.

Performance comparison of RETEA with TRIA using TFBS data.

TF	Expected	Observed S2	P-value	Observed T2	P-value
Abf1	870/6229	42/51	3.36E-12	56/66	8.56E-12
Cin5	986/6229	10/23	1.50E-03	14/37	9.59E-04
Fkh1	1431/6229	17/23	3.04E-07	25/36	3.69E-09
Fkh2	916/6229	6/11	2.37E-03	12/35	3.02E-03
Rap1	515/6229	20/41	1.20E-11	23/36	3.54E-12
Swi4	1731/6229	13/20	5.62E-04	12/20	2.51E-03
Swi5	2918/6229	13/26	4.48E-01	16/23	2.35E-02
Swi6	2206/6229	33/48	2.47E-06	6/9	5.65E-02

Table 5.

Performance comparison of RETEA with Garten et al’s method using TFBS data.

TF	Expected	Observed S3	P-value	Observed T3	P-value
Cin5	986/6229	15/34	8.35E-05	21/47	2.52E-06
Fkh2	916/6229	20/34	3.30E-09	9/16	1.33E-04
Mbp1	792/6229	46/77	2.74E-12	2/13	5.06E-01
Mcm1	148/6229	6/13	2.43E-07	15/24	1.29E-11
Rap1	515/6229	19/30	8.06E-12	43/66	9.36E-12
Swi4	1731/6229	28/34	5.93E-11	21/34	3.44E-05
Swi5	2918/6229	16/27	1.35E-01	21/41	3.42E-01
Swi6	2206/6229	43/57	7.14E-10	24/29	2.12E-07

Determination of the thresholds used in correlation and partial correlation analysis

The threshold Th1 is determined as follows. We compute the Pearson correlations of all possible gene pairs in the yeast genome to form a distribution of the expression correlation between two genes. Then the threshold Th1 is chosen as the correlation value that is at the top 1% of the distribution. Similarly, the threshold Th2 is determined as follows. We choose all the gene pairs whose correlations are larger than Th1. For each of these gene pair, we compute the partial correlation between the gene pair and each of the 203 TFs in yeast. Then we collect all the computed partial correlations to form a distribution. The threshold Th2 is chosen as the partial correlation value that is at the top 10% of the distribution.

The threshold values are determined by the following procedure. We ran RETEA using 12 different settings of the correlation threshold (Th1) and partial correlation threshold (Th2) values. The result is summarized in Table 6. In the table, 9/11 means that for nine of the eleven cell cycle TFs the B⁺R⁺ is more enriched in the cell cycle-regulated genes (with P-value <0.005) than that of B⁺R⁻. It could be seen that RETEA performs well when Th1 is chosen at the top 1% of the correlation distribution no matter which Th2 is used. However, when Th1 is chosen at the top 3% or 5%, the performance of RETEA is bad. Therefore, we used Th1 (top 1%) and Th2 (top 10%) as the default parameter setting for RETEA.

Table 6.

Performance comparison of RETEA using different correlation threshold (Th1) and partial correlation threshold (Th2) values.

	Th1 (top 1%)	Th1 (top 3%)	Th1 (top 5%)
Th2 (top 5%)	9/11	4/11	0/11
Th2 (top 10%)	9/11	4/11	0/11
Th2 (top 15%)	9/11	4/11	0/11
Th2 (top 20%)	8/11	2/11	0/11

Factors that affect the performance of RETEA

Two kinds of factors can affect the performance of RETEA. The first kind is the threshold values used in RETEA. We tried 12 different settings of the correlation threshold (Th1) and partial correlation threshold (Th2) values and found a good one (Th1 at the top 1% and Th2 at the top 10%) that can make RETEA capable of extracting the plausible regulatory targets from the binding targets of 11 cell cycle TFs. The other kind of factors that affects RETEA is the protein activity profiles of TFs. Since the protein activity profiles of TFs are not available in the public domain, they need to be estimated by computational methods. In this study, the protein activity time profile of a TF is estimated by using the average of the gene expression time profiles of all the genes whose expressions are affected by the deletion of that TF (inferred from the mutant data). Our way to estimate the protein activity profiles of TFs may not be optimal and there is still much room for improvement. However, this issue will become minor when the experimental technology for measuring the protein activity profiles is developed in the future.

Applying RETEA to identify plausible regulatory targets of oxidative stress-response TFs

In this paper, RETEA is applied to identify regulatory targets of eleven cell cycle TFs. For showing the generality of RETEA, we demonstrated that RETEA also performs well for cell-cycle irrelevant regulators. In this regard, we applied RETEA to identify regulatory targets of TFs that are involved in the oxidative stress response. The genome-wide gene expression and ChIP-chip data under the oxidative stress were downloaded from Gasch et al’s paper²² and Harbison et al’s,¹⁵ respectively.

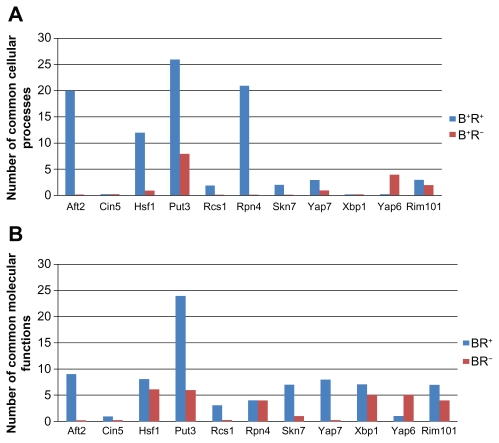
Using GO term finder in SGD²¹ with FDR <0.05, we found that in most cases (8/11), the number of enriched common cellular processes in B⁺R⁻ is larger than that in B⁺R⁻ (see Fig. 3A). Besides, using GO term finder in SGD with FDR <0.05, we found that in most cases (9/11), the number of enriched common molecular functions in B⁺R⁻ is larger than that in B⁺R⁻ (see Fig. 3B). This result suggests that RETEA performed well not only for cell cycle TFs but also for cell cycle-irrelevant TFs.

Figure 3.

Testing for the enrichment for the common cellular processes and common molecular functions in B⁺R⁺ and B⁺R⁻ for eleven oxidative stress-response TFs.

Conclusions

In this study, an algorithm called RETEA is developed to identify the plausible regulatory targets of a TF from its binding targets. Since the binding of a TF to a gene does not necessarily imply regulation, algorithms like RETEA are needed in solving this ambiguity. We validated the effectiveness of RETEA by checking the enrichments for cell cycle-regulated genes, the common cellular processes and common molecular functions. Besides, the performance of RETEA was shown to be better than three published methods (MA-Network, TRIA, and Garten et al’s method). In addition, we showed that RETEA performed well not only for cell cycle TFs but also for cell cycle-irrelevant TFs. Taken together, we are confident that RETEA has the ability to find biologically relevant results and can be useful in systems biology study.

Appendix

Statistical test used in Table 2

A model based on hypergeometric distribution⁷ is used to test whether the enrichment of the cell cycle- regulated genes in B⁺R⁻ is statistically higher than that in B⁺R⁻. The formula is as follow:

$$P(m_a,m_b,n_a,n_b)=\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill m_a\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b\hfill \\ \hfill m_b\hfill \end{array}\right)}{\left(\begin{array}{c}{n}_a+n_b\\ m_a+m_b\end{array}\right)}=\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill m_a\hfill \end{array}\right)\left(\begin{array}{c}N-n_a\\ M-m_a\end{array}\right)}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill M\hfill \end{array}\right)}$$

where N = n_a + n_b, M = m_a + m_b, n_a (n_b) is the number of genes in B⁺R⁺ (B⁺R⁻), m_a (m_b) is the number of the cell cycle-regulated genes in B⁺R⁻ (B⁺R⁻), and $\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill m_a\hfill \end{array}\right)\triangleq \frac{n_a!}{m_a!(n_a-m_a)!}$. We then consider all possible combinations of x_a, x_b such that ${\displaystyle \sum _{i=\{a,b\}}}{x}_i={\displaystyle \sum _{i=\{a,b\}}}{m}_i=M$ and sum all probabilities calculated as above where x_a ≥ m_a, which is taken as the P-value for rejecting the null hypothesis that enrichment of the cell cycle-regulated genes in B⁺R⁺ is not statistically higher than that in B⁺R⁻.

$$\begin{array}{c}p=P(x_a\ge m_a)=\sum _{x_a\ge m_a}\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill x_a\hfill \end{array}\right)\left(\begin{array}{c}\hfill N-n_a\hfill \\ \hfill M-x_a\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill M\hfill \end{array}\right)}\\ =1-\sum _{x_a=0}^{m_a-1}\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill x_a\hfill \end{array}\right)\left(\begin{array}{c}\hfill N-n_a\hfill \\ \hfill M-x_a\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill M\hfill \end{array}\right)}\end{array}$$ (1)

Statistical test used in Tables 3, 4, and 5

The proportions of genes whose promoter regions contain the high-confidence binding site of the TF under study are calculated for S₁ (S₂,S₃) and T₁ (T₂,T₃), where S₁ (S₂,S₃) is the set of regulatory targets of the TF under study that are identified by RETEA but not by MA-Network (TRIA, Garten et al’s method) and T₁ (T₂,T₃) be the set of regulatory targets of the TF under study that are identified by MA-Network (TRIA, Garten et al’s method) but not by RETEA. Note that only those TFs that are studied by both RETEA and previous methods can be used to do the performance comparison.

The high-confidence TFBSs were downloaded from MacIsaac et al’s paper.¹⁹ These TFBSs were derived by using six motif discovery methods, under the requirement for conservation across at least two of the four related yeast species. The yeast genome has 6229 ORFs. Only 870 genes contain Abf1 binding site, 986 genes contains Cin5 binding site, 1431 genes contain Fkh1 binding site, 916 genes contain Fkh2 binding site, 792 genes contain Mbp1 binding site, 515 genes contain Rap1 binding site, 1731 genes contain Swi4 binding site, 2918 genes contain Swi5 binding site, and 2206 genes contain Swi6 binding site.¹⁹

We tested over-representation of the high-confidence TFBS in S₁ (S₂, S₃) and T₁ (T₂, T₃). The cumulative hypergeometric distribution is used to determine the statistical significance. The P-value is defined as in Equation (1), where N = 6229 is the number of genes in the yeast genome, M is the number of genes in G, where G = S₁ (S₂, S₃) or T₁(T₂, T₃), (eg, M = 24 for Fkh2 if G = S₁ and M = 19 for Fkh2 if G = T₁; M = 11 for Fkh2 if G = S₂ and M = 35 for Fkh2 if G = T₂; M = 34 for Fkh2 if G = S₃ and M = 16 for Fkh2 if G = T₃), n_a is the number of genes in the yeast genome that contain the TFBS of the TF under study (eg, n_a = 916 for Fkh2) and m_a is the number of genes in G that contain the binding site of the TF under study (eg, m_a = 13 for Fkh2 if G = S₁ and m_a = 13 for Fkh2 if G = T₁; m_a = 6 for Fkh2 if G = S₂ and m_a = 12 for Fkh2 if G = T₂; m_a = 20 for Fkh2 if G = S₃ and m_a = 9 for Fkh2 if G = T₃).