Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Jan 12.
Published in final edited form as: J Membr Biol. 2009 Jul 15;230(1):49–55. doi: 10.1007/s00232-009-9185-1

HILL COEFFICIENT ANALYSIS OF TRANSMEMBRANE HELIX DIMERIZATION

Ricky Soong 1,+, Mikhail Merzlyakov 1,+, Kalina Hristova 1,*
PMCID: PMC3020080  NIHMSID: NIHMS152260  PMID: 19603128

Abstract

Here we employ the Hill equation, used broadly to characterize cooperativity in protein-ligand binding, to describe the dimerization of transmembrane (TM) helices in hydrophobic environments. The Hill analysis of wild-type FGFR3 TM domain dimerization gives a Hill coefficient of ~1 for lipid bilayers, but only ~0.2 for SDS micelles. We propose that this finding is indicative of heterogeneity in FGFR3 TM dimer structure and stability in SDS micelles. We further speculate that: (1) The Hill equation can be used as a tool to assess the existence of multiple structural states of TM dimers in different hydrophobic environments, and (2) The structural heterogeneity, detectable by Hill analysis, may be the underlying reason for the broad peaks and the low resolution in 2-D NMR studies of peptides in detergents.

Introduction

Despite the fact that 30% of the open reading frames in organisms encode membrane proteins [Liu and Rost, 2001;Wallin and von Heijne, 1998], our knowledge of their folding and their structure-function relationship is limited [MacKenzie, 2006;White et al., 2001;White and Wimley, 1999;Popot and Engelman, 2000], due to limited biophysical tools used in the studies [White et al., 1998;MacKenzie, 2006]. The limitations are obvious in the studies of the lateral association of TM helices - the simplest, yet a critically important interaction that occurs in the hydrophobic membrane environment. While methods are now available to measure the energetics of TM helix dimerization (i.e., the dimer stability) in vesicles and supported lipid bilayers [Li et al., 2005;Li et al., 2006;You et al., 2006] and in bacterial membranes [Duong et al., 2007;Finger et al., 2006], high resolution TM dimer structures are often sought in detergents. However, only a few high resolution structures have been solved so far in detergent micelles, including the structure of the GpA TM dimer in DPC [MacKenzie et al., 1997] and the structure of the ζζ TM dimer in 5:1 DPC:SDS [Call et al., 2006], due to challenges associated with broad NMR peaks and low experimental resolution.

A review article by Engelman and colleagues reminds us that “the constraints of the lipid bilayer are poorly imitated by the detergents used to study membrane proteins” [Matthews et al., 2006]. A question therefore arises whether the detergent environment may significantly alter the association of TM helices, such that the structure and interactions in detergents and in membranes are principally different [Walkenhorst et al., 2009]. Do TM helices, which form structurally well-defined dimers in membranes, exist in multiple structural states in detergent micelles, such that the dimer does not have a well-defined structure in detergent? Can this be the reason for the poor resolution in the NMR experiments?

Here we address the above questions using FGFR3 TM domain as a model dimerizing helix. The dimerization of FGFR3 TM domain has been studied extensively in lipid systems of various compositions [You et al., 2006;Li et al., 2006;You et al., 2007;Merzlyakov and Hristova, 2008]. FGFR3 is a receptor tyrosine kinase which conducts biochemical signals across the plasma membrane via lateral dimerization. Its TM domain has a propensity to form sequence-specific dimers in bilayers, but this propensity is rather weak [Li et al., 2005]. FGFR3 TM domain mutations, such as the Ala391→Glu mutation linked to Crouzon syndrome with acanthosis nigricans, increase the stability of the dimer [Li and Hristova, 2006;Li et al., 2006]. The dimerization of wild-type FGFR3 TM domain and all studied mutants in bilayers is well described as an equilibrium reaction [Li et al., 2005;You et al., 2005;Merzlyakov et al., 2006b;Li et al., 2006;Merzlyakov et al., 2006a]. Thus, the FGFR3 TM domain is a good model protein for the current study because (1) it is very “well-behaved” in bilayer systems and (2) its dimerization propensity is weak, and therefore the nature of the hydrophobic environment may affect the stability and the structure of the dimer.

Here we use the Hill equation formalism as a quantitative tool to gain new knowledge about FGFR3 TM domain dimerization in both detergents and lipid bilayers. We show that the Hill equation can be used to describe FGFR3 TM domain interactions in both hydrophobic environments. The Hill analysis of wild-type FGFR3 TM domain dimerization gives a Hill coefficient of ~1 for lipid bilayers, but only ~0.2 for SDS micelles. We interpret these results as an indication for FGFR3 dimer heterogeneity in detergent micelles, and we discuss the implications of this finding. Also, we speculate that: (1) The Hill equation can be used as a tool to assess the existence of multiple structural states of TM dimers in different hydrophobic environments and (2) The heterogeneity, detected using the Hill coefficient analysis presented here, may be the underlying reason for the broad peaks and the low resolution in NMR experiments in detergents.

Materials and Methods

Hill coefficient analysis of TM helix dimerization

The dimerization of TM helices is described by an association constant K, defined as:

K=[D][M]2, (1)

where [M] and [D] are the monomer and dimer concentrations, respectively. If [T] = 2[D] + [M] is the total protein concentration, the fraction of proteins in the dimeric state is:

f=2[D][T]=2[M]2[M]+1/K (2)

Now we rearrange equation (2) and obtain:

f1−f=2K·[M] (3)

Taking the logarithm, we write:

ln(f1−f)=ln(K)+ln[2M] (4)

Equation (4) follows directly from equation (1), and therefore it also describes an equilibrium between monomers and dimers.

We now examine equation (4) more closely by comparing it to the Hill equation. The Hill equation,

ln(Θ1−Θ)=ln(K)+nln[L] (5)

is frequently used in biochemistry to describe multivalent ligand binding to proteins. In this equation Θ is the fraction of protein binding sites filled with the ligand, K is the binding constant, [L] is the concentration of ligand and n is the Hill coefficient which describes the cooperativity of binding. If binding does not depend on the number of ligands bound to the protein, binding is considered “non-cooperative” and the Hill coefficient has a value of 1. A value greater than 1 indicates positive cooperativity (binding is enhanced by the presence of other ligands), while less than 1 means negative cooperativity (binding affinity decreases once a ligand is bound).

While the Hill equation was derived to describe the cooperative binding of oxygen to hemoglobin [Hill, 1910], the comparison between equations (4) and (5) suggests that the Hill equation may be also used to describe TM helix dimerization. We see that equation (4) is very similar to the Hill equation, with n = 1 and L = 2M, suggesting that the association of two monomers into a dimer can be considered analogous to the binding of a ligand to a protein binding site. The comparison suggests that the fraction of TM helices in the dimeric state f is equivalent to the fraction of protein binding sites occupied by the ligand, i.e. f = Θ; and the concentration of free ligand is equivalent to twice the concentration of monomers (free “ligands”), [L] = 2[M]. The latter can be rationalized because two monomers are required to form a TM helix dimer, but only one ligand is needed for protein-ligand binding.

In studies of protein-ligand interactions, measured values of ln[Θ/(1−Θ)] as a function of ln(L) are fitted to equation (5) to obtain n, and determine the degree of cooperativity. Can a similar fit be used to provide new insights into the TM helix dimerization process? With this question in mind, we re-write equation (4) in a more generalized way, following the well-established Hill analysis formalism:

ln(f1−f)=ln(K)+n·ln[2M] (6)

Within the Hill formalism, this equation can be fitted to experimental measurements of ln(f/(1−f)) as a function of 2M to determine n.

FRET measurements of dimerization in detergent

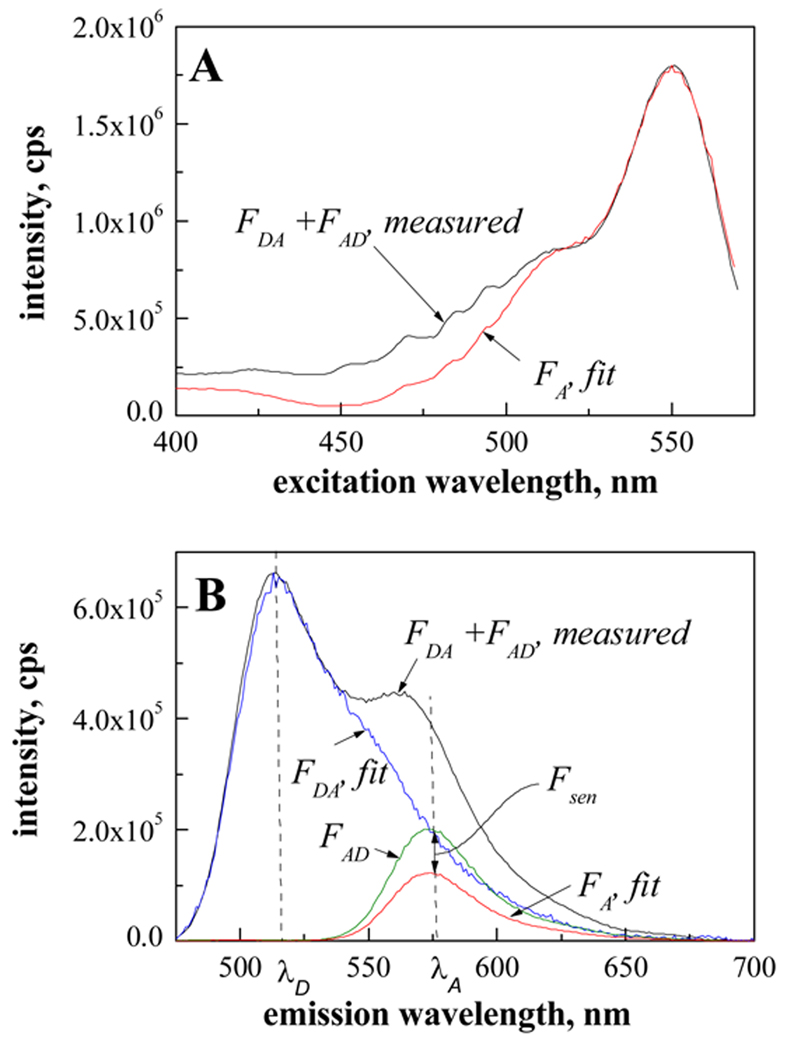
The FRET efficiency between FGFR3 TM domains labeled with either fluorescein (donor) or rhodamine (acceptor) was measured as described [You et al., 2005]. The peptide concentration range was 4 to 400 µM, and the SDS concentration was 200 mM. High label concentrations, such as the ones required in this study of weak interactions, lead to inner-filter effects (i.e., absorbance of the excitation and emission light by the sample), even when measurements are performed in a 10 µl microcuvette. To minimize this effect, a small sample volume (4 µl) was sandwiched between two quartz slides resulting in a path length of approximately 40 µm or less. The slides were mounted on a homemade slide holder [Merzlyakov et al., 2006a]. Emission and excitation scans, such as the spectra shown in Figure 2 A and B, were recorded with a Fluorolog-3 fluorometer (Jobin Yvon, Edison, NJ). The background signal from the quartz slides and the detergent was below 15000 cps and was subtracted from the measured spectra prior to data evaluation. The FRET efficiency was calculated as shown in Figure 3. The calculation is based on comparison of the FRET emission and excitation spectra to standard spectra of the donor and the acceptor at known concentrations (standard spectra, not shown). To calculate the FRET efficiency, the measured FRET excitation spectrum is fitted to the standard acceptor excitation spectrum at wavelengths longer than 530 nm where the donor is not excited. As discussed in [Merzlyakov et al., 2007;Merzlyakov and Hristova, 2008], this step gives the direct emission of the acceptor in the absence of the donor, FA. Next, the FRET emission spectrum is split into two components, the spectra of the donor and the acceptor in the presence of their FRET partners, FDA and FAD. This was accompished by fitting the standard donor emission spectrum to the measured FRET spectrum, FDA + FAD, at wavelengths shorter than 520 nm where the acceptor is not emitting. Finally, the sensitized fluorescence of the acceptor, Fsen, is determined as Fsen = FAD − FA, and the FRET efficiency is calculated as E≅Fsen(λA)FDA(λD)+Fsen(λA), see [Merzlyakov et al., 2007] for details. The donor-to-acceptor ratios and the acceptor fraction χa are determined by comparing the amplitudes of FD and FA to the standard spectra [Merzlyakov et al., 2007].

Figure 2.

Figure 2

Open in a new tab

(A) Excitation and (B) emission spectra, recorded for 200 µM Ala391Glu TM in 200 mM SDS at different donor to acceptor ratios.

Figure 3.

Figure 3

Open in a new tab

FRET efficiency calculation from fluorescence spectra. The calculation is based on comparison of the FRET emission and excitation spectra to standard spectra of the donor and the acceptor at known concentrations (standard spectra, not shown). FDA and FD are the measured fluorescence spectra of the donor in the presence and absence of the acceptor; FAD and FA are the measured fluorescence spectra of the acceptor in the presence and in absence of the donor; λD are λA are the emission peak wavelengths of the donor and the acceptor. The black curves show the measured FRET excitation spectrum (A) and the FRET emission spectrum (B) of 200 µM Ala391Glu TM in 200 mM SDS (donor to acceptor ratio of 1). The background signal from the quartz slides and the detergent is below 15000 cps and was subtracted from the measured spectra prior to data evaluation. To calculate the FRET efficiency, the measured FRET excitation spectrum is fitted to the standard acceptor excitation spectrum at wavelengths longer than 530 nm where the donor is not excited. This step gives the direct emission of the acceptor, FA. Next, the FRET emission spectrum is split into two components, FDA and FAD, by fitting the standard donor emission spectrum to the measured FRET spectrum, FDA + FAD, at wavelengths shorter than 520 nm where the acceptor is not emitting. Finally, the sensitized fluorescence of the acceptor, Fsen, is determined as Fsen = FAD − FA, and the FRET efficiency is calculated as E≅Fsen(λA)FDA(λD)+Fsen(λA), see [Merzlyakov et al., 2007]. The donor-to-acceptor ratios and the acceptor fraction χa are determined by comparing the amplitudes of FD and FA to the standard spectra (see (22) for details).

The measured FRET efficiency was corrected for FRET that arises due to random co-localization of donors and acceptors (proximity effects) [Li et al., 2006;You et al., 2005;Posokhov et al., 2008]. An estimate of this proximity contribution was obtained by measuring FRET between fluorescein- and rhodamine labeled lipids in SDS micelles (data not shown). Since there are no specific interactions between lipids, the observed FRET between labeled lipids is only due to random co-localization of the two dyes. Under all conditions studied, this contribution did not exceed ~15 % of the measured FRET.

Results

Analysis of dimerization in bilayers

We first verify that equation (4) holds for both wild-type FGFR3 TM domain and the Ala391Glu mutant, using previous FRET measurements in POPC liposomes. FRET measurements give the dimer and monomer concentrations, [D] and [M], as a function of the total concentration [T]. In Figure 1 we replot published data [Li et al., 2006], plotting measured values of ln [f/(1−f)] as a function of ln[2M] (shown as symbols in Figure 1A for the wild-type and in Figure 1B for the Ala391Glu mutant). Since the equilibrium constants K had been measured as well, we also plot the function ln(K) + ln[2M] as a function of ln[2M] (solid lines in Figures 1A and 1B). Inspection of Figures 1A and B shows that despite scatter, the data are generally consistent with the theoretical curves given by equation (4). Alternatively, we can fit the data (shown with symbols) in Figures 1A and B to the generalized equation (6), with n being unknown. The fits are shown with the dotted lines. The calculated Hill coefficients are n = 1.1 ± 0.2 for the wild-type (Figure 1A) and n = 0.8 ± 0.4 for the mutant (Figure 1B).

Figure 1.

Figure 1

Open in a new tab

The Hill plots for POPC: Natural logarithm of f/(1−f) versus the logarithm of 2M, where f is the fraction of peptides in the dimeric state, for the wild-type FGFR3 TM domain (A) and for the Ala391Glu mutant (B). Values for M, D and T are from [Li et al., 2006]. Experimental data were fitted to the generalized equation (6), with n being the unknown. The fit is shown with the dotted line and it gives n = 1.1 ± 0.2 for the wild-type (A) and n = 0.8 ± 0.4 for the mutant (B). The slope of the solid lines equals one (n = 1.0).

Thus, the presented analysis shows that the Hill equation, with L substituted by 2M, described the dimerization of FGFR3 TM domain in POPC vesicles. Furthermore, the Hill coefficients obtained for both wild-type FGFR3 TM domain and the Ala391Glu mutant are close to 1.

Analysis of dimerization in detergent

Next, the dimerization of wild-type FGFR3 TM domain and the Ala391Glu mutant were studied in SDS following the protocol described in Materials and Methods. The FRET efficiency was calculated as shown in Figure 3. The measured FRET efficiency was corrected for FRET that arises due to random co-localization of donors and acceptors (proximity effects) [Li et al., 2006], see Materials and Methods. As discussed previously [Adair and Engelman, 1994;Merzlyakov et al., 2007], the corrected FRET efficiency E is proportional to 1−(1−χa)m−1, where χa is the acceptor fraction and m is the oligomer size (m = 2 for a dimer). Therefore, measurements of E as a function of χa at a constant peptide concentration give the size of the oligomer [Adair and Engelman, 1994;Li et al., 1999]. In particular, a linear dependence of E on χa is indicative of dimer formation, and the existence of monomers and dimers only. Such linear dependence is shown in Figure 4A for the wild-type and in Figure 4B for the mutant, demonstrating that both peptides form dimers in detergent (m = 2).

Figure 4.

Figure 4

Open in a new tab

FRET efficiency as a function of acceptor fraction χa for two different samples: (A) 4 µM wild-type FGFR3 TM domain in 200 mM SDS; (B) 200 µM Ala391Glu in 200 mM SDS. The acceptor fraction was determined as shown in Figure 3. The linear dependence of the FRET efficiency on χa is indicative of dimer formation. Such linear dependence was observed for all peptide concentrations studied, 4, 40, 200 and 400 µM.

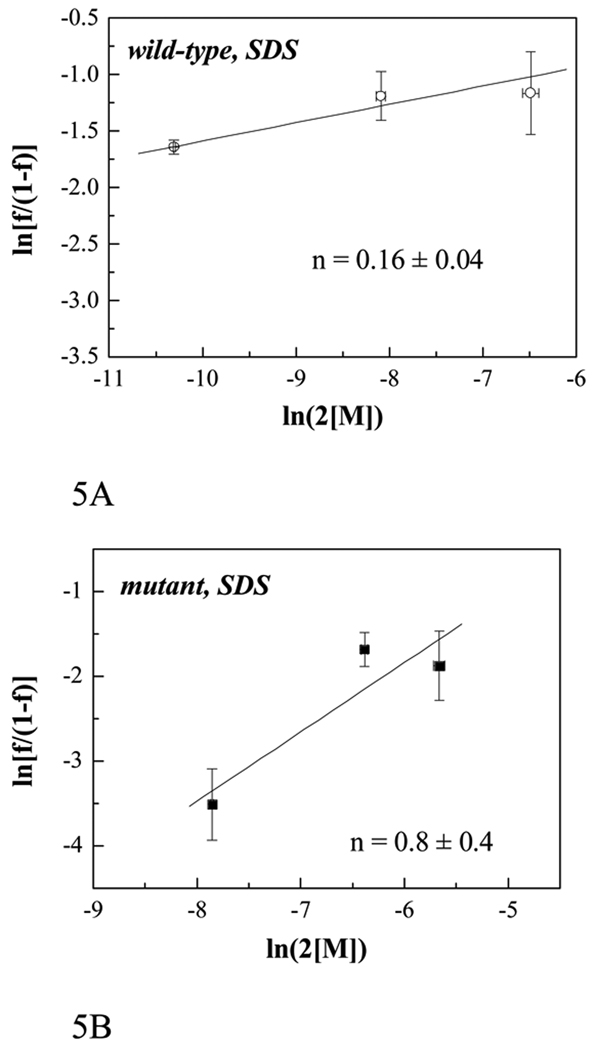
To create the Hill plots, we calculated the fraction of peptides in the dimeric state f as f = E/χa, while keeping the donor-to-acceptor ratio constant at 1:1 and varying the total peptide concentration [T]. The total protein concentration [T] was known as aliquoted, and the monomer concentration was calculated as [M] = [T](1−f). Figure 5 shows the Hill plots for the wild-type FGFR3 TM domain and the Ala391Glu mutant in SDS. Experimental values (shown with symbols) were fitted to equation (6). The solid lines are the fits, with Hill coefficient values of n = 0.16 ± 0.04 for the wild-type and n = 0.8 ± 0.4 for the Ala391Glu mutant.

Figure 5.

Figure 5

Open in a new tab

The Hill plots for SDS: Natural logarithm of f/(1−f) versus logarithm of 2[M] for the wild-type FGFR3 TM domain (4, 40 and 200 µM) (A) and for the Ala391Glu mutant (40, 200 and 400 µM) (B), both in 200 mM SDS. The solid lines are given by equation (6); the Hill coefficient n is determined by fitting the solid lines to the experimental data. The error bars shown are the standard deviations calculated from three different experiments at a given concentration.

Thus, while the Hill coefficient for the Ala391Glu mutant is ~1 in both lipid vesicles and detergents, the value for the wild-type in detergent is ~0.2. In the formalism of the Hill equation, the latter corresponds to anti-cooperative binding.

Discussion

Previously, we have shown that FGFR3 TM domain forms dimers in POPC bilayers [Li et al., 2005;Li et al., 2006]. Now we show that this dimerization process can be described by the Hill equation with Hill coefficient equal to one. We also find that FGFR3 forms dimers in SDS (see Figure 4). The Hill coefficient for the wild-type FGFR3 TM domain, however, is only 0.16 ± 0.04 in SDS (Figure 5). We propose that this finding is indicative of heterogeneity in the interactions between the helices in the wild-type FGFR3 dimer in SDS. We further propose that the observed heterogeneity in dimerization thermodynamics is associated with heterogeneity in dimer structure. This concept can be rationalized within the general concept of anti-cooperative binding: if multiple dimer structures exist, then the formation of a dimer interface between two TM helices will exclude all other possible interactions between them. Within this framework, the measured Hill coefficient of ~1 in POPC bilayers is indicative of a single dimeric state with well-defined structure and stability. A single dimeric structure is also observed for the Ala391Glu mutant in both lipids and detergents, most likely stabilized by Glu391-medited hydrogen bonds. Note that the maximum value of n is the number of binding sites, and thus the maximum value of n is 1 in the context of dimerization.

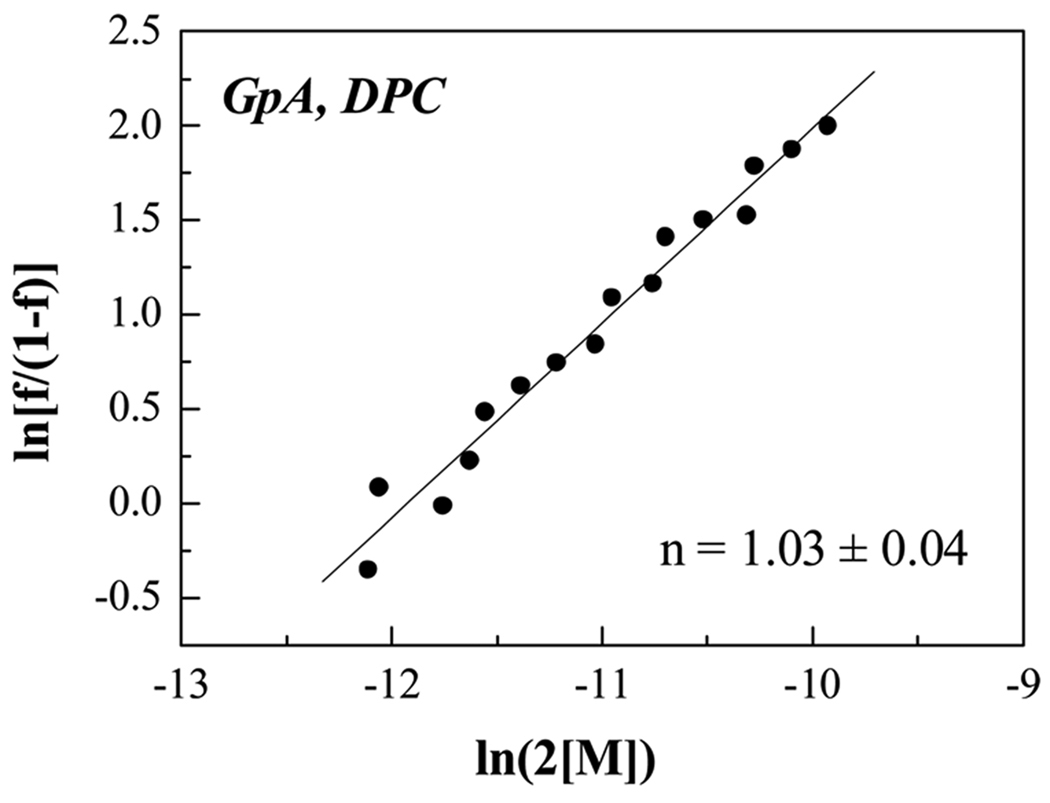
Despite the fact that wild-type FGFR3 TM domain forms “well-behaved” dimers in lipid bilayers, its dimers in SDS are characterized by various degrees of heterogeneity. While the exact nature of this heterogeneity is unknown, it can be expected that a family of different dimer structures exist, and these structures are associated with different dimerization propensities. Furthermore, SDS micelles may contain both parallel and anti-parallel dimers, exhibiting different FRET efficiencies. It is also possible that the micelle population is heterogeneous [Walkenhorst et al., 2009], such that the peptides encounter different environments, and this in turn leads to different structures and stabilities. We propose that such structural heterogeneity in detergents is not limited to the FGFR3 TM domain in SDS, but is a general feature of weakly bonded TM dimers in detergents. We further propose that this heterogeneity may be the underlying reason for the broad peaks and the low resolution in NMR detergent experiments. Thus, the presented Hill analysis may provide a means to evaluate the likelihood of success in dimer structure determination in detergent using NMR. We note that the Hill analysis of glycophorin A dimerezation in DPC (data of Fisher and Engelman, [Fisher et al., 1999]) gives a Hill coefficient of n = 1.03 ± 0.4, consistent with this view (see Figure 6).

Figure 6.

Figure 6

Open in a new tab

The Hill plots for GpA in DPC, replotted data from [Fisher et al., 1999]. The structure of the GpA dimer in DPC has been solved by NMR [MacKenzie et al., 1997], and the analysis of previously published energetics measurements [Fisher et al., 1999] gives a Hill coefficient of 1.

In summary, detergent micelles may be unsuitable for structural and thermodynamic characterization of some non-covalently bonded TM dimers (particularly weak dimers), and the presented method is a tool to evaluate the utility of a given detergent system in the characterization of a particular TM helix dimer. The structure and stability of weak TM dimers in detergents may be different from the structure and stability in membranes, and therefore experiments in detergents may not report on the native interactions in the cellular membrane. It should be kept in mind that the presented measurements are carried out in SDS, a detergent that is well-known to denature membrane proteins, and thus the discussions about the suitability of different detergent systems in studies of membrane proteins should continue. Finally, it should be noted that lipid bicelles have been used to solve the structure of TM dimers in lipid environment [Bocharov et al., 2007;Bocharov et al., 2008b;Bocharov et al., 2008a], thus demonstrating that lipid systems are a viable alternative to detergent solutions in the quest for high resolution TM dimer structures.

Acknowledgments

Supported by NIH grant GM068619 and Research Scholar Grant # RSG-04-201-01 from the American Cancer Society to K.H.

Reference List

  1. Adair BD, Engelman DM. Glycophorin a helical transmembrane domains dimerize in phospholipid bilayers - a resonance energy transfer study. Biochemistry. 1994;33:5539–5544. doi: 10.1021/bi00184a024. [DOI] [PubMed] [Google Scholar]
  2. Bocharov EV, Mayzel ML, Volynsky PE, Goncharuk MV, Ermolyuk YS, Schulga AA, Artemenko EO, Efremov RG, Arseniev AS. Spatial Structure and pH-dependent Conformational Diversity of Dimeric Transmembrane Domain of the Receptor Tyrosine Kinase EphA1. J Biol Chem. 2008a;283:29385–29395. doi: 10.1074/jbc.M803089200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bocharov EV, Mineev KS, Volynsky PE, Ermolyuk YS, Tkach EN, Sobol AG, Chupin VV, Kirpichnikov MP, Efremov RG, Arseniev AS. Spatial structure of the dimeric transmembrane domain of the growth factor receptor ErbB2 presumably corresponding to the receptor active state. J Biol Chem. 2008b;283:6950–6956. doi: 10.1074/jbc.M709202200. [DOI] [PubMed] [Google Scholar]
  4. Bocharov EV, Pustovalova YE, Pavlov KV, Volynsky PE, Goncharuk MV, Ermolyuk YS, Karpunin DV, Schulga AA, Kirpichnikov MP, Efremov RG, Maslennikov IV, Arseniev AS. Unique dimeric structure of BNip3 transmembrane domain suggests membrane permeabilization as a cell death trigger. J Biol Chem. 2007;282:16256–16266. doi: 10.1074/jbc.M701745200. [DOI] [PubMed] [Google Scholar]
  5. Call ME, Schnell JR, Xu CQ, Lutz RA, Chou JJ, Wucherpfennig KW. The structure of the zeta zeta transmembrane dimer reveals features essential for its assembly with the T cell receptor. Cell. 2006;127:355–368. doi: 10.1016/j.cell.2006.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Duong MT, Jaszewski TM, Fleming KG, MacKenzie KR. Changes in apparent free energy of helix-helix dimerization in a biological membrane due to point mutations. J Mol Biol. 2007;371:422–434. doi: 10.1016/j.jmb.2007.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Finger C, Volkmer T, Prodohl A, Otzen DE, Engelman DM, Schneider D. The stability of transmembrane helix interactions measured in a biological membrane. J Mol Biol. 2006;358:1221–1228. doi: 10.1016/j.jmb.2006.02.065. [DOI] [PubMed] [Google Scholar]
  8. Fisher LE, Engelman DM, Sturgis JN. Detergents modulate dimerization, but not helicity, of the glycophorin A transmembrane domain. J Mol Biol. 1999;293:639–651. doi: 10.1006/jmbi.1999.3126. [DOI] [PubMed] [Google Scholar]
  9. Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol. 1910;40:iv–vii. [Google Scholar]
  10. Li E, Hristova K. Role of receptor tyrosine kinase transmembrane domains in cell signaling and human pathologies. Biochemistry. 2006;45:6241–6251. doi: 10.1021/bi060609y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Li E, You M, Hristova K. SDS-PAGE and FRET suggest weak interactions between FGFR3 TM domains in the absence of extracellular domains and ligands. Biochemistry. 2005;44:352–360. doi: 10.1021/bi048480k. [DOI] [PubMed] [Google Scholar]
  12. Li E, You M, Hristova K. FGFR3 dimer stabilization due to a single amino acid pathogenic mutation. J Mol Biol. 2006;356:600–612. doi: 10.1016/j.jmb.2005.11.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Li M, Reddy LG, Bennett R, Silva ND, Jr, Jones LR, Thomas DD. A fluorescence energy transfer method for analyzing protein oligomeric structure: Application to phospholamban. Biophys J. 1999;76:2587–2599. doi: 10.1016/S0006-3495(99)77411-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Liu JF, Rost B. Comparing function and structure between entire proteomes. Protein Science. 2001;10:1970–1979. doi: 10.1110/ps.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. MacKenzie KR. Folding and stability of alpha-helical integral membrane proteins. Chem Rev. 2006;106:1931–1977. doi: 10.1021/cr0404388. [DOI] [PubMed] [Google Scholar]
  16. MacKenzie KR, Prestegard JH, Engelman DM. A transmembrane helix dimer: Structure and implications. Science. 1997;276:131–133. doi: 10.1126/science.276.5309.131. [DOI] [PubMed] [Google Scholar]
  17. Matthews EE, Zoonens M, Engelman DM. Dynamic helix interactions in transmembrane signaling. Cell. 2006;127:447–450. doi: 10.1016/j.cell.2006.10.016. [DOI] [PubMed] [Google Scholar]
  18. Merzlyakov M, Chen L, Hristova K. Studies of receptor tyrosine kinase transmembrane domain interactions: The EmEx-FRET method. J Membr Biol. 2007;215:93–103. doi: 10.1007/s00232-007-9009-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Merzlyakov M, Hristova K. Forster Resonance Energy Transfer Measurements of Transmembrane Helix Dimerization Energetics. Fluorescence Spectroscopy. 2008;450:107–127. doi: 10.1016/S0076-6879(08)03406-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Merzlyakov M, Li E, Casas R, Hristova K. Spectral Forster resonance energy transfer detection of protein interactions in surface-supported bilayers. Langmuir. 2006a;22:6986–6992. doi: 10.1021/la061038d. [DOI] [PubMed] [Google Scholar]
  21. Merzlyakov M, You M, Li E, Hristova K. Transmembrane helix heterodimerization in lipids bilayers: probing the energetics behind autosomal dominant growth disorders. J Mol Biol. 2006b;358:1–7. doi: 10.1016/j.jmb.2006.01.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Popot J-L, Engelman DM. Helical membrane protein folding, stability, and evolution. Annu Rev Biochem. 2000;69:881–922. doi: 10.1146/annurev.biochem.69.1.881. [DOI] [PubMed] [Google Scholar]
  23. Posokhov YO, Merzlyakov M, Hristova K, Ladokhin AS. A simple "proximity" correction for Forster resonance energy transfer efficiency determination in membranes using lifetime measurements. Analytical Biochemistry. 2008;380:134–136. doi: 10.1016/j.ab.2008.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Walkenhorst WF, Merzlyakov M, Hristova K, Wimley WC. Polar residues in transmembrane helices can decrease electrophoretic mobility in polyacrylamide gels without causing helix dimerization. Biochim Biophys Acta. 2009;1788:1321–1331. doi: 10.1016/j.bbamem.2009.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wallin E, von Heijne G. Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms. Protein Sci. 1998;7:1029–1038. doi: 10.1002/pro.5560070420. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. White SH, Ladokhin AS, Jayasinghe S, Hristova K. How membranes shape protein structure. J Biol Chem. 2001;276:32395–32398. doi: 10.1074/jbc.R100008200. [DOI] [PubMed] [Google Scholar]
  27. White SH, Wimley WC. Membrane protein folding and stability: Physical principles. Annu Rev Biophys Biomol Struc. 1999;28:319–365. doi: 10.1146/annurev.biophys.28.1.319. [DOI] [PubMed] [Google Scholar]
  28. White SH, Wimley WC, Ladokhin AS, Hristova K. Protein folding in membranes: Determining the energetics of peptide-bilayer interactions. Methods Enzymol. 1998;295:62–87. doi: 10.1016/s0076-6879(98)95035-2. [DOI] [PubMed] [Google Scholar]
  29. You M, Li E, Hristova K. The achondroplasia mutation does not alter the dimerization energetics of FGFR3 transmembrane domain. Biochemistry. 2006;45:5551–5556. doi: 10.1021/bi060113g. [DOI] [PubMed] [Google Scholar]
  30. You M, Li E, Wimley WC, Hristova K. FRET in liposomes: measurements of TM helix dimerization in the native bilayer environment. Analytical Biochemistry. 2005;340:154–164. doi: 10.1016/j.ab.2005.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. You M, Spangler J, Li E, Han X, Ghosh P, Hristova K. Effect of pathogenic cysteine mutations on FGFR3 transmembrane domain dimerization in detergents and lipid bilayers. Biochemistry. 2007;46:11039–11046. doi: 10.1021/bi700986n. [DOI] [PubMed] [Google Scholar]

RESOURCES