Abstract
Many diagnostic tools and goodness-of-fit measures, such as the Akaike information criterion (AIC) and the Bayesian deviance information criterion (DIC), are available to evaluate the overall adequacy of linear regression models. In addition, visually assessing adequacy in models has become an essential part of any regression analysis. In this paper, we focus on a spatial consideration of the local DIC measure for model selection and goodness-of-fit evaluation. We use a partitioning of the DIC into the local DIC, leverage, and deviance residuals to assess local model fit and influence for both individual observations and groups of observations in a Bayesian framework. We use visualization of the local DIC and differences in local DIC between models to assist in model selection and to visualize the global and local impacts of adding covariates or model parameters. We demonstrate the utility of the local DIC in assessing model adequacy using HIV prevalence data from pregnant women in the Butare province of Rwanda during 1989-1993 using a range of linear model specifications, from global effects only to spatially varying coefficient models, and a set of covariates related to sexual behavior. Results of applying the diagnostic visualization approach include more refined model selection and greater understanding of the models as applied to the data.
Keywords: Bayesian statistics, DIC, spatial statistics, hierarchical models, linear models, HIV, Rwanda
Introduction
Many diagnostic tools are available to evaluate the adequacy of a linear model. Model residuals are used to assess model fit, while diagnostics such as leverage values, Cook's distances, DFFITS, and DFBETAS are used to identify outlying and influential observations. Residuals provide a well-known tool for identifying outlying data points and summarizing the contribution of each individual observation to the overall fit of a model, thus providing valuable elements for constructing model diagnostics. To aid in the evaluation of a model, diagnostic values are frequently presented in scatter plots with fitted values or covariates to identify observations that may be suspect according to one or more model characteristic (Neter et al., 1996). In fact, visually assessing lack of fit in models has become an essential part of any regression analysis. This is evident in many diagnostic works in statistics, including that of Cook and Weisberg (1999), who use model checking plots to evaluate the appropriateness of the linear model. The model checking plot is a scatter plot of the fitted outcome and a function of the predictors, along with the ordinary least squares fit and a lowess fit. Cook and Weisberg (1994) also use added-variable plots, scatter plots for visually assessing whether a variable has explanatory power when added to the regression model of the outcome on another variable. These added-variable plots, along with ARES (Adding REgressors Smoothly) plots (Cook and Weisberg, 1994), are useful diagnostic plots for model selection. For visually identifying influential observations, Cook's distances are plotted against predictor values or are used to highlight certain observations in a plot of residuals versus predictors in generalized additive models (Hastie and Tibshirani 1990). In spatial analyses, residuals themselves are also often mapped over the study unit to inspect for significant spatial autocorrelation of errors, a violation of the independence assumption of residuals in a linear model.
In addition to model diagnostic tools assessing the impact of individual observations, methods of assessing overall goodness of fit and model complexity also have been developed for linear models, such as Akaike information criterion (Akaike, 1973). The AIC is defined as AIC = D(θ̂)+2k, the combination of the deviance evaluated at the maximum likelihood estimate of the parameters θ and a penalty defined as twice the number of model parameters. The deviance D(θ̂) is a general measure of fit defined as D(θ̂) = −2log p(y|θ̂), with log p(y|θ̂) denoted as the maximized log likelihood. The AIC fits into the broad literature of classical covariate selection and model choice (Burnham and Anderson, 2002). There are also a variety of statistical assessments of overall model fit in the Bayesian paradigm, including Bayes factors (Kass and Raftery, 1995), Bayesian information criterion (BIC: Schwarz, 1978), deviance information criterion (DIC: Spiegelhalter et al., 2002), among others (Gelman and Pardoe, 2006). As a generalization of the AIC, the DIC is appropriate for model comparison in complex hierarchical models where the number of parameters is unknown, such as the models used in spatial analysis, with disease mapping examples found in Zhu and Carlin (2000) and Best et al. (1999). As with the AIC, the DIC is a measure of model fit or adequacy with a penalty for model complexity. An advantage of the DIC is that one can easily calculate it from the Markov chain Monte Carlo (MCMC) simulation samples generated when drawing samples from the posterior distribution of a parameter in a Bayesian model. Another key advantage of the DIC is that it can be partitioned into individual contributions from observations in the data, as few diagnostic tools currently exist in the statistical literature to assess the local importance of additional model covariates within groups or subsets of data. The partitioning of the DIC into individual data contributions is outlined in Spiegelhalter et al. (2002). While the work of Spiegelhalter et al. (2002) provides the components necessary for an approach to local diagnosis of Bayesian model fit, an approach for visually diagnosing local spatial model fit has not been previously explored.
A local partitioning of the DIC is especially relevant in spatial model applications, such as in disease mapping, where relatively strong priors concerning spatial correlation among study units are often used. In the applied spatial statistical literature, there has been a recent emphasis on methodology that models local covariate effects, often spatially correlated, instead of the more traditional models that represent relationships with fixed effects across a study area. In reality, the association between a covariate and the occurrence of an outcome may vary between geographic and demographic subsets of individuals. Examples of reported differences in covariate and health outcome associations within a study population include: 1) prevalence of Hepatitis C virus among drug users across two geographic regions in Belgium (Mathei et al., 2004), 2) engagement in high risk sexual behavior among men who have sex with men within different subgroups and geographic locations throughout the United States (McFarland et al., 2001; Leone et al., 2004; Guenther-Grey et al., 2005), and 3) prevalence of human immunodeficiency virus (HIV) among injecting drug users in urban and rural Scotland (Haw and Higgins, 1998). Such studies suggest that the impact of a determinant within a subset of individuals or a subset of the study area may drive an overall significant association and falsely suggest an association for the entire population. Conversely, parameter estimates based on the entire population may mask an influential impact limited to a subset of the population. Some methodology in spatial statistics recognizing the potential for these situations and allowing for regression relationships that vary over space are Bayesian spatially varying coefficient (SVC) models (Gelfand et al., 2003; Banerjee et al., 2004) and geographically weighted regression (Fotheringham et al., 2002). In practice, spatially varying coefficient models can be computationally demanding to fit, and local diagnostic tools that justify the additional computational effort in terms of improved local fit and more accurate representation of relationships are needed. In addition, local diagnostic methods to identify situations of differential fit and influence among spatial subgroups are currently not well developed. Related to this is subset analysis, which examines the effects of two or more treatments within each of several subsets, or subgroups, of data along with an overall assessment (Shafer and Olkin, 1983). An issue in subgroup analysis is that a large number of subgroups may be identified within a typical data set, which raises concern about multiplicity effects (Dixon and Simon, 1991). Partitioning of the DIC may be helpful in identifying areas or data subgroups where a specified spatial model is ill-fitting or not particularly appropriate, i.e. where data are not in agreement with the prior.
In this paper, we focus on a spatial consideration of local DIC statistics for model selection and goodness-of-fit evaluation. We expand on the DIC partitioning approach of Spiegelhalter et al. (2002) to explore its applicability to visually assessing and quantifying local model fit with individual and groups of spatial data. We use a partitioning of the DIC to assess local model fit and data influence in a Bayesian framework for both individual observations and groups of observations, with groups corresponding to predefined spatial units. The interest in a partitioned DIC is to identify whether some models fit differently in certain areas and highlight any local, rather than global, impacts of covariate effects. In our approach to local model diagnosis, we introduce mapping of the partitioned, or local, DIC to explore spatial patterns of model fit over different spatial areas. We also map differences in local DIC values between models to examine the impact of adding additional covariates or model parameters. In addition, we plot the local DIC components of deviance residuals and leverage values and link plots of DIC components to maps of local DIC values. The novelty of this work involves building diagnostic tools out of available components in a typical Bayesian analysis to strengthen data analysis, an area of rich results from linear models (Cook and Weisberg, 1994; 1999). We demonstrate the utility of the local diagnostics with an example analyzing HIV type-1 (HIV-1) prevalence among pregnant women in the Butare province of Rwanda during 1989-1993. We fit several models to the Butare HIV data and visualize local DIC values to assist in model selection, moving from a regression model with a global intercept to a spatially varying coefficient regression model in one analysis, and then adding covariates in another analysis. In addition, we explore relationships between local DIC, local leverage, and deviance residuals in the dataset.
Methods
Partitioning the DIC
Heretofore, the DIC has been primarily used for overall model comparisons in a Bayesian setting, for example with public health data (Congdon, 2005; 2007). As a model comparison criterion, it combines model fit and complexity, where model fit describes how well model predictions match the data, and complexity, in a Bayesian sense, is a term coined to describe the relative structure of and associated difficulty of fitting a given model. The DIC is a Bayesian measure of fit, D̄(θ), penalized by the effective number of parameters, pD:
| (1) |
where the Bayesian deviance is
| (2) |
for observed data y, likelihood p(y | θ), parameter vector θ, and the sampling distribution evaluated at the observed data, f(y). The effective number of parameters may be expressed as
| (3) |
where D̄(θ) denotes the mean deviance and D(θ̄) denotes the deviance of the means of the model parameters calculated from the posterior parameter distribution.
While the DIC has been primarily used as an overall, or global, measure of model fit, the DIC can be partitioned into contributions from individual observations to provide a finer level of detail of model inadequacy. Following Spiegelhalter et al. (2002), the partitioning of the DIC according to individual observations is
| (4) |
where D̄i(θ) is the mean deviance for observation i and pDi is considered the amount of information observation i contributes to its own fitted value. The with n individual observations. The term pDi is also known as the leverage. In classical linear regression, leverage values identify points that may change conclusions about the linear model if removed, i.e. points that disproportionably influence for the model conclusions.
In linear model diagnostics, leverage values are the diagonal values of the hat matrix H, the matrix that projects the data onto the fitted values. Leverages also have been used to estimate the effective number of parameters as the trace of the hat matrix in smoothing spline applications (Wahba 1990) and in generalized additive models (Hastie and Tibshirani, 1990). In smoothing, outliers in covariate space are referred to as leverage points and in resistant smoothing the influence of these outlying points is minimized (Hastie and Tibshirani, 1990). In the DIC, we estimate individual leverage values from the individual mean deviance and deviance of the mean parameters,
| (5) |
The DIC may also be partitioned at other levels of the data when there is a clear hierarchy in the data to get another view of model inadequacy. As an example of partitioning the DIC at multiple levels of the data, we briefly turn to our application of HIV status in Rwanda. For n observations with a Bernoulli random variable, HIV status, with parameter pi, for each observation, the deviance is
| (6) |
To partition the DIC by administrative unit, or sector, in Butare, Rwanda, one can calculate the local DIC for each sector by aggregating over observations in each sector,
| (7) |
where nj is the number of observations in sector j and the observations are sorted by sector. To calculate the effective number of parameters or leverage for each sector one can partition the overall model complexity,
| (8) |
Given these equations, one can assess DIC, deviance, and leverage at the individual level or the sector level. By grouping observations into areas or sectors, we can identify outlying areas that have a large influence on the overall DIC. Often in small area public health applications, disease or case counts are aggregated to the area level; hence, a typical analysis would use partitioned DIC and leverage values at the area level. While one can observe the partitioned Bayesian deviance for a model, it may be more informative to inspect the deviance residuals, the individual contributions to the overall mean deviance. The deviance residual , with the sign depending on the sign of yi − E[yi|θ̄] (Spiegelhalter et al., 2002). Deviance residuals may be used in general to identify where a particular model may be lacking in fit and maps of deviance residuals can highlight spatial units for which the model fit is poor. The deviance can be expressed as the sum of squared individual Bayesian deviance residuals dr,
| (9) |
Visualizing the Partitioned DIC Components
As demonstrated repeatedly in the linear model diagnostics literature, visualization of model diagnostics is beneficial for evaluating model adequacy in a variety of ways. In addition, visualization of model output and diagnostics is particularly useful in the spatial analysis literature. Visualization is especially important when spatial data are modeled and there are multiple spatial scales in the data in order to explore the local variation in model adequacy. The approach of visualization of diagnostics described here is in accord with the philosophy of exploratory data analysis expressed by Tukey (1977) and Chambers et al. (1983).
Having previously defined the partitioned DIC at multiple levels of data, we next outline approaches for visualizing partitioned components of the DIC in several interesting ways to gain insight into the local fit characteristics of the models considered in an analysis. The approach suggested here includes using a combination of linked maps and graphs of diagnostics to assess individual model fit and to compare the fits of multiple models. The role of linked plots, or dynamic plots, in exploratory data analysis is described by Tierney (1990) and Cleveland and McGill (1988). Briefly, linked plots enable one to interactively select observations of interest in one graph and simultaneously highlight these observations in all other linked graphs to better visualize the relationships between certain diagnostic components. This technique of data brushing is innate in geographic information system (GIS) software packages such as ArcGIS (ESRI 2005) and GeoDa (Anselin 2003).
An obvious first step in visualizing the partitioned DIC with spatial data is to map the local DIC at an available spatial scale for any model of interest and look for relatively large values. With individual level data matched to census units, the local DIC values could be mapped for census block groups or census tracts, for example. The areas with the largest local DIC values contribute the most to the overall model lack-of-fit. These local DIC maps may be compared for several different models. Also when comparing models, scatter plots of local DIC values for pairs of models may be instructive in showing specific areas where one model improves on the fit of another model. Of course, the points in the plot must be labeled with an area identifier. The information provided by this type of scatter plot would not be available with a simple difference in overall DIC for two models. Another useful graph when comparing models is a map of differences in local DIC values by area between pairs of models. Graduated color maps of these local DIC differences not only highlight areas with large differences in adequacy for two models but also indicate the magnitude of the differences. When comparing models with the DIC and AIC measures, Spiegelhalter et al. (2002) and Burnham and Anderson (2002), respectively, consider a difference in DIC of 2-3 and above as meaningful. One could conservatively use this guideline to suggest meaningful differences in local DIC values when comparing models.
In addition to maps and plots of local DIC values, one can construct several graphs with local DIC components. One possible plot is a scatter plot of leverages versus local DIC values to highlight the most influential and ill-fitting observations or areas. This plot could be linked to an area map of local DIC values to inspect for any clear spatial patterns in the areas that appear to be outliers. When using a spatial model that considers spatial dependence, areas with high leverage could be areas that are quite distinct from their adjacent, or neighboring, areas. Another useful plot of local DIC components is a scatter plot of leverages against deviance residuals with contours for reference DIC values, such as 2, 3, or more (Spiegelhalter et al. 2002). Points outside of the meaningful DIC contour lines would be identifiable as potential outliers and the composition of the outlier, in terms of leverage and lack of fit, would be apparent. If this scatter plot is constructed at the area level from aggregated sample points within areas, the local DIC could be driven largely by the number of points inside each area. In this case, it will be useful to include another scatter plot of leverages versus deviance residuals with symbols proportional to the number of individual observations within each area.
Taken together, these dynamic scatter plots and maps can be combined effectively to evaluate and compare model adequacy with respect to a number of difference criteria. These graphs can all be created easily in a GIS software package after importing the local DIC component values derived from the MCMC samples. This approach is novel in the context of Bayesian spatial data analysis in that it combines (spatially) local statistical diagnostic tools with exploratory data analysis tools for model assessment. In the next section, we provide an example of modeling HIV status in Rwanda using several models and plot the partitioned DIC, deviance residuals, and leverage values for individual observations and sectors to visually assess outliers in model adequacy.
Analysis of HIV in Rwanda
Rwanda HIV Data
Human immunodeficiency virus type-1 infection in sub-Saharan Africa has been identified as a significant public health issue for more than two decades and continues to be of extreme importance today. According to the Joint United Nations Programme on HIV/AIDS (UNAIDS), Rwanda is one of nine African countries most severely affected by the HIV/AIDS epidemic. In the mid-1980s, HIV infection was estimated to be 88% among sex workers (Van de Perre et al., 1985) and 29 - 33% among women of childbearing age in the capital city of Kigali (Allen et al., 1991; Bucyendore et al., 1993). While reports regarding HIV-1 infection among subpopulations in Africa appear in the literature, few focus on HIV-1 infection and associated regional and local risk factors among pregnant women of childbearing age from a geographical perspective (Boerma et al., 1999; Hickson, 2005).
Between 1989 and 1993, the Department of Epidemiology at Johns Hopkins University School of Hygiene and Public Health and the National University of Rwanda School of Medicine conducted an epidemiologic study among pregnant women attending five ante-natal clinics and residing in the Butare province of Rwanda to estimate HIV incidence and prevalence and to identify socio-demographic and sexual history factors associated with HIV infection. In the present study, 7,444 women living in 54 sectors within a 25 kilometer radius of the town of Butare, Rwanda were included in the analysis. Variables collected included HIV infection status, residential location, marital status, history of sexually transmitted disease (STD), history of sexual intercourse as a source of income, sexual partner's circumcision status, current syphilis infection status, and whether the woman had sexual partners other than her husband/regular partner within five years. Residency information was of particular interest because it allowed the investigator to map estimates of HIV infection. Here, residency information allows us to identify sub-groups within the data and to assess model fit within these data groupings to explore local impacts of covariates effects. The study area is displayed in Figure 1, with the 54 sectors shaded corresponding to the percent of surveyed women who were HIV positive.
Figure 1. Percent women sampled with HIV infection in each of 54 sectors in Butare, Rwanda.
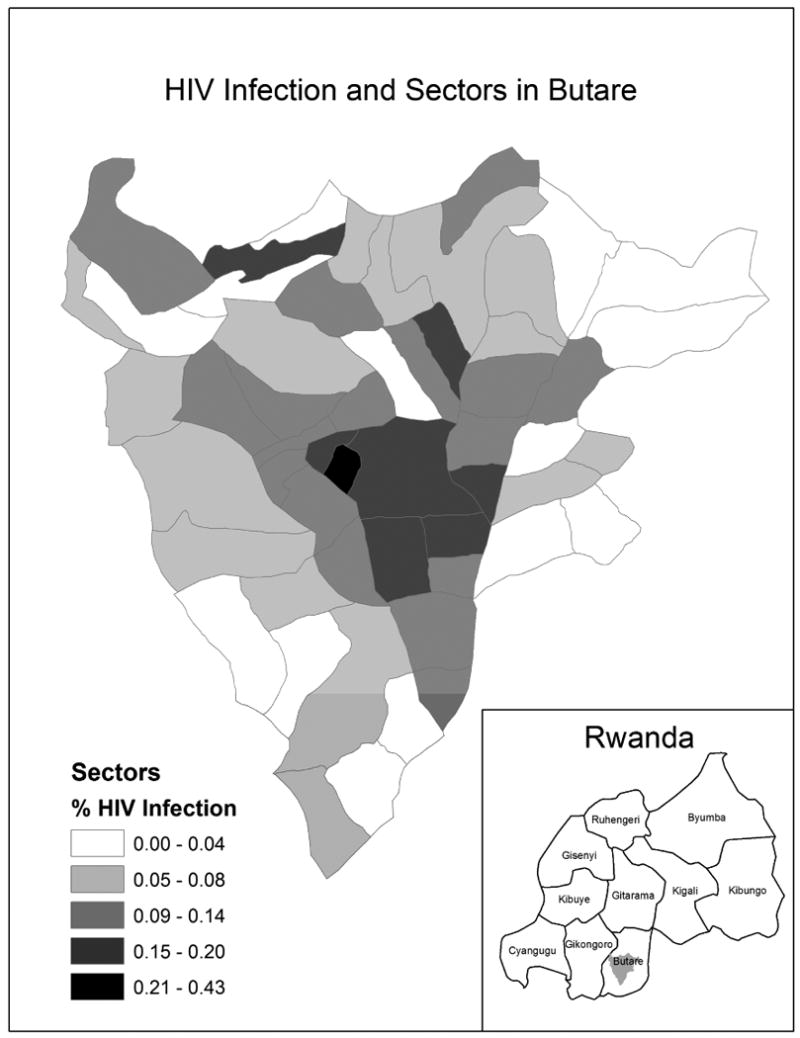
Study results have been presented previously and reveal geographical differences in the prevalence of HIV infection and several high risk sexual behaviors among this sample of pregnant women (Chao et al., 1994; Bulterys et al., 1994; Hickson, 2005). Hickson (2005) reports an increased risk of HIV-1 infection for women who have ever engaged in sexual intercourse to support themselves. A relatively large percentage of women who reside in several of the urban sectors reported engaging in this high risk sexual behavior. However, there is no particular geographical pattern in the percentage of women who engage in this high risk sexual behavior by spatial sector and possible spatial variation in the association between HIV serostatus and this risky behavior, as well as others, helps motivate our research.
There were several explanatory variables in the dataset with missing values due to non-response. To address the missingness in the data, we performed Bayesian multiple imputation. To do so, we simulated covariate values for observations missing data by treating the missing covariate values as unknown parameters with a prior mean for each covariate centered on the observed data mean. After simulating an adequate number of samples from the posterior distribution, we took a random draw from the posterior and used the selected values for missing observations. In the modeling analysis that follows, we use a complete dataset, comprised of mostly observed values and some imputed values for missing covariate values.
Models for HIV Status
In this analysis of HIV prevalence, we evaluate the partitioned DIC for several Bayesian hierarchical models fitted to HIV status. We start the analysis with one covariate, earned money for sex, and fit models increasing in complexity from a global intercept to spatially varying coefficients with spatial correlation. An objective here is to not just compare the overall DIC among models as is typically done, but to compare the spatial patterns of local DIC estimates among models to determine the local impacts of differences in specific model specifications. We assume that HIV status is a Bernoulli random variable with probability pij for each sampled individual i, Yij ∼ Bernoulli(pij). The subscript j in the following models indicates the sector in which each individual woman resides. We use a logit link function to model the probability of HIV status as a linear function of data and parameters, defined by θij in logit(pij) =θij. The initial candidate models are
Model 1: θij = α0,
Model 2: θij = α0 + β1xi1,
Model 3: θij = α0 + β1xi1 + γj,
Model 4: θij = α0 + β1xi1 + φj,
Model 5: θij = α0 + βj1xi1,
Model 6: θij = αj + βj1xi1.
Model 1 has an intercept only (α0), while Model 2 includes a covariate, x1= ever engaged in sexual intercourse to support oneself, and an overall effect. Model 3 has exchangeable random effects for sectors, γ ∼ N(0, τ), where τ is the precision. Model 4 has spatially correlated random effects, with spatial correlation specified through an intrinsic conditional autoregressive (CAR) prior, φ ∼ CAR(τ1), where τ1 is the precision. The CAR distribution may be expressed as
| (10) |
where mj is the number of adjacent areas for area j. The conditional mean of the distribution is φ̄j = Σlinδjφl, where δj is the set of neighbors adjacent to area j. In Model 5, the covariate effect is allowed to vary over sectors, where the spatially varying covariate effects have a CAR prior, β1 ∼ CAR(τ2), where τ2 is the precision. In Model 6, the intercept may also vary by sector, and the intercept and covariate effects are specified together with an intrinsic multivariate CAR, or MCAR prior, that models spatial correlation as well as correlation between regression terms. Rewriting the varying intercept to be βj1 and the single covariate to be βj2, the MCAR prior for the vector of two spatially dependent random effects in each area j, βj = (βj1,βj2)′, has a multivariate conditional distribution
| (11) |
where β̄j = (β̄j1, β̄j2)′, β̄jk = Σl∈κj βlk/mj, κj is the set of neighboring areas for area j, and mj is the number of neighbors for area j. The diagonal elements of Σβ are the conditional variances of the βk's and the off-diagonal elements are the conditional covariances between pairs of βk's. See Besag et al. (1991) for additional details about the intrinsic CAR model and Mardia (1988), Gelfand and Vounatsou (2003), and Banerjee et al. (2004) for details on the MCAR model. In a secondary analysis, we will later add additional covariates to some of the models described above and inspect the local differences in DIC that result from adding one covariate to the model.
Prior distributions are required to complete the Bayesian models and allow for posterior parameter estimation. The prior distributions for the non-varying regression terms are normal and vague, for example, the prior for the intercept is α0 ∼ N(0, τ0). The priors for the precisions of the regression terms are gamma, for example, τ0 ∼ G(1,1). The priors for the precisions of the CAR priors are also gamma, τ1 ∼ G(1,1) and τ2 ∼ G(1,1). The G(1,1) prior is a popular, conjugate hyperprior for CAR precisions (Banerjee et al. 2004). The prior for the within-area, between-coefficient variance-covariance matrix Σβ in the MCAR prior is assigned a vague inverse Wishart distribution with hyperparameter scale matrix set to 0.02·I2×2, where I is the identity matrix, and degrees of freedom ν = 2, Ω ∼ IW(ν, 0.02·I). While the results and inferences may be sensitive to the choice of hyperparameters, the choice of hyperparameters will not change our relative conclusions in the comparisons of model results, i.e. our focus is on relative fit of the models and we do not change hyperparameter values between models. We fit the Bayesian hierarchical models using WinBUGS (Spiegelhalter et al., 2003) software with MCMC simulation to provide samples of model parameter values from their joint posterior distribution. We use a “burn-in” period of 1,000 iterations and 5,000 subsequent samples from the joint posterior distribution to calculate posterior median estimates of the parameters for each model. We generate the sector adjacency list required in the CAR and MCAR priors in GeoBUGS (Thomas et al., 2004).
Rwanda HIV Model Results
Overall DIC
The overall DIC for each of the six initial models described above is listed in Table 1. In this table itself there are several interesting results. In comparing models, we follow the guidelines in Spiegelhalter et al. (2002) and Burnham and Anderson (2002) and use a meaningful difference in DIC of 3 and above. As expected, the intercept-only model has the highest DIC. The relatively large difference in DIC between models 1 and 2 indicates that ever having sex to support oneself is a significant factor in explaining HIV status for women studied in this region of Rwanda. The substantial difference (26.3) in DIC between Model 2 and Model 5 suggests that the ever having sex to support oneself effect varies significantly over sectors and that it is worthwhile to include a spatially varying coefficient for this variable. Model 3 and Model 4 have much lower DIC values than Model 2, which suggests that it is beneficial to include a random effect for each sector. That Model 3, in turn, has an appreciably lower DIC than Model 4 reveals that introducing spatial correlation in the random effects through the popular CAR prior is not beneficial in fitting HIV status, given that the effective number of parameters are almost the same (38.6 for Model 3 versus 39.5 for Model 4), i.e. the mean deviances explain the difference in DIC values. There are of course other available spatial models and our conclusion about spatial correlation applies only to the CAR-based models considered. The result that Model 3 and Model 4 have lower DIC values than Model 5 indicates that the random intercept by sector assists more in fitting HIV infection status than does a spatially varying effect for money for sex with no random intercept. This suggests that important covariates are left out of the model, as the sector-specific random effects represent some local unmeasured risk factors. Model 6, the spatially varying coefficient model, has the lowest DIC. This supports earlier conclusions that the effect of ever having sex to support oneself varies spatially and that potentially important risk factors have not been included in the model.
Table 1. Local DIC, mean deviance, and effective number of parameters for models 1 through 6.
| Model | DIC | D̄(θ) | pD |
|---|---|---|---|
| 1 | 4659.6 | 4658.6 | 1.0 |
| 2 | 4533.7 | 4531.7 | 1.9 |
| 3 | 4297.6 | 4259.0 | 38.6 |
| 4 | 4303.7 | 4264.2 | 39.5 |
| 5 | 4507.4 | 4483.6 | 23.7 |
| 6 | 4290.9 | 4257.5 | 33.4 |
Local DIC
While comparing the overall DIC values provides interesting interpretations and provides evidence to rule out some models, our primary interest is in the patterns of local DIC values by sector. The local DIC for each sector for Models 1-6 is mapped in Figure 2. The sectors are labeled with identification numbers in the local DIC map for Model 1 and are shaded by local DIC value using a natural break classification scheme based on the values for Model 2. The overall pattern in local DIC values for Model 1 shows clear spatial variation in DIC, with higher DIC values tending to be found in the urban center areas and lower DIC values located in the peripheral urban areas. For this study, the overall pattern in DIC by sector can be at least partly explained by the number of women sampled residing in each sector, as the aggregated observations in more populous areas, where more women were sampled, tend to result in larger DIC values. In general, however, plotting local DIC values should be illuminating to any pattern in model adequacy.
Figure 2. Local DIC for models 1 through 6 with sectors labeled by identifiers in the Model 1 map.
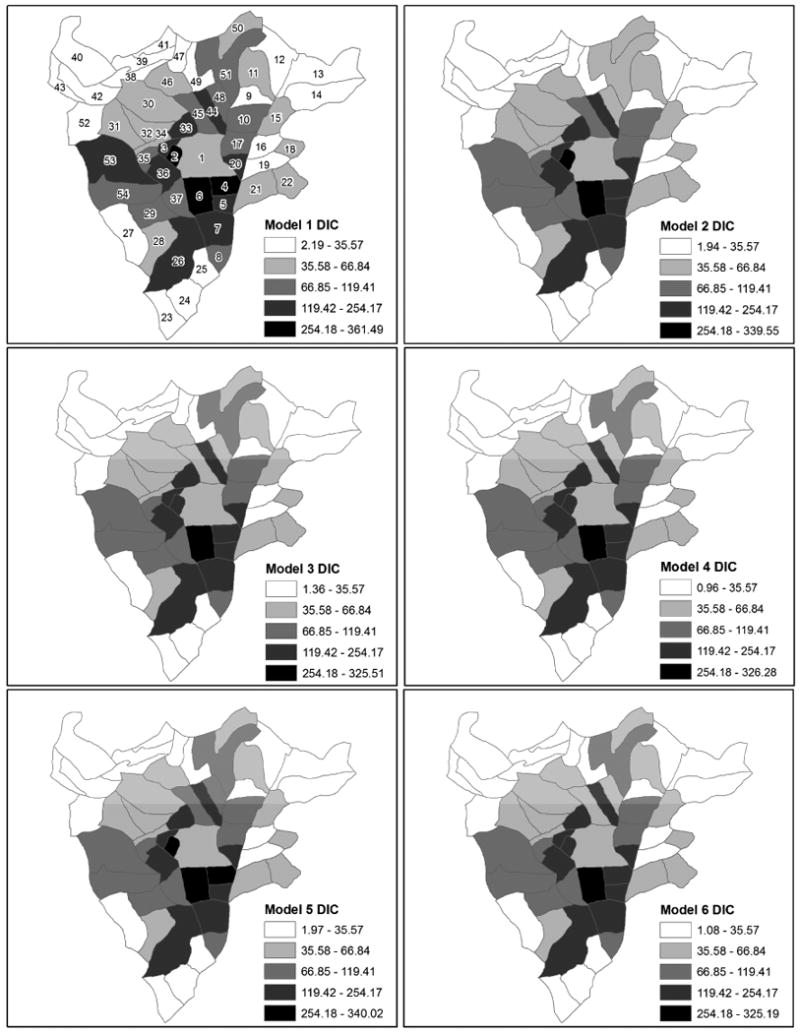
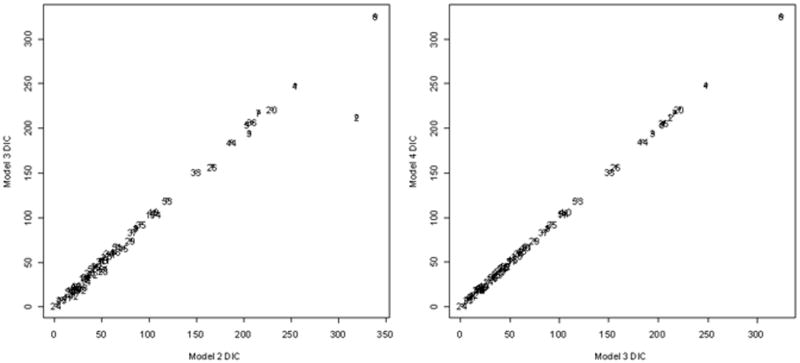
Perhaps more interesting in this analysis, is the relative comparison of patterns of local DIC among models. According to the overall DIC values, Model 2 improves on Model 1 overall, however, in comparing the local DIC maps for models 1 and 2, it is clear that adding the sex for money covariate in Model 2 has reduced the DIC from Model 1 in certain areas, such as sectors 4, 51, 48, and 53. Sector 4, coincidently, has one of the highest counts of women who have ever exchanged sex for money in order to support themselves. In a similar comparison, Model 3 reduced the DIC in sectors 2 and 45. These visual comparisons are revealing, although they do not show precisely how much local DIC values change between models. We later address this with maps of local DIC differences between models. There appear to be no differences in local DIC values between models 3 and 4 using the current choropleth classification. The difference in overall DIC between these models is approximately 6, coming from an aggregation over 54 sectors, so it is not surprising that the patterns in local DIC are similar. In addition, the pattern in local DIC values for Model 6 is similar to models 3 and 4. Again, there is a relatively little difference in overall DIC between these models. To closer look at differences in local DIC between pairs of models, the local DIC values for Model 3 versus Model 2 and Model 4 versus Model 3 are plotted in Figure 3. These scatter plots show that the main decrease in local DIC from Model 2 to Model 3 comes in sector 2, and that there is no noticeable change in DIC for any sector when going from Model 3 to Model 4. This latter result again illustrates that it is not necessary to induce correlation in the random effects with these data. While in practice, based on the overall DIC values, one would select Model 3 over Model 4, partitioning the DIC by sector reveals that the decrease in DIC from using Model 3 is not derived from one sector or a group of sectors in particular, but rather from small decreases across the entire study area.
Figure 3. Local DIC for Model 3 versus Model 2 (left) and Model 4 versus Model 3 (right).
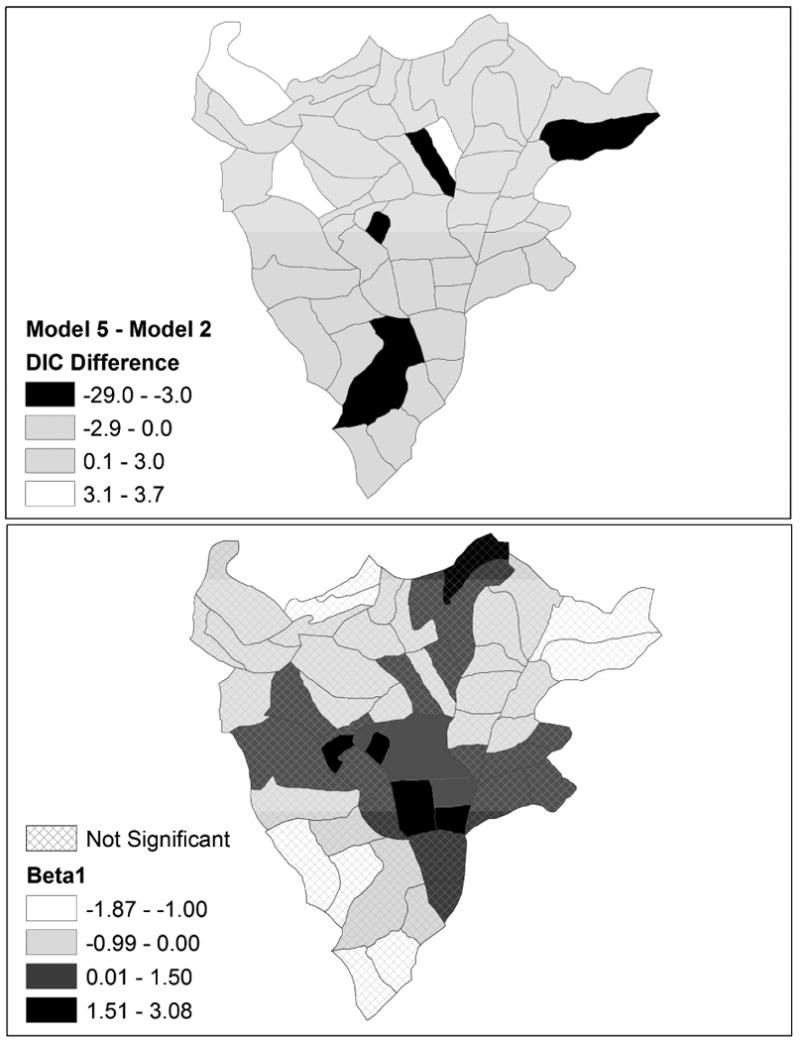
As mentioned, the relatively large difference in overall DIC values for models 2 and 5 suggests that the sex for money covariate effect varies over sectors. We investigate this variation further through looking at the local DIC differences in the models. The pattern of local DIC differences between two nested models with different types of effects (global or local) on a common covariate may indicate that the particular predictor variable is important in some sectors and not in others. It may, however, result more from substantial differences in observed covariate and response values in sectors. To visualize the patterns in local DIC differences and estimated coefficients, the differences in DIC for models 5 and 2 and the estimated regression coefficients β̂j1 from Model 5 are plotted in Figure 4. The top map shows with positive differences in DIC greater than 3 plotted in white, negative differences greater than 3 in magnitude plotted in black (meaningful improvement in the DIC with Model 5), and insignificant differences shaded gray. The bottom map shows the posterior median estimates of the sex for money effect, with coefficients that are not significant based on the 95% credible intervals shaded with a crosshatch pattern. There are four sectors that have meaningfully lowered DIC with Model 5; these are sectors 2, 14, 26, and 44. However, the major improvement in DIC is with sector 2, which has a reduction of 29.0 in DIC with Model 5. Sector 2 is an outlier in that it has by far the highest response variable value, with 43 percent of sampled women in that sector having a positive HIV status. Furthermore, this sector has a high concentration of commercial sex workers, a university with a population of over 4,000 male students (at the time of the original study) and a military base (Chao et al. 1994). This sector also has the largest estimated coefficient for the sex for money variable, with β̂2,1 = 3.08. Clearly, allowing the coefficient for the sex for money variable to increase for this sector relative to other sectors improves model fit meaningfully. There are seven sectors that have significant coefficients for the sex for money covariate based on the 95% credible intervals and they are all located in the center of Butare and all have a positive estimated coefficient for the sex for money variable. Inspecting these two maps together is beneficial for conveying the nature of the relationship between the response variable and the covariate of interest and also emphasizing the areas of greatest improvement in model fit with a spatially varying effect.
Figure 4. Local DIC difference in models 5 and 2 (top) and posterior median estimates of the sex for money covariate with insignificant effects shaded with crosshatching (bottom).
Local DIC Components
In addition to mapping the local DIC values, it is worthwhile to visualize the local DIC components and look for any patterns. Figure 5 contains a scatter plot of the leverage versus the local DIC by sector from Model 3 linked to a map of local DIC values. There is a curvilinear relationship between leverage and local DIC. The plots have highlighted the sectors with the largest DIC and leverage. These sectors contribute most to the overall DIC and are relatively more influential in the linear expression used to estimate HIV status. The selected sectors are somewhat clustered in the central and south central sections of Butare. Given the hierarchy in the Rwanda HIV data, we also plot the relationship between leverage and the deviance residuals for individual observations from Model 5 in Figure 6 with parabolas for DICi = 1, 2, or 3 where points on a parabola contribute an equal amount (1, 2, or 3) to the overall DIC, given that . Points located outside the outer parabola contribute more than 3 to the overall DIC. In the left plot in Figure 6, the individual observations are labeled by their sector identifier. There can be several occurrences of a sector ID in the plot due to using individual observations instead of sectors, for which deviance residuals are not available. For example, there is an observation from sector 50 with a negative deviance residual just outside the parabola corresponding to DICi = 1 and another observation from that sector with a positive deviance residual outside the parabola for DICi = 2. While not apparent, there are several overlapping observations from the same sector at various locations in the plot. To address this, the right plot in Figure 6 contains graduated symbols that indicate the number of observations for each sector with the same coordinates of the deviance residuals and leverages in the left plot. In the right plot, it is clear sector 2 is contributing a relatively large number of observations with DICi > 3 and dri > 2. Sector 6 also has a relatively large number of observations with DICi > 2.
Figure 5. Local DIC for Model 3 with a scatter plot of local leverage versus local DIC. Sectors with high leverage and DIC are highlighted.
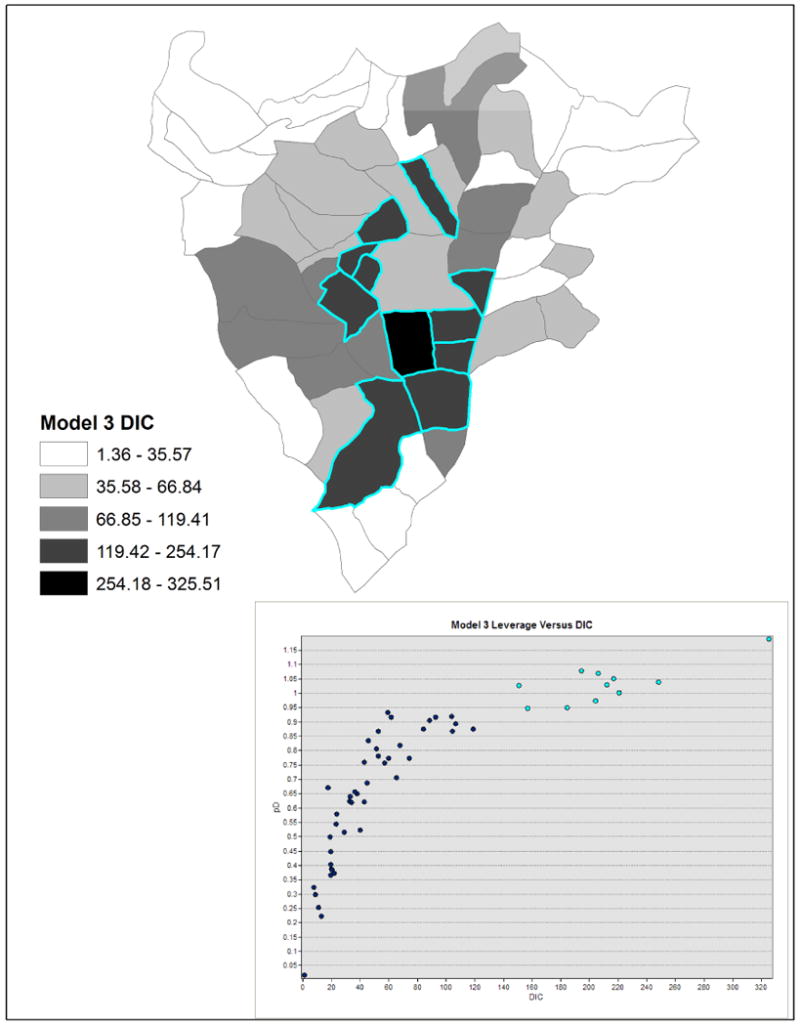
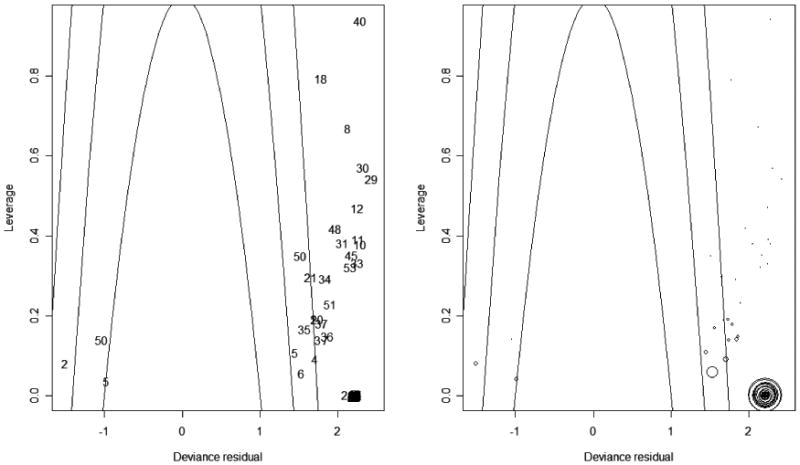
Figure 6. Leverages versus deviance residuals for individual observations labeled with sector identifiers in the left plot and graduated symbols for the number of observations per sector with the same leverage and deviance residual where the parabolas indicate contributions of 1, 2, or 3 to the overall DIC.
Local DIC and Variable Selection
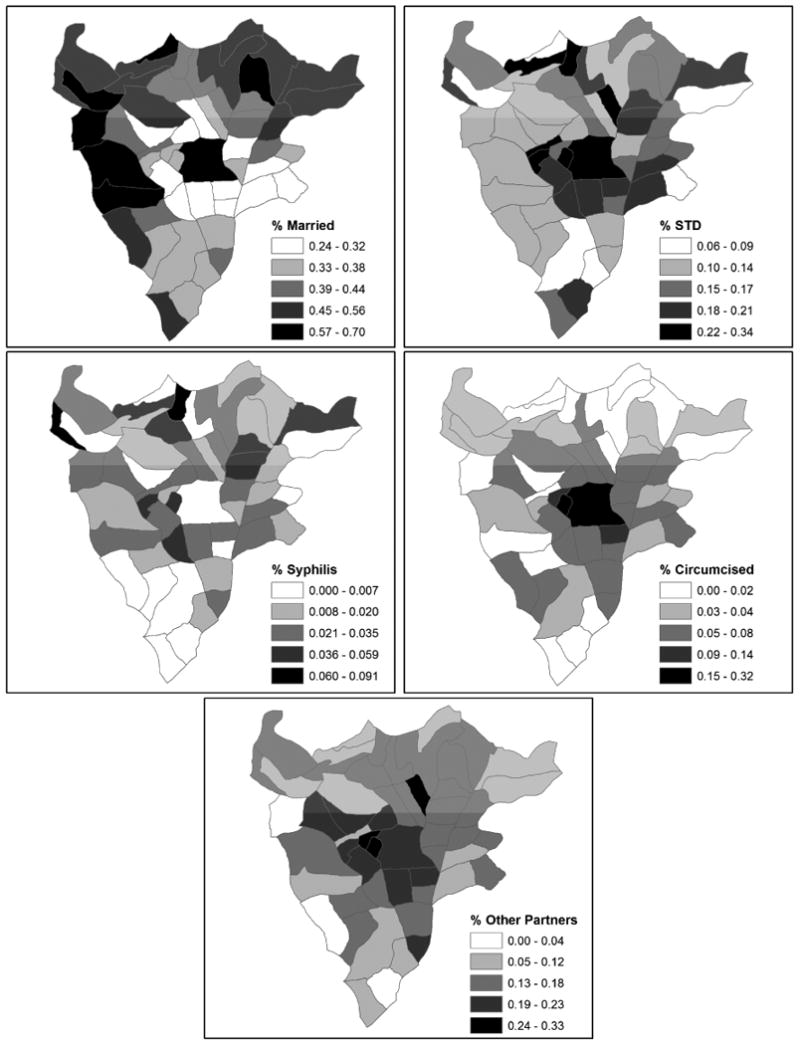
In addition to using the local DIC components for comparing models with different effects, it is potentially worthwhile to use the pattern of local DIC to select other covariates to include in the model. Given that local DIC values are higher in the urban areas, it seems sensible to add covariates displaying a concentration, in either high or low values, in these areas. To this end, we plot the sector-level covariate values in Figure 7 for percent married, percent with an STD, percent testing positive for syphilis, percent with circumcised partners, and percent having had a sexual partner other than their husband/regular partner within five years. In looking at the patterns of the covariates, it appears there is some co-patterning with the local DIC values from the models with percent married, percent STD, and percent having other sexual partners. Percent married appears low where local DIC values are high in urban areas. Conversely, percent with an STD and percent with other sexual partners appear high in these more urbanized areas. To determine if these variables will lower the DIC, we add each of the five covariates plotted in Figure 7 to Model 3 separately to create five new models. We use Model 3 as the base model to focus on the impact of a adding a new overall covariate effect. The new models include the following new variable, Model 7: marriage status, Model 8: STD status, Model 9: syphilis status, Model 10: circumcised partner, Model 11: other sexual partner. These models are defined generally as
Figure 7. Percentages by sector for five covariates used in models 7 through 11.
| (12) |
where Xi is the row vector of covariates for subject i and β is the column vector of corresponding regression coefficients.
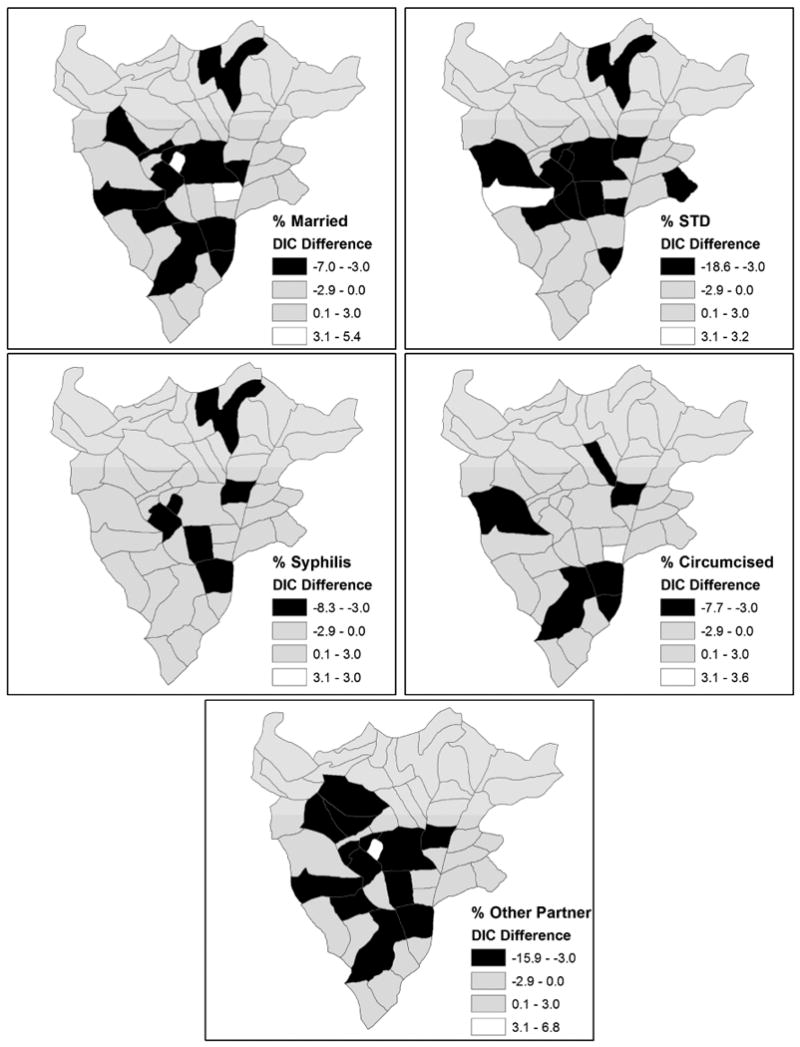
The overall DIC, effective number of parameters, and mean deviance for each of the five models are listed in Table 2. According to the DIC and mean deviance values, the model with STD (Model 8) fits HIV status the best, followed by the model with other sex partner (Model 11), and then the model with marriage status (Model 7), and there are meaningful differences in fit among the models. The effective number of parameters is essentially the same with rounding (39) for the models, as expected. More interesting than the overall DIC values, however, are the differences in local DIC estimates in each sector for the new models and Model 3. These differences effectively show where an additional covariate has utility for improving model fit within a given sector. The differences in DICj for models 7 through 11 and Model 3 are mapped in Figure 8. The first of the maps in Figure 8 shows ; the others are of similar form. The model with the greatest overall decrease in DIC, Model 8, decreases the local DIC in the sector with the largest DIC in Model 3, sector 6. This model also has the largest decrease in local DIC for any sector (18.6). Adding the STD variable also decreases the DIC in several of the other high-DIC sectors from Model 3, including 2, 3, 5, and 36. Model 11 significantly decreases the local DIC in the high-DIC sectors 3, 6, 7, 26, and 36. Adding the married covariate decreases the local DIC in several sectors with high DIC in Model 3, such as sectors 3, 7, 8, 20, 26, 36. Adding the syphilis variable (Model 9) also decreases the DIC in the sector with the largest DIC in Model 3 (sector 6). It is worth mentioning that the DIC with all six covariates included in an exchangeable model (Model 3 type) is 4056. All global covariate effects are significant in the model with intuitive signs, in that only the married covariate effect is negative, the rest are positive. For a SVC model (Model 6 type) with all six covariates included, the overall DIC for is 4027. Therefore, there is substantial evidence for spatially varying effects for at least some of the variables.
Table 2. Local DIC, mean deviance, and effective number of parameters for models 7 through 11.
| Model | DIC | D̄(θ) | pD |
|---|---|---|---|
| 7 | 4218.7 | 4179.4 | 39.2 |
| 8 | 4201.3 | 4162.9 | 38.5 |
| 9 | 4269.5 | 4230.2 | 39.3 |
| 10 | 4272.0 | 4233.4 | 38.7 |
| 11 | 4208.4 | 4169.7 | 38.8 |
Figure 8. Local DIC differences between models 7 through 11 and Model 3.
Discussion
The DIC is a summary of global fit and complexity for models with complex hierarchical structures. We present a partitioning of the DIC into local deviance and leverage components to be used as diagnostic tools for local model adequacy. We propose visualization tools in the form of linked plots and maps of diagnostics to aid in the assessment of local model fit and influence for both individual observations and aggregated observations in Bayesian hierarchical models. Plotting local DIC values or the deviance residuals shows any observations or areas that are especially poorly fitted and plotting leverages is beneficial in identifying observations with disproportionally strong impact on particular covariate values. Through visualizing the local DIC for each model and comparing it across several models, we can assess comparative local model fit and identify local impacts of model parameters. This is the case in our illustrative application of modeling HIV infection status in Butare, Rwanda, where the partitioned DIC identifies local impacts of a covariate effect. The sector-specific DIC estimates suggest evidence in favor of a spatially varying effect for the variable of women who engage in sexual intercourse to support themselves. The local DIC differences also show the value in selecting several covariates to add to a model, including syphilis status, marriage status, and women who have had sex with someone other than their husband or primary partner. When working with large datasets or complex models, this visual approach to model selection may prove useful, and at least should offer focused insights to model behavior in the same spatial context as the analysis.
Our approach for diagnosing spatial hierarchical models uses a combination of Bayesian statistical modeling and geographic information systems. Geographic information system technology is increasingly being utilized in public health research for exploring spatial relationships in disease. Bayesian statistical modeling is useful for quantifying trends and explaining spatial variation in disease rates. Taken together, we obtain a powerful set of tools for the statistical analysis of spatially-referenced data. In order to take full advantage of these tools, our model diagnostics should utilize the richness of the Bayesian output as well as the visualization capabilities of GIS in order to bring the same level of spatial visualization to model diagnostics as is often applied to display model output. As we have described, in the Bayesian framework the partitioned DIC components for individual observations or areas are easily attained from the MCMC simulation routine and can then be mapped to evaluate patterns in local DIC. Some mapping of diagnostics is possible directly in the Bayesian analysis software WinBUGS through GeoBUGS, although more flexibility is found in GIS software, such as ArcGIS. Our analysis of HIV infection data from Butare, Rwanda demonstrates that using Bayesian hierarchical models in combination with GIS technology can reveal spatial patterns in local model fit and highlight areas of high influence and poor fit in both individual observations and aggregations of observations in areas.
While use of the partitioned DIC for assessing model adequacy looks promising, several concerns have been expressed regarding the DIC as a measure of model fit and complexity (Spiegelhalter et al. 2002). One apprehension with pD for some is that it is not invariant to the selected parameterization, as the model deviances may change with using posterior medians for example instead of posterior means. Spiegelhalter et al. (2002) suggest calculating the DIC with several different estimators to address this issue. Another concern with the DIC is the fact that pD can be negative for some models, which does not have a clear interpretation when considering it as a measure of model complexity. Typically, this anomaly occurs in models with very asymmetric posterior distributions where the posterior mean is a poor summary statistic (Carlin and Louis, 2009, p. 214). Others have also expressed unease that the DIC is not asymptotically consistent; it will not always select the true model from a set as sample size increases. While negative pD was not an issue in the models fitted to the Rwanda HIV data, issues with the DIC will be present with the partitioned DIC and modelers should not use this tool uncritically.
This work proposes a step forward in the development and utilization of a suite of local diagnostics for hierarchical linear models, and for spatial hierarchical models in particular. Similar partitions of model fit criteria, such as Bayes Factors, could possibly be utilized to assess local model fit. While a partitioning of the DIC by geographic areas is the most natural in our study, one could imagine other underlying structural features, such as socioeconomic status, ethnicity, environmental exposure, and health clinic type. The approach is flexible to different types of partitions of the data. Given our experience, the development and application of additional local diagnostics and creative methods of visualization merits attention in future research.
References
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. 2nd international symposium on information theory; Budapest. 1973. pp. 267–281. [Google Scholar]
- Allen S, Van de Perre P, Serufiliram A, Lepage P, Carael M, DeClercq A, Tice J, Black D, Nsengumuremyi F, Ziegler J, Levy L, Hulley S. Human immunodeficiency virus and malaria in a representative sample of childbearing women in Kigali, Rwanda. Journal of Infectious Diseases. 1991;164:67–71. doi: 10.1093/infdis/164.1.67. [DOI] [PubMed] [Google Scholar]
- Anselin L. GeoDa 0.9 User's Guide 2003 [Google Scholar]
- Banerjee S, Carlin B, Gelfand A. Hierarchical modeling and analysis for spatial data. Chapman & Hall/CRC; Boca Raton, Florida: 2004. [Google Scholar]
- Besag J, York J, Mollie A. Bayesian image restoration, with two applications in spatial statistics (with discussion) Annals of the Institute of Statistical Mathematics. 1991;43:1–59. [Google Scholar]
- Best NG, Arnold RA, Thomas A, Waller LA, Conlon EM. Bayesian models for spatially correlated disease and exposure data. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian statistics 6. Oxford University Press; Oxford, UK: 1999. pp. 131–156. [Google Scholar]
- Boerma JT, Urassa M, Senkoro K, Klokke A, Ngweshemi JZ. Spread of HIV infection in a rural area of Tanzania. AIDS. 1999;13:1233–1240. doi: 10.1097/00002030-199907090-00013. [DOI] [PubMed] [Google Scholar]
- Bucyendore A, Van de Perre P, Karita E, Nziyumvia A, Sow I, Fox E. Estimating the seroincidence of HIV-1 in the general adult population in Kigali, Rwanda. AIDS. 1993;7:275–277. doi: 10.1097/00002030-199302000-00018. [DOI] [PubMed] [Google Scholar]
- Bulterys M, Chao A, Habimana P, Dushimimana A, Nawrocki P, Saah A. Incident HIV-1 infection in a cohort of young women in Butare, Rwanda. AIDS. 1994;8:1585–1591. doi: 10.1097/00002030-199411000-00010. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model selection and multimodel inference: a practical information-theoretic approach. 2nd. Springer-Verlag; New York: 2002. [Google Scholar]
- Carlin BP, Louis TA. Bayesian methods for data analysis. 3rd. Chapman & Hall/CRC; Boca Raton, Florida: 2009. [Google Scholar]
- Chambers JM, Cleveland WS, Kleiner B, Tukey PA. Graphical methods for data analysis. Wadsworth & Brooks/Cole; Pacific Grove, California: 1983. [Google Scholar]
- Chao A, Bulterys M, Musanganire F, Habimana P, Nawrocki P, Taylor E, Dushimimana A, Saah A. Risk factors associated with prevalent HIV-1 infection among pregnant women in Rwanda. International Journal of Epidemiology. 1994;23:371–380. doi: 10.1093/ije/23.2.371. [DOI] [PubMed] [Google Scholar]
- Cleveland WS, McGill ME. Dynamic graphics for statistics. Wadsworth; Monterey, CA: 1988. [Google Scholar]
- Congdon P. Bayesian predictive model comparison via parallel sampling. Computational Statistics & Data Analysis. 2005;48:735–753. [Google Scholar]
- Congdon P. Mixtures of spatial and unstructured effects for spatially discontinuous health outcomes. Computational Statistics & Data Analysis. 2007;51:3197–3212. [Google Scholar]
- Cook RD, Weisberg S. An introduction to regression graphics. Wiley; New York: 1994. [Google Scholar]
- Cook RD, Weisberg S. Applied regression including computing and graphics. Wiley; New York: 1999. [Google Scholar]
- Dixon DO, Simon R. Bayesian subset analysis. Biometrics. 1991;47:871–881. [PubMed] [Google Scholar]
- ESRI. ArcGIS 9.1 Users Guide 2005 [Google Scholar]
- Gelfand AE, Kim H, Sirmans CF, Banerjee S. Spatial modeling with spatially varying coefficient processes. Journal of the American Statistical Association. 2003;98:387–396. [Google Scholar]
- Gelfand A, Vounatsou P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics. 2003;4:11–25. doi: 10.1093/biostatistics/4.1.11. [DOI] [PubMed] [Google Scholar]
- Gelman A, Pardoe I. Bayesian measure of explained variation and pooling in multilevel (hierarchical) models. Technometrics. 2006;48:241–251. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. second. Chapman & Hall/CRC; Boca Raton, Florida: 2004. [Google Scholar]
- Guenther-Grey CA, Varnell S, Weiser JI, Mathy RM, O'Donnell LO, Stueve A, Remafedi G, Community Intervention Trial for Youth (CITY) Study Team Journal of the National Medical Association. 2005;97:38S–43S. [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R. Generalized additive models. Chapman & Hall; London: 1990. [DOI] [PubMed] [Google Scholar]
- Haw S, Higgins K. A comparison of the prevalence of HIV infection and injecting risk behaviour in urban and rural samples in Scotland. Addiction. 1998;93:855–863. doi: 10.1046/j.1360-0443.1998.9368557.x. [DOI] [PubMed] [Google Scholar]
- Hickson DA. Dissertation. Emory University, Department of Biostatistics; Atlanta, GA: 2005. Multilevel (hierarchical) analysis of the human immunodeficiency virus and high risk sexual behavior: Assessing model fit with the deviance information criterion and generalized coefficient of determination. [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. Journal of the American Statistical Association. 1995;90:773–795. [Google Scholar]
- Leone P, Hightow L, Owen-O'Dowd J, Phillip S, Gray P, Jones B, Fitzpatrick L, Millet G, Jones K, Stall R, Holmberg S, Greenberg A. HIV transmission among black college student and non-student men who have sex with men - North Carolina, 2003. MMWR. 2004;53:731–734. [PubMed] [Google Scholar]
- Mardia KV. Multi-dimensional multivariate Gaussian Markov random fields with application to image processing. Journal of Multivariate Analysis. 1988;24:265–284. [Google Scholar]
- Mathei C, Robaeys G, Van Damme P, Buntinx F, Verrando R. Prevalence of hepatitis C in drug users in Flanders: determinants and geographic differences. Epidemiology Infections. 2004;133:127–136. doi: 10.1017/s0950268804002973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland W, Katz MH, Stoyanoff SR, Shehan DA, LaLota M, Celentano DD, Koblin BA, Torian LV, Thiede H. MMWR. 2001;50:440–444. [Google Scholar]
- Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. Applied linear regression models. Irwin; Chicago: 1996. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–466. [Google Scholar]
- Shafer G, Olkin G. Adjusting p values to account for selection over dichotomies. Journal of the American Statistical Association. 1983;78:674–678. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, Series B. 2002;64:583–639. With discussion. [Google Scholar]
- Spiegelhalter DJ, Thomas A, Best NG, Lunn D. WinBUGS user manual, version 1.4. MRC Biostatistics Unit; Cambridge: 2003. [Google Scholar]
- Thomas A, Best N, Lunn D, Arnold R, Spiegelhalter D. GeoBUGS user manual, version 1.2. MRC Biostatistics Unit; Cambridge: 2004. [Google Scholar]
- Tierney L. LISP-STAT: An object oriented environment for statistical computing and dynamic graphics. Wiley; Chichester: 1990. [Google Scholar]
- Tukey JW. Explanatory data analysis. Addison-Wesley; Reading, MA: 1977. [Google Scholar]
- Van de Perre P, Clumeck N, Carael M, Nzabihimana E, Robert-Guroff M, De Mol P, Freyens P, Butzler JP, Gallo RC, Kanyamupira JB. Female prostitutes: a risk group for infection with human T-cell lymphotropic virus type III. Lancet. 1985;ii:524–526. doi: 10.1016/s0140-6736(85)90462-3. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline models for observational data. Society for Industrial and Applied Mathematics; Philadelphia: 1990. [Google Scholar]
- Zhu L, Carlin BP. Comparing hierarchical models for spatio-temporally misaligned data using the deviance information criterion. Statistics in Medicine. 2000;19:2265–2278. doi: 10.1002/1097-0258(20000915/30)19:17/18<2265::aid-sim568>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]


