Punishing and abstaining for public goods

Abstract

The evolution of cooperation within sizable groups of nonrelated humans offers many challenges for our understanding. Current research has highlighted two factors boosting cooperation in public goods interactions, namely, costly punishment of defectors and the option to abstain from the joint enterprise. A recent modeling approach has suggested that the autarkic option acts as a catalyzer for the ultimate fixation of altruistic punishment. We present an alternative, more microeconomically based model that yields a bistable outcome instead. Evolutionary dynamics can lead either to a Nash equilibrium of punishing and nonpunishing cooperators or to an oscillating state without punishers.

Public goods pose a riddle from the evolutionary viewpoint. Individuals who do not contribute, but exploit the public goods, fare better than those who pay the cost by contributing. Thus, the defectors have a higher payoff. If more successful strategies spread, cooperation will vanish from the population, and the public goods along with it. A strong body of theoretical and empirical evidence points to the importance of punishment as a major factor for sustaining cooperation in public goods games (1-8). But how can such an altruistic trait emerge, if the act of punishing non-contributors is costly?

An interesting suggestion has been made in ref. 9. It is based on the assumption that players can voluntarily decide whether to take part in the joint enterprise or not (10-12). They can obtain an autarcic income independent of the other players' decision. Thus, in addition to cooperators, defectors, and punishers, there exists a fourth type, the loners. Loners do not participate in the public goods enterprise. Those who participate include the defectors, who do not contribute their part, but exploit the contributions of the other participants. Cooperators contribute but do not punish. Punishers also contribute to the public good but punish all those participants who fail to contribute, or who fail to punish defectors. (The latter assumption serves to prevent cooperators from “free-riding” on the punishers.) According to ref. 9, punishers will invade and take over.

This result, however, is based on a model that effectively allows single individuals to play a public goods game with themselves. By contributing, they obtain a payoff that is higher than that of loners, and as high, in fact, as if the whole population consisted of cooperators. Thus, “a mutant cooperator can invade a population of non-participants [= loners],” and “a single punisher can invade a population of non-participants” (9). Moreover, in a population consisting only of cooperators and punishers, the cooperators will be punished, although they did not fail to punish defectors (because none were present). These problems can be avoided by using the modeling assumptions from ref. 10. In this approach, a sample of N players is randomly selected from the population, and the members of this sample can decide to play a public goods game or not. If a single member wants to play, but all others refuse, then the single player is reduced to the autarkic income, i.e., forced to act like a loner.

The differences in the modeling approach lead to different conclusions. In contrast to ref. 9, altruistic punishers will not always come to dominate a population of contributors, defectors, and loners. We emphasize that we do not believe that this result reduces the importance of punishment, but rather that its emergence is still offering theoretical challenges.

Methods

Let x be the frequency of cooperators (who contribute but do not punish), y that of defectors, z the loners, and w the punishers (who contribute, and punish by reducing the payoff of defectors by an amount β, and that of nonpunishing cooperators by an amount αβ, at a cost γ resp αγ to themselves). We normalize the payoffs such that the cost for contributing is 1. Each contribution is multiplied by a constant factor r, and the resulting total is divided equally among all participants of the public goods game (irrespective of whether they contributed or not). The autarkic payoff is σ. We assume that N > r > (1 + σ) and β > 1 > α > 0 (other cases are of less interest). With P_x, P_y, etc., we denote the average payoff for cooperators, defectors, etc.

According to ref. 9, the payoffs are P_z = σ,

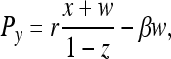[1]

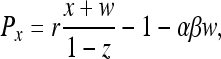[2]

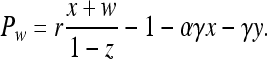[3]

Following the approach in ref. 10 instead, we compute the payoffs as P_z = σ,

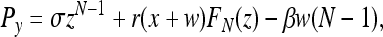[4]

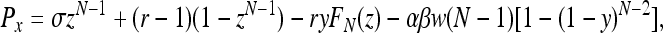[5]

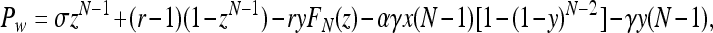[6]

where

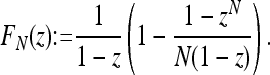[7]

These expressions are, of course, considerably less simple. In ref. 9, the whole population (which is assumed to be very large) is presented with the public goods game. In the absence of defectors, a single cooperator or punisher will obtain r - 1 from playing the public goods game, which is larger than the payoff obtained by a non-participant. Moreover, in a population without defectors, contributors will be punished, although they did obviously not fail to punish defectors. Taking account of these modeling issues yields the terms with z^N-1 and (1 - y)^N-2, respectively. The different equations lead to distinct replicator dynamics (see Figs. 1 and 2). This dynamical system, which describes the evolution of the frequencies in the unit simplex S₄ where x + y + z + w = 1, is given by ẋ = x(P_x - P̄), etc., where P̄:= xP_x + yP_y + zP_z + wP_w is the average payoff in the population.

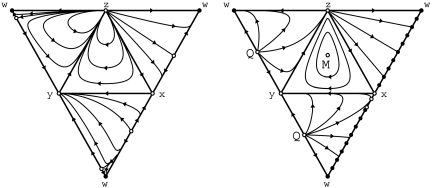
Fig. 1.

Replicator dynamics on the boundary faces of the simplex S₄ for the payoff expressions in ref. 9 (Left) and in our model (Right). Filled circles represent stable fixed points, and open circles unstable fixed points. Parameter values are in both cases r = 3, α = 0.1, β = 1.2, γ = 1, and σ = 1. Furthermore, n = 5. Note the differences in the faces w = 0 and z = 0. But in both cases, cooperators, defectors, and loners form a rock-paper-scissors cycle.

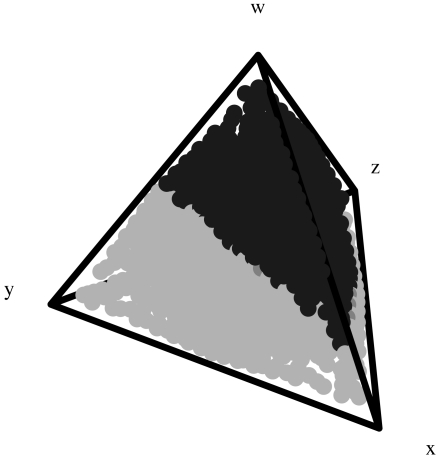
Fig. 2.

Replicator dynamics in the interior of the state space S₄ for the payoff expressions given by our model. The parameter values are as before. The initial states marked by dark dots lead to the attractor A (mixtures of cooperators and punishers); the initial states marked by bright dots lead to the attractor B (periodic orbits with no punishers).

The main differences are the following. (i) In ref. 9, the fixed point w = 1 (punishers only) is asymptotically stable. It corresponds to a strict Nash equilibrium. In contrast, here, the xw edge consists of fixed points, and all those with k/β < w ≤ 1 are stable, but not asymptotically stable, where

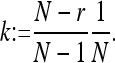[8]

(ii) More importantly, on the face w = 0, ref. 9 has a homoclinic cycle: all orbits in the interior of this face converge to z = 1 for t → +∞ and t → -∞. In ref. 10, however, this face contains a fixed point M, which is surrounded by periodic orbits. The time averages of the payoff values P_x, P_y, and P_z are all equal, and therefore equal to σ. In our model, this point M is saturated in the sense of ref. 13, and therefore a Nash equilibrium. Indeed, at M, one has P_x = (r - 1)(1 - z^N-1) + σz^N-1 - ryF_N(z) = P_z = P̄ = σ, and therefore P_w - P̄ = -γ(N - 1)[y + αx(1 - (1 - y)^N-2)] < 0. Moreover, any orbit o with period T in the face w = 0 is attracting orbits from the interior of S₄, in the sense that the time average of the “transversal growth rate,” i.e., of P_w - P̄, is negative. This result can be shown as before, by noting that the time-averages along o satisfy the equalities P̂_x = P̂_y = P̂_z = P̄̂ = σ, so that

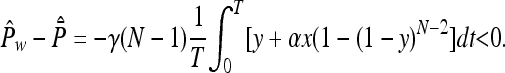[9]

The periodic orbit o is thus saturated in this sense, i.e., transversally stable, and even attracting. We note that, for very large orbits, the state spends most of the time close to z = 1. The transversal eigenvalue, there, is 0.

Results and Discussion

In ref. 9, the dynamics always lead to the fixation of the punishers in the population. In contrast, our model displays a bistable behavior. Depending on the initial condition, the state converges either to a Nash equilibrium consisting of cooperators and punishers, or to a periodic orbit in the face w = 0 (no punishers), where the frequencies of loners, defectors, and cooperators oscillate endlessly. More precisely, let us denote by A the segment x = y = 0, k/β ≤ w ≤ 1, which consists of (nonstrict) Nash equilibria, and by B the interior of the face w = 0, which consists of periodic orbits. Orbits in the interior of the state space (i.e., with all types initially present) converge either to A or to B. We are unable to delimit analytically the basins of attractions of A and B, but numerical simulations show that, as a rule of thumb, the fraction of initial states leading to A is given by (β - k)/(β + γ), which corresponds to the w-value of the fixed point Q on the wy-edge. It should be noted that, if the state converges to A, all members of the population end up with payoff r - 1 whereas, if the state converges to B, the time averages are only σ. Punishers are important for the sake of the society, but they cannot invade a population consisting only of defectors. The reason why, in ref. 9, the outcome is different from ours is that the odds, in ref. 9, favor punishers in two ways. On the one hand, cooperators will be punished even if there are no defectors around, and thus will be unable to invade a population of punishers by neutral drift. On the other hand, in the absence of punishers, the state z = 1 (loners only) is a homoclinic attractor. Each invasion of contributors is quickly repressed so that, up to rare, intermittent bursts of cooperation, the population is reduced to the autarkic way of life. Because it is allowed, additionally, that even “a single punisher can invade a population of loners” (9), the ultimate domination by punishers is greatly furthered.

Of course there are many ways that a public good may depend on the number of contributors and defectors. It is by no means necessary to assume, as we have done in our model, that, in a group of two cooperators and no defectors, the payoff is as high as in a group of a hundred cooperators and no defectors. But the model should always reflect that contributing to a public goods enterprise is a risky investment, whose eventual return depends on other players. An isolated public goods contributor should not obtain single-handedly more than a non-participant.

There is another reason why it is plausible to assume that any given public goods game is offered only to a small fraction of the population, a sample of size N (with N a one- or two-digit number). During most of human evolution, total population numbers were fairly large (in the ten thousands and more), but it is unlikely that, in the absence of modern institutions, more than a few dozens, or hundreds, could have been presented with the same joint endeavor. In this sense, our model has the advantage of being based on an explicit microeconomical foundation.

Fowler's idea in ref. 9, of analyzing the interplay between (i) abstaining from participating and (ii) punishing the exploiters, offers considerable interest. Our model shows that both abstaining and punishing are possible as long-term outcomes.