Abstract
Purpose
To evaluate setup, interfraction, and intrafraction organ motion error distributions and simulate intrafraction intervention strategies for prostate radiotherapy.
Methods and Materials
Seventeen patients were setup and monitored using Calypso system during radiotherapy. On average, prostate tracking measurements were performed over 8 minutes per fraction for 28 fractions for each patient. For both patient couch shift data and intrafraction organ motion data, the systematic and random errors were obtained from the patient population. PTV margins were calculated using van Herk formula. Two intervention strategies were simulated using the tracking data: deviation-threshold and time-period. The related PTV margins, time costs and prostate position “fluctuation” were presented.
Results
The required treatment margins for the left-right, superior-inferior and anterior-posterior axes were 8.4, 10.8, and 14.7 mm for skin-mark-only setup and 1.3, 2.3 and 2.8 mm with online setup correction. Prostate motion significantly correlated among the SI and AP directions. Fourteen patients had 91.6% or higher total tracking time that prostate motion was within 5 mm of the initial setup position. The treatment margin decreased to 1.1, 1.8, 2.3 mm with 3 mm threshold correction and to 0.5, 1.0, 1.5 mm with every–two-minute correction. The periodic corrections significantly increase treatment time and increase the number of instances when the setup correction was made during transient excursions.
Conclusions
The residual systematic and random error due to intrafraction prostate motion is small after online setup correction. Threshold-based and time-based intervention strategies both reduce PTV margins. The time-based strategies increases treatment time and in-fraction position fluctuation.
Keywords: Patient setup, Intrafraction motion, Tracking, PTV Margin, Intervention Strategies
INTRODUCTION
In external-beam prostate radiotherapy, target position uncertainty can affect the efficacy of the treatment (1–2). Uncertainty arises from inaccuracies in the daily setup procedure, daily movement of the prostate with respect to the setup landmarks, and intrafraction motion. To mitigate its impact, a margin is added to the clinical target volume (CTV) to define the planning target volume (PTV). A well-defined margin should reflect anticipated prostate position variations relative to the intended target position for the particular setup procedure in use. For example, if setup is based on daily alignment to skin marks, the margin should accommodate daily and intrafraction prostate motion relative to those marks; if internal fiducial markers are used for daily image-guided setup, the margin should accommodate intrafraction organ movement following initial alignment. The correct margin should be based on actual observations of prostate movement for each setup scenario and should also reflect the fact that the setup procedure itself has intrinsic instrumental and measurement uncertainties.
The prostate position for a particular patient can change in a systematic way over the complete course of treatment while fluctuating randomly around its mean daily position. Similar systematic and random variations can occur during a single fraction. By observing and measuring these patterns of fluctuation in a population of patients, one can establish the expected target position uncertainty for any given setup procedure. Appropriate margins can then be estimated from population-based rules that ensure acceptable target coverage for, e.g., 90% of the patients.
It is now possible to track the position of the prostate continuously during each treatment fraction using the Calypso 4D localization system (Calypso Medical Technologies, Inc. Seattle, WA). This system is a wireless electromagnetic system that utilizes a radiofrequency source/receiver array to localize implanted transponders. Several investigators (3–7) have evaluated the Calypso system localization accuracy in a phantom or have analyzed prostate motion data acquired using this system. Balter et al. (3) concluded that the Calypso system has sub-millimeter localization accuracy in both stationary and moving phantoms. Litzenberg et al. (6) analyzed data from eleven prostate cancer patients implanted with Calypso transponders and demonstrated the influence of intrafraction prostate motion on the PTV margin.
We have used the Calypso system to make a clinical study of interfraction and intrafraction prostate movement during radiotherapy for a cohort of 17 patients. Then we used our observations to estimate appropriate margins for various daily patient alignment scenarios. Finally, we have used our data to simulate various intervention strategies to improve alignment accuracy and reduce the margins while accounting for the time costs (increase of treatment time) and potential increases in prostate position fluctuations for some patients.
METHODS AND MATERIALS
The Calypso 4D localization system localizes and tracks electromagnetic transponders implanted in the patient’s target volume. The overall system components and operating principles have been described by Balter et al (3). This system can measure the target position with sub-millimeter accuracy at a rate of 10 Hz. As a part of the research agreement between Virginia Commonwealth University (VCU) and Calypso Medical, the digital tracking data were exported from the 4D tracking station and converted into readable format by a software program provided by Calypso Medical.
Patient information
This study, under an institutional internal review board approved protocol, analyzed tracking data from 17 consecutive prostate cancer patients who were prescribed and treated with implanted Calypso transponders between 2007 and 2008 at VCU. All patients were educated about transponder implantation and Calypso System operation during the treatment. For each patient, three transponders were implanted into the prostate gland at the right base, left base and apex, using a transrectal ultrasound-guided procedure. CT simulation was performed one week after the implantation to minimize the influence of transponder drift. Permanent skin marks for localizing the isocenter via room lasers were placed at the time of simulation. The CT images were imported into the Pinnacle treatment planning system (Philips Medical Systems, Fitchburg, WI). The coordinates of the transponders and the planned treatment isocenter point, usually the centroid of the transponders, were obtained from the treatment planning system and manually inputted into the Calypso 4D tracking station computer.
Patient setup and tracking
At the start of each treatment fraction the patient was initially set up to the skin marks placed during CT simulation. Then the patient was localized using the Calypso system. The treatment target deviation from the machine isocenter was determined from the detected transponder positions in the left-right (LR), superior-inferior (SI) and anterior-posterior (AP) directions and reported as a translational displacement (Δx, Δy, Δz) of the isocenter position from that measured during simulation CT. Radiation therapists then manually adjusted the treatment table position by (Δx, Δy, Δz) to approximately zero the deviation prior to treatment.
During each treatment fraction the Calypso system continued monitoring the position of the planned isocenter point. Whenever the intrafraction position deviated by more than 5 mm from the setup position for more than 25 seconds on any axis, our policy was to interrupt treatment and adjust the treatment couch. However, this procedure was not uniformly implemented. Our analysis was able to identify only 14 treatment sessions that had intrafraction couch adjustments. To avoid biasing our analysis, the datasets of these patients were processed to recover the patient’s original prostate motion trajectories as if no adjustments had been made.
While processing the tracking data for this study, some of the tracking files were corrupted. On average, there were about 28 tracking sessions per patient, each of about 8 minutes duration. Population histograms of intrafraction prostate motion along each axis were obtained. Cumulative probabilities of prostate deviating from initial setup positions in 3D distances and along each axis were also calculated.
To evaluate the directional properties of prostate motion for each tracking session, we calculated the correlation coefficients among the position data of three axes using following equation:
| (1) |
X and Y represent the prostate position history along the LR, SI or AP axes in each treatment fraction, Cov(X,Y) is the covariance between the two histories, Var(X), Var(Y) are their individual variances, for each pair of coordinate axes. To investigate prostate displacement trend with time, the fraction of time in each minute bin that the prostate displaced beyond distance thresholds (3, 5, 7, 10 mm) was analyzed as a function of monitoring elapsed time since initial interfraction setup.
Statistical analysis of the inter and intrafraction position data and their reduction to margin estimates
During treatment session i of patient j, tracking measurement k was obtained from Calypso system. If we denote patients as j ∈ {1,2,⋯,N} and each patient’s treatment session as i ∈ {1,2,⋯,Mj} and each tracking measurement as k ∈ {1,2,⋯, Oij}, then during a treatment, the CTV location is
| (2) |
where Sij is setup error and Xij (tk) is organ motion error for patient j, fraction i at k-th moment. From this we obtained
| (3) |
| (4) |
| (5) |
| (6) |
For interfraction setup error only, denotes the difference between the isocenter coordinates measured by Calypso for ith fraction of the jth patient and those measured during simulation CT. For intrafraction organ motion error only, denotes the difference between the isocenter coordinates measured by Calypso for ith fraction of the jth patient at kth moment and those at beginning of tracking.
Several investigators (8–11) have developed population-based geometric rules to determine the optimal margin for setup errors when the random error σ and the systematic error Σ are known for a cohort of similar patients all treated via the same setup procedure. The analysis of Van Herk et al. (10, 11) determined that a PTV margin of 2.5Σ + 0.7σ will ensure that at least 90% of all patients receive at least 98% equivalent uniform dose. The dominant influence of the systematic error component compared to the random component reflects the fact that, over the course of treatment, the random deviations blur the dose distributions while the systematic deviations result in a geometric miss.
Simulated intervention strategies
The prostate tracking data were used to evaluate the impact of several hypothetical intervention strategies to correct prostate excursions during the treatment, including deviation threshold-based and time-based approaches. The threshold-based approach interrupted treatment and repositioned the patient whenever the prostate excursion exceeded a preset distance (3 or 5 mm) along any of the three axes for a preset duration (20 seconds). In the time-based approach, the patient was repositioned at preset time intervals (every 2 minutes and every 4 minutes) regardless of the spatial magnitude of setup discrepancy. In both approaches, the related time costs were calculated based on both in-room treatment couch adjustment (45 seconds) and remote adjustment (15 seconds) (12). Using these parameters, a program written in Matlab (The MathWorks, Inc., Natick, Massachusetts) was used to simulate each type of intervention and compare the errors against tracking data with no intrafraction couch adjustments other than the initial interfraction adjustment. For each of the four simulated excursion correction datasets, systematic and random components of the intrafraction prostate motion errors were calculated and the corresponding margins were presented. The maximum, minimum and average time cost were calculated for both in-room and remote couch adjustment.
For each patient, the 3D mean prostate position over all fractions was obtained by averaging the 3D distance over all treatment time. Similarly, for each patient, the root-mean-squared deviation (SD) over all the treatment fractions was obtained using Equation 7. The quadrature average SD represented the magnitude of fluctuation within fractions. Same analysis was performed on datasets obtained from simulated threshold-based and time-based intervention approaches and compared to those of original tracking data. These comparisons can evaluate the impact of intervention strategies on each individual patient, especially when prostate motion fluctuation could not be ignored, i.e., in hypofractionated radiotherapy.
| (7) |
RESULTS
Prostate interfraction setup error and intrafraction motion
The systematic and random components of patient initial setup and prostate motion errors are shown in Table 1. The magnitude of both the systematic (Σinter) (σinter) component, 2.3, 3.4, 4.7 mm and 3.7, 2.7, 3.5 mm, respectively, were much larger than their intrafraction counterparts (0.3, 0.5, 0.6 mm for Σintra and 0.7, 1.4, 1.9 mm for σintra).
Table 1.
Systematic and random components for both patient initial setup errors and intrafraction prostate motion errors.
| LR (mm) | SI (mm) | AP (mm) | ||
|---|---|---|---|---|
| Population Mean Inter-fraction Setup Error | 0.6 | 0.5 | 2.7 | |
| Inter-fraction Setup Error | Systematic | 2.3 | 3.4 | 4.7 |
| Random | 3.7 | 2.7 | 3.5 | |
| Population Mean Intra-fraction Organ Motion Error | 0.0 | −0.1 | −0.4 | |
| Intra-fraction Organ Motion Error | Systematic | 0.3 | 0.5 | 0.6 |
| Random | 0.7 | 1.4 | 1.9 | |
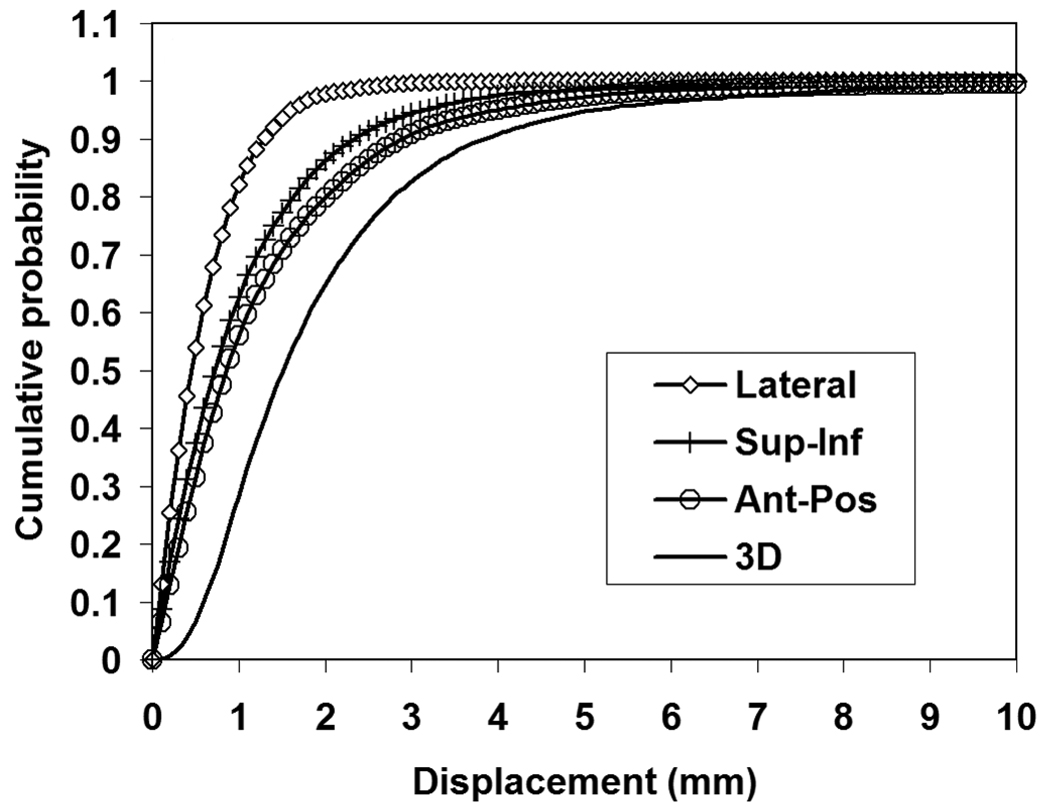
The distributions of intrafraction motion measurements along LR, SI and AP axes were approximately Gaussian. Their cumulative probabilities of deviation from initial setup positions are presented in Figure 1. Magnitude of the prostate motion was larger in the AP and SI directions than in the LR direction of the patients. The prostate displacements were 0.0±0.7 mm in LR, −0.1±2.4 mm in SI and −0.4±3.9 mm in AP directions. Table 2 shows, for each patient, the fraction of time that the prostate was displaced by more than the indicated 3D distance. Patient 15 showed a significantly more time fraction (31.6%) in which the prostate was displaced at least 5 mm from the desired treatment isocenter compared to other patients.
Figure 1.
Cumulative probability intrafraction prostate motion along each axis and in 3D distance.
Table 2.
Percentage of time of that 3D prostate displacement exceeds 10, 7, 5 and 3 mm for each of the 17 patients.
| Patient No. | 3D > 10 mm (%) | 3D > 7mm (%) | 3D > 5 mm (%) | 3D > 3 mm (%) |
|---|---|---|---|---|
| 1 | 0.0 | 0.1 | 0.2 | 0.9 |
| 2 | 0.0 | 0.0 | 2.8 | 26.9 |
| 3 | 0.1 | 1.6 | 4.0 | 4.5 |
| 4 | 2.3 | 8.0 | 14.1 | 36.8 |
| 5 | 0.1 | 1.5 | 4.6 | 12.7 |
| 6 | 0.0 | 0.0 | 0.1 | 6.0 |
| 7 | 0.0 | 0.0 | 0.8 | 9.2 |
| 8 | 0.1 | 0.8 | 3.4 | 17.5 |
| 9 | 0.0 | 0.0 | 0.0 | 4.5 |
| 10 | 0.4 | 2.2 | 8.4 | 32.8 |
| 11 | 0.0 | 0.0 | 0.1 | 2.9 |
| 12 | 0.2 | 0.9 | 6.0 | 22.1 |
| 13 | 0.1 | 9.7 | 14.7 | 40.2 |
| 14 | 0.0 | 0.1 | 1.9 | 7.3 |
| 15 | 8.5 | 18.6 | 31.6 | 52.2 |
| 16 | 0.0 | 0.0 | 0.1 | 1.4 |
| 17 | 0.0 | 0.0 | 0.2 | 17.2 |
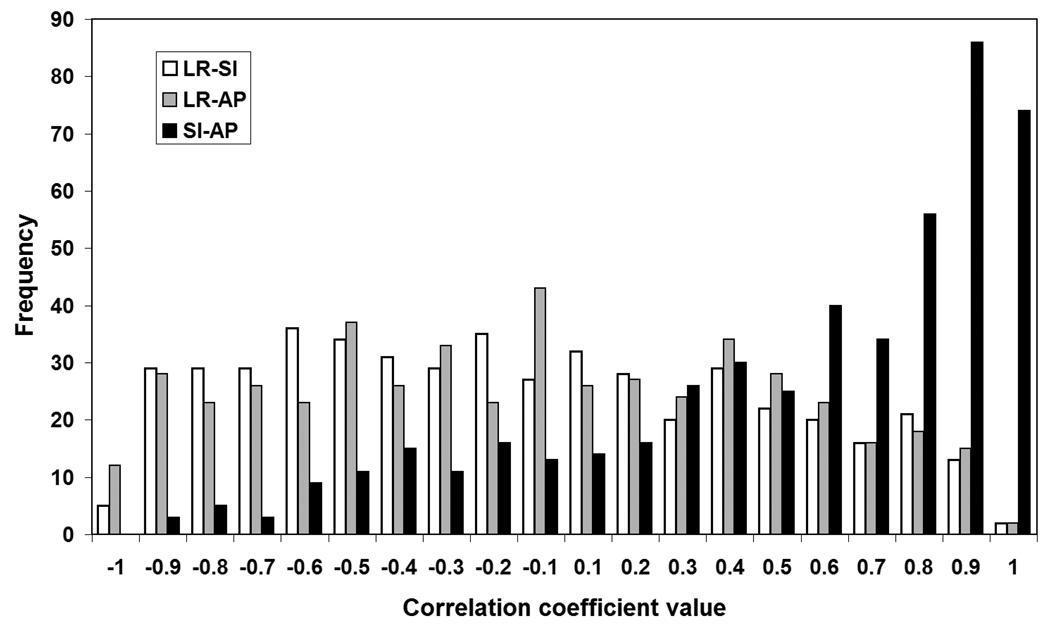
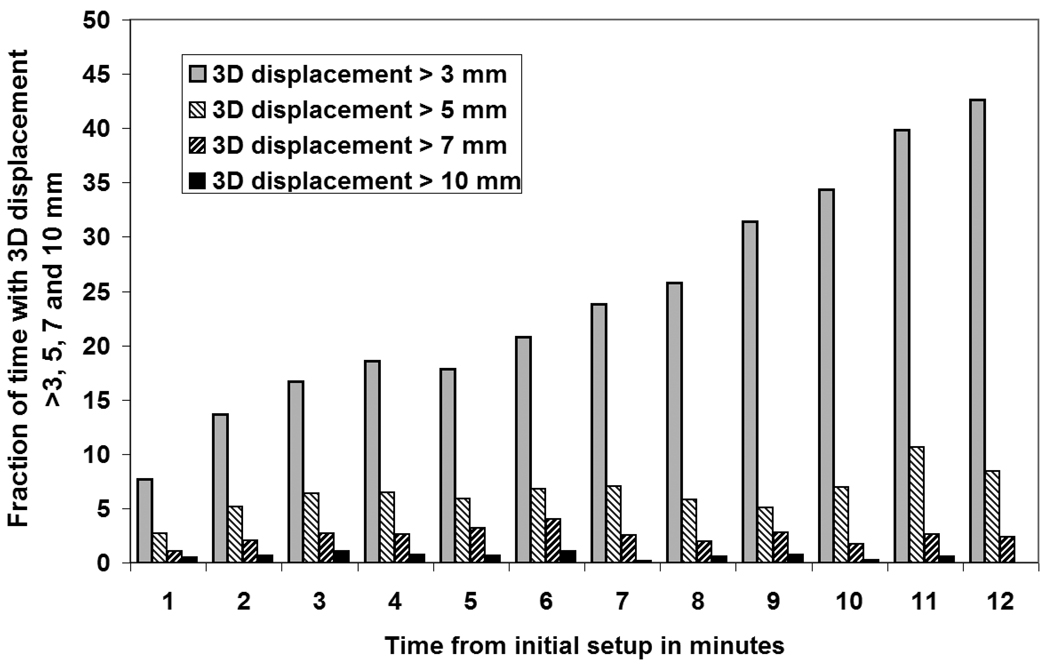
Correlation coefficients between each two axes were obtained for all treatment sessions and presented in Figure 2. Clearly, there is a significant positive correlation of prostate motion between each patient AP and SI directions, which indicates that the prostate had a tendency to move in the AP/SI plane. Figure 3 shows this prostate displacement trend with time. The fraction of time for displacements exceeding 3 mm increased linearly with time. However, for larger 3D displacement thresholds, the time fraction did not vary systematically with time but fluctuated between 0 and 10 percent.
Figure 2.
Motion correlations among the three different axes for all the treatment sessions of the patient population.
Figure 3.
Time fraction of prostate 3D displacement greater than 3, 5, 7 and 10 mm as a function of elapsed time since initial interfraction error adjustment. The time fraction displaced was estimated for 1 minute time bins.
Margins
The margins with and without patient initial setup correction are presented in Table 3. Without the online correction before each treatment session, the required margins were 8.4, 10.8 and 14.7 mm in the patient’s LR, SI and AP directions, respectively. With the online correction, the systematic and random errors associated with skin marks setup and interfraction prostate motion were largely eliminated. Thus, the remaining treatment errors were due to the intrafraction motion of the prostate, Calypso measurement errors (including marker identification on CT), prostate deformation errors, and prostate delineation errors. Considering only the intrafraction error component, margins of 1.3, 2.3 and 2.8 mm in the LR, SI and AP directions, respectively, would be needed.
Table 3.
Margins required for skin mark setup and online corrections with transponders.
| Margins | LR (mm) | SI (mm) | AP (mm) |
|---|---|---|---|
| Skin Mark Setup | 8.3 | 10.5 | 14.2 |
| Skin Mark Setup with Intra-fraction Motion Consideration | 8.4 | 10.8 | 14.7 |
| Online Correction using Calypso Transponders | 1.3 | 2.3 | 2.8 |
Intervention strategie
Table 4 shows both the margins and time-cost associated with each intervention strategy. Of the four strategies, the 5 mm threshold approach yielded the least benefit wheras, the 3 mm threshold one yielded modest improvements compared to the margins required when no intrafraction adjustments were made. On the other hand, making adjustments at a fixed time frequency reduced the margin to two thirds and half of the original margins, for 4 and 2 minutes repositioning intervals, respectively. However, the associated time-cost for the time-based approaches were significantly higher than those of threshold-based approaches. The treatment time increased more than 50% for the every-2-minute correction approach with the in-room couch adjustment method. For the remote couch adjustment method, the time cost was reduced significantly compared to the in-room adjustment but it still exceeded 10%. While a 12% penalty in exchange for a 2-fold intrafraction margin reduction is a reasonable trade, such margin adjustments will add clinical value only if other sources of targeting error are reduced to comparable levels.
Table 4.
PTV margins of each intervention technique and its corresponding treatment time increases (given as percent of the original treatment time) due to couch adjustments.
| Margin | In-Room Cost | Remote Cost | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Strategy | LR (mm) | SI (mm) | AP (mm) | Average(%) | Max(%) | Min(%) | Average(%) | Max(%) | Min(%) |
| Original Data | 1.3 | 2.3 | 2.8 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 mm Threshold | 1.2 | 2.1 | 2.6 | 2.6 | 18.6 | 0 | 0.5 | 3.7 | 0 |
| 3 mm Threshold | 1.1 | 1.8 | 2.3 | 6.9 | 31.5 | 0 | 1.4 | 6.3 | 0 |
| Every 4 minutes | 0.8 | 1.4 | 1.9 | 23.4 | 29.0 | 18.5 | 4.7 | 5.8 | 3.7 |
| Every 2 minutes | 0.5 | 1.0 | 1.5 | 53.8 | 58.7 | 47.9 | 10.8 | 11.7 | 9.6 |
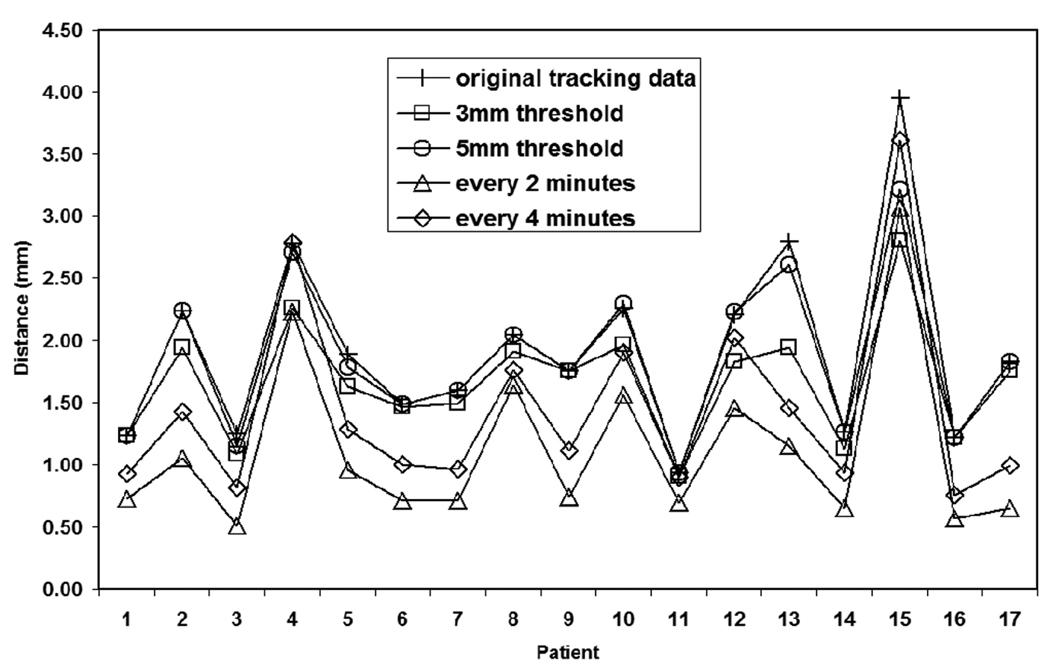
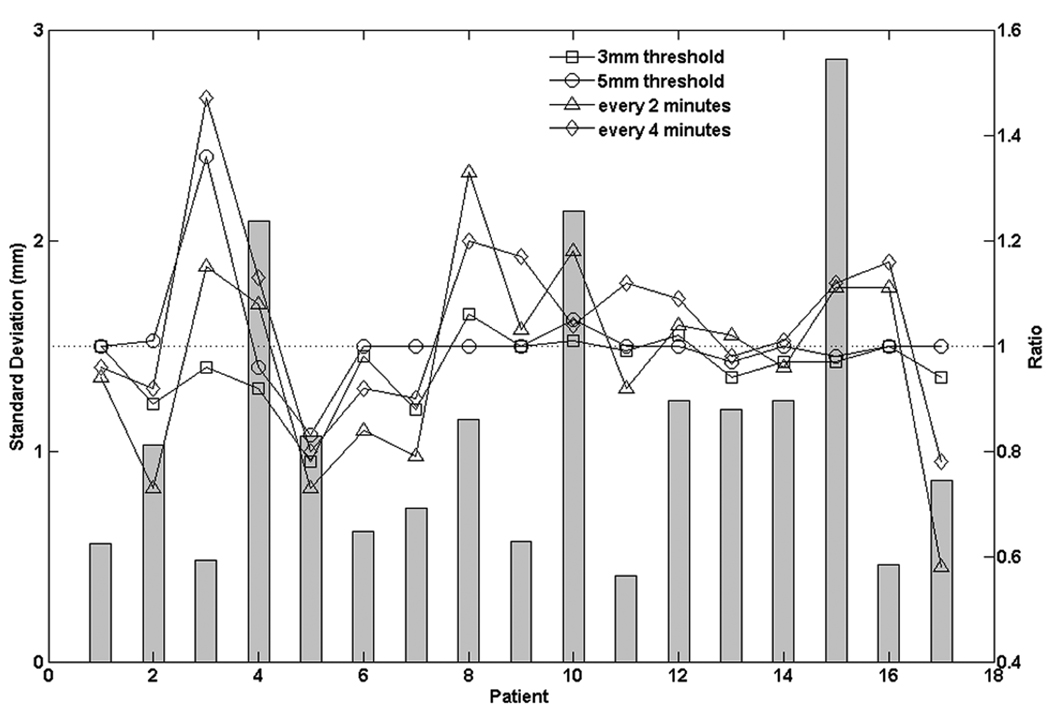
Figure 4 shows the patient-specific mean 3D prostate displacements average over all observations for the various intervention techniques. In general, all intervention strategies succeeded in reducing the mean prostate excursion distance from the target position during the course of treatment. The every-2-minute approach caused the most significant reduction in the mean excursion distance except for patient 15. For 13 of the 17 patients, the every-4-minute intervention approach out-performed (more reduction of mean excursion distance) the threshold-based approaches. Figure 5 shows the quadrature-averaged σintra over all the treatment fractions of the original tracking data for each patient and the ratio of for each intervention approach to that of the original data. Interestingly, for 8 patients, making excursion corrections at fixed time intervals increased compared to the original tracking data. Also for 7 patients (5 were the same patients of the above 8 patients), the time-based approaches had larger than the deviation threshold-based approaches.
Figure 4.
3D Displacement of isocenter from planned location for each patient, averaged over all measurements and fractions, each intervention technique.
Figure 5.
The quadratic mean of fraction standard deviation for every patient of the original tracking data (bar symbols) and its ratios of each intervention technique to the original tracking data (hollow symbols).
DISCUSSION
In image-guided prostate radiotherapy, prostate localizations before or during treatment are performed with different techniques: kV/MV 2D radiographic/fluoroscopic imaging of implanted markers (13–16, 18), kV 3D imaging and detection of implanted electro-magnetic transponder (6, 17, 23). Intrafraction prostate motion was also studied by using cine-MRI with time duration comparable to typical radiation treatment (20–22). Online setup correction and target monitoring using electromagnetic transponders has the advantages of non-ionizing radiation target localization and real-time target monitoring with high sampling rate compared to other target localization and monitoring techniques.
Table 5 listed PTV margins for both setup and organ motion errors of several investigators (6, 13–19) using various target positioning and/or monitoring techniques. Interfraction only margins varied up to two fold among different localization techniques. For intrafraction only margin, even though Nederveen et al. (16) and Kitamura et al. (14) have relatively frequent intrafraction prostate motion data, the total imaging time was only about 2 to 3 minutes. Furthermore, only one marker at the apex of the prostate was tracked in the Kitamura et al. study. Nevertheless, these findings confirmed that the intrafraction prostate motion errors were much smaller than interfraction errors. Compared to continuous tracking data, the EPID inter-beam or difference between pre-treatment and post-treatment techniques may over/under estimate the intrafraction motion because they assume the measured prostate deviation lasts between images. Litzenberg et al. (6) investigated prostate interfraction and intrafraction motion of 11 patients using Calypso system. They simulated pre-beam implanted marker correction strategy, in which they simulated realignment of the patient before each treatment beam. This pre-beam re-alignment was similar to our simulations of the every-2-minute intervention strategy; however, they included a 1 mm Gaussian setup uncertainty for pre-beam re-alignments. They reported margins of 1.4 mm in LR, 1.8 mm in SI and 2.3 mm in AP directions, which is about 0.8 mm larger (agreed with 0.7*1 mm) in all three directions than ours.
Table 5.
PTV margins calculated from interfraction and intrafraction errors of this study and other investigators using margin formula: 2.5Σ + 0.7σ.
| Margin | |||||
|---|---|---|---|---|---|
| Study (First Author) | Method | Time(min) | LR (mm) | SI (mm) | AP (mm) |
| Inter-fraction Setup Error Only (after skin mark setup) |
|||||
| Van den Heuvel et al. | EPID | 13 | 12.5 | 11.6 | |
| O'Daniel et al. | kV CT | 5.8 | 9.9 | 12.3 | |
| Litzenberg et al. | Calypso | 8 | 10 | 7.3 | |
| This Study | Calypso | 8.3 | 10.5 | 14.2 | |
| Intra-fraction Organ Motion Error Only (after online correction using markers) |
|||||
| Nederveen et al. | EPID Cine Images | ~2–3 | 0.24 | 2 | 1 |
| Kitamura et al. | kV Fluoro | ~2 | 0.2 | 1.2 | 0.6 |
| Aubry et al. | EPID pre & Post Tx | 1.1 | 1.7 | 2.7 | |
| McNair et al. | EPID pre & Post Tx | 3.1 | 3.4 | 3.6 | |
| Schallenkamp et al. | EPID inter-beam | 3.4 | 2.2 | 3.1 | |
| Litzenberg et al. | Calypso | ~8 | 1.8 | 7.1 | 5.8 |
| Litzenberg et al. | Calypso (every 2 mins) | ~8 | 1.4 | 1.8 | 2.3 |
| This Study | Calypso | ~8 | 1.3 | 2.3 | 2.8 |
| This Study | Calypso (every 2 mins) | ~8 | 0.5 | 1 | 1.5 |
Mah et al. (20) acquired cine-MRI in the sagittal and axial planes through the center of the prostate for about 9 minutes. They tracked posterior, lateral and superior edges of the prostate relative to initial prostate position. They observed prostate displacements of 0.0±1.5 mm in LR, 0.0±3.4 mm in SI and 0.2±2.9 mm in AP directions. These results are in good agreement with our findings: 0.0±0.7 mm in LR, −0.1±2.4 mm in SI and −0.4±3.9 mm in AP directions, with the considerations of different tracking methods and 20s break between cine-MRI frames. Padhani et al. (21) confirmed correlation between prostate motion and rectal distention and movement using axial cine-MRI. Ghilezan et al. (22) examined prostate motion for both empty and full rectum patient using sagittal cine-MRI, they demonstrated that the status of rectal fillings is the most significant predictor for intrafraction prostate motion. They also demonstrated the increase in probability of prostate displacement with elapsed time. This trend (at least for >3 mm case) can be observed from Figure 3 of this study.
Langen et al. (23) reported intrafraction prostate motion from a 17 patient study using the Calypso system. The maximum percentages of all the patients have 3D displacements >10, >7, >5 and >3 mm were 1.3%, 3.1%, 10.9% and 36.2%, respectively. This is similar to our findings. Langen et al. also reported that, for the patient population, prostate 3D displaced by >3 mm and >5 mm was approximately 14% and 3% of the time, respectively. Similarly, our study (Figure 1) indicates 17.3% and 5.2% of the corresponding displacements. Our fraction of time in each 1 minute interval that the prostate exceeded 3mm in 3D distance increased almost linearly with observation time. However, there was no such trend observed for the cases of 5, 7 and 10 mm excursion distances. Intuitively, these observations indicated that there are both systematic drifts and random excursions of prostate intrafraction motion.
We reported margins of both original prostate trajectories and of different interventional strategies, however, there is a caveat using them without further investigations of other residual error sources, which were not included in these simulations and margin calculation, i.e., isocenter calibration of Calypso system to coincide with machine isocenter; transponder identification in CT images; system localization accuracy (random error in the target alignment); single-point rigid body model used for prostate only (without seminal vesicles) and with no rotation and deformation considerations. All these factors will increase the PTV margins either by increasing its systematic or random components. Thus, these margins mainly served as a comparison metric for different intervention strategies.
Table 4 showed that both the threshold-based and the time-based intervention strategies reduced PTV margins. However, the time-based strategies achieved more margin reductions than the threshold-based strategies. This is due to the fact that time-based approach made corrections in a given time interval to all patients regardless of their prostate locations. This effectively reduced the systematic component of intrafraction motion error for the patient population. On the other hand, threshold-based performance depended on both the preset threshold and patients’ intrafraction motion magnitude. Large margin reductions can be achieved by setting tighter thresholds, although with increased treatment time cost. Selection of time-based or threshold-based strategy for intrafraction prostate motion management depends on many factors in a clinic. i.e., patient load (affordable treatment time for each patient), remote couch shift function availability and understanding of other residual errors in the treatment simulation, target delineation and treatment planning processes.
The margin data in this study are based on regular fractionation (about 30 to 40 fractions) in prostate radiotherapy of a patient population. In a hypo-fractionated prostate radiotherapy, i.e., 5 fractions or less, the distinction between random and systematic error blurs. The increased standard deviation of each fraction caused by time-based correction strategies may play a greater role in patient dosimetry. Using kV imaging sequences from CyberKnife (Accuray, Sunnyvale, CA) hypofractionated intensity modulated radiation therapy (IMRT) treatment for the prostate, Hossain et al. (24) simulated multileaf collimator (MLC) based intensity modulated radiation therapy (IMRT) hypofractionated treatment. They concluded that when sporadic prostate movements greater than 5mm were present in any one direction, significant target underdose was found. Interestingly, in our simulations, although the time-based correction strategies outperformed the threshold based ones in terms of reduction of PTV margins, they introduced a higher degree of “fluctuations” for almost half of the patient population, i.e., patients 4, 13 and 15, etc (Figure 5). These increased fluctuations can be partially explained by the correction interventions made during a transient prostate excursion. For example, passing gas may cause the prostate to deviate temporarily from the aligned position. If a time-based correction were to be made to zero this offset at this moment, then the prostate would be at an offset position, as indicated by the tracking system, and would remain in that offset position until the time of next correction; However, if a threshold-based correction was made, when gas passed, it would respond to this new offset prostate position and zero this offset, if it exceeded the preset threshold. These increased “fluctuations” may increase the “sporadic” motions if the patient is treated with hypofractionation with time based correction. Thus, prostate motion correction strategies during hypofractionated treatment may be patient specific and worth further investigations.
CONCLUSIONS
We analyzed 17 patient prostate interfraction setups and intrafraction motion data acquired by the Calypso system. Online correction largely eliminated the interfraction setup and prostate motion errors in all axes. The systematic and random components of intrafraction prostate motion error were much smaller than those of the interfraction. The corresponding PTV margins were about 2 to 3 mm for 90% of the patient population that receives a minimum dose to the CTV of at least 95% of the nominal dose. It appears that motion in SI direction correlated well with motion in the AP direction with a large range of prostate motion in the AP direction. Several patients in the cohort exhibited significant large motion consistently through treatments. Simulations of threshold-based and time-based strategies revealed that time-based strategies led to smaller PTV margins but longer treatment time, especially with the in-room correction approach. Furthermore, time-based corrections introduce more prostate trace fluctuation for some patients with very active prostate motion. Further investigations of correction strategies and their dosimetric consequences are needed to examine their impact on hypofractionated prostate radiotherapy.
Acknowledgements
This project has been supported in part by NIH grant P01 CA116602 and in part by Calypso Medical, Inc.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest:
None.
REFERENCES
- 1.Byrne T. A Review of Prostate Motion with Considerations for the Treatment of Prostate Cancer. Medical Dosimetry. 2005;30(3):155–161. doi: 10.1016/j.meddos.2005.03.005. [DOI] [PubMed] [Google Scholar]
- 2.Langen KM, Jones DTL. Organ Motion and its Management. Int J Radiat Oncol Biol Phys. 2001;50(1):265–278. doi: 10.1016/s0360-3016(01)01453-5. [DOI] [PubMed] [Google Scholar]
- 3.Balter JM, Wright JN, Newell LJ, et al. Accuracy of a Wireless Localization System For Radiation Therapy. Int J Radiat Oncol Biol Phys. 2005;61(3):933–937. doi: 10.1016/j.ijrobp.2004.11.009. [DOI] [PubMed] [Google Scholar]
- 4.Kupelian PA, Willoughby TR, Mahadevan A, et al. Multi-institutional Clinical Experience with the Calypso System in Localization and Continuous Real-time Monitoring of the Prostate Gland During External Radiotherapy. Int J Radiat Oncol Biol Phys. 2007;67(4):1088–1098. doi: 10.1016/j.ijrobp.2006.10.026. [DOI] [PubMed] [Google Scholar]
- 5.Li HS, Chetty I, Enke CA, et al. Dosimetric Consequences of Intrafraction Prostate Motion. Int J Radiat Oncol Biol Phys. 2008;71(3):801–812. doi: 10.1016/j.ijrobp.2007.10.049. [DOI] [PubMed] [Google Scholar]
- 6.Litzenberg DW, Balter JM, Hadley SW, et al. Influence of Intrafraction Motion on Margins for Prostate Radiotherapy. Int J Radiat Oncol Biol Phys. 2006;65(2):548–553. doi: 10.1016/j.ijrobp.2005.12.033. [DOI] [PubMed] [Google Scholar]
- 7.Willoughby TR, Kupelian PA, Pouliot J, et al. Target Localization and Real-time Tracking using the Calypso 4D Localization System in Patients with Localized Prostate Cancer. Int J Radiat Oncol Biol Phys. 2006;65(2):528–534. doi: 10.1016/j.ijrobp.2006.01.050. [DOI] [PubMed] [Google Scholar]
- 8.Craig T, Moiseenko V, Battista J, et al. The Impact of Geometric Uncertainty on Hypofractionated External Beam Radiation Therapy of Prostate Cancer. Int. J Radiat Oncol Biol Phys. 2003;57(3):833–842. doi: 10.1016/s0360-3016(03)00638-2. [DOI] [PubMed] [Google Scholar]
- 9.Stroom JC, de Boer HC, Huizenga H, et al. Inclusion of Geometrical Uncertainties in Radiotherapy Treatment Planning by Means of Coverage Probability. Int. J Radiat Oncol Biol Phys. 1999;43(4):905–919. doi: 10.1016/s0360-3016(98)00468-4. [DOI] [PubMed] [Google Scholar]
- 10.van Herk M, Remeijer P, Rasch C, et al. The Probability of Correct Target Dosage: Dose Population Histograms for Deriving Treatment Margins in Radiotherapy. Int J Radiat Oncol Biol Phys. 2000;47(4):1121–1135. doi: 10.1016/s0360-3016(00)00518-6. [DOI] [PubMed] [Google Scholar]
- 11.van Herk M, Remeijer P, Lebesque JV, et al. Inclusion of Geometric Uncertainties in Treatment Plan Evaluation. Int J Radiat Oncol Biol Phys. 2002;52(5):1407–1422. doi: 10.1016/s0360-3016(01)02805-x. [DOI] [PubMed] [Google Scholar]
- 12.Malinowski KT, Noel C, Roy M, et al. Efficient use of continuous, real time prostate localization. Physics in Medicine and Biology. 2008;53:4959–4970. doi: 10.1088/0031-9155/53/18/007. [DOI] [PubMed] [Google Scholar]
- 13.Aubry JF, Beaulieu L, Girouard LM, et al. Measurements of Intrafraction Motion and Interfraction and Intrafraction Rotation of Prostate by Three-dimensional Analysis of Daily Portal Imaging with Radiopaque Markers. Int J Radiat Oncol Biol Phys. 2004;60(1):30–39. doi: 10.1016/j.ijrobp.2004.02.045. [DOI] [PubMed] [Google Scholar]
- 14.Kitamura K, Shirato H, Seppenwoolde Y, et al. Three-dimentional Intrafractional Movement of Prostate Measured During Real-time Tumor-tracking Radiotherapy in Supine and Prone Treatment Positions. Int J Radiat Oncol Biol Phys. 2002;53(5):1117–1123. doi: 10.1016/s0360-3016(02)02882-1. [DOI] [PubMed] [Google Scholar]
- 15.McNair HA, Hansen VN, Parker CC, et al. A Comparisonof the use of Bony Anantomy and Internal Markers for Offline Verification and an Evaluation of the Potential Benefit of Online and Offline Verification Protocols for Prostate Radiotherapy. Int J Radiat Oncol Biol Phys. 2008;71(1):41–50. doi: 10.1016/j.ijrobp.2007.09.002. [DOI] [PubMed] [Google Scholar]
- 16.Nederveen AJ, van der Heide UA, Dehnad H, et al. Measurements and Clinical Consequences of Prostate Motion During a Radiotherapy Fraction. Int J Radiat Oncol Biol Phys. 2002;53(1):206–214. doi: 10.1016/s0360-3016(01)02823-1. [DOI] [PubMed] [Google Scholar]
- 17.O'Daniel JC, Dong L, Zhang L, et al. Dosimetric Comparison of Four Target Alignment Methods for Prostate Cancer Radiotherapy. Int J Radiat Oncol Biol Phys. 2006;66(3):883–891. doi: 10.1016/j.ijrobp.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 18.Schallenkamp JM, Herman MG, Kruse JJ, et al. Prostate Position Relative to Pelvic Bony Anatomy based on Intraprostatic Gold Markers and Electronic Portal Imaging. Int J Radiat Oncol Biol Phys. 2005;63(3):800–811. doi: 10.1016/j.ijrobp.2005.02.022. [DOI] [PubMed] [Google Scholar]
- 19.van den Heuvel F, Fugazzi J, Seppi E, et al. Clinical application of a repositioning scheme, using gold markers and electronic portal imaing. Radiotherapy and Oncology. 2006;(79):94–100. doi: 10.1016/j.radonc.2006.03.002. [DOI] [PubMed] [Google Scholar]
- 20.Mah D, Freeman G, Milestone B, et al. Measurement of Intrafractional Prostate Motion using Magnetic Resonance Imaging. Int J Radiat Oncol Biol Phys. 2002;54(2):568–575. doi: 10.1016/s0360-3016(02)03008-0. [DOI] [PubMed] [Google Scholar]
- 21.Padhani AR, Khoo V, Suckling J, et al. Evaluating the Effect of Rectal Distension and Rectal Movement on Prostate Gland Position using Cine MRI. Int J Radiat Oncol Biol Phys. 1999;44(3):525–533. doi: 10.1016/s0360-3016(99)00040-1. [DOI] [PubMed] [Google Scholar]
- 22.Ghilezan MJ, Jaffray D, Siewerdsen J, et al. Prostate Gland Motion Assessd with Cine-Magnetic Resonance Imaging (Cine-MRI) Int J Radiat Oncol Biol Phys. 2005;62(2):406–417. doi: 10.1016/j.ijrobp.2003.10.017. [DOI] [PubMed] [Google Scholar]
- 23.Langen KM, Willoughby TR, Meeks SL, et al. Observations on Real-time Prostate Gland Motion using Electromagnetic Tracking. Int J Radiat Oncol Biol Phys. 2008;71(4):1084–1090. doi: 10.1016/j.ijrobp.2007.11.054. [DOI] [PubMed] [Google Scholar]
- 24.Hossain S, Xia P, Chuang C, et al. Simulated real time image guided intrafraction tracking-delivery for hypofractionated prostate IMRT. Medical Physics. 2008;35(9):4041–4048. doi: 10.1118/1.2968333. [DOI] [PubMed] [Google Scholar]