Finding undetected protein associations in cell signaling by belief propagation

Abstract

External information propagates in the cell mainly through signaling cascades and transcriptional activation, allowing it to react to a wide spectrum of environmental changes. High-throughput experiments identify numerous molecular components of such cascades that may, however, interact through unknown partners. Some of them may be detected using data coming from the integration of a protein–protein interaction network and mRNA expression profiles. This inference problem can be mapped onto the problem of finding appropriate optimal connected subgraphs of a network defined by these datasets. The optimization procedure turns out to be computationally intractable in general. Here we present a new distributed algorithm for this task, inspired from statistical physics, and apply this scheme to alpha factor and drug perturbations data in yeast. We identify the role of the COS8 protein, a member of a gene family of previously unknown function, and validate the results by genetic experiments. The algorithm we present is specially suited for very large datasets, can run in parallel, and can be adapted to other problems in systems biology. On renowned benchmarks it outperforms other algorithms in the field.

Signaling cascades, an exemplar of which is the phosphorylation MAPK kinase pathways, consist of sequential reactions starting at receptor proteins and transmitted through protein interactions to effector proteins. Activation of these effectors leads to cellular changes, notably at the transcriptional level, and results in the adaptation of the cell to its surroundings (1). Identifying signaling pathways is particularly important for medical studies because their malfunction is responsible for many diseases, such as cancer (2) or Alzheimer’s disease (3).

From an engineering point of view, signaling cascades present interesting properties: They provide signal filtering (4) and amplification (5). Their global interconnected organization equips the cell with an integrated sensor network where pathways can modulate one another through crosstalk and retroactions. In this complex system, signal specificity is maintained by scaffold proteins (6, 7) acting as connectors of particular reactions. Finally, the output of the information carried by the transduction network allows for another layer of regulation—namely combinatorial control in gene expression (8). A purely experimental approach to the identification of all components of a pathway, or all components of a functional gene module, would need long and costly experiments. Such a process would greatly benefit from the extraction of indirect information about pathways from producible large-scale data, such as expression, sequencing, and protein interaction data. Indeed, even if the correlation between signaling pathway activity and expression data may be weak (although this may be case-dependent; see ref. 9as an interesting example), expression data are available in shear quantity. By introducing a parameter weighting the relative importance given to expression data with respect to reliable protein–protein interaction data or in general established pathways knowledge, we hope to be able to enrich the existing knowledge by the small amount of information needed to reveal unknown interactions. To this scope, important aspects like the varying reliability of interaction data and the proliferation of alternative paths, require the development of heuristic algorithmic techniques which need to be efficient on large-scale datasets.

Here we propose a method for the inference of hidden components of functional networks and signaling pathways from large-scale transcriptomics and protein interaction data. Such functional networks, composed of proteins acting together in given environmental conditions, are an integrated way of describing information processes in the cell. This problem has enormous potential applications and has already been addressed in several works (10–13), leading to interesting theoretical predictions. In these works, the underlying methodology consists of separately identifying single signaling pathways and then collecting them in an aggregated network. The methodology proposed here attempts instead to extract information on an entire network, defined as a connected subgraph of the full protein interaction network. This technique was roughly sketched in a biological inference context (14). Here we present a complete, in-depth description and analysis of the approach, including in particular algorithmic and experimental validations, and a comparison with results from a previous work along the same lines. We also give full details of the algorithmic framework we use, which may allow implementation of the same ideas to similar systems biology problems.

We state the functional network inference problem in a rather simple and general graphical form. Given a graph G = (V,E)—the protein interaction network (PIN)—with positive costs over edges {c_e: e∈E} and positive prizes over vertices {b_i: i∈V}, find a connected subgraph G^′ = (V^′,E^′) that minimizes the following function:

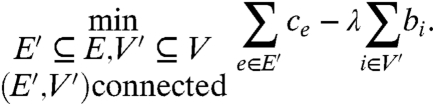[1]

To our purpose the costs of edges c_e are chosen so that high confidence interactions (protein interactions verified in small-scale experiments or found in many large-scale datasets) have lower value with respect to low confidence ones (interactions experimentally shown only once in a large-scale experiment). The node prizes are computed by b_i = - log p_i, where p_i is the p-value of differential expression of node i in the corresponding microarray. The parameter λ regulates the trade-off between the edge costs and vertices prizes, and its value indirectly controls the size of the subgraph G^′.

In spite of its apparent simplicity, the problem of solving Eq. 1, known as the prize-collecting Steiner tree problem (PCST), is computationally intractable (NP-Hard), and heuristic algorithms need to be developed in order to solve instances arising from large datasets. Satisfying the connectivity constraint on the optimization task constitutes a major computational difficulty. The problem remains intractable even in the case in which b_i∈{0,L} for a large L > 0, because this limit case corresponds to the better known minimum Steiner tree problem (MSTT) on graphs, which is also NP-Hard.

Modeling ideas related to our work are discussed in refs. 15–18. These studies rely on different algorithmic techniques—namely on a combination of linear programming relaxation solvers, branch and bounds optimization methods, and preprocessing of the underlying biological network. A detailed comparison shows essentially that the difference in performance between LP-based methods and the one presented here increases dramatically with the problem size. Additionally, the computational cost of our approach scales roughly linearly with the size of the problem, and the algorithm is fully parallelizable. These two facts suggest that the method proposed here may be particularly well-suited to study problems defined on large networks.

The paper is organized as follows: First we present the general problem of identifying optimal subgraphs as a technique for integrating different data types. Then we discuss an algorithmic approach based on belief propagation: We provide benchmark performances together with a specific application to pheromone response data in yeast. Finally, we describe in detail the experimental validation of the predictions relative to the functional role of a family of genes (COS). Complete details are given in SI Appendix.

Results

A Message-Passing algorithm for PCST.

In ref. 19, a statistical physics analysis of the properties of Steiner trees on different ensembles of large random graphs was presented. Here we generalize this work and introduce an algorithm that can be used to identify signaling pathways in transduction PINs. A detailed discussion is given in SI Appendix. Minimizing Eq. 1 gives access to connected networks that include reliable edges and, at the same time, nodes that are significantly differentially expressed (see Fig. 1). This cost function could easily be generalized to other types of interactions; e.g., gene-based information such as results of knockout experiments. Biological priors such as the relative position of proteins (nodes) along the tree or their expected degree could also be easily included in the same scheme.

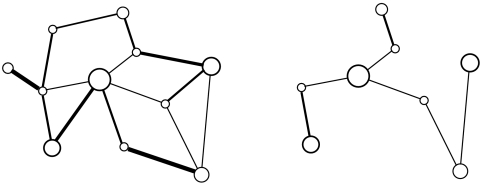
Fig. 1.

An example of a prize-collecting Steiner tree. Larger nodes mean larger prizes; thickness of the edges is proportional to their cost. A prize-collecting minimum Steiner tree (right) picks as many as possible of the larger nodes while simultaneously picking the thinnest links and maintaining connectivity. The analyzed yeast protein network has approximately 5,000 nodes and 22,000 edges.

One main difficulty with an optimization over connected subgraphs is that the connectivity condition is global rather than local; i.e., it can not be verified by a set of simple local checks over the graph. This problem is dealt with here by switching to a richer description of the subgraph that includes an extra variable for each graph node, which essentially denotes when (if ever) nodes would be visited by an algorithm that explores the subgraph from a given starting “root” node. While such representations are in one-to-one correspondence to connected subgraphs, the connectivity condition does have an expression as a set of simple local conditions for the new variables.

The proposed algorithm consists of a set of functional equations for estimating the probabilities that individual links belong to the optimal subgraph at a given distance from the starting node. Such equations can be written in a computationally efficient form that is solved by iteration in a so-called message-passing procedure. The general derivation and other details are given in SI Appendix, whereas the source code is available for download (www.polito.it/cmp). A proof that in certain limit cases the algorithm provides optimal results can be found in ref. 20.

Tests and Data Analysis.

In order to assess the general efficacy of the algorithm, it was tested against the collection of MSTT benchmark problems in the SteinLib dataset (21), which defines the state of the art in the field. Though the benchmarks problems are not of a biological nature, they are both large and difficult to solve and therefore particularly useful for comparing the performance of different algorithms. Quite surprisingly the best-known cost of almost all of the open problems could be improved in a fraction of the computational time (details and complete tables in SI Appendix). Most of the heuristic algorithms with the previously best-known performance are based on linear programming (LP) relaxations complemented with preprocessing of the underlying graph and a branch-and-bound strategy; e.g., ref. 15 (details in SI Appendix). Further direct comparisons between such methods and our approach suggest that already for moderate-sized networks the LP-based methods become highly inefficient (details in SI Appendix).

As a second preliminary test, on biological data, we have compared our technique to another method for the inference of linear signaling pathways based on color coding (11), the optimization criterion of which is a restriction of ours to the edge cost part. We have assessed our algorithm performance relative to ref. 11 with the same data and optimization criterion. Essentially, the same pathways were found much more efficiently (due to the fact that the computational cost does grow only linearly with the chain length and not exponentially as in ref. 11), and it was possible to recover their variability by adjusting the chain length (details in SI Appendix), thereby proving the capacity of our algorithm to recover known biology.

Pheromone Response Data.

Finally, we have applied the algorithm to analyze pheromone sensing on a yeast protein network built by fusion of the Munich Information Center for Protein Sequences (MIPS) (22) and Database of Interacting Proteins (DIP) (23) networks by using 56 large-scale expression datasets created to reconstruct the pheromone pathway experimentally by studying the expression of strains deleted for key genes in the pathway (24). This system was chosen as a case study by virtue of a preexisting good theoretical understanding of its functioning. The pheromone response system is in fact a well-studied MAPK kinase cascade, which permits communication previous to mating in haploid yeasts. Upon sensing a pheromone, the cell cycle is arrested, the cytoskeleton and membrane structure are modified, and finally mating occurs by fusion of two cells of opposite sexual type.

The identification of optimal subnetworks was done for a range of λ values, giving us variable structures going from the backbone of the network to a very detailed picture of each subpathway. The root of the trees was defined to be STE2, the α-pheromone receptor and entrance of the entire pheromone pathway (25, 26).

The biological coherence of our results was assessed by showing that the average number of GO Slim annotations shared between neighbors in the inferred trees is significantly superior to those of random trees (t-test, p < 5.10^-7, see SI Appendix). The results obtained from each one of the 56 expression patterns have been merged, leading to a final network with links that are weighted by their frequency of appearance. For each identified tree there is also a direction associated to each link toward the chosen root (not displayed in Fig. 2 for clarity).

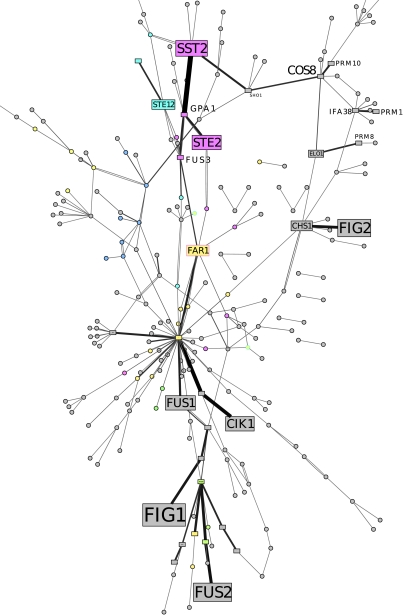
Fig. 2.

This graph is a subnetwork of the protein–protein interaction map, obtained by including nodes that appear more than 30% of the time on the 56 inferred Steiner trees for λ = 0.2, with link intensity proportional to the number of times the specific connection was found and node size proportional to average prize. The layout was decided in order to minimize crossings with the Graphviz suite. Afterwards, colors were added denoting the main GO annotation: actin (light green), cell cycle (yellow), chromatin structure (blue), spindle checkpoint (dark green), cell wall (cyan), and pheromone sensing (magenta). The annotations were obtained from the SGD project Saccharomyces Genome Database http://www.yeastgenome.org/.

The network we found (see Fig. 2) contains known pathways, whose completeness depends on λ. It shows signaling going from STE2, to the cell cycle module (starting from CDC28), proteins involved in cell polarity and cytoskeleton reorganization (RVS161 and RVS167), and another branch containing essentially PRM proteins and proteins involved in sphingolipid synthesis (ELO1) or cell wall (CHS1). A closer look at the structure of the inferred subnetwork shows that it is constituted of two types of proteins: proteins differentially expressed during pheromone response, already discovered by transcriptomic studies, and protein bridging between subparts of the network, while having a stable expression level in these conditions. These proteins, that will be called herein Steiner proteins in reference to Steiner nodes in the MSTT, are not detected by classical transcriptomics but may have an informative or signaling role nonetheless: They allow signal propagation between modules of the transduction network and can be discovered only through a combined analysis of the protein interaction and transcriptomics data.

One such protein we found is COS8, a gene of unknown function, which appears at the head of the third main branch starting from STE2, linking between the standard pheromone pathway and a group of proteins related to membrane structure. To ensure that COS8 frequent occurrence is not due to a bias of our optimization criterion to predict proteins having high connectivity (12), we assessed the statistical significance of the Steiner proteins by bootstrap experiments with noisy costs and prizes. Interestingly, the COS8 protein appears frequently enough to be considered as significant and biologically relevant. Given the interest in uncovering a role for a member of a large gene family in yeast (the COS family contains 11 highly similar members), we therefore attempt to infer its biological role using its neighborhood in the inferred trees.

COS8 is suggested to be the target of the STE2-GPA1-SST2-SHO1 cascade. Because SHO1 is also a sensor involved in the filamentous growth and osmolarity pathway, COS8 could be an actor of more than just the pheromone system and could provide crosstalk between these different pathways. Out of 48 proteins experimentally shown to interact with it, a small subset appear in most simulations, composed of the membrane protein PRM10, the fatty acid elongases ELO1, SUR4, and FEN1—involved in the first steps of sphingolipid synthesis—and other components of the secretion pathway and ceramide synthesis such as AUR1, LAC1 and IFA38. Such homogeneity in the uncovered interactions of COS8, relative to the diversity in the 48 interactants set, allows us to putatively predict both localization and the role of COS8: It should be an endoplasmic reticulum (ER) protein involved in sphingolipid synthesis. Concerning localization, these predictions corroborate the results of a previous study using GFP fluorescence, that localized COS8 either in the ER or the nucleus (27). Moreover, the single hint about COS8 function, uncovered in a large-scale transcriptomic experiment, and not experimentally verified, is an undetermined role in the unfolded protein response, a process occurring in the ER (28), in agreement with our results.

As for the role of COS8, sphingolipids are essential components of the membrane, being part of the lipid rafts microdomains (29). To check the relevance of COS8 for the sphingolipid synthesis, and more generally for membrane structure, we analyzed with the same algorithm another large-scale dataset (30) testing for response to caffeine or rapamycin stress, which are also known to inhibit the TOR pathway (31) and therefore to disrupt membrane structure. Consistently with the pheromone results, COS8 was also detected as a Steiner protein and was significantly enriched in the resulting subgraphs with the same interacting partners. We therefore decided to check experimentally our predictions about COS8 interactions and their putative role.

Experimental Validation.

We proceeded to genetic experiments in strains with disrupted COS8 or containing a plasmid overexpressing (Fig. 3). We tested interactions with the main components of sphingolipid synthesis, in various conditions.

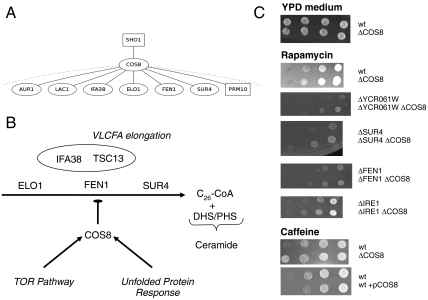
Fig. 3.

(A) The main proteins interacting with COS8 in our signaling tree. Squares stand for membrane proteins. The dotted lines show that many protein interactions are never found in our tree. (B) A global scheme of the putative negative regulatory role of COS8, at the interface between very long chain fatty acid elongation (VLFCA), TOR signaling, and the unfolded protein response (see text). (C) A subset of the genetic experiments showing (i) the rescue of ΔYCR061W, ΔSUR4, ΔFEN1, and ΔIRE1 by ΔCOS8 in rapamycin medium; (ii) the effects of either the disruption or the overexpression of COS8 in a caffeine medium.

We made the ΔCOS8 strain for this study, by replacing the chromosomal copy of this gene by cos8∷LEU2 deletion cassette. For the overexpression study, we cloned COS8 gene in multicopy plasmid pRS426 (with URA3 marker). To obtain double mutants used in this study cos8∷LEU2 deleted BY4741 strain was crossed with a strain from YKO collection (ORF∷KAN). The resultant diploid was dissected and segregants having KAN and LEU2 markers were selected and used for further experiments. Details concerning all the experiments are given in SI Appendix.

We found that deleting COS8 rescued completely the phenotype of ΔFEN1 and ΔYCR061W strains in rapamycin medium—as well as caffeine—and partially the phenotype of ΔSUR4 in the same conditions. Oppositely, a strain overexpressing COS8 is hypersensitive to caffeine and presents the same phenotype as FEN1 deletion. This shows a clear interaction between TOR signaling, COS8, and long chain fatty acid elongation and hints at a negative regulation of very long chain fatty acid (VLCFA) elongation by COS8. As a control experiment, we checked for genetic interactions with IRE1, the master regulator of unfolded protein response, which is the annotated role of COS8 (28), and we also found this interaction (see Fig. 3). Finally, we tested for growth defect in ΔCOS8 strains in media containing myriocin. Myriocin is a very potent inhibitor of serine palmitoyltransferase (32), the first step in sphingosine biosynthesis and slow sphingolipid synthesis. We compared the sensitivity of ΔCOS8 and WT strains to this antibiotic. After 36 h of incubation in liquid YPD media with 0.1 mM of myriocin we observed a transient but clear positive effect of COS8 deletion on cell growth (see Table 1).

Table 1.

OD600 of the WT strain and the ΔCOS8 strain in myriocin and control medium

Strain	Control (SD 0.8)	0.1 mM myriocin (SD 0.45)
WT	20	1.9
ΔCOS8	20.8	6.7

Weak but reproducible increase of myriocin resistance for ΔCOS8 could also be seen on solid YPD media. This can be interpreted if COS8 indeed regulates negatively the sphingolipid production, via VLCFA synthesis: In these conditions the cell growth rate should become dependent on the efficiency of VLCFA elongation, which is less restricted in ΔCOS8 strains, therefore leading to smaller effects of myriocin. We therefore conclude that the function of COS8 is indeed related to sphingolipid metabolism and probably regulates negatively the VLCFA synthesis and therefore the sphingolipid production.

Discussion

Algorithmic predictions and genetic experiments show interactions between sphingolipid synthesis, particularly ceramide, pheromone response, and TOR signaling. Sphingolipids have recently been involved in the TOR-regulated network (33, 34): TOR is able to activate the reaction of synthesis of ceramide from dihydrosphingosine. The molecular mechanisms of this regulation are still unknown but are coherent with our experimental results about a negative role of COS8 in VLCFA elongation, because ΔCOS8 strains are resistant to caffeine and rapamycin—two components known to inhibit the TOR pathway. Because sphingolipids are now known to be both essential membrane components and signaling molecules, understanding the regulation of their synthesis by various pathways, and the potential crosstalk they could provide, is a crucial issue. Here, regulation of sphingolipid synthesis by COS8 would provide the cell with the ability to integrate a signal from the pheromone pathway, the osmolarity pathway, and the TOR pathway in order to modify its membrane structure. Finally, COS8 is a member of a gene family of 11 highly similar members. Further investigations would be needed to identify the functional role of other members of the family, considering that both our predictions and experiments seem to indicate that COS8 has a major effect among all members of the COS family.

Conclusions

We have presented a previously undescribed computational technique, inspired from statistical physics, that can efficiently extract useful information about interactions in signaling pathways (from gene expression and protein–protein data) by solving an appropriately defined optimization problem on graphs. Our method not only provides candidate networks linking proteins of known function, the method also suggests new roles for proteins of previously unknown function. As a test case we specifically predict a functional role for the COS8 protein (a member of a large gene family with yet unknown functional role) both in sphingolipid synthesis and in the TOR pathway in Saccharomyces cerevisiae. We have validated the prediction by providing experimental evidence showing that COS8 is involved in a regulatory loop at the level of ceramide synthesis. Our algorithmic technique has several properties that should make it of significant value to optimization problems in systems biology: efficiency (nearly linear time complexity), simplicity (it is based on a fixed point equation), parallelizability, and the ability to include other biological priors, such as synthetic lethal interactions or phosphoproteomics data. Moreover, the technique outperforms the best-known techniques in the field: We tested it on unsolved instances of the best-known library (SteinLib), and it achieved better optima than were known previously. Finally, it is relatively easy to adapt the technique to a large class of network reconstruction problems, including many which arise in systems biology.

Materials and Methods

Full methods are in SI Appendix. They include: (i) algorithm design (the model, derivation of the message-passing cavity equations, the max-sum limit, computation of marginals, iterative dynamics and reinforcement, a note on directness); (ii) numerical results on benchmark problems and direct comparison with LP-based techniques; (iii) data source and results (including data concerning GO annotation enrichment); (iv) experimental protocols (strains, media and culture conditions, construction of multicopy plasmid with COS8 chromosomal allele, construction of the COS8 deleted strain, construction of double mutants, drug sensitivity assays); and (v) algorithm comparison with previous data.