Quantitative Mitral Valve Modeling Using Real-Time Three-Dimensional Echocardiography: Technique and Repeatability

Abstract

Background

Real-time three-dimensional (3D) echocardiography has the ability to construct quantitative models of the mitral valve (MV). Imaging and modeling algorithms rely on operator interpretation of raw images and may be subject to observer-dependent variability. We describe a comprehensive analysis technique to generate high-resolution 3D MV models and examine inter-operator and intraoperator repeatability in humans.

Methods

Patients with normal MVs were imaged using intraoperative transesophageal real-time 3D echocardiography. The annulus and leaflets were manually segmented using a TomTec Echo-View workstation. The resultant annular and leaflet point cloud was used to generate fully quantitative 3D MV models using custom Matlab algorithms. Eight images were subjected to analysis by two independent observers. Two sequential images were acquired for 6 patients and analyzed by the same observer. Each pair of annular tracings was compared with respect to conventional variables and by calculating the mean absolute distance between paired renderings. To compare leaflets, MV models were aligned so as to minimize their sum of squares difference, and their mean absolute difference was measured.

Results

Mean absolute annular and leaflet distance was 2.4 ± 0.8 and 0.6 ± 0.2 mm for the interobserver and 1.5 ± 0.6 and 0.5 ± 0.2 mm for the intraobserver comparisons, respectively. There was less than 10% variation in annular variables between comparisons.

Conclusions

These techniques generate high-resolution, quantitative 3D models of the MV and can be used consistently to image the human MV with very small interoperator and intraoperator variability. These data lay the framework for reliable and comprehensive non-invasive modeling of the normal and diseased MV.

Two-dimensional echocardiography (2DE) has been the mainstay of preoperative and intraoperative assessment of mitral valve structure and function [1]. Accurate measurement of mitral annular variables by multiplane 2DE is contingent on correct alignment of imaging planes and recognition of anatomic landmarks [2]. Real-time three-dimensional echocardiography (rt-3DE) has the potential to generate manipulable three-dimensional (3D) geometric models of the normal and pathologic MV, and thereby unburden clinical imaging of the MV.

Since the first 3D ultrasound of the heart by Dekker and colleagues in 1974 [3], significant advances have been made in the field of 3D technology. Recent development of matrix-array transducers has made rt-3DE a clinically applicable tool. Multiple studies have shown 3DE to be feasible and accurate at assessing MV anatomy [4–10]. Real-time 3DE obviates the need for obtaining multiple views and aligning imaging planes as required for standard 2DE. As such, the American Society of Echocardiography has proposed a full clinical practice protocol for rt-3DE use [11].

Real-time 3DE has enhanced our understanding of MV geometry and dynamics, has demonstrated that the mitral annulus is not flat but saddle-shaped [12, 13], has allowed investigators to predict leaflet mechanical stress [14], and has impacted MV repair strategies [15, 16]. Several research groups have described techniques for analysis of rt-3DE data that have led to better understanding of the pathophysiology of MV disease [12, 13, 17–22]. However, reconstruction techniques for the MV are multistep and user-dependent and thus prone to variability.

We have developed an analytic technique that uses rt-3DE images to perform a comprehensive quantitative assessment of the MV. This methodology is not influenced by viewing plane selection and therefore enables a clinically relevant and consistent measure of annular, leaflet, and subvalvular pathologic disease. This report describes the 3D analysis techniques and demonstrates their reproducibility.

Patients and Methods

Image Acquisition

Patients with normal MV function and anatomy undergoing cardiac surgery for indications unrelated to the MV were imaged using intraoperative transesophageal rt-3D. The protocol was approved by the University of Pennsylvania School of Medicine Institutional Review Board. All studies were performed after induction of general anesthesia and before initiation of cardiopulmonary bypass. The rt-3DE data sets were acquired through a mid-esophageal view with an iE-33 platform (Philips Medical Systems, Andover, MA) equipped with a 2- to 7-MHz X7-2t transesophageal echocardiography matrix-array transducer. Electrocardiographically gated full-volume images were acquired during four consecutive cardiac cycles. Care was taken to include the mitral apparatus in its entirety throughout the acquisition. The volumetric frame rate was set at 17 to 30 Hz with an imaging depth of 12 to 16 cm. For purposes of interacquisition variability analysis, two images were acquired for the same patient consecutively under similar physiologic conditions (1 to 2 minutes apart).

Repeatability between analysts was studied by subjecting the same echocardiographic image (acquisition) to analysis by two independent observers (n = 8). Repeatability between echocardiographic acquisitions (intraobserver) was studied by subjecting two sequentially collected images to analysis by a single observer (n = 6).

Image Segmentation

Each full-volume data set was exported to an Echo-View 5.4 (TomTec Imaging Systems, Munich, Germany) software workstation for image analysis. This customized software allows for the interactive manipulation including rotation, translation, surface rendering, and measurement of fully 3D data sets. All analysis was performed at midsystole. For interobserver comparison, each observer independently selected a frame at midsystole of each acquisition (n = 8). For interacquisition comparison, the two consecutively acquired images from the same patient were subjected to analysis by the same observer (n = 6).

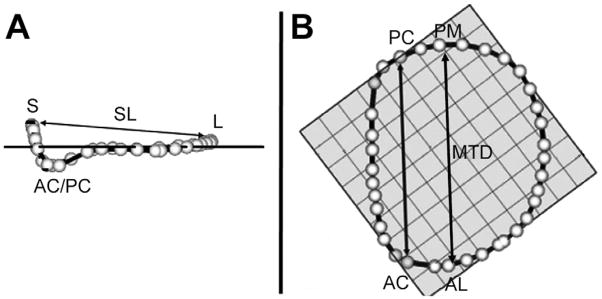
First, the plane of the MV orifice was rotated into a short-axis view. The geometric center of the MV orifice was then translated to the intersection of two long-axis planes corresponding to the intercommissural and septolateral axes of the MV orifice. A rotational template consisting of 18 long-axis cross-sectional planes separated by 10-degree increments was superimposed on the 3D image. Two annular points intersecting each of the 18 long-axis rotational planes were then identified by means of orthogonal visualization of each plane and marked interactively (Fig 1A). The anterior and posterior commissures were defined as annular points at the junction between the anterior and posterior leaflets (middle of commissural region) and interactively identified. The two leaflets were traced separately in parallel long-axis cross-sections, 1 mm apart and sufficient to encompass the entire MV from commissure to commissure (Fig 1B). The coaptation zone between the two leaflets was independently identified in each parallel cross-section view across the entire extent of the MV. The Cartesian coordinates of each point were exported to Matlab (The Mathworks, Inc, Natick, MA) to perform quantitative analysis. Total segmentation time for each valve was 4 to 6 hours.

Fig 1.

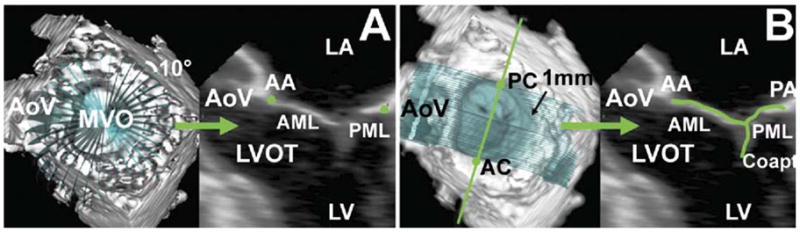
Technique for annular and leaflet segmentation. (A) Annular delineation using rotational cross sections at 10-degree increments, centered on the geometric center of the mitral valve. (B) Leaflet segmentation using transverse cross sections every 1 mm along the intercommissural axis. In each panel, the three-dimensional rendered echocardiographic volume containing the mitral valve is displayed on the left, with cross-sectional planes; the two-dimensional resulting cross section is displayed on the right. (AA = anterior mitral annulus; AC anterior commissure; AML = anterior mitral leaflet; AoV = aortic valve; Coapt = mitral leaflet coaptation; LA = left atrium; LV = left ventricle; LVOT = left ventricular outflow tract; MVO = mitral valve orifice; PA = posterior mitral annulus; PC posterior commissure; PML = posterior mitral leaflet.)

Annular Analysis

The center of gravity of the resultant 36-point annular data set was translated to the origin. The least squares plane of the 3D data set was then calculated by means of orthogonal distance regression, and the annular model was rotated such that the MV orifice plane was aligned with the x–y plane. Anatomic landmarks (Fig 2) were identified: the septum was identified as the anterior horn of the annulus at the aortic valve, anterior commissure and posterior commissure coordinates were superimposed onto the annulus rendering to divide the annulus into anterior and posterior portions, and the lateral annulus was located at the middle of the posterior annulus circumference. Finally, with the annular model rotated such that the commissures were aligned along the y-axis, the maximum and minimum y-values of the annulus were identified as the anterolateral and posteromedial annular points.

Fig 2.

Annular modeling, with intercommissural (A) and transvalvular (B) views of a real-time three-dimensional derived mitral annular model. The 36 annular data points (white spheres) have been included. The least squares plane has been superimposed on the annulus in both views. (A) The graph illustrates the manner in which the septolateral diameter (SL) is determined for each valve. (B) The graph illustrates the manner in which the intercommissural width (CW) and the mitral transverse diameter (MTD) are determined for each valve. (AC = anterior commissure; AL = anterolateral point; L = lateral annulus; PC = posterior commissure; PM = posteromedial point; S = septum.)

Geometric variables were calculated as follows (Fig 2). Septolateral diameter was defined as the distance separating the septum and lateral annulus. Commissural width was defined as the distance between the commissures. Mitral transverse diameter was the widest diameter of the MV and was calculated as the distance between the anterolateral annulus and posteromedial annulus. Mitral annular area was defined as the area enclosed by the two-dimensional projection of a given annular data set onto its corresponding least squares (MV orifice) plane. Mitral annular circumference was defined as the total 3D length of the annulus.

To determine the mean absolute difference between two annuli (MAD_A), both annuli were aligned as described above, and their centers of gravity superimposed. The 3D distance between the two annuli was then measured at 1-degree intervals around the annular circumference, and the MAD_A was calculated as the mean of those distances.

Leaflet Analysis

The leaflet point clouds representing the anterior and the posterior leaflet were then transformed such that their geometric center coincided with the origin and their least-squares-fit plane lay on the x–y plane. To compare two geometric MV models, each was remeshed using a 0.1-mm square grid projected from the x–y plane, and then each was translated and rotated around the z-axis to minimize the mean sum of squares difference in the z-coordinate over the leaflet surfaces. Once two models were thus optimally aligned, a mean absolute z-coordinate distance between the two leaflets (MAD_L, ie, a standard deviation between the paired MV models compared at n_leaflets corresponding points over the surfaces of both leaflets) was calculated as follows:

$${\mathit{MAD}}_L=\sqrt{\sum _{\mathit{leaflets}}\frac{{(z_1-z_2)}^2}{n_{\mathit{leaflets}}}}$$

Data Analysis and Statistics

All continuous data is presented as mean ± standard deviation. Student’s paired t test was used to evaluate for statistically significant difference (p < 0.05) between measurements. Pearson correlation analysis was performed to assess correlation between measurements within each group, presented as Pearson’s correlation coefficient (R). Bland–Altman analysis was performed [23], and mean difference (bias) was calculated; results are presented as bias ± 2 standard deviations. Also, for each annular variable, the percent difference between the two measurements was calculated. All calculations and statistics were performed using Matlab and Microsoft Excel (Microsoft Corporation, Redmond, WA).

Results

Interobserver Comparison

Results for interobserver comparison are summarized in Table 1. The MAD_A and mean absolute distance between paired leaflets were found to be 2.38 ± 0.76 mm and 0.60 ± 0.17 mm, respectively.

Table 1.

Interobserver Comparison

Variable	Observer 1 Mean ± SD	Observer 2 Mean ± SD	p Value	Correlation Coefficient (R)	% Difference Mean ± SD
Commisural width (mm)	33.52 ± 3.17	34.26 ± 3.65	0.67	0.83	4.82 ± 3.00
Septolateral dimension (mm)	29.21 ± 1.42	29.96 ± 3.72	0.60	0.81	7.61 ± 4.46
Mitral transverse diameter (mm)	35.02 ± 2.59	35.72 ± 3.38	0.65	0.91	3.40 ± 2.71
Mitral annular area (mm2)	803.53 ± 101.93	825.33 ± 174.84	0.77	0.88	9.00 ± 7.13
Annular circumference (mm)	107.69 ± 6.45	113.90 ± 17.58	0.36	0.80	7.47 ± 6.57

SD = standard deviation.

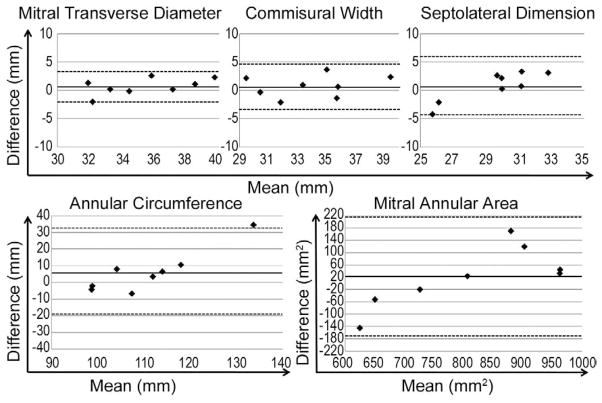
Bland–Altman analysis plots for inter-observer comparisons are depicted in Figure 3. Bias ± 2 standard deviation for various annular variables are as follows: commissural width, 0.74 ± 3.92 mm; septolateral dimension, 0.75 ± 5.39 mm; maximum transverse diameter, 0.70 ± 2.96 mm; mitral annular area, 21.80 ± 195.89 mm²; and mitral annular circumference, 6.21 ± 25.93 mm.

Fig 3.

Bland–Altman analysis: interobserver comparison. For each image, the mean of the two observations (by each observer) is plotted along the x-axis; the difference between the measurements of the two observers is plotted along the y-axis. Solid line indicates bias; dotted lines indicate two standard deviations above and below bias.

Interacquisition Comparison

Results for interacquisition comparison are summarized in Table 2. The MAD_A and mean absolute distance between paired leaflets (Fig 4) were found to be 1.45 ± 0.62 mm and 0.46 ± 0.21 mm, respectively.

Table 2.

Intraobserver Comparison

Variable	Acquisition 1 Mean ± SD	Acquisition 2 Mean ± SD	p Value	Correlation Coefficient (R)	% Difference Mean ± SD
Commissural width (mm)	32.67 ± 2.58	33.47 ± 4.89	0.73	0.93	4.81 ± 5.09
Septolateral dimension (mm)	28.86 ± 2.97	27.89 ± 2.35	0.54	0.54	6.49 ± 5.97
Mitral transverse diameter (mm)	34.65 ± 3.12	34.47 ± 4.24	0.93	0.92	4.17 ± 2.95
Mitral annular area (mm2)	771.12 ± 161.87	757.06 ± 177.13	0.89	0.88	7.55 ± 9.24
Annular circumference (mm)	112.18 ± 20.20	104.80 ± 11.28	0.45	0.87	6.76 ± 7.54

SD = standard deviation.

Fig 4.

Mean Absolute Distance between paired Leaflets (MADL). Leaflet renderings of the two different images (meshed vs shadow) of the same mitral valve traced by the same observer are overlaid after minimizing their mean sum square difference. Agreement between the two renderings is apparent both from a viewing point situated above the posterior commissure (A) and from above the anterior horn of the mitral valve (B). (AL = anterior leaflet; PL = posterior leaflet.)

Bland–Altman analysis plots for intraacquisition comparisons are depicted in Figure 5. Bias ± 2 standard deviation for various annular variables are as follows: commissural width, −0.80 ± 5.36 mm; septolateral dimension, 0.97 ± 5.24 mm; maximum transverse diameter, 0.18 ± 3.72 mm; mitral annular area, 14.07 ± 171.78 mm²; and mitral annular circumference, 7.38 ± 23.66 mm.

Fig 5.

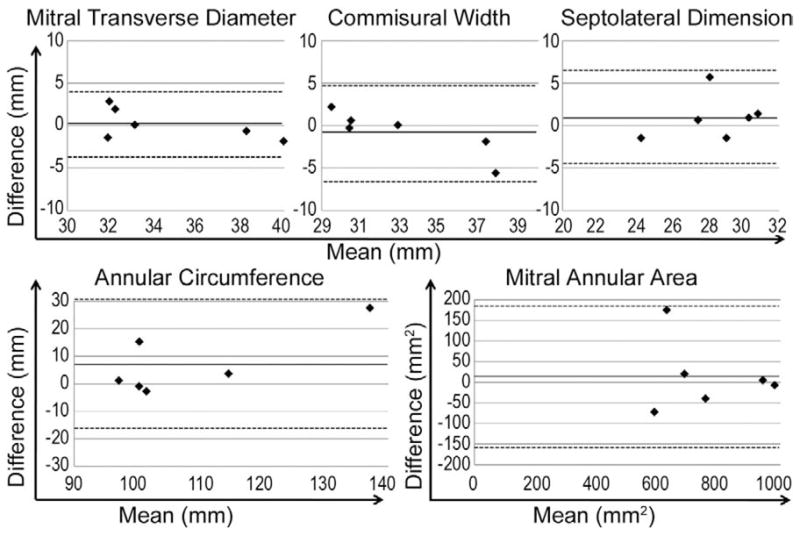
Bland–Altman analysis: intraobserver comparison. For each valve, the mean of the two observations (from two images analyzed by same observer) is plotted along the x-axis; the difference between the measurements obtained from the two images is plotted along the y-axis. Solid line indicates bias; dotted lines indicate two standard deviations above and below bias.

Comment

Fully 3D methods of MV imaging and modeling are emerging as potentially superior methodologies to conventional 2DE. Foster and associates [2], for example, demonstrated that as compared with cardiac computed tomography, conventional 2DE is unreliable for measuring mitral annular geometry owing to imaging plane alignment errors. Although some annular variables (commissural width, septolateral dimension, mitral transverse diameter) can be obtained by 2DE, their accuracy may be compromised by incorrect viewing plane selection or regional valvular asymmetry. Meanwhile, measurement of other variables (mitral annular area, mitral annular circumference, global assessment of annular shape) is unique to 3D imaging approaches. Among novel 3D imaging methods, including cardiac magnetic resonance imaging and cardiac computed tomography, rt-3DE has the distinct advantages of no radiation or magnetic field exposure, no contrast administration, ability to perform transthoracic studies at the bedside, ability to perform intraoperative studies in the operating room, and real-time availability of imaging results. Unfortunately, most of the current literature concerning the clinical utility of rt-3DE in MV function and disease has been limited to visualization of mitral components using image processing capabilities integrated into vendors’ ultrasound modules. The term reconstruction, in particular, seems generous at best and misleading at worst when applied to simple rendering of the mitral leaflets in real time using “on-board” visualization algorithms. However, we are unaware of any attempt at validation of fully 3D modeling of the entire MV including its annulus and leaflets.

The current study describes rigorous geometric reconstruction of the MV from rt-3DE scan data, for invariant measurement of mitral annular and leaflet variables and for construction of a 3D MV model. In the process, this work validates the repeatability of the technique and—in particular—its steps that require human observers. We have developed a new analytic technique that uses rt-3DE images to perform a comprehensive quantitative assessment of all anatomic components of the MV annulus and leaflets. This methodology is not influenced by viewing plane selection, regional asymmetry, or annular dilatation, and therefore represents a potentially useful, clinically relevant, and consistent measure of MV anatomy and pathologic changes. The manual segmentation technique described in this report yields 600 to 1,200 data points on the mitral annulus and leaflet surface. The reconstructed model from this Cartesian coordinate data set is fully quantitative and can be subjected to assessment of standard and unique MV variables. Finally, a high degree of repeatability in the measurement of annular variables with less than 10% variability between two observations—both interobserver and interacquisition—is demonstrated.

This research presents an approach to comparison of 3D MV models using MAD_A and mean absolute distance between paired leaflets. These measures represent global quantitative comparisons to assess geometric similarity. This methodology can also be used to compare more than two valves (ie, to assess the mean variability σ in a group of i = 1 to m MV leaflet models) by modifying the calculations for MAD to the following:

$$\sigma =\sqrt{\sum _{\mathit{leaflets}}\frac{{\displaystyle \sum _i}\frac{{(\overline{z}-z_i)}^2}{m}}{n_{\mathit{leaflets}}}}$$

Although the patients in this study have normal, competent MVs, the techniques are also applicable to pathologic MVs. Furthermore, the technique is not bound by the need to define the coaptation in every segmentation plane; independent identification of the anterior and posterior leaflets will allow for direct anatomic measurement of the regurgitant orifice in incompetent valves. We have recently used this technique to evaluate a cohort of patients with ischemic mitral regurgitation to compare them with a cohort of patients with normal MVs for precise 3D assessment of annular size, annular shape, leaflet tethering, regurgitant orifice, and subvalvular papillary muscle remodeling (M Vergnat, unpublished data).

One limitation of these techniques is the need for time-consuming off-line analysis. Therefore, work is in progress to develop automated segmentation techniques that will allow image processing and MV leaflet segmentation in minutes, rather than hours. The current study lays the framework for validation of such techniques as they are developed and tested.

Three-dimensional MV modeling holds great promise in a number of clinical scenarios. Among them is the description of myxomatous valves before surgical repair for operative planning, and postoperatively for assessment of repair [10]. Several studies have tried to predict recurrent mitral regurgitation after repair of ischemic mitral regurgitation [24–27], but to date the use of 2DE to predict recurrent ischemic mitral regurgitation has not become routine and has not had a positive impact on repair durability. The pathologic anatomy of MV is complex and three-dimensional. Real-time 3DE has the potential to contribute to the assessment of MV anatomy, to the prediction of MV repair durability, and to overcome many of the limitations inherent in 2DE.