High relaxivity MRI contrast agents part 1: Impact of single donor atom substitution on relaxivity of serum albumin-bound gadolinium complexes

Abstract

Rationale and objectives

The donor atoms that bind to gadolinium in contrast agents influence inner-sphere water exchange and electronic relaxation, both of which determine observed relaxivity. These molecular parameters impact relaxivity greatest when the contrast agent is protein bound. We sought to determine an optimal donor atom set to yield high relaxivity compounds.

Methods

Thirty-eight Gd-DOTA derivatives were prepared and relaxivity determined in presence and absence of human serum albumin as a function of temperature and magnetic field. Each compound had a common albumin-binding group and differed only by substitution of different donor groups at one of the macrocycle nitrogens. O-17 relaxometry at 7.05T was performed to estimate water exchange rates.

Results

Changing a single donor atom resulted in changes in water exchange rates ranging across 3 orders of magnitude. Donor groups increased water exchange rate in the order: phosphonate ~ phenolate > α-substituted acetate > acetate > hydroxamate ~ sulfonamide > amide ~ pyridyl ~ imidazole. Relaxivites at 0.47T and 1.4T, 37 °C, ranged from 12.3 to 55.6 mM^-1s^-1 and from 8.3 to 32.6 mM^-1s^-1 respectively. Optimal relaxivities were observed when the donor group was an α-substituted acetate. Electronic relaxation was slowest for the acetate derivatives as well.

Conclusions

Water exchange dynamics and relaxivity can be predictably tuned by choice of donor atoms

INTRODUCTION

Magnetic resonance (MR) imaging contrast agents are unique among diagnostic imaging probes in that the imaging agent is detected indirectly. The contrast agent catalytically relaxes solvent water hydrogen atoms that it encounters, and this relaxation enhancement generates image contrast on T₁- or T₂-weighted images. The extent to which a contrast agent can affect the relaxation rate of tissue water (1/T₁ or 1/T₂) is termed relaxivity (r₁ or r₂) and is given by equation 1, where [CA] is the concentration of the contrast agent.

$$\frac{1}{T_i}=\frac{1}{T_i^0}+r_i\left[CA\right];i=1,2$$ (1)

Tissue has an inherent relaxation rate (1/T₁⁰), so in order to generate readily observable contrast the r₁[CA] product should be at least 10% of the inherent rate. For commercial extracellular fluid agents like Gd-DTPA, r₁ is on the order of 4 mM^-1s^-1 and as a result very large doses of contrast agent are required to affect T₁. Increasing relaxivity would enable contrast-enhanced MRI to be performed at lower doses and may lower the risk of gadolinium (Gd)-induced toxicity. The importance of gadolinium-associated toxicity has been recently emphasized by recognition of an association of Gd-based contrast agents with nephrogenic systemic fibrosis.^1-3 In addition to safety, molecular imaging is driving improvements in relaxivity.^4-7 For a targeted imaging agent, higher relaxivity would allow lower concentration targets to be detected by MRI. Unlike nuclear medicine where the number of photons emitted at a fixed radiochemical concentration is known and constant, relaxivity is not a static effect but depends on the molecular properties of the contrast agent.^8,9

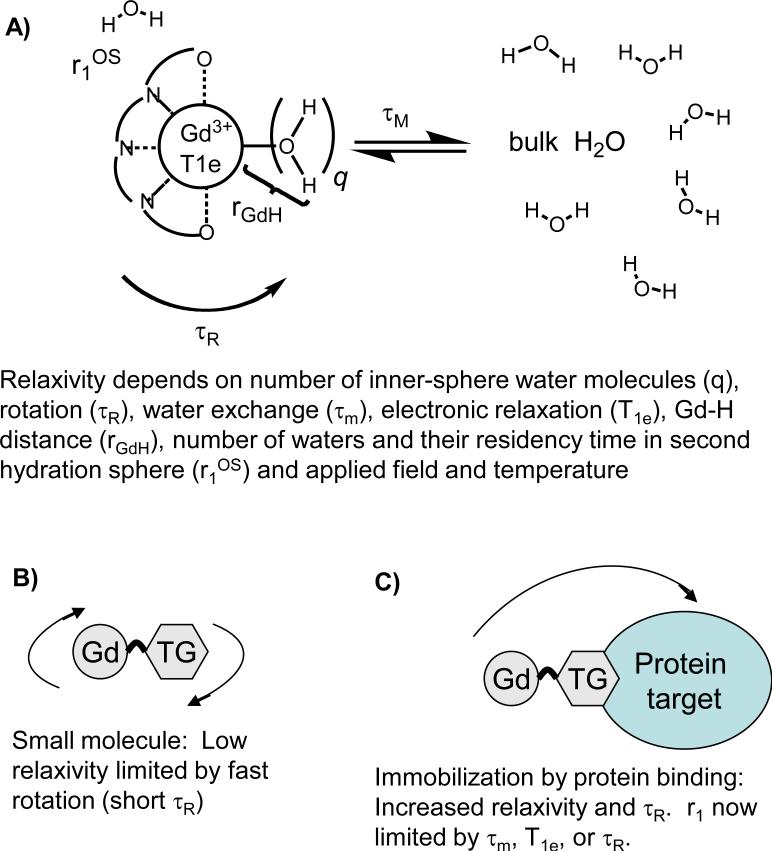
For gadolinium (Gd)-based contrast agents, relaxivity depends on extrinsic factors like applied field and temperature. It also depends on intrinsic factors such as the number of water molecules in the inner-coordination sphere (i.e. directly bonded to the Gd and denoted q), the mean residency time of such water molecules (τ_m whose inverse is the water exchange rate, k_ex = 1/τ_m), the number of water molecules or exchangeable hydrogen atoms in the second and subsequent coordination spheres and their residency times, see Figure 1A. Gd-induced longitudinal relaxation is a dipolar process that depends on the gadolinium to hydrogen distance as the inverse 6^th power (r_GdH^-6). In order to induce nuclear relaxation, the contrast agent creates a fluctuating magnetic field. This fluctuation can arise from the tumbling of the molecule in solution and for compounds tumbling isotropically this is described by a characteristic rotational correlation time, τ_R. The fluctuating field can also be a result of the electrons in the Gd³⁺ ion undergoing excitation and relaxation. At fields of 0.1T and higher, nuclear (hydrogen) relaxation is modulated by the longitudinal electronic relaxation time T1e. Electronic relaxation is also field dependent and 1/T_1e decreases with the square of increasing field. The mechanism for electronic relaxation is transient zero-field splitting (ZFS) modulation where ligand field about the Gd³⁺ ion is transiently distorted due to vibrations and solvent collisions resulting in electronic relaxation. The magnitude of this distortion is given by a term denoted Δ_t² (square of trace of ZFS tensor) and is modulated by a correlation time termed τ_v. The fluctuating field can also be a result of the water molecule coming into contact with the metal complex.

Figure 1.

A) Relaxivity of gadolinium complexes depends on a range of intrinsic molecular factors. B) For fast tumbling complexes, relaxivity is limited by fast rotation and it is not possible to determine how much relaxivity will be increased if rotation were slowed, e.g. by protein binding. C) Relaxivity is increased when the complex is immobilized by binding to a large protein, but other factors may now limit relaxivity.

Relaxivity is obviously a complex phenomenon involving inner-sphere (r₁^IS) and outer-sphere (r₁^OS) mechanisms as explained above. Often the effect due to the inner-sphere water molecule(s) is factored out.^8,9 Inner-sphere relaxivity can be described by a two-site exchange model as shown in equation 2, where T_1m is the T₁ of the bound water molecule. At imaging fields of 0.1T and higher, the relaxation rate of the bound water is given by equation 3 where 1/T_1m depends on several physical constants (C), the Gd-water hydrogen distance (r_GdH), a correlation time for the magnetic fluctuation (τ_c), and the Larmor frequency (ω_H).⁸ The correlation time for the magnetic fluctuation (τ_c) is a function of rotational, electronic and exchange correlation times. The shortest correlation time will dominate τ_c as shown by equation 4.

$$r_1=r_1^{IS}+r_1^{OS}=\frac{q∕\left[H_{2}O\right]}{T_{1m}+{\tau }_m}+r_1^{OS}$$ (2)

$$\frac{1}{T_{1m}}=\frac{C}{r_{GdH}^6}\left[\frac{3{\tau }_c}{1+{\omega }_H^2{\tau }_c^2}\right]$$ (3)

$$\frac{1}{{\tau }_c}=\frac{1}{{\tau }_R}+\frac{1}{T_{1e}}+\frac{1}{{\tau }_m}$$ (4)

For small molecules like Gd-DTPA at clinical field strengths, the relevant correlation time is always the rotational correlation time τ_R which is on the order of 50 – 200 ps at 37 °C.^10,11 When one computes T_1m for such small molecules it is always large (several microseconds) compared to the mean residency time of the water bound to Gd (typically sub-microsecond at 37 °C, so T_1m >> τ_m). The GdH distance has been investigated by electron nuclear double resonance techniques and does not vary significantly amongst all the compounds studied.^12-14 As a result, for small molecules inner-sphere relaxivity is well approximated by equation 5 and depends only on the number of inner-sphere water (q) molecules and the rotational correlation time (τ_R), where C’ is a constant, Figure 1B.

$$r_1^{IS}=C^{\prime }\times q\times {\tau }_R$$ (5)

It is well known that increasing the rotational correlation time, e.g. by protein binding, will increase relaxivity.^9,15 As rotational motion is slowed, relaxivity will begin to be limited by other parameters (Figure 1C). For example τ_m becomes greater than T_1m in eqn 2 or T_1e or τ_m becomes the dominant correlation time in eqn 4. This represents a challenge in identifying new high relaxivity Gd complexes. Simply screening the complexes as small molecules will give results largely dependent on hydration number and molecular weight (proportional to rotational correlation time). While it is possible to measure τ_m and T_1e using other physical methods,^11,13,16-18 it is not obvious whether these parameters will be unchanged when the complex is targeted to a protein. For instance, it has been shown that water exchange can be slowed upon protein binding^19,20 and electronic relaxation may be overestimated in small molecules.^21,22

In this report we describe an approach to identifying high-relaxivity Gd chelates by using a common framework based on the thermodynamically stable GdDOTA complex. Each of the complexes has a common, high affinity serum albumin binder attached via a substituted acetate. One donor group at N7 in the cyclen ring (Figure 2) is varied to explore the effect of donor group on water exchange kinetics, second-sphere hydration, and electronic relaxation and its cumulative effect on relaxivity. The compounds are screened by measuring relaxivity at 0.47 and 1.4T in the presence (immobilized) and absence of human serum albumin. A subset of the complexes are further studied by variable temperature proton nuclear magnetic relaxation dispersion (NMRD) and variable temperature O-17 relaxometry, and the data analyzed to extract the molecular determinants of relaxivity.

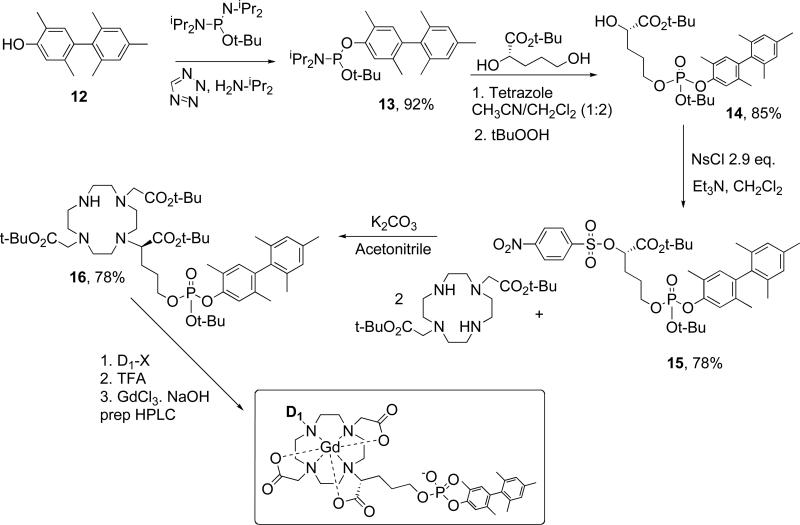
Figure 2.

General synthetic scheme for the compounds described in this report.

MATERIALS AND METHODS

Compound synthesis

Compounds Gd2a, Gd3b and Gd6c were described previously, ^23,24 and the other compounds used in this report have been described in a patent application.²⁵ Here, the synthesis of the advanced intermediate used to prepare all the compounds is described in detail (see Figure 2 for scheme and numbering).

Synthesis of diisopropyl-phosphoramidous acid tert-butyl ester 2,5,2′,4′,6′-pentamethyl-biphenyl-4-yl ester, 13

was achieved using phosphorylation conditions described by Bannwarth.^26,27 Pentamethyl hydroxybiphenyl 12 was synthesized as described previously.²⁸ Biphenyl 12 (3.55 g, 14.8 mmol) was dissolved in anhydrous acetonitrile (40 ml) and tert-butyl tetraisopropylphosphorodiamidite (5.94 g, 19.5 mmol, 1.3 eq.) was added at once. Diisopropylammonium tetrazolide²⁹ (3.80 g, 22.2 mmol, 1.5 eq.) was added at once under argon at room temperature (RT). The reaction was monitored by ³¹P NMR (136.1 ppm: starting material and 131.9 ppm: product) and by thin layer chromatography (TLC). After 5h the solvent was evaporated and the residue was triturated with ether (100 mL). The white precipitate was filtered off and was rinsed with ether (2 × 25 mL). Evaporation of ether gave 8.77 g of crude phosphoramidite, which was purified by short flash chromatography on silica gel (ethyl acetate(EtOAc)/hexane(Hex) 9:1 to 8.5:1.5 to 4:1) to give 6.00 g (92%) of desired phosphoramidite as a white solid.

Synthesis of (S)-5-[tert-Butoxy-(2,5,2′,4′,6′-pentamethyl-biphenyl-4-yloxy)-phosphoryloxy]-2-hydroxypentanoic acid tert-butyl ester, 14

(S)-2,5-dihydroxypentanoic acid tert-butyl ester^30,31 (0.79 g, 4.2 mmol, 1 eq.) and phosphoramidite 13 (1.66 g, 3.7 mmol, 0.9 eq.) were dissolved in 1:2 mixture of acetonitrile/methylene chloride (12 mL) and 4Å molecular sieves (3.5 g) were added under argon. 3% 1H-Tetrazole in acetonitrile (0.32 g, 4.6 mmol, 1.1 eq.) was added at once at –40°C and the reaction mixture was stirred for 4h between –40°C and 15°C. The reaction was monitored by ³¹P NMR (136.5 ppm, s: starting material and 131.0 ppm, d: product). tert-Butylhydroperoxide (1.15 mL, 8.3 mmol, 2eq.) was added and the oxidation was complete (³¹P NMR: -12.8 ppm) in 40 minutes. The molecular sieves and the white solid formed were filtered off and the filtrate was diluted with EtOAc (100 mL) then washed successively with 10% sodium bisulfite (Na₂S₂O₃) twice, with saturated sodium hydrogenocarbonate (NaHCO₃) and with brine. The organic layer was dried over sodium sulfate (Na₂SO₄). Evaporation of solvents gave 3.06 g of crude phosphotriester as an orange-yellow oil that was purified by flash chromatography on silica gel (1% triethylamine in Hexanes/EtOAc 3:1 to 1:1) to give 1.75 g (85%) of desired phosphotriester 14 as a racemic mixture at the phosphorus center.

Synthesis of (S)-5-[tert-Butoxy-(2,5,2′,4′,6′-pentamethyl-biphenyl-4-yloxy)-phosphoryloxy]-2-(4-nitrobenzenesulfonyloxy)-pentanoic acid tert-butyl ester, 15

Compound 14 (2.16g, 3.9 mmol) was dissolved in methylene chloride (50 mL) and triethylamine (1.0 mL, 7.2 mmol, 1.8 eq.) was added at once. 4-Nosyl chloride (2.50 g, 11.3 mmol, 2.9 eq.) was added at once at 0°C and the solution was stirred for 1h at 0°C and was warmed to RT in 2 h. The reaction mixture was washed with saturated NaHCO₃ and the organic layer was dried over Na₂SO₄. Evaporation of solvent gave the crude nosylate as an orange oil, which was purified by flash chromatography on silica gel (0.1% Et₃N in Hexanes / EtOAc 9:1 to 3:1) to give 2.26 g (78%) of desired nosylate 15 as a foaming white solid.

Synthesis of 2-(4,10-Bis-tert-butoxycarbonylmethyl-1,4,7,10-tetraaza-cyclododec-1-yl)-5-(R)-[tertbutoxy-(2,5,2′,4′,6′-pentamethyl-biphenyl-4-yloxy)-phosphoryloxy]-pentanoic acid tert-butyl ester, 16

1,7-DO2A bis-(tert-butyl ester) (2.29 g, 5.7 mmol, 2 eq.) was obtained from Macrocyclics (Dallas, TX) and dissolved in anhydrous acetonitrile (10 mL) and potassium carbonate (K₂CO₃) (0.79 g, 5.72 mmol, 2 eq.) was added under argon. Nosylate 15 (2.10 g, 2.9 mmol, 1 eq.) dissolved in acetonitrile (6 mL) was added dropwise over 50 minutes at room temperature. The mixture was stirred for 25 h and the acetonitrile was evaporated. The residue was triturated in ether (50 mL) and the solid was filtered off. The ether layer was washed successively with 0.5% citric acid (2 × 50 mL), saturated NaHCO₃ (50 mL) and with brine (50 mL). The organic layer was dried over Na₂SO₄. Evaporation of solvent gave 2.37 g of a 8:1 mixture of desired mono phosphate and bis phosphate that was used directly in the next step without any further purification. The pH of the citric acid extracts was adjusted to 9 with saturated NaHCO₃ and then the aqueous layer was extracted with EtOAc (4 × 30 mL). The combined organic fractions were washed with brine (30 mL) and dried over Na₂SO₄. Evaporation of solvent gave 0.86 g of recovered 1,7-DO₂A bis-(tert-butyl ester). MS monophosphate: [M+1]= 931.5; bisphosphate: [M+1]= 1461.7

Synthesis of Gd1g

Alkylation conditions varied depending on the donor group being introduced. However all deprotection and chelation reactions followed a common procedure. Here the synthesis of Gd1g is given as an example. Advanced intermediate 16 (100 mg, 0.11 mmol, 1 eq) and dimethyl bromomalonate (36 mg, 0.17, 1.5 eq.) were dissolved in acetonitrile (0.5 mL). Diisopropylethylamine (40 mL, 0.22 mmol, 2 eq.) was added and the solution was stirred at RT for 24h. The solvent was evaporated under reduced pressure. The residue was re-dissolved in EtOAc. The organic layer was washed successively with water and brine and was dried over Na₂SO₄. The solvent was removed under reduced pressure to give the desired crude protected ligand 1g. MS: [M+1] = 1061.7 The protected ligand (1g) was dissolved in trifluoroacetic acid (TFA)/methanesulfonic acid/phenol (95:2.5:2.5, 2 mL) and the reaction stirred at RT for 2 hr to remove the t-butyl groups. TFA was evaporated and the residue was suspended in water. The pH was adjusted to 12 with 1N NaOH to saponify the ethyl esters. The reaction was monitored by LC-MS. After 4h the reaction mixture was lyophilized to give the crude ligand (1g) as a brown solid. MS: [M+1] = 787.4.

The ligand (1g) was dissolved in H₂O and the pH adjusted to 6 with a 1N NaOH solution. A 245 mM solution of GdCl₃ was added (1 eq based on ligand weight) and the pH adjusted to 6. The reaction mixture was stirred at 45°C for 5 hours and the chelation monitored by LC-MS. EDTA solution was added to chelate the excess Gd³⁺ and the product was purified by preparative-HPLC on a C-18 column using a gradient of 50 mM aqueous ammonium formate and acetonitrile. After lyophilization of the pure fractions, Gd1g (16 mg) was obtained. MS: [M+1] = 961.2 with expected isotopic mass distribution.

Sample preparation and concentration determination

Human serum albumin (Fraction V, Sigma) was dissolved in 50 mM HEPES buffered saline (HBS) of 150 mM sodium chloride content (pH 7.4) to reach a final protein solution of ~6% (w/v). Protein concentration was estimated from absorbance at 280 nm compared to a series of albumin standards (Sigma). This stock solution was used to prepare 4.5% (w/v) HSA solutions (0.67 mM) by appropriate dilution with a gadolinium chelate stock solution (5 – 10 mM) and HBS. For relaxivity determinations, the Gd concentration ranged from 0 – 0.1 mM and for nuclear magnetic relaxation dispersion (NMRD) and protein binding studies the Gd concentration was 0.1 mM. All gadolinium concentrations were determined by inductively coupled plasma mass spectroscopy (ICP-MS) on an Agilent 7500a system.

Ultrafiltration Measurements of Protein Binding

Solutions of 0.1 mM Gd compound and 4.5% HSA (400 μL total) were added to a 5000 MW ultra-filtration unit (regenerated cellulose membrane, Millipore, Bedford, MA). The samples were incubated at 37°C for thirty minutes, placed in pre-warmed centrifuge buckets and centrifuged for seven minutes at 3500G and 37°C using a Jouan GT 4 22 centrifuge. The filtrates were analyzed for gadolinium concentration by ICP-MS. The concentration of bound complex in the protein samples was determined by subtracting the gadolinium concentration (unbound complex) found in the filtrate from the gadolinium concentration of the initial solution. Experiments were performed in duplicate.

Relaxivity

Water proton relaxation rates (1/T₁ and 1/T₂) were determined at 20 MHz (0.47 T) and 60 MHz (1.41 T) using a Bruker NMS 120 Minispec and a Bruker mq60 Minispec, respectively. Samples, 200 μL, were pipetted into glass vials and were equilibrated for at least 20 minutes at 37°C before being measured at 37°C. T₁ was measured with an inversion recovery pulse sequence using 10 different TI times; the pre-acquisition delay was always set to at least 5T₁. T₂ was measured using a Carr Purcell Meiboom Gill (CPMG) sequence with 300 to 500 echoes collected. The ¹H NMRD profiles were recorded at 5°, 15°, 25°, and 35°C on a field cycling relaxometer³² at NY Medical College over the frequency range 0.01-50 MHz (0.0002 – 1.2 tesla). Each dispersion curve consisted of a total of 22 data points.

O-17 NMR

H₂¹⁷O transverse relaxation rates were determined for a PBS buffer solution in the presence and absence of ca. 10 mmolal gadolinium complex (exact concentration determined by ICP-MS) as a function of temperature (-5 – 95 °C) on a Varian Unity 300 NMR operating at 40.6 MHz. Probe temperatures were determined from ethylene glycol or methanol chemical shift calibration curves. T₂ was determined by a CPMG pulse sequence

RESULTS

Synthesis

The t-butyl protected, advanced intermediate 16 shown in Figure 2 was synthesized in 48% overall yield over 4 steps. The pentamethyl hydroxybiphenyl 12 was used previously for serum albumin targeting and was known to provide good affinity when linked to a metal complex via a phosphodiester.²⁸ Phosphoramidite chemistry, similar to what was reported previously^28,33 was used to prepare the phosphodiester 14. The reaction with (S)-2,5-dihydroxypentanoic acid tert-butyl ester is regiospecific for the primary alcohol. Compound 14 was converted to the nosylate for further reaction with protected 1,7-DO2A. The nosylate provided a good balance of reactivity with shelf stability. We used an excess of DO2A to the nosylate (2:1) to favor alkylation of only one nitrogen, but most of the excess DO2A could be recovered.

This advanced intermediate 16 could then be further alkylated at the N7 position with a range of functional groups denoted D₁ in Figure 2. Regioisomers may be prepared if the 1,4-DO2A is used and one example of a regioisomer with 1,4-substitution was synthesized following a similar synthetic protocol but starting from 1,4-DO2A.³⁴ Further conversion to the gadolinium complex followed three common steps: acid deprotection of the tert-butyl groups, neutralization, metallation with gadolinium chloride, then preparative HPLC to give the final purified compound. Compounds were assessed for purity by LC-MS and stock solutions then prepared for biophysical studies with accurate gadolinium concentration determined by ICP-MS.

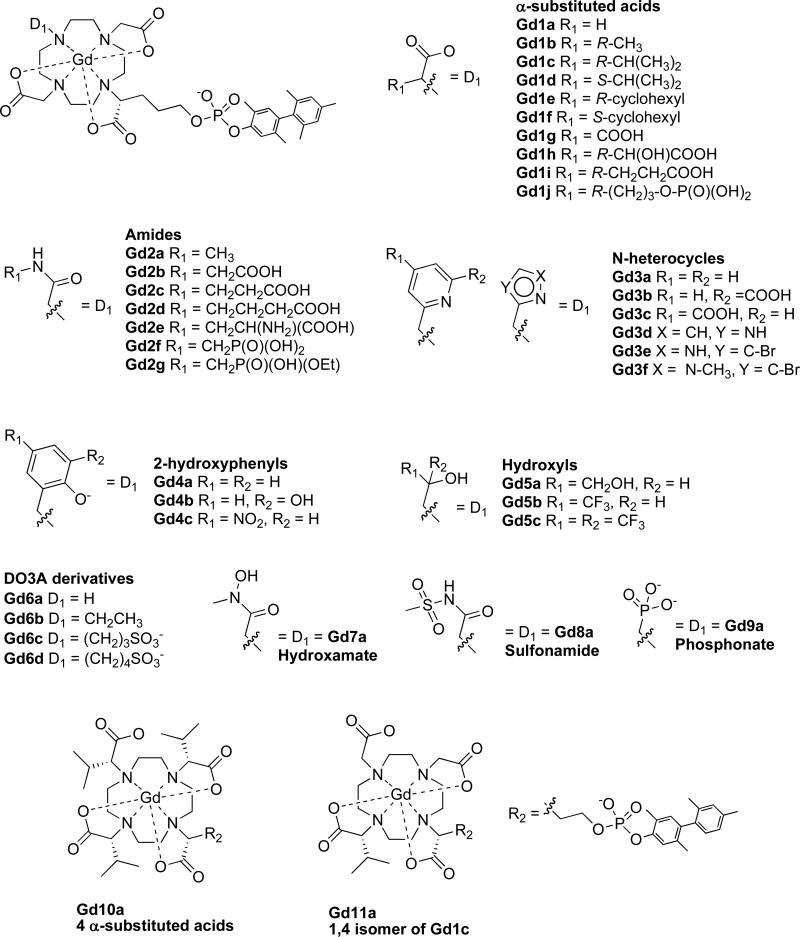
A range of compounds were prepared and analyzed and are shown in Figure 3. A series of alpha-substituted acetates explores whether the size or charge of the substituent influences relaxivity. Two sets of diastereomers Gd1c/Gd1d and Gd1e/Gd1f were also evaluated to determine if chirality at this center influenced relaxivity. A series of amide donors with different substituents was prepared to determine how these substituents may affect relaxivity through second sphere effects. Donor atoms based on basic nitrogen heterocycles (e.g. pyridine and imidazole derivatives) were employed. A series of three hydroxyl donors were prepared with 0, 1, or 2 trifluoromethyl groups alpha to the hydroxyl group in order to assess the role of the electron withdrawing CF₃ group on oxygen coordination to gadolinium and subsequent relaxivity. Examples of negatively charged oxygen atom donors (phenolates, hydroxamate, and phosphonate) were screened as was a negatively charged nitrogen atom donor, the methylsulfonamide, which coordinates Gd via the deprotonated nitrogen. Some examples of compounds without a donor atom for Gd in position N7 were prepared (compounds Gd6a-d) which were expected to have 2 inner-sphere waters. The effect of having 4 substituted acids was explored (Gd10a). Finally the regiochemical isomer of Gd1c (Gd11a) where 1,4-DO2A was used for the synthesis provided an example of the effect this isomerism may have on relaxivity. Of the compounds listed in Figure 3, three were reported previously: Gd2a, Gd3b and Gd6c.^23,24

Figure 3.

Chemical structures of the compounds studied in this report arranged by different donor groups.

Protein Binding

Binding of the complexes to human serum albumin (HSA) was assessed under standard conditions of 0.1 mM complex, 0.67 mM HSA (4.5% w/v), pH 7.4 50 mM HEPES buffered saline (HBS) at 37 °C by ultrafiltration across a membrane with a 5000 MW cutoff. The initial (total) gadolinium concentration and the gadolinium concentration in the filtrate (unbound) were assessed by ICP-MS. The unbound fraction is simply the ratio of unbound:total, and the protein-bound fraction is one minus this unbound fraction. For all the gadolinium complexes in this study, there was greater than 98% of complex bound to HSA under these conditions. These findings suggest that the dissociation constant for the albumin bound complex, K_d < 12 μM for all the compounds studied here. While the various D₁ substituents may alter the albumin affinity, the measurement of full binding isotherms for each compound was beyond the scope of this study.

Relaxivity

Longitudinal proton relaxation rates (R1) were measured in HEPES buffer, pH 7.4, 37 °C at two proton Larmor frequencies, 20 MHz and 60 MHz corresponding to 0.47 and 1.41T, respectively. Measurements were made with gadolinium concentrations ranging from 0 to 0.1 mM and either no HSA or with 0.67 mM HSA. Relaxivity (r₁) was calculated from the slope of the R1 dependence on concentration. Relaxivities in HSA reported are all “observed” relaxivities, i.e. the relaxivity obtained from the R1 dependence and not calculated to reflect the relaxivity of the protein-bound species. However since the fraction bound to HSA is very high under the conditions used (>98%), the observed relaxivity is essentially that of the protein-bound species.

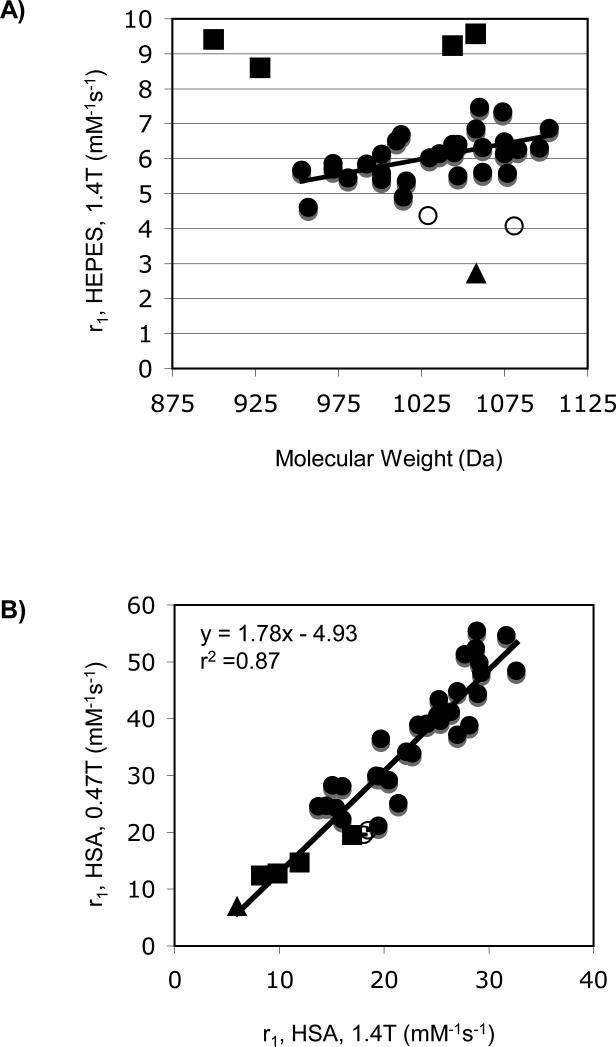
Figure 4a shows the relaxivity of these compounds in HEPES buffer at 1.4T plotted versus molecular weight. As expected, most relaxivities are similar and increase with increasing molecular weight.³⁵ There are clearly some outliers in Figure 4a and these are denoted by different symbols. Gd3b which is contains a pyridyl donor with a carboxylate group ortho to the pyridine is known to be q = 0 (both the pyridine N and carboxylate O atoms coordinate to Gd) and the relaxivity is low as a result.²⁴ The compounds Gd6a-d have D₁ groups that do not coordinate to Gd(III) and are expected to be q = 2 and Gd6c was shown previously to be q = 2.²⁴ The additional inner-sphere water would account for the higher relaxivity. Finally there are some compounds like Gd4a and Gd5c (open circles) that show lower than expected relaxivity but do not appear to be q = 0. They may exist as a mixture of q = 0 and q = 1 species.

Figure 4.

A) Relaxivities determined in HEPES buffer, pH 7.4, 37 °C at 1.4T plotted versus compound molecular weight. B) Relaxivities determined in HSA solution at 37 °C showing the correlation between r₁ at 0.47T (y-axis) and 1.4T (x-axis). Squares represent suspected q = 2 compounds Gd6a-d; triangle is known q = 0 compound Gd3b; open circles are outliers Gd4a and Gd5c.

Figure 4b shows the relaxivity of these compounds in HSA solution with the relaxivity measured at 0.47T plotted versus that at 1.4T. There is a strong correlation between the two albumin bound relaxivities for all compounds. Interestingly the 4 compounds with the highest relaxivity in the absence of protein (Gd6a-d, squares) all have the lowest relaxivity when bound to protein (except for Gd3b which is q = 0). Previously it was shown that the two inner-sphere water molecules in Gd6c were displaced by a protein side chain upon binding to HSA.²⁴ It is likely that protein side chain from a glutamate or aspartate residue is displacing the inner-sphere water molecules in Gd6a, Gd6b, and Gd6d. Similar effects have been reported for other q = 2 complexes non covalently bound to albumin.³⁶

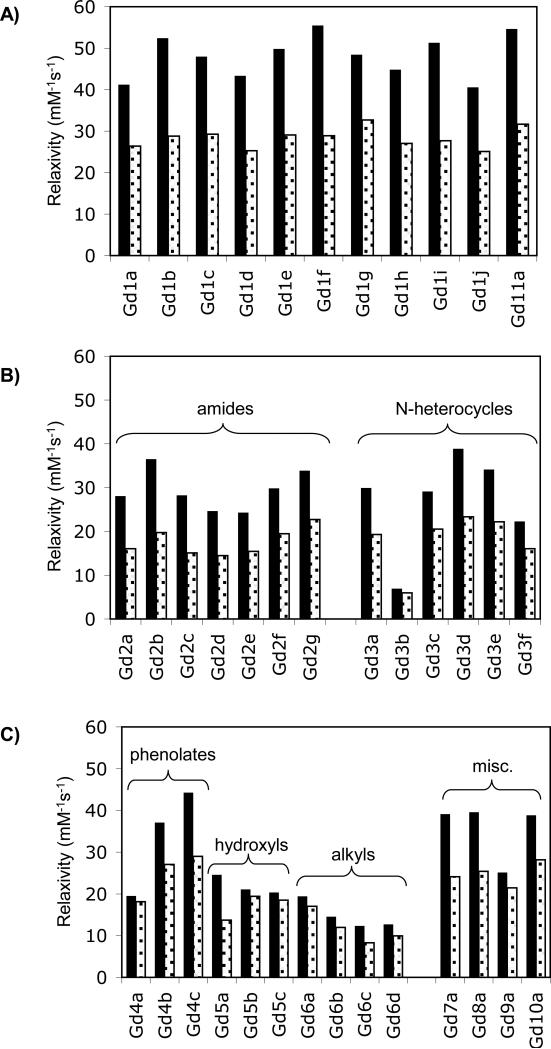
Figure 5 shows the relaxivities measured in HSA plotted according to donor type. The highest relaxivities at both fields were seen with the alpha-substituted acetates, Figure 5a. Relaxivities as high as 55.5 mM^-1s^-1 (Gd1f) at 0.47T and 32.6 mM^-1s^-1 (Gd1g) at 1.4T were observed. There were small differences among the different substitutions. For instance the diasteromeric pairs Gd1c and Gd1d or Gd1e and Gd1f showed some difference in relaxivities that were mainly evident at 0.47T. The regioisomers Gd1c and Gd11a also showed some differences. However as a class, all of these alpha-substituted acetates showed higher relaxivity than the other donor types.

Figure 5.

Relaxivities determined in HSA solution (0.1 mM Gd, 0.67 mM HSA) at 37 °C at 0.47T (black bars) and 1.4T (grey bars). A) Alpha-substituted acetate donors; B) Amide and N-heterocycle donors; C) all other donor groups.

The amide group (Figure 5b) showed lower relaxivities, but there were sharp differences among the amide substituents. For instance going from N-CH₃ (Gd2a) to N-CH₂COOH (Gd2b) resulted in an increase of 30% in relaxivity, but an additional methylene unit N-CH₂CH₂COOH (Gd2c) showed similar relaxivity to the N-CH₃ derivative. The N-methylenephosphonate derivatives (Gd2f and Gd2g) also showed higher relaxivity relative to the N-methyl suggesting that there may be an additional second-sphere contribution to relaxivity arising from exchangeable hydrogen (waters) with long residency times (>1 ns) in the second coordination sphere. This second-sphere contribution in tetra-substituted amides has been noted before.³⁷

Of the nitrogen heterocycles, the best example for relaxivity was the imidazole derivative Gd3d. The phenolate donor gave good relaxivity for the para-nitro derivative Gd4c but rather poor relaxivity for the unsubstituted phenolate Gd4a (Figure 5c). The hydroxyl derivatives all showed rather low relaxivity. The alkyl substituted compounds had quite low relaxivity as discussed above and this is likely a result of them being q = 0 when bound to protein. Finally the hydroxamate (Gd7a), sulfonamide (Gd8a), and tetra(alpha-substituted) acid (Gd10a) derivatives showed intermediate relaxivity. When D₁ was methylphosphonate, the relaxivity was low.

Nuclear Magnetic Relaxation Dispersion (NMRD)

Nuclear magnetic relaxation dispersion (NMRD) is a measure of longitudinal relaxivity (or relaxation rate) as a function of magnetic field or Larmor frequency. To better understand the differences in relaxivity among these compounds, NMRD profiles of 26 of these compounds (0.1 mM) in HSA solution (0.66 mM, pH 7.4) were recorded each at 4 temperatures: 5, 15, 25, and 35 °C. The HSA solutions alone also show a field dependence on relaxation rate.³² The NMRD relaxivity was calculated for each magnetic field and temperature using equation 1, and subtracting the appropriate diamagnetic relaxation rate for HSA solution at that same field and temperature.

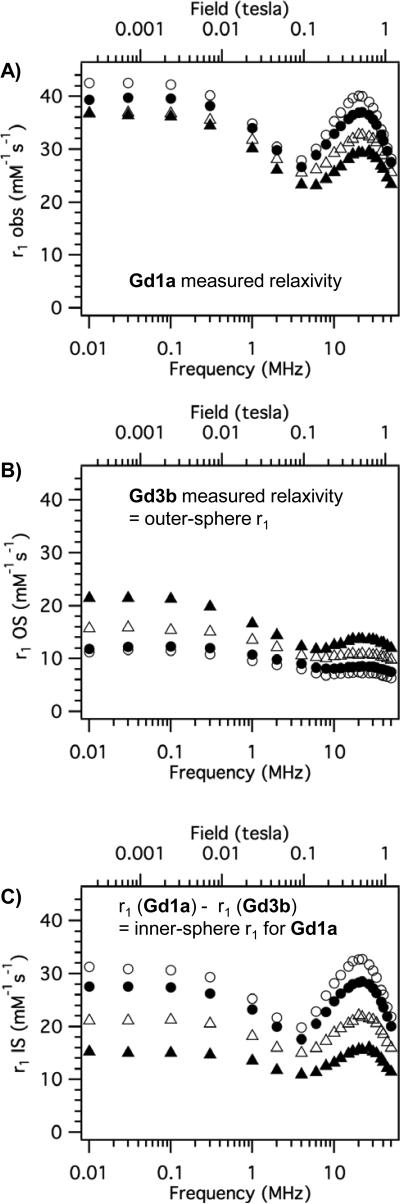
Examples of NMRD relaxivities in HSA solution are shown in Figure 6a and 6b for compounds Gd1a and Gd3b, respectively. As discussed above, it is convenient for the purpose of analysis to factor relaxivity into contributions arising from the inner-sphere water and from contributions from second-sphere and outer-sphere water. It was assumed that the contributions to relaxivity arising from second- and outer-sphere water could be estimated from the relaxivity of Gd3b in HSA, since it contains no inner-sphere water. The relaxivity of Gd3b then was subtracted from the relaxivity of each compound at the corresponding temperature and field strength. As an example, Figure 6c shows this difference for Gd1a, which reflects the inner-sphere contribution to relaxivity for Gd1a. The inner-sphere relaxivity of Gd1a decreases with decreasing temperature. This indicates that the system is in slow exchange (T_1m < τ_m) and that analysis of this data should provide an accurate estimate of the water residency time τ_m.

Figure 6.

A) Variable temperature NMRD profile for Gd1a in HSA solution. B) Variable temperature NMRD for q = 0 complex Gd3b in HSA solution. C) Estimated inner-sphere relaxivity of Gd1a obtained by subtracting each curve in B from corresponding curve in A. t = 35 °C (open circles); t = 25 °C (filled circles); t = 15 °C (open triangles); t = 5 °C (filled triangles).

The variable temperature NMRD data was analyzed as follows. First, the higher field NMRD data only were considered (ν_H ≥ 6 MHz). At these fields, the contribution to electronic relaxation from the static zero-field splitting (ZFS) is negligible and use of modified Solomon-Bloembergen-Morgan theory is appropriate.^38,39 We found it necessary to apply the Lipari-Szabo modification of the spectral density term to account for internal motion.⁴⁰ At these proton frequencies (6 MHz and up), the contribution to relaxation dependent on the electronic Larmor frequency, ω_s, has dispersed and the relaxation of the inner-sphere water is given by equation 6

$$\frac{1}{T_{1m}}=\frac{2}{15}\left(\frac{{\mu }_0}{4\pi }\right)\frac{{\gamma }_H^2{g}_e^2{\mu }_B^{2}S(S+1)}{r_{GdH}^6}\lfloor \frac{3F^2{\tau }_c}{1+{\omega }_H^2{\tau }_c^2}+\frac{3(1-F^2){\tau }_f}{1+{\omega }_H^2{\tau }_f^2}\rfloor$$ (6)

where τ_f is a correlation time that takes into account fast local motion (1/τ_f = 1/τ_c + 1/τ_l) and τ_l is a correlation time for fast motion; F² is an order parameter (often denoted S², but here F is used to avoid confusion with the spin quantum number). ω_H is the Larmor frequency of the proton (rad/s), γ_H is the proton magnetogyric ratio, g_e is the electronic g-factor (g_e = 2 for Gd(III)), μ_B is the Bohr magneton, and μ₀ is the permittivity of vacuum. The field dependence on T_1e is given by equation 7.

$$\frac{1}{{\mathrm{T}}_{1\mathrm{e}}}=\frac{{\Delta }_t^2[4S(S+1)-3]}{25}\left[\frac{{\tau }_v}{1+{\omega }_s^2{\tau }_v^2}+\frac{4{\tau }_v}{1+4{\omega }_s^2{\tau }_v^2}\right]$$ (7)

The various correlation times should all be temperature dependent, however we found that because rotation is already slow because of protein binding and did not limit relaxivity, the data could be well fit with a single, temperature independent τ_R (i.e. the temperature dependence on τ_R was not well defined). Similarly it is known from previous work that τ_v has a weak temperature dependence^11,21 and we found that all the variable temperature NMRD data could be well fit with a single τ_v. We also found that the data was insensitive to the fast internal motion correlation time τ_l, which was always very short (≤100 ps). Under these conditions the (1-F²)τ_f/(1+ω_H²τ_f²) term tends to zero and introducing a term for the temperature dependence of τ_l is meaningless. The data are however very sensitive to τ_m and its temperature dependence is given by equation 8 where τ_m³¹⁰ is the water residency time at 37 °C and ΔH^‡ is the activation energy for water exchange.

$$\frac{1}{{\tau }_m}=k_{ex}=\frac{T}{310.15{\tau }_m^{310}}\left[\frac{\Delta H^{◻}}{R}\left(\frac{1}{T}-\frac{1}{310.15}\right)\right]$$ (8)

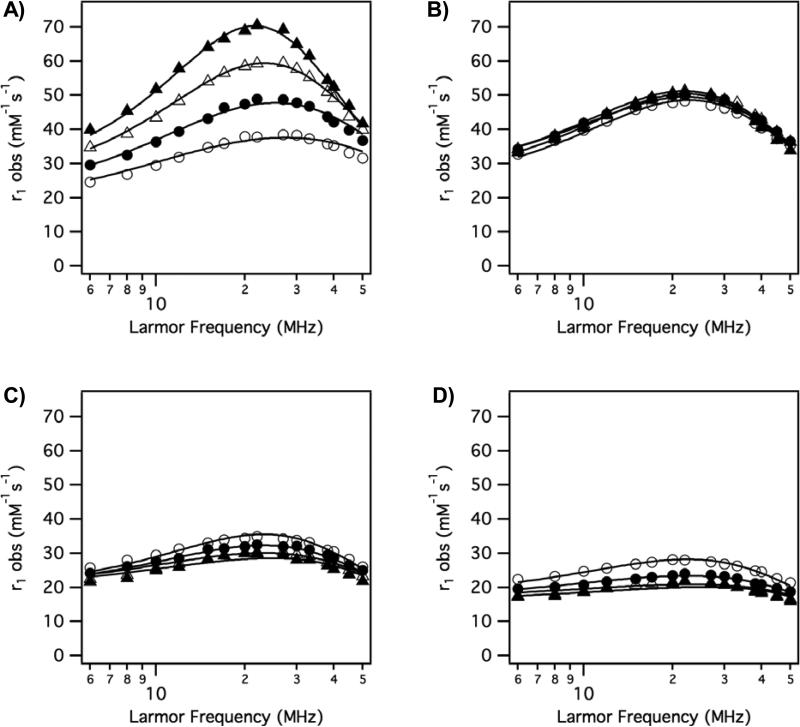
Altogether the variable temperature NMRD data (4 temperatures, 60 data points) could be well fit using 6 parameters: τ_R, τ_v, τ_m³¹⁰, ΔH^‡, Δ², and F². NMRD data for each compound was simultaneously fit to equations 2, 6, 7, and 8 with the relaxivity of Gd3b assumed to be equal to the contribution to relaxivity from second/outer-sphere water. Examples of the observed NMRD relaxivities and the fitted data are shown in Figure 7. Figure 7 shows the range of behaviors encountered. Figure 7A shows relaxivity of Gd4b (phenolate donor) where the relaxivity is increasing as temperature decreases. This indicates that the system is in fast exchange (T_1m > τ_m). At 5 °C very high relaxivities were observed with this compound but at 35 °C, relaxivity appears limited by water exchange that is too fast. Figure 7B shows data for the alpha-substituted (isopropyl) acetate derivative Gd1c. Here relaxivity is high and practically independent of temperature. Recall from Fig 6B that the second/outer-sphere relaxivity is increasing as temperature decreases, and so the inner-sphere component must actually decrease slightly with decreasing temperature. Figure 7C shows data for the hydroxamate derivative Gd7a. The relaxivities are lower and the highest relaxivities are observed at 35 °C. This suggests this system is limited by slow water exchange, since as the temperature is lowered τ_m will increase and dominate the (T_1m + τ_m) term. Figure 7D shows NMRD data for the amide derivative Gd2c. This is one of the lowest relaxivities observed and again, the relaxivity decreases with decreasing temperature, suggesting relaxivity limited by slow water exchange. The very flat NMRD profile at lower temperatures is also typical of a system dominated by very slow exchange.

Figure 7.

Representative variable temperature (t = 35 °C (open circles); t = 25 °C (filled circles); t = 15 °C (open triangles); t = 5 °C (filled triangles)) NMRD with solid lines as fits to the data as described in the text. A) Gd4b; B) Gd1c; C) Gd7a; D) Gd2c

In total, NMRD data for 25 compounds was analyzed. The results of these six parameter NMRD analyses are given in Table 1 along with the estimated standard deviation for each parameter in parentheses. The water residency time at 37 °C (τ_m³¹⁰) ranged from 0.7 to 612 ns, or over three orders of magnitude. In Table 1 the mean parameter values for all 25 compounds are listed along with relative standard deviations (RSD). There is wide variability in the water residency times, but much less variation among the other parameters. The values of τ_R are in the range reported for other complexes non-covalently bound to serum albumin.^21,41,42 It was necessary to use the Lipari-Szabo approach, although the correlation time for fast motion could not be determined accurately and only an upper limit of 0.1 ns could be given. The values of τ_v are also similar to reported numbers for these types of gadolinium complexes.^11,43,44 The Δ² numbers are much smaller by a factor of 3-5 than what is typically reported for fast tumbling GdDOTA derivatives, i.e. electronic relaxation of the protein bound compounds is slower than may have been anticipated from the literature. This inconsistency may arise from the use of approximate theories for the relaxivity of small complexes where the effect of the static ZFS is neglected. It has been shown that when the fast rotational motion is included as source of modulation of static ZFS, smaller Δ² values are always obtained.²² Furthermore, more thorough analyses of multifrequency EPR and NMRD of [Gd(DOTA)(H₂O)]^2- which take static ZFS into account show lower values of Δ².^16,17,45

Table 1.

Molecular parameters derived from simultaneous fitting of variable temperature NMRD of albumin-bound gadolinium complexes. See text for details. Numbers in parentheses represent one standard deviation. RSD = relative standard deviation.

	τR (ns)	τm310 (ns)	τv (ps)	ΔH‡ (kJ/mol)	Δ2 (1018 s-2)	F2
Gd1a	4.3 (0.2)	108 (14)	18 (2)	42.2 (2.5)	2.80 (0.14)	0.49 (0.02)
Gd1b	3.7 (0.2)	34.1 (6.7)	22 (3)	42.3 (4.2)	3.39 (0.12)	0.46 (0.01)
Gd1c	4.3 (0.2)	16.4 (1.8)	19 (2)	43.7 (2.8)	3.23 (0.09)	0.56 (0.01)
Gd1d	5.1 (0.2)	49.2 (2.5)	19 (1)	56.2 (1.2)	3.85 (0.07)	0.59 (0.01)
Gd1e	4.2 (0.2)	19.8 (2.6)	20 (2)	31.6 (3.3)	3.45 (0.08)	0.54 (0.01)
Gd1f	5.7 (0.2)	75.3 (.57)	18 (1)	41.3 (1.6)	3.97 (0.11)	0.68 (0.01)
Gd1g	4.7 (0.2)	9.8 (0.7)	18 (1)	43.3 (2.4)	3.56 (0.09)	0.54 (0.01)
Gd1h	4.3 (0.2)	37.6 (4.3)	21 (2)	47.9 (2.5)	3.93 (0.10)	0.52 (0.01)
Gd1i	3.8 (0.2)	24.0 (3.7)	21 (3)	47.9 (3.5)	3.36 (0.11)	0.46 (0.01)
Gd1j	3.9 (0.2)	64.7 (8.9)	21 (2)	40.1 (2.8)	3.33 (0.11)	0.48 (0.01)
Gd2b	7.6 (1.9)	441 (67)	17 (3)	31.3 (3.0)	4.47 (0.73)	0.62 (0.14)
Gd2c	11.6 (6.5)	579 (99)	18 (5)	30.9 (3.4)	5.97 (1.68)	0.8 (0.34)
Gd2d	11.4 (5.9)	570 (92)	17 (4)	30.6 (3.2)	5.71 (1.46)	0.8 (0.32)
Gd2f	13.8 (7.3)	536 (91)	18 (4)	23.9 (2.9)	6.22 (1.57)	0.8 (0.32)
Gd3a	7.7 (3.0)	499 (108)	21 (3)	10.8 (2.9)	7.9 (2.2)	0.8 (0.31)
Gd3c	7.2 (1.9)	612 (86)	28 (7)	13.4 (2.1)	10.4 (2.5)	0.72 (0.20)
Gd3f	5.0 (0.6)	574 (74)	28 (3)	33.3 (4.6)	7.1 (1.0)	0.53 (0.09)
Gd4a	20 (9.8)	0.7 (0.1)	26 (3)	34.9 (2.4)	5.56 (0.24)	0.48 (0.01)
Gd4b	17.2 (6.2)	1.9 (0.1)	23 (2)	30.5 (2.7)	4.20 (0.10)	0.62 (0.01)
Gd4c	11.0 (1.9)	2.4 (0.1)	25 (2)	33.8 (2.9)	4.32 (0.11)	0.61 (0.01)
Gd7a	6.2 (1.4)	281 (71)	17 (3)	23.2 (4.1)	4.82 (0.72)	0.60 (0.12)
Gd8a	8.0 (2.1)	370 (60)	16 (3)	32.1 (3.2)	4.84 (0.75)	0.66 (0.14)
Gd9a	7.0 (2.7)	1.4 (0.1)	30 (6)	27.4 (4.1)	4.94 (0.36)	0.53 (0.01)
Gd10a	5.6 (1.0)	2.1 (0.1)	24 (3)	31.2 (4.1)	4.00 (0.15)	0.69 (0.01)
Gd11a	4.2 (0.2)	54 (12)	19 (2)	24.5 (3.9)	3.20 (0.13)	0.69 (0.02)
Mean	7.5	199	21	33.9	4.74	0.61
Std dev	4.4	238	4	10.5	1.75	0.11
RSD	58%	120%	19%	31%	37%	18%

The most uncertainty in the fitted parameters arose for compounds where water exchange was either very fast or very slow. In the former case, the short residency time τ_m is the dominant correlation time for relaxation (see equation 4). As a result, the NMRD profile is less sensitive to the slow rotational correlation time and τ_R is less well defined. On the other extreme, when water exchange is very slow (τ_m > T_1m), the NMRD profile is not very sensitive to the relaxation time of the bound water molecule (T_1m) and as a result τ_R, τ_v, and Δ² are less well defined. Nonetheless the fact that similar τ_R values are obtained among all 25 compounds appears to validate the use of a common albumin-binding group to immobilize these complexes.

Oxygen-17 relaxometry

Typically water exchange rates at gadolinium complexes are estimated from the temperature dependence of the O-17 transverse relaxation rate of bulk water in the presence and absence of the complex. The O-17 technique is generally not sensitive enough to measure water exchange of protein-bound complexes. This is because of solubility limitations of the protein and also because the baseline relaxation rate of water in concentrated protein solution is already quite high. Although it has been shown that protein-binding can alter the water exchange rate of the complex,²⁰ a series of O-17 studies was performed without HSA to determine if the same general trends in water exchange rate were seen in the absence of protein.

The data treatment has been amply described previously.²¹ For Gd³⁺ complexes, where the paramagnetic chemical shift of the bound water is small compared to its transverse relaxation time, the so-called reduced relaxation rate (1/T_2r) is given by equation 9, where R_2p and R_2d are the relaxation rates measured in the presence and absence of gadolinium complex, respectively.

$$\frac{1}{T_{2r}}=\frac{(R_{2p}-R_{2d})}{(q∕\left[H_{2}O\right])}=\frac{1}{T_{2m}+{\tau }_m}$$ (9)

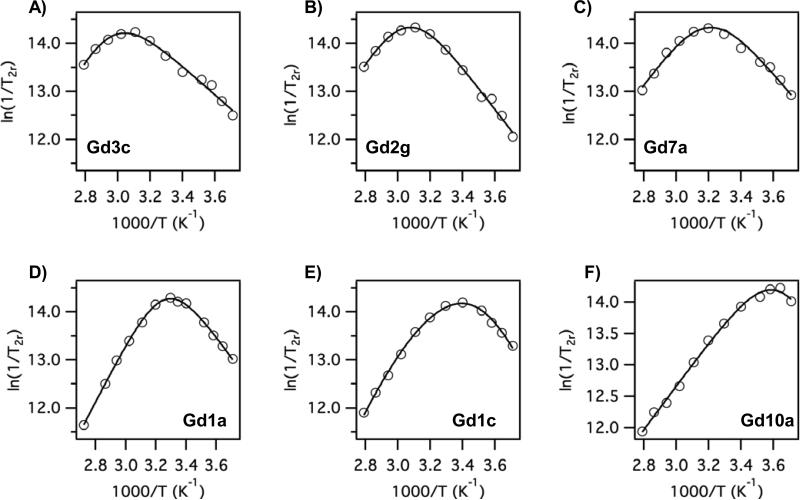
At low temperatures where the slow exchange limit (τ_m >> T_2m) is reached, the reduced relaxation rate becomes the water exchange rate, i.e. 1/T_2r = 1/τ_m. Figure 8 shows variable temperature O-17 data for 6 compounds where the water exchange rate is increasing from Figure 8A through 8F. The maximum (where τ_m = T_2m) moves increasingly to lower temperatures from Fig 8A through to 8F, and if one inspects the low temperature limit (right side, slow exchange limit) of each graph, it is obvious that the water exchange rate is increasing through this series. The donor atom series in Figure 8 from A to F is pyridyl, amide, hydroxamate, acetate, substituted acetate, and then Gd10a, which has 4 substituted acetate donors. The water exchange parameters are listed in Table 2 and are in reasonable agreement with those estimated for the protein-bound complexes.

Figure 8.

Reduced O-17 T2 relaxation rates versus reciprocal temperature (symbols) and fits to estimate water exchange parameters determined in the absence of HSA. A) Gd3c; B) Gd2g; C) Gd7a; D) Gd1a; E) Gd1c; F) Gd10a

Table 2.

Water exchange parameters determined from variable temperature O-17 NMR relaxation data on gadolinium complexes in the absence of protein.

	Gd1a	Gd1c	Gd2f	Gd3f	Gd7a	Gd10a
τm310 (ns)	85 (17)	46.5 (3.3)	622 (51)	777 (64)	330 (50)	9.1 (0.4)
ΔH‡ (kJ/mol)	56.1 (2.9)	56.4 (0.7)	34.4 (1.9)	22.7 (2.0)	31.6 (3.2)	26.1 (1.3)

DISCUSSION

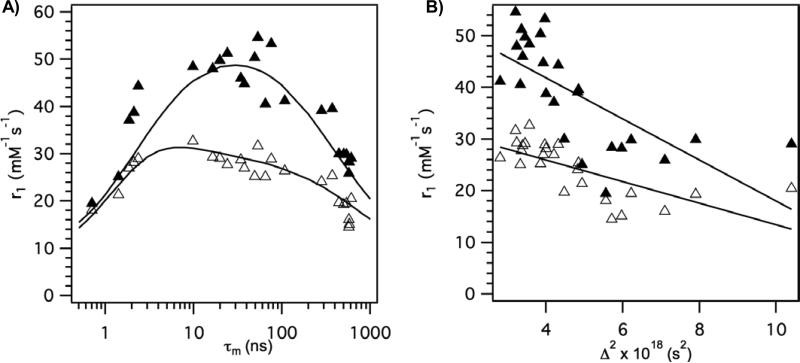
The overall approach to identifying high relaxivity compounds appears justified. The derivatives where the D₁ group was an alpha-substituted acetate gave the highest relaxivities at both fields. Relaxivities in the 45 – 55 mM^-1s^-1 range at 0.47T and 26 – 32 mM^-1s^-1 at 1.4T were observed with this group. Other donor atom substitutions either made water exchange too fast or too slow. In Figure 9A the measured relaxivities at both fields are plotted versus τ_m values obtained from the NMRD fits. The observed behavior is exactly as predicted by theory wherein there is an optimal range for τ_m with respect to relaxivity. The solid lines in Figure 9A were generated from the average values for the rotational and electronic relaxation parameters in Table 1. Although it is likely that each compound has slightly different rotational dynamics, the reasonably good agreement of this composite curve in Figure 9A with the data validates the overall approach of screening compounds with a common albumin binding group. Figure 9A also experimentally demonstrates that the optimal water exchange regime is much smaller at 0.47T than it is at 1.4T. Optimization of water exchange is clearly much more important at low fields. This point has been made previously based on simulations,^8,46 and this study provides experimental data to support those simulations. Note also that at 1.4T the optimum value for water residency time is shifted compared to 0.47T.

Figure 9.

A) Relaxivity of complexes in HSA solution at 37 °C plotted versus measured water residency time at 37 °C with data at 0.47T (filled symbols) and 1.4T (open symbols). Solid lines are curves generated using the mean molecular parameters listed in Table 1. B) Relaxivity of complexes in HSA solution at 37 °C plotted versus measured transient zero field splitting parameter Δ², a measure of electronic relaxation rate, with data at 0.47T (filled symbols) and 1.4T (open symbols). Solid lines are linear regressions.

Figure 9B shows the correlation between the electronic relaxation parameter Δ² and measured relaxivity. There is a good negative correlation (r = -0.69 for both fields) between relaxivity and Δ². This may be expected since as Δ² becomes smaller, T_1e becomes longer. At low fields T_1e is, or contributes significantly to the overall correlation time, see equation 4. Increasing T_1e will increase relaxivity. However T_1e will increase with the square of the applied field (eq 7), so at high fields, the contribution of T_1e to the overall correlation time τ_c becomes smaller, and the importance of Δ² on relaxivity decreases with increasing field. This is apparent in Figure 9B where the slope of correlation line at low field (0.47T) is twice as great as at 1.4T.

The magnitude of Δ² determined in this study is smaller by a factor of 3 to 4 compared with values reported for DOTA derivatives, which were not bound to proteins.^11,44 For slow tumbling compounds Δ² strongly influences where the peak in the NMRD curve will occur. The values of Δ² in the literature would predict a relaxivity maximum occurring between 0.8 – 0.9T (35 – 40 MHz) while we typically observed maxima at ca. 0.5T.

Other parameters such as τ_v and the order parameter F² did not correlate with relaxivity. τ_v is the correlation time for modulation of the transient zero field splitting. The origin of this picosecond correlation time is believed to be either from vibrational modes of the metal complex or solvent collisions. Since the complexes are all very similar in structure as DOTA derivatives, one may expect similar vibrational energies; similarly the rate of solvent collisions should not differ among the different complexes. Differences in the order parameter may simply be due to differences in internal motion. For instance, the donor group may also interact with the protein and serve to rigidify the chelate:protein complex and reduce internal motion. Another possibility is differences in second-sphere relaxivity among the compounds. Mathematically, the order parameter F² scales the spectral density function. If some compounds had higher or lower second-sphere relaxivity than that of the q = 0 compound Gd3b then the order parameter would have been higher or lower, respectively, in order to compensate.

Overall the relaxivities are not as high as predicted by theory. This is certainly a result of internal motion. The rotational correlation times estimated from NMRD are shorter than those anticipated for a protein the size of albumin. This phenomenon has been seen before and the reduced τ_R values likely reflect internal motion along the bonds from the biphenyl binding group to the metal complex. It is also known that the coordinated water itself undergoes rotation and this will further serve to limit relaxivity.^47,48 Reducing internal motion should lead to higher relaxivities. Consider Gd4b whose water exchange rate was too fast at 37 °C. At lower temperatures, the exchange rate for this compound enters the optimal range; at the same time, all motion is slowing down as the temperature is lowered. Relaxivities as high as 71 mM^-1s^-1 were observed for Gd4b at 5 °C and this demonstrates the potential low field relaxivities that may be obtained.

Structure – Activity Relationships

In general, the effect of donor group on water exchange rate was in accord with what has been reported in the literature. Donor groups increased water exchange rate in the order: phosphonate ~ phenolate > α-substituted acetate > acetate > hydroxamate ~ sulfonamide > amide ~ pyridyl ~ imidazole. There are examples of DOTA derivatives with a single phosphonate,⁴⁴ phenolate,⁴⁹ α-substituted acetate,⁵⁰ sulfonamide,⁵¹ amide,^11,52 and pyridyl⁵³ substitution, and in the cases where water exchange data were reported,¹⁸ the values are in a similar range to what is observed here. The hydroxamate donor and some of the N-heterocycles had not been reported to our knowledge. Replacing an acetate with a neutral donor slowed down water exchange in all cases and resulted in lower relaxivity. The phosphonate and phenolate substitutions increased water exchange to the point that fast water exchange limited relaxivity. It is known that sequential replacement of acetate groups by phosphonate groups will eventually lead to a reduction in coordination number from 9 to 8 and there will no longer be a coordinated water. In the case of the single phosphonate substitution it may be that the 8-coordinate transition state is sufficiently stabilized to lead to facile water exchange via a dissociative mechanism, and a very fast exchange rate was also reported for a related phosphonate derivative.⁴⁴

Among the alpha-substituted acetates, we compared the effect of chirality on relaxivity and its molecular determinants. Gd1c/Gd1d and Gd1e/Gd1f are both diastereomeric pairs with R- and S-substituted acetates, respectively. In all the compounds the protein binding group is branched from an acetate with R configuration. Thus Gd1c is an R,R diastereomer and Gd1d is an R,S diasteromer. In both cases the R,R diastereomers showed 3-4 fold faster water exchange than the corresponding R,S analog. However differences in relaxivity among these compounds were minor since the exchange rates were all within the optimal range. Similarly the regioisomers Gd1c and Gd11a differed by the placement of the substituted acetate. The former was on N7 while the latter was substituted at N4. Again, small differences in water exchange rate were observed but relaxivities were similar. It is well established that DOTA derivatives can adopt two conformational isomers: square antiprism (SAP) where, looking down the water oxygen to gadolinium bond, the 4 nitrogens form one square and the 4 acetate oxygens form another square that is staggered 45° from the nitrogen containing square; and a twisted square antiprism (TSAP) where this angle is reduced.^54,55 The TSAP isomers usually have faster water exchange kinetics. The distribution between SAP and TSAP isomerism was not investigated in this study, but it may be behind the differences in water exchange rate observed in the various alpha-substituted acetates where τ_m³¹⁰ ranged from 10 to 75 ns. Increasing the number of alpha-substituted acetates is known to increase the water exchange rate,^54-56 and a similar effect was observed here with Gd10a where τ_m³¹⁰ was only 2 ns.

For the neutral donors where water exchange was slow it is not possible to definitively rank these donor groups in terms of effect on water exchange because the uncertainty in τ_m for these compounds is of the same order as the differences among them. Similarly, the effect of a phenolate or phosphonate donor on water exchange appears comparable.

There are clear trends in terms of the electronic relaxation parameter Δ². It seems that this is related to symmetry. The lowest value of Δ² (longest T_1e) was found with the unsubstituted acetate, where the ligand field created by the 4 cyclen N, 4 carboxylate O, and water O donors would have apparent C_4v symmetry. The substituted acetates all showed the next lowest values of Δ², likely due to the all acetate donor set. The next tier could be defined as non-acetate oxygen donor atoms (amide, phenolate, etc). The compounds with the largest value of Δ² were those with a neutral nitrogen donor atom.

This study did not explicity address second-sphere contributions to relaxivity. It is known that exchangeable hydrogen atoms in the second sphere, either from waters of hydration or protonated acids, can make significant contributions to relaxivity. For instance an albumin-bound complex with no inner-sphere water was reported to have relaxivities greater than 20 mM^-1s^-1 at 0.47T.⁵⁷ Among the amide series in this study (Gd2a-g), we noted higher than expected relaxivity for the amide derived from glycine (Gd2b). Its relaxivity was 30% higher compared to Gd2a which had no pendant carboxylate groups. The relaxivity of Gd2b was also significantly higher than Gd2c or Gd2d which had pendant carboxylates but also additional methylene units. Higher relaxivity was also noted for the methylenephosphonate derivatives Gd2f and Gd2g. Indeed the tetra-amide compound, where each amide has a methylenephosphonate group shows high, pH-dependent relaxivity even though the inner-sphere water is undergoing extremely slow water exchange.^37,58,59 The high relaxivity of these tetraamides must be attributed to second-sphere effects.

Utilizing amide substituents to organize the second hydration sphere would seem a useful strategy to increase relaxivity further. Unfortunately, amide donors have a negative effect on inner-sphere water exchange rate in terms of gadolinium relaxivity. In a subsequent paper, we will explore the potential of using amide substituents to increase second-sphere relaxivity while varying the other donor groups to optimize the inner-sphere water exchange rate and in turn, inner-sphere relaxivity.⁶⁰

CONCLUSION

Overall this study demonstrates that the water exchange rate at GdDOTA derivatives can be exquisitely tailored over 3 orders of magnitude by the choice of donor atom. Donor atom choice has a predictable effect on electronic relaxation as well through the parameter Δ². For protein bound complexes this results in a range of relaxivities where the alpha-substituted acetate was the preferred donor group. Other donor groups resulted in relaxivity that was limited by too fast a water exchange rate (e.g. phenolate or phosphonate donor groups) or too slow a water exchange rate (e.g. amide or pyridyl). Differences among compounds with the same donor atom may be ascribed to differences in second-sphere relaxivity and this avenue may be explored for further gains in relaxivity. However, even with an optimal water exchange rate, relaxivities observed in this study were still limited by fast internal motions.