Patient-specific radiation dose and cancer risk estimation in CT: Part I. Development and validation of a Monte Carlo program

Abstract

Purpose: Radiation-dose awareness and optimization in CT can greatly benefit from a dose-reporting system that provides dose and risk estimates specific to each patient and each CT examination. As the first step toward patient-specific dose and risk estimation, this article aimed to develop a method for accurately assessing radiation dose from CT examinations.

Methods: A Monte Carlo program was developed to model a CT system (LightSpeed VCT, GE Healthcare). The geometry of the system, the energy spectra of the x-ray source, the three-dimensional geometry of the bowtie filters, and the trajectories of source motions during axial and helical scans were explicitly modeled. To validate the accuracy of the program, a cylindrical phantom was built to enable dose measurements at seven different radial distances from its central axis. Simulated radial dose distributions in the cylindrical phantom were validated against ion chamber measurements for single axial scans at all combinations of tube potential and bowtie filter settings. The accuracy of the program was further validated using two anthropomorphic phantoms (a pediatric one-year-old phantom and an adult female phantom). Computer models of the two phantoms were created based on their CT data and were voxelized for input into the Monte Carlo program. Simulated dose at various organ locations was compared against measurements made with thermoluminescent dosimetry chips for both single axial and helical scans.

Results: For the cylindrical phantom, simulations differed from measurements by −4.8% to 2.2%. For the two anthropomorphic phantoms, the discrepancies between simulations and measurements ranged between (−8.1%, 8.1%) and (−17.2%, 13.0%) for the single axial scans and the helical scans, respectively.

Conclusions: The authors developed an accurate Monte Carlo program for assessing radiation dose from CT examinations. When combined with computer models of actual patients, the program can provide accurate dose estimates for specific patients.

INTRODUCTION

Computed tomography (CT) is the single largest source of medical radiation exposure to the U.S. population, constituting half of the total medical exposure in 2006.¹ The past few years have witnessed growing societal efforts to manage radiation dose in CT, particularly efforts to adapt CT scanning technique to patient sizes.^{2, 3, 4} These efforts can greatly benefit from a dose-reporting system that provides radiation dose and potential cancer risk estimates that are specific to each patient and each CT scan. Such a system could serve as the basis for individualized protocol design and optimization. For patients who undergo sequential examinations over an extended period of time, the knowledge of dose and risk could also aid in deciding the necessity and frequency of examinations. Moreover, as there is an increasing call for radiation dose tracking from medical examinations and procedures,^{5, 6} patient-specific dose and risk estimations could offer an additional opportunity to be accountable for serial examinations.

The first step in enabling patient-specific dose and risk estimation is to accurately assess patient dose from CT examinations. Due to the lack of practical techniques to measure dose directly from patients, Monte Carlo simulations are often used to estimate the dose from computational patient models.^{7, 8, 9, 10, 11, 12, 13} Monte Carlo simulations can be very accurate, provided that the simulation code has been carefully benchmarked against experimental measurements. Several groups in the past have benchmarked their Monte Carlo programs using the standard CT dose index (CTDI) phantoms.^{14, 15} That approach is limited in that standard CTDI phantoms are made of a single material and provide dose information at only two or three different radial distances from the central axis. Recently, Monte Carlo dose results have also been validated in anthropomorphic phantoms.^{16, 17} However, the validations were limited either to single axial scans¹⁷ or to the surface of an anthropomorphic phantom.¹⁶

To enable patient-specific dose and risk estimation, the goal of this study was to develop and validate a Monte Carlo method for accurately assessing dose from CT examinations. A Monte Carlo program was developed to model a modern CT system. Its accuracy was first validated against ion chamber measurements in a custom-designed cylindrical phantom, which allowed dose measurements at seven different radial distances from its central axis. The accuracy of the Monte Carlo program was then validated against measurements made with thermoluminescent dosimetry (TLD) chips at various organ locations in two anthropomorphic phantoms for both axial and helical scanning modes.

MATERIALS AND METHODS

CT scanner

A multidetector array CT scanner (LightSpeed VCT, GE Healthcare, Waukesha, WI) was used in all measurements and simulations. The CT scanner was equipped with 64 arrays∕rows of detectors, allowing the user to select a beam collimation of 1.25–40 mm. It could operate in both axial and helical scanning modes with a helical pitch of 0.516–1.375. Three bowtie filters (small, medium, and large) were available on the scanner to provide size-adapted compensation for the variation of body thickness from the center to the periphery of the scan field-of-view (SFOV) in order to reduce dose and achieve more uniform x-ray intensity at the detector. The appropriate bowtie filter could be selected based on patient size and scanned body region via the proper choice of SFOV type. The scanner automatically switched between a large and a small focal spot size based on tube current. The distance between the focal spot and the isocenter was 54.1 cm. The user could select a tube potential of 80, 100, 120, or 140 kVp and a gantry rotation period of 0.4–2.0 s. While tube-current modulation techniques were available on the CT scanner, this study focused on fixed-tube-current techniques.

CT system modeling

Analytical simulation of x-ray energy spectra

The x-ray energy spectra at the exit of the x-ray tube and before filtration by the bowtie filter (referred to as the prebowtie spectra) were simulated by an x-ray modeling program (xSpect, version 3.3, Henry Ford Health System, Detroit, MI). An initial set of prebowtie spectra for the four kVp values was simulated for constant∕high-frequency tube potentials based on the target material, target angle, and inherent tube filtration data provided by the manufacturer (under a nondisclosure agreement). The prebowtie spectra were then numerically filtered by the thinnest central region of the small bowtie filter to obtain a set of postbowtie spectra. The half-value layers (HVLs) of the postbowtie spectra estimated using xSpect were matched to the HVLs reported by the manufacturer at the center of the beam by making small adjustments to the amount of inherent aluminum filtration used in the simulations. The above procedure was implemented to ensure that the beam qualities in our simulations match that in the actual CT scanner.

Monte Carlo simulation of radiation transport

Monte Carlo code

We developed a Monte Carlo program to simulate radiation transport in the CT system. The program was based on a benchmarked Monte Carlo subroutine package for photon, electron, and positron transport (PENELOPE, version 2006, Universitat de Barcelona, Spain).^{18, 19} The example main program PENMAIN.F included in the standard PENELOPE distribution was modified to simulate radiation transport in the bowtie filter, to model x-ray tube motions during axial and helical scans, and to transport radiation through voxel geometry. All material definition files used in the simulations were generated by running the program MATERIAL.F of PENELOPE, which has a large database of predefined common materials in addition to allowing the user to input the atomic compositions and mass densities of user-defined materials.

Radiation transport in bowtie filters

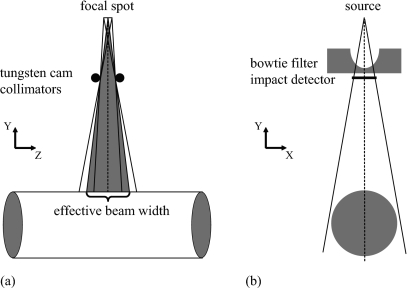
Based on the geometry data provided by the manufacturer, each bowtie filter available on the CT scanner was modeled using the geometry package PENGEOM of PENELOPE as a group of simple objects limited by quadric surfaces. In the actual CT scanner, a cone beam of x-ray with a half-cone angle of 27.5° first passes through the bowtie filter and is subsequently restricted by a pair of tungsten cam collimators.²⁰ In our simulations, the collimators were not explicitly modeled, but a fan beam of x-ray defined by the collimators was transported through the bowtie filter. Using a point source, we chose an effective beam width to account for the dose delivered by both the umbra and the penumbra regions of the beam [Fig. 1a]. The effective beam width was measured using a ready-pack x-ray film. The methods are detailed in the Appendix0. The half-fan angle of the fan beam was chosen to be broad enough to cover the imaging object [Fig. 1b]. A pseudoimpact detector (nonexistent in the actual CT system) was added below the bowtie filter at the level of the tungsten cam collimators to register the state (type of particle, energy, position coordinates, directional cosines, weight, etc.) of each incident particle in a phase-space file²¹ for use in the subsequent simulations of axial and helical scans. The width of the impact detector was equal to the aperture of the tungsten cam collimators and its length was just slightly larger than the divergence of the x-ray beam [Fig. 1b].

Figure 1.

(a) A point source and an effective beam width were used in the simulations to account for the dose delivered by both the umbra and the penumbra regions of the beam. (b) The fan beam was chosen to be just broad enough to cover the imaging object. A pseudoimpact detector was added below the bowtie filter at the level of the tungsten cam collimators to register the information of each incident particle in a phase-space file for use in the subsequent simulations of axial and helical scans.

Axial and helical scans

To model the effect of x-ray tube motion during an axial or helical scan, the impact detector was “moved” parallel to the x-ray tube trajectory to serve as a source. This was achieved by first reading the initial state of each particle from the precalculated phase-space file. Before the particle was released for transport in the imaging object, rotational and translational transforms were performed on the initial coordinates and the directional cosines of the particle with rotational angle and translational distance calculated as

$$\beta =\alpha \text{RAND}\text{and}d=\frac{\beta }{2\pi }s+z_0,$$ (1)

respectively, where α is the total gantry rotation angle during the scan and equals 2π for single axial scans, RAND is a random value between 0 and 1, s is the table increment per gantry rotation (equals zero for a single axial scan), and z₀ is the start location of the scan. Considering that the statistical errors of the Monte Carlo outputs were dependent on the number of particles stored in the phase-space file, which had a limited file size, we employed particle splitting, a variance-reduction technique, to reduce the variances of the results without increasing the simulation time.²¹ Each particle in the phase-space file was split into 12 equivalent particles with weights equal to 1∕12 of the original particle weight at the beginning of the particle track. We have verified using a cylindrical phantom that the dose results simulated with and without the particle splitting technique agreed within the statistical constraints of the Monte Carlo simulation.

Radiation transport in voxel geometry

Realistic representation of human anatomy in Monte Carlo simulations frequently requires the use of voxel geometry. Earlier computer models of patients were generated from direct segmentation of the three-dimensional matrices of voxels in the patients’ tomographic data sets;^{22, 23, 24, 25} every voxel was assigned to the appropriate organ or tissue based on grayscale values. Modern computer modeling of human anatomy employs more flexible mathematical surfaces, most notably the nonuniform rational B-spline (NURBS) surfaces, which are fits to the segmented tomographic data.²⁶ The complexity of such surfaces, however, prohibits particle locations to be solved efficiently during Monte Carlo simulations. As such, NURBS surfaces based computer models are often voxelized before inputting into Monte Carlo simulations.¹³

As it is impractical and inefficient to individually define all the planes and voxels in a voxel geometry using the original geometry routine PENGEOM of PENELOPE, we developed a new geometry routine, named PENVOME (i.e., PENGEOM for voxelized models). PENVOME conveniently labels each voxel by its matrix indices; boundary planes of the voxel are only calculated when the voxel is reached by a particle. This circumvents the need to store surface∕body definitions and to sort through a genealogical tree of a large number of bodies. The accuracy of PENVOME was validated against PENGEOM in terms of simulated dose in a simple object of 18 voxels and the results were identical within the statistical constraints of the Monte Carlo simulation. As such, the Monte Carlo program can be used to transport radiation for dose simulation in both quadric and voxel geometries.

Dose measurements

A series of dose measurements were performed to calibrate and validate the accuracy of our CT model and Monte Carlo code.

Dose measurements in air

To quantify the absolute outputs of the x-ray tube for converting Monte Carlo results to absolute dose, free-in-air exposure was measured for all combinations of bowtie filters and kVps with a calibrated ion chamber (6.6 mm long, 0.18 cm³ active volume, model 10×5-0.18∕9015, Radcal Corporation, Monrovia, CA). The ion chamber was positioned at the isocenter of the CT scanner with its long axis aligned with the axis of gantry rotation. Single axial scans were performed with the x-ray beam centered on the active volume of the ion chamber. For each combination of bowtie filter and kVp, five to seven repeated measurements were taken at a beam collimation of 40 mm, a tube current of 30 or 60 mA, and a gantry rotation period of 1 s, and the results were averaged. All measured exposures in Roentgen (R) were converted to dose in cGy using 1 R=0.876 cGy.

Dose measurements in a cylindrical phantom

It is well known that a single axial scan generally delivers more radiation dose to the periphery than the center of a cylindrical phantom, affected by beam quality, phantom attenuation, and the spatial variation of beam intensity. We were motivated by this fact to design a CT dose phantom that allows center-to-periphery dose distributions to be measured for comparison with Monte Carlo simulated results. Initially focused on pediatric CT applications, we built a cylindrical phantom to represent a pediatric torso [Fig. 2a]. The phantom was made of a 7 in. diameter and 7 in. long polymethylmethacrylate (PMMA) cylinder. Seven through-holes, 1.4 cm in diameter, were drilled parallel to its long axis to allow the placement of ion chambers at incremental distances away from the central axis. The holes, which could be filled with similar diameter PMMA rods, were arranged in a spiral pattern to minimize their overlap in the CT projections.

Figure 2.

(a) Custom-designed CT dose phantom for measuring center-to-periphery dose distributions. The locations of the seven drill holes are numbered. (b) Measurements of dose distribution in the custom-designed phantom. The phantom was attached to one end of the CT table and positioned so that its long axis matched the axis of gantry rotation.

Radial dose distributions in the phantom from single axial scans were measured with the ion chamber. The phantom was attached to one end of the CT table using a phantom holder supplied with the CT system and positioned so that its long axis matched the axis of gantry rotation [Fig. 2b]. Exposure was measured for each hole individually with the ion chamber positioned midway inside the hole and the x-ray beam centered on the active volume of the ion chamber. The remaining volume of that hole was filled with two half-length PMMA rods. All other holes also were filled. For each of the three bowtie filters, dose distribution was measured at the four kVp values with a beam collimation of 40 mm, a tube current between 200 and 300 mA, and a gantry rotation period of 1 s. Five to seven repeated measurements were taken at each hole location, and the results were averaged.

Dose measurements in anthropomorphic phantoms

To further validate the accuracy of our Monte Carlo method for dose estimation in human anatomical structures, we measured dose in two anthropomorphic phantoms, a pediatric one-year-old phantom and an adult female phantom (ATOM, Models 704-D and 702, CIRS, Norfolk, VA), shown in Figs. 3a, 3b.

Figure 3.

Dose measurements in (a) pediatric one-year-old CIRS phantom and (b) adult female CIRS phantom. (c) The phantoms were composed of axially sliced, 25 mm thick, contiguous sections. Each section contained one or more 5 mm diameter through-holes at various organ locations.

The phantoms were composed of axially sliced, 25 mm thick, contiguous sections. Each section contained one or more 5 mm diameter through-holes at various organ locations [Fig. 3c]. The holes could be filled with similar size plugs or dosimeter holders. We used TLD chips (Harshaw TLD-100, Thermoscientific, Oakwood Village, OH), which were calibrated against a precalibrated ion chamber (6 cm³ active chamber volume, model 10×5-6∕9015, Radcal Corporation, Monrovia, CA) at appropriate beam energies; calibration was performed either in the CT beam of interest or in an x-ray beam of a radiography system where the beam was hardened with a copper filter to match the half-value layer of the CT beam at the tube potential of interest. At each selected organ location, the hole plug was removed, cut in half, and used to sandwich a pair of two TLD chips before refilling the hole. The average of the two TLD readings at each organ location was used as the measured dose at that location; the standard deviation of the two readings was used to assess the uncertainty of the measurement. For each anthropomorphic phantom, two sets of TLD chips were used to measure dose from a single axial scan and a helical scan, respectively (Table 1). The single axial scan was centered on a chest section in which TLD chips were embedded. The helical scan was a full-body scan for the pediatric phantom and a chest scan for the adult female phantom. Compared to the typical clinical protocols for a one-year-old pediatric patient and a small adult patient, the protocols in Table 1 had much higher tube current and gantry rotation period and much lower pitch values. These high-dose scan parameters were used to improve the precisions of the dose measurements. Furthermore, in a helical scan, the x-ray tube starting angle is not fixed and thus different each time (per private communication with the manufacturer). Using pitch values close to 0.5 also helped reduce the dose uncertainties associated with the random∕unknown tube starting angle. To test the accuracy of our Monte Carlo program, relatively independent of the effect of tube starting angle, these pitch values, not typical of clinical practice, were used.

Table 1.

Scan protocols used to collect TLD dose measurements from the pediatric one-year-old and the adult female phantoms.

	Pediatric phantom		Adult female phantom
	Single axial	Helical	Single axial	Helical
Body region	Chest	Whole body	Chest	Chest
kVp	100	100	120	120
mA	250a	250	250	250
Gantry rotation period (s)	1	1	1	1
Scan FOV (bowtie filter)	Pediatric body (small bowtie)	Pediatric body (small bowtie)	Large body (large bowtie)	Large body (large bowtie)
Collimation (mm)	40	20	40	40
Pitch	–	0.531	–	0.516
Slice thickness (mm)	2.5	2.5	5	5
Reconstruction interval (mm)	2.5	2.5	5	5

^aThe high tube current, high gantry rotation period, and low pitch values in the table are not typical of clinical scan parameters for pediatric and small adult patients. They were used for the purposes of validating the Monte Carlo program (see Sec. 2C3).

Dose simulations

The dose measurements conducted in the air and in the three phantoms were simulated using the developed Monte Carlo program.

Dose simulations in the air and in the cylindrical phantom

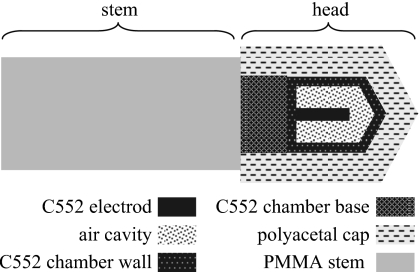
Computer models of the ion chamber (6.6 mm long, model 10×5-0.18) and the cylindrical phantom were created using the geometry package PENGEOM. The head of the ion chamber was modeled as a group of simple objects limited by quadric surfaces (Fig. 4), based on the chamber geometry data provided by Radcal Corporation. The stem of the ion chamber, which contains metal conductors, was not explicitly modeled but was approximated by a small PMMA cylinder (Fig. 4). The small air gaps left in between the ion chamber and the phantom were also assumed to be filled with PMMA.

Figure 4.

Model of the ion chamber (6.6 mm long, 0.18 cm³ active volume, model 10×5-0.18∕9015, Radcal Corporation, Monrovia, CA) used in the Monte Carlo simulations. “C552” here refers to C552 air-equivalent plastic. Material data file for polyoxymethylene was used for the polyacetal cap.

Energy deposited in the air cavity of the ion chamber was accumulated and used to calculate dose. When choosing simulation parameters, we referenced the recipe prescribed by Sempau et al.²⁷ Analog simulation was employed in the air cavity and a speedup parameter²⁷ of a=1 was used for the chamber wall. Table 2 summarizes the simulation parameters and variance-reduction techniques used. In the polyacetal cap and the PMMA stem, electrons were not transported but were assumed to be absorbed locally when produced. This is because even if electrons were transported in these objects, they could not arrive at the air cavity, thus having no effect on the air cavity dose. For the same reason, electrons were not transported in the PMMA phantom. For each combination of bowtie filter and kVp, center-to-periphery dose distribution in the phantom was obtained by running the simulation seven times with the ion chamber placed in a different hole each time. For all simulations in the phantom, the number of photon histories was chosen to obtain relative errors in dose of 1% or below. The relative error was defined as one standard deviation divided by the average tally result. When simulating the in-air measurements, the volume occupied by the phantom was replaced by air, leaving only the model of the ion chamber; the number of photon histories was chosen to obtain relative errors of 0.5% or below.

Table 2.

Simulation parameters and variance-reduction techniques used for dose simulations in the air and the cylindrical phantom.

	Electron absorption energy (keV)	Photon absorption energy (keV)	Speedup parameteraa	Variance-reduction techniqueb
Air cavity	5c	kVp energy∕1000	0	Photoelectric interaction forcer=50; Compton interaction forcer=50
Chamber wall	5	kVp energy∕1000	1	Photoelectric interaction forcer=50; Compton interaction forcer=50
Chamber base	5	kVp energy∕1000	1	No
Polyacetal	kVp energy	kVp energy∕1000	N∕A	No
PMMA	kVp energy	kVp energy∕1000	N∕A	No

^aReference ²⁷.

^bReference ²¹.

^cThe absorption energy of electrons in the air was chosen to be 5 keV, half the kinetic energy of an electron that has a continuous slowing down approximation (CSDA) range approximately equal to the thickness of the air in the cavity (Ref. ²⁷).

The above simulations produced air cavity dose in the unit of cGy per photon emitted from the source. The total number of photons emitted from the source during a CT scan was calculated as

$$N=n\cdot \Omega \cdot \text{mAs},$$ (2)

where n, the number of photons emitted from the source per solid beam angle per mA s, was calculated from the energy spectra simulated by xSpect, and Ω is the solid angle of the fan beam. Absolute dose values in the unit of cGy were then equal to

$$D_{\text{sim}}=d_{\text{sim}}\cdot N,$$ (3)

where d_sim is Monte Carlo simulated dose in the unit of cGy per photon emitted from the source. We first calculated the absolute dose for each of the in-air dose simulations and compared it with the corresponding measured dose. The ratio of the measured to the simulated in-air dose was defined as an output correction factor (OCF)

$$\text{OCF}=\frac{D_{\text{meas},\text{in-air}}}{D_{\text{sim},\text{in-air}}}.$$ (4)

As mentioned in Sec. 2B1, HVL matching served to ensure the accurate shapes (beam qualities) of the prebowtie spectra. Here the OCF values serve to correct for the inaccuracy in the magnitudes of the prebowtie spectra. In other words, they correct for the inaccuracy in the values of n. Such inaccuracy existed because the exact (proprietary) compositions and densities of the filtration materials in the x-ray tube were unknown and thus the materials used in the analytical simulation (Sec. 2B1) differed somewhat from that in the actual x-ray tube even after HVL matching. To calculate the absolute dose for all simulations in the cylindrical and anthropomorphic phantoms, the total number of photons emitted from the source was calculated as

$$N^{\prime }=N\cdot \text{OCF}.$$ (5)

Dose simulations in the anthropomorphic phantoms

A full-body computer model was created for each anthropomorphic phantom based on the phantom’s CT images. The method was similar to that reported recently for creating NURBS models of pediatric CT patients²⁸ and is briefly described below. Initially, the images of each phantom were segmented using a graphical software application developed in our laboratory. Segmented organs and tissues included soft tissue, lung, bone, spinal cord, and spinal disk. The brain of the pediatric phantom, the breasts of the adult female phantom, and large unfilled air holes were also segmented. The TLD chips were not explicitly segmented, but each was modeled as a 1 mm tall cylinder with a 3 mm diameter to emulate the actual dimensions of the TLD chips. Following the segmentation, three-dimensional polygon models were created for each structure using the marching cubes algorithm.^{29, 30} Typically, three-dimensional NURBS surfaces would then be fit to the polygon models to provide a more compact and flexible definition for each structure. The advantage of using NURBS surfaces would be to allow for the simulation of anatomical variations or motion. In this case, since only static phantoms were needed for dose simulation purposes, each phantom was left as a collection of polygon models. As only the chest part of the adult female phantom was scanned during the TLD dose measurements, the initial computer model of that phantom only included this region. To simulate dose to organ locations outside the chest scan image volume, images of the entire adult female phantom were acquired (after the TLD chips were removed) to allow the remaining parts of the phantom to be modeled.

To account for the effect of CT table attenuation on dose, a computer model of the CT table (table case and table interior) was also created via manual segmentation of the table from a patient CT image with a large reconstruction field-of-view.

The model of each phantom with the table attached was voxelized at resolutions comparable to the original image resolutions. Each organ and structure was assigned a material based on the elemental composition and mass density information tabulated in the CIRS manual. Soft tissue material was used for the tissue-equivalent TLD chips. The interior of the CT table (acrylic foam) was modeled as low-density acrylic per information provided by the manufacturer. The case of the CT table (carbon fiber) was modeled as carbon with density of 1.7 g∕cm³.

The location and coverage of the axial and helical scans in the actual experiments were reproduced in the simulations. For the helical scans, the total scan length was calculated as the total image coverage plus the over-ranging distance (additional scan length necessary for data interpolation in helical reconstruction).³¹ The over-ranging distance was estimated from the scanner console parameters as “table speed (cm∕s)×total scan time(s)−image coverage (cm).” As the tube starting angles in the actual experiments were unknown, each helical scan was simulated six times, with the tube starting angle differing by 60° each time. For each organ location where the TLD chips were embedded, the simulated dose values at individual tube starting angles and the average across tube starting angles were compared to measurements.

For the range of photon energies in CT, the ranges of the secondary electrons in tissue materials are generally much smaller than the voxel sizes in the phantoms. Therefore, electrons were not transported during the simulations; their energies were deposited locally immediately after they were produced. The transport of a photon was terminated if the photon energy dropped below 1∕1000 of the kVp energy.²¹ Energy deposited in the TLD chips was tallied and used to calculate dose, following the procedure of dose calculation performed for the cylindrical phantom (Sec. 2D1). The number of photon histories was chosen to obtain relative errors in dose of 5% or below.

RESULTS

In-air results

Simulated dose in the air was lower than measured dose for all combinations of kVps and bowtie filters (Table 3), resulting in OCF values [Eq. 4] greater than unity. As OCFs calibrated the magnitudes of the prebowtie spectra, they had little dependence on bowtie filter type; the coefficients of variation across bowtie filters were less than 1.5% (Table 3). As such, the OCF values were averaged across bowtie filters for use in subsequent dose calculations.

Table 3.

Measured and simulated in-air dose at the isocenter of the LightSpeed VCT scanner for single axial scans. Error figures reflect one standard deviation.

kVp	Bowtie filter	In-air dose (cGy∕100 mAs)		OCF		Standard deviationa	Coefficient of variationa b, b (%)
		Measured	Simulated	Eq. 4	Meana
80	Small	1.145±0.004	0.896±0.004	1.278	1.290	0.020	1.5
	Medium	1.151±0.003	0.900±0.004	1.279
	Large	0.835±0.003	0.636±0.003	1.313
100	Small	1.901±0.003	1.515±0.006	1.255	1.270	0.014	1.1
	Medium	1.907±0.004	1.498±0.006	1.273
	Large	1.481±0.003	1.155±0.005	1.283
120	Small	2.776±0.004	2.337±0.009	1.188	1.196	0.016	1.4
	Medium	2.775±0.005	2.340±0.009	1.186
	Large	2.262±0.001	1.862±0.008	1.215
140	Small	3.744±0.006	3.187±0.013	1.175	1.177	0.003	0.3
	Medium	3.736±0.007	3.178±0.013	1.176
	Large	3.144±0.005	2.664±0.012	1.180

^aThe mean, standard deviation, and coefficient of variation of the OCF values across bowtie filters.

^bCoefficient of variation=(standard deviation∕mean)×100%.

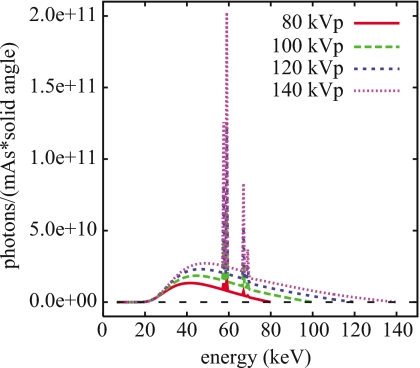
Figure 5 illustrates the results of our analytical simulations of the x-ray energy spectra at the exit of the x-ray tube and before filtration by the bowtie filter. The magnitudes of the spectra have been corrected using the OCF results.

Figure 5.

Simulated x-ray energy spectra at the exit of the x-ray tube and before filtration by the bowtie filter (prebowtie spectra).

Cylindrical phantom results

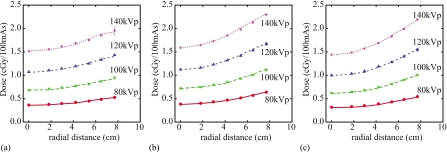
Comparisons between measured and simulated dose distributions in the custom-designed cylindrical phantom are shown in Fig. 6. Across all bowtie filter and kVp settings, simulations agreed very well with measurements. Percent differences between simulations and measurements at individual data points ranged from −4.8% to 2.2% with an average magnitude of 1.3%.

Figure 6.

Measured and simulated dose distributions in the custom-designed cylindrical phantom for single axial scans at four kVp values using the (a) small, (b) medium, and (c) large bowtie filters and a 40 mm beam collimation. Simulated dose values are shown by lines. Measured dose values are shown by symbols and their error bars reflect one standard deviation. Most error bars are too small to appreciate.

Anthropomorphic phantom results

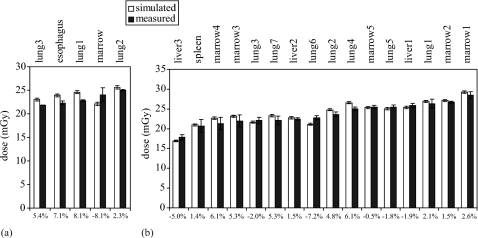
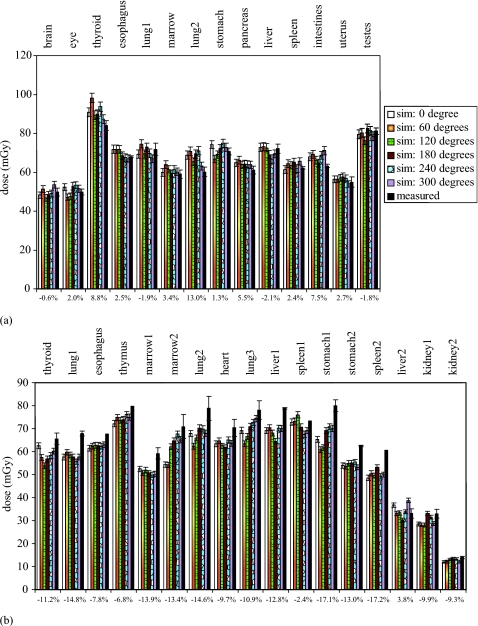
Figures 78 illustrate measured and simulated dose values in the pediatric and adult female anthropomorphic phantoms. For the axial scans performed in both phantoms, excellent match was found between simulations and measurements at all organ locations. For the helical scans, simulations agreed well with measurements for the pediatric phantom, yet slightly underestimated measurements for the adult female phantom. Results are also summarized in Table 4.

Figure 7.

Measured and simulated dose from a single axial scan in (a) the pediatric and (b) the adult female phantoms. Error bars reflect one standard deviation. Percent discrepancies between simulation and measurement are labeled on the bottom. The high dose values reported here were results of the high-dose scan parameters (Table 1) used in the measurements and simulations and were not typical of clinical dose values.

Figure 8.

Measured and simulated dose from (a) a full-body helical scan in the pediatric phantom and (b) a chest scan in the adult female phantom. Error bars reflect one standard deviation. The degrees are x-ray tube start angles relative to 12 o’clock. Percent discrepancies between simulation (averaged over tube starting angles) and measurement are labeled on the bottom. At four organ locations in the adult female phantom, one of the two TLD chips was cracked during the experiment; dose uncertainty could not be assessed for these four locations. The high dose values reported here were results of the high-dose scan parameters (Table 1) used in the measurements and simulations and were not typical of clinical dose values.

Table 4.

Summary of discrepancies between simulated and measured dose in the cylindrical and anthropomorphic phantoms.

	Cylindrical phantom	Pediatric phantom		Adult female phantom
	Single axial	Single axial	Helicala	Single axial	Helicala
Range	(−4.8%, 2.2%)	(−8.1%, 8.1%)	(−2.1%, 13.0%)	(−7.2%, 6.1%)	(−17.2%, 3.8%)
Average magnitudeb	1.3%	6.2%	4.0%	3.4%	11.1%

^aSimulated dose averaged across tube starting angles was used to calculate the percent discrepancies.

^bThe average of the absolute values.

DISCUSSION

Toward the goal of patient-specific dose and risk estimation, we developed and validated a Monte Carlo program for assessing dose from CT examinations. To ensure the accuracy of the simulated dose, we modeled a CT system in great detail, including explicit modeling of the x-ray source energy spectra, the three-dimensional geometry of the bowtie filters and the CT table, and the trajectories of CT tube motions during axial and helical scans.

The results of our dose simulation showed good agreement with ion chamber and TLD measurements. An excellent match (Fig. 6) was found between simulated and measured radial dose distributions in the cylindrical phantom for all combinations of kVp and bowtie filter settings (discrepancy<4.8%). As radial dose distribution is highly dependent on the quality of the x-ray beam and the filtration of the CT system, these results are strong evidence of the accuracy of our spectrum and filtration models.

To our knowledge, this work is the first effort to validate Monte Carlo simulated dose inside anthropomorphic phantoms for helical scans. Prior work was limited either to single axial scans^{14, 15, 17} or to the surface of an anthropomorphic phantom.¹⁶ For the pediatric phantom in our study, excellent agreement was found between simulations and measurements for both axial and helical scans [Figs. 7a, 8a] (discrepancy<13%). Our simulations showed that the tube starting angle has a discernable effect on dose even at a helical pitch value close to (∼0.5), contributing to the uncertainty in dose estimation. Such dependence has also been reported recently at other pitch values (0.75–1.5) and has been exploited as dose reduction strategies.³² For the adult female phantom, simulations agreed well with measurements for the single axial scan (discrepancy<7.2%), yet slightly underestimated measurements for the helical scan (discrepancy<17.2%). Nevertheless, considering the complexity of the simulations and the large number of factors that influence both the simulation and measurement results, discrepancies of less than 20% from measurements are generally considered as good matches.¹⁷ Furthermore, as these discrepancies were associated with the dose to the small TLD chips, we expect the discrepancies for organ dose values to be lower. As mentioned earlier, the computer models of the two anthropomorphic phantoms were created from their CT data using a method similar to that reported recently for creating patient models from clinical CT data.²⁸ Therefore, we expect similar accuracy in simulated dose when applying our Monte Carlo program to models of actual patients.

We note that the dose values reported in this study (Figs. 78) were much higher than the typical clinical dose values (see Part II of this work on application to patients³³). The high dose values were results of the high tube current, high gantry rotation period, and low helical pitch values (Table 1) used in the dose measurements and simulations. These high-dose scan parameters were used for the purposes of validating our Monte Carlo program (see Sec. 2C3). One should not interpret these results as being representative of clinical CT dose values.

Our study is limited to a single CT scanner model. However, the methods developed in our study can be readily extended to other CT scanner models. Furthermore, other authors have shown, with small numbers of patients and scanner models, that when organ dose estimates are normalized by CTDI values, the variations across CT scanner models are small.^{34, 35} Thus, our Monte Carlo program can be used to provide normalized dose results independent of scanner models, although this requires further testing and validation. While our study is limited to fixed-tube-current scans, the Monte Carlo program explicitly models the trajectory of x-ray tube motion and therefore can be easily adapted to simulate tube-current-modulated scans.

CONCLUSION

Our work has demonstrated that radiation dose from axial and helical CT examinations can be accurately estimated using a Monte Carlo program that employs accurate x-ray energy spectra calibrated in terms of both spectral shape and magnitude and provides detailed modeling of system geometry, bowtie filtration, CT table, and x-ray tube trajectories. The Monte Carlo program can be readily adapted to model different CT scanners and scan modes. When combined with realistic models of CT patients, the program can be applied in patient-specific dose and risk estimations.

APPENDIX: EFFECTIVE BEAM WIDTH MEASUREMENTS

We determined the effective beam widths (along z direction) for the small and large focal spots and for three most commonly used collimation settings: 40, 20, and 10 mm.

Methods

At each combination of collimation and focal spot settings, a ready-pack x-ray film (PPL, Eastman Kodak Co., Rochester, NY) was centered on the surface of the gantry bore and exposed in a single axial scan that delivered dose values within the responsive range of the film. The developed film was digitized (Expression 10000 XL, Seiko Epson Corporation, Japan) at a resolution of 72 points per inch, resulting in a 16-bit image. From the image, three pixel intensity profiles were measured across the x-ray beam along the beam width (z) direction. The pixel intensity profiles were converted into net optical density profiles, which were linearly proportional to the dose profiles over the range of net optical densities in our experiment. As each film was exposed twice in a single axial scan at two different source-to-film distances, each dose profile was the superposition of two profiles, representing the divergences of the beam at two source-to-film distances. The effective beam width at each source-to-film distance was defined as the distance between two points where the dose fell off most rapidly. Such two points were determined by differentiating the dose profile to find the points of maximum/minimum slopes. The effective beam widths measured at the two source-to-film distances were then converted to that at the isocenter of the CT scanner using known source-to-isocenter distance and gantry bore size.

Results

Results of effective beam width measurements are summarized in Table 5. These results are consistent with those reported earlier by other authors, who measured the effective beam widths on the LightSpeed VCT scanner using rod optically stimulated luminescence dosimeters.³⁶ Good agreements were found between the results derived from the two source-to-film distances. Furthermore, the effect of focal spot size was not statistically significant (p=0.06–0.94). We defined the penumbra of the beam as the effective beam width minus the nominal collimation setting. As the differences between the penumbras at different focal spot and collimation settings were small, the results were averaged to obtain a single penumbra value. This value was added to each collimation setting to serve as the effective beam width at each collimation setting for the Monte Carlo simulations.

Table 5.

Effective beam widths measured for both focal spot sizes and for three most commonly used collimation settings.

Focal spot size	Collimation (mm)	Effective beam width at isocenter (mm)			Penumbrab (mm)
		Derived from near SFDa	Derived from far SFD	Average
Small	40	42.2±0.6	42.4±0.2	42.3	2.3
Large	40	41.9±0.0	42.7±0.2	42.3	2.3
Small	20	22.1±0.6	21.7±0.2	21.9	1.9
Large	20	22.1±0.6	23.1±0.2	22.6	2.6
Small	10	12.7±0.0	12.1±0.0	12.4	2.4
Large	10	12.7±0.0	12.8±0.4	12.7	2.7
				Average=2.3

^aSFD=source-to-film distance.

^bPenumbra is defined here as the effective beam width minus the nominal collimation setting.