Homonuclear Mixing Sequences for Perdeuterated Proteins

Abstract

We test the performance of several ¹³C homonuclear mixing sequences on perdeuterated microcrystalline ubiquitin. All sequences were applied without ¹H decoupling and at relatively low MAS frequencies. We found that RFDR gave the highest overall transfer efficiency and that DREAM performs surprisingly well under these conditions being twice as efficient in the aliphatic region of the spectrum than the other mixing sequences tested.

Introduction

²H isotope labeling (perdeuteration) is an established technique in protein liquid-state NMR and its great potential for solid-state NMR has been demonstrated by several studies in the last decade [1–5]. Most important for solid-state NMR is that perdeuteration leads to narrow ¹H linewidths of the remaining protons, which enables high resolution spectroscopy of this important nucleus. Furthermore, high-power ¹H decoupling becomes unnecessary in perdeuterated samples and low power liquid-state NMR type pulse sequences become useful. However, perdeuteration also comes at a price. The gain in signal-to-noise ratio (S/N) due to ¹H-¹³C cross polarization (CP) is reduced if present at all. Therefore, direct excitation of the ¹³C spins using a 90° pulse instead of a CP is sometimes performed. The spin-lattice relaxation time T₁ of ¹H and ¹³C alike can become quite long in perdeuterated samples. This problem can be overcome by adding paramagnetic centers that shorten the T₁ [6]. A third aspect is that a dense proton network, which is absent in perdeuterated samples, is a key instrument facilitating ¹³C-¹³C polarization transfer in many pulse sequences, such as proton driven spin diffusion (PDSD) [7], dipolar-assisted rotational resonance (DARR) [8], mixed rotational and rotary resonance (MIRROR) [9], or proton assisted recoupling (PAR) [10]. In the light of this last point, it becomes necessary to either re-evaluate the homonuclear mixing sequences previously developed for fully protonated systems or to find new techniques that replace PDSD and DARR.

Several recent papers illustrate successful recoupling of carbons in perdeuterated proteins. In one study, radio-frequency-driven recoupling (RFDR) was carried out with sample spinning at 20 kHz and a field of 800 MHz to obtain broadband recoupling on a 95% perdeuterated sample of microcrystalline ubiquitin, (with labile hydrogens exchanged with protonated solvent) [11]. Agarwal & Reif used an adiabatic TOBSY (total though-bond correlation spectroscopy) sequence with sample spinning at 20 kHz and a magnetic field of 600 MHz and achieved broadband ¹³C mixing on perdeuterated SH3 crystals in the context of a 3D HCCH experiment. In their sample, only 10% of the labile protons exchanged back to ¹H [12]. Recently, Akbey and co-workers proposed a new pulse sequence called DONER. Similar to DARR, this sequence recouples protons and deuterons at the rotational resonance condition during the ¹³C-¹³C mixing. DONER spectra recorded on perdeuterated SH3 crystals (40% of the protons exchanged back) at 10 kHz MAS and a ¹H Larmor frequency of 400 MHz lead to much higher transfer efficiency as compared to DARR or PDSD [13]. However, no comparative study has been done comparing the efficiency of these pulse sequences for perdeuterated samples.

In the present study, we try to determine the optimal homonuclear mixing sequence by comparing such mixing sequences namely RFDR, TOBSY, adiabatic TOBSY, SPC5, DREAM, DARR, DONER, and PDSD in perdeuterated microcrystalline ubiquitin. In the absence of strong proton couplings, many of these pulse sequences lead to high transfer efficiencies at low MAS frequencies without the need of any ¹H decoupling as illustrated below.

Many homonuclear mixing sequences have been developed (for recent reviews see reference [14]). A key in developing homonuclear mixing sequences has been good performance, despite the presence of strong ¹H-¹³C and ¹H-¹H couplings. On the other hand, theoretical descriptions and numerical simulations of homonuclear recoupling sequences often assume perfect ¹H decoupling, neglecting all parts of the Hamiltonian involving proton spins [15–17]. Experimentally, efficient ¹H decoupling during ¹³C recoupling is non-trivial and should be optimized with care [18,19]. In perdeuterated systems i.e. in the absence of ¹H-¹³C couplings, homonuclear mixing sequences are expected to behave more closely to the numerical and theoretical predictions that assume perfect ¹H decoupling. One of the oldest sequences is RFDR, in which one 180° pulse per rotor period restores ¹³C homonuclear dipolar couplings, which would otherwise be averaged by MAS [20]. RFDR and variants of this pulse sequences are still widely used. Another class of mixing sequences is based on windowless phase-modulated radio frequency pulse trains, which are known as C and R sequences [21,22]. These sequences can be used to recouple different parts of the Hamiltonian; for example the $C{7}_2^1$ (C7) or super cycled $C{5}_2^1$ (known as SPC5) sequence are popular sequences that restore homonuclear dipolar couplings [15,16]. Other C and R sequences introduce the full J-coupling Hamiltonian, including for example the TOBSY sequence [23,24]. This pulse sequence, which is similar to the TOCSY sequence in liquid-state NMR, and its adiabatic variants [25,26], have proven to be very efficient. Another class of recoupling sequences is based on non phase modulated spin-lock fields. For example, the DREAM sequence, an adiabatic amplitude sweep through the HORROR condition (ω₁= 1/2 ω_r; were ω₁ is the spin-lock field strength and ω_r the MAS frequency), gives very high transfer efficiencies [27,28]. However, due to the restriction in rf-field, DREAM is better suited for high MAS frequencies [29,30].

For protonated systems, all of these mixing sequences were shown to depend heavily on efficient ¹H decoupling during the mixing and detection periods. The need for strong decoupling can limit their efficiency, and lead to stresses on the probe and the sample. One successful class of experiments obviates the need for high power decoupling by emplying high MAS frequencies with low power ¹H decoupling [30,31]. Fast MAS also has other advantages, for example for suppressing CSAs at high magnetic fields. However, better averaging of dipolar couplings at fast MAS posed a different problems to spin diffusion based pulse sequences, which has been partly addressed by recently developed efficient recoupling schemes such as PAR or MIRROR. A second solution to the stress of high power proton decoupling is to reduce rf-induced sample heating by using modern probes that dramatically reduce the E-field inside the coil and thereby prevent sample heating [32,33]. A third approach to avoiding the damage due to high power ¹H decoupling involves high ¹³C recoupling rf-field strengths such as CMAR [34], R-TOBSY [35], and $\text{Post}-C{20}_6^3$ [36]. These recoupling sequences were shown to work even without ¹H decoupling, but either require relatively fast MAS frequencies (CMAR, R-TOBSY), or are less efficient than similar sequences with high-power ¹H decoupling ( $\text{Post}-C{20}_6^3$). Finally, another very convenient solution to this problem is sample perdeuteration, since no ¹H decoupling is presumably necessary in the absence of protons. However, most known homonuclear mixing sequences were developed to perform under strong heteronuclear ¹H couplings. The present manuscript evaluates the performance of these sequences on perdeuterated ubiquitin, since heteronuclear couplings are absent in perdeuterated samples.

Results and Discussion

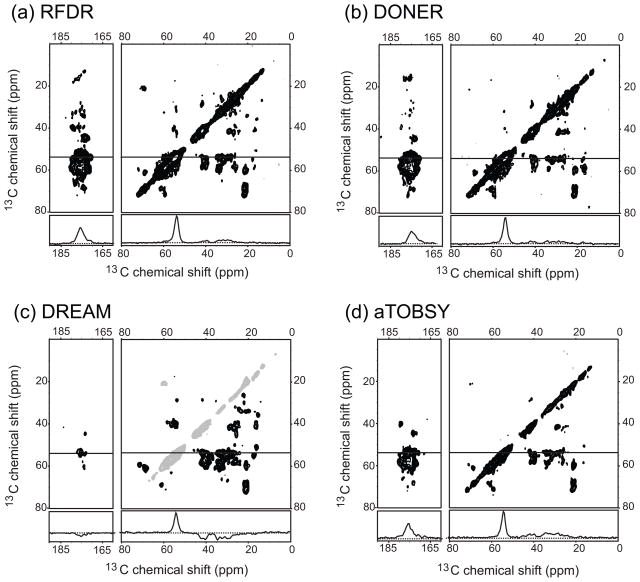
To compare the transfer efficiency of different homonuclear mixing sequences, we recorded a series of 2D ¹³C-¹³C correlation spectra on ²H-¹³C-¹⁵N labeled, human ubiquitin, which was crystallized from a fully protonated buffer. Considering that the sample was perdeuterated except of the back-exchanged amid protons, the ¹H-¹³C CP at the beginning of all 2D spectra transferred mostly magnetization to C′ and C_α. Figure 1 shows the results we got for the RFDR, DONER, DREAM, and adiabatic TOBSY (aTOBSY) sequences. All spectra were recorded under essentially the same conditions i.e. on a 400MHz spectrometer, at 8 kHz MAS (8.333 kHz for aTOBSY) and with neither proton nor deuterium decoupling during t₁, t₂, and the mixing time. The complete absence of decoupling made all these sequences easy to set up as compared to protonated samples were the careful optimization of ¹H decoupling is often essential to obtain acceptable transfer efficiencies. The MAS frequencies of 8 and 8.333 kHz were chosen to avoid the C′-C_α rotational resonance condition at about 11.5 kHz. (Spinning above all rotational resonance conditions was not practical using a standard 4 mm setup.) The 8.333 kHz made sense in the case of the C and R type sequences such as aTOBSY, since it led to even pulse lengths. Except for DREAM and SPC5, all mixing sequence were optimized by dephasing the C′ line and observing of the magnetization buildup over time. (Typical 1D time arrays used to determine the mixing time are shown in Supplemental Figure 1.) For DONER and DARR, we used the same mixing time (50 ms) as Akbey and co-workers under very similar conditions. This mixing time is also close to the optimal mixing time in the 1D time arrays. For RFDR, we used a slightly longer mixing time (3 ms) than for the maximal C′ intensity as a good compromise between transfer within the aliphatic region of the spectrum and transfer to C′, and also to achieve a good balance between one- and two-bond transfers (see Supplemental Figure 2). For aTOBSY, we picked the mixing time (4.3 ms) that gave the best compromise between transfer and magnetization decay. DREAM and SPC5 were optimized by the maximum in the negative signals from the double quantum transfer (2 ms and 1 ms, respectively). These mixing times are good compromises between transfer within the entire aliphatic region of the spectrum and the overall polarization decay.

Figure 1.

2D ¹³C-¹³C correlation spectra of perdeuterated ubiquitin microcrystals recorded with different ¹³C recoupling sequences at 400 MHz. 1D slices, cut at δ₁ = 54 ppm, are shown below the corresponding 2D spectra. (a) RFDR, (b) DONOR, (c) DREAM, and (d) adiabatic TOBSY. RFDR, DONER, and adiabatic TOBSY spectra show strong Cα to C′ and relatively weak peaks between Cα and the side-chain carbons. The DREAM spectrum, on the other hand, showed intense Cα to alphatic cross peaks and less intense Cα to C′ correlations.

Generally, the homonuclear mixing sequences show similar recoupling patterns (i.e. relative cross peak intensities) on our perdeuterated sample as on comparable protonated samples under high power ¹H decoupling. Except for the DREAM sequence, all recoupling techniques gave strong Cα-C′ correlations and less intense cross peaks in the aliphatic region of the spectrum. This behavior is expected for broadband recoupling sequences, since they do not lead to equal distribution of magnetization, but rather to a magnetization maximum at the end of the carbon chain (e.g. the carbonyl of peptides) [16].

The DREAM sequence on the other hand, generated more and stronger cross peaks within the aliphatic region (e.g. Cα – Cβ) as compared to RFDR, DONER, and aTOBSY spectra. At 8 kHz MAS, the HORROR condition is at the relatively weak spin lock field of 4 kHz leading to a more band selective recoupling. However, even with this low spin-lock field we observed Cα-C′ cross-peaks i.e. correlation between resonance ~11.5 kHz apart.

To quantify the transfer efficiency, we integrated the intensity of all cross peaks at the δ₁ slice at 54 ppm shown in Figure 1 and of the additional PDSD, DARR, SPC5, and TOBSY spectra shown in Supplemental Figure 3. To correct for relaxation during the mixing time, we compared the cross peak intensities to the diagonal peak of a 2D spectrum without any ¹³C-¹³C mixing. The result of this analysis, separated in overall transfer efficiency, transfer efficiency within the aliphatics, and from the aliphatics to the carbonyls and aromatic side chains, is shown in Table 1. The RFDR and DONER sequence show the highest overall (Cα-side chain + Cα– C′) transfer efficiencies and also the highest cross peak intensity for the Cα-C′ region of the spectrum. DREAM, on the other hand, proved to be the best sequence for magnetization transfer within the aliphatic region being twice as efficient as all the other sequences tested. Repeating this analysis for δ₁ slices other than 54 ppm led to essentially the same results given in Table 1 (data not shown).

Table 1.

Comparison of transfer efficiencies of different recoupling sequences based on the 1D slice corresponding to δ₁ of 54 ppm (Figure 1). The total transfer efficiencies as well as the transfer efficiencies from Cα to C′, the side-chain (aliphatic) and aromatic carbons are given. All transfer efficiencies are calculated as % of the diagonal peak at δ₁ of 54 ppm from a ¹³C-¹³C spectrum without mixing. RFDR generated the highest overall transfer efficiency but led, as most of the other sequences, primarily to strong Cα-C′ peaks. DREAM on the other hand proved to be more than twice as efficient for the aliphatic carbons as all the other sequences. Therefore, DREAM is the pulse sequence of choice if high transfer between C and other aliphatic carbons such as sidechain carbons is needed.

Pulse sequence	Total transfer efficiency	Transfer to C′	Transfer to aliphatic	Transfer to aromatic
RFDR	48 (±4) %	33 (±1) %	14 (±2) %	1 (±1) %
DONER	42 (±4) %	26 (±1) %	14 (±2) %	2 (±1) %
DARR	38 (±4) %	25 (±1) %	13 (±2) %	-
PDSD	19 (±4) %	9 (±1) %	10 (±2) %	-
TOBSY	29 (±4) %	22 (±1) %	7 (±2) %	-
aTOBSY	31 (±4) %	18 (±1) %	13 (±2) %	-
SPC5	16 (±4) %	8 (±1) %	8 (±2) %	-
DREAM	37 (±4) %	4 (±1) %	33 (±2) %	-

Both the hard pulsed TOBSY and the adiabatic TOBSY showed low transfer efficiencies in our experiments. This can be explained by the strong relaxation during the mixing time of the TOBSY sequence: TOBSY is a mostly T_1ρ limited sequence because of the longer optimal mixing times required by the relatively weak J coupling. Therefore, we observed a stronger overall magnetization decay during the TOBSY mixing than for DREAM and the T₁ limited sequences RFDR and DONER. This explains why the TOBSY and aTOBSY sequence give only 25% overall absolute transfer efficiency when the transfer efficiency is calculated as described above. (In contrast, if we compared the transfer between cross peaks and diagonal within the same spectrum, i.e. without relaxation correction, we would obtain apparent transfer efficiencies of 71% and 61% for TOBSY and aTOBSY, respectively.) The SPC5 sequence also showed low absolute transfer efficiency because most of the magnetization decayed during the mixing time (If we compared the transfer between cross peaks and diagonal within the same spectrum, we would obtain apparent transfer efficiencies of 69%). Similar magnetization losses during continuous phase modulated, i.e. C and R-type, mixing sequences have been observed by others [37]. These magnetization losses probably come from pulse imperfections and could be instrument dependent.

All 2D spectra shown in Figure 1 are asymmetric because we used ¹H-¹³C CP as preparation sequence. CP leads to strong Cα, C′ magnetization at short contact times since these are the carbon spins closest to the only proton source, the amide protons. The Cβ peaks are stronger than Cγ, Cδ peaks due to the same reason. During the mixing time, magnetization mainly transfers from C′ to Cα and side chain carbons, and also from Cα to C′ and the side chain carbons, but not from the sidechain carbons causing an asymmetric appearance of the spectrum. DREAM spectra are also inherently asymmetric even at equal carbon magnetization at the beginning of the recoupling [38]. Therefore, the DREAM spectrum in Figure 1 is clearly asymmetric. Nevertheless, virtually all of the cross peaks are present on one side of the diagonal or the other, when compared with protonated ubiquitin 2D spectrum taken by Zech and coworkers [39] (with only a very few Val, Leu, and Ile Cγ and Cδ cross peaks as exceptions, see Supplemental Figure 4).

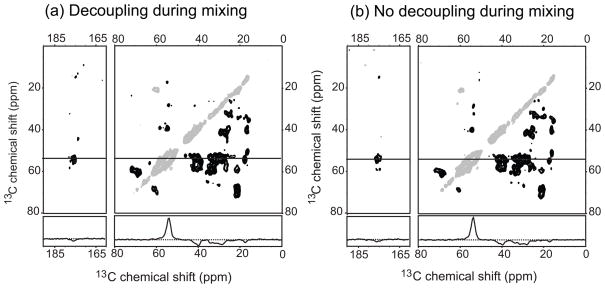
The data presented above show that, generally, perdeuteration permits ¹³C-¹³C mixing without the need of ¹H or ²H decoupling at relatively low MAS frequencies with high efficiency. To further prove this point, we recorded a DREAM spectrum with and without high-power ¹H decoupling during the DREAM recoupling step. As can be seen in Figure 2, both spectra look essentially the same. The transfer efficiency within the aliphatic, and from the aliphatic to carbonyl at δ₁ slice at 54 ppm decrease about 1% each. This similarity in transfer efficiency is a remarkable result considering that ¹H-¹³C cross polarization still gives a higher signal than direct ¹³C excitation, i.e. ¹H-¹³C dipolar couplings are present in our sample.

Figure 2.

2D DREAM ¹³C-¹³C correlation spectra of perdeuterated ubiquitin microcrystals at 400 MHz. (a) Spectrum recorded with 95 kHz CW proton decoupling during DREAM mixing. (b) Spectrum recorded without proton decoupling. Note that the transfer efficiency is similar (check 1D slice at δ₁ = 54 ppm) and the transfer pattern is relatively complete in both spectra. This figure shows that high-power proton decoupling during the DREAM mixing time is not necessary for perdeuterated proteins.

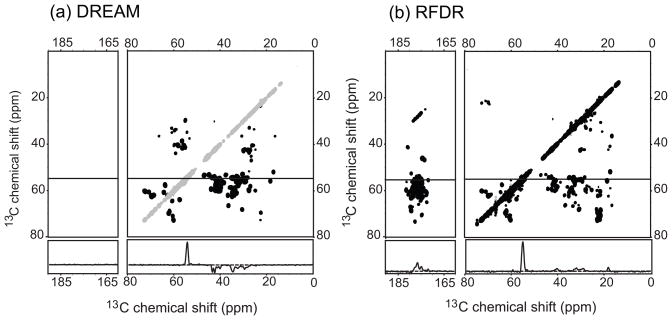
The results obtained on a 400 MHz spectrometer appear to translate well to higher fields, as illustrated with RFDR and DREAM spectra collected at 750 MHz and 14 kHz MAS shown in Figure 3. The overall transfer profile is the same under these conditions: RFDR leads to broadband mixing and relatively strong Cα-C′ cross peaks, DREAM leads to very high transfer efficiency in the aliphatic region of the spectrum.

Figure 3.

2D DREAM (a) and RFDR (b) ¹³C-¹³C correlation spectra of perdeuterated ubiquitin microcrystals recorded on a Bruker 750 MHz spectrometer. The transfer efficiency is good and the transfer pattern is relative complete in the case of both sequences. In that respect the result is very similar compared to the data recorded at 400 MHz. On the other hand the resolution is superior as expected and comparable to spectra recorded on fully protonated ubiquitin under high-power proton decoupling at 750 MHz (see Supplemental Figure 4).

Residual ¹H and ²H couplings during t₁ and t₂ could influence the linewidths of the peaks in these spectra. Nevertheless, as can be seen from Supplemental Figure 5 and 6 neither ¹H nor ²H decoupling, nor the decoupling of both ¹H and ²H had a relevant influence on the linewidth of our spectra. These results are similar to the results of Morcombe and co-workers [11], who recorded high-resolution spectra of perdeuterated ubiquitin without the need of any ¹H nor ²H decoupling at a ¹H Larmor frequency of 800 MHz and 20 MHz MAS.

In summary, except for PDSD and DARR, i.e. sequences which essentially rely on the presence of a dense ¹H bath, all sequences perform well on perdeuterated proteins and show similar magnetization transfer patterns as when applied to fully protonated samples. RFDR, among the most robust and easy to set up pulse sequences tested, showed the highest overall transfer efficiency. However, broad banded mixing sequences typically lead to an accumulation of magnetization at the end of carbon chains [16] and, therefore, to strong Cα-C′ cross peaks. This can be a problem since strong Cα-C′ cross peaks lower the sensitivity of Cα-side chain cross peaks, which are often the main focus of the investigation especially when the Cα-C′ cross peaks are unresolved. The Cα-CX cross peaks are often better resolved than Cα-C′ cross peaks and contain important information about secondary structure. DREAM is the mixing sequence of choice to get the most intense Cα-CX cross peaks since it has by far the highest transfer efficiency in the aliphatic region of the spectrum. The negative cross peaks associated with the double quantum transfer make DREAM straight forward to optimize in a 1D version of the experiment. The high performance of the DREAM sequence is particularly noteworthy since a spin-lock field as low as ~4 kHz at the HORROR condition was employed without dramatic magnetization decay. Furthermore, the DREAM recoupling was not limited to the aliphatic region, but also clear Cα-C′ cross peaks in the spectra recorded at 400 MHz. Therefore, the combination of perdeuteration with the DREAM sequence makes it possible to record intense, low power 2D ¹³C-¹³C correlation spectra at moderate MAS frequencies. Moreover, only a double-resonance probe was used, and potentially a single channel probe could be used.

What is the prospect of these results at high MAS frequencies? DREAM was shown to work especially well at high MAS frequencies extending its recoupling bandwidth to the entire ¹³C chemical shift range [29]. Furthermore, both DREAM and RFDR were shown to perform well without the need of ¹H decoupling at high MAS frequencies even on fully protonated samples [30,31]. We expect them to work equally well on perdeuterated samples under the same conditions. In this manuscript we showed that fast MAS is not essential, and that perdeuteration and slow MAS constitute a good alternative to fast MAS, since they permit high-resolution 2D spectra with good transfer efficiencies and without sample heating due to MAS or high power ¹H decoupling.

Conclusions

Apart from proton assisted pulse sequences such as DARR and PDSD all homonuclear-mixing sequences tested, performed very well on perdeuterated ubiquitin at relatively modest MAS frequencies and without any ¹H and ²H decoupling. Therefore, perdeuteration makes it possible to record high quality 2D homonuclear correlation spectra with virtually no sample heating coming from MAS or ¹H decoupling. We found that RFDR showed the highest overall transfer efficiency and DREAM gave the most intense cross peaks in the aliphatic region of the spectrum. Both sequences are robust and easy to set up and, therefore, form a very good alternative to DARR for perdeuterated samples.

Experimental

NMR

Solid-state NMR spectra at 400 MHz were recorded on a Varian Infinityplus spectrometer. DREAM and RFDR were performed using a 4 mm Apex (Chemagnetics) probe. For all the other sequences, we used a 4 mm T3 probe. Depending on the pulse sequence, samples were spun at a MAS frequency of 8 kHz or 8.333 kHz. The sample temperature was ~2°C (VT= 0°C). The CP rf-field strengths for all pulse sequences were 50 and 58 kHz for ¹³C and ¹H, respectively, with a contact time of of 1 ms. ¹³C and ¹H hard-pulses were done with rf-field strengths of 50 and 100 kHz, respectively. The amplitude of the DREAM sweep was approximately 4 kHz (shape parameters: β/2π=1.4 kHz, Δ/2π=0.7 kHz following [40]) and the mixing time was 2 ms. The RFDR mixing time was 3 ms. The DONER sequence follows the conditions described by Akbey and co-workers: ¹H and ²H were irradiated simultaneously using a rotary resonance condition (ω_1H = ω_2H = 8 kHz). The mixing time for DONER, DARR, and PDSD sequences was 50 ms.

The non-adiabatic TOBSY was recorded using a Post C9¹₃ mixing sequence with 8.333 kHz MAS, a ¹³C rf-field strength of 50 kHz, and a mixing time of 7.5 ms [23]. The adiabatic TOBSY was recorded using a Wurst inverse Wurst (WiW) C9¹₁₈ mixing sequence with 8.333 kHz MAS and a mixing time of 4.3 ms [25]. The 120 μs long Wurst pulses were done with an exponent of q=9, and a maximum rf-field strength of 70 kHz. As for the other sequences, no ¹H decoupling was applied during the TOBSY mixing.

The SPC5 spectrum was recorded with 8 kHz MAS using a ¹³C rf-field strength of 40 kHz and a mixing time of 1 ms [41].

The spectral width was 40 kHz in both the direct and indirect dimensions, and 512 and 300 points were acquired in the t₁ and t₂ dimensions, respectively. No ¹H and ²H decoupling was employed during t₁ and t₂.

The high-resolution 2D DREAM, and 2D RFDR spectra (shown in Figure 3 and Supplemental Figure 4 and 5) were recorded on a Bruker 750 MHz Advance II spectrometer using a 4 mm triple resonance HXY probe operating at 14 kHz MAS. The CP rf-field strengths for all the pulse sequences were 40 and 54 kHz for ¹³C and ¹H, respectively and the contact time of the CP was 1 ms. ¹³C and ¹H hard-pulses were performed with rf-field strengths of 40 and 100 kHz, respectively. The amplitude of the DREAM sweep was approximately 7 kHz and the mixing time was 2 ms. The RFDR mixing time was 3 ms. The spectral width was 94 kHz in both the direct and indirect dimension, and 2048 and 768 points were acquired in the t₁ and t₂ dimensions, respectively. For some of the spectra waltz decoupling of 5 kHz on ¹H and 2.5 kHz on ²H was applied during t₁ and t₂. No decoupling was applied during the ¹³C mixing sequences.

NMR spectra were processed and analyzed using the following programs: NMRPipe, SPARKY, SciPy.

Protein Expression

The expression of uniformly ²H, ¹³C, and ¹⁵N labeled ubiquitin was done following a protocol similarly to the one described by Tugarinov and co-workers except that E. coli cells were slowly adapted to deuterated M9 minimal medium by going from a starter culture in 50 ml LB, 0% D₂O into a sequence of M9 minimal media containing varying amounts of D₂O: 350 ml 0% D₂O, 2 l 70% D₂O, and 1 l 97–99% D₂O. After the expression, ubiquitin was purified as follows: The cell pellet was redissolved in 20 ml glacial acetic acid. The cell lysate was centrifuged at 4,000 g for 1 hr. The supernatant of this spin was neutralized to pH ~ 5 with addition of 5 M KOH. This solution was then dialyzed twice against deionized water and a third time against 50 mM pH 4.5 ammonium acetate solution. The cell lysate was loaded onto a SP sepharose column equilibrated with 50 mM ammonium acetate, pH 4.5 and eluted with 50 mM ammonium acetate, pH 5.5. Purity and labeling degree of ubiquitin was confirmed by mass spectrometry. Purified ubiquitin was crystallized at 4°C by a batch method in 51% 2-methyl-2,4-pentanediol (MPD), 10% ethylene glycol, and 20mM citrate buffer, pH 4.0–4.2. Protonated buffers and solutions were used during purification (including a protein unfolding step) and crystallization, leading to an essentially complete introduction of protons in all amides and exchangeable sidechain moieties.