Further Studies on the Anisotropic Distribution of Collagen in Articular Cartilage by μMRI

Abstract

To further study the anisotropic distribution of the collagen matrix in articular cartilage, microscopic MRI (μMRI) experiments were carried out on articular cartilages from the central load-bearing area of three canine humeral heads at 13-μm resolution across the depth of tissue. Quantitative T₂ images were acquired when the tissue blocks were rotated, relative to B₀, along two orthogonal directions, both perpendicular to the normal axis of the articular surface. The T₂ relaxation rate (R₂) was modeled, by three fibril structural configurations (solid cone, funnel and fan), to represent the anisotropy of the collagen fibrils in cartilage from the articular surface to the cartilage/bone interface. A set of complex and depth-dependent characteristics of collagen distribution was found in articular cartilage. In particular, there were two anisotropic components in the superficial zone and an asymmetrical component in the radial zone of cartilage. A complex model of the 3D fibril architecture in articular cartilage is proposed, which has a leaf- or layer-like structure in the radial zone, arises in a radial manner from the subchondral bone, spreads and arches passing the isotropic transitional zone, and exhibits two distinct anisotropic components (vertical and transverse) in the surface portion of the tissue.

Introduction

Structural architecture of articular cartilage plays a critical role in the biomechanical functions and morphological properties of the tissue as a load-bearing material in joints (1–6), whose degradation is the hallmark of clinical joint diseases such as osteoarthritis. Since the collagen fibril is the principal macromolecule that provides a depth-dependent structural integrity to articular cartilage (7), continuing efforts have been focused on the specific features of the 3D collagen structure in cartilage. Histologically, the collagen matrix in non-calcified cartilage is commonly considered to contain three structural zones from the articular surface to the cartilage-bone interface, namely, the superficial zone (SZ) with the collagen fibrils parallel with the tissue surface, the transitional zone (TZ) with mostly random fibrils, and the radial zone (RZ) with the perpendicular fibrils anchored to the underlining bone. These depth-dependent features of the collagen matrix become the fundamental components in several fibril models in literature, including the arcade model (8) where the collagen fibrils arise in a radial manner from the subchondral bone, pass towards the surface through the TZ obliquely, and return to the bone; the columnar arrangement (9,10) where the collagens are arranged in a columnar manner, which could be traced from the calcified cartilage to their oblique orientation in the tangential tissue matching the concept of the arcade model; and the leaf model (3,5,10,11), where the collagens are arranged in a series of closely packed layers or leaves in the RZ and arches in the TZ to form the horizontally orientated leaves in the SZ.

The structural orientation of collagen matrix in cartilage can result in various anisotropic appearances in modern imaging experiments (7), such as the magic angle effect in magnetic resonance imaging (MRI) (12,13) and the birefringence in polarized light microscopy (PLM) (14,15). Since the values of T₂ relaxation in MRI of tendon and cartilage is known to be sensitive to collagen structure and fibril orientation relative to the static magnetic field B₀ (16–20), T₂ has been used as a molecular-level parameter to assess the structural integrity of the tissue (21,22). The use of T₂ to quantitatively monitor the collagen distribution in cartilage requires the rotation of the tissue block in B₀ and the analysis of the anisotropy of T₂ at different orientations.

For any 3D object in the Cartesian coordinate, there are in general three rotational axes, termed as the regular (x), cross (y) and planar (z) rotations in this report (Fig 1). In most MRI rotational experiments of articular cartilage, the specimen is rotated in either regular or cross direction relative to B₀, which is in parallel with the surface normal axis (z). Coupled with an imaging slice perpendicularly to the rotational axis, a single 2D image will contain all three histologic zones of the tissue (12). Neither regular nor cross rotation, however, could determine the structural orientation of the collagen within the SZ cartilage, a phenomenon termed as the ‘ambiguity of the surface collagen orientation’ in literature (20). Recently, a quantitative Microscopic MRI (μMRI) study mainly by planar rotation was completed (23), which revealed the anisotropic distribution of the collagen fibrils within the surface layer of cartilage.

Fig 1.

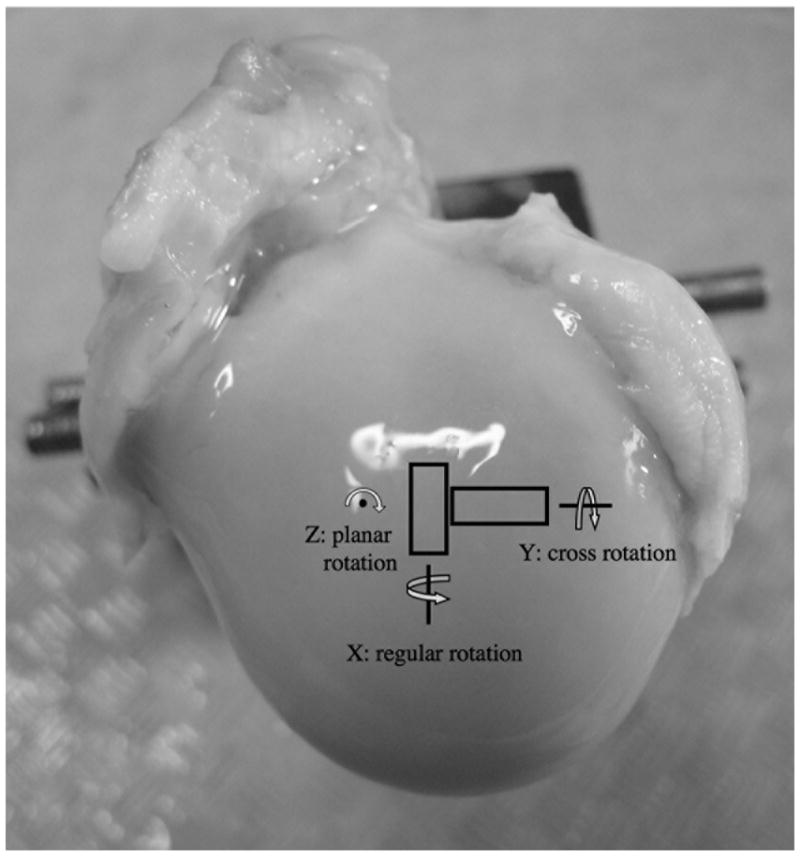
The orientations of the tissue blocks on the humeral head and the two rotational axes (regular and cross) of the imaging experiments. B₀ is in the normal direction of the cartilage surface, in parallel with the z direction. (The planar rotation was not carried out in this project.)

This work further investigated the 3D structural anisotropy of the collagen matrix in articular cartilage from SZ to RZ, by rotating the cartilage along two orthogonal axes (regular rotation and cross rotation in Fig 1) relative to B₀, both perpendicular to the normal axis of the articular surface. A collagen matrix with a z-axial symmetry would produce an identical result in both regular and cross rotations. Any difference between these two rotations would consequently indicate an anisotropic structure of 3D collagen matrix along the z-axis. To the best of knowledge, an investigation of this type of tissue anisotropy had not been systematically carried out. μMRI experiments in this project were completed at 13 μm resolution along the direction of the tissue depth (z). Quantitative T₂ anisotropy data were fitted with three fibril structural models to determine the 3D anisotropic distribution of the collagen matrix in articular cartilage.

Materials and Methods

Cartilage Specimens

Seven specimens of full thickness of articular cartilage that was still attached to the underlying bone were harvested from three canine humeral heads and kept at −20°C until the μMRI experiments. These dogs were skeletally mature and healthy, sacrificed for an unrelated experimental study. From the central load-bearing area of each humeral head, one pair of cartilage specimens was harvested in such a way that the two specimens were located next to each other and perpendicular to each other lengthwise, as shown schematically in Fig 1. Each specimen had a dimension of about 1.75 mm (width)× 2 mm (depth) × 4 mm (length). The two specimens in each pair were used for the regular and cross rotational experiments, respectively. One additional specimen was harvested from one of the joints, used first for the regular rotational experiment and trimmed afterwards for the cross rotational experiment. All specimens were bathed in physiological saline with 1 % protease inhibitor (Sigma, Missouri) and sealed in precision glass tubes with an internal diameter of 2.34 mm.

Microscopic MRI Method

Microscopic MRI experiments were conducted at room temperature on a Bruker AVANCE II 300MHz NMR spectrometer equipped with a 7-Tesla/89-mm vertical-bore superconducting magnet and micro-imaging accessory (Bruker Instrument, Billerica, MA). A homemade 3-mm solenoid coil was used to image all specimens under the identical experimental parameters for the quantitative T₂ mapping where a rotational device was incorporated into the system (20). Briefly, at each specimen orientation, the specimen was imaged using a magnetization-prepared T₂ imaging sequence (12,19,22) which had a well-separated CPMG T₂-weighting segment that contained no gradient pulse, and a subsequent spin-echo imaging segment where all timings were kept constant. This sequence is capable of the measurement of the intrinsic T₂ in the tissue (22). The echo spacing in the CPMG T₂-weighting segment was 1 ms, and the number of echoes was 2, 4, 12, 50, 100, which corresponded to five echo delays of 2, 4, 12, 50, 100 ms respectively for the five T₂-weighted images. The imaging parameters were: the echo time in the imaging segment was 7.2 ms; the field of view was 0.32 cm × 0.32 cm; the imaging matrix size was 128 × 256 (256 was in the readout direction), which resulted in a pixel resolution of 26 μm × 13 μm (13 μm was in the cartilage depth direction); the slice thickness was 1 mm; the spectral bandwidth was 50 kHz, corresponding to a readout sampling dwell time of 20 μs; 0.8 ms and 0.507 ms hermite shape pulses were used as excitation and refocusing pulse in the imaging segment, respectively; the repetition time (TR) of the imaging experiment was 2 seconds. From these intensity images, the T₂ relaxation in cartilage was calculated by a single exponential fitting of the data on a pixel-by-pixel basis, which is based on the assumption that there is only one T₂ component in articular cartilage (22).

Modeling the Anisotropy of T₂ Relaxation

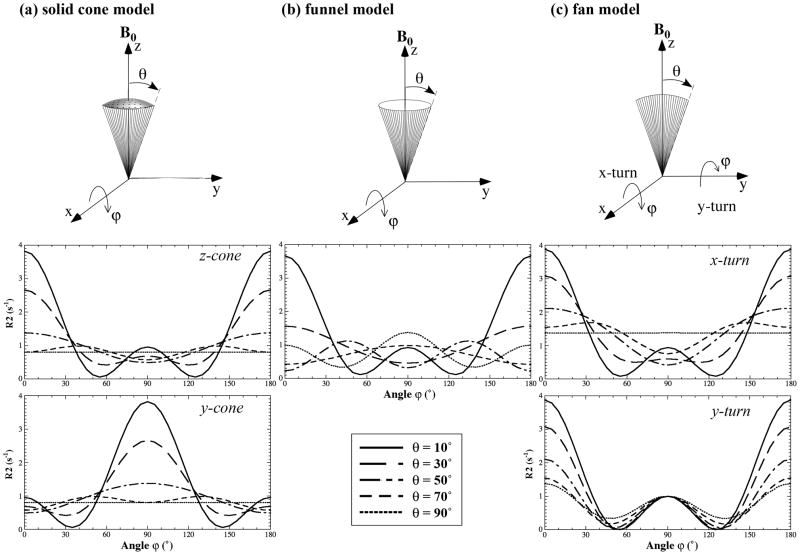
To probe the T₂ anisotropy at different depths in cartilage during specimen rotations, three distributions of collagen were developed, schematically shown in Fig 2 as the solid cone distribution (Fig 2a), the funnel distribution (Fig 2b) and the fan distribution (Fig 2c). Each fibrillar distribution has a (half) span angle θ and contains an identical ‘shadow’ part pointing in the opposite direction from the viewpoint of dipolar interaction. When θ becomes 90°, for example, the cone model in Fig 2a will have the shape of a half spherical ball, which is equivalent to a full spherical ball because of the ‘shadow’ portion of the dipolar interaction. The major difference between the solid cone and the funnel model is that the fibrils in the funnel are distributed on the funnel edge wall whereas the fibrils in the solid cone are distributed homogeneously inside the cone. The cone can be oriented along the z-axis (z-cone) or y-axis (y-cone). The fan can be rotated along the x-axis (x-rotation) or y-axis (y-rotation). These models were constructed based on our results of the collagen distribution (20,23) and adapted some structural elements from other studies in literature (3,5,8–11). The length of the lines in these models has an arbitrary unit, reflecting the ‘amount’ of the fibrils that play an active role in the T₂ anisotropy.

Fig 2.

The schematics of the collagen distribution models: (a) the solid cone model, (b) the funnel model, and (c) the fan model. θ and ϕ represent the half span angle of the fibril configuration and the rotational angle of the fibril structure, respectively. The plots under each fibril model are the simulated results using Eq. (1).

The T₂ relaxation rate R₂ (R₂ = 1/T₂) follows the square of the dipolar interaction, R₂ ∝(1−3cos² α)², where α is the inclination angle between the directions of B₀ and an individual dipole moment (19,24–26). Consequently, the following equation was used for any given distribution function f(α,β),

$$R_2\propto a+b\underset{0}{\overset{\pi }{\int }}\underset{0}{\overset{2\pi }{\int }}f(\alpha ,\beta ){(1-3{cos}^2\alpha )}^{2}d\alpha d\beta$$ (1)

where a and b are two constants representing the isotropic and anisotropic ‘amount’ of the collagen matrix involved in the calculation, respectively; and β refers to the azimuth angle of the direction of an individual dipole moment. The modeling of the experimental data was implemented with the MatLab codes (MathWorks, Natick, MA). Note that the symmetry of the fibril distributions along the opposite direction is assured with the square function in Eq. (1).

Results

The anisotropies of R₂ were simulated using Eq. (1) (a = 0, b = 1) with a 5° increment of rotational angle ϕ from 0° to 180° based on the three models of the collagen configuration. Five representative data are shown in Fig 2. For the cone model of fibril configuration (Fig 2a), a θ of zero (i.e., a bundle of fibrils along the z axis) results in the maximum anisotropy and a θ of 90° (i.e., a spherical ball of fibrils) results in no anisotropy. The anisotropy of the y-cone is phase-shifted in ϕ from the anisotropy of the z-cone by 90°. For the funnel model of fibril configuration (Fig 2b), a θ of zero results in the maximum anisotropy as expected (i.e., identical to the solid cone at θ = 0°), and a θ of 90° (i.e., a circular sheet of fibrils in the x-y plane) will still result in a finite anisotropy. For the fan model of fibril configuration (Fig 2c), small θs (e.g., 10°) result in nearly identical anisotropy for both x-rotation and y-rotation (also nearly identical to the cone and funnel at θ ~ 0°). At θ of 90° (i.e., a circular sheet of fibrils in the y-z plane), the x-rotation of the fan configuration will cause no anisotropy, but the y-rotation will result in a finite anisotropy that is identical to the funnel model at θ = 90°, except for a 90° phase shift in ϕ.

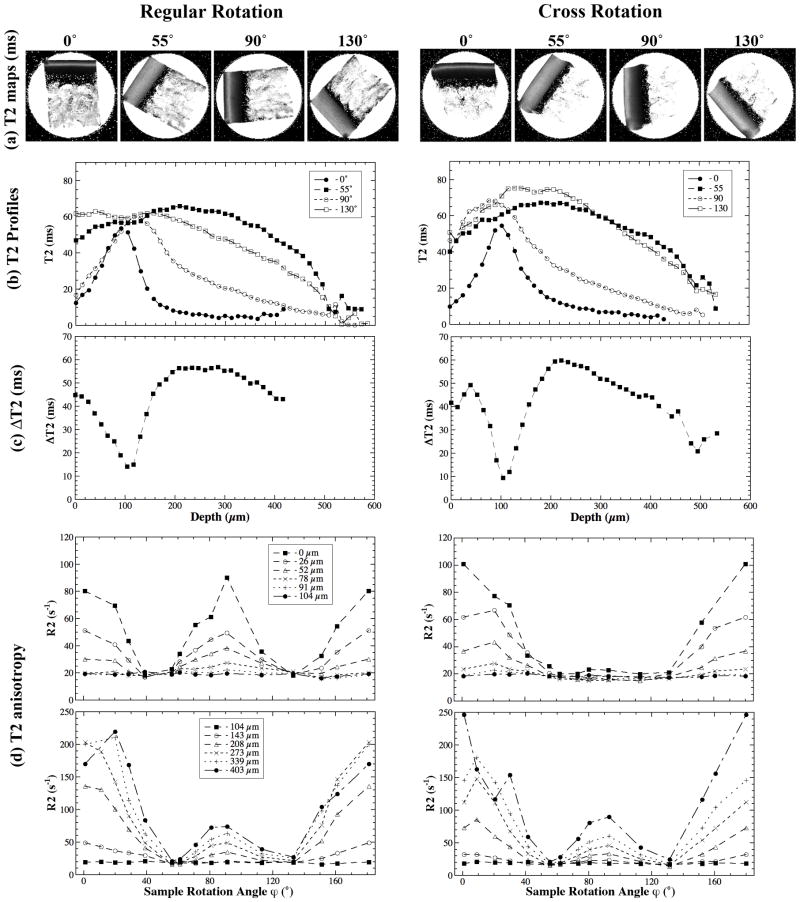
Fig 3 summarizes the experimental results of the regular and cross rotations from a pair of representative specimens, which were similar to those from a single specimen in both regular and cross rotational experiments. The T₂ images and profiles shown in Fig 3a and 3b are highly consistent with the previous observations of cartilage characteristics in μMRI (19), where a laminar appearance of cartilage is clearly visible when the tissue is oriented at 0° (the angle between the surface normal axis and B₀). The minimization of the dipolar interaction at 55° restored the image intensity to a relatively uniform appearance. Fig 3c shows the maximum variation of T₂ among all rotational angles during the regular and cross rotation as a function of the tissue depth. The minimum of ΔT₂ value in both rotational experiments occurred at around 100 μm from the cartilage surface, which is approximately the center of the transitional zone based on our previous PLM study, using the nearly identical specimens (15).

Fig 3.

T₂(R₂) anisotropy of articular cartilage during regular and cross rotations. (a) T₂ images at selected orientations. (b) T₂ profiles as the function of tissue depth relative to cartilage surface. (c) The max variation of the T₂ at each tissue depth. (d) The depth-dependent anisotropy profiles of R₂ at some selected tissue depths.

By plotting the R₂ values as a function of the specimen rotational angle (ϕ) at each pixel location (every 13 μm) along the tissue depth, we have examined the characteristics of the R₂ anisotropy in the specimen due to the regular and cross rotations over the entire tissue depth, summarized in the four plots in Fig 3d. Clearly, the R₂ anisotropy was different between the regular rotation and cross rotation. Several distinct features can be identified from these anisotropic profiles.

Firstly, the T₂ anisotropy for the SZ tissue had significant difference between the regular rotation and the cross rotation (the plots of 0 μm, 26 μm, 52 μm from the cartilage surface in Fig 3d), which demonstrates the anisotropic distribution of the collagen fibers in the SZ when viewed from these two orthogonal directions. Secondly, the R₂ value at ϕ = 90° was similar to or even slightly higher than that at 0° for the SZ cartilage during the regular rotation (the top left plot in Fig 3d), which suggested that a collagen model with two fibril bundles, the main axis of one bundle at 0° and the other at 90° relative to B₀, should be used in data modeling. At the same time, the R₂ value at ϕ = 0° was much higher than that at ϕ = 90° for the SZ cartilage during the cross rotation (the top right plot in Fig 3d), which suggested that a collagen model with only one bundle with its main axis at 0° relative to B₀ could be used in data modeling. Thirdly, the R₂ anisotropy in the TZ (located approximately from 80 μm to 120 μm from the cartilage surface for this type of canine tissue) was not very obvious, which confirms the general understanding that the collagen organization in the TZ is approximately isotropic. Consequently, the differences between the regular and cross rotational experiments were small for the TZ cartilage. Finally, the T₂ anisotropies in the RZ were strong and had comparable profiles for the two rotational experiments. Since the relative value of R₂ at 0° and 90° is different between the regular and cross rotational experiments, a symmetric model (e.g. the solid cone model (Fig 2a) and the funnel model (Fig 2b)) cannot be used to model the results because of its symmetric property during x-rotation and y-rotation. Instead, a fan model best predicted the measured R₂s.

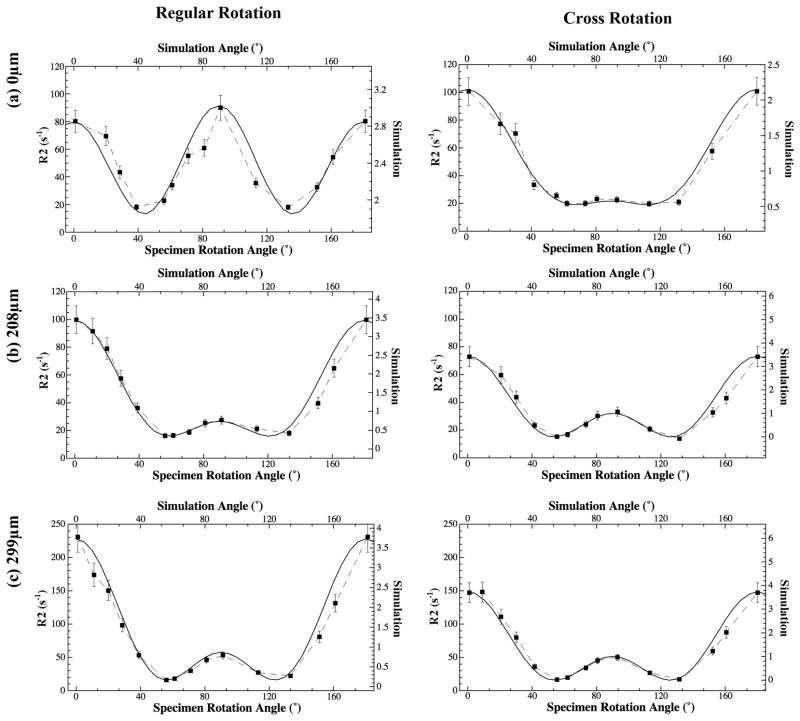
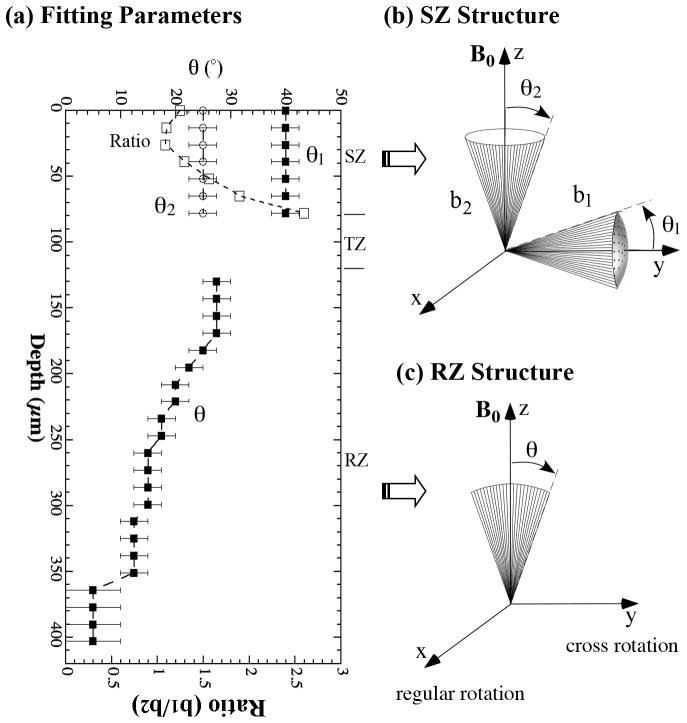
The modeling of these anisotropic profiles was carried out at each tissue depth from the cartilage surface (every 13 μm) using all experimental rotation data, where two simple criteria were applied during modeling. First, the number of fibril elements used to simulate the experimental data should be as few as possible. Second, and most importantly, a set of common fitting parameters (including span angle and the relative amount of different modeling elements) must be valid for both the regular and cross rotation results at each tissue depth. A set of representative fittings is shown in Fig 4, and all fitting parameters are summarized in Fig 5a, together with the schematic models in Fig 5b and Fig 5c.

Fig 4.

The representative fitting of the R₂ anisotropy profiles using Eq.(1), (a) the articular surface, (b) the upper part of radial zone, and (c) the middle part of the tissue (in the radial zone).

Fig 5.

The trends of the orientation fitting parameters as the function of tissue depth, using the schematic models shown in Fig 2. The fibril structure in the superficial zone and radial zone are shown schematically in (b) and (c) respectively.

For the SZ cartilage (approximately from 0 μm to 80 μm), two collagen bundles are best to model the R₂ anisotropy as the function of the rotational angle ϕ (Fig 5b). The span angles of the horizontal bundle (a solid cone model) and vertical bundle (a funnel model) were ~ 40° and 25°, respectively. An interesting observation was the ratio of the two anisotropic amount of collagen fibrils (b₁/b₂, where b₁ and b₂ are the relative amounts of horizontal and vertical bundles, which were adjusted manually to best fit the experimental data) increased from about 1.25 at the 0-μm depth to about 2.6 at the 78-μm depth. The data in the TZ cartilage (~ 80 μm–120 μm) was not fitted due to the lack of sizeable anisotropy. For the RZ cartilage (≥ 130 μm), the best model to simulate both regular and cross rotations simultaneously was a single fan configuration (Fig 5c), whose span angle decreased from about 27° at the 130-μm depth to about 12° at the 351-μm depth. A smaller angle between 0° and 10° could be used for the tissue beyond the depth of 351 μm in the RZ, which confirms that the deep part of the RZ cartilage indeed contains very organized fibrils perpendicular to the cartilage surface. The subtle differences in the R₂ anisotropy between the regular and cross rotations suggested that the collagen structure in the RZ cartilage was not completely symmetrical in the x-y plane (which is in parallel with the articular surface), which implied the need for a leaf- or layer-structure in the RZ.

Discussion

In this project, the regular and cross rotational experiments were performed to study the anisotropic property of cartilage tissue from the central load-bearing area of the humeral head, respectively. If the collagen structure in cartilage had a symmetric 3D structure about its surface normal axis, one would expect that the results from these two orthogonal rotational experiments to be identical. The results in this project clearly showed distinct differences between these two rotational experiments, especially for the superficial zone of the tissue, discussed in the following for each histological zone.

In the SZ cartilage, the collagen distribution in the modeling contained two anisotropic components. One anisotropic component (the b₁ bundle in Fig 5b) was aligned approximately along the transverse (y) direction of the humeral head, and the other anisotropic component (the b₂ bundle in Fig 5b) was aligned perpendicular to the cartilage surface along the z direction (the direction of the surface normal axis). The transverse y-bundle is highly consistent with the results in one of our previous studies (23), which represents the non-random distribution of the horizontal fibrils in the SZ cartilage and relates in some way to the split-line appearance of the cartilage surface (1,3,27–32). The identification of the vertical z-bundle in the SZ cartilage, which was the strongest near the cartilage surface (the smallest ratio in Fig 5a), was unmistakable since the y-bundle had no effect on the R₂ variation during the cross rotation. As one moves away from the articular surface, the relative amount of the transverse y-bundle actually increased (bigger ratios), which seems to be counter-intuitive according to the knowledge of the fibril structure. However, we emphasize that both “transverse y-bundle” and “vertical z-bundle” are just the anisotropic components, and that the absolute amount of both bundles decrease significantly with an increase of tissue depth (in other words, the isotropic component increases), which is evident by the increase of average T₂ values during rotation in Fig 3b and the decrease of ΔT₂ in Fig 3c with the increase of depth.

In the TZ cartilage, the collagen distribution was relatively isotropic, which is consistent with the general understanding in the literature (33,34). The anisotropic variation of R₂ relaxation during regular and cross rotations in this project was smaller than that in one of our previous MRI projects (23) when the nearly identical tissue block was rotated along the planar (z) direction. These smaller variations in the R₂ anisotropy among different rotational axes could be due to several factors, such as different sensitivities towards the fibril alignment during different rotational schemes. In a PLM project (15) where the retardation of the tissue was mapped, the TZ cartilage was found to have a small but finite value of retardance, which suggested that the randomness of the fibrils in the TZ is not completely perfect (3,35,36).

In the RZ cartilage, it is very interesting to find that the R₂ variation in the RZ cartilage during regular rotation is slightly different from that during cross rotation. The use of a fan model most closely matched this difference. Combined with the previous planar rotation result (23) which also showed the fan distribution of collagen in the upper part of RZ, it seems clear that the collagen fibrils are distributed in RZ in the form of an arched leaf-like structure, with a span angle from about 27° in the upper part of RZ to about 5°–10° in the deeper part of RZ.

Putting together the modeling parameters from this project (Fig 5a) and several previous reports of cartilage rotational experiments from our previous work (15,19,20,23), and referring to the cartilage structure models suggested by different models in literature (e.g., arcade model (8), leaf model (3,5,10,11) and columnar model (9,10)), the anisotropic part of the 3D collagen fibril architecture in articular cartilage from the central load-bearing area of a humeral head can be postulated to have the following configuration. Starting from the subchondral bone, the collagen fibrils are well organized, with a slight distortion along the y direction, hence adapting to a structure of so-called layer- or leaf-like shapes in literatures (3,5,10,11) (Fig 5c). The fibrils arise in a radial manner towards the transitional zone, with an increasing spreading of the fan structure only along the y direction. At the same time, the fibrils are increasingly arching away from the radial direction. Passing the transition zone with a nearly isotropic distribution of collagen, the combination of a vertical z-bundle and a transverse y-bundle was the best to describe the anisotropic distribution of collagen in the SZ.

Several subtle points should be emphasized here. First, the current rotational experiments only monitor the anisotropic part of the collage distribution. In other words, the isotropic component of the tissue configuration was not investigated. In reality, the amount of the isotropic collagen would dominate the configuration in some part of the tissue such as the TZ. Second, our simulation suggested that the leaf- or layer-like structure exists only in the RZ. Thirdly, there was often more than one option of the fibril model to simulate the same anisotropy data. For example, both cone model and funnel model could simulate the transverse and vertical bundles with slightly different span angles and relative quantities in the SZ. The final choice of the solid cone model for the horizontal bundle and the funnel model for the vertical bundle in SZ was based on the knowledge about collagen distribution in literature and the consistency among the neighboring pixels. Finally, there were some small (about 10%) but noticeable degrees of tissue degradation during the course of the quantitative imaging experiments, which was evident when comparing the quantitative T₂ of cartilage from two identical imaging experiments (both at 0°), one at the onset of the imaging series and one at the end the imaging series. The effect of tissue degradation on the T₂ measurements was compensated in the post-processing according to the order of individual experiments based on the assumption that the duration of degradation had a linear influence on T₂ (37).

Conclusion

In summary, the μMRI rotational experiments along two orthogonal directions (the longitude x and transverse y directions of the humeral head) were performed to study the architecture of the collagen matrix in articular cartilage from superficial zone to radial zone. The experimental data from microscopic imaging was used to formulate a complex model to describe the collagen fibril orientation in articular cartilage. In this architecture, the collagen fibrils have a leaf- or layer-like shape distribution in RZ, which arises in a radial manner from the subchondral bone, spreads and arches toward the isotropic transitional zone; in the SZ, a vertical z-bundle and a transverse y-bundle are needed to describe the anisotropic distribution of collagen in SZ. To the best of our knowledge, this collagen architecture is different from any other models in the literature, which could contribute to a better understanding of the fibril structure and its disruption in the event of clinical diseases such as osteoarthritis.