Abstract
Unicellular organisms are typically found to have a characteristic cell size. To achieve a homeostatic distribution of cell sizes over many generations requires that cell length is actively sensed and regulated. However, the mechanisms by which cell size is controlled remain poorly understood. Recent experiments in fission yeast have shown that cell length is controlled in part by polar gradients of the protein Pom1 together with localized measurement of concentration at midcell. Dilution as the cell grows leads to a reduction in the midcell protein concentration, which lifts a block on mitosis. Here we analyze the precision of this mechanism for length sensing in the presence of inevitable intrinsic noise in the processes leading to formation and measurement of this gradient. We find that the use of concentration gradients allows for more robust length sensing than a comparable spatially uniform system, and allows for reliable length determination even if the average protein concentration throughout the cell remains constant as the cell grows. Optimal values for the gradient decay length and receptor dissociation constant emerge from maximizing sensitivity while minimizing the impact of density fluctuations.
Introduction
Under any given environmental conditions, cells are typically found to have a characteristic range of sizes (1). In proliferating cells, this distribution of sizes can be stable over several generations. Because cell growth and division will inevitably have some random variation, we would naturally expect this distribution of sizes to broaden over time. The observed invariance of cell size distributions means that size must be actively sensed and regulated (2). However, many questions remain about the molecular mechanisms by which growth and division are coupled (1).
It has long been believed that the cell cycle of fission yeast, Schizosaccharomyces pombe, is regulated by cell-size-dependent checkpoints at the G1/S transition and the initiation of mitosis (3–5). Recent experiments have clarified the mechanism of the mitotic size checkpoint (6,7). The protein Pom1 forms polar concentration gradients within the cell (8). Pom1 is an inhibitor of cell division, acting to localize the division factor Mid1 to the cell midplane (9,10). In addition, Pom1 phosphorylates and suppresses the activity of Cdr2, a promoter of mitosis, which localizes in nodes near midcell (6,7). In short cells the concentration of Pom1 at midcell is high, and hence Cdr2 activity is inhibited. As the cell grows, the concentration of Pom1 at midcell decreases; consequently Cdr2 becomes activated and the cell proceeds into mitosis. The Pom1 gradients in fission yeast appear similar to those of division inhibitors in bacteria, such as MipZ in Caulobacter crescentus (11) and MinCD in Bacillus subtilis (12,13) and Escherichia coli (14,15), raising the possibility that this is a more general mechanism for size control in unicellular organisms.
The use of concentration gradients of morphogen proteins to provide positional information in developmental systems is well established (16,17). In addition to promoting differentiation and specifying cell fate (18), some morphogens also regulate cell growth and proliferation (19,20), thereby providing positional cues for tissue growth. More recently, subcellular concentration gradients have also been observed in a wide variety of systems (21–24). It has also been shown theoretically that diffusion together with the localization of enzymes has the potential to generate gradients of protein activity (25) and concentration (26,27), and to regulate intracellular processes based on cell size and shape (28,29).
To determine whether the mechanism of length-sensing proposed by Martin and Berthelot-Grosjean (6) and Moseley et al. (7) is viable in vivo, it is important to analyze its robustness to biochemical noise. The formation of the protein gradient together with the measurement of the protein concentration will be subject to inevitable fluctuations due to the finite protein copy number, the discrete nature of biochemical reactions, and the intrinsic randomness of physical processes such as diffusion. These fluctuations will limit the precision with which any subcellular system can measure and regulate cell length. Previous analyses have addressed how reliably absolute position can be encoded in concentration gradients (30,31), and analyzed how noise in downstream reactions can affect position specification (32). In this article we analyze a simple model of the length-sensing mechanism proposed by Martin and Berthelot-Grosjean (6) and Moseley et al. (7) and estimate both the precision with which concentration gradients are able to provide information about cell length, and the precision with which this information can be decoded by a downstream detector.
To investigate the use of intracellular concentration gradients for size sensing, we consider a simple mathematical model of gradient formation on the cell membrane consisting of localized protein influx, diffusion, and uniform dissociation, and a detector which responds to the local concentration of the gradient protein at midcell. We show that the use of concentration gradients together with a localized concentration readout allows for more precise size-sensing than a comparable spatially uniform system of concentration measurement over a biologically relevant range of parameter values. Additionally, if the protein in question is constitutively expressed, such that its average concentration in the cell is held constant as the cell grows, spatial gradients still allow the cell to detect changes in length while a uniform system is no longer viable. Importantly, this means that the level of such a protein need not be regulated over the cell cycle. We show that these conclusions apply both for the protein gradient itself and the readout of this gradient by downstream signaling proteins. Finally, the simple model suggests that appropriate choices of the gradient length scale and detector dissociation constant can maximize the precision of length sensing.
Model
We consider a simple model of a bipolar concentration gradient on the membrane of a rod-shaped cell. As a starting point for our analysis we take a model for the dynamics of Pom1 recently considered by Padte et al. (10). In this model Pom1 associates with the membrane at cell poles. Once on the membrane, it is able to diffuse until spontaneous dissociation returns the protein to the cytoplasm. In the cytoplasm, Pom1 again diffuses until it returns to the cell pole and reassociates with the cell membrane. This cycle of localized membrane attachment and global dissociation is similar to mechanisms proposed by Lipkow and Odde (26) and Daniels et al. (27) for the establishment of intracellular concentration gradients via localized kinase and distributed phosphatase activity. However, here we are concerned not with the overall density of total protein, but only with the gradient of membrane proteins which is naturally generated in this model. We therefore make a number of simplifications to this model to simplify and generalize our analysis.
First, although Padte et al. (10) postulated a second polar inhibitor molecule to explain the symmetric positioning of Mid1 despite asymmetry in the Pom1 gradient, we instead consider only a single species of protein which forms a symmetric gradient by associating with the membrane at both cell poles. This is also reminiscent of the largely symmetrical gradients which are observed for bacterial cell-division inhibitors MipZ and MinCD (11–13).
Second, because we are primarily concerned with the effects of concentration gradients on the cell membrane, we neglect the explicit dynamics of the protein within the cytoplasm. Instead we simply model this recycling as an influx of proteins onto the membrane at the two cell poles. The appropriate choice for this flux will be discussed below. The model is shown schematically in Fig. 1.
Figure 1.
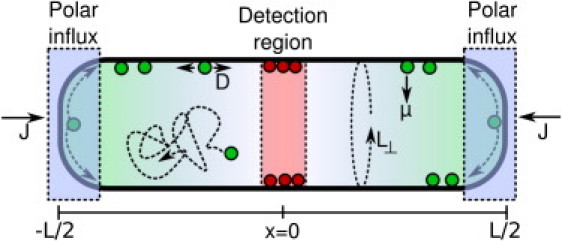
A schematic depiction of the model of protein dynamics within the cell, incorporating membrane diffusion and dissociation. Cytoplasmic diffusion and the details of polar reassociation are coarse-grained out, replaced by a polar influx of proteins. The concentration of the gradient protein is measured by detectors localized at midcell.
The long-axis of the cell extends from x = – L(t)/2 to x = L(t)/2, where growth is represented by the cell length L(t) increasing with time. We suppose that the cell wishes to identify when a target length, LT, is reached. The circumference of the cell is taken to be L⊥. Proteins are injected into the cell at each pole with rate J/2, such that the total protein influx is j = J/L⊥. On the cell membrane, proteins diffuse with diffusion constant D. Dissociation is modeled as removal of proteins with a constant rate μ, independent of position. The average density of membrane-associated proteins, ρ (x, t), is then described by the reaction-diffusion equation
| (1) |
together with the boundary conditions describing the protein sources,
| (2) |
If cell growth is slow, the concentration profile can be taken to be in quasi-steady state as the cell grows. This assumption appears reasonable in many cell types, where the doubling time is tens of minutes (for E. coli) to hours (for fission yeast) whereas the time required for the gradient to reach steady state will typically be a few tens of seconds. The average density profile at a given length is then given by
| (3) |
where is the characteristic decay length of the gradient and N = J/μ is the mean number of proteins located on the cell membrane.
Although the model has been outlined above in terms of protein production and decay reactions, we emphasize that the addition and removal of proteins from the membrane population should be interpreted in terms of exchange with the cytoplasmic pool, and not de novo translation and degradation. A single protein may therefore cycle many times between the membrane and cytoplasm. Nevertheless, the irreversibility of the exchange cycle implies that the system operates out of equilibrium, and must consume energy to maintain the membrane gradient.
We assume that the cell measures and responds to the concentration of the gradient protein only at the position x = 0. We will not concern ourselves with how the cell is able to localize the detection machinery to this position. In the case of fission yeast, the Pom1 gradient itself contributes to localization of the Cdr2-containing foci (6,7) and Mid1 (9,10). In bacterial systems, the cooperative self-assembly of FtsZ may also lead to effective confinement of FtsZ to midcell in response to the gradient (33). The average concentration at x = 0 is given by
| (4) |
For comparison, the same number of proteins distributed uniformly throughout the cell and diluted by growth would have a mean density
| (5) |
The midcell density for a bipolar gradient is always lower than if the same total number of proteins were uniformly distributed along the length of the cell, and this difference becomes more pronounced as the decay length λ decreases, or as the cell grows.
It remains now to specify how the effective protein influx J, or alternatively the number of proteins at the cell membrane N, should be chosen. In general, this will depend on the precise dynamics of the gradient protein, and the rates of protein production and degradation. In this article we shall assume that the overall concentration of the protein of interest within the cell is constant as the cell grows; then the total copy number Ntot(L) increases linearly with L. Experiments have found no change in the expression level of Pom1 over the cell cycle (34), although its activity may change over time (35).
Because diffusion of proteins within the cytoplasm (with typical diffusion constants ∼10 μm2 s–1) is much faster than diffusion at the membrane (diffusion constants of ∼0.1 μm2 s–1), we assume that on the timescale of dissociation events, proteins in the cytoplasm have time to diffuse throughout the cell. Therefore, neglecting the nonuniform distribution of positions at which proteins dissociate from the membrane, the net reassociation flux is given approximately by
where Ncyt(L) = Ntot(L) – N(L) is the number of proteins in the cytoplasm, κ describes the effective polar association rate, and the factor of L–1 represents the probability of a cytoplasmic protein being found in a polar region where it is able to reassociate with the membrane. Under our quasi-steady-state approximation, the fraction of proteins on the cell membrane, F(L) = N(L)/Ntot(L), can be found by matching the influx J with the net dissociation flux, μN(L); this leads to F(L) = 1/(1 + αL), where α–1 = κ /μ parameterizes the rate of polar reassociation. Then the polar influx takes the form J = μNtot(L)/[1 + αL].
We will focus on two limiting cases.
In the first instance we take the flux to be a constant, J = J0, independent of cell length. This corresponds to the limit of slow polar reassociation or large α, for which the membrane fraction decreases as F(L) ∼ L–1; as a result, the number of proteins on the membrane, N(L) = N0, is constant. We denote the gradient profile with this choice of N(L) by ρn(x, L).
The second case we shall consider is the limit of small α, or fast reassociation, for which F(L) ∼1 is independent of length. The protein influx and the number of proteins on the membrane will then increase linearly with the cell length, such that the mean concentration on the membrane is constant. We choose N(L) = N0 L/LT and denote the corresponding concentration profile by ρc(x, L). In this way we compare the two cases on the basis of the same concentration profile at the target length, (LT) = (LT).
In addition to the protein forming the concentration gradient, we also consider a simple model for the detection of this gradient. We assume that the detector molecule has active and inactive states. To achieve a switchlike response of the detector as a function of the density of the gradient protein, the gradient protein cooperatively promotes switching of the detector to the active state with cooperativity parameter γ ≥ 1. Active detectors spontaneously switch back to the inactive state with a constant rate. For a population of Nd detectors switching independently, the average number of active detectors, a, can then be described by
| (6) |
where k+ and k– are the rates of detector activation and deactivation respectively. If we again assume that the switching dynamics of the detector are fast compared to changes in cell length, we can write the average fraction of active detectors as
| (7) |
where K = (k–/k+)1/γ is the density at which the fractional detector activity is one-half.
From a measurement of the midcell concentration or detector activity, the cell length can be inferred by inverting Eq. 4 or Eq. 7. The target cell length LT can be identified when a threshold value of the density ρ0(LT) or detector activity a(LT) is reached. However, such a measurement will always be subject to numerous sources of noise. The processes of diffusion, dissociation, and reassociation which determine the concentration of the gradient protein are intrinsically stochastic, as are the binding reactions of the protein to its downstream detector and the (in)activation of this detector. This noise will lead to some error in our estimate of the cell length. The variance in the estimate of this length can be related to the noise in the measured quantity z, which could be the midcell concentration or detector activity, by
| (8) |
where and σ2z(L) are, respectively, the mean and variance of z at length L and represents evaluated at L = LT. The two terms on the right-hand side of Eq. 8 have a straightforward interpretation. The first is the coefficient of variation in z; a higher coefficient of variation means that the value of z at a particular length is more variable over time in a single cell and between different cells, and hence the expected error in estimating L increases. The second term describes the sensitivity of to changes in the cell length; increasing the sensitivity allows for different lengths to be more reliably distinguished.
To examine whether the model proposed above is compatible with experimentally observed variability in cell length, typically ∼±5–10% in fission yeast (5–7,36), we will consider the following representative parameter values: LT = 14 μm, L⊥ = 10 μm, and N0 = 4000 copies of the gradient protein on average at the target length (a typical number for regulators of cytokinesis in fission yeast (37)). We take D = 0.2 μm2 s–1, representative of a membrane-associated protein. Except when examining the dependence of the length uncertainty on the parameter λ, we will choose λ = 2 μm.
Results
Uncertainty due to noise in the protein concentration
In the remainder of this article we will examine the contributions of different sources of noise to uncertainty in length determination, and ask whether the precision which can be achieved by this model is consistent with observed variability in cell size. First we shall consider uncertainty in estimating the cell length due solely to fluctuations in the concentration of the protein gradient at midcell, ΔLconc. This corresponds to a lower bound on the total uncertainty, which would be achieved if the cell were able to measure the concentration with perfect accuracy.
The diffusion, production, and decay processes which make up the dynamics in the gradient model described above are each Poissonian. For this simple model we would therefore expect that the protein concentration at any point will also be Poisson-distributed (30,38). That is, the number of proteins within an area (Δx)2 centered at position x will have a mean 〈n(x)〉 = 〈ρ(x)〉(Δx)2 and variance σn2 = 〈n(x)〉. In general, the exchange of proteins between the membrane and cytoplasm may lead to correlations between protein dissociation events and subsequent association reactions, which would in turn lead to deviations from purely Poisson density statistics. However, in the parameter range of interest for the known intracellular protein gradients, stochastic simulations show that local density fluctuations are well described by σn2 = 〈n(x)〉, as noise is dominated by the diffusive transport of proteins to the detection volume (see the Supporting Material). The variance in the concentration at midcell in a cell of length L will then be given by (30)
The coefficient of variation therefore decreases with increasing concentration, as one would expect for a Poisson-distributed variable. We can identify Δx as the size of the detector which reads out the protein concentration. In the case of Pom1, this will be approximately the size of a Cdr2 protein cluster.
We first consider the case where the signal protein is uniformly distributed throughout the cell membrane. Substituting ρu(L) from Eq. 5 into Eq. 8, we find
| (9) |
As we would expect, increasing the protein concentration reduces the impact of the Poisson density fluctuations. In addition we see that increasing Δx reduces the uncertainty in estimating the cell length, effectively providing spatial averaging of fluctuations in the protein density.
We now turn to the system employing spatial concentration gradients. Taking the case of a constant number of membrane proteins, with midcell concentration (L), the uncertainty in cell length is given by
| (10) |
Fig. 2 shows that an optimal value of the gradient length scale exists which minimizes the uncertainty in estimating cell length. This optimum can be understood as a result of a trade-off between increasing sensitivity and increasing noise as λ is varied. The noise in the protein density,
and the sensitivity,
are both monotonically decreasing functions of λ. When λ is small and decreasing, the increase in noise in the protein density dominates over the increase in sensitivity ∼λ−1, and so the uncertainty in cell length increases. For large λ both the noise and sensitivity tend to constant values, and so the uncertainty in cell length varies little with λ. However, there is an intermediate regime around λ ∼ LT/2 where the reduction in sensitivity as λ is increased remains ∼λ−1, while the change in the average midcell density, and therefore the reduction in noise, is small. The change in sensitivity therefore dominates, leading to the increase in with increasing λ which can be seen in Fig. 2. The existence of an optimal gradient length-scale for the determination of cell length parallels similar observations for the accuracy of position determination (30) and the specification of gene expression domains (32). Interestingly, the optimal length scale of λ ≈ LT/6 is similar to the ratios observed for the division inhibitors Pom1 in fission yeast, where λ ∼2 μm and LT ∼ 14 μm (6,7,9,10), and MipZ in Caulobacter, where λ ∼ 0.25 μm in a cell body of length LT ∼ 2.5μm (11).
Figure 2.
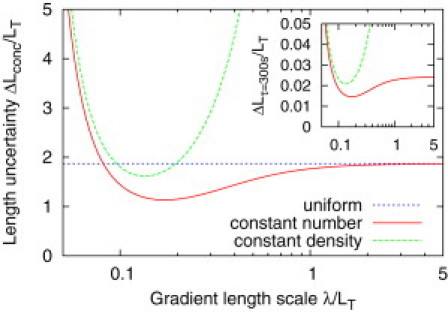
Uncertainty in cell length due to fluctuations in protein concentration as a function of the gradient length scale. (Dotted line) ()2 given by Eq. 9. (Solid line) ()2 given by Eq. 10. (Dashed line) ()2 given by Eq. 13. The gradient model allows for higher precision than the uniform system, and shows an optimum as a function of λ. (Inset) Length uncertainty after time-averaging over τ = 300 s. Parameter values are as described in Model (see text).
Comparing the results of Eqs. 9 and 10, we can see that the ratio of uncertainties in the two models is
| (11) |
From Fig. 2 we can see that for λ larger than ∼LT /12 the bipolar gradient allows for more accurate estimation of cell length than the corresponding spatially uniform system. This is despite the fact that the midcell concentration is lower in the gradient model, and hence the effective noise in the concentration is larger. Indeed the improvement in precision comes about because the midcell concentration in the gradient model decreases more rapidly with increasing cell length than in the uniform model. At around the optimal gradient length scale of λ ≈ LT /6, the variance in length estimates for the gradient model is reduced by approximately a factor of three compared to the uniform model. For small λ ≲ LT /12, the uniform model achieves greater precision. In this regime the protein concentration at midcell becomes very low in the gradient model, and hence the higher noise in the protein levels severely compromises precision. Finally, when diffusion is fast and λ ≳ LT /2 the two models become equivalent, as the concentration in the gradient model becomes approximately uniform.
We now turn to the case, discussed in Model, above, where the number of proteins located at the membrane increases linearly with cell length. It is clear that then if the signal protein is uniformly distributed ∂Lρu(LT) = 0 and ΔLconc → ∞; because the mean concentration is constant, measuring concentration provides no information about cell length. However, for the bipolar gradient model the midcell concentration does vary with length,
| (12) |
Substituting into Eq. 8 the length uncertainty for this modified model is
| (13) |
We can see that is always larger than . This is because the increase in the number of proteins counteracts dilution as the cell grows, reducing the sensitivity of the midcell concentration to changes in length. From Fig. 2 we can also see that the precision of length estimation is much more sensitive to parameter variations if the number of proteins on the membrane increases with length: the observed minimum in the uncertainty as a function of λ becomes much more pronounced. This is because as λ is increased the protein gradient approaches a uniform concentration profile, for which the sensitivity to changes in cell length vanishes. The position of the minimum shifts to a slightly shorter length scale; however, this change is small, and the resulting optimal value of λ is still comparable to the observed length scales of in vivo gradients.
The results presented here for the limiting cases of large and small α are qualitatively unchanged for intermediate values. We note that choosing N to be linear in L provides a worst-case scenario for the estimation of cell length: if the total number of proteins within the cell increases linearly with cell length the value of |∂Lρ0|, and consequently also the sensitivity, will be smallest when F(L) = 1. Our results show that through the use of concentration gradients together with localized detectors, the cell can nevertheless use a concentration-sensing mechanism to estimate cell length even though the average concentration of the measured protein within the cell or on the cell membrane remains constant.
Given the above results, we can ask whether or not cells are able to achieve a level of precision which is compatible with experimentally observed variability in cell length. Using representative parameter values for Pom1 (see Model, above) we find for the gradient model with a constant number of membrane proteins. For a spatially uniform protein distribution, or in the case of a gradient with constant mean concentration, > 1.6. A reliable estimate of cell length cannot be achieved from a single instantaneous measurement of the concentration, even if this measurement is perfectly accurate.
Time averaging
To reduce the impact of intrinsic noise in protein concentrations, biochemical detection systems often exploit temporal averaging. We suppose that the detector integrates the concentration of the gradient protein at midcell over some period τ. The appropriate averaging timescale is set by the process which detects and reads out the concentration of the gradient protein, which will be considered below. In effect, in the period τ a detector is able to perform τ/τD independent measurements of the protein concentration (39), where τD is the correlation time of fluctuations in the protein density or alternatively the timescale on which the area sampled by the detector is refreshed. The variance of the averaged density measurements is reduced compared to an instantaneous measurement by a factor τ/τD. For the two-dimensional system we are considering here, we take τD = (Δx)2/D (ignoring logarithmic corrections which have a negligible effect on the averaging time (30)). Then the uncertainty in estimating cell length, , will be
| (14) |
| (15) |
We can see that if D is increased, while also increasing μ so as to hold constant, the uncertainty in cell length is reduced. This is because faster diffusion allows for more rapid refreshing of the environment of the detector reading out the concentration, increasing the number of independent measurements which can be made. Varying μ while holding D constant, we find (Fig. 2, inset) that the uncertainty still has a minimum as a function of λ. We also note that, because τD is the same in both cases, time averaging does not affect the relative precision of the gradient models with different flux conditions. For the uniform model the effect of time averaging is less clear; the appropriate averaging time may depend on both diffusion and (uniform) exchange between membrane and cytoplasm. However, the latter is likely to occur on a longer timescale than diffusion over the short length scales assumed here for the detector size, Δx, and as such it is unlikely that time averaging will be able to reduce Δ below Δ if LT/10 ≲ λ ≲ LT.
Again using parameters for Pom1, the uncertainty in length from time-averaged measurements is Therefore, cells will be able to reduce the uncertainty in cell length to ∼±5% by averaging over a time τ ∼50 s, even for the less accurate constant-density gradient model. Parameter values for the detection of Pom1 by Cdr2 or other downstream proteins, and in particular the averaging timescale on which these interactions take place, are not known. The required timescales are sufficiently short that these levels of precision could be reached during one cell cycle. However, it should be noted that with a doubling time of ∼2 h, the cell length would itself change by a few percent during an integration period τ ∼10 min, potentially leading to systematic errors in the estimated length.
Uncertainty due to detector switching
We have seen above that by employing a detector which is able to integrate over fluctuations on the protein concentration, a cell is able to greatly improve the precision of length sensing. However, the interaction of the gradient and detector proteins will itself be stochastic. It is therefore important to consider also the limit that the noise in these detection reactions places on the accuracy of length determination, ΔLsw. This represents a different lower bound on the total precision of the system from that calculated above, which corresponds to the limit that fluctuations in the protein concentration are negligible.
We use Eq. 8 to estimate the uncertainty in cell length for the detector switching model (described in Model, above) in terms of fluctuations in the number of active detectors, a(L). For a population of Nd independent detectors, the number of active detectors will have a binomial distribution, with the probability of each individual detector being active equal to f (L), given by Eq. 7. In particular, the variance in the total detector activity will be σa2 = Ndf (1 – f). Assuming that Nd is a constant independent of cell length, we find
| (16) |
Combining these results and Eq. 7, the uncertainty in cell length is given by
| (17) |
The dependence of the uncertainty on the detector dynamics is contained in the factor
It was recently shown (40) that the precision with which ligand-receptor binding is able to provide information about concentration fluctuations is optimized when K matches the mean background concentration. Similarly, we find that the error in length detection can be minimized for a fixed gradient profile by choosing K = ρ0(LT), as shown in Fig. 3 a.
Figure 3.
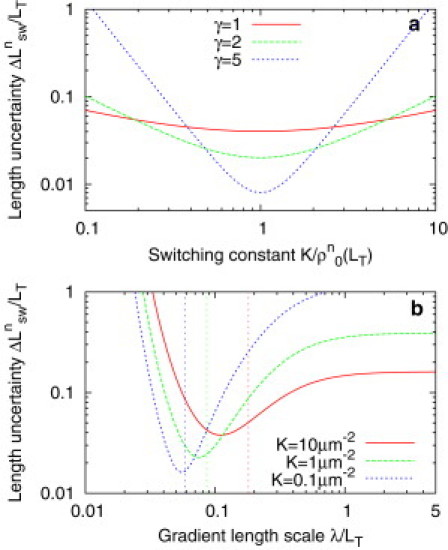
Uncertainty in cell length due to detector switching dynamics. (a) For a fixed density profile, uncertainty is minimized by choosing K = ρ0(LT). This effect is most pronounced for larger cooperativity in detector activation, γ. (b) For fixed K, an optimal gradient length scale λ exists. Each curve corresponds to a different value of K with γ = 1. (Vertical dotted lines) Value of λ for which (LT) = K. In each case, the minimum of Δ is at a smaller value of λ. Parameters are as described in Model (see text) and Nd = 200.
Substituting (LT) into Eq. 17 we find that for fixed K the uncertainty again has a minimum as a function of λ. The position and depth of this minimum depend on the other parameters of the model, including K: from Fig. 3 b we can see that the optimal value decreases and the minimum becomes more pronounced as K increases. Note, however, that the optimal value of λ does not correspond to choosing By choosing a slightly smaller value of λ, one can both decrease the noise in the state of the detector population and increase the sensitivity of the system. Using the constant-density model instead gives qualitatively similar results (data not shown). As we saw for the uncertainty due to density fluctuations, in this case the uncertainty as a result of detector switching is slightly larger and more sensitive to changing λ. This is again because increasing protein levels partially compensate for dilution, reducing sensitivity of the detector output to changes in length.
As before, we can compare this with a spatially uniform system, for which we have
| (18) |
As shown in Fig. 4, we find that for large regions of parameter space the gradient model is able to achieve significantly higher precision than the corresponding uniform system—only for small λ does the gradient model perform worse. This is in part because the different models provide different concentrations at LT, and therefore have different optimal choices for K. However, we note that even if the optimal value of K = ρu(LT) for the uniform model is chosen, the gradient model is still able to achieve greater precision over a wide, and biologically relevant, range of λ.
Figure 4.
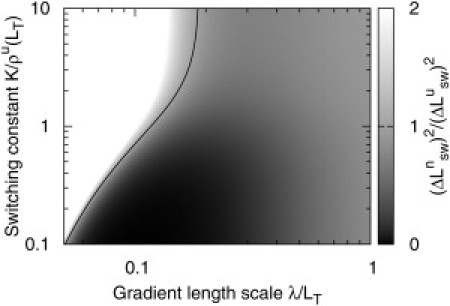
Comparison of the uncertainty due to detector switching for the gradient and uniform models. (Grayscale) Ratio of uncertainties ()2/()2 as K and λ are varied, for γ = 2. (Left of solid line) Uniform model allows for higher precision. (Right of solid line) Gradient model performs better.
To estimate a lower bound on the uncertainty due to noise in detector switching for the Pom1 system, we choose the optimal value for K =, where is calculated using the parameters described previously. The resulting uncertainty is
meaning that precision of ±5% of LT could be achieved with Nd ∼130 independent detectors with only linear binding kinetics, γ = 1, if there were no fluctuations in the concentration of the gradient protein. This value appears comparable to the number of Cdr2-containing clusters which is observed experimentally (6,7). The addition of cooperativity greatly reduces the number of required detectors: for a highly cooperative response with γ = 10, a couple of detector clusters may be sufficient to achieve the required accuracy. If we apply the same procedure for a spatially uniform system we find that the number of detectors required to reach the same level of precision is ∼10-fold larger than for the gradient model.
Combining diffusive and switching noise
In reality, the state of the gradient read-out mechanism will be affected by both the intrinsic randomness of switching and by extrinsic fluctuations in the density of the gradient protein. For each detector, the intrinsic contribution to the noise will simply be f (1 – f), while the extrinsic contribution will have the form (41)
Here τf = [k+ρ0(L)γ + k–]–1 is the correlation time for detector switching, which sets the timescale over which the state of the detector is influenced by previous values of the density, and therefore also the time interval over which density fluctuations are integrated. The variance in the activity of the population of detectors will be approximately
| (19) |
where the sums run over detectors, δi,j is the Krönecker delta, and Ci, j is the covariance of the time-averaged density at detectors i and j. In general this will be a function of the distribution of distances between detectors and the averaging time τf. Here we will simply assume that each detector is perfectly correlated with a fraction φ of the total population of detectors, and is uncorrelated with the remaining detectors. In particular, we would expect correlations between detectors which are separated by because in a time τf diffusing proteins will be able to visit both detector sites, and negligible correlations between detectors at more distant sites. Additionally, if τf μ >> 1 the typical distance that a protein will diffuse before dissociating is limited to ∼λ, and hence so too is the density correlation length, leading to φ ∼ λ2/A, where A is the area of the membrane where detectors can be found. For the Pom1-Cdr2 system, φ ∼ λ2/(L⊥ × 4 μm) ∼0.1. Different assumptions about the correlations between detectors do not qualitatively change our conclusions below, but may change the value of φ. Taking additionally τf >> τD, the overall variance in the total detector activity becomes
| (20) |
where the last term can be interpreted as the averaging of density fluctuations over a number φ –1 of effectively independent detectors.
The overall length uncertainty then has the form
| (21) |
This equation shows that the two components of the uncertainty are largely independent. Strategies which reduce intrinsic detector noise, such as increasing Nd or γ, have little effect on the uncertainty due to density fluctuations. Conversely, density fluctuations can be reduced principally by increasing τf, which in itself does not affect intrinsic switching noise. Because we saw previously that for realistic parameter combinations the two individual uncertainties could each be reduced to the level of a few percent of the cell length, it follows from Eq. 21 that the combined uncertainty can also reach this level of precision.
At the level of the reaction parameters we once again find a nonmonotonic dependence on the dissociation constant K. Substituting into Eq. 21 gives
| (22) |
where
ΔLtot is minimized by choosing (varying k– while holding k+ constant)
| (23) |
which differs slightly from the value at which sensitivity is maximized, K = ρ0(LT). This is because choosing a slightly smaller value of K reduces the impact of noise in the protein density through two effects: First, moving the target concentration away from the most sensitive regime of the detector means that the variability in detector activity due to density fluctuations is reduced. Second, decreasing k– increases the correlation time of the detector, increasing the effective time over which density fluctuations are integrated. These effects become increasingly important as the correlations between detectors increase, because this increases the contribution of noise in the protein density to the overall uncertainty.
Discussion
In this article, we have analyzed a mechanism of size regulation by polar protein gradients, which was recently described in fission yeast by Martin and Berthelot-Grosjean (6) and Moseley et al. (7). We have calculated the expected uncertainty in length estimation based on the inevitable intrinsic noise in the physical processes and chemical reactions of formation and detection of a protein concentration gradient. Our results show that this mechanism is able to perform with a greater accuracy than a simpler spatially uniform model. We have seen that cells can still reliably detect changes in cell length even if the overall density of proteins within the cell is unchanged. Importantly, therefore, the use of concentration gradients potentially allows a cell to regulate its size, and cell cycle progression, with proteins whose expression are not themselves under cell cycle control. Furthermore, the accuracy of the system can be improved by matching the dynamics of the gradient and detector proteins. We find that the optimal value of K represents a compromise between maximizing the sensitivity of the system and reducing the impact of fluctuations in the concentration of the gradient protein.
The analysis presented here indicates that the measurement of cell length itself can be sufficiently accurate to achieve experimentally observed levels of variability in cell length (6,7). From Eq. 21 we find that for realistic parameters—averaging density fluctuations over a timescale of a minute with ∼100 detectors—precision in length sensing can reach a few percent of cell length. A significant contribution to this error comes from noise in the density of the gradient protein, which can be difficult to reduce if there are significant correlations between fluctuations at different detectors. Instead, density fluctuations must be managed by time-averaging. However, there may be an upper limit to the timescale over which the cell can integrate: if this time is so long that there is significant growth during the integration period, then errors in the length at which cell cycle events occur may be introduced due to fluctuations in the growth rate or integration time itself. Our results therefore suggest that density fluctuations may impose a significant limit on the precision with which length can be sensed in vivo.
There are likely to be many additional sources of inaccuracy which also contribute to the observed variation in cell length, but have not been included in this model. Among the most significant will be cell-to-cell variability in the copy numbers of the gradient and detector proteins. These extrinsic fluctuations in protein numbers will lead to differences between the effective target lengths of different cells. Another potential source of inaccuracy is variability in the time taken between the initiation of mitosis and the completion of cell division. These different sources of error could potentially be resolved experimentally by examining the correlations between cell length and the timing of events nearer the initiation of mitosis such as formation of mitotic spindle, or the activity of Cdr2 as measured, for example, via Förster resonance energy transfer.
Here we have considered the error with which the target length can be estimated at the level of the gradient read-out. In general, the decision on whether the target cell length has been reached could instead be made at a downstream step of the signaling pathway. Each additional step in the signaling cascade would allow the cell to integrate over fluctuations in the upstream reactions, reducing transmitted noise. However, each additional reaction would also introduce a source of intrinsic noise which would contribute to the overall length uncertainty. This includes the ultimate decision step, which one might expect to always be limited by binomial-type switching statistics, as considered here for the protein readout. It is therefore not clear that moving the decision of whether the target length has been reached downstream could significantly improve the precision of length sensing.
We have found that cells may be able to exploit the characteristic length-scale of an intracellular gradient to achieve greater precision in the sensing of cell length than a spatially uniform system relying solely on dilution. Importantly, concentration gradients are also able to reliably specify the position at which cell division should occur (10,30), thereby allowing one system to perform two crucial tasks in cell division and removing the need for separate processes dedicated to each. However, we did not consider the mechanism by which the detector molecules are localized near midcell. Pom1 is known to play a role in the correct localization of Cdr2 and other regulators of mitosis such as Mid1 (6,7,9,10), and it remains to be seen whether this could lead to significant changes in the noise properties of the system. We note that the model discussed here does not rely on the specific localization of the detector proteins at midcell, rather than any other fixed position within the cell. However, it seems most straightforward to localize the detector proteins to the region of lowest concentration, which occurs at midcell, than to any other specific position. Furthermore, the symmetry of the gradient means that the concentration of the signal protein is relatively constant over a region around midcell, and therefore localization of the detector protein need not be exceedingly precise for the system to function reliably.
There remain many aspects of the Pom1 system which are poorly understood. For example, what is the effect of clustering of Cdr2 and other downstream signaling proteins? In the current analysis the only role of clustering is to increase the effective Pom1 detector size, reducing noise in the concentration measurement via spatial averaging. Once time-averaging is taken into account, the uncertainty is largely insensitive to the detector size; in this case, clustering effectively reduces the number of detectors and increasing intrinsic noise, while providing no benefit for reducing extrinsic noise. Instead, clustering may be important for the reliable transmission of the Cdr2 signal downstream.
The model discussed here cannot by itself account for the variability of cell size which is observed in different growth media or at different growth rates (42,43). A different mean cell length could be achieved by altering the relative levels of Pom1, Cdr2, or other downstream proteins, or their activities, in response to varying environmental conditions. These properties may be subject to active regulation depending on nutrient availability (43). However, the Pom1 gradient will also not be the only regulator of mitotic entry, as demonstrated by the relatively large division size of pom1 knock-out strains (6,7). It will be important to study these different regulation mechanisms to understand the precise role of the Pom1 gradient in natural environments.
Acknowledgments
I thank Jose Alvarado and Pieter Rein ten Wolde for careful reading of the manuscript and valuable comments.
This work is part of the research program of the Stichting voor Fundamenteel Onderzoek der Materie (FOM), which is financially supported by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO).
Supporting Material
References
- 1.Jorgensen P., Tyers M. How cells coordinate growth and division. Curr. Biol. 2004;14:R1014–R1027. doi: 10.1016/j.cub.2004.11.027. [DOI] [PubMed] [Google Scholar]
- 2.Fantes P.A., Nance P. Division timing: controls, models and mechanisms. In: John P.C.L., editor. The Cell Cycle. Cambridge University Press; Cambridge, UK: 1981. pp. 11–33. [Google Scholar]
- 3.Fantes P.A. Control of cell size and cycle time in Schizosaccharomyces pombe. J. Cell Sci. 1977;24:51–67. doi: 10.1242/jcs.24.1.51. [DOI] [PubMed] [Google Scholar]
- 4.Nurse P., Thuriaux P. Controls over the timing of DNA replication during the cell cycle of fission yeast. Exp. Cell Res. 1977;107:365–375. doi: 10.1016/0014-4827(77)90358-5. [DOI] [PubMed] [Google Scholar]
- 5.Sveiczer A., Novak B., Mitchison J.M. The size control of fission yeast revisited. J. Cell Sci. 1996;109:2947–2957. doi: 10.1242/jcs.109.12.2947. [DOI] [PubMed] [Google Scholar]
- 6.Martin S.G., Berthelot-Grosjean M. Polar gradients of the DYRK-family kinase Pom1 couple cell length with the cell cycle. Nature. 2009;459:852–856. doi: 10.1038/nature08054. [DOI] [PubMed] [Google Scholar]
- 7.Moseley J.B., Mayeux A., Nurse P. A spatial gradient coordinates cell size and mitotic entry in fission yeast. Nature. 2009;459:857–860. doi: 10.1038/nature08074. [DOI] [PubMed] [Google Scholar]
- 8.Bähler J., Pringle J.R. Pom1p, a fission yeast protein kinase that provides positional information for both polarized growth and cytokinesis. Genes Dev. 1998;12:1356–1370. doi: 10.1101/gad.12.9.1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Celton-Morizur S., Racine V., Paoletti A. Pom1 kinase links division plane position to cell polarity by regulating Mid1p cortical distribution. J. Cell Sci. 2006;119:4710–4718. doi: 10.1242/jcs.03261. [DOI] [PubMed] [Google Scholar]
- 10.Padte N.N., Martin S.G., Chang F. The cell-end factor pom1p inhibits mid1p in specification of the cell division plane in fission yeast. Curr. Biol. 2006;16:2480–2487. doi: 10.1016/j.cub.2006.11.024. [DOI] [PubMed] [Google Scholar]
- 11.Thanbichler M., Shapiro L. MipZ, a spatial regulator coordinating chromosome segregation with cell division in Caulobacter. Cell. 2006;126:147–162. doi: 10.1016/j.cell.2006.05.038. [DOI] [PubMed] [Google Scholar]
- 12.Marston A.L., Thomaides H.B., Errington J. Polar localization of the MinD protein of Bacillus subtilis and its role in selection of the mid-cell division site. Genes Dev. 1998;12:3419–3430. doi: 10.1101/gad.12.21.3419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marston A.L., Errington J. Selection of the midcell division site in Bacillus subtilis through MinD-dependent polar localization and activation of MinC. Mol. Microbiol. 1999;33:84–96. doi: 10.1046/j.1365-2958.1999.01450.x. [DOI] [PubMed] [Google Scholar]
- 14.Raskin D.M., de Boer P.A.J. Rapid pole-to-pole oscillation of a protein required for directing division to the middle of Escherichia coli. Proc. Natl. Acad. Sci. USA. 1999;96:4971–4976. doi: 10.1073/pnas.96.9.4971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hu Z., Lutkenhaus J. Topological regulation of cell division in Escherichia coli involves rapid pole to pole oscillation of the division inhibitor MinC under the control of MinD and MinE. Mol. Microbiol. 1999;34:82–90. doi: 10.1046/j.1365-2958.1999.01575.x. [DOI] [PubMed] [Google Scholar]
- 16.Wolpert L. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 1969;25:1–47. doi: 10.1016/s0022-5193(69)80016-0. [DOI] [PubMed] [Google Scholar]
- 17.Tabata T., Takei Y. Morphogens, their identification and regulation. Development. 2004;131:703–712. doi: 10.1242/dev.01043. [DOI] [PubMed] [Google Scholar]
- 18.Ashe H.L., Briscoe J. The interpretation of morphogen gradients. Development. 2006;133:385–394. doi: 10.1242/dev.02238. [DOI] [PubMed] [Google Scholar]
- 19.Rogulja D., Irvine K.D. Regulation of cell proliferation by a morphogen gradient. Cell. 2005;123:449–461. doi: 10.1016/j.cell.2005.08.030. [DOI] [PubMed] [Google Scholar]
- 20.Towers M., Mahood R., Tickle C. Integration of growth and specification in chick wing digit-patterning. Nature. 2008;452:882–886. doi: 10.1038/nature06718. [DOI] [PubMed] [Google Scholar]
- 21.Robbins J.R., Monack D., Theriot J.A. The making of a gradient: IcsA (VirG) polarity in Shigella flexneri. Mol. Microbiol. 2001;41:861–872. doi: 10.1046/j.1365-2958.2001.02552.x. [DOI] [PubMed] [Google Scholar]
- 22.Bastiaens P., Caudron M., Karsenti E. Gradients in the self-organization of the mitotic spindle. Trends Cell Biol. 2006;16:125–134. doi: 10.1016/j.tcb.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 23.Maeder C.I., Hink M.A., Knop M. Spatial regulation of Fus3 MAP kinase activity through a reaction-diffusion mechanism in yeast pheromone signaling. Nat. Cell Biol. 2007;9:1319–1326. doi: 10.1038/ncb1652. [DOI] [PubMed] [Google Scholar]
- 24.Fuller B.G., Lampson M.A., Kapoor T.M. Midzone activation of Aurora B in anaphase produces an intracellular phosphorylation gradient. Nature. 2008;453:1132–1136. doi: 10.1038/nature06923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Brown G.C., Kholodenko B.N. Spatial gradients of cellular phospho-proteins. FEBS Lett. 1999;457:452–454. doi: 10.1016/s0014-5793(99)01058-3. [DOI] [PubMed] [Google Scholar]
- 26.Lipkow K., Odde D.J. Model for protein concentration gradients in the cytoplasm. Cell. Mol. Bioeng. 2008;1:84–92. doi: 10.1007/s12195-008-0008-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Daniels B.R., Perkins E.M., Wirtz D. Asymmetric enrichment of PIE-1 in the Caenorhabditis elegans zygote mediated by binary counterdiffusion. J. Cell Biol. 2009;184:473–479. doi: 10.1083/jcb.200809077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Meyers J., Craig J., Odde D.J. Potential for control of signaling pathways via cell size and shape. Curr. Biol. 2006;16:1685–1693. doi: 10.1016/j.cub.2006.07.056. [DOI] [PubMed] [Google Scholar]
- 29.Neves S.R., Tsokas P., Iyengar R. Cell shape and negative links in regulatory motifs together control spatial information flow in signaling networks. Cell. 2008;133:666–680. doi: 10.1016/j.cell.2008.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tostevin F., ten Wolde P.R., Howard M. Fundamental limits to position determination by concentration gradients. PLOS Comput. Biol. 2007;3:e78. doi: 10.1371/journal.pcbi.0030078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saunders T.E., Howard M. Morphogen profiles can be optimized to buffer against noise. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:041902. doi: 10.1103/PhysRevE.80.041902. [DOI] [PubMed] [Google Scholar]
- 32.Erdmann T., Howard M., ten Wolde P.R. Role of spatial averaging in the precision of gene expression patterns. Phys. Rev. Lett. 2009;103:258101. doi: 10.1103/PhysRevLett.103.258101. [DOI] [PubMed] [Google Scholar]
- 33.Lan G., Daniels B.R., Sun S.X. Condensation of FtsZ filaments can drive bacterial cell division. Proc. Natl. Acad. Sci. USA. 2009;106:121–126. doi: 10.1073/pnas.0807963106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rustici G., Mata J., Bähler J. Periodic gene expression program of the fission yeast cell cycle. Nat. Genet. 2004;36:809–817. doi: 10.1038/ng1377. [DOI] [PubMed] [Google Scholar]
- 35.Bähler J., Nurse P. Fission yeast Pom1p kinase activity is cell cycle regulated and essential for cellular symmetry during growth and division. EMBO J. 2001;20:1064–1073. doi: 10.1093/emboj/20.5.1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Miyata H., Miyata M., Ito M. The cell cycle in the fission yeast Schizosaccharomyces pombe. I. Relationship between cell size and cycle time. Cell Struct. Funct. 1978;3:39–46. [Google Scholar]
- 37.Wu J.-Q., Pollard T.D. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310:310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- 38.Lepzelter D., Wang J. Exact probabilistic solution of spatial-dependent stochastics and associated spatial potential landscape for the bicoid protein. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;77:041917. doi: 10.1103/PhysRevE.77.041917. [DOI] [PubMed] [Google Scholar]
- 39.Berg H.C., Purcell E.M. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hu B., Chen W., Levine H. Physical limits on cellular sensing of spatial gradients. Phys. Rev. Lett. 2010;105:048104. doi: 10.1103/PhysRevLett.105.048104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tănase-Nicola S., Warren P.B., ten Wolde P.R. Signal detection, modularity, and the correlation between extrinsic and intrinsic noise in biochemical networks. Phys. Rev. Lett. 2006;97:068102. doi: 10.1103/PhysRevLett.97.068102. [DOI] [PubMed] [Google Scholar]
- 42.Fantes P., Nurse P. Control of cell size at division in fission yeast by a growth-modulated size control over nuclear division. Exp. Cell Res. 1977;107:377–386. doi: 10.1016/0014-4827(77)90359-7. [DOI] [PubMed] [Google Scholar]
- 43.Petersen J., Nurse P. TOR signaling regulates mitotic commitment through the stress MAP kinase pathway and the Polo and Cdc2 kinases. Nat. Cell Biol. 2007;9:1263–1272. doi: 10.1038/ncb1646. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


