Ion Selectivity Mechanism in a Bacterial Pentameric Ligand-Gated Ion Channel

Abstract

The proton-gated ion channel from Gloeobacter violaceus (GLIC) is a prokaryotic homolog of the eukaryotic nicotinic acetylcholine receptor that responds to the binding of neurotransmitter acetylcholine and mediates fast signal transmission. Recent emergence of a high-resolution crystal structure of GLIC captured in a potentially open state allowed detailed, atomic-level insight into ion conduction and selectivity mechanisms in these channels. Herein, we have examined the barriers to ion conduction and origins of ion selectivity in the GLIC channel by the construction of potential-of-mean-force profiles for sodium and chloride ions inside the transmembrane region. Our calculations reveal that the GLIC channel is open for a sodium ion to transport, but presents a ∼11 kcal/mol free energy barrier for a chloride ion. Our collective findings identify three distinct contributions to the observed preference for the permeant ions. First, there is a substantial contribution due to a ring of negatively charged glutamate residues (E-2′) at the narrow intracellular end of the channel. The negative electrostatics of this region and the ability of the glutamate side chains to directly bind cations would strongly favor the passage of sodium ions while hindering translocation of chloride ions. Second, our results imply a significant hydrophobic contribution to selectivity linked to differences in the desolvation penalty for the sodium versus chloride ions in the central hydrophobic region of the pore. This hydrophobic contribution is evidenced by the large free energy barriers experienced by Cl⁻ in the middle of the pore for both GLIC and the E-2′A mutant. Finally, there is a distinct contribution arising from the overall negative electrostatics of the channel.

Introduction

Nicotinic acetylcholine receptors (nAChRs) mediate fast signal transduction throughout the central and peripheral nervous systems (1–4). Their principal function is to bind the neurotransmitter acetylcholine and alter the transmembrane (TM) potential through selective permeation of ions. Therefore, it is of both fundamental and practical importance to understand how these molecular devices (ion channels) operate at the molecular level. The action of the receptors can be conceptually subdivided into three elementary steps: ligand recognition, channel gating, and ion conduction. Although ligand recognition and channel gating involve interconversion among several conformational states (separated by microsecond-to-millisecond free energy barriers) (5,6), only one of these states—the open state—can effect conduction of ions. The advent of patch-clamp recording enabled the measurement of electrical currents resulting from ion transport across the TM region of nAChR channels on timescales as brief as tens of microseconds (7).

Despite the enormous utility of electrophysiology measurements and the large existing body of biochemical knowledge regarding nAChRs, detailed mechanistic understanding of ion translocation through nAChR and related channels remains an outstanding challenge for both experiment and theory (8–11). nAChRs conduct Na⁺ and K⁺ ions (and in some subunit combinations, Ca²⁺ ions) while effectively precluding passage for anions such as Cl⁻. The structural origin of this selectivity is still an unresolved problem. Early mutagenesis studies attributed the charge selectivity to the intracellular end of the channel (12). For instance, insertion of a proline residue into the −2′ position in the α7 nAChR together with G1′A and V13′T mutation converts nAChR from a cation-selective to an anion-selective channel (13,14). However, work that is more recent has suggested that important structural determinants of selectivity may lie in other regions of the receptor. Charge reversal experiments on 5-HT3 receptors suggested that the intracellular MA loop reduced cation permeation, but did not invert the selectivity between monovalent anions and cations (15). Potential of mean force (PMF) calculations on the α7 nAChR showed that the extracellular entrance of the TM domain, in particular the negatively charged girdle of glutamate residues in position 20′, could facilitate cation flow through the channel (16). More recent computational studies, combined with experiments, implied that the extracellular domain of nAChR may also exert an influence on ion conductance (17).

The slow progress toward mechanistic understanding of ion conduction can, to a large extent, be attributed to poor structural understanding of nAChR in its functional state (9). Until this is resolved, insights into the function of nAChR would necessarily have to come from studies of homologous proteins with known structures. Recently, the crystallization of a pentameric ligand-gated ion channel from Erwinia chrysanthemi (ELIC) has been reported (18), followed by structural determination of another homologous channel from Gloeobacter violaceus (GLIC) (19,20). ELIC and GLIC resemble mammalian ligand-gated ion channels with analogous symmetrical arrangement of five M2 helices surrounding a central pore that plays a role in ion conduction. The helices in the prokaryotic channels exhibit somewhat tighter packing compared to eukaryotic nAChR. The cryo-electron microscopy (cryo-EM) structure of nAChR from Torpedo marmorata identified a hydrophobic obstruction in the middle of the channel pore comprising residues Val-13′, Leu-9′ in the pore-lining M2 helices (9).

This hydrophobic girdle of residues has the capacity to impede ion flow and has been proposed to function as the putative gate of the channel (21). The cryo-EM structure of nAChR and the ELIC crystal structure are thought to correspond to the closed state. By contrast, the GLIC structure is assumed to have been captured in an open state in response to the low pH gradient imposed at both sides of the membrane. With respect to the ELIC structure, the five M2 helices in GLIC are tilted by ∼7°, thus leading to a potentially open conformation where the hydrophobic constriction has been removed. The overall funnel-shaped GLIC channel narrows substantially at the intracellular end where a ring of glutamate residues (E-2′) is found with the side chains pointing toward the center of the pore. This region appears even more constrictive than the hydrophobic girdle region in the cryo-EM nAChR structure. However, unlike a hydrophobic constriction, the glutamate residues are capable of coordinating cations. Therefore, the narrow intracellular region may act as a selectivity filter. However, if the E-2′ residues bind too strongly to cations (especially divalent ones) or the disruption of the E-2′ side-chain packing is too costly, the intracellular end could also block cation conduction.

In this study, we provide insight into the ion transport mechanism in GLIC using molecular dynamics (MD) simulation combined with umbrella sampling and continuum electrostatic calculations. The high-resolution GLIC structure captured in a potentially open state paved the way for new simulations of this system that could put the static structural information in the context of a working molecular machine (22–24). Among the pertinent questions such simulations may address are:

• 1.Is the GLIC crystal structure indeed captured in a conducting state?
• 2.How are the ions distributed along the pore?
• 3.How does the electrostatics of the pore environment contribute to selectivity?
• 4.What is the role of ion hydration and protein dynamics in the ion transport process?

Moreover, the GLIC crystal structures revealed two distinct conformations for the E-2′side chains, with one defining a more constrictive pore (0.4 Å; PDB code: 3ehz) than the other (2.0 Å; PDB code: 3eam) (19,20). Previous Brownian dynamics (BD) simulations by Song and Corry (23) further showed that this structural difference plays a key role in determining the conduction properties of the two GLIC structures, and might be the final step of the conformational change involved in channel gating. Our simulations probe the conformational dynamics of E-2′ in two different protonation states (corresponding to different pH conditions), and thus help elucidate its role in ion conduction and selectivity.

Materials and Methods

Molecular dynamics

The protonation states of the titratable residues were determined by a combined pK_a calculation using the Karlsberg webserver (http://agknapp.chemie.fu-berlin.de/karlsberg/) and manually checking for hydrogen-bonding residues nearby. GLIC has been shown to be activated by a decrease in the extracellular pH (19,25). To mimic this pH gradient across the membrane, the titratable residues near the intracellular exit were modeled at pH 7 whereas the residues at the extracellular entrance were modeled at pH 4. At physiological pH 4–7, there are six potentially titratable residues in each transmembrane subunit: E222 (−2′), H235, E243 (19′), E272, H277, and E282. Briefly, E282 is located at the intracellular end with its side chain exposed to the bulk solvent, so was assigned in a deprotonated state, whereas E243(19′) and E272 are located at the extracellular end with their side chains pointing toward the helix packing, so were assigned in a protonated state. Both H235 and H277 were neutral: for partially buried H235 the Nɛ atom was protonated to hydrogen bond with the neighboring I259 backbone, whereas for intracellular H277 the proton was on the Nδ atom. For E222(−2′), both the protonated and deprotonated states were simulated to see how the protonation state of E222 will influence the protein dynamics. The protonation states of the extracellular titratable residues are given in Table S1 in the Supporting Material.

MD simulations were performed with two full-length GLIC structures (PDB code: 3eam) embedded in a fully hydrated 120 × 120 Å POPC (palmitoyl-2-oleoyl-sn-glycerol-phosphatidylcholine) bilayer, one with deprotonated Glu-2′ (corresponding to a high pH) and the other with protonated Glu-2′ (corresponding to a low pH). This resulted in a total of ∼300 POPC molecules and ∼37,200 water molecules. Charge neutralization was accomplished with the addition of 120 Cl⁻ ions for the protonated simulation, and 115 Cl⁻ ions for the deprotonated simulation, resulting in a ∼0.1 M solution for both systems. Partially missing POPC lipid molecules were built, minimized, and equilibrated to fill the gap between the M4 and M1–3 helices. The solvated systems then underwent four equilibration steps:

• 1.Two-thousand steps of energy minimization with protein backbone fixed;
• 2.Five cycles of a 500-step minimization with decreasing positional restraints on the protein C_α atoms;
• 3.Gradual temperature increase from 50 K to 310 K in 10,000 steps of constant-volume MD (NVT ensemble) simulation with harmonic restraints (with force constant of 3 kcal·mol⁻¹·Å⁻²) on the protein C_α atoms; and
• 4.Two-nanosecond constant surface-area ensemble MD equilibration with decreasing positional restraints on the C_α atoms.

After equilibration, a 30-ns production run was collected for both simulations. All the MD simulations were performed with the NAMD 2.7 program (26) and the CHARMM27 force field (with backbone potential CMAP correction) (27). A short-range cutoff of 9 Å was used for nonbonded interactions, and long-range electrostatic interactions were treated with a particle mesh Ewald method (28). Langevin dynamics and a Langevin piston algorithm were used to maintain the temperature at 310 K and a pressure of 1 atm. The r-RESPA multiple-time-step method was employed, with time steps of 2 fs for bonded, 2 fs for short-range nonbonded, and 4 fs for long-range electrostatic forces (29). The bonds between hydrogen and heavy atoms were constrained with the SHAKE algorithm (30). All simulations were conducted on the Jaguar XT4 supercomputer at the National Center for Computational Science (http://www.nccs.gov/).

Umbrella samples calculations

Umbrella sampling calculations (31) were performed for both Na⁺ and Cl⁻ inside the GLIC and E-2′A mutant channels. Only the TM domain of the protein was simulated (Fig. 1) for two reasons:

• 1.Reduction of computational cost; and
• 2.Previous studies have shown that the extracellular domain only plays a minor role in discriminating among ion types, although it could help concentrate cations at the entrance of the pore (23).

Figure 1.

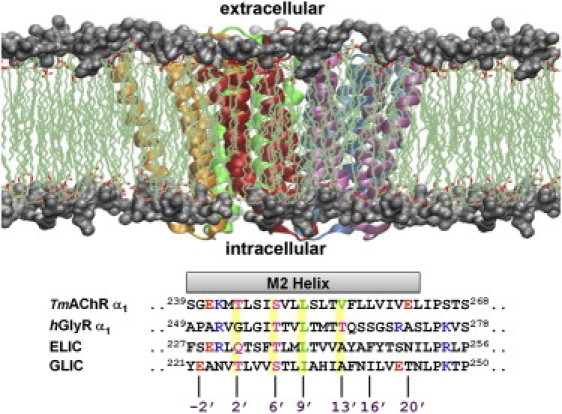
(Top) Structure of the transmembrane domain of GLIC with the five subunits highlighted in different colors; the headgroup region of the lipid bilayer is shown in silver surface representation. (Bottom) The sequence alignment of the pore-lining M2 (α2) residues from α1 T. marmorata nAChR, α1 GlyR, ELIC, and GLIC.

The truncated system was taken from the full-length GLIC simulations along with equilibrated membrane lipid bilayer and pore water molecules. Five intracellular E-2′ residues were deprotonated. The GLIC simulations were carried out in 59 windows of length 1 Å along the membrane-normal z direction and were sufficient to cover the entire length of the TM domain, whereas the E-2′A simulations were performed with 35 windows that cover the intracellular part of the pore (−5 Å < z ≤ 30Å).

Individual ions for each window were inserted into different z positions along the channel axis, followed by solvation, neutralization, and equilibration of the entire system. After 1-ns equilibration, a spring constant of 5 kcal·mol⁻¹ was applied to the z coordinate of the ion, followed by a 2-ns production run. During the umbrella sampling simulations, other ions were excluded from the pore (by a 3 kcal·mol⁻¹·Å⁻² positional harmonic restraint) to compute the free energy profiles assuming a single-ion transport mechanism. For windows with z ≤ −16 Å or z ≥ 20 Å, a cylindrical restraint was applied to prevent the ion from drifting too far from the axis of the pore laterally. Harmonic restraints (with force constant of 3 kcal·mol⁻¹·Å^-2) were applied to six C_α atoms on each subunit (three at the extracellular end and three at the intracellular end of the TM domain). These restraints are not coupled to the reaction coordinate through common atoms so that they have no direct influence on the PMF calculation. A total of ∼400 ns of simulation data was collected for the subsequent weighted histogram analysis method to generate PMFs (32). To estimate the statistical uncertainty, the total data set was split into four parts, then for each part a PMF was computed. The standard deviation of the four PMFs was used as a rough estimate of the error.

Born energy calculations

The Born energy calculations were carried out using the Adaptive Poisson Boltzmann Solver package (33). The charge and radius parameters for Adaptive Poisson Boltzmann Solver were assigned by using PDB2PQR server (34). The Poisson equation was solved for the transmembrane part of the protein in a focusing scheme, staring with a coarse-grid solution (grid length 139 Å × 136 Å × 95 Å) followed by a finer one (grid length 10 Å × 10 Å × 10 Å), both with grid points of 193 × 193 × 129. The fine grid was centered at the position of the ion. The Born energy was calculated as the difference of three electrostatic energies: E_Born = E_protein+ion − E_protein − E_ion. The dielectric constants of protein and water were set to be 2.0 and 60, respectively, by following previous studies that have shown this choice was appropriate for nAChR (23,35). The ionic concentration was set to 0 M (36). The Born energies were calculated for 500 representative frames (including the appropriately positioned ion) selected from each umbrella window.

The density profiles were calculated by binning the z-coordinate positions of the atoms for each species (lipid tail carbon, lipid headgroup nitrogen, phosphorus, ester oxygen atoms, and water oxygen atoms) to construct a histogram. The bin size was 0.2 Å, and density was normalized by the volume of a 0.2 Å wide slab of the simulation box oriented perpendicular to the bilayer-normal. The coordination number was calculated from the radial distribution function (RDF) of water oxygen atoms surrounding the ion,

$$g_j\left(r\right)=\frac{1}{N}\sum _{i=1}^N\langle \delta \left(\left|r_{ij}\right|-r\right)\rangle ,$$

where r_ij represents the distance between the ion j and the water oxygen i, and 〈…〉 denotes the ensemble average over the entire trajectory. The first hydration shell was defined as the first minimum of the RDF. Then the coordination number was determined by integrating the RDF up to the first minimum r_m,

$$N_{coor}=\underset{0}{\overset{r_m}{\int }}dr{g}_j\left(r\right).$$

Mean force decomposition

Individual contributions to the total PMF can be computed by integration of the corresponding mean forces F_α along the channel z-axis direction (37),

$$W_{\alpha }\left(z\right)=W_{\alpha }\left(z\right)-\underset{z_0}{\overset{z}{\int }}d{z}^{\prime }\langle F_{\alpha }\left(z^{\prime }\right)\rangle .$$

The PMFs are decomposed into individual contributions from the ion's interactions with its first solvation shell water (defined as 3.3 Å from sodium and 4.1 Å from chloride), the protein, and the residues E-2′ and E19′. Pair interactions (van der Waals and electrostatic forces along z direction) between two groups of atoms are calculated using the PairInteraction option in NAMD (26) for the MD trajectories generated in the umbrella sampling simulations.

Pore radius profiles were calculated with the HOLE program (38). The program VMD (39) was used in the visualization and analysis of the results.

Results and Discussion

We performed PMF calculations on the TM domains of the GLIC and an E-2′A mutant using MD simulation combined with umbrella sampling to determine free energy profiles for single ion transport through the channel (Fig. 1). Although it has been implied that the charge state of E-2′ might affect the gating behavior and ion conduction of the GLIC channel (23), our PMF calculations have only been focused on the deprotonated E-2′ system because we reasoned the deprotonated state of E-2′ might be more realistic in the physiological condition, as discussed further below. The z coordinate of the ion (along the membrane-normal direction) was chosen as the reaction coordinate. The computed PMFs for both Na⁺ and Cl⁻ ions allow us to probe specific ion-protein and ion-water interactions that determine ion selectivity.

As shown in Fig. 2, the resulting PMF displays no significant barrier for Na⁺ translocation through the GLIC channel. The PMF is largely flat over a broad region at the extracellular vestibule, and shows ∼1 kcal/mol increase in the middle of the pore (in the position corresponding to hydrophobic residue I9′). On the extracellular side, the M2 helices expose three rings of apolar residues (I16′, A13′, and I9′, Fig. 1) toward the interior of the pore, which could potentially render this region hydrophobic.

Figure 2.

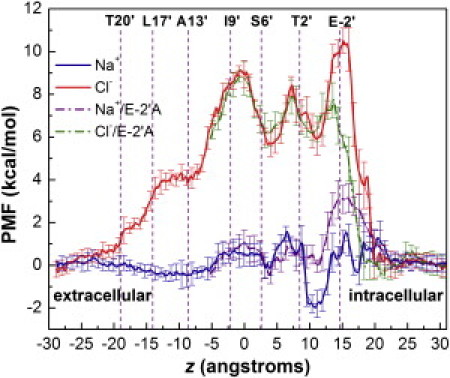
PMFs of sodium and chloride by umbrella sampling. The PMFs were shifted such that the curves match at the intracellular end. Positions of M2 pore-lining residues are shown with purple lines and labeled at the top of the graphs. The error bars correspond to the standard deviations.

However, the computed PMF indicates no hydrophobic restriction present for Na⁺ in this segment of the pore. This is in contrast to previous simulations of nAChR channels where the hydrophobic barrier featured very prominently (16,40). It has been suggested that the tilting motion of the M2 helices opens the hydrophobic constriction in the case of GLIC (19,20). Indeed, its central pore radius is 0.5 Å wider than Unwin's EM structure of the nAChR channel and 2 Å wider than ELIC. On the intracellular part, the PMF shows two stabilization regions corresponding to two layers of polar residues. A small minimum at position 4 Å corresponds to a binding site formed by S6′, whereas a ∼2 kcal/mol stabilization at position 10 Å is due to the interactions with T2′. In the T2′ site, Na⁺ can also be simultaneously stabilized by E-2′, albeit occasionally. Both binding sites seem to correspond well to the electron density of cations observed in the crystal structure (19). Snapshots from the trajectories showing these interactions are presented in Fig. S1 (top panel). Intracellular exit of Na⁺ involves the disruption of interactions with the E-2′ side chains, giving rise to a bumpy free energy profile toward the intracellular end. However, the five glutamate residues overall do not appear sufficiently attractive (∼2 kcal/mol) to impede the passage of Na⁺ ions.

The PMF for Cl⁻ inside the GLIC pore is clearly distinct from the one for Na⁺, displaying a broad barrier throughout the intracellular part of the pore. The overall barrier is ∼10 kcal/mol, leading to a channel effectively closed to anions. The initial gradual rise in the PMF is likely due to the overall negative electrostatic environment in the TM domain. An abrupt increase that reaches a maximum at position 0 Å corresponds to two rings of apolar residues A13′ and I9′, indicating the presence of a hydrophobic constriction for Cl⁻, which is possibly due to a more significant disruption of its first solvation shell compared to Na⁺. Further details of the Na⁺ and Cl⁻ hydration differences inside the pore will be discussed below.

Due to the funnel shape of the pore, the PMF displays the largest barrier for Cl⁻ upon entry into the intracellular vestibule. Movement of a Cl⁻ ion across this region is impeded by strong unfavorable interactions with E-2′ side chains and is accompanied by side-chain rearrangements. Similar to the calculation for Na⁺, two small stabilizing regions are also observed in the chloride PMF, corresponding to the two binding sites formed by S6′ and T2′, respectively (Fig. S1, bottom panel). However, under normal physiological condition, these metastable binding sites can rarely be reached by a Cl⁻ ion due to the large free energy barriers for accessing them. Compared with the sodium PMF, the most significant barrier for Cl⁻ is located at the intracellular end of the pore, suggesting that the narrow intracellular entry, especially the negatively charged E-2′ residues (previously referred to as the intermediate ring of charge (12)), may play a dominant role in selecting Na⁺ over Cl⁻ in the GLIC channel.

To gain deeper insight into the role of E-2′ in ion selectivity, we performed additional PMF calculations on an E-2′A mutant. The resulting PMF profiles are shown in Fig. 2. For Na⁺ (purple dashed line), the E-2′A mutation increases the barrier height by ∼3 kcal/mol at the intracellular end (at position15 Å) and destabilizes the T2′ binding site by ∼2 kcal/mol. This result predicts a decrease in the cation flow through the mutant channel, due to the absence of favorable electrostatic interactions of Na⁺ with the five glutamate residues. By contrast, the chloride PMF (green dashed line) reveals a barrier reduction by ∼3 kcal/mol at the same position. The E→A mutation has two effects that may lower the Cl⁻ barrier. First, the unfavorable electrostatics of E-2′ is eliminated. Second, compared with the bulky glutamate side chains, the alanine side chains are smaller and thus rearrange more easily to allow ion movement. Overall, the PMFs for the E-2′A mutant indicate that the substitution of glutamate by alanine residues alters both Na⁺ and Cl⁻ conductions in an opposite direction, which is consistent with the BD simulations of Song and Corry (23). These results confirm that E-2′ contributes substantially to the charge selectivity of the GLIC channel, providing theoretical support to the experimental proposals that the intracellular end of the Cys-loop family receptors function as a selectivity filter (12,41).

It is also important to note in the chloride PMF that although the mutation reduces the intracellular (largest) barrier, the hydrophobic barrier is still present and now becomes dominant. Only upon the removal of this constriction, the channel would become conductive to Cl⁻, which seems to be supported by experimental findings that the simultaneous mutation of the middle valine residue to a threonine is required to reverse charge selectivity in nAChR. Triple mutation at positions −1′ (E/A), −2′ (insertion P), and 13′ (V/T) has been shown to reverse charge selectivity in α7 nAChR (13), α1 GlyR (14), and 5HT3(42) receptors, highlighting the importance of the middle hydrophobic region of the M2 helix to ion selectivity, in addition to the intracellular end.

To identify the electrostatic role of the TM domain in ion conduction, we computed Born energy profiles for both Na⁺ and Cl⁻ inside the GLIC channel. The Born energy profiles in Fig. S2 reveal that there is little electrostatic stabilization/destabilization in GLIC on the extracellular part of the pore, in agreement with the PMF profiles that also show no stabilization for Na⁺, and correspondingly slight destabilization for Cl⁻. By contrast, our previous PMF and continuum electrostatic calculations on nAChR have revealed a strong stabilization for Na⁺ at the extracellular region due to primarily exposed glutamate residues (16).

We reason that two factors could give rise to the observed difference in GLIC. First, the five extracellular glutamate residues (E19′) in the GLIC crystal structure do not point toward the pore center and are partially buried between helices; second, all E19′ side chains were chosen to be protonated to be consistent with their partially buried conformation and the experimental low pH condition (19,25). Together, these two factors significantly diminish the contribution of the E19′ residues toward electrostatic stabilization of the permeant cations. At the intracellular end, the Born energy profiles reveal a pronounced energy well for Na⁺ and a broad energy barrier for Cl⁻, corresponding to the ring of E-2′.

It is worth noting that the glutamate residues in the 2′ position were modeled as negatively charged to adequately reflect the pH gradient across the membrane resulting in higher pH at the intracellular side of the membrane (19,25). The significant negative charges from the girdle of E residues would be expected to concentrate the permeating Na⁺ and repel the oppositely charged Cl⁻. Hence, in contrast to the extracellular protonated E19′, the electrostatics of the appropriately charged intracellular E-2′ clearly contributes to the selectivity of the GLIC channel, as also supported by the BD simulations of GLIC in which the charge of E-2′ was manually changed from 1.0e to 0 (23). However, the pronounced asymmetry between the Na⁺ and Cl⁻ PMF profiles implies that the electrostatics is not the sole determinant of ion selectivity but is rather coupled with side-chain dynamics and hydration. These additional factors will be discussed further below.

To assess the role of pore hydration, we calculated density profiles for different types of atoms along the bilayer-normal in the GLIC channel. The profiles show that water molecules penetrate the entire length of the channel pore, and water density is minimal at the center of the pore (z coordinate between −3 and 3 Å) corresponding to a ring of I9′ residues (Fig. 3). Compared with the nAChR pore, the GLIC pore is wider in the hydrophobic region and lined with two rings of serine and threonine residues in the following layers, thus it is more hydrated at the center. The extracellular end of the GLIC pore (z coordinate below −9 Å) is especially well hydrated, whereas the intracellular half shows a somewhat reduced water density, corresponding to the narrowest section of the GLIC pore at T2′ position along the M2 helix (z coordinate 10 Å). At the narrow intracellular end, the presence of ions changes the packing of E-2′ and T2′ side chains, leading to a somewhat reduced water density.

Figure 3.

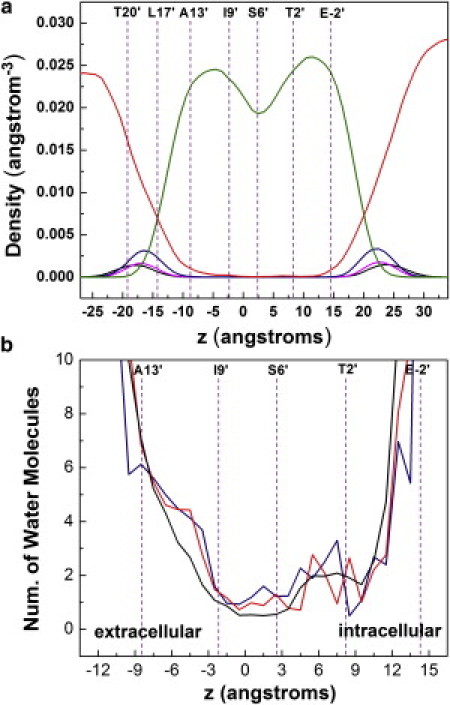
(a) Density profiles along the lipid bilayer-normal for lipid tail carbon (olive), lipid headgroup nitrogen (magenta), phosphorus (black), and ester oxygen atoms (blue) as well as water oxygen atoms (red). (b) Amplified version of the density profiles for water oxygen atoms in unbiased simulation (black), umbrella simulation with sodium (blue), and umbrella simulation with chloride (red). Positions of the M2 pore-lining residues (purple lines), labeled at the top of the graphs.

We also calculated coordination number for individual ions at different z positions. From Fig. S3, it is evident that the coordination for both Na⁺ and Cl⁻ is reduced in the central hydrophobic region of the pore, whereas the corresponding pore radius in this region is not the narrowest. In the bulk, the coordination number for a sodium ion is ∼5.8, whereas that for a chloride ion is ∼8.1. The comparison shows that in the central part of the pore, Cl⁻ is stripped of more water molecules (∼0.3 on average) relative to the bulk than Na⁺, which might contribute to the higher hydrophobic barrier for Cl⁻. Fig. S3 also shows the separation of the hydration shell into the contributions from water oxygen, protein nitrogen, and oxygen atoms. The sharp decrease at the intracellular end of the Na⁺ profile (blue dashed line) indicates that the E-2′ carbonyl oxygen atoms can take the role of the water oxygen atoms and tightly interact with Na⁺, which may facilitate partially hydrated cations to pass through the narrowest region of the pore. For Na⁺, the difference between the solid and dashed lines extends toward the center of the pore, suggesting the following two layers of polar residues S6′ and T2′ also provide partial solvation. For Cl⁻, smaller difference between the two lines indicates that the ion does not interact with E-2′ and only intermittently with the other two polar residues.

When pore-lining residues cannot sufficiently solvate the ion, an increase of the pore radius might occur such that fewer coordinated water molecules will be stripped off in the course of ion passage (43). In Fig. 4, color-coded changes in pore radius along the channel axis are depicted as a function of different ion positions (from different umbrella sampling windows). It is evident that the size of the pore fluctuates in response to the presence of ions. In both the profiles for Na⁺ and Cl⁻, two horizontal blue stripes (at z positions 0 Å and 10 Å) indicate the narrowest regions (with pore radius of ∼2.4 Å), which correspond to the rings of I9′ and T2′, respectively. The pore appears to dilate temporarily as the ion passes these positions, and reverts to its initial size after the passage. Furthermore, the pore radius seems to increase slightly more during the passage of Na⁺ compared to Cl⁻ in the hydrophobic region (green circles highlighted in Fig. 4), which explains in part why Cl⁻ is stripped of more water molecules than Na⁺ in the middle of the pore. These results are in good correspondence with those from previous simulation of nAChR (43), underlining the importance of pore dynamics to ion conduction that allows for a lower free energy path through the hydrophobic region.

Figure 4.

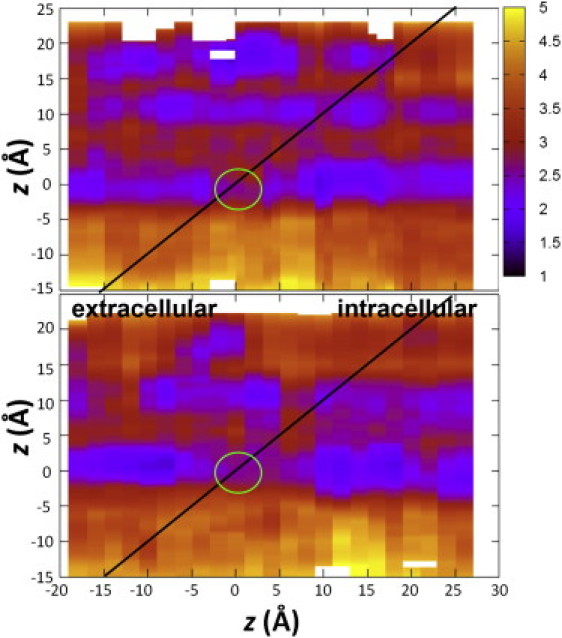
Dynamic fluctuations of the pore radius along the channel pore (vertical axis) from different umbrella sampling windows (horizontal axis) for the translocation of a Na⁺ ion (top) and a Cl⁻ ion (bottom). (Green circles) Passage through the hydrophobic region. The pore radius is color-coded. (Red) Large values. (Blue) Small values.

The pore radius also shows a widening in the E-2′ position (at z position 17 Å) during the passage of Na⁺ (Fig. 4 a), whereas the same region is widened throughout for Cl⁻ (Fig. 4 b). Detailed inspection reveals that in the chloride simulations, the E-2′ side chains have already folded away, assuming a different conformation from the starting one. Recent crystal structures of GLIC have also revealed two distinct conformations for the E-2′ residues (19,20): in one structure, the five glutamate side chains assume an up-conformation that folds back into the pore, leading to a very constrictive pore (pore radius 0.4 Å), whereas in the other structure they are all in a down-conformation that points toward the cytoplasm, leading to a wider opening (pore radius 2 Å). The BD simulations by Song and Corry (23) have revealed that the two conformations lead to a sharp difference in their conduction properties.

To gain further insight into the E2′ side-chain dynamics and its implication for ion conduction, we performed two additional 30-ns MD simulations of the full-length GLIC. Both simulations were started from the down-conformation (PDB code: 3eam), one with protonated E-2′ (corresponding to a low pH condition) and the other with deprotonated E-2′ (corresponding to a high pH condition). As illustrated in Fig. 5, the E-2′ side chains are quite dynamic, alternating among three different conformations, including the up- (C-C_α-C_β-C_γ: 60°), down- (C-C_α-C_β-C_γ: −60°), and a transient anti-conformation (C-C_α-C_β-C_γ: 180°).

Figure 5.

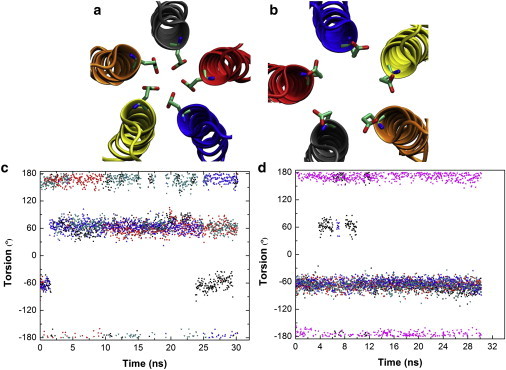
E-2′ side-chain dynamics during the simulations of the full-length GLIC. The up- (a) and down- (b) conformations of E-2′ side chain in the crystal structure. Five pore-lining helices are shown in cartoon representation, and five E-2′ residues are shown in licorice representation. Time trajectories of five E-2′ side-chain torsions (C-C_α-C_β-C_γ) during the simulations, with E-2′ in protonated (c) and deprotonated (d) states.

Different populations observed in the two simulations indicate that the E-2′ side-chain dynamics strongly depends on its protonation state. Whereas the down-conformation is preferred when E-2′ are deprotonated (Fig. 5 b), the up-conformation is favored when protonated (Fig. 5 a). When starting from the down-conformation, all the five protonated E-2′ residues quickly depart from their initial configurations and fluctuate between the up- and anti-conformations, frequently forming a more constrictive pore structure. These results lend some support to Song and Corry's proposal (23) that the more constrictive side-chain conformation of E-2′ (19) might have been influenced by the low intracellular pH during crystallization, and thus the down-conformation (corresponding to deprotonated E-2′) (19,20) most likely represents the experimentally determined open channel. The results also implicate that the proton exchange at E-2′ that shifts the up/down equilibrium of the E-2′ side-chain conformation may be coupled with ion conduction through the channel, which is worth further study in the future.

To further quantify the relative importance of various factors in contributing to charge selectivity, we decomposed the PMFs into individual contributions from the ion's interactions with its solvation shell, the residues E-2′ and E19′, and the protein excluding E-2′ and E19′ by integration of mean forces. Fig. 6 shows large opposing contributions from the protein and the solvation shell water (a complete decomposition of PMFs is given in Fig. S4). Evident preference for Na⁺ and repelling of Cl⁻ toward the intracellular end of the pore arise from the mean forces exerted by the protein. There is a strong attractive free energy contribution for Na⁺ centered at E-2′ position, whereas a slightly weaker repulsion is present for Cl⁻ at the same location.

Figure 6.

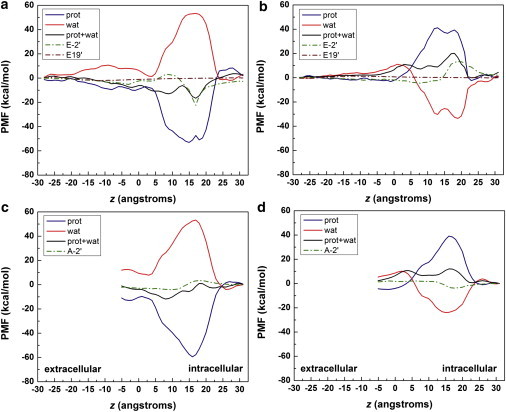
Mean force decomposition of the PMFs due to interactions of the ion with its first solvation shell (wat), the residues E-2′ and E19′, and the protein excluding E-2′ and E19′ (prot) for (a) Na⁺; (b) Cl⁻; (c) Na⁺ in the mutant E-2′A channel; and (d) Cl⁻ in the mutant E-2′A channel.

The results support that the E-2′ residues play an important role in charge selectivity—they contribute nearly 30% of the total energetic barrier/well seen in Fig. 6 (top panel, navy and olive lines). After mutation to alanine residues, their contributions become markedly diminished and nonspecific (Fig. 6, bottom panel). In the hydrophobic region, water hydration increases the PMF barrier by ∼4–5 kcal/mol for Cl⁻ when compared with Na⁺ (red lines in Fig. 6), possibly arising from the reduced number of water molecules and/or an unfavorable alignment of water molecules around the anion. The remaining PMF differences for Na⁺ and Cl⁻ in this region may come from the protein (navy line in Fig. 6), likely due to the overall negative electrostatic environment of the TM region. So, in addition to the hydration differences, the overall electrostatics contributes to the large free energy differences observed in hydrophobic regions for Na⁺ and Cl⁻.

Conclusions

Our calculations are consistent with the notion that the GLIC crystal structure was indeed captured in an active (open) state. Although it allows passage of sodium ions, it prevents chloride ions from entering the channel. We identified three major factors that determine the charge selectivity in the TM domain of GLIC—the E-2′ residue located at the intracellular exit and the hydrophobic region at the center of the pore, in agreement with the two regions of low ion concentration revealed by previous BD simulations of GLIC (23). Additionally, the overall negative electrostatic environment of the TM region also contributes to ion selectivity. The crucial role of E-2′ for ion selectivity was confirmed by the E-2′A mutant simulations that show an increase in the energy barrier for Na⁺ and a decrease in the barrier for Cl⁻ translocation. By contrast, the glutamates in position 19′ play only a minor role in determining ion selectivity due to their neutral protonation state (under physiological conditions) and lack of direct interactions with solvated ions. Our PMF calculations also predicted the existence of two low affinity binding sites for both Na⁺ and Cl⁻ at positions S6′ and T2′, in accordance with the two cation binding sites identified in the crystal structure (19).

Our results provide further insights into the interplay between pore hydration and ion permeation. Water density profiles showed that the GLIC channel is completely water-filled, and the presence of ions inside the channel tends to increase the pore size in predominantly hydrophobic confinement regions. Although the translocation of a sodium ion through the channel only experiences a negligible hydrophobic barrier, the same is not true for solvated anions. Indeed, the chloride PMF revealed a hydrophobic restriction with a significant barrier (∼9 kcal/mol) in the middle of the pore. The different hydrophobic barriers between Na⁺ and Cl⁻ have also been noted previously (16,40), and can be primarily attributed to a combined effect of local water hydration and the overall electrostatics of the channel.

Besides ion hydration, dynamical fluctuations of the GLIC channel appear crucial for ion transport as well. Instantaneous increase of pore size in the narrow hydrophobic regions coupled with the presence of ions promotes water filling, and thus facilitates ion transport. At the intracellular end, the structural rearrangements of the E-2′ side chains are quite facile. As a result, even though the intracellular end of the pore appears constrictive in the crystal structure, the energetic barrier for sodium transport is small.

The confluence of several structural, dynamical, and energetic factors enable preferential translocation of cations and exclusion of anions from the TM pore of the GLIC receptor:

• 1.Presence of a ring of negatively charged glutamate residues (E-2′) at the narrow intracellular end of the receptor;
• 2.Differential effects of the hydrophobic constriction on water coordination by sodium and chloride ions;
• 3.Overall negative electrostatic environment in the TM region; and
• 4.To some degree, the dynamics of the pore-lining residues and its crucial influence on the pore radius and ion hydration.

Additional studies are now needed to determine to what extent the mechanistic insights gleaned in the GLIC channel can translate to understanding of the nAChR and other Cys-loop family receptors.