Abstract
Purpose
Quantification of hepatic tracer kinetics by PET requires measurement of tracer input from the hepatic artery (HA) and portal vein (PV). We wished to develop a method for estimating dual tracer input without the necessity to sample PV blood.
Methods
Pigs weighing 40 kg were given bolus doses of C15O (CO), 2-[18F]fluoro-2-deoxy-D-glucose (FDG), [11C]-methylglucose (MG), 2-[18F]fluoro-2-deoxy-D-galactose (FDGal) or H2 15O (H2O). Tracer concentration 3-min time courses were measured in the femoral artery and PV by blood sampling. Blood flow was measured in the HA and PV using flow-meters. A model for transfer of tracer through the splanchnic circulation was used to estimate values of a tracer-specific model parameter β. Tracer-specific mean values of β were used to estimate tracer concentration time courses in the PV from the measured arterial concentration. A model-derived dual-input was calculated using the mean HA flow fraction (0.25) and validated by comparison of the use of the measured dual-input and a kinetic model with a fixed ”true” K 1 true, i.e. clearance of tracer from blood to liver cells.
Results
The rank order of the means of β was CO < FDG ≈ MG < FDGal < H2O, reflecting their different splanchnic mean transit times. Estimated K 1 est was not significantly different from “true” K 1 true.
Conclusion
The hepatic dual tracer input, which is of great importance for the assessment of processes such as transfer across the plasma-hepatocyte membrane or hepatic blood perfusion, can be well approximated in pigs without the necessity to sample PV blood and measure hepatic blood flow; only arterial blood sampling is needed.
Keywords: Splanchnic circulation, Liver kinetics, Molecular imaging, Pharmacokinetics, PET, Portal model, Radioactive tracers
Introduction
Molecular imaging with positron emission tomography (PET) provides unique possibilities for in vivo quantification of blood perfusion, transmembrane transport and tissue metabolism. A quantitative PET study comprises bolus administration of a positron-emitting tracer immediately followed by dynamic recording of the tracer concentration time-courses in tissue by PET and in the blood supply by blood sampling. Physiological parameters are calculated by fitting a mathematical model of tracer distribution and metabolism to the data. Application of this approach to the liver is complicated, however, due to dual input of tracer from the hepatic artery (HA) and the portal vein (PV), comprising 25% and 75%, respectively. The tracer concentration time-course in the PV is initially delayed and dispersed compared to that in the HA due to transfer of tracer through the splanchnic circulation. If there is no metabolism of the tracer in the organs drained by the PV, hepatic steady-state metabolism may be assessed by dynamic PET using solely the arterial input of tracer. This has been validated for 2-[18F]fluoro-2-deoxy-d-glucose (FDG) [1, 2] and 2-[18F]fluoro-2-deoxy-d-galactose (FDGal) in pigs [3] and used in studies of hepatic FDG metabolism in humans [4–6]. Processes such as transfer across the highly permeable plasma-hepatocyte membrane or hepatic blood perfusion must be assessed using the initial dynamic part of tracer concentration time-courses before steady-state metabolism dominates the recordings, however. This requires successive measurement of blood tracer activity concentration in the PV immediately after tracer administration, as well as of the fractional blood flow in the PV and HA [1]. The most reliable method is to measure tracer concentration time-courses in both an artery and the PV by invasive blood sampling combined with invasive measurements of blood flow in the HA and PV. This is only possible in animal studies, however [1–3, 7, 8], and various studies have addressed the challenge of how to assess the initial dynamic tracer input from the HA and PV for human studies. Choi et al. [4] suggested the use of a single arterial input with a time delay to account for the delay of the PV input, but this does account for the dispersion of the PV tracer input. However, Munk et al. [1] showed that knowledge of the tracer input from both vessels, the so-called dual-input, is needed to obtain unbiased kinetic parameter estimates that are in agreement with independent measurements of hepatic blood flow and hepatic blood volume.
PET image-derived methods have been used in several studies [9–12] and seem attractive because they are completely noninvasive and thus applicable to humans. However, the image-derived dual-input tracer concentration time-course is prone to errors caused by partial volume effects where the tracer concentration time-courses in the PV and the aorta, used as arterial input, are affected by tracer activity in the surrounding tissue due to limited spatial resolution compared with the size of the vessels and respiratory motion [4, 9, 10]. Mathematical–physiological models describing the transfer of tracer from the intestinal arteries to the PV do not rely on the dynamic tissue PET image data. Various mathematical PV models have been proposed such as a one-compartmental model [13] and a double gamma-variate model [8].
We have previously developed PV models that included only parameters with direct physiological interpretations and which were validated by means of sets of measured tracer concentration time-courses in arterial blood and the PV [14]. However, these models have never been used to calculate the dual-input for kinetic modelling of liver physiology. One of these PV models (method 4 in ref. 14) is particularly useful and robust for calculating the model-derived tracer concentration time-course in the PV from that in arterial blood as it provides a full description of the tracer concentration time-course in the PV using only a single tracer-specific parameter, β, which reflects tracer-specific mean splanchnic transit time for the tracer from the intestinal arteries to the PV. Therefore we tested the use of this PV model in the present study.
The aim of the present study was to estimate population means of β for five tracers with a wide range of mean splanchnic transit times and to calculate the dual input from the tracer-specific mean values of β and an estimated mean of the HA blood flow fraction. The model-derived dual input was validated by fitting a simple kinetic model to a simulated tracer concentration time-course in liver tissue. We chose clearance of tracer from blood to liver cells, K 1, as our test parameter because the K 1 estimate is particularly sensitive to the initial dynamic shape of the dual-input curve [1]. Thus any errors produced by using the PV model in kinetic modelling will be reflected in the estimated K 1. Moreover, K 1 for MG, FDG and FDGal may be used as a measure of hepatic blood perfusion [1, 3]. The overall aim of the study was to develop and validate a simple method – based solely on blood sampling from a peripheral artery, tracer-specific means of β and an estimated mean HA blood flow fraction – with which to estimate the combined tracer input to the liver from the HA and PV for use in PET studies of initial hepatic tracer kinetics.
Materials and methods
The investigations were performed in nine pigs given C15O (CO) by inhalation. Five of the pigs also received intravenous injections of H152O (H2O). In addition, the study included analysis of raw data from previously published studies in six pigs which each received intravenous injections of FDG and [11C]methylglucose (MG) [1], and ten pigs which received intravenous injections of FDGal [3]. In each study the tracer concentration time-course was measured simultaneously in a femoral artery and the PV, and blood flow was measured in the HA and PV for the first 3 min following tracer administration using surgically placed ultrasound transit time flow-meters.
All studies were approved by the Danish Ministry of Legal Affairs and performed in accordance with European Union, national, and institutional guidelines for animal welfare.
Experimental procedures
Female pigs (Danish Landrace and Yorkshire cross-breed; body weight 38–42 kg) were fasted for 16 h with free access to water. Anaesthesia was maintained by a constant intravenous infusion of 240 mg propofol, 200 mg S-ketamine and 40 mg midazolam per hour and the animal was ventilated with air/oxygen 2.2:1 by mechanical respiration. Catheters were inserted into a femoral artery (blood sampling) and a femoral vein (intravenous administration). The abdomen was opened and ultrasound transit-time flow-meter probes (12 mm and 4 or 6 mm, respectively; CardioMed; In vivo Aps, Norway) were positioned around the PV and HA (in some cases two HA vessels) for continuous measurement of blood flow [15, 16]. A 5.3F polyethylene catheter (William Cook, Denmark) was inserted directly into the PV for blood sampling; it was placed downstream of the flow-meter probe so as not to disturb the flow measurements. Physiological parameters were maintained as follows: body temperature 38.5–39.5°C, arterial pCO2 3.5–7.0 kPa, pO2 18.0–25.0 kPa, pH 7.35–7.45 and blood glucose 5.0–6.7 mmol/l. The experiments were terminated by intravenous injection of 4 g pentobarbital sodium.
Tracer administration and blood concentration measurements
C15O (400 MBq) was administered as a 10-s inhalation via the respirator; H152O (300 MBq) was administered as a 15-s intravenous injection. To assess reproducibility, these tracers were administrated twice in each pig. Starting at the beginning of tracer administration, arterial blood was drawn from the catheter in the femoral artery by an automated blood sampling apparatus and the blood concentration of tracer determined every 0.5 s (Allogg, Mariefred, Sweden), correcting for delay and dispersion in the sampling catheters [17]. In order not to disturb blood flow in the HA, the samples were collected from a femoral artery (the concentration of tracer in the femoral artery is identical to that in the HA; Keiding, unpublished observations). PV blood samples (1 ml) were collected manually from the PV catheter every 5th second 18 times and then every 15th second 6 times (3 min). Tracer concentrations in blood (kBq/ml) were measured using a well counter (Packard Instruments, Meriden, CT). All tracer concentration measurements were corrected for radioactive decay back to the start of tracer administration.
With the FDG [1], MG [1] and FDGal [3] studies, tracer concentrations were measured in successive blood samples drawn manually from the femoral artery and PV over a period of 45–90 min. However, in the present study only measurements from the initial 3 minutes were used. For none of the five tracers were metabolites detectable in the blood [1, 3] and accordingly the measured tracer activity concentrations in the blood were used directly in the calculations.
Model considerations and calculations
With each administration of tracer the following calculations were performed:
1.
The HA blood flow fraction, f HA, was calculated from the flow-meter measurements of blood flow in the HA, F HA (millilitres blood per minute), and in the PV, F PV (millilitres blood per minute), as
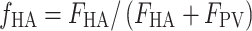 |
1 |
The f
HA in individual experiments deviated by less than 1% per minute, and an individual mean value of f
HA was used in the individual experiments (Section 2, below). For the calculations of the model-derived dual-input,  , a mean value for all experiments, denoted
, a mean value for all experiments, denoted 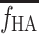 (=0.25±0.07, mean±SEM), was used (Section 5, below).
(=0.25±0.07, mean±SEM), was used (Section 5, below).
2.
The measured dual-input, C dual(t), was calculated from the tracer concentration time-courses in HA blood, C HA(t), equivalent to the individually measured tracer concentration time-courses in arterial blood, C A(t), and PV blood, C PV(t), and f HA, as
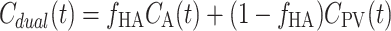 |
2 |
3.
We describe the passage of a bolus from the arterial system through the splanchnic circulation to the PV using a previously validated impulse response function based on a distribution of washout rate constants. The full impulse response function has two parameters: a final washout rate constant, k 0, and β, that determine the mean transit time and the standard deviation of transit times for the passage of tracer from the intestinal arteries to the PV [14]. Thus, the model parameters have a clear physiological interpretation. In the limit of a slow final washout constant, k 0 → 0, the full impulse-response function is reduced to a power law function with the single parameter β. This one-parameter impulse response function provided a robust description of the tracer concentration time-course in the PV for CO and MG [14]. In the present study we accordingly estimated β of this PV model for each tracer administration by nonlinear regression analysis of the relationship between C PV(t) and C A(t):
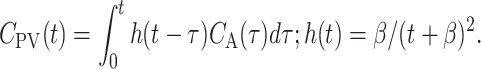 |
3 |
With CO and H2O, agreement between the double determinations of β was good (see Results) and the mean value for each animal was used.
4.
The mean of β, denoted 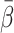 , was used as an estimate of a population mean of β for each tracer and used to calculate individual PV model-derived tracer concentration time courses in the PV,
, was used as an estimate of a population mean of β for each tracer and used to calculate individual PV model-derived tracer concentration time courses in the PV, 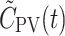 , from C
A(t) as:
, from C
A(t) as:
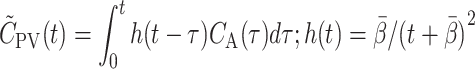 |
4 |
5.
The model-derived dual-input, 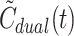 , was calculated from C
A(t),
, was calculated from C
A(t), 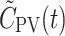 and
and 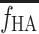 , as:
, as:
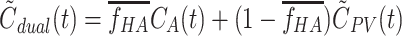 |
5 |
6.
The use of 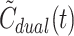 instead of C
dual(t) when estimating hepatic tracer kinetics was assessed by means of individual simulated tracer activity concentration time courses in liver tissue,
instead of C
dual(t) when estimating hepatic tracer kinetics was assessed by means of individual simulated tracer activity concentration time courses in liver tissue, 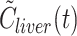 , using the first 3 minutes of the measured C
dual(t) and a one-tissue compartmental model with a fixed set of ”true” parameters: K
1
true, clearance of tracer from blood to liver cells (1 ml blood per millilitre liver tissue per minute); k
2, rate constant for backflux of tracer from cells to blood (2/min); and V
0, vascular volume of the liver (0.40 ml blood per millilitre liver tissue). The model was fitted to
, using the first 3 minutes of the measured C
dual(t) and a one-tissue compartmental model with a fixed set of ”true” parameters: K
1
true, clearance of tracer from blood to liver cells (1 ml blood per millilitre liver tissue per minute); k
2, rate constant for backflux of tracer from cells to blood (2/min); and V
0, vascular volume of the liver (0.40 ml blood per millilitre liver tissue). The model was fitted to 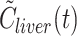 using the
using the 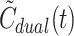 as input for estimation of K
1
est with no parameters fixed. The error associated with the use of
as input for estimation of K
1
est with no parameters fixed. The error associated with the use of 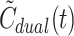 rather than C
dual(t) in the kinetic fitting procedure was assessed by the relative deviation of K
1
est from K
1
true: (K
1
est − K
1
true)/K
1
true, which assesses how well the fixed K
1
true is recovered. Although the one-tissue compartmental model was not physiologically correct for all tracers in the present study, we used it to generate a simulated tissue curve for testing the effect of replacing C
dual(t) by
rather than C
dual(t) in the kinetic fitting procedure was assessed by the relative deviation of K
1
est from K
1
true: (K
1
est − K
1
true)/K
1
true, which assesses how well the fixed K
1
true is recovered. Although the one-tissue compartmental model was not physiologically correct for all tracers in the present study, we used it to generate a simulated tissue curve for testing the effect of replacing C
dual(t) by 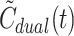 in the analysis of initial hepatic tracer kinetics.
in the analysis of initial hepatic tracer kinetics.
Statistical analysis
Normally distributed data are expressed in terms of the mean ± standard error of the mean (SEM) unless otherwise stated, and statistical analysis of intergroup differences was performed by ANOVA analysis. For multiple comparisons, the Bonferroni post-hoc test was used for data with equal variance and the Tamhane T2 test for data with unequal variance. Differences with a p value <0.05 were considered statistically significant.
Results
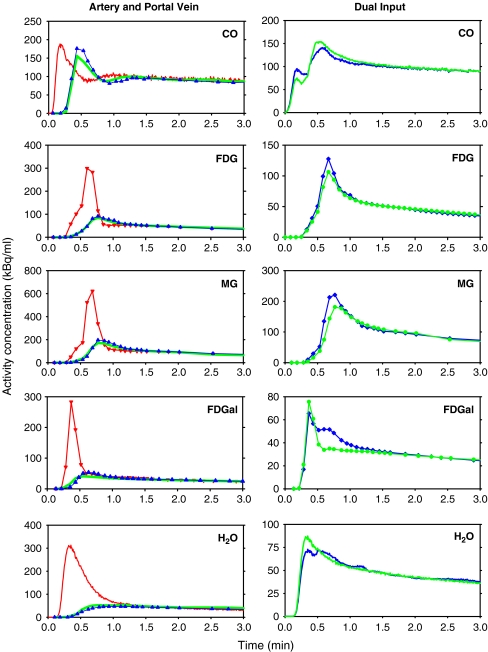
Examples of the measured tracer concentration time-course in the PV, C
PV(t), are shown in Fig. 1 (left) which illustrates the delay and the dispersion of the peak compared to that in arterial blood, C
A(t). The 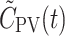 derived from the PV model (Eq. 4) well reflects the measured C
PV(t).
derived from the PV model (Eq. 4) well reflects the measured C
PV(t).
Fig. 1.
Left Examples of blood tracer activity concentration time-courses following bolus administration of tracers to pigs measured in a femoral artery, C
A(t) (red curves); measured in the PV, C
PV(t) (blue curves); PV model-derived, 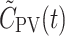 (green curves) calculated from C
A(t) using means of the tracer-specific parameters for the passage of the tracer from the intestinal arteries to the PV,
(green curves) calculated from C
A(t) using means of the tracer-specific parameters for the passage of the tracer from the intestinal arteries to the PV, 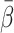 s (Eq. 4). Right For each tracer, the measured dual input, C
dual(t) (blue curves), was calculated from C
A(t) and C
PV(t) shown on the left and the individually measured HA blood flow fractions, f
HA (Eqs. 1 and 2). The corresponding model-derived dual input,
s (Eq. 4). Right For each tracer, the measured dual input, C
dual(t) (blue curves), was calculated from C
A(t) and C
PV(t) shown on the left and the individually measured HA blood flow fractions, f
HA (Eqs. 1 and 2). The corresponding model-derived dual input, 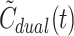 (green curves), was calculated from C
A(t) and
(green curves), was calculated from C
A(t) and 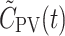 and the mean HA blood flow fraction, f
HA (=0.25; Eq. 5)
and the mean HA blood flow fraction, f
HA (=0.25; Eq. 5)
With CO (nine tracer administrations) the degree of agreement between the double determinations of 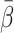 , expressed as an intraclass correlation, was 0.90. The corresponding figure for H2O (five tracer administrations) was 0.86. Thus, the estimate of β could be accurately reproduced in each animal. For the administration of both FDG and MG in each of six pigs two-way ANOVA showed that the variation between the pigs accounted for 79.0% of the total variance (p=0.0591). In other words, the accuracy of the estimated β was good enough to demonstrate variation between the animals. The variation associated with
, expressed as an intraclass correlation, was 0.90. The corresponding figure for H2O (five tracer administrations) was 0.86. Thus, the estimate of β could be accurately reproduced in each animal. For the administration of both FDG and MG in each of six pigs two-way ANOVA showed that the variation between the pigs accounted for 79.0% of the total variance (p=0.0591). In other words, the accuracy of the estimated β was good enough to demonstrate variation between the animals. The variation associated with 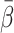 accordingly can be ascribed to physiological and experimental differences between animals which contribute to the error of
accordingly can be ascribed to physiological and experimental differences between animals which contribute to the error of 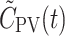 . The tracer-specific means of
. The tracer-specific means of 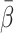 , are shown in Table 1. The rank order for
, are shown in Table 1. The rank order for 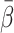 was CO < FDG ≈ MG < FDGal < H2O.
was CO < FDG ≈ MG < FDGal < H2O.
Table 1.
Values of 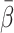 (tracer-specific means of β) in pigs. The data are presented as means±SEM
(tracer-specific means of β) in pigs. The data are presented as means±SEM
| Tracer | Number of tracer administrations |
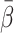 (min) (min) |
|---|---|---|
| CO | 9 | 0.10±0.02 |
| FDG | 6 | 0.50±0.05 |
| MG | 6 | 0.57±0.09 |
| FDGal | 10 | 0.82±0.08 |
| H2O | 5 | 2.17±0.13 |
As illustrated in Fig. 1 (right), the dual input, 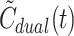 , derived from the model (Eq. 5) well reflects the measured dual input, C
dual(t) (Eq. 2).
, derived from the model (Eq. 5) well reflects the measured dual input, C
dual(t) (Eq. 2). 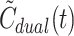 even reproduced the biphasic shape of C
dual(t) for CO. In some cases,
even reproduced the biphasic shape of C
dual(t) for CO. In some cases, 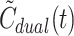 slightly over- or underestimated the peak value of C
dual(t) more than would be expected from the good agreement between
slightly over- or underestimated the peak value of C
dual(t) more than would be expected from the good agreement between 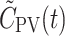 and C
PV(t). No systematic tendencies were apparent, probably because individual values of f
HA were used to calculate C
dual(t), whereas the mean value
and C
PV(t). No systematic tendencies were apparent, probably because individual values of f
HA were used to calculate C
dual(t), whereas the mean value 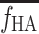 was used to calculate
was used to calculate 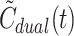 .
.
The error associated with using 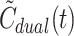 rather than C
dual(t) to estimate K
1
est did not differ significantly from zero with any of the tracers (Table 2). Individual estimates of K
1
est may, however, be biased because the individual (unknown) parameters β and f
HA may deviate from the tracer-specific mean
rather than C
dual(t) to estimate K
1
est did not differ significantly from zero with any of the tracers (Table 2). Individual estimates of K
1
est may, however, be biased because the individual (unknown) parameters β and f
HA may deviate from the tracer-specific mean 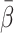 and the mean
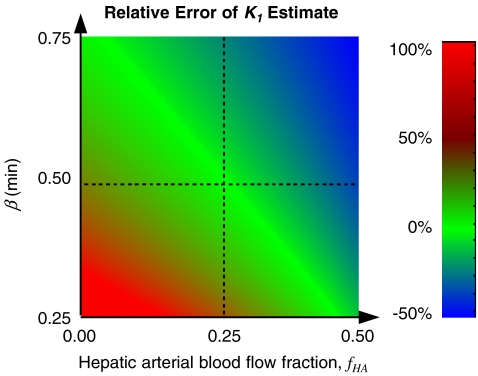
and the mean 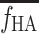 for all tracer administrations. As an example, Fig. 2 shows a plot of the error of K
1
est as a function of β and f
HA for MG with
for all tracer administrations. As an example, Fig. 2 shows a plot of the error of K
1
est as a function of β and f
HA for MG with 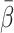 = 0.5 and
= 0.5 and 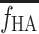 = 0.25. There were wide ranges of β and f
HA values which only induce a modest error in K
1
est. In general, K
1
est is overestimated when the individual β is lower than
= 0.25. There were wide ranges of β and f
HA values which only induce a modest error in K
1
est. In general, K
1
est is overestimated when the individual β is lower than 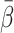 and vice versa.
and vice versa.
Table 2.
Fractional error of model-derived clearance of tracer from blood to liver cells
| Tracer | No. of studies | K 1 est fractional errora | p value |
|---|---|---|---|
| CO | 9 | 0.02 ± 0.05 | 0.71 |
| FDG | 6 | 0.23 ± 0.23 | 0.36 |
| MG | 6 | -0.04 ± 0.09 | 0.67 |
| FDGal | 10 | -0.09 ± 0.13 | 0.51 |
| H2O | 5 | 0.17 ± 0.09 | 0.16 |
aModel-derived dual input was validated by comparing the estimated clearance of tracer from blood to liver cells, K
1
est, with the fixed “true” clearance, K
1
true. K
1
est was calculated by fitting a one-tissue compartmental liver kinetic model to a simulated tracer concentration time-course in liver tissue, 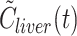 , using the model-derived dual input,
, using the model-derived dual input, 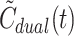 ; see text for further details. The data are presented as means±SEM.
; see text for further details. The data are presented as means±SEM.
Fig. 2.
Plot of the error associated with the use of model-derived dual input, 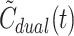 , rather than measured dual input, C
dual(t), (see Fig. 1, right) for fitting hepatic kinetics. The plot provides an example with
, rather than measured dual input, C
dual(t), (see Fig. 1, right) for fitting hepatic kinetics. The plot provides an example with 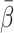 equal to that for MG (0.5 min) and
equal to that for MG (0.5 min) and 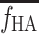 the mean of all experiments (0.25), using a simulated activity concentration time-course in liver tissue calculated according to a one-tissue compartmental model with fixed K
1
true (K
1, clearance of tracer from blood to liver cells) using C
dual(t) as input (see text for further details). Next K
1
est was estimated by fitting the model to the simulated liver tissue curve using
the mean of all experiments (0.25), using a simulated activity concentration time-course in liver tissue calculated according to a one-tissue compartmental model with fixed K
1
true (K
1, clearance of tracer from blood to liver cells) using C
dual(t) as input (see text for further details). Next K
1
est was estimated by fitting the model to the simulated liver tissue curve using 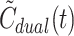 as input. The relative deviation of K
1
est from K
1
true, (K
1
est−K
1
true)/K
1
true, illustrates how well the fixed K
1
true is recovered by K
1
est, and is plotted as a function of sets of β (tracer-specific parameter of the PV model, minutes) and f
HA (HA blood flow fraction)
as input. The relative deviation of K
1
est from K
1
true, (K
1
est−K
1
true)/K
1
true, illustrates how well the fixed K
1
true is recovered by K
1
est, and is plotted as a function of sets of β (tracer-specific parameter of the PV model, minutes) and f
HA (HA blood flow fraction)
Discussion
The main result of this study was that estimates of the time-course of the model-derived 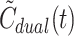 based on tracer-specific means of β combined with the mean HA blood flow fraction,
based on tracer-specific means of β combined with the mean HA blood flow fraction, 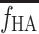 , agreed well with invasively measured C
dual(t). The use of
, agreed well with invasively measured C
dual(t). The use of 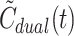 instead of C
dual(t) to estimate clearance of tracer from blood to liver cells, K
1, was successful for all tracers. Dual input of tracer to the liver can thus be estimated solely by sampling blood from a peripheral artery, thereby obviating the need to sample blood from the PV and perform invasive measurement of blood flow.
instead of C
dual(t) to estimate clearance of tracer from blood to liver cells, K
1, was successful for all tracers. Dual input of tracer to the liver can thus be estimated solely by sampling blood from a peripheral artery, thereby obviating the need to sample blood from the PV and perform invasive measurement of blood flow.
The tracer-specific β (minutes) is related to the transit time of tracer through the splanchnic circulation and may be interpreted as the inverse of the most frequent rate (min−1) by which tracer molecules enter the PV bloodstream from the intestinal arteries [14]. The study included five tracers differing widely in splanchnic mean transit time from purely intravascular CO to freely diffusible H2O. A high mean transit time yields a high β, as reflected in the rank order of 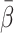 for the tracers, i.e. CO < FDG ≈ MG < FDGal < H2O (Table 1). The low
for the tracers, i.e. CO < FDG ≈ MG < FDGal < H2O (Table 1). The low 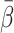 for CO (0.10±0.02 min) is in agreement with a low mean splanchnic transit time due to firm binding to erythrocytes and with the previously recorded value of 0.11±0.02 min in pigs [14].
for CO (0.10±0.02 min) is in agreement with a low mean splanchnic transit time due to firm binding to erythrocytes and with the previously recorded value of 0.11±0.02 min in pigs [14]. 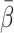 was significantly higher for H2O than for all the other tracers (p<0.0001), in accordance with the fact that water is freely diffusible and thus has the greatest volume of distribution and slowest passage through the splanchnic circulation, i.e. a high transit time. Tracer-specific means of β, i.e.
was significantly higher for H2O than for all the other tracers (p<0.0001), in accordance with the fact that water is freely diffusible and thus has the greatest volume of distribution and slowest passage through the splanchnic circulation, i.e. a high transit time. Tracer-specific means of β, i.e. 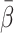 , could be estimated with all five tracers and the PV model adequately described the transfer of the tracers from the intestinal arteries to the PV, thus indicating general applicability of the PV model.
, could be estimated with all five tracers and the PV model adequately described the transfer of the tracers from the intestinal arteries to the PV, thus indicating general applicability of the PV model.
The validity of the PV model relies on two assumptions: (1) no trapping of tracer in the intestines, and (2) no production of blood-born metabolites in the intestines. If one of these assumptions is violated then there is no longer a mass balance between the tracer activity concentration on the arterial side and on the PV side, and this must be taken into account, e.g. by multiplying a loss term to the impulse-response function in Eq. 3. We did not include a loss term because all five tracers in this study allowed direct use of the PV model (Fig. 1, left). However, if other tracers are used this modification may be required. Moreover, some PET tracers, e.g. 13N-ammonia, produce blood-born metabolites outside the intestines that must be taken into account when analysing dynamic PET data of the liver [20]. For such tracers the PV model should be applied separately for the tracer and the metabolites.
The mean HA flow fraction found in this study, 0.25, is similar to the value of 0.26±0.02 (n=7) determined in humans with no liver disease by means of ultrasound transit-time flow-meters [21], and of 0.25±0.02 (n=8) determined in healthy humans by hepatic scintiangiography [22]. This indicates that a HA flow fraction of 0.25 is applicable to human studies. Likewise, the mean transit time for CO through the splanchnic circulation determined in pigs, 0.35±0.05 min [21], is similar to that in humans, 0.37±0.05 min [22]. These similarities for key physiological features are promising for translation of the present modelling to human studies, but this needs to be examined further.
A key question is to what extent will possible errors introduced by the use of the model-derived dual input, 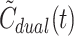 , rather than the measured dual input, C
dual(t), propagate into errors of the estimated liver kinetic parameters. We examined this question by using simulated liver tissue activity concentration time-courses rather than experimental PET data, the rationale being that simulated data are not influenced by the experimental uncertainty associated with measured activity concentration time-course in liver tissue or the possible shortcomings of compartmental models of hepatic tracer kinetics. We therefore generated a simulated activity concentration time-course in liver tissue,
, rather than the measured dual input, C
dual(t), propagate into errors of the estimated liver kinetic parameters. We examined this question by using simulated liver tissue activity concentration time-courses rather than experimental PET data, the rationale being that simulated data are not influenced by the experimental uncertainty associated with measured activity concentration time-course in liver tissue or the possible shortcomings of compartmental models of hepatic tracer kinetics. We therefore generated a simulated activity concentration time-course in liver tissue, 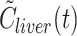 , using a one-tissue compartmental model of the hepatic tracer kinetics with fixed “true” parameters and the “correct” individually invasively measured dual input, C
dual(t). The model was then fitted to the simulated liver tissue curve
, using a one-tissue compartmental model of the hepatic tracer kinetics with fixed “true” parameters and the “correct” individually invasively measured dual input, C
dual(t). The model was then fitted to the simulated liver tissue curve 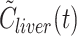 using
using 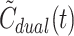 to test how well the fixed “true” parameter K
1
true could be reproduced. Full kinetics of experimentally measured PET data should be analysed using kinetic models appropriate to the metabolism of the specific tracer [1–3, 18, 19]. For the evaluation of the PV model, however, all five tracers distribute flow-limited in the liver and therefore the use of the one-tissue compartmental model is relevant for the initial kinetics for all five tracers.
to test how well the fixed “true” parameter K
1
true could be reproduced. Full kinetics of experimentally measured PET data should be analysed using kinetic models appropriate to the metabolism of the specific tracer [1–3, 18, 19]. For the evaluation of the PV model, however, all five tracers distribute flow-limited in the liver and therefore the use of the one-tissue compartmental model is relevant for the initial kinetics for all five tracers.
The finding that the mean deviation of K
1
est from K
1
true was not significantly different from zero for any of the five tracers (Table 2) demonstrates that the modelling of the dual input yielded accurate estimates of K
1 for each group of tracer experiments. The next question is to what extent the error in K
1 for individual subjects depends on the individual (unknown) values of β and f
HA compared with 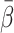 and
and 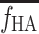 . Fig. 2 gives an example of how deviation in true individual β and f
HA from
. Fig. 2 gives an example of how deviation in true individual β and f
HA from 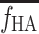 and
and 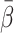 propagate into errors of K
1
est. The relationship is complicated due to correlations between the one-tissue compartmental model parameters (K
1, k
2, V
0) and the model-derived dual-input parameters
propagate into errors of K
1
est. The relationship is complicated due to correlations between the one-tissue compartmental model parameters (K
1, k
2, V
0) and the model-derived dual-input parameters 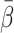 and
and 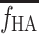 . Nevertheless, wide ranges of β and f
HA exist that only induce a modest error in K
1
est. However, large deviations in β from
. Nevertheless, wide ranges of β and f
HA exist that only induce a modest error in K
1
est. However, large deviations in β from 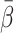 and in f
HA from
and in f
HA from 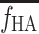 will lead to significant errors in the estimation of K
1. This emphasizes the importance of using a well-established set of
will lead to significant errors in the estimation of K
1. This emphasizes the importance of using a well-established set of 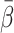 and
and 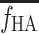 when performing kinetic analyses without PV blood samples. Thus, the model-derived dual input
when performing kinetic analyses without PV blood samples. Thus, the model-derived dual input 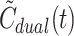 can only be used for a group of subjects for whom estimates of
can only be used for a group of subjects for whom estimates of 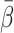 and
and 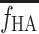 are available.
are available.
Compared to previous models [4, 7–13], our method is very robust, relying on only a single tracer-specific parameter 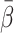 . It makes no assumption about the shape of the arterial input curve, is independent of the liver kinetic model and is unaffected by possible undesirable features of the PET image-derived input such as partial volume effects and artefacts due to patient motion. The robustness of the model and the similarities between the splanchnic circulation in pigs and humans indicate the potential for transferring the method to PET studies of initial tracer kinetic processes such as blood-cell exchange and hepatic blood perfusion in liver physiology and metabolism in humans.
. It makes no assumption about the shape of the arterial input curve, is independent of the liver kinetic model and is unaffected by possible undesirable features of the PET image-derived input such as partial volume effects and artefacts due to patient motion. The robustness of the model and the similarities between the splanchnic circulation in pigs and humans indicate the potential for transferring the method to PET studies of initial tracer kinetic processes such as blood-cell exchange and hepatic blood perfusion in liver physiology and metabolism in humans.
Conclusion
In the present study we developed a method to estimate a model-derived dual-input using the one-parametric PV-model, a tracer-specific mean parameter 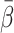 for the transfer of tracer from the intestinal arteries to the PV and the HA blood flow fraction
for the transfer of tracer from the intestinal arteries to the PV and the HA blood flow fraction 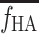 = 0.25. Although the five tracers examined here differ markedly in splanchnic mean transit time, the PV-model could be successfully applied to each of the tracers. Validation of the model for a wide range of tracers did not reveal any systematic deviations in parameters of the initial hepatic tracer kinetics by using the model-derived compared with the invasively measured dual-input. The study thus shows that the dual input of tracer to the liver from the HA and PV can be well approximated without the necessity to sample blood from the PV and perform invasive measurement of blood flow in the HA and PV. Our new method only requires measurement of the tracer concentration in a peripheral artery during a dynamic PET study of the liver and estimates of the mean
= 0.25. Although the five tracers examined here differ markedly in splanchnic mean transit time, the PV-model could be successfully applied to each of the tracers. Validation of the model for a wide range of tracers did not reveal any systematic deviations in parameters of the initial hepatic tracer kinetics by using the model-derived compared with the invasively measured dual-input. The study thus shows that the dual input of tracer to the liver from the HA and PV can be well approximated without the necessity to sample blood from the PV and perform invasive measurement of blood flow in the HA and PV. Our new method only requires measurement of the tracer concentration in a peripheral artery during a dynamic PET study of the liver and estimates of the mean 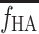 and tracer-specific population mean
and tracer-specific population mean 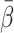 .
.
Acknowledgments
This study was supported by the National Institutes of Health (R01-DK074419), the Danish Medical Research Council (09-067618), the Novo Nordisk Foundation (R121-A10313), Aase and Ejnar Danielsen’s Foundation (106309), Helga and Peter Korning’s Foundation, and the A. P. Møller Foundation for the Advancement of Medical Science.
The authors wish to thank Prof. Ludvik Bass, University of Queensland, Brisbane, Australia, for encouraging us to use the tracer-specific portal vein model to determine the noninvasive dual-input tracer concentration for studies of liver kinetics.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Abbreviations
- CO
[15O]-Carbon monoxide
- FDG
2-[18F]Fluoro-2-deoxy-d-glucose
- MG
[11C]Methylglucose
- FDGal
2-[18F]Fluoro-2-deoxy-d-galactose
- H2O
[15O]-Water
- HA
Hepatic artery
- PV
Portal vein
- FHA
Blood flow in the hepatic artery (ml blood/min)
- FPV
Blood flow in the portal vein (ml blood/min)
- fHA
Hepatic arterial blood flow fraction
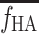
Mean f HA for all experiments
- h(t)
Impulse-response function of the portal vein model
- β
Tracer-specific parameter of the portal vein model (min)
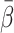
Population mean of β for each tracer (min)
- CA(t)
Measured tracer concentration time-course in peripheral arterial blood (kBq/ml blood)
- CHA(t)
Tracer concentration time course in hepatic arterial blood (kBq/ml blood); tracer concentration is equal to that in C A(t)
- CPV(t)
Measured tracer concentration time course in the portal vein (kBq/ml blood)
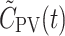
PV model-derived tracer concentration time course in the portal vein (kBq/ml blood)
- Cdual(t)
Measured dual-input tracer concentration time course (kBq/ml blood)
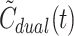
Model-derived dual-input tracer concentration time course (kBq/ml blood)
- Cliver(t)
Measured activity concentration time course in liver tissue (kBq/ml liver tissue versus min)
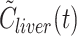
Simulated activity concentration time course in liver tissue (kBq/ml liver tissue versus min)
- K1
Clearance of tracer from blood to liver cells (ml blood/ml liver tissue/min)
References
- 1.Munk OL, Bass L, Roelsgaard K, Bender D, Hansen SB, Keiding S. Liver kinetics of glucose analogs measured in pigs by PET: importance of dual-input blood sampling. J Nucl Med. 2001;42:795–801. [PubMed] [Google Scholar]
- 2.Iozzo P, Jarvisalo MJ, Kiss J, Borra R, Naum GA, Viljanen A, et al. Quantification of liver glucose metabolism by positron emission tomography: validation study in pigs. Gastroenterology. 2007;32:531–42. doi: 10.1053/j.gastro.2006.12.040. [DOI] [PubMed] [Google Scholar]
- 3.Sørensen M, Munk OL, Mortensen FV, Olsen AK, Bender D, Bass L, et al. Hepatic uptake and metabolism of galactose can be quantified in vivo by 2-[18F]fluoro-2-deoxy-galactose positron emission tomography. Am J Physiol Gastrointest Liver Physiol. 2008;295:G27–G36. doi: 10.1152/ajpgi.00004.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Choi Y, Hawkins RA, Huang S-C, Brunken RC, Hoh CK, Messa C, et al. Evaluation of the effect of glucose ingestion and kinetic model configurations of FDG in the normal liver. J Nucl Med. 1994;35:818–823. [PubMed] [Google Scholar]
- 5.Keiding S, Hansen SB, Rasmussen HH, Gee A, Kruse A, Roelsgaard K, et al. Detection of cholangiocarcinoma in primary sclerosing cholangitis by positron emission tomography. Hepatology. 1998;28:700–706. doi: 10.1002/hep.510280316. [DOI] [PubMed] [Google Scholar]
- 6.Prytz H, Keiding S, Björnsson E, Broomé U, Almer S, Castedal M, et al. Dynamic FDG-PET is useful for detection of cholangiocarcinoma in patients with PSC listed for liver transplantation. Hepatology. 2006;44:1572–1580. doi: 10.1002/hep.21433. [DOI] [PubMed] [Google Scholar]
- 7.Slimani L, Kudomi N, Oikonen V, Jarvisalo M, Kiss J, Naum A, et al. Quantification of liver perfusion with [15O]H2O-PET and its relationship with glucose metabolism and substrate levels. J Hepatol. 2000;48:974–982. doi: 10.1016/j.jhep.2008.01.029. [DOI] [PubMed] [Google Scholar]
- 8.Brix G, Ziegler SI, Bellemann ME, Doll J, Schosser R, Lucht R, et al. Quantification of [18F]FDG uptake in the normal liver using dynamic PET: impact and modeling of the dual hepatic blood supply. J Nucl Med. 2001;42:1265–1273. [PubMed] [Google Scholar]
- 9.Chen S, Ho C, Feng D, Chi Z. Tracer Kinetic Modeling of 11C-acetate applied in the liver with positron emission tomography. IEEE Trans Med Imaging. 2004;23:426–432. doi: 10.1109/TMI.2004.824229. [DOI] [PubMed] [Google Scholar]
- 10.Cui Y, Bai J. Comparison of parameter estimations using dual-Input and arterial-input in liver kinetic studies of FDG metabolism. Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference Shanghai, China, 1–4 September 2005: pp. 2345–2348. [DOI] [PubMed]
- 11.Kudomi N, Jarvisalo MJ, Kiss J, Borra R, Viljanen A, Viljanen T, et al. Non-invasive estimation of hepatic glucose uptake from [18F]FDG PET images using tissue-derived input functions. Eur J Nucl Med Mol Imaging. 2009;36:2014–2024. doi: 10.1007/s00259-009-1140-y. [DOI] [PubMed] [Google Scholar]
- 12.Kudomi N, Slimani L, Jarvisalo MJ, Kiss J, Lautamäki R, Naum GA, et al. Non-invasive estimation of hepatic blood perfusion from H215O PET images using tissue-derived arterial and portal input functions. Eur J Nucl Med Mol Imaging. 2008;35:1899–1911. doi: 10.1007/s00259-008-0796-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Taniguchi H, Oguro A, Koyama H, Masuyama M, Takahashi T. Analysis of models for quantification of arterial and portal blood flow in the human liver using PET. J Comput Assist Tomogr. 1996;20:135–144. doi: 10.1097/00004728-199601000-00025. [DOI] [PubMed] [Google Scholar]
- 14.Munk OL, Keiding S, Bass L. Impulse-response function of splanchnic circulation with model-independent constraints: theory and experimental validation. Am J Physiol Gastrointest Liver Physiol. 2003;285:G671–G680. doi: 10.1152/ajpgi.00054.2003. [DOI] [PubMed] [Google Scholar]
- 15.Laustsen J, Pedersen EM, Terp K, Steinbrüchel D, Kure HH, Paulsen PK, et al. Validation of a new transit time ultrasound flowmeter in man. Eur J Vasc Endovasc Surg. 1996;12:91–96. doi: 10.1016/S1078-5884(96)80282-6. [DOI] [PubMed] [Google Scholar]
- 16.Mortensen FV, Rasmussen JS, Viborg O, Laurberg S, Pedersen EM. Validation of a new transit time ultrasound flowmeter for measuring blood flow in colonic mesenteric arteries. Eur J Surg. 1998;164:599–604. doi: 10.1080/110241598750005705. [DOI] [PubMed] [Google Scholar]
- 17.Munk OL, Keiding S, Bass L. A method to estimate dispersion in sampling catheters and to calculate dispersion-free blood time-activity curves. Med Phys. 2008;35:3471–3481. doi: 10.1118/1.2948391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Munk OL, Keiding S, Bass L. Capillaries within compartments: microvascular interpretation of dynamic positron emission tomography data. J Theor Biol. 2003;225:127–141. doi: 10.1016/S0022-5193(03)00227-3. [DOI] [PubMed] [Google Scholar]
- 19.Munk OL, Bass L, Feng H, Keiding S. Determination of regional flow using intravascular PET tracers: microvascular theory and experimental validation for pig livers. J Nucl Med. 2003;44:1862–1870. [PubMed] [Google Scholar]
- 20.Keiding S, Sørensen M, Bender D, Munk OL, Ott P, Vilstrup H. Brain metabolism of 13 N-ammonia during acute hepatic encephalopathy in cirrhosis measured by PET. Hepatology. 2006;43:42–50. doi: 10.1002/hep.21001. [DOI] [PubMed] [Google Scholar]
- 21.Doi R, Inoue K, Kogire M, Sumi S, Takaori K, Suzuki T, et al. Simultaneous measurements of hepatic arterial and portal venous flows by transit time ultrasound volume flowmetry. Surg Gynecol Obstet. 1988;167:65–69. [PubMed] [Google Scholar]
- 22.Fine DR, Glasser D, Hildebrandt D, Esser J, Lurie RE, Chetty N. An anatomic and physiological model of hepatic vascular system. J Appl Physiol. 1995;79:1008–1026. doi: 10.1152/jappl.1995.79.3.1008. [DOI] [PubMed] [Google Scholar]