Abstract
Missing covariate data present a challenge to tree-structured methodology due to the fact that a single tree model, as opposed to an estimated parameter value, may be desired for use in a clinical setting. To address this problem, we suggest a multiple imputation algorithm that adds draws of stochastic error to a tree-based single imputation method presented by Conversano and Siciliano (Technical Report, University of Naples, 2003). Unlike previously proposed techniques for accommodating missing covariate data in tree-structured analyses, our methodology allows the modeling of complex and nonlinear covariate structures while still resulting in a single tree model. We perform a simulation study to evaluate our stochastic multiple imputation algorithm when covariate data are missing at random and compare it to other currently used methods. Our algorithm is advantageous for identifying the true underlying covariate structure when complex data and larger percentages of missing covariate observations are present. It is competitive with other current methods with respect to prediction accuracy. To illustrate our algorithm, we create a tree-structured survival model for predicting time to treatment response in older, depressed adults.
Keywords: regression trees, classification trees, survival trees, survival analysis, missing data, imputation
1. Introduction
Binary tree-structured algorithms recursively divide a sample into disjoint subsets, two at a time, resulting in sets of empirically derived classification groups according to an outcome of interest. These tree models can be used to predict the outcomes of new cases based on their corresponding covariate observations and thus can be useful for investigators who are required to make qualitative decisions. In a clinical setting, tree-structured survival models are particularly advantageous because they can be used to predict risk for new patients so that specific treatment strategies can be employed on a case-to-case basis.
Although classification trees were introduced as early as 1963 [1], the first comprehensive algorithm for creating tree-structured models was developed by Breiman et al. [2]. Their algorithm, called ‘Classification and Regression Trees’ (CART), allows users to generate tree models with both continuous and categorical outcome variables. Gordon and Olshen [3], Davis and Anderson [4], Segal [5], and LeBlanc and Crowley [6, 7] extended the CART algorithm to generate trees with censored time-to-event outcomes.
As with all multivariate modeling techniques, missing covariate data present a challenge to tree-structured methodology. One particular challenge is that a single tree algorithm, as opposed to an estimated parameter value, may be desired for use in a clinical setting. To address this problem, Breiman et al. [2] and Therneau et al. [8, 9] use surrogate splitting in their tree-structured algorithms, CART and rpart, respectively. Although surrogate splitting is practical because it retains the output in the form of a tree-structured model, it only utilizes one surrogate covariate to classify the cases with missing observations. As a result, it does not allow the modeling of complex or nonlinear structures between covariates, which we view as a common occurrence in public health data due to the number of interconnected clinical and demographic factors.
As an alternative to surrogate splitting, single imputation procedures can be used to model more complex covariate structures, at which point standard complete data methodology can be utilized. However, it is well known that multiple imputation can more realistically represent missing observations because it allows for the incorporation of imputation uncertainty [10]. Therefore, we propose a multiple imputation method that accommodates a complex and nonlinear covariate structure yet still results in a single tree model. The methodology expands upon a tree-structured single imputation method previously proposed by Conversano and Siciliano [11] by adding stochastic error to create multiple imputations.
This paper is structured as follows. After summarizing basic binary tree methodology, we provide details on how our multiple imputation algorithm can be implemented in tree-structured analyses with missing covariate data. Due to the paucity of literature evaluating the abilities of the different methods for modeling missing covariate data in tree-structured analyses, we also present a simulation study designed to evaluate both the current and proposed methodologies in a variety of scenarios. Finally, we illustrate our methodology with data from a clinical trial for treating depression in the elderly.
2. Tree notation and methodology
Growing a binary tree, H, consists of recursively splitting the predictor space, , into disjoint binary subsets called nodes. At a node, h, there are many possible binary splits, sh, that could divide the predictor space, . The set of all possible splits at node h is denoted as Sh. A splitting statistic, G(sh), is used to quantify the predictive improvement resulting from each potential split, sh ∈ Sh, and subsequently to identify the one best split, , that will actually divide the node.
The selection of a splitting statistic depends largely on the nature of the outcome of interest. For continuous outcomes, Breiman et al. [2] developed binary regression trees by maximizing the reduction in squared deviance. LeBlanc and Crowley [6] extended the concept of a within-node splitting criterion to censored survival outcomes by selecting the split that maximizes the reduction in the full exponential likelihood deviance. Alternatively, Segal [5] and LeBlanc and Crowley [7] proposed maximizing a measure of between-node separation, as quantified by the absolute value of the test statistic of any two-sample rank test from the Harrington Fleming [12] family.
Regardless of the splitting statistic selected for use, the best split, , divides the node into disjoint left and right daughter nodes, each of which may subsequently go through the same splitting procedure. The splitting continues for each new node until the largest possible tree, HMAX, has been created. However, it is often the case that HMAX is too large to be clinically meaningful. In such cases, pruning algorithms may be used to select the best subtree. Further details on tree growing and pruning algorithms are given by Breiman et al. [2] and LeBlanc and Crowley [6] for within-node splitting statistics and LeBlanc and Crowley [7] for between-node splitting statistics.
After growing and pruning a tree, H, the nodes that are not split are called terminal nodes; the set of terminal nodes in a tree, H, is denoted as H̃.
3. Single and multiple imputation methodology for tree-structured analyses
One advantage of tree-structured methodology is that it allows one to classify outcomes with respect to covariates which themselves could have extreme outliers, multicollinearity, skewed distributions and/or nonlinear relationships with other covariates. Therefore, any imputation model selected to estimate missing observations in such covariates should also be able to accommodate these characteristics. One particularly advantageous model is the tree-structured single imputation method proposed by Conversano and Siciliano [11]. In this section, we first summarize the single imputation method and then propose our extension to create a tree-based multiple imputation algorithm.
3.1. Conversano and Siciliano's tree-structured single imputation method
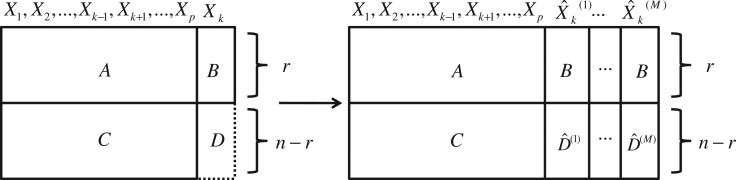
Consider a covariate matrix, Xn×p, containing r cases with completely observed covariates and n − r cases with a continuous covariate, Xk, unobserved. As shown in the left side of Figure 1, Xn×p can be separated into four submatrices, such that submatrices A and B contain data for the completely observed cases, submatrix C contains the observed data corresponding to the cases missing Xk and submatrix D represents the missing Xk data.
Figure 1.
Data structure for Xn×p, before and after multiple imputation.
Conversano and Siciliano [11] fit a regression tree model, Hk, using covariate data from A to model the corresponding observed Xk data in B. The observed mean for each terminal node, h ∈ H̃k, is denoted as X̄kh. Using observed data in C, each of the n−r cases with missing Xk data is classified into a terminal node, h ∈ H̃k. For a case, i, classified into a terminal node, h ∈ H̃k, the associated terminal node mean, X̄kh, is used to impute the missing xik value.
Conversano and Siciliano's methodology [11] can be extended to impute categorical covariates by fitting a classification tree, as detailed by Breiman et al. [2], to be used for the imputation model.
3.2. An extension to a multiple imputation algorithm
When imputing continuous covariates that will be used in a tree-structured analysis, it is important to represent the missing data as accurately as possible so that the true splitting value can be selected and the observations can be classified into the correct node. Conversano and Siciliano's method [11] can only impute as many unique values as there are terminal nodes in the tree-structured imputation model. Although this may be appropriate for covariates with a limited number of possible values (e.g. categorical covariates), we do not view this as an effective imputation strategy for covariates with a larger set of possible values (e.g. continuous covariates) because it is not likely to realistically represent the variability in the missing observations. Thus, we propose a new tree-based imputation strategy for continuous covariates, where draws of stochastic error are added to the predicted mean value from the terminal node to create multiple imputations.
3.2.1. Generating multiple imputation estimates
As in Conversano and Siciliano's method [11], we begin with an Xn×p data matrix with n−r cases missing covariate Xk divided into four submatrices, pictured in the left side of Figure 1. Using these data, we create an imputation tree, Hk, using A as the predictor space and B as the outcome. For each terminal node, h ∈ H̃k, we calculate a mean value,
| (1) |
and a set of residuals,
| (2) |
where is the set of rh individuals in terminal node h and .
Using the observed data in C, we classify each of the n−r cases with missing Xk data into a terminal node, h ∈ H̃k. For a case, i, classified into a terminal node, h ∈ H̃k, we create M imputation estimates,
| (3) |
where represents one draw of stochastic error.
We propose both an explicit (model-based) approach and an implicit (algorithm-based) approach as possible methods to draw values of the stochastic error. In the explicit approach, the errors are assumed to come from a normal distribution with a mean of zero and a variance equal to the variance of the observed residuals in terminal node h, i.e.,
The explicit approach is reasonable under the assumption of normality and homoscedasticity of the outcome variable, Xk, in each terminal node. For situations where this assumption is not met, we present an implicit approach where we randomly sample, with replacement, from the observed residuals of the terminal node, i.e., randomly assign each a value such that . In both the implicit and explicit approaches, we create M multiple imputation estimates for each of the missing observations in D. The data structure after multiple imputation is shown in the right side of Figure 1.
When multiple covariates have missing observations, the covariate with the fewest missing observations is imputed first. The covariate with the next fewest missing observations is imputed second, using methodology proposed in Section 3.2.2 to incorporate the M multiple imputation vectors into the imputation model. This process continues iteratively until each covariate with missing observations is represented by M multiple imputation vectors.
3.2.2. Incorporating multiple imputations into a single tree model
When detecting the best split at any node, h, we must consider possible splits on the non-imputed covariates as well as the multiply imputed covariate. We first identify the best split, , and associated splitting statistic, , based only on the non-imputed covariates, X j, j≠k. Next, we identify the best split, , and associated splitting statistic, , for each imputed vector, , m = 1, . . . , M. The median of the M splitting values, denoted by , represents the best split for covariate Xk. Similarly, the median of the M splitting statistics, denoted by , represents the splitting statistic associated with the best split on covariate Xk.
To select the overall best split, , we compare the median best splitting statistic from the M imputed vectors to the best splitting statistic from the non-imputed covariates, as follows:
| (4) |
When , the overall best split, , is randomly assigned to equal either or .
If the overall best split, , occurs on one of the non-imputed covariates, Xj, j≠k, the tree-growing process can proceed as usual and all observations are sent to either the left child node, hL, or right child node, hR, depending on whether their Xj value is less than or equal to or greater than , respectively. If the overall best split occurs on the imputed covariate, Xk, the r cases with observed Xk values can be assigned to a node as usual. However, for each case, i, with M imputed values representing their missing xik value, a node assignment, hi, is made as follows:
| (5) |
where
| (6) |
The criterion, M/2, corresponds to sending the case, i, to the left node when it is less than or equal to the splitting value, , for the majority of imputation vectors. If M is selected to be an even number and ai = M/2, the case, i, is sent to the child node with more observations; the case is randomly assigned to either hL or hR if the child nodes have equal numbers of observations. This algorithm continues iteratively at each node further down the tree.
The algorithm can be extended to accommodate the situation where two or more covariates are represented by multiple imputation vectors. For each of the covariates with missing data, we identify the best splitting statistic and associated splitting value for each of the M multiply imputed vectors. Then, separately for each multiply imputed covariate, we calculate the median of the M splitting values as well as the median of the M splitting statistics. Each of the median statistics from the imputed covariates is then compared to the best splitting statistic from the non-imputed covariates. The split associated with the largest splitting statistic is selected to divide the node. If this split is on one of the multiply imputed covariates, equations (5) and (6) are used to assign nodes to cases with multiply imputed values.
As discussed previously, the largest tree possible, HMAX, often needs to be pruned to create a more parsimonious model. It is straightforward to extend the proposed multiple imputation algorithm to accommodate the various pruning algorithms. If a split occurs on a multiply imputed covariate, the median splitting statistic is used to calculate pruning statistics. Equations (5) and (6) can be used to classify multiply imputed observations from a cross-validation, bootstrap, or independent test sample.
4. Simulation study
Simulation study objectives were (i) to evaluate the accuracy of our multiple imputation algorithm in comparison to other currently used methods for accommodating missing covariate data in tree models and (ii) to develop a better understanding of the abilities of current methods for handling missing covariate data under a variety of data scenarios. To accomplish these objectives, we assessed our proposed methodology, as well as currently used methodology, with three percentages of missing at random (MAR) covariate data, (10, 25, and 40 per cent), two splitting statistics (reduction in full exponential likelihood deviance (FLD) [6] and two-sample log rank (LR) [5, 7]) and two types of covariate relationships (simple and complex).
Our strategy was to first generate a ‘complete’ dataset and then remove a proportion of the observations in one covariate. We refer to the data not removed as the ‘observed’ dataset, and to the subset of the observed dataset that contains only the cases with completely observed data as the ‘completely observed’ dataset. Based on these datasets, we compared five different methods for accommodating missing covariate values:
Using the completely observed dataset to grow trees (COBS).
Using surrogate splits to grow trees with the observed dataset (SS).
Imputing the observed dataset with Conversano and Siciliano's single imputation method and using the resulting dataset to grow trees (CS).
Imputing the observed dataset using our multiple imputation method with M = 1 draw of normally distributed error and using the resulting dataset to grow trees (MI-1).
Using our multiple imputation algorithm with M = 10 draws of normally distributed error to grow trees based on the observed dataset (MI-10).
For standard multiple imputation procedures, Rubin [13] notes that as few as five, and sometimes only three, multiple imputation estimates may be sufficient, with no clear advantage shown for more than 10 multiple imputation estimates. Thus, we used a value of M = 10 multiple imputation estimates for our simulation study. For comparison purposes, we also grew trees using the complete dataset before removing a proportion of the data to create missing observations (COMP).
4.1. Data generation
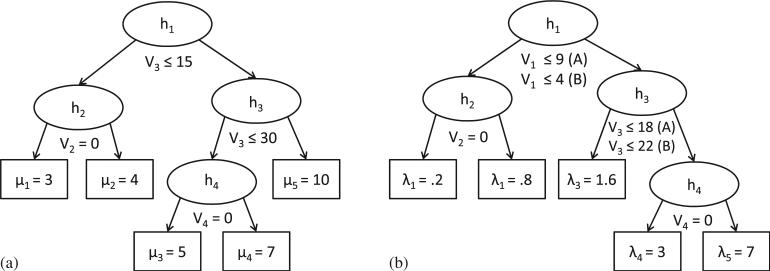
We generated continuous and binary covariates to be used in the true survival tree models, as well as extraneous continuous and binary covariates to be used as noise (Table I). Model A had a simple, linear structure between covariates V1 and V3. Model B had a more complex, nonlinear structure between covariates such that the mean value of covariate V1 for each observation was determined by the algorithm given by tree (a) in Figure 2. For models A and B, we generated three missing data indicators to create datasets that contained approximately 10, 25, and 40 per cent MAR observations in covariate V1.
Table I.
Simulated data structure for models A and B.
| Model A | Model B | |
|---|---|---|
| Model covariates | V1~N(10, 2) | V1~N(μh, 3)* |
| V2~Bin(0.6) | V2~Bin(0.6) | |
| V3~N(13 + 0.5V1, 4) | V3~N(25, 6) | |
| V4~Bin(0.5) | V4~Bin(0.5) | |
| Extraneous covariates | V5~N(20, 5) | V5~N(20, 5) |
| V6~Bin(0.7) | V6~Bin(0.7) | |
| V7~Bin(0.5) | V7~Bin(0.5) | |
| V8~Bin(0.4) | V8~Bin(0.4) | |
| Missingness indicators for covariate V1 | M1~Bin(0.2I(V3<18)) | M1~Bin(0.2I(V3<25)) |
| M2~Bin(0.5I(V3<18)) | M2~Bin(0.5I(V3<25)) | |
| M3~Bin(0.8I(V3<18)) | M3~Bin(0.8I(V3<25)) | |
| Event time p.d.f. | Exp(λh)† | Exp(λh)† |
| Censoring time p.d.f. | f(c)=0.1, if c=1/4, 1/2, 1, 2; =0.2, if c=4, 8, 16 | f(c)=0.1, if c=1/4, 1/2, 1, 2; =0.2, if c=4, 8, 16 |
Figure 2.
(a) Algorithm to determine the mean of covariate V1 in model B. (b) Algorithm to determine the parameter value for the true event times in models A and B. Cases answering ‘yes’ to each split are sent to the left child node.
The distributions of the true event times, T, were exponential with the differing parameters determined by tree (b) in Figure 2. We arranged this tree model so that the covariate with missing data (V1) split node h1 and the covariate associated with the missingness (V3) split below it at node h3. To reflect a practical application, we generated discrete censoring times with a lower probability at earlier time points (Pr(C=c)=.1 for times c=0.25, 0.5, 1, 2) and a higher probability at later time points (Pr(C=c)=0.2 for times c=4, 8, 16). The observed outcome time was calculated as the minimum of the event and censoring times.
Altogether, we simulated 1000 datasets of N =300 observations for models A and B. The 1000 datasets created for model A had, on average, 16.15 per cent censored observations and missingness indicators to create datasets with 9.95, 24.93, and 40.07 per cent missing observations in covariate V1. The 1000 datasets created for model B had, on average, 17.82 per cent censored observations and missingness indicators to create 10.05, 24.94, and 40.08 per cent missing observations in covariate V1. The statistical package, R [14], was used for all data generation.
4.2. Computing methods
We used the ‘rpart()’ function with the ‘method=anova’ option in R to create the single and multiple tree-structured imputation models for the CS, MI-1, and MI-10 methods [8, 9]. In these imputation models, the observed values in covariate V1 were used as the outcome and all other covariates (V2−V8) were used as predictors. We required at least 10 observations in each terminal node; other than this specification the trees were grown and pruned using the standard parameters in the ‘rpart()’ function.
We wrote functions in R to create the survival trees for all methods [14]. For the trees grown with the FLD splitting statistic, we used the function ‘rpart()’ specifying the option ‘class=exp’ to determine the best split at each node [8, 9]. We wrote our own function in R to create survival trees based on the LR statistic due to the fact that rpart does not incorporate this statistic. The surrogate splitting algorithms for both splitting statistics were based on the work by Therneau et al. [8, 9] and Breiman et al. [2]. For all survival models, a split was only considered if it would result in at least 10 observations per child node. This resulted in some lower nodes not being able to split due to not enough observations being sent down the tree. To focus on the abilities of each imputation method to detect the correct splits at nodes h1−h4, we did not prune the trees.
4.3. Assessment measures
All methods were assessed using criteria based on both structural and predictive accuracies. We selected structural accuracy as a criterion because a tree-structured model that displays the true covariate hierarchy will identify meaningful and stable prognostic groups that can be used to inform clinical management. We selected predictive accuracy as a criterion because a tree may still result in a relatively accurate survival prediction even if its structure is not exactly correct.
Structural accuracy was measured by the proportion of models that identified the correct covariate at each of nodes h1, h2, h3, and h4. For nodes h2−h4, this proportion was conditional on the model reaching the designated node of interest through the correct covariates; denominator values were adjusted accordingly. Therefore, a descendant node could only be identified as splitting on the correct covariate if all its ancestor nodes also split on the correct covariates. The specific value of the covariate split did not affect its identification as being correct. We also calculated the total proportion of models that split on all four correct covariates and the associated 95 per cent confidence interval.
Predictive accuracy of the tree models was measured by the mean integrated squared error (MIE). We classified each new observation in a test sample of N =200 into one of the terminal nodes of a survival tree created with a learning sample of N =300. The estimated survival function at each of the five terminal nodes identified by tree (b) in Figure 2 was calculated based on the observations in the test sample that were classified into that node. We then calculated the MIE by integrating the squared difference between the true and estimated survival distributions with respect to time and averaging over all 200 observations in the test sample [15]. Due to computational constraints, we used 250 pairs of test and learning samples to assess each scenario. The median and interquartile range of the MIE from these 250 pairs of samples are reported.
4.4. Results
4.4.1. Selection of the correct covariate at each node
Simulation results regarding the correct covariate selection at each node are displayed in Table II. Recall that in the true survival tree structure (tree (b) in Figure 2) node h1 split on the covariate with missing data and node h3 split on the covariate associated with the missingness.
Table II.
Percentage of tree models that identified the correct splitting covariate: assessed separately at each node and also for all four possible splits combined. Simulation results from models A and B, based on 1000 datasets of N = 300 observations each.
| Statistic* (per cent Missing) | Model A |
Model B |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method† | h1 | h2‡ | h3‡ | h4§ | Total (95 per cent CI) | h1 | h2‡ | h3‡ | h4§ | Total (95 per cent CI) | |
| FLD (0 per cent) | COMP | 100 | 97.60 | 99.90 | 91.69 | 89.3 (85.80, 92.80) | 100 | 83.80 | 97.60 | 98.16 | 80.3 (75.80, 84.80) |
| FLD (10 per cent) | COBS | 100 | 95.40 | 99.30 | 91.64 | 86.5 (82.42, 90.58) | 100 | 79.10 | 93.70 | 97.44 | 72.1 (66.75, 77.45) |
| SS | 100 | 94.90 | 99.70 | 92.08 | 87.1 (83.31, 90.89) | 100 | 57.00 | 93.90 | 97.44 | 51.5 (45.84, 57.16) | |
| CS | 99.80 | 94.29 | 99.80 | 92.07 | 86.5 (82.63, 90.37) | 100 | 74.80 | 98.00 | 97.35 | 71.3 (66.18, 76.42) | |
| MI-1 | 99.70 | 95.89 | 100 | 92.08 | 87.9 (84.21, 91.59) | 99.90 | 73.37 | 97.60 | 97.74 | 69.6 (64.39, 74.81) | |
| MI-10 | 99.90 | 95.90 | 99.90 | 92.18 | 87.9 (84.21, 91.59) | 100 | 76.20 | 97.80 | 97.96 | 72.7 (67.66, 77.74) | |
| FLD (25 per cent) | COBS | 100 | 90.70 | 93.70 | 90.72 | 77.4 (71.94, 82.86) | 100 | 66.70 | 80.10 | 96.63 | 51.7 (44.97, 58.03) |
| SS | 99.80 | 84.57 | 97.29 | 91.56 | 74.8 (69.89, 79.71) | 99.70 | 27.88 | 82.65 | 96.84 | 22.1 (17.40, 26.80) | |
| CS | 97.30 | 79.96 | 99.08 | 89.42 | 69.9 (64.71, 75.09) | 98.10 | 50.25 | 96.63 | 94.20 | 45.8 (40.16, 51.43) | |
| MI-1 | 95.70 | 86.65 | 99.90 | 91.54 | 75.6 (70.73, 80.46) | 97.60 | 55.33 | 98.67 | 96.16 | 51.6 (45.94, 57.26) | |
| MI-10 | 97.30 | 85.30 | 99.90 | 92.29 | 76.2 (71.38, 81.02) | 98.70 | 56.74 | 98.28 | 96.62 | 53.9 (48.26, 59.54) | |
| FLD (40 per cent) | COBS | 100 | 79.50 | 60.40 | 88.08 | 41.7 (34.50, 48.90) | 100 | 51.40 | 37.30 | 91.15 | 17.7 (12.12, 23.28) |
| SS | 99.00 | 69.90 | 72.83 | 89.04 | 43.9 (38.28, 49.52) | 97.80 | 11.96 | 39.47 | 91.71 | 5.1 (2.61, 7.59) | |
| CS | 90.90 | 53.14 | 82.51 | 84.53 | 38.3 (32.80, 43.80) | 92.50 | 26.92 | 88.54 | 90.96 | 22.5 (17.7, 27.23) | |
| MI-1 | 82.30 | 73.03 | 99.88 | 90.88 | 54.6 (48.97, 60.23) | 83.30 | 29.65 | 99.28 | 95.16 | 23.7 (18.89, 28.51) | |
| MI-10 | 87.10 | 67.16 | 99.77 | 92.06 | 53.7 (48.06, 59.34) | 87.60 | 29.79 | 98.63 | 95.14 | 24.9 (20.00, 29.79) | |
| LR (0 per cent) | COMP | 99.90 | 95.70 | 99.90 | 90.68 | 86.4 (81.40, 89.40) | 100 | 86.40 | 96.80 | 97.31 | 81.5 (77.11, 85.89) |
| LR (10 per cent) | COBS | 99.90 | 93.29 | 99.00 | 90.39 | 83.3 (78.85, 87.75) | 100 | 82.60 | 91.80 | 96.41 | 73 (67.70, 78.30) |
| SS | 99.80 | 93.89 | 99.40 | 90.73 | 84.7 (80.63, 88.77) | 100 | 64.90 | 92.00 | 96.85 | 57.8 (52.21, 63.39) | |
| CS | 99.20 | 88.41 | 99.40 | 89.45 | 79.4 (74.82, 83.98) | 100 | 71.60 | 97.10 | 95.57 | 66.4 (61.05, 71.75) | |
| MI-1 | 99.50 | 93.27 | 99.80 | 90.94 | 84.1 (79.96, 88.24) | 99.90 | 78.18 | 96.80 | 97.00 | 72.7 (67.34, 77.46) | |
| MI-10 | 99.50 | 94.17 | 99.90 | 90.74 | 84.9 (80.85, 88.95) | 100 | 78.40 | 97.50 | 96.62 | 73.6 (68.61, 78.59) | |
| LR (25 per cent) | COBS | 100 | 90.00 | 92.80 | 89.22 | 74.6 (68.91, 80.29) | 100 | 68.9 | 76.20 | 95.80 | 50.5 (43.97, 57.03) |
| SS | 99.60 | 84.94 | 96.69 | 90.34 | 73.7 (68.72, 78.68) | 99.30 | 35.55 | 78.55 | 95.51 | 25.8 (20.85, 30.75) | |
| CS | 94.80 | 68.57 | 96.20 | 87.17 | 58.2 (52.62, 63.78) | 96.40 | 41.49 | 93.88 | 93.48 | 38.3 (32.80, 43.80) | |
| MI-1 | 93.80 | 85.29 | 99.89 | 90.18 | 72.3 (67.24, 77.36) | 94.20 | 57.64 | 97.66 | 95.43 | 51.6 (45.94, 58.55) | |
| MI-10 | 94.80 | 82.17 | 99.89 | 91.13 | 70.6 (65.49, 75.76) | 96.00 | 58.75 | 98.02 | 95.54 | 52.9 (47.25, 58.55) | |
| LR (40 per cent) | COBS | 99.90 | 79.38 | 53.45 | 83.15 | 35.0 (28.03, 41.97) | 100 | 38.0 | 28.60 | 83.92 | 8.7 (4.58, 12.82) |
| SS | 97.70 | 72.26 | 67.35 | 86.62 | 41.4 (35.83, 46.97) | 96.00 | 19.90 | 31.25 | 86.33 | 5.8 (3.16, 8.45) | |
| CS | 90.70 | 43.66 | 68.47 | 81.00 | 28.3 (23.20. 33.40) | 89.30 | 18.14 | 72.79 | 87.23 | 13.3 (9.46, 17.14) | |
| MI-1 | 75.10 | 66.31 | 98.27 | 88.89 | 44.7 (39.07, 50.33) | 74.20 | 34.50 | 91.71 | 94.16 | 23.8 (18.98, 28.62) | |
| MI-10 | 80.00 | 62.63 | 97.75 | 91.56 | 45.4 (39.77, 51.03) | 78.60 | 34.35 | 96.69 | 93.55 | 24.8 (19.91, 29.69) | |
FLD, reduction in full exponential likelihood deviance; LR, two-sample log rank.
COMP, full simulated data; COBS, completely observed cases only; SS, surrogate splitting; CS, Conversano and Siciliano's single imputation; MI-1, multiple imputation with one draw of normal error; and MI-10, multiple imputation with 10 draws of normal error.
Correct variable selection at nodes h2 and h3 is conditional on correct variable selection at node h1.
Correct variable selection at node h4 is conditional on correct variable selection at both nodes h1 and h3.
At node h1, the non-imputation methods (COBS, SS) tended to be more accurate than the imputation methods (CS, MI-1, MI-10). However, at node h3, the imputation methods tended to be more accurate than the non-imputation methods. These trends were most pronounced with larger percentages of missing data and the more complex data structure (Model B).
4.4.2. Selection of all four correct covariates
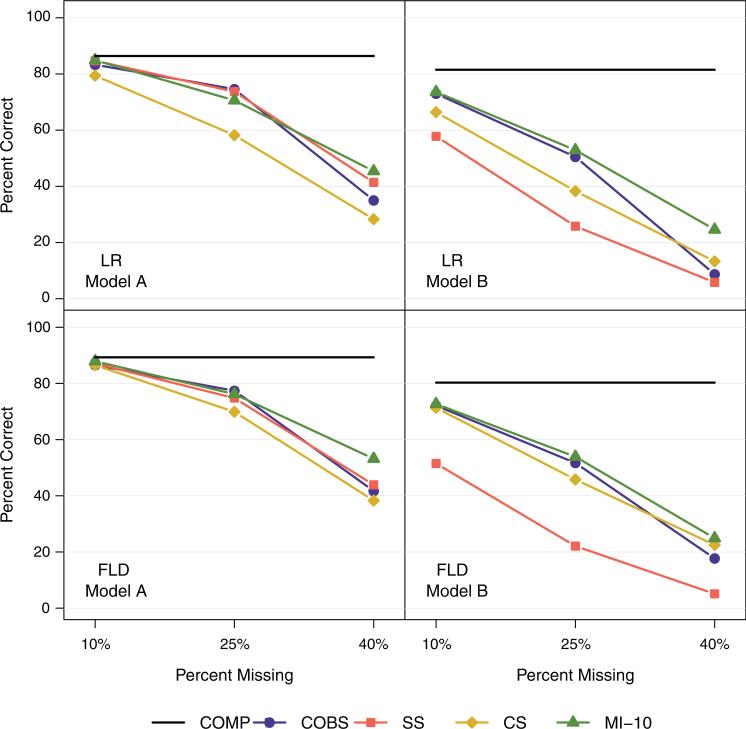
Results for Models A (simple covariate structure) and B (complex covariate structure) are displayed in Figure 3 and Table II. Overall, the FLD statistic tended to be more accurate than the LR statistic and Model A tended to be more accurate than Model B. The tree models based on complete data (COMP) were similar in accuracy to the tree models based on datasets with 10 per cent missing data, and were significantly more accurate than the tree models based on datasets with 25 or 40 per cent missing data. Our multiple imputation method tended to be most advantageous with a more complex data structure and larger percentages of missing data.
Figure 3.
Percentage of models that identified the correct splitting covariate at all four nodes. FLD, reduction in full exponential likelihood deviance statistic; LR, two-sample log rank statistic; COMP, full simulated data; COBS, completely observed cases only; SS, surrogate splitting; CS, Conversano and Siciliano's single imputation; MI-1, multiple imputation with one draw of normal error; MI-10, multiple imputation with 10 draws of normal error.
Model A: With 10 per cent missing, all methods were similar when using both the FLD and LR statistics. With 25 per cent missing, all methods were more accurate than the CS method when using the LR statistic; there were no significant differences among the five methods with 25 per cent missing when using the FLD statistic. With 40 per cent missing, the multiple imputation (MI-1, MI-10) methods were more accurate than the CS method when using both splitting statistics; the SS method was also more accurate than the CS method when using the LR statistic with 40 per cent missing.
Model B: When using the FLD statistic, all methods were more accurate than the SS method, regardless of the percentage of missingess. None of the four other missing data methods (COBS, CS, MI-1, MI-10) were significantly different from one another when using the FLD statistic. When using the LR statistic with 10 per cent missing, the COBS and multiple imputation (MI-1, MI-10) methods were more accurate than the SS method. When using the LR statistic with 25 per cent missing, the COBS and multiple imputation methods were more accurate than both the SS and CS methods; the CS method was also more accurate than the SS method. When using the LR statistic with 40 per cent missing, the multiple imputation methods were more accurate than all other methods; the CS method was also more accurate than the SS method. The overall inaccuracy of the SS method may be due to the nonlinear relationship between V1 and V3, as shown in tree (a) of Figure 2. This relationship was not detected using the SS method because only one surrogate covariate could be used to identify which observations should be sent to the left and right nodes.
4.4.3. Prediction accuracy
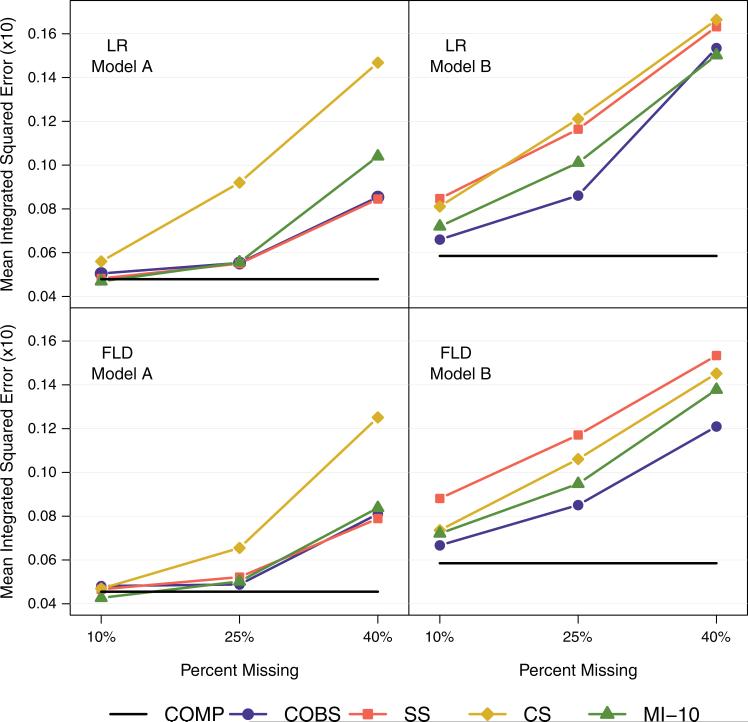
The median and interquartile range of the MIE from both Model A (simple covariate structure) and Model B (complex covariate structure) are displayed in Table III and Figure 4. Overall, Model A tended to result in better predictive accuracy (lower MIE) than Model B, and the FLD statistic tended to result in better predictive accuracy than the LR statistic.
Table III.
Median (IQR)× 10 of the mean integrated squared error for 250 pairs of learning and test samples of size 300 and 200, respectively.
| Model A |
Model B |
||||
|---|---|---|---|---|---|
| Per cent missing | Method† | FLD* | LR | FLD | LR |
| 0 | COMP | 0.0455 (0.0315) | 0.0479 (0.0343) | 0.0585 (0.0499) | 0.0585 (0.0496) |
| 10 | COBS | 0.0481 (0.0367) | 0.0505 (0.0608) | 0.0667 (0.0616) | 0.0660 (0.0549) |
| SS | 0.0466 (0.0385) | 0.0482 (0.0378) | 0.0881 (0.0745) | 0.0847 (0.0709) | |
| CS | 0.0469 (0.0457) | 0.0560 (0.0584) | 0.0736 (0.0658) | 0.0811 (0.0722) | |
| MI-1 | 0.0461 (0.0371) | 0.0502 (0.0397) | 0.0735 (0.0694) | 0.0711 (0.0622) | |
| MI-10 | 0.0427 (0.0337) | 0.0469 (0.0370) | 0.0721 (0.0625) | 0.0720 (0.0613) | |
| 25 | COBS | 0.0488 (0.0462) | 0.0553 (0.0473) | 0.0851 (0.0663) | 0.0861 (0.0636) |
| SS | 0.0522 (0.0501) | 0.0550 (0.0529) | 0.1171 (0.0567) | 0.1164 (0.0636) | |
| CS | 0.0655 (0.0732) | 0.0920 (0.0809) | 0.1061 (0.0815) | 0.1211 (0.0850) | |
| MI-1 | 0.0569 (0.0562) | 0.0599 (0.0668) | 0.1094 (0.0830) | 0.1139 (0.0833) | |
| MI-10 | 0.0502 (0.0480) | 0.0556 (0.0522) | 0.0948 (0.0652) | 0.1011 (0.0747) | |
| 40 | COBS | 0.0810 (0.0618) | 0.0854 (0.0713) | 0.1210 (0.0852) | 0.1535 (0.0691) |
| SS | 0.0789 (0.0697) | 0.0845 (0.0736) | 0.1534 (0.0621) | 0.1632 (0.0767) | |
| CS | 0.1251 (0.1005) | 0.1468 (0.0807) | 0.1452 (0.0901) | 0.1664 (0.0854) | |
| MI-1 | 0.9470 (0.0807) | 0.1053 (0.0962) | 0.1612 (0.0982) | 0.1701 (0.1078) | |
| MI-10 | 0.0838 (0.0813) | 0.1040 (0.0915) | 0.1378 (0.0766) | 0.1502 (0.0924) | |
FLD, reduction in full exponential likelihood deviance statistic; LR, two-sample log rank statistic.
COMP, full simulated data; COBS, completely observed cases only; SS, surrogate splitting; CS, Conversano and Siciliano's single imputation; MI-1, multiple imputation with one draw of normal error; and MI-10, multiple imputation with 10 draws of normal error.
Figure 4.
Mean integrated squared error (×10). FLD, reduction in full exponential likelihood deviance statistic; LR, two-sample log rank statistic; COMP, full simulated data; COBS, completely observed cases only; SS, surrogate splitting; CS, Conversano and Siciliano's single imputation; MI-1, multiple imputation with one draw of normal error; MI-10, multiple imputation with 10 draws of normal error.
Model A: All the methods had better predictive accuracy than the CS method, regardless of the splitting statistic used or the level of missingness. Other methods had relatively similar predictive accuracy, with the exception of a worsening in accuracy of the multiple imputation methods with 40 per cent missing, particularly when using the LR statistic. The MI-10 method consistently had better predictive accuracy than the MI-1 method.
Model B: The COBS method tended to have the best predictive accuracy across each level of missing data and both splitting statistics, followed by one or both of the multiple imputation methods (MI-10, MI-1). The only exception was with 40 per cent missing using the LR statistic, where the MI-10 method had slightly better predictive accuracy than the COBS method. The MI-10 method consistently had better predictive accuracy than the MI-1 method with the exception of using the LR statistic with 10 per cent missing.
5. Application to late-life depression
Missing data are common in psychiatric research due to the patient burden required for many studies. To illustrate the utility of our proposed method in this context we use data from a two-year randomized clinical trial for treating depression in the elderly (PROSPECT—Prevention of Suicide in Primary Care Elderly: Collaborative Trial [16]). The cohort included depressed older adults with either major or minor depression, as defined by the DSM-IV modified by requiring four depressive symptoms, a 24-item Hamilton Rating Scale for Depression score of 10 or higher and duration of at least 4 weeks. These individuals were randomized to either a depression care manager intervention or usual care and were observed at baseline, 4, 8, 12, 16, and 24 months. Further details regarding the two treatment arms and study design are given by Bruce et al. [16].
Our aim was to create a tree-structured survival model for time to depression remission using baseline covariates shown in Table IV. The PROSPECT sample used in the main results paper [16] contained 599 individuals. However, for purposes of illustrating our methodology, we included only those participants with complete data for all characteristics in Table IV, except for in the health-related coping strategies scale [17]. As a result, our sample included 422 individuals, with 37.68 per cent (n =159) missing health-related coping strategies data.
Table IV.
Baseline characteristics.
| Characteristic (Scale)* | Median (IQR) | Characteristic | Per cent endorsed (n) |
|---|---|---|---|
| Use of health-related coping strategies (OPSC) | 31 (28–35) | Assigned intervention | 51.18 (216) |
| Depression (HRSD) | 17 (13–22) | Living with someone | 59.0 (249) |
| Anxiety (CAS) | 3 (1–7) | Female | 71.09 (300) |
| Physical comorbidity (CCI) | 2 (1–4) | White | 70.14 (296) |
| Hopelessness (BHS) | 7 (4–11) | ||
| Cognitive impairment (MMSE) | 28 (26–29) | ||
| Age | 70.02 (64.51–76.35) |
OPSC, Optimization in Primary and Secondary Control Survey; HRSD, Hamilton 24-Item Rating Scale for Depression; CAS, Clinical Anxiety Scale; CCI, Charlson Comorbidity Index; BHS, Beck Hopelessness Scale; and MMSE, Mini Mental State Exam.
The health-related coping strategies scale includes eight questions on a 5-point likert scale, with possible scores ranging from 8 to 40. Higher values of the scale indicate greater use of positive health coping strategies, such as putting in effort to get better, asking others for advice, and not blaming oneself for health problems [17].
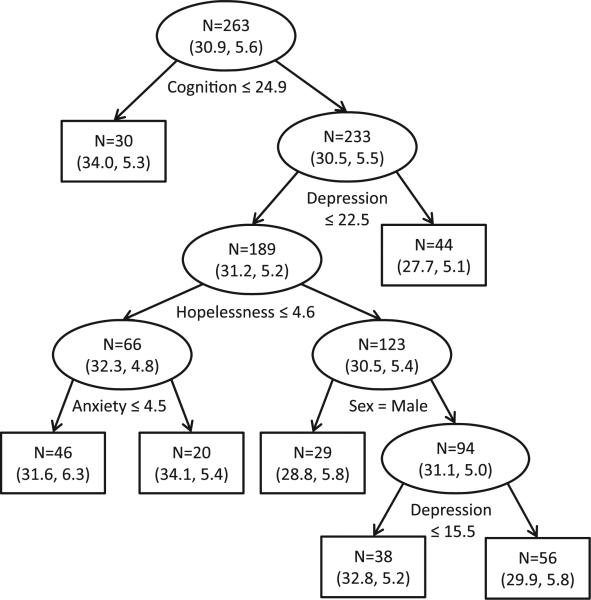
We first created an imputation model using only the 263 observations with no missing data (see Figure 5). Depression severity was selected to split multiple nodes on the imputation tree, suggesting a possible nonlinear relationship with health-related coping strategies. Observed health-related coping strategy scores were approximately normally distributed at each terminal node.
Figure 5.
Regression tree used for imputation of missing health-related coping strategies data. Nodes display sample size (N) as well as the estimated mean and standard deviation (). Cases answering ‘yes’ to each split are sent to the left child node.
The imputation tree was used to classify the 159 individuals with missing health-related coping strategies data into terminal nodes. We drew 10 normally distributed realizations of stochastic error for each individual with missing data based on the terminal-node-specific means and standard deviations indicated in Figure 5. The result was M = 10 multiple imputation estimates for each individual with missing health-related coping strategies information.
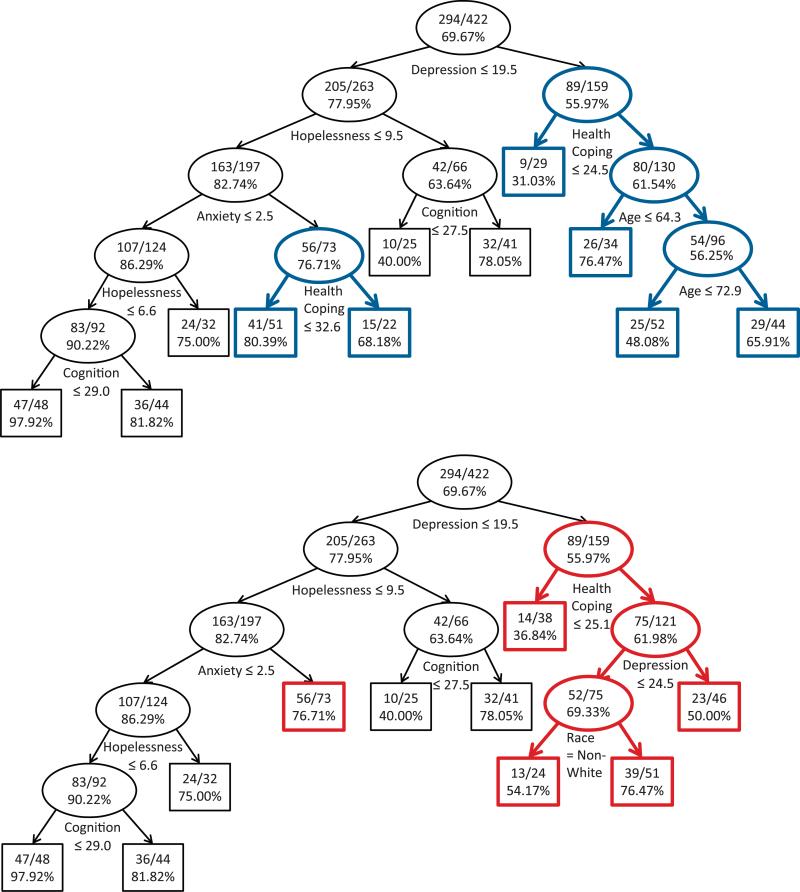
After multiple imputation, we used our proposed methodology to model time to remission with covariates from Table IV. The resulting model is shown in the top of Figure 6. We repeated a similar analysis using SS methodology, with results shown in the bottom of Figure 6. For both tree models, we used the FLD splitting statistic [5, 7], required at least 60 observations to split a node and at least 20 observations in each terminal node, and only allowed a split to occur if it would result in a reduction in full exponential likelihood deviance of at least 3 per cent.
Figure 6.
Survival tree created using multiple imputation (top panel) or surrogate split (bottom panel) methodology. Each node displays [number remitted in node]/[sample size in node] and per cent remission. Cases answering ‘yes’ to each split are sent to the left child node.
The two resulting models are similar for individuals with lower baseline depression, with the only difference being an additional split on health-related coping strategies in the tree created using multiple imputation. However, the tree models are very different for individuals with higher baseline depression because of the subsequent split on the health-related coping strategies covariate. Specifically, the tree created using surrogate splitting divides further on depression and race, whereas the tree created with multiple imputation splits on age. These differences in the two tree models highlight the cascading effect that missing data can have on the structure of a tree model when the covariate with missing data is a strong predictor of the outcome relative to other covariates in the model.
6. Conclusions
In this manuscript, we proposed a multiple imputation algorithm to accommodate missing covariate data in tree-structured methodology. Unlike previously proposed methods, this algorithm allows for the modeling of complex and nonlinear covariate relationships while still resulting in a single tree-structured model. Our methodology was shown to be most advantageous for identifying the correct covariate structure of a survival model with more complex data structures and higher percentages of missing data. Our methodology was competitive with other currently used methods with respect to prediction accuracy.
Although results from our simulation study are promising with respect to the abilities of our proposed multiple imputation algorithm, there are many different data structures that could alter the accuracy of the methods, and they should be more closely examined before further conclusions are made regarding a preferred method. Specifically, we believe that the accuracy of any method for managing missing covariate data in tree-structured analyses hinges upon the strength of the relationship between the covariate with missing data and the outcome, as indicated by its position in the tree. When a covariate with missing data has a relatively strong relationship with the outcome it may split near the top of the tree. Any cases that are incorrectly classified at this node could cause a cascading effect of inaccuracy further down the tree. Alternatively, if the covariate with missing data has a relatively weak relationship with the outcome it may split near the bottom of the tree. As a result, there are fewer nodes below it that could be negatively affected by misclassified cases. Our application provided an example of the former situation. The variable with missing data (a health coping strategies scale) was a strong predictor of time to remission. Thus, the two methods for handling missing covariate data resulted in different covariate splits on the nodes further down the tree.
The accuracy of our method and other competing methods may also depend on the number of covariates with missing observations and to how many other covariates their missingness mechanisms are related. Simulation results showed that our proposed multiple imputation method was less accurate than other methods when selecting the correct covariate at nodes that split on the imputed covariate, but more accurate than other methods when selecting the splits at descendant nodes. Thus, the overall accuracy of our method could change depending on which covariates split the nodes in the tree, and may be further compounded by the positioning of these covariates within the tree, as discussed above.
The fact that our methodology was weak in its ability to identify a split on the imputed covariate should be investigated further. Although worse overall, the CS method was more accurate than our proposed method when splitting on the imputed covariate. This finding suggests that the inaccuracy of our proposed multiple imputation method was not due to the tree-structured nature of the imputation model, but rather the addition of stochastic error. However, we did see an improvement when the number of draws of error was increased from 1 to 10, leading us to believe that if we used an even larger number of draws of stochastic error our method would further improve. Of course, tree-structured analysis is already computationally intensive, so it is important to determine the minimum number of multiple imputations that would be needed to create accurate models.
The abilities of the missing data methods need to be evaluated when model assumptions are violated. Both the FLD statistic and the LR statistic require assumptions of proportional hazards and random censoring. Because these assumptions are often violated in practice, future work should assess the robustness of our proposed method and also other competing methods in the face of model misspecification.
Acknowledgements
The authors thank the anonymous referees, whose comments helped to improve the reporting of the methodology and results, as well as the design of the simulation experiments. The authors also thank the PROSPECT team for the use of their data. PROSPECT is a collaborative research study funded by the National Institute of Mental Health. The three collaborative groups include the Advanced Centers for Intervention and Services Research of the following: Cornell University (PI: George S. Alexopoulos, M.D. and CO-PIs: Martha L. Bruce, Ph.D., M.P.H. and Herbert C. Schulberg, Ph.D.; R01 MH59366, P30 MH68638), University of Pennsylvania (PI: Ira Katz, M.D., Ph.D. and Co-PIs: Thomas Ten Have, Ph.D. and Gregory K. Brown, Ph.D.; R01 MH59380, P30 MH52129) and University of Pittsburgh (PI: Charles F. Reynolds III, M.D. and CO-PI: Benoit H. Mulsant, M.D.; R01 MH59381, P30 MH52247). Additional grants for PROSPECT came from Forest Pharmaceuticals and the Hartford Foundation.
The authors were supported by the following contract/grant sponsors and contract/grant numbers: NIMH: 5-T32-MH073451, NIMH: 5-T32-MH16804, NIH: 5-U10-CA69974, NIH: 5-U10-CA69651.
References
- 1.Morgan J, Sonquist J. Problems in the analysis of survey data, and a proposal. Journal of the American Statistical Association. 1963;58(304):415–434. [Google Scholar]
- 2.Breiman L, Friedman J, Olshen R, Stone C. Classification and Regression Trees. Wadsworth; California: 1984. [Google Scholar]
- 3.Gordon L, Olshen R. Tree-structured survival analysis. Cancer Treatment Reports. 1985;69:1065–1069. [PubMed] [Google Scholar]
- 4.Davis R, Andersen J. Exponential survival trees. Statistics in Medicine. 1989;8:947–961. doi: 10.1002/sim.4780080806. [DOI] [PubMed] [Google Scholar]
- 5.Segal M. Regression trees for censored data. Biometrics. 1988;44:35–47. [Google Scholar]
- 6.LeBlanc M, Crowley J. Relative risk trees for censored survival data. Biometrics. 1992;48:411–425. [PubMed] [Google Scholar]
- 7.LeBlanc M, Crowley J. Survival trees by goodness of split. Journal of the American Statistical Association. 1993;88(422):457–467. [Google Scholar]
- 8.Therneau T, Atkinson E. Technical Report 61. Section of Biostatistics, Mayo Foundation; Rochester, MN: 1997. An introduction to recursive partitioning using the rpart routine. [Google Scholar]
- 9.Therneau TM, Atkinson B, Ripley B. rpart: Recursive Partitioning. 2008 r package version 3.1-41. Available from: http://mayoresearch.mayo.edu/mayo/research/biostat/splusfunctions.cfm.
- 10.Little R, Rubin D. Wiley Series in Probability and Statistics. Wiley Interscience; New Jersey: 2002. Statistical analysis with missing data. [Google Scholar]
- 11.Conversano C, Siciliano R. Technical Report. Department of Mathematics and Statistics, University of Naples; Naples, Italy: 2003. Tree-based classifiers for conditional incremental missing data imputation. [Google Scholar]
- 12.Harrington D, Fleming T. A class of rank test procedures for censored survival data. Biometrika. 1982;69(3):553–566. [Google Scholar]
- 13.Rubin DB. Multiple imputation after 18+ years. Journal of the American Statistical Association. 1996;91(434):473–489. [Google Scholar]
- 14.R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2008. Available from: http://www.R-project.org. ISBN 3-900051-07-0. [Google Scholar]
- 15.Hothorn T, Lausen B, Banner A, Radespiel-Troger M. Bagging survival trees. Statistics in Medicine. 2004;23:77–91. doi: 10.1002/sim.1593. [DOI] [PubMed] [Google Scholar]
- 16.Bruce ML, Ten Have TR, Reynolds CF, III, Katz IR, Schulberg HC, Mulsant BH, Brown GK, McAvay GJ, Pearson JL, Alexopoulos GSA. Reducing suicidal ideation and depressive symptoms in depressed older primary care patients. Journal of the American Medical Association. 2004;291:1081–1091. doi: 10.1001/jama.291.9.1081. [DOI] [PubMed] [Google Scholar]
- 17.Schulz R, Heckhausen J. Technical Report. University of Pittsburgh; Pittsburgh, PA: 1998. Health-specific optimization in primary and secondary control scales. [Google Scholar]