3D sensitivity encoded ellipsoidal MR spectroscopic imaging of gliomas at 3T

Abstract

Purpose

The goal of this study was to implement time efficient data acquisition and reconstruction methods for 3D magnetic resonance spectroscopic imaging (MRSI) of gliomas at a field strength of 3T using parallel imaging techniques.

Methods

The point spread functions, signal to noise ratio (SNR), spatial resolution, metabolite intensity distributions and Cho:NAA ratio of 3D ellipsoidal, 3D sensitivity encoding (SENSE) and 3D combined ellipsoidal and SENSE (e-SENSE) k-space sampling schemes were compared with conventional k-space data acquisition methods.

Results

The 3D SENSE and e-SENSE methods resulted in similar spectral patterns as the conventional MRSI methods. The Cho:NAA ratios were highly correlated (P<.05 for SENSE and P<.001 for e-SENSE) with the ellipsoidal method and all methods exhibited significantly different spectral patterns in tumor regions compared to normal appearing white matter. The geometry factors ranged between 1.2 and 1.3 for both the SENSE and e-SENSE spectra. When corrected for these factors and for differences in data acquisition times, the empirical SNRs were similar to values expected based upon theoretical grounds. The effective spatial resolution of the SENSE spectra was estimated to be same as the corresponding fully sampled k-space data, while the spectra acquired with ellipsoidal and e-SENSE k-space samplings were estimated to have a 2.36–2.47-fold loss in spatial resolution due to the differences in their point spread functions.

Conclusion

The 3D SENSE method retained the same spatial resolution as full k-space sampling but with a 4-fold reduction in scan time and an acquisition time of 9.28 min. The 3D e-SENSE method had a similar spatial resolution as the corresponding ellipsoidal sampling with a scan time of 4:36 min. Both parallel imaging methods provided clinically interpretable spectra with volumetric coverage and adequate SNR for evaluating Cho, Cr and NAA.

1. Introduction

Brain cancer is a devastating disease with 20,500 new cases each year within the United States alone and 1 year median survival for the highest grade lesions [1]. Gliomas are the most common type of brain tumor and arise from the glial cells of the brain, which are the support cells for neurons. 3D Magnetic resonance spectroscopic imaging (MRSI) has been successfully employed to extract information about brain tumor cellularity, cell membrane breakdown, tissue energetics and neuronal activity through its ability to differentiate signals from choline (Cho), creatine (Cr) and N-acetyl aspartate (NAA) molecules. Previous studies have reported higher Cho, variable Cr and lower NAA values in the tumor regions compared to normal brain tissue [2]. Higher lactate and lipid values were also observed in high grade gliomas, which indicate the presence of necrosis and cell death [3]. Addition of MRSI data to the conventional magnetic resonance (MR) imaging has been shown to improve brain tumor diagnosis, localization, treatment planning and evaluation of disease progression [4-7].

One limitation of acquiring 3D MRSI data for brain tumor patients is the long acquisition time associated with using conventional phase encoding. For clinical applications, it is desirable to acquire MRSI data in less than 10 min and although the higher sensitivity obtained at 3T is sufficient to reduce the acquisition time, this would require the implementation of alternative k-space sampling techniques. Restricting the phase encoding to a central, ellipsoidal region of k-space (ellipsoidal sampling) has been used to reduce the scan time for 3D MRSI [3,8-12] by a factor of two. Sensitivity encoding (SENSE) is another method that has been shown to reduce scan time for 2D MRSI [13,14] by acquiring fewer phase encoding steps and using coil sensitivity profiles from phased-array coils to resolve spatial aliasing. The application of 2D and 3D SENSE MRSI with or without ellipsoidal sampling has been reported in phantoms and the brain of healthy volunteers [14-16] but it has not been applied for the acquisition of 3D matrices with small fields of view for brain tumor patients. The use of a k-space shutter, which restricts the k-space acquisition to a certain region, in conjunction with the SENSE technique was reported to reduce the scan time by 25% for a cylindirical shutter and 50% for a spherical k-space shutter [16]. The combination of time-varying spectroscopic readout gradients and parallel imaging approaches, such as SENSE with echo planar spectroscopic imaging (SENSE-PEPSI) [17], generalized autocalibrating partial parallel acquisition (GRAPPA) with EPSI encoding [18,19] and SENSE with spiral trajectories [20], have also been proposed for achieving fast scan times. These fast techniques have not yet been fully evaluated in terms of SNR, volumetric coverage and possible artifacts in conjunction with their impact on estimates of metabolite levels for clinical applications.

The aim of this study was to implement 3D ellipsoidal sampling and 3D SENSE with full and with ellipsoidal sampling (e-SENSE) schemes on a 3T whole body scanner and to evaluate the metabolic profiles of spectra obtained from patients with brain tumors. To evaluate the robustness of each method, we compared metabolite intensities that were estimated using multiple approaches within the same subject. The parameters considered were the point spread function, signal-to-noise ratio (SNR), nominal voxel size, variation in Cho:NAA ratio and lipid contamination.

2. Materials and methods

2.1. Data acquisition

A phantom, eight volunteers (seven females, one male, mean age=26 years) and 19 patients (15 Grade IV, 3 Grade III, 1 Grade II, 6 female, 13 male, mean age=50 years) were scanned on a 3T whole body MR scanner (GE Healthcare, Milwaukee, WI, USA) equipped with an eight-channel RF phased-array coil (MRI Devices, Gainesville, FL). The eight-channel coil consisted of eight surface coils equidistantly located in a circular frame. All the subjects provided informed consent prior to scanning. The imaging protocol included the acquisition of axial T1-weighted spoiled gradient (SPGR) (TR=26 ms, TE=3 ms, 3 mm slice thickness, 256×256×64 voxels, FOV=24×24×19.2 cm, flip angle=40°), T2-weighted fluid-attenuated inversion recovery (FLAIR) (TR=10002 ms, TE=127 ms, TI=2200 ms, 3 mm slice thickness, 256×256×48 voxels, FOV=24×24×14.4 cm) and proton-density weighted fast gradient echo coil sensitivity images (TR=150 ms, TE=2.1 ms, 5 mm slice thickness, 64×64×36 voxels, FOV=30×30×18 cm, flip angle=20°). T1 SPGR images were acquired both pre-contrast and after the administration of gadolinium.

SENSE, ellipsoidal and the combination of SENSE and ellipsoidal (e-SENSE) sampling strategies were implemented for 3D ¹H MRSI data acquisition in conjunction with a traditional point resolved spectroscopy (PRESS) [21] volume localization sequence. Chemical shift selective (CHESS) [22] pulses were utilized for water suppression and very selective suppression [23] pulses for outer volume suppression. The spectroscopic data acquisition parameters were as follows: TR=1.1s, TE=144 ms, spectral bandwidth=2000 Hz, number of frequency points=1024 and 1×1×1-cm³ spatial resolution. For the ellipsoidal sampling, the k-space points were acquired using the following formula:

$${\mathit{acq}}_{\text{Ellipsoidal}}(k_x,k_y,k_z)=\left(\sqrt{\frac{k_x}{{\mathrm{PE}}_x}+\frac{k_y}{{\mathrm{PE}}_y}+\frac{k_z}{{\mathrm{PE}}_z}}\le k_{\mathrm{rad}}\right)$$ (1)

where k_x, k_y and k_z are the respective coordinates of the k-space along the three axes, k_rad is the radius of the ellipsoid that will encompass the acquired k-space points, PE_x, PE_y and PE_z are the total number of phase encoding steps along the three axes, and acq_Ellipsoidal(k_x,k_y,k_z) is the flag that controls the data acquisition. k_rad was set to 1.1 for our data acquisition resulting in a total data acquisition time of 17:32 min for a 16×16×8 spectral array and 9:36 min for a 12×12×8 spectral array.

For the SENSE sampling, only even k_x and k_y points were acquired, resulting in a reduction factor (R) of 2 in both x and y directions and a total of a fourfold scan time reduction. For a 16×16×8 spectral array, SENSE sampling resulted in a scan time of 9:28 min. For the e-SENSE sampling scheme, only even k-space points along k_x and k_y (R_x=2, R_y=2) that fell into a central ellipsoidal region were acquired. A fully sampled 16×16×8 k-space array would have consisted of 2048 k-space points. With a TR of 1.1 s this would have resulted in a scan time of 37:42 min. The radius of the ellipsoid that encompassed the acquired k-space points (k_rad) was set to 1.1 for the e-SENSE data acquisition resulting in the sampling of 238 k-space points (11% of the fully sampled data) with a total scan time of 4:36 min.

The subject population was divided into two groups for the SENSE and e-SENSE spectroscopic imaging. The first group comprised five volunteers (5 females, mean age=25) and thirteen glioma patients (11 Grade IV, 1 Grade III, 1 Grade II, 5 female, 8 male, mean age=49). Although it would have been desirable to use 16×16×8 matrix sizes for the full and ellipsoidal encoding it was not practical to perform all of these studies on the same individuals because of limitations on scan time. As a compromise, three types of k-space sampling strategies were used in the volunteers. These comprised full (12×12×8 spectral array, FOV=12×12×8 cm, 1×1×1 cm³ nominal spatial resolution, 21:12 min), ellipsoidal (12×12×8 spectral array, FOV=12×12×8 cm, 1×1×1 cm³ nominal spatial resolution, 9:36 min) and SENSE (16×16×8 spectral array, R_x=2, R_y=2, FOV=16×16×8 cm, 1×1×1 cm³ nominal spatial resolution, 9:28 min). For the patients in this group, only the ellipsoidal and SENSE spectra were acquired.

The second group of subjects comprised three volunteers (two females, one male, mean age=26) and six patients diagnosed with glioma (four Grade IV, two Grade III, 1 female, 5 male, mean age=53). e-SENSE (16×16×8 spectral array, FOV=16×16×8 cm, R_x=2, R_y=2, 4:36 min) and ellipsoidal (16×16×8 spectral array, FOV=16×16×8 cm, 17:32 min) sampling were used for the phantom and volunteers, with the smaller ellipsoidal array (12×12×8 spectral array, FOV=12×12×8 cm, 9:36 min) being used for patients. Table 1 summarizes the data acquisition schemes for the patients and volunteers in the SENSE and e-SENSE groups.

Table 1.

Data acquisition schemes for SENSE and e-SENSE volunteers and patients

	Patients			Volunteers
	Sampling	Matrix	Time	Sampling	Matrix	Time
Group 1 (SENSE)	Ellipsoidal	12×12×8	9:36 min	Ellipsoidal	12×12×8	9:36 min
	SENSE	16×16×8	9:28 min	SENSE	16×16×8	9:28 min
				Full	12×12×8	21:12 min
Group 2 (e-SENSE)	Ellipsoidal	12×12×8	9:36 min	Ellipsoidal	16×16×8	17:32 min
	e-SENSE	16×16×8	4:36 min	e-SENSE	16×16×8	4:36 min

2.2. Spatial response function simulations

The effective spatial resolution of the ellipsoidal, SENSE and e-SENSE samplings were investigated through simulations of the spatial response function (SRF). A 16×16×8 array and a 12×12×8 array with a point source located at the origin were simulated resulting in a k-space representation with constant values of 1 at all k-space locations. A binary sampling mask that has ones at the sampled points and zeros elsewhere was generated for each of the ellipsoidal (16×16×8 and 12×12×8 k-space array), SENSE (16×16×8 k-space array, R_x=2, R_y=2) and e-SENSE (16×16×8 k-space array, R_x=2, R_y=2) sampling schemes. The sampling masks were multiplied with the k-space representation of the object to retrieve subsampled k-space images of the object for each of the sampling schemes. The resultant k-space arrays were zero filled to 48 times the size of the original array in each dimension for the 12×12×8 arrays and 32 times the size of the original array for the 16×16×8 arrays to result in 576×576×384 and 512×512×256 arrays, respectively. Zero filling increased the number of simulated points in a given volume for a finer grid in the 3D space, but the spatial resolution remained the same. The zero filling factor was smaller for the 16×16×8 arrays due to limitations on memory. The resultant arrays were inverse Fourier transformed into the spatial domain and the spatial resolution was calculated following the definition of Maudsley et al. [12]. Briefly, the volume integral of the number of points that had intensity higher than 50% of the maximum absolute peak intensity was calculated and normalized by the respective zero filling factors (48³ and 32³) to estimate the effective spatial resolution. Table 2 lists the spatial resolution for the sampling schemes considered in this article.

Table 2.

Effective spatial resolution calculated via the spatial response function simulations

Sampling	Matrix	FOV (cm)	Spatial resolution (cm3)	Time (min)
Full	16×16×8	16×16×8	1.019	37:42
Full	12×12×8	12×12×8	1.017	21:12
Ellipsoidal	16×16×8	16×16×8	2.366	17:32
Ellipsoidal	12×12×8	12×12×8	2.473	9:36
SENSE	16×16×8	16×16×8	1.029	9:28
e-SENSE	16×16×8	16×16×8	2.369	4:36

2.3. Data processing

Regions of normal appearing white matter (NAWM) were contoured from the white matter on the contralateral side of the tumor using an interactive image analysis program developed in our laboratory. Contrast-enhancing (CE) areas were segmented from the postcontrast T1-weighted SPGR images and the regions of T2 hyperintensity (FL) were segmented from the T2-weighted FLAIR images using a semi-automated region growing algorithm [24] for the patients.

In-house software [25] was used to reduce the anatomy related nonuniformities in the coil sensitivity maps. A mask of the anatomy was created using the Canny method [26] to find the edges of the brain in the combined (sum of squares) coil sensitivity images. This mask was applied to the individual and the combined coil sensitivity images. Individual coil images were then divided by the combined images and smoothed by consecutively applying median and low-pass homomorphic filters. The resultant images were dilated by a 3×3 kernel to preserve the edges and resampled to 32×32×8-cm FOV images with 1-cm³ spatial resolution located at the same center with the spectra.

Ellipsoidal and full spectra from individual coil elements were apodized with a 4 Hz Lorentzian filter, inverse Fourier-transformed along the spatial and frequency dimensions and combined using coil sensitivity weighting [27]. SENSE and e-SENSE spectral data points were first placed on a respective 16×16×8 rectangular grid. These spectra then were preprocessed in a similar manner to the ellipsoidal and full spectra to generate aliased spectral images for each coil element. The resulting parallel spectra were unaliased and combined with SENSE spectral data reconstruction to generate an array with double the original size along the reduced directions (32×32×8 spectral array) to take into account the lipid aliasing problem of small FOV spectroscopy [25]. Cartesian SENSE spectral data reconstruction with Tikhonov’s simple regularization [14,25,28,29] was implemented using MATLAB 7.0 (The Mathworks, Natick, MA, USA) as follows,

$$v={(S^H{\psi }^{-1}S+\lambda I)}^{-1}{S}^H{\psi }^{-1}A,$$ (2)

where S is the coil sensitivity matrix, H is the complex conjugate transpose, ψ is the receiver noise matrix, the symbol −1 represents the pseudo-inverse operator, λ is the Tikhonov’s simple regularization parameter, I is the identity matrix, A is the aliased spectrum and v is the unaliased spectra.

The receiver noise matrix contained noise variances of single coils at the diagonal, and the noise cross-correlation of the coils in the off-diagonal entries [13]. Noise from the last 20 points of the spectra in the central 7×7×3 voxels in the spectral array were used to calculate the noise receiver matrix. The final noise receiver matrix was calculated by averaging the noise receiver matrices of the selected central 147 voxels. For a given voxel, only the coils that had coil sensitivities higher than the 20% of the maximum coil sensitivity for that given voxel are employed in the unaliasing. The geometry factor, g, maps were also calculated to estimate the noise amplification due to the data reconstruction using SENSE as,

$$g=\sqrt{{\left(S^H{\psi }^{-1}S\right)}^{-1}\left(S^H{\psi }^{-1}S\right)}.$$ (3)

Several Tikhonov’s regularization parameters in the range of 0.01 to 100 were assessed qualitatively to set the regularization parameter. All the regularization parameters were observed to condition the matrix inversion and reduce the noise in the resultant unaliased spectra. While increasing the residual lipid aliasing, higher regularization parameters were observed to result in a reduction in the energy of the spectrum. This feature was used to relatively reduce the lipid intensity in the spectra. Each spectrum was divided into two parts; the first segment included metabolites with resonant frequencies between 0 and 1.7 ppm, while the second section contained metabolites that resonate at frequencies higher than 1.7 ppm. Higher regularization parameters were utilized for the lipid region to suppress the residual aliasing lipid peaks. The regularization parameter was set to 1 for the Cho, Cr and NAA region, and 4 for the lipid region.

For each spectrum, frequency and phase corrections were applied and the water baseline was removed using in-house software as described previously [6]. The SNR of Cho, Cr, NAA and lipid peaks were estimated by normalizing their heights with the standard deviation of the spectral noise calculated from the left end of the spectrum, which was devoid of peaks.

2.4. Data analysis

Metabolite SNRs of the SENSE and ellipsoidal spectra were compared with that of the fully sampled spectra in volunteers by using the following formula,

$$\begin{array}{cc}\hfill & {\mathit{SNR}}_{\text{SENSE}}\frac{g\Delta v_{\text{Full}}\sqrt{{\text{time}}_{\text{Full}}}}{\Delta v_{\text{SENSE}}\sqrt{{\text{time}}_{\text{SENSE}}}}={\mathit{SNR}}_{\text{Full}}=\hfill \\ \hfill & {\mathit{SNR}}_{\text{Ellipsoidal}}\frac{\Delta v_{\text{Full}}\sqrt{{\text{time}}_{\text{Full}}}}{\Delta v_{\text{Ellipsoidal}}\sqrt{{\text{time}}_{\text{Ellipsoidal}}}}\hfill \end{array}$$ (4)

where Δv_SENSE, Δv_Full and Δv_Ellipsoidal are the effective voxel sizes of the respective samplings estimated by the SRF simulations, and g is the respective g-factor value for the given voxel. Similarly, e-SENSE spectral metabolite intensities were compared with that of the ellipsoidal spectra as,

$$\begin{array}{cc}\hfill & {\mathit{SNR}}_{\text{EllipsoidalSENSE}}g∕\left(\Delta v_{\text{EllipsoidalSENSE}}\sqrt{{\text{time}}_{\text{EllipsoidalSENSE}}}\right)\hfill \\ \hfill & ={\mathit{SNR}}_{\text{Ellipsoidal}}∕\left(\Delta v_{\text{Ellipsoidal}}\sqrt{{\text{time}}_{\text{Ellipsoidal}}}\right).\hfill \end{array}$$ (5)

Spearman rank correlation coefficients were computed to assess if the Cho, Cr or NAA ratios between the tumor and NAWM were similar for the ellipsoidal and the SENSE spectra. A Mann–Whitney rank sum test was utilized to assess if the tumor regions had significantly higher Cho:NAA values than NAWM for SENSE and e-SENSE or ellipsoidal spectra for the patients. Voxels with lipid contamination were defined as having spectra with absolute lipid peak height bigger than the absolute NAA peak height within regions of normal appearing white matter from the same subject. A Spearman rank correlation coefficient was computed to assess the similarity of the Cho:NAA ratio between the ellipsoidal and the SENSE and e-SENSE spectra over the PRESS selected region.

3. Results

The raw median SNR of Cho, Cr and NAA peaks calculated from the full, ellipsoidal and SENSE spectra in the white matter region of the normal volunteers for the first part of the study are shown in Table 3. The median absolute SNR of lipid were below 3 for all three spectral data sets. After correcting for the time and unit volume differences and the g factor as noted in Eq. (4), the median ratios of the full corrected SNR to the unregularized SENSE and the ellipsoidal corrected SNRs were very close to 1. This observation supported the results of the simulation and indicated that the effective spatial resolution of the SENSE spectra was similar to that of the full spectra (1 cc) and that the effective voxel size was around 2.4 times larger for the ellipsoidal than the full k-space data. Fig. 1 shows the corrected NAA SNR calculated from the SENSE spectra versus the full spectra after they were corrected for differences in acquisition time and the effect of the geometry factors for a volunteer from the whole PRESS box. It was observed that the slope of the regression was 1.0382, which is very close to the expected value of 1.0. Adding Tikhonov’s regularization to SENSE reconstruction was observed to reduce the noise in the spectra and resulted in 25% higher corrected SNR values for SENSE spectra than the theoretical estimate.

Table 3.

The raw median SNR values and the time, g factor and unit volume corrected median SNR ratios of the spectra in the white matter region of the volunteers, showing an excellent agreement between the simulations and the empirical data

	Cho	Cr	NAA
SNRFull	20.4±3.3	19.8±2.4	47.4±4.2
SNRSENSE	14.1±2.0	12.2±1.4	31.3±2.1
SNREllipsoidal	34.0±5.5	29.7±1.6	73.6±2.8
SNREllipsoidalSENSE	22.7±1.5	17.6±1.9	47.5±1.7
Fullcorr/SENSEcorr	0.99±0.14	1.00±0.14	0.97±0.17
Fullcorr/Ellipsoidalcorr	0.98±0.07	0.99±0.06	0.98±0.07

Fig. 1.

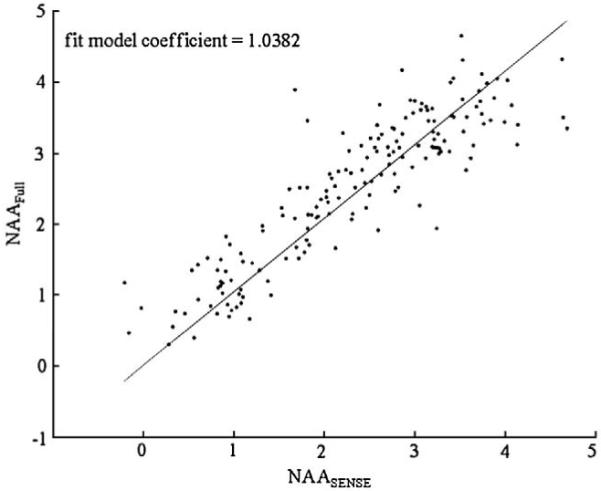
The linear fit of the NAA intensities calculated from a volunteer’s SENSE versus full spectra. The fit model coefficient was 1.0382 indicating high similarity between the intensities calculated from the two data sets.

The geometry factor was reduced by unfolding the SENSE spectra twice into a bigger FOV. The median geometry factor was 1.59±0.11 (max=2.38) in volunteers and 1.58±0.10 (max=2.72) in patients when the SENSE spectra were unaliased into the original FOV (16 cm). The median geometry factors were reduced to 1.20±0.09 (max=1.38) for the volunteers and 1.21±0.19 (max=1.87) for the patients after unaliasing the SENSE spectra into a FOV (32 cm) that was twice as big in-plane as the original FOV.

Table 4 displays the median Cho:NAA values in FL, CE and NAWM regions for the patients as well as the P values of the Mann-Whitney rank sum test of the differences in Cho:NAA ratios between tumor and normal regions. Both CE and FL regions had significantly higher (P<.05) Cho:NAA ratios than NAWM for SENSE and the ellipsoidal spectra. Table 5 displays the ratios of the median Cho, Cr and NAA levels in the FL and CE regions versus the NAWM region and their correlations. The metabolite parameters estimated from different sampling methods were highly correlated.

Table 4.

Median Cho:NAA values and the p values of the differences between Cho: NAA in the NAWM and FLAIR FL and in NAWM and CE regions for the nine patients scanned with ellipsoidal and SENSE methods

	Ellipsoidal	SENSE
Median±S.D.
Cho:NAA
NAWM	0.54±0.07	0.49±0.12
FL	0.96±0.19	0.89±0.18
CE	1.36±0.3	1.26±0.32
P values
NAWM versus FL	4.09e-05	2.08e-05
NAWM versus CE	1.07e-04	1.07e-04

Table 5.

Median ratio of the median values of Cho, Cr and NAA in FL versus NAWM, and CE versus NAWM regions as calculated from patients scanned with ellipsoidal and SENSE methods along with their Spearmen rank correlation coefficients (r) and P value of the correlation (P)

	Cho	Cr	NAA
FL/NAWM
Ellipsoidal	0.87±0.23	0.66±0.30	0.41±0.21
SENSE	0.96±0.41	0.71±0.36	0.41±0.18
(r, P)	(0.67, 0.01)	(0.65, 0.01)	(0.91, 1.40e-05)
CE/NAWM
Ellipsoidal	0.77±0.29	0.44±0.26	0.23±0.12
SENSE	0.81±0.43	0.46±0.23	0.24±0.10
(r, P)	(0.98, 7.76e-09)	(0.95, 1.12e-06)	(0.95, 1.12e-06)

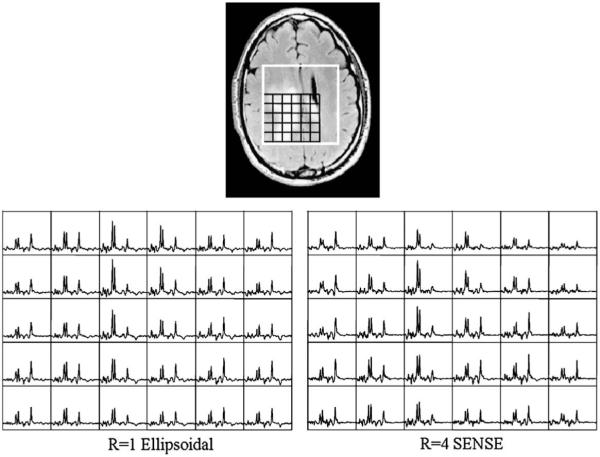
Fig. 2 shows the spectra of a patient with a glioblastoma multiforme. The levels of Cho were observed to be higher and NAA levels were lower in tumor relative to normal regions. The spatial extent of the metabolic lesion and distribution of peak heights were similar for both data sets.

Fig. 2.

A 40-year-old male patient diagnosed with glioblastomamultiforme. T2-weighted FLAIR image is shown on the top, and ellipsoidal and SENSE spectra from the black grid are shown on the bottom. Both spectra depict similar tumor regions with high Cho and Cr and low NAA.

The findings from the comparison between ellipsoidal and e-SENSE data were similar to those of the SENSE data. In this case, median of the geometry factors was 1.25±0.04 (max=1.3) for the volunteers and 1.33±0.11 (max=1.55) for the patients. The median raw SNR of NAA calculated from e-SENSE spectra of the volunteers was 47.52 (range 45.01–48.42). The raw SNR of the e-SENSE was slightly higher than the theoretical expectation due to the noise reduction effect of the Tikhonov’s regularization. The increase in raw SNR above the theoretical level was 10.5% for the volunteers and 8.5% for the patients. The median Cho:NAA ratios for ellipsoidal and e-SENSE data were identical in the volunteers (0.48) and similar in the patients (0.74 and 0.70, respectively) and the voxel-by-voxel comparison of ratios for the two sets of spectra were significantly (P<.001) correlated for each individual subject.

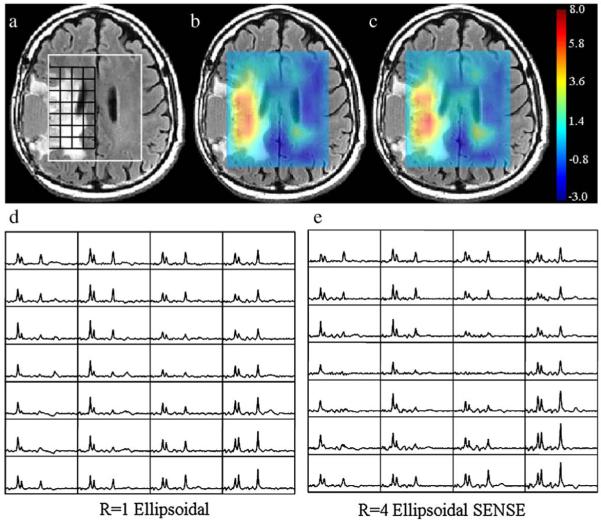
Fig. 3 displays a slice of the e-SENSE and ellipsoidal spectra from a patient diagnosed with glioblastoma multiforme and corresponding choline to NAA index (CNI) [30] maps overlaid on T2 FLAIR image. The CNI index is the distance between the Cho:NAA ratio for a given voxel and the regression line fit of the Cho:NAA ratios of normal voxels in a given subject. The CNI maps calculated from the ellipsoidal and e-SENSE spectra both showed similar regions of high CNI values, indicating tumor. e-SENSE and ellipsoidal spectra both depicted high Cho and low NAA within the tumor region and had highly correlated Cho:NAA ratios (r=0.86, P<.001).

Fig. 3.

A 53 year old male patient diagnosed with glioblastoma multiforme. The top row shows a T2 weighted FLAIR image with the PRESS box in white and a selected spectral region in black (a) and overlaid CNI maps calculated from ellipsoidal (b) and e-SENSE (c) spectra. Ellipsoidal (d) and e-SENSE (e) spectra from the spectral grid are shown at the bottom left and right, respectively.

4. Discussion

Previous results had shown that the higher field strength and use of multi-channel RF coil could provide an increase in signal to noise ratio of as much as twofold over 3D MRSI data that had been acquired using a 1.5-T whole body scanner [31]. This increase in sensitivity may be used to reduce scan time, improve spatial coverage or decrease voxel size. With a 3D acquisition matrix, the number of phase encodes is the limiting factor in determining scan time. This can be addressed with parallel imaging methods such as SENSE using fewer phase encode steps and taking advantage of the differences in sensitivity profiles of individual coil elements to provide information on spatial localization. In this study, we implemented data acquisition and reconstruction methods for 3D SENSE MRSI and 3D e-SENSE MRSI on a whole body 3-T scanner and evaluated their performance in normal volunteers and patients with gliomas.

One of the main limitations of the SENSE based spectral data acquisition techniques was expected to be the lower SNR associated with the so-called geometry factor. With the eight-channel head coil and unfolding the spectra into a larger FOV in the reconstruction, the geometry factor gave a 20–30% loss in SNR for the SENSE and e-SENSE spectra compared with the level that was expected based upon scan time. As can be seen in the normal and patient data, the parallel imaging methods provided spectral data with similar information to the full k-space matrices and equal or improved spatial resolution compared to the ellipsoidal data. Although the computational time for reconstruction is longer than the conventional Fourier transform, the size of the spectral array is modest in comparison to many fast imaging methods and so this is not likely to be a limiting factor for clinical applications.

A second concern is that the relatively small fields of view associated with the 3D SENSE and e-SENSE data would result in increased lipid contamination. Lipid peaks located at the scalp are close to individual coil elements and are therefore challenging to suppress completely using out of voxel saturation. With the 3D field of view and size of the matrix being considered, the SENSE based techniques can cause lipids to alias into the PRESS selected volume. Imperfections in the empirical coil sensitivity maps and reconstruction algorithm mean that these may not be completely eliminated. A postprocessing method that used Tikhonov’s simple regularized inversion was used with a higher parameter for the range of spectral frequencies corresponding to lipid. This was effective in reducing contamination but may have limited the potential for identifying regions within the lesion that contained lipid due to the presence of necrosis or treatment effects. If the quantification of such lipid peaks is of interest for diagnosis or evaluation of prognosis, other rapid k-space sampling techniques such as spiral [32] and echo planar MRSI [33] should be considered. The echo planar MRSI encodes the chemical shift and one spatial dimension while spiral MRSI can encode two spatial dimensions along with the chemical shift within one repetition time. Time saved by such encodings can be used to increase the spatial coverage in the other phase encode directions and the lipid regions can be contained within the FOV to prevent lipid aliasing. However, both echo planar and spiral MRSI might suffer from a limited spectral bandwidth resulting in spectral aliasing unless interleaving is used. The combination of time-varying spectroscopic readout gradients and parallel imaging approaches, like combining SENSE with echo planar spectroscopic imaging (SENSE-PEPSI) [17], GRAPPA with EPSI [18,19] and SENSE with spiral trajectories [20], have also been proposed for achieving an even faster scan time. However, the application of these fast techniques for clinical applications might need more evaluation for the SNR, volumetric coverage, possible artifacts and their impact on the metabolite levels and the disease extent definition.

The ellipsoidal sampling is a well-established method for reducing the scan time for MR imaging. The simulation and empirical data results presented here have shown that the volumetric matrices have a 2.4-fold lower spatial resolution than full encoding. Note that the spectra obtained using 3D SENSE were calculated to have a better effective spatial resolution than ellipsoidal k-space sampling data obtained within a similar acquisition time. This is particularly important for the evaluation of small or heterogeneous lesions. If speed of acquisition is the priority rather than the spatial resolution, 3D e-SENSE is the method of choice, because those data can be obtained in less than 5 minutes. Note that the 3D e-SENSE MRSI has the same limitations as 3D SENSE MRSI in terms of quantification of lipid, but it is able to provide high quality spectra with clear differences in the levels of choline, creatine and NAA between regions of tumor and normal appearing white matter.

5. Conclusion

The 3D SENSE and e-SENSE spectra were able to reduce scan times to clinically acceptable times of 9:28 and 4:36 min, respectively. The reduced scan time can be used to enable spectral scans with multiple echo times in a single patient visit or to shorten the length of the exam. Now that higher magnetic field scanners are widely available, SENSE-based MRSI techniques are likely to be of interest for routine clinical applications. Faster MRSI data acquisition is expected to result in reduced patient discomfort and reduced motion artifacts, as well as higher throughput for MR scanners. Future studies will investigate the application of 3D e-SENSE method for lactate editing and higher spatial resolution using high field MR scanners.