Abstract
Meniscal attachments are ligamentous tissues anchoring the menisci to the underlying subchondral bone. Currently little is known about the behavior of meniscal attachments, with only a few studies quantitatively documenting their properties. The objective of this study was to quantify and compare the tensile mechanical properties of human meniscal attachments in the transverse direction, curve fit experimental Cauchy stress-stretch data to evaluate the hyperelastic behavior, and couple those results with previously obtained longitudinal data to generate a more complete constitutive model. Meniscal attachment specimens were tested using a uniaxial tension test with the collagen fibers oriented perpendicular to the loading axis. Tests were run until failure and load-optical displacement data was recorded for each test. The medial posterior attachment was shown to have a significantly greater elastic modulus (5.38±0.77 MPa) and ultimate stress (1.73±0.32 MPa) when compared to the other three attachments. The Mooney-Rivlin material model was selected as the best fit for the transverse data and used in conjunction with the longitudinal data. A novel computational approach to determining the transition point between the toe and linear regions is presented for the hyperelastic stress stretch curves. Results from piece-wise non-linear longitudinal curve fitting correlate well with previous linear elastic and SEM findings. These data can be used to advance the design of meniscal replacements and improve knee joint finite element models.
Keywords: Meniscus, knee, enthesis, modulus, mechanical properties, material model, transverse, longitudinal
1. INTRODUCTION
The menisci provide fundamental support in the human knee and encompass an array of functions, essentially regulating the load transmission across the knee joint (Walker and Erkman 1975; Shrive, O’Connor et al. 1978; Messner and Gao 1998). Menisci contain collagen fibers that are circumferentially aligned to distribute loading on the tibial plateau, intrinsically facilitating articular cartilage fortification and osteoarthritis prevention (Messner and Gao 1998). The menisci are joined to the tibia by means of ligamentous structures known as meniscal attachments (Messner and Gao 1998). With a ground substance matrix comprised of proteoglycans, elastin, glycolipids, fibroblasts and ~60-70% water (Woo 1982; Villegas, Maes et al. 2007) and collagen fibers as reinforcement; meniscal attachments serve as transitions from meniscal body fibrocartilage into the underlying subcondral bone (Villegas, Hansen et al. 2008). Loads sustained by the meniscus are diffused into these insertion sites, which reduce the stress concentrations by gradually transitioning soft tissue into the bone and increasing interface contact area (Messner and Gao 1998). Previous research has shown that meniscal attachments are important for retaining joint functionality (Haut Donahue, Hull et al. 2003) and their mechanical behavior directly affects stability of the knee (Chen, Branch et al. 1996; Goertzen, Gillquist et al. 1996; Alhalki, Howell et al. 1999; Haut Donahue, Hull et al. 2003), however, limited research has been conducted on this unique biological structure to date.
Previous mechanical testing has only been performed in the longitudinal direction of the collagen fibers in the attachments (Villegas, Hansen et al. 2008; Hauch, Villegas et al. 2010), despite implications that the anterior attachment is primarily in tension, while the posterior attachment is thought to be subjected to both tension and compression (Benjamin, Evans et al. 1991; Gao, Oqvist et al. 1994). Furthermore, the presence of aggrecan in the attachment suggests that the attachments are likely subjected to compression (Benjamin and Ralphs 1998; Villegas, Hansen et al. 2008). Since ligamentous material is known to be mechanosensitive, the strength of each attachment may vary based on the external loading environment (de Boer, Selby et al. 2007; Provenzano, Alejandro-Osorio et al. 2007). Thus, understanding the transverse mechanical properties of the meniscal attachments is imperative for further elucidating the load distribution of the human meniscus. Previous studies of time-dependent and failure properties of meniscal attachments in the longitudinal direction (Villegas, Hansen et al. 2008; Hauch, Villegas et al. 2010) coupled with these transverse properties will enable tissue engineering replacement design and aid in three-dimensional modeling of the human knee joint (Haut Donahue, Hull et al. 2003). Furthermore, developed constitutive models from this data will aid in a greater understanding of the human meniscus during common injury loading scenarios (Gardiner and Weiss 2003). Thus, the first objective of this study was to measure the tensile mechanical properties of the human meniscal attachments along the transverse direction. Posterior meniscal attachments are hypothesized to have higher transverse moduli than the anterior attachments due to their hypothesized in vivo loading conditions.
A hyperelastic material model can be used to represent the attachments’ non-linear tendencies in the transverse direction (Quapp and Weiss 1998; Gardiner and Weiss 2003). The second objective of this study was to characterize the constitutive behavior of the meniscal attachments using three independent hyperelastic models evaluated against the experimental data. Given previous studies (Quapp and Weiss 1998), it is hypothesized that the higher parameter models will better describe the hyperelastic transverse material properties of the specimens. Additionally, previous longitudinal stress-strain data obtained by our laboratory has examined the linear elastic and time-dependent properties along this axis; however, due to the organization of the tissue, both matrix and fibers were examined simultaneously. By isolating the matrix via transverse testing, its contribution alone can be accounted for and a hyperelastic, transversely isotropic material model can be utilized to describe the material performance for each human meniscal attachment in the longitudinal direction.
2. MATERIALS AND METHODS
Transverse specimen preparation
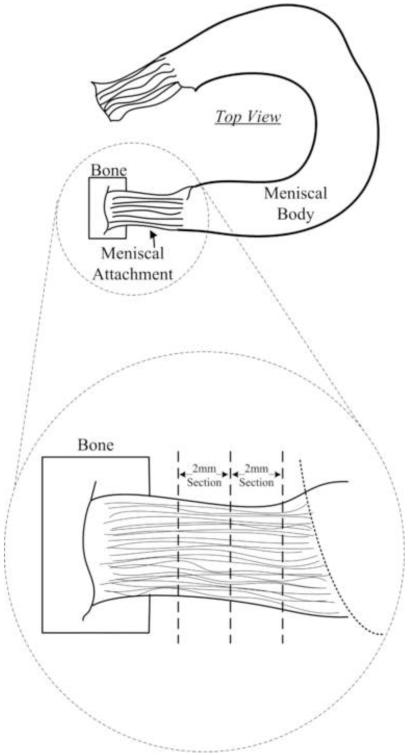
Five healthy human knees (males, ages 50-65, avg. age 58) (NDRI, Philadelphia, PA) were procured, wrapped in saline soaked gauze and frozen at −20°C until the time of dissection. All surrounding tissue was cut away from each knee until the tibial plateau and meniscal bodies were exposed (Figure 1). The medial anterior (MA), medial posterior (MP), lateral anterior (LA), and lateral posterior (LP) attachments were extracted and stored in 0.9% saline solution at 4°C. A custom drop-cutter was used for preparing the individual specimens by slicing 1 or 2 mm thick sections of the meniscal attachment, depending on attachment size (Figure 1). Sections were cut perpendicular to the orientation of collagen fibers. Specimens were then blotted dry and four parallel ink lines were applied, for optical tracking purposes and slip detection, such that there would be a line located below each grip face and 1mm interiorly. Specimens were rehydrated and stored in saline prior to testing.
1.
Schematic showing where specimens were excised from between the tibial plateau and meniscal body (Villegas, Hansen et al. 2008). 1-2mm sections were removed based on tissue availability.
Transverse test setup
Specimens were loaded into modified thin-film grips (Imada, Northbrook, IL) with the collagen fibers oriented perpendicular to the direction of load (Figure 2A). A scale was etched on the outer surface of each grip for dimensioning. Each grip face was serrated and roughened to eliminate slippage. Specimens were loaded such that the aspect ratio was maximized, while providing ample material to secure each specimen; approximately 3 mm of each specimen was inside the grip faces (Figure 2).
2.
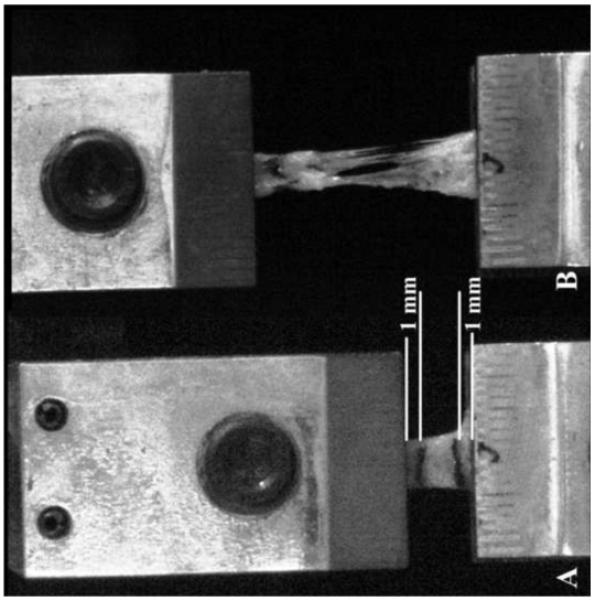
Representative meniscal attachment A) prior to initiation of test, and B) immediately following mid-substance failure of specimen. White lines indicate where ink lines were placed to track strain. Failure of specimen can be seen tearing midsubstance with no appearance of lines placed just below the grip face, indicating no slippage during testing.
Grips were attached to a 44.5 N S-beam load cell (Futek, Irvine, CA) and stationary base holding block. The load cell was attached to a servo-hydraulic uniaxial materials testing machine (Model 8872, Instron Corp, Canton, MA). A pre-load of approximately 0.025 N was applied to the specimen and initial gauge length between the ink lines and width were measured using a scale. Previous studies have shown that strain rate in the transverse direction does not affect mechanical properties of tendons, so a constant strain rate of 10 mm/min was set for all testing (Lynch, Johannessen et al. 2003). No preconditioning was performed on the specimens due to the load being perpendicular to the fiber orientation (Lynch, Johannessen et al. 2003). A charge-couple video camera (Model MicroPix M-1024 CCD camera, Ann Arbor, MI) was utilized to track the motion of the ink lines through testing.
Transverse testing analysis
Load and optical displacement data was recorded for each specimen and processed using a custom MATLAB program (MATLAB R2008a, Natick, MA). Given initial gauge width, thickness, and length, mechanical properties were calculated from user-selected points on the load-displacement curve. Elastic modulus was calculated from the linear region of the stress-strain curve using Hooke’s Law. The ultimate stress and strain were measured at failure (Figure 3) using machine displacement as the tracking lines became marred during failure, optical data was crosschecked against machine data to ensure good correlation.
3.
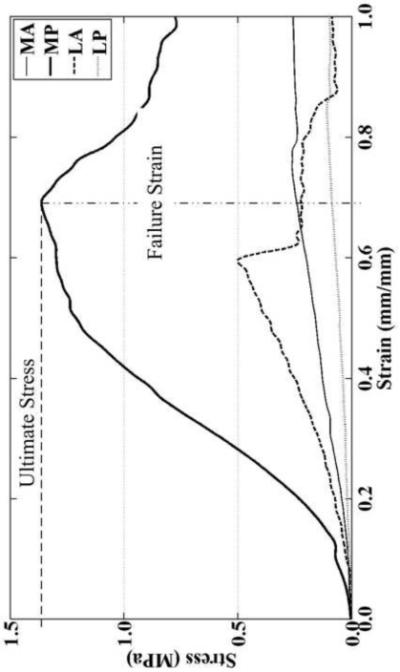
Representative tensile stress-strain curves in the transverse direction for human meniscal attachments using machine displacement to obtain ultimate stress and failure strain. Elastic moduli were computed from optical data (not shown) that was comparable to machine displacement. On average, the medial and lateral posterior attachments exhibited the greatest ultimate stress and failure strain, respectively.
In addition to linear elastic properties, the stress-strain data was analyzed to determine hyperelastic behavior of the meniscal attachments in the transverse direction. The experimentally-measured stress, 2nd Piola-Kirchhoff stress (S11), was converted to Cauchy stress (T11) using Equation 1 for a uniaxial test. The 1-direction is defined as the direction of the tensile tests, that is, in the transverse direction of the attachments. The uniaxial strain in the testing direction (ε) was converted to stretch (λ) using Equation 2. Datasets were then compiled into a single set for each attachment site, four in total. The Neo-Hookean (Equation 3), Mooney-Rivlin (Equation 4), and Ogden (Equation 5) hyperelastic models were fit to the attachment site specific datasets using the MATLAB Optimization Toolbox.
| (1) |
| (2) |
Neo-Hookean (Weiss, Maker et al. 1996; Quapp and Weiss 1998; Holzapfel 2000):
| (3) |
Mooney-Rivlin (Weiss, Maker et al. 1996; Quapp and Weiss 1998; Holzapfel 2000):
| (4) |
Ogden (Holzapfel 2000; Ogden R. W. 2004):
| (5) |
The MATLAB program utilized the experimental Cauchy stress and stretch data to produce hyperelastic curves that fit the test data. The unknown coefficients C1, C2, μp and αp were calculated for each respective model.
Longitudinal analysis
Longitudinal data was procured by means of a pull to failure test. In brief, 6 healthy human knees were potted and aligned in a fixture that mimicked in situ loading conditions. A custom-made freeze clamp gripped the menisus at the transition line between meniscal tissue and attachment. Each attachment was preconditioned for 10 cycles at 10 mm/min between 0% and 3% of the gauge length. Pull to failure was then performed using displacement control at a rate of 2%sec−1. We previously reported local elastic and failure properties of these attachments (Hauch, Villegas et al. 2010). In this study, Weiss’ ligament model for an incompressible, hyperelastic, transversely isotropic biological composite was used to describe to behavior of the meniscal attachments (Weiss, Maker, et al., 1996)
| (6) |
Where Ψm and Ψf represent the matrix and fiber contributions, respectively, and Ψm-f embodies the matrix-fiber interaction. This last term is ignored as it pertains to shearing effects and its contribution can be considered relatively insignificant for the attachments. Rewriting in terms of principal stretch the matrix portion is obtained by means of the aforementioned transverse testing and analysis. A piece-wise function is required for the fiber contribution in order to encapsulate the non-linear phase, when uncrimping of the collagen fibers occurs, and linear phase such that
| (7) |
Where λ* represents the stretch at the point the collagen fibers become taut. Curve fitting was performed on longitudinal data for all samples at a given attachment site. Determination of λ* was achieved by minimizing the objective function
| (8) |
where, the first two experimental points are fit to the exponential equation and the remaining points with the linear function. The process is then iterated upon by removing the first point from the linear portion and appending it to exponential set. The lowest resultant for all iterations using (8) identifies the value of λ*.
Statistical analysis
One way Analysis of Variance (ANOVA) was performed to determine differences between each anatomical meniscal attachment for mechanical properties. When significant results were identified by ANOVA, a post-hoc Student’s two-tailed t-test was performed to compare individual meniscal attachment region variances to one another. The goodness-of-fit of the evaluated hyperelastic material models was determined using a Student’s t-test to evaluate the null hypothesis that the mean of the standardized variance is zero; a higher p-value represents a better model fit for the data set (Morrow, Haut Donahue et al. 2010).
3. RESULTS
Specimen failure occurred mid-substance (Figure 2B) and no slippage in the grips was observed during the testing procedure, as evidenced by no ink line excursion from the grip face. Stress-strain curves were typical of ligamentous-type tissues with a characteristic toe-region (Figure 3) preceding an elastic region until failure. There were no significant differences in gauge length and cross-sectional area between different specimens. The average gauge length and cross-sectional area (mean ± standard error) for all specimens tested (n=20) were 6.1±0.4 mm and 3.7±0.4 mm2, respectively. The anterior attachments of both the medial and lateral menisci exhibited similar behavior during testing (Table 1). The MP attachment was approximately five times stiffer than the other attachment sites (Table 1). Failure strains for all attachments coincided with one another; however ultimate stresses were found to be significantly different, with the MP ultimate stress being approximately five times greater than the MA and LP attachments (Table 1).
Table 1.
Experimental transverse tensile properties of human meniscal attachments. Elastic modulus is derived from optically tracked strain data, ultimate stress and failure strain are determined using test machine strain data. MA=medial anterior, MP=medial posterior, LA=lateral anterior, LP=lateral posterior. Mean +/− Standard error
| Elastic Modulus (MPa) |
Ultimate Stress (MPa) |
Failure Strain (mm/mm) |
|
|---|---|---|---|
| MA | 1.35±0.76 * | 0.34±0.12 * | 0.82±0.13 |
| MP | 6.42±0.78 | 1.73±0.32 | 0.49±0.06 |
| LA | 1.21±0.48 * | 0.56±0.04 *^ | 0.81±0.17 |
| LP | 1.21±0.56 * | 0.33±0.06 * | 0.94±0.11 |
= significantly different than MP
= significantly different than LP
P< 0.05
A non-linear toe region for Cauchy stress-stretch data was seen in the transversly stretched meniscal attachments (Figure 4). The Neo-Hookean (NH), Mooney-Rivlin (MR) and Ogden (OG) hyperelastic material models were optimized for each sample tested(Figure 4). The material parameters of each hyperelastic model varied between the attachment zones (Table 2). The NH model resulted in the lowest p-value for all attachment sites while OG and MR produced comparable p-values. Since MR quantiatively outperformed OG, transverse MR parameters were used in conjunction with longitudinal data (Figure 5).
4.
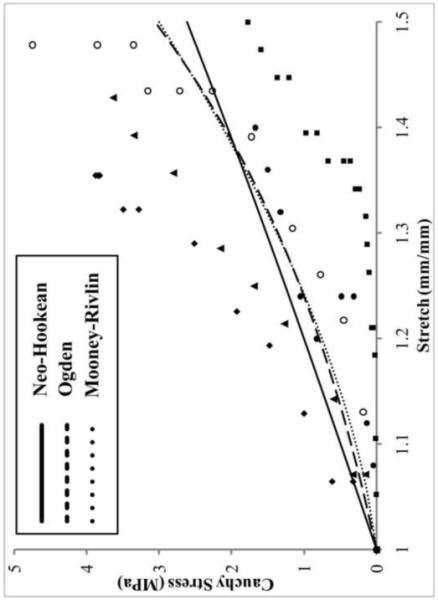
Cauchy stress-stretch curve showing hyperelastic curve fits to the experimental data for the medial posterior attachment site. Solid line = Neo-Hookean, dashed line= Ogden, dotted line = Mooney-Rivlin, symbols = testing data points for each specimen. The latter two models fit the trend of the data well. Mooney-Rivlin tends to describe samples with a large toe region better than Ogden, which favors specimens that have less compliant linear regions.
Table 2.
Calculated coefficient parameters and p-value for each evaluated hyperelastic material model. MA=medial anterior, MP=medial posterior, LA=lateral anterior, LP=lateral posterior. Mooney-Rivlin model consistently resulted in a better fit, as indicated by a higher p-value
| Ogden | Mooney-Rivlin | Neo-Hookean | ||||||
|---|---|---|---|---|---|---|---|---|
| μ 1 | α 1 | p-value | C1 | C2 | p-value | C1 | p-value | |
| MA | 0.1081 | 3.1915 | 0.8741 | 0.1904 | −0.1227 | 0.9275 | 0.1003 | 0.7933 |
| MP | 0.4360 | 4.9310 | 0.9432 | 2.2485 | −1.9525 | 0.9941 | 0.8621 | 0.6334 |
| LA | 0.1114 | 6.1978 | 0.8604 | 1.1192 | −1.0787 | 0.9790 | 0.3171 | 0.3593 |
| LP | 0.0982 | 4.3606 | 0.5486 | 0.3808 | −0.3136 | 0.7542 | 0.1389 | 0.2809 |
5.
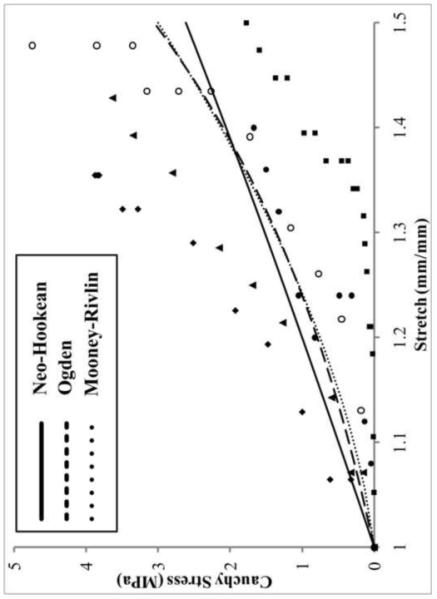
Cauchy stress-stretch curve showing hyperelastic curve fits for the longitudinal data for the medial anterior attachment site. Symbols = test data, solid line = curve fit. The piece-wise function used to fit the data performs a good fit for all data sets considered.
All longitudinal datasets analyzed using the piece-wise material model were optimized to meet the statistical evaluation criteria during the fitting process (Figure 5). The transition point, λ*, was the highest for the anterior attachment sites with the MA reaching over 10% strain. The non-linear scaling coefficient, C3, was also greatest for the MA and lowest for both the posterior attachments. The rate of collagen uncrimping, C4, was higher for the lateral attachments. Anterior attachment sites possessed a linear elastic constant, C5, at least double that of the posterior (Table 3). C6 is an offset factor to ensure continuity at λ* and thus bears no physiological relevance.
Table 3.
Calculated coefficient parameters (C3-C6) and transition point (λ*) from non-linear (toe) to linear regions using Mooney-Rivlin material model for matrix performance (C1, C2). MA=medial anterior, MP=medial posterior, LA=lateral anterior, LP=lateral posterior
| Toe Region | Linear Region | ||||
|---|---|---|---|---|---|
| λ* | C3 | C4 | C5 | C6 | |
| MA | 1.1088 | 8.7418 | 9.7111 | 246.3200 | −256.3306 |
| MP | 1.0579 | 2.7881 | 7.0331 | 29.2884 | −29.5832 |
| LA | 1.0797 | 5.6253 | 13.0889 | 210.9640 | −217.4616 |
| LP | 1.0427 | 2.4003 | 17.7646 | 90.4355 | −90.2595 |
4. DISCUSSION
The results of this study show significant differences in the transverse mechanical properties between meniscal attachments. Namely, the elastic modulus and ultimate stress in MP attachments were significantly greater than all other attachments, which may support theories that this region endures larger compressive loads during dynamic activity compared to others (Benjamin, Evans et al. 1991; Gao, Oqvist et al. 1994). Additionally, failure strains and elastic moduli for both anterior attachments were approximately equal in this study, supporting previous findings of comparable GAG content between anterior attachments (Benjamin, Evans et al. 1991; Villegas, Hansen et al. 2008). However, these conclusions are based on a material which demonstrates compressive-tensile non-linearity, and these cues may not be directly translatable. Additionally, on average the MP attachment reported the lowest failure strains. This may explain why previous clinical studies show more posterior meniscal root tears compared to anterior in humans (Brody, Lin et al. 2006; Jones, Houang et al. 2006; Choi, Son et al. 2008; Lee, Jee et al. 2008; Ahn, Lee et al. 2009; De Smet, Blankenbaker et al. 2009). Scanning electron microscopy of transverse sections of the meniscal attachments has revealed a network of large planar collagen fibers sheathed in loose membrane septae comprised of thinner, randomly oriented, and interwoven fibrils (Villegas, Haut Donahue 2010). While most collagen fibers are aligned with the longitudinal axis, some can be seen diverging in the transverse direction, however, no quantitative analysis has been performed comparing the prevalence of these deviated fibers in the different attachment sites. Future studies should investigate this to elucidate the differences found here.
Mechanical properties obtained from this study agree with previous studies of other ligamentous materials tested in the transverse direction. Human interosseous ligament and medial collateral ligament (MCL) exhibited elastic moduli of 11.02±3.57 MPa and 1.82±2.93 MPa, respectively (Quapp and Weiss 1998; Stabile, Pfaeffle et al. 2004). These moduli values are comparable to those of the attachments tested in this study. Another study conducted on lapine patellar tendons in the transverse directions gave an elastic moduli and ultimate stress value of 1.27 MPa and 0.37 MPa, respectively (Yamamoto, Hayashi et al. 2000). Additionally, ultimate stresses from the transversely strained MCL were 1.69±0.53 MPa (Quapp and Weiss 1998), which is comparable to that of the MP attachment. The failure strain of lapine patellar tendon (0.41 mm/mm) (Yamamoto, Hayashi et al. 2000) was comparable to that of the MP attachment (0.49 mm/mm).
The meniscal attachments exhibited hyperelastic behavior when strained in the transverse direction. Of the three evaluated hyperelastic material models, the OG model can have the highest number of material parameters, and thus has the potential to describe the most complex material behavior. For this study, the OG material model was evaluated with p=1, 2 and 3 to compare the relative accuracy. Increasing the number of material parameters in the OG model did not increase the goodness-of-fit. Therefore, the two-coefficient model only was reported and analyzed. The NH material model did not fit the convex hyperelastic nature of the experimental data, resulting instead in a more linear shape. The MR model involved two unknown coefficients for the hyperelastic curve-fitting and consistently reported the highest resulting p-value for each attachment site. Qualitatively, by comparison, there was little difference between the two complex material models, MR and OG, with the former being more adept at assessing the low stretch (λ < 1.2) phase and the latter more accurately encapsulating the tail end of the stretch-stress curve. Due to better quantitative results and superior computational efficiency the MR model was used in conjunction with the longitudinal data.
Traditionally, determining λ* is performed qualitatively and consistency is dependent on the person assessing the data (Quapp and Weiss 1998). Here, a novel approach to determining λ* has been employed which entails an exhaustive computational method, providing a more robust, user independent evaluation of λ*. The results of this study show that the anterior attachments exhibited the greatest amount of non-linear stretch during longitudinal testing. Imaging techniques have shown that these locations exhibit more mobility during loading, potentially due to a more compliant microstructure (Thompson, et al. 1991; Vedi, et al. 1999). Additionally, the higher rate of uncrimping exhibited by the lateral attachments correlates with SEM findings that the collagen crimp length is longest at these locations, hence the response time required before the collagen fibers become taut is decreased (Villegas, Haut Donahue 2010). Lastly, the initial study conducted on the failure properties of meniscal attachments in the longitudinal direction (Hauch, Villegas et al. 2010) reported elastic moduli values of 169±130 MPa and 91±67 MPa for the anterior and posterior attachments, respectively. The more complex assessment performed here found similar results with the LA and MA attachments possessing the highest longitudinal linear elastic moduli (C5). The anterior and posterior attachments moduli were well within their respective standard deviations from the previous study; evidence that the piece-wise material model corresponds well with commonplace linear elastic evaluation.
This is the first study to examine the mechanical properties of meniscal attachments in the transverse direction. Results suggest that there are significant mechanical differences between attachments. While it is not believed that the attachments are loaded in pure tension in the transverse direction, this transverse mechanical data, coupled with longitudinal data, was used to improve upon previous constitutive modeling of the mechanical behavior of meniscal attachments. Future studies are needed to determine if the different transverse properties of the MP attachment translates into clinically meaningful effects. These data are vital to engineer meniscal replacements, as the apparent anisotropic nature of the meniscal attachments is an important feature that likely needs to be replicated during meniscal tissue engineering.
Acknowledgements
This study was supported in part by the National Institutes of Health (R15AR051906-02).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
The authors affirm that they have no financial affiliation or involvement with any commercial organization that has direct financial interest in any matter included in this manuscript.
References
- 1.Ahn JH, Lee YS, et al. Arthroscopic all inside repair of the lateral meniscus root tear. Knee. 2009;16(1):77–80. doi: 10.1016/j.knee.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 2.Alhalki MM, Howell SM, et al. How three methods for fixing a medial meniscal autograft affect tibial contact mechanics. Am J Sports Med. 1999;27(3):320–8. doi: 10.1177/03635465990270030901. [DOI] [PubMed] [Google Scholar]
- 3.Benjamin M, Evans EJ, et al. Quantitative differences in the histology of the attachment zones of the meniscal horns in the knee joint of man. J Anat. 1991;177:127–34. [PMC free article] [PubMed] [Google Scholar]
- 4.Benjamin M, Ralphs JR. Fibrocartilage in tendons and ligaments--an adaptation to compressive load. J Anat. 1998;193(Pt 4):481–94. doi: 10.1046/j.1469-7580.1998.19340481.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brody JM, Lin HM, et al. Lateral meniscus root tear and meniscus extrusion with anterior cruciate ligament tear. Radiology. 2006;239(3):805–10. doi: 10.1148/radiol.2393050559. [DOI] [PubMed] [Google Scholar]
- 6.Chen MI, Branch TP, et al. Is it important to secure the horns during lateral meniscal transplantation? A cadaveric study. Arthroscopy. 1996;12(2):174–81. doi: 10.1016/s0749-8063(96)90007-9. [DOI] [PubMed] [Google Scholar]
- 7.Choi NH, Son KM, et al. Arthroscopic all-inside repair for a tear of posterior root of the medial meniscus: a technical note. Knee Surg Sports Traumatol Arthrosc. 2008;16(9):891–3. doi: 10.1007/s00167-008-0581-3. [DOI] [PubMed] [Google Scholar]
- 8.de Boer MD, Selby A, et al. The temporal responses of protein synthesis, gene expression and cell signalling in human quadriceps muscle and patellar tendon to disuse. J Physiol. 2007;585(Pt 1):241–51. doi: 10.1113/jphysiol.2007.142828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.De Smet AA, Blankenbaker DG, et al. MR diagnosis of posterior root tears of the lateral meniscus using arthroscopy as the reference standard. AJR Am J Roentgenol. 2009;192(2):480–6. doi: 10.2214/AJR.08.1300. [DOI] [PubMed] [Google Scholar]
- 10.Gao J, Oqvist G, et al. The attachments of the rabbit medial meniscus. A morphological investigation using image analysis and immunohistochemistry. J Anat. 1994;185(Pt 3):663–7. [PMC free article] [PubMed] [Google Scholar]
- 11.Gardiner JC, Weiss JA. Subject-specific finite element analysis of the human medial collateral ligament during valgus knee loading. J Orthop Res. 2003;21(6):1098–106. doi: 10.1016/S0736-0266(03)00113-X. [DOI] [PubMed] [Google Scholar]
- 12.Goertzen D, Gillquist J, et al. Tensile strength of the tibial meniscal attachments in the rabbit. J Biomed Mater Res. 1996;30(1):125–8. doi: 10.1002/(SICI)1097-4636(199601)30:1<125::AID-JBM16>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 13.Hauch KN, Villegas DF, et al. Geometry, time-dependent and failure properties of human meniscal attachments. J Biomech. 2010;43(3):463–8. doi: 10.1016/j.jbiomech.2009.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haut Donahue TL, Hull ML, et al. How the stiffness of meniscal attachments and meniscal material properties affect tibio-femoral contact pressure computed using a validated finite element model of the human knee joint. J Biomech. 2003;36(1):19–34. doi: 10.1016/s0021-9290(02)00305-6. [DOI] [PubMed] [Google Scholar]
- 15.Holzapfel GA. Nonlinear solid mechanics : a continuum approach for engineering. Wiley; Chichester; New York: 2000. [Google Scholar]
- 16.Jones AO, Houang MT, et al. Medial meniscus posterior root attachment injury and degeneration: MRI findings. Australas Radiol. 2006;50(4):306–13. doi: 10.1111/j.1440-1673.2006.01586.x. [DOI] [PubMed] [Google Scholar]
- 17.Lee SY, Jee WH, et al. Radial tear of the medial meniscal root: reliability and accuracy of MRI for diagnosis. AJR Am J Roentgenol. 2008;191(1):81–5. doi: 10.2214/AJR.07.2945. [DOI] [PubMed] [Google Scholar]
- 18.Lynch HA, Johannessen W, et al. Effect of fiber orientation and strain rate on the nonlinear uniaxial tensile material properties of tendon. J Biomech Eng. 2003;125(5):726–31. doi: 10.1115/1.1614819. [DOI] [PubMed] [Google Scholar]
- 19.Messner K, Gao J. The menisci of the knee joint. Anatomical and functional characteristics, and a rationale for clinical treatment. J Anat. 1998;193(Pt 2):161–78. doi: 10.1046/j.1469-7580.1998.19320161.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Morrow DA, Haut Donahue T, Odegard G, Kaufman K. A method for assessing the fit of a constitutive material model to experimental stress-strain data. Comput Methods Biomech Biomed Engin. 2010:1. doi: 10.1080/10255840903170686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ogden RW, Sgura SG., I Fitting hyperelastic models to experimental data. Computational Mechanics. 2004;34(6):18. [Google Scholar]
- 22.Provenzano PP, Alejandro-Osorio AL, et al. Systemic administration of IGF-I enhances healing in collagenous extracellular matrices: evaluation of loaded and unloaded ligaments. BMC Physiol. 2007;7:2. doi: 10.1186/1472-6793-7-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Quapp KM, Weiss JA. Material characterization of human medial collateral ligament. J Biomech Eng. 1998;120(6):757–63. doi: 10.1115/1.2834890. [DOI] [PubMed] [Google Scholar]
- 24.Shrive NG, O’Connor JJ, et al. Load-bearing in the knee joint. Clin Orthop Relat Res. 1978;(131):279–87. [PubMed] [Google Scholar]
- 25.Stabile KJ, Pfaeffle J, et al. Bi-directional mechanical properties of the human forearm interosseous ligament. J Orthop Res. 2004;22(3):607–12. doi: 10.1016/j.orthres.2003.05.002. [DOI] [PubMed] [Google Scholar]
- 26.Thompson WO, Thaete FL, et al. Tibial meniscal dynamics using three-dimensional reconstruction of magnetic resonance images. American Journal of Sports Medicine. 1991;19(3):210–5. doi: 10.1177/036354659101900302. [DOI] [PubMed] [Google Scholar]
- 27.Villegas DF, Hansen TA, et al. A quantitative study of the microstructure and biochemistry of the medial meniscal horn attachments. Ann Biomed Eng. 2008;36(1):123–31. doi: 10.1007/s10439-007-9403-x. [DOI] [PubMed] [Google Scholar]
- 28.Villegas DF, Maes JA, et al. Failure properties and strain distribution analysis of meniscal attachments. J Biomech. 2007;40(12):2655–62. doi: 10.1016/j.jbiomech.2007.01.015. [DOI] [PubMed] [Google Scholar]
- 29.Villegas DF, Haut Donahue TL. Collagen Morphology in human meniscal attachments: a SEM study. Connective Tissue Research. 2010 doi: 10.3109/03008200903349639. In Press. [DOI] [PubMed] [Google Scholar]
- 30.Walker PS, Erkman MJ. The role of the menisci in force transmission across the knee. Clin Orthop Relat Res. 1975;(109):184–92. doi: 10.1097/00003086-197506000-00027. [DOI] [PubMed] [Google Scholar]
- 31.Weiss JA, Maker BN, et al. Finite element implentation of incompressible, transversely isotropic hyperelasticity. Comput methods in applied mechanics adn engineering. 1996;135(1-2):21. [Google Scholar]
- 32.Woo SL. Mechanical properties of tendons and ligaments. I. Quasi-static and nonlinear viscoelastic properties. Biorheology. 1982;19(3):385–96. doi: 10.3233/bir-1982-19301. [DOI] [PubMed] [Google Scholar]
- 33.Vedi V, Williams A, et al. Meniscal movement: An in-vivo study using dynamic mri. The Journal of Bone & Joint Surgery. 1999;81(1):37–41. doi: 10.1302/0301-620x.81b1.8928. [DOI] [PubMed] [Google Scholar]
- 34.Yamamoto E, Hayashi K, et al. Effects of stress shielding on the transverse mechanical properties of rabbit patellar tendons. J Biomech Eng. 2000;122(6):608–14. doi: 10.1115/1.1319660. [DOI] [PubMed] [Google Scholar]