Role of Excited States in Low Energy Electron (LEE) Induced Strand Breaks in DNA Model Systems: Influence of Aqueous Environment

Radiation induced ionizations and excitations of DNA represent the initial steps in DNA radiation damage that lead to resulting biological effects.^1,2 Radiation induced low energy electrons (LEEs), below 15 eV, are produced in large numbers (4 × 10⁴ per MeV energy deposited)³ along the tracks of the ionizing radiation and have been recognized as a potential significant contributor to the DNA damage. Recently, Sanche and coworkers discovered that these LEEs even below 4 eV can produce single-strand breaks (SSB) in plasmid DNA.⁴ Subsequently, these LEEs were also found to cause a variety of damages in DNA model compounds.^4,5 While LEEs clearly result in strand breaks in DNA, it is well known from pulse radiolysis that in aqueous environment solvated electrons do not cause strand breaks on attachment to DNA.^6,7 To add insight to these experiments,^{4 - 7} a number of theoretical efforts have been reported in the recent years and have added some understanding of potential underlying mechanisms of strand break formation and base release.^{8 - 15}

Based on Hartree-Fock (HF) level of theory, Simons and coworkers⁸ proposed a mechanism for the SSB formation in which an excess electron primarily attaches into the π* molecular orbital (MO) of the DNA base (shape resonance) and subsequently transferred to the C-O bond region (joining the sugar-phosphate groups) during the bond dissociation processes. Using B3LYP/DZP++ level of theory Gu et al.⁹ also supported a similar mechanism⁸ for SSB formation. A second mechanism of SSB formation was proposed by Li et al.¹² in which an excess electron directly attaches to the sugar phosphate backbone using a sugar-phosphate-sugar (S-P-S) model and initiates the bond dissociation processes having a barrier height of ca. 10 kcal/mol. In their model, the initial state was found to be a dipole bond state.¹² More recently, using B3LYP/6-31G* level of theory the C_5′-O_5′ bond breaking was studied¹³ in vertical (transient negative ion (TNI) at the optimized geometry of the neutral) and adiabatic states of 5′-dTMPH radical anion as a simple model of DNA. This calculation found a lower barrier for C-O bond breaking (ca. 9 kcal/mol) along a vertical path than for the adiabatic path (ca. 15 kcal/mol). In this case, the excess electron is located on the DNA base, in a valence bound state. Further, in a very recent study,¹⁴ we calculated the potential energy surfaces (PES) of C_5′-O_5′ bond cleavage for the excited states of 5′-dTMPH radical anion in their vertical (mimicking TNI formation) and adiabatic states in the gas phase using BHandHLYP/6-31G* level of theory.

An important conceptual base of this present work and our previous work¹⁴ is that the interaction of LEE with a molecule creates resonances which are equivalent to the vertical excited states of the electron adduct of the parent molecule. In our previous work,¹⁴ we calculated the excited states of TNIs of adenine, uracil, cytosine and thymine, as a test case, and found that the calculated transition energies were in good agreement to those experimentally observed shape resonance energies found from electron transmission spectroscopy (ETS) by Aflatooni et al.¹⁶ (see Table T1 in supporting information). Further, we found that below 2 eV there is a dissociative σ* state localized on the PO₄group of 5′-dTMPH radical anion that leads to a facile strand break formation (see Table T1 and Figure X1 in the supporting information). Therefore, our earlier¹⁴ work clearly demonstrated that excited state calculations are useful in the elucidation of the role of low energy electrons in DNA strand break formation. In this work we carry this method forward to include the treatment of the influence of the aqueous environment on these states so important to LEE induced reactions.

We note that in dealing with the valence bound state of anions, the choice of the basis set is very important in these calculations. Since such excitations/resonances, in the gas phase, are likely in the continuum, we employ compact basis set (6-31G*) to avoid the mixing of valence bound states with dipole bound states and the continuum.¹⁷ The use of compact basis sets (such as 6-31G*) to study resonances, TNIs and negative electron affinities of DNA bases is well documented in the literature.^14,17-19 However, we note that in solution the anion states are stabilized by solvation by several eV creating stable ground and excited states.

In this communication, we have investigated the excited states of 2′-deoxy-guanosine-3′,5′-diphosphate(3′,5′-dGDP), 2′-deoxyadenosine-3′,5′-diphosphate (3′,5′-dADP), 2′-deoxythymidine-3′,5′-diphosphate (3′,5′-dTDP) and 2′-deoxycytidine-3′,5′-diphosphate (3′,5′-dCDP) radical anions in their TNI and adiabatic states. The transition energies were calculated in the gas phase and in solution using time-dependent density functional theory (TD-DFT). We present the first theoretical study to show that while in gas phase these dissociative (σ*) states are accessible by LEEs, in solution these σ* states are blue-shifted towards the higher energy and are not accessible to LEEs with energies under 4 eV. The blue shifting of σ* states on solvation (relative to the gas phase) is not unusual. It is well known that anions on solvation are more stable energetically in comparison to the gas phase. Thus a higher detachment energy is needed in solution as compared to the gas phase. As a result, the photoelectron spectra (PES) of solvated anions have their peaks blue-shifted.²⁰

The geometries of 3′,5′-dGDP, 3′,5′-dADP, 3′,5′-dTDP and 3′,5′-dCDP in their neutral and radical anionic states, in gas phase and in the presence of 2 and 3 water molecules, were fully optimized using B3LYP method and 6-31G* basis set. In all the molecules, the negatively charged PO₄ groups were protonated and the C_5′- and C_3′- ends were terminated by the methyl groups. The effect of bulk water (ε = 78.34) on the hydrated structures were incorporated by the use of integral equation formalism-polarized continuum model (IEF-PCM). Considering the B3LYP/6-31G* optimized geometries, the lowest vertical π→π*, π→σ* excited states as well as core excitation of all the molecules were calculated using TD-BHandHLYP/6-31G* method in gas phase and in the presence of aqueous media. All the calculations were done using Gaussian 03 suite of programs²¹ and GaussView²² was used to plot the MOs. In recent years, TD-DFT is widely used as a routine to study the excited states of molecules in a variety of states.^{14, 23} However, as pointed out by Head-Gordon et al.^24a TD-DFT largely underestimates the long-range coulomb interactions in charge transfer excited states with hole and electron separation in an overall neutral molecule. Fortunately, the use of increased HF exchange (50% in BHandHLYP) is found to give a good description of charge transfer excited states.²⁴ In an encouraging very recent study by Félix and Voityuk,^23c the BHandHLYP computed excitation energies of stacked DNA bases in radical anionic states were found to be comparable to MS-PT2 (multistate formulation of CASPT2) computed excitation energies.

The B3LYP/6-31G* optimized geometries of 3′,5′-dGDP, 3′,5′-dADP, 3′,5′-dTDP and 3′,5′-dCDP radical anions in their gas phase and in the presence of water molecules are shown in Figures A1 and A2 in the supporting information. We found that our B3LYP/6-31G* optimized gas phase geometries are in close agreement with those calculated using B3LYP/DZP++ level of theory by Gu et al.²⁵

As pointed out above, the excited states of radical anions are of utmost importance to the understanding of LEE interactions with a molecule and it is the excitations of the TNIs (i.e., electron adducts to the optimized neutral molecule) that are most pertinent to LEE effects. In Figures 1 and V1 – V3 (see the Supporting information), we present the excited states of TNIs of 3′,5′-dADP, 3′,5′-dGDP, 3′,5′-dTDP and 3′,5′-dCDP in gas phase and in aqueous media (ε = 78.34). The vertical excited states of 3′,5′-dADP radical anions in gas phase and in the presence of aqueous media (ε = 78.34) are presented in Figures 2, respectively, while the excited states of 3′,5′-dGDP and 3′,5′-dTDP and 3′,5′-dCDP radical anions are presented in Figures A1-A3 (see the supporting information), respectively. From Figures 1, 2, A3 - A5 and V1 – V3, it is clearly evident that the singly occupied molecular orbital (SOMO) is of π-type in ground state and localized on the base representing valence bound nature as expected by ESR studies.¹ Using B3LY/DZP++ level of theory Gu et al.²⁵ also calculated the adiabatic electron affinities (AEAs) of 3′,5′-dADP, 3′,5′-dG^•−DP, 3′,5′-dCDP and 3′,5′-dTDP as 0.10, 0.24, 0.27 and 0.35 eV, respectively, however, the corresponding vertical electron affinities (VEA) were found to be 0.02, 0.14, 0.03 and 0.17 eV, respectively. The quite small VEA values of 3′,5′-dADP (0.02 eV) and 3′,5′-dCDP (0.03 eV) show that the excess electron is weakly bound with the parent (neutral) molecules. A plot of the SOMOs of 3′,5′-dADP^•−, 3′,5′-dCDP^•− and 3′,5′-dTDP^•− radical anions show a mixed valence bound and diffuse nature with molecular orbitals mainly localized on base and the phosphate groups of these molecules; however, 3′,5′-dG^•−DP^•− was characterized as typically dipole bound (see Figure 1 of ref. 25) by the authors.²⁵

Figure 1.

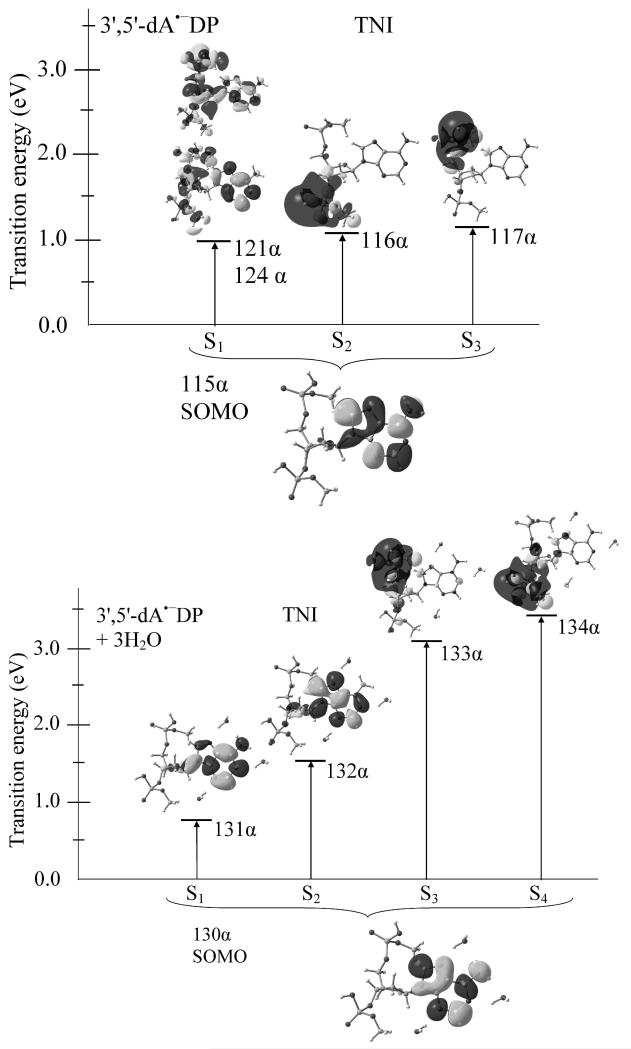
TD-BHandHLYP/6-31G* computed transition energies in TNI state of 3′,5′-dADP in gas phase (above) and aqueous solution (lower). The effect of bulk water solvent was considered using IEF-PCM model on the trihydrated 3′,5′-dA^•− DP system. Transition occurs from SOMO to different MOs (shape resonance) are shown. Transition energies are given in eV.

Figure 2.

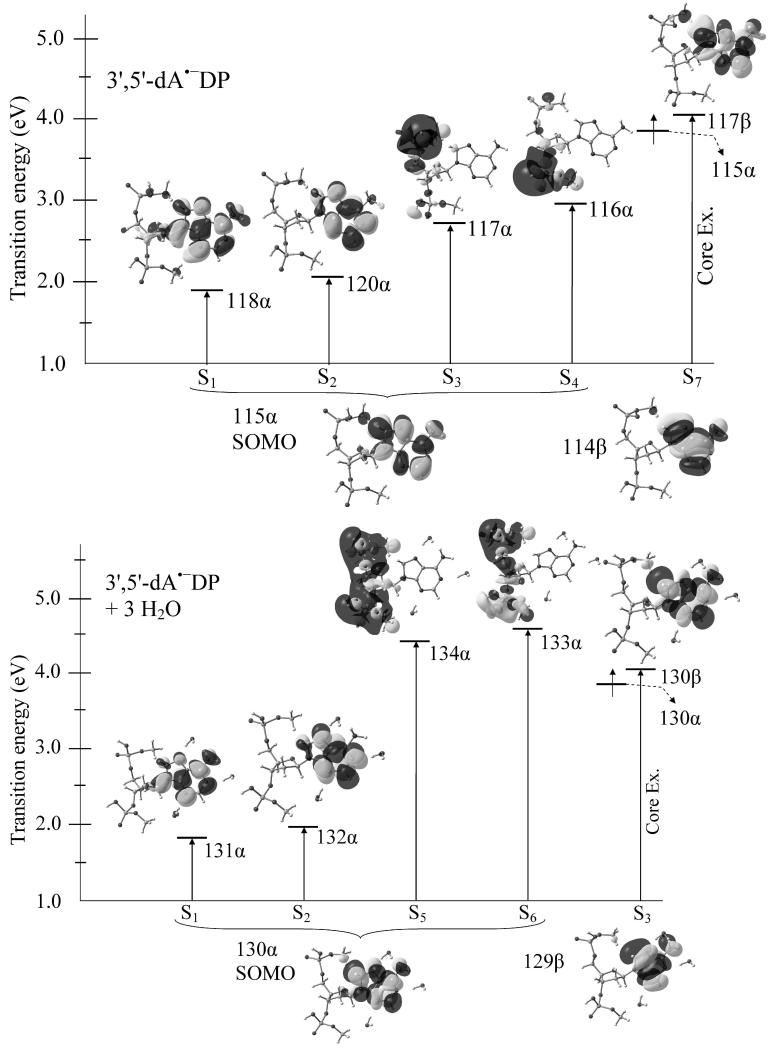
TD-BHandHLYP/6-31G* computed transition energies in an adiabatic state of 3′,5′-dA^•−DP in gas phase (above) and aqueous solution (lower). The effect of bulk water solvent was considered using IEF-PCM model on the trihydrated 3′,5′-dA^•−DP system. Transition occurs from SOMO to different MOs and from an inner shell MO to higher MO (core excitation) are shown. Transition energies are given in eV.

The BHandHLYP/6-31G* calculated excited states of TNIs of 3′,5′-dTDP, 3′,5′-dCDP, 3′,5′-dADP and 3′,5′-dGDP in gas phase predicted lowest two transitions (S₁ and S₂) as π→σ* for 3′,5′-dTDP, 3′,5′-dCDP and 3′,5′-dGDP while for 3′,5′-dADP these transitions are π→π* and π→σ* in nature (See Figures 1 and Figures V1 – V3 in supporting information). As a representative case, we presented the excited states of TNI of 3′,5′-dADP in gas phase and in solvation in Figure 1. In gas phase, the lowest three transitions of 3′,5′-dADP are π(A)→π(A)*, π(A)→σ(3′-PO₄)* and π(A)→σ(5′-PO₄)* in nature and occur at 0.99, 1.07 and 1.14 eV, respectively. Transition S₁ takes place from SOMO(π)→(121α and 124α) MOs having contributions ca. 25% and 50% (see Figure 1). The other two transitions S₂ and S₃ are singly dominant transition having contributions ca. 90% each and are localized on the 3′- and 5′- ends of the PO₄ group of 3′,5′-dADP. In comparison to the gas phase, the excited states of TNI of solvated (3′,5′-dADP + 3 H₂O) is quite different and we found that the lowest two transitions (S₁ and S₂) are π→π* in nature and have the transition energies 0.76 and 1.54 eV. Transitions S₃ and S₄ are π→σ* type and shifted towards high energy (blue shift) by ca. 2 eV to their corresponding gas phase transition energy values (see Figure 1). For 3′,5′-dTDP the three lowest transitions S1 – S3 are π(T)→σ(3′-PO₄)*, π(T)→σ(5′-PO₄)* and π(T)→π(T)* type and have the transition energies 1.18, 1.46 and 1.60 eV, respectively, (Figure V1 in supporting information). The excited state of 3′,5′-dCDP in TNI state has the transition energies S1(1.25), S2(1.66) and S3(1.77) and are π(C)→σ(5′-PO₄)*, π(C)→σ(3′-PO₄)* and π(C)→π(C)* in nature (see Figure V2). In the case of 3′,5′-dGDP the transitions are π(G)→σ(3′-PO₄)*, π(G)→σ(5′-PO₄)* and π(G)→π(G)* and have very low transition energies as 0.35, 0.46 and 1.11 eV. Except 3′,5′-dGDP, the π→σ* transitions of 3′,5′-dADP, 3′,5′-dTDP and 3′,5′-dCDP lie in the range 1.1 – 1.7 eV and the π→π* transitions occur between 1.0 – 1.8 eV, respectively. Using ETS aflatooni et al.¹⁶ estimated the π* resonances of DNA bases (thymine (T), cytosine (C), and adenine (A)) and found that π₂* shape resonance in these bases lie at 1.71(T), 1.53(C) and1.36(A) eV, respectively. Our calculated lowest π→π* transition energies (corresponding the π₂* shape resonance) 1.60 (S3, 3′,5′-dTDP), 1.77 (S3, 3′,5′-dCDP) and 0.99 (S1, 3′,5′-dADP) are in good agreement with the ETS values.¹⁶ Recently, Burrow et. al.²⁶ also studied the resonances of several phosphate containing molecules using ETS and they found that the resonances localized on the PO₄ group are σ* in nature and this is supported from our present (see Figures 1, 2, V1 - V4 and A1 - A4) and earlier studies.¹⁴ Further, our calculated π→σ* transition energies, lying between 1.1 – 1.7 eV, are, also, in good agreement with our theoretically calculated σ* resonance energies of the PO₄ group in 5′-dTMPH radical anion.^13,14 However, our calculated π→σ* transition energies (1.1 – 1.7 eV) are about 1 eV lower than those reported by Burrow et al.²⁶ which are in the range 1.9 – 2.8 eV. This difference is not unexpected since we consider different structures than Burrow et al.²⁶ Interestingly, we found that in the presence of solvation these σ* states in all the molecules shifted towards the higher energy by ca. 2 eV in comparison to their corresponding gas phase excitation energy values. However, the transition energies of the π* states are almost unaffected under solvation (see Figures 1 and V1 – V3 in the supporting information).

The excited states of 3′,5′-dA^•−DP in adiabatic state in gas phase and in solvation are shown in Figure 2. For 3′,5′-dA^•−DP (in gas phase), BHandHLYP predicts four lowest transitions as π(A)→π(A)*, π(A)→π(A)*, π(A)→σ(5′-PO₄)* and π(A)→σ(3′-PO₄)* and have transition energies 1.89, 2.05, 2.71 and 2.97 eV, respectively. The next core excited state (S₇) having transition energy 4.07 eV is π(A)→π(A)* in nature and occurs from the inner shell electron having β-spin (see Figure 2). Also, we found that these transitions (S₁ - S₄, and S₇) involve dominant single excitations having ~77%, ~81%, ~81%, ~81% and ~72% contributions, respectively. Further, the excited states of fully solvated (3′,5′-dA^•−DP + 3H₂O) (shown in Figure 2) has first three lowest transitions (S₁ – S₃) as π(A)→π(A)* in nature and transition S₃ corresponds to the core excitation. Transitions (S₅ and S₆) are π(A)→σ(5′-PO₄)* and π(A)→σ(3′-PO₄)* and localized on both of the phosphate groups. The corresponding transition energies (S₁ - S₃, S₅ and S₆) are 1.82, 1.97, 4.08, 4.45 and 4.60 eV, respectively. Transitions S₁ and S₂ are almost degenerate (having a difference of 0.15 eV) and thus have almost equal contributions (> 52%) in each transitions. Similarly, the excited states of 3′,5′-dG^•−DP, 3′,5′-dT^•−DP and 3′,5′-dC^•−DP in their adiabatic states are shown in Figures A3 – A5 in the supporting information.

From Figures (1, 2, A3 – A5 and V1 – V4) we see that in gas phase π→σ* states, localized on PO₄ group at 5′- and 3′-ends, lie below 4 eV, in all the nucleotides in their TNI and adiabatic radical anion states. The presence of these σ*-states are of interest because of their dissociative nature, as already been established in the literature²⁷ and recently shown by us¹⁴ its role to cause strand break formation in 5′-dTMPH radical anion as a model of DNA. It is, also, found in all nucleotides investigated here that the π→σ(5′-PO₄)* and π→σ(3′-PO₄)* states have almost similar transition energies (the largest difference is ~0.4 eV). It is expected that the LEE created excited state of the TNI in these σ(PO₄)* states would undergo facile cleavage of the C - O bond leading to strand cleavage as predicted by theoretical work^9,12,13 and found to occur in experimental work by Sanche and co-workers.²⁸

The calculated π→σ* excited states in all the nucleotides are blue-shifted on solvation by ca. 2 eV over the corresponding gas phase transition energy values (see Figures 1, 2, A3 – A6 and V1 – V4). This variability of the transition energies for π→ σ* states with solvation are in contrast to the π→π* and core excited states that are essentially invariant with solvation in both TNI and adiabatic states.

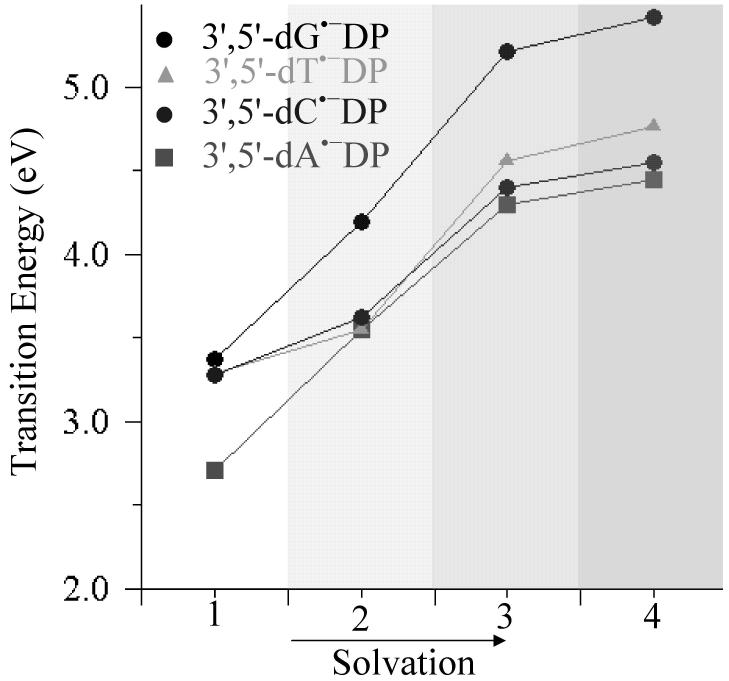
In Figures 3, A7 and A8 (in supporting information), we show the variation of π→σ* transition energies, located on the MOs localized on phosphates at 5′- and 3′-ends of the nucleotides, (1) in the gas phase, with (2) three discrete water molecules, and (3,4) bulk solvent with at two dielectric values ε = 7 and ε = 78.4 in their TNI and adiabatic states. From Figures 3, A7 and A8, it is clear that transition energies of π→σ* states increase with increasing solvation and become less accessible to LEEs with energies < 4 eV.

Figure 3.

Variation of transition energies (eV) of the π→σ(5′-PO₄)* excited state of nucleotides in adiabatic state with increasing solvation. Different solvation levels labeled on X-axis are: 1- gas phase, 2- three discrete water molecules , 3- three waters and a continuous dielectric (ε = 7.0) and 4- three waters and a continuous dielectric (ε = 78.4).

In summary, the present study confirms previous work^4b which reported that in the gas phase LEEs with energies < 4 eV have accessible PO₄ (σ*) states which lead to strand break formation through a dissociative electron attachment (DEA) mechanism.^13,14 The σ* states for TNIs are found to be at 1.1 - 1.7 eV (in gas phase) which is in close agreement with experimental threshold value of 0.8 ± 0.3 eV for creating a SSB.^4b However, most importantly this study shows that in solution these dissociative (σ*) states increase in energy by several eVs. This clearly suggests that solvation of DNA would reduce the direct cleavage of DNA by LEEs in the energy range 0 to 4 eV. This suggests that the sensitivity of living systems to LEE would be less that expected from work on model systems with low levels of hydration.