Organization of the Macaque Extrastriate Visual Cortex Re-Examined Using the Principle of Spatial Continuity of Function

T N Aflalo; MSA Graziano

doi:10.1152/jn.00795.2010

. 2010 Nov 10;105(1):305–320. doi: 10.1152/jn.00795.2010

Organization of the Macaque Extrastriate Visual Cortex Re-Examined Using the Principle of Spatial Continuity of Function

T N Aflalo ¹, MSA Graziano ^1,^✉

PMCID: PMC3023372 PMID: 21068269

Abstract

How is the macaque monkey extrastriate cortex organized? Is vision divisible into separate tasks, such as object recognition and spatial processing, each emphasized in a different anatomical stream? If so, how many streams exist? What are the hierarchical relationships among areas? The present study approached the organization of the extrastriate cortex in a novel manner. A principled relationship exists between cortical function and cortical topography. Similar functions tend to be located near each other, within the constraints of mapping a highly dimensional space of functions onto the two-dimensional space of the cortex. We used this principle to re-examine the functional organization of the extrastriate cortex given current knowledge about its topographic organization. The goal of the study was to obtain a model of the functional relationships among the visual areas, including the number of functional streams into which they are grouped, the pattern of informational overlap among the streams, and the hierarchical relationships among areas. To test each functional description, we mapped it to a model cortex according to the principle of optimal continuity and assessed whether it accurately reconstructed a version of the extrastriate topography. Of the models tested, the one that best reconstructed the topography included four functional streams rather than two, six levels of hierarchy per stream, and a specific pattern of informational overlap among streams and areas. A specific mixture of functions was predicted for each visual area. This description matched findings in the physiological literature, and provided predictions of functional relationships that have yet to be tested physiologically.

INTRODUCTION

The cerebral cortex is organized such that similar functions are generally spatially near each other. A possible adaptive advantage of this “like attracts like” organization is that it minimizes wiring length between interconnected neurons (Cherniak 1994; Kaas 2000; Klyachko and Stevens 2003; Van Essen 1997; Young 1992). The principle of maximum functional continuity can explain features of cortical organization at the largest and smallest scales. At the largest scale, function is clumped into cortical sectors devoted mainly to vision, audition, movement, and other major information categories. At a slightly smaller scale, within the visual modality, cortical areas may be clustered together by similar function (Kolster et al. 2009; Wandell et al. 2007). Visual areas are also clustered together according to the density of their anatomical interconnectivity (Young 1992). At an even smaller scale, within a cortical area, the principle of functional continuity can explain topography such as retinotopic or somatotopic maps (Kaas and Catania 2002; Kohonen 1982; O'Leary and McLaughlin 2005; Saarinen and Kohonen 1985). At the smallest scale of cortical organization, the columnar level, the complex pinwheel arrangement of orientation and ocular dominance columns in V1 is apparently an optimal solution to the problem of local continuity of function (Chklovskii 2000; Durbin and Mitchison 1990; Koulakov and Chklovskii 2001). Although most studies on the optimal continuity principle of organization relate to the visual system, a similar organizational principle can be demonstrated in other cortical systems. Recently the overarching topographic arrangement of the primary motor cortex, premotor cortex, supplementary motor cortex, frontal eye field, and supplementary eye field was successfully reconstructed by reducing a macaque monkey's highly dimensional movement repertoire onto the cortical surface following the principle of maximum functional continuity (Aflalo and Graziano 2006; Graziano and Aflalo 2007). In all of the cases summarized in the preceding text, the simple underlying principle of functional continuity can explain complex spatial arrangements across the cortical surface.

Most of the studies described in the preceding text were focused on testing the validity of the principle of optimal cortical organization, for example testing whether cortical areas really are organized in a manner that minimizes connectional length (Klyachko and Stevens 2003) or testing whether functional properties really are arranged spatially in a manner that optimizes functional continuity (Durbin and Mitchison 1990). In the present study, we provisionally accepted the principle as correct and asked whether it could be used to deduce new information about cortical function. The principle that functions are arranged to optimize spatial continuity provides a quantitative relationship between function and topography. In many regions of the cortex, much more is known about the topographic organization of cortical areas than about their functional properties. Can the principle of functional continuity be used as a tool to deduce information about functions, given information about topography?

The topography of the macaque monkey extrastriate visual cortex has been intensively studied. Although there is still debate about the exact boundaries between areas and the best way to subdivide areas, the basic layout of areas across the cortex is understood (e.g., Baylis et al. 1987; Boussaoud et al. 1990; Desimone and Ungerleider 1989; Felleman and Van Essen 1991; Galletti et al. 1999, 2005; Lewis and Van Essen 2000; Lyon and Kaas 2002). Much less well established is the functional relationships among areas. Is vision divided into several major information domains, such as object recognition and spatial processing, that form hierarchical streams? If so, just how many streams and substreams exist? What is the relative hierarchical ranking of visual areas within and across streams? What is the informational overlap between streams? Does TEO contain any motion information, in addition to object identity information? Just how much shape information is present in the intraparietal sulcus?

These questions of the distribution of information across the visual cortex lend themselves to an analysis of topography. If information is distributed across cortex in a manner that optimizes cortical continuity, then the relative locations of areas on cortex provides a clue to their functional relationships. For example, areas MT and MST both emphasize motion information and are topographically adjacent to each other. This adjacency is an obvious example of the continuity of function across the cortical surface. It adheres to the general principle that similar functions are arranged near each other. Given a sophisticated enough analytical machinery, can any inferences be drawn about the amount of motion information present in other areas based on their spatial relationship to MT and MST? Can other aspects of functional organization be inferred from the extrastriate topography?

In the present study, we used an analytical approach to infer functional relationships among areas based on their topographic relationships. In this approach, one begins with a specific hypothesis about the functional relationships among cortical areas. Using standard mathematical tools, the hypothesized set of functions is arranged onto a model of the cortex in a manner that optimizes spatial continuity. If we have a correct description of the functional relationships among areas, then the resulting map should accurately reconstruct the target cortical topography. If, however, our description of the functional relationships among areas is faulty or incomplete, then when we mathematically lay them onto the cortex according to the principle of optimal continuity, we should arrive at a wrong or incomplete topography. With this method as a guide, it is possible to test hypotheses about the functional relationships among visual areas, rejecting some hypotheses, fine-tuning others, until we arrive at one that passes the test—a description of the functional similarities and dissimilarities among extrastriate visual areas that is consistent with their topographic relationships.

The goal of the present study was to find the correct number of processing streams into which visual areas are grouped, the correct pattern of informational overlap among streams, and the correct hierarchical ordering of areas, such that the principle of functional continuity would reproduce a target version of the topographic arrangement of visual areas. To accomplish this goal, we tested a series of increasingly refined models including a two-stream model, a four-stream model, and an optimized four-stream model. Each model was tested by arranging it onto a three-dimensional model of the folded extrastriate visual cortex according to the principle of optimal continuity. Through a systematic search, we obtained a model of the functional relationships among visual areas that successfully recreated the topographic relationships among visual areas. The final outcome of the study, the optimized four-stream model, provided a detailed, quantitative description of the informational relationships among 15 principle visual areas. This derived information matched physiological findings on the properties of visual areas and also provided specific predictions of functional properties that have yet to be tested physiologically.

METHODS

This study tested three models of the macaque extrastriate visual cortex: a two-stream model, a four-stream model, and an optimized four-stream model. For each model, the method combined three components. First, we used an information structure that represented the functional relationships among visual areas (including the number of functional streams into which the areas were grouped, the informational overlap among streams, and the hierarchical relationships among visual areas). Second we used a model cortical sheet that resembled the macaque extrastriate visual cortex. Third, we used an algorithm for mapping the information structure onto the model cortex in a manner that optimized nearest neighbor similarity. The model cortical sheet and the mapping algorithm are described in the following text. For clarity of presentation, the three information structures are described in the results section.

Model cortical sheet

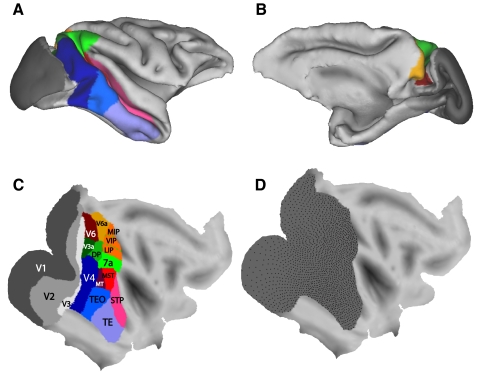
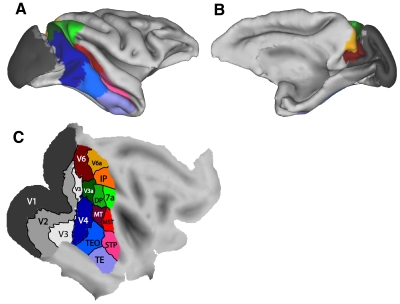
To model the visual cortex, we used a three-dimensional (3-D) model of the cortical sheet (based on the surface half-way through the cortical thickness), from structural MRI data of a macaque monkey, using the Caret software from the work of Van Essen and colleagues (monkey F99, right hemisphere reconstruction, from http://brainvis.wustl.edu/wiki/index.php/Caret:About) (see also Van Essen et al. 2001). This model cortical sheet is shown in Fig. 1. Figure 1, A and B, shows views in which the sulci are in their normal folded configuration. Figure 1C shows the cortical sheet flattened using the Caret software with a large cut through the center of V1.

Fig. 1. — The macaque visual cortex. A: a lateral view of the folded cortex based on the anatomical images and Caret software of Van Essen and colleagues (2001). The surface is taken from the depth half-way through the cortical thickness. Some of the main visual areas are displayed in color and labeled. B: a medial view of the same cortical model as in *A. C*: a flattened version of the same model shown in A and *B. D*: the down-sampled set of 1,892 nodes, distributed across the visual cortex, used in the functional mapping algorithm.

Figure 1 shows one possible rendering of some of the known visual areas (Baylis et al. 1987; Boussaoud et al. 1990; Desimone and Ungerleider 1989; Felleman and Van Essen 1991; Galletti et al. 1999, 2005; Lewis and Van Essen 2000; Lyon and Kaas 2002). To construct this summary map, for ventral areas, we relied more heavily on Desimone and Ungerleider (1989), and for medial areas, we relied more heavily on the recent detailed mapping work of Galletti et al. (1999, 2005). This summary map therefore captures at least the general outlines of the complex mosaic of extrastriate cortex. We acknowledge that there are differences of opinion about the borders of areas and the subdivision of areas into smaller areas. In the discussion, we consider how additional divisions of cortex, not shown in Fig. 1, might relate to the present study. The areas shown in Fig. 1 represent the target topography that we attempted to re-construct using the self-organizing map techniques.

The cortical surface was defined in the Caret software by the spatial location of 35,946 nodes. In the present study, this full set of nodes was used for all spatial transformations of the model cortex, including flattening or inflating the cortex and calculating distances across the cortex. However, for some of the computations in the Kohonen algorithm described in the following text, the total number of nodes was prohibitively high. We therefore created a second rendering of the visual cortical sheet at a down-sampled number of nodes. The down-sampling was performed as follows. The cortex was first inflated into a sphere using the Caret software. The sphere was then populated by 5,000 equally spaced nodes. The region of the striate and extrastriate cortex contained 1,892 nodes. This array of 1,892 nodes representing the visual cortex is displayed on the flat map in Fig. 1D. The Kohonen algorithm, described in the following text, rendered a multidimensional information space onto this down-sampled set of 1,892 nodes.

Kohonen mapping algorithm

We used the Kohonen method (Kohonen 2001) to arrange the multidimensional information structure onto the 1,892 nodes of the model visual cortical sheet. The Kohenen network is a standard tool for solving the problem of dimensionality reduction or the problem of representing a multidimensional space on a lower dimensional space such that neighbor relationships are optimized. The technique is well established, heavily used in information technology applications, and instructions for implementing it are available in book form (Kohonen 2001) and on-line (http://www.cis.hut.fi/projects/somtoolbox/). Here we first describe the general concept of the Kohonen method and then provide details on those aspects of the technique for which there was more than one possible way to implement the method, requiring us to choose the approach that suited our particular application.

In essence, the Kohonen method takes an N-dimensional data set and arranges it onto a 2-D array of nodes. Three mathematical objects are defined. First, the information structure to be flattened is a set of data points arranged in an N-dimensional space. Each data point in that data set is called an input vector. Second, the node array is the 2-D arrangement of nodes, in this case, the model cortex, onto which the information structure is to be flattened. Third, each node in the node array has a codebook vector. The codebook vector is N-dimensional and indicates the part of the information structure that is represented by that node. The Kohonen algorithm uses an iterative series of steps to alter the codebook vectors of all nodes until the node array contains a representation of the information structure that is optimized for topographic smoothness.

As a simple example, consider the case in which the 2-D space of the retina is mapped onto the 2-D space of the cortex. The information structure consists of a set of points sampled across the retina. The Kohonen algorithm can arrange these points onto the cortical sheet such that points near each other on the retina are represented near each other on cortex. The emergent result is a smooth, topographic map of the retina on the cortex (e.g., Kohonen 1982). The map is topologically simple and smooth because the dimensionality of the retina matches the dimensionality of the cortex. This example helps to illustrate the underlying concept of the Kohonen method, but the real usefulness of the method arises in applications for which the information structure is more complex and therefore its optimal mapping onto the cortex is less intuitively obvious.

As another example, consider the case in which the information structure consists of data points clustered into five categories. When mapping the information structure onto the cortical sheet, the Kohonen algorithm will tend to arrange the data points such that each category forms a distinct area on the cortex. This clustering of information into areas maximizes the similarity of neighboring cortical points within an area while minimizing the discontinuous border between neighboring zones. The exact size and shape of these areas on the cortex will depend on factors such as the relative number of data points in each category and the informational relationships among categories. This issue of the size and shape of cortical areas rendered by the Kohonen method is discussed again throughout results.

When rendering a complicated, multidimensional, multicategory information space onto the cortical surface, the optimization problem becomes so complex that the result can be an apparent chaos of areas, something like a Jackson Pollock painting, with no easy intuitive explanation for why a particular area may have a particular location or shape. Such was the case, for example, when rendering the multidimensional space of a macaque monkey's movement repertoire onto the cortical surface to reconstruct the complex, idiosyncratic topography of the primary, premotor, and supplementary motor cortex (Graziano and Aflalo 2007). Yet even in that case, the optimality principle seemed to reconstruct the known cortical topography.

In essence, the Kohonen method involves local and iterative reorganization that follows the principle of optimizing continuity. As a result, a global map emerges. The map may have a variety of topographic properties and symmetries, but the true organizational rule is a local one (continuity), not a global one. It is therefore often a matter of simplification or approximation to try to determine why any particular large-scale feature of the map emerged. Why did a visual area map to this instead of that location, and why did it acquire this shape instead of that shape? It is usually possible to speculate as to why the local principle of continuity would result in particular, large-scale map features, but such explanations are usually ad hoc and difficult to confirm.

The Kohonen algorithm that we employed in the present study was the batch computation variant of the self-organizing map. In the batch computation algorithm, the entire set of input vectors is employed during each update step of the nodes. We used 300 update steps. In initial tests, we used a range from 100 to 3,000 update steps and found that 300 was sufficient to cause the map topography to converge.

A defining feature of the self-organizing map is that as each node of the map updates, it also updates its surrounding nodes. The extent to which nodes influence each other is given by a neighborhood function of which several forms can be applied. Following one standard method, we used a Gaussian neighborhood function that takes the form $h_{c, j} = \exp (\frac{- d^{2} (c, i)}{2 σ^{2} (t)})$ where c and i specify two nodes, d(c,i) specifies the physical distance between the two nodes in the array, and σ(t) specifies the time-dependent SD of the Gaussian (where time during the optimization process is measured in update steps). The time dependence of σ allows for a large initial neighborhood for the purposes of a global reordering of the network. The neighborhood then shrinks with time to allow for convergence on local smoothness. In our case, the initial value of sigma was set to half the height of the map, following standard procedures. The height in tangential distance across the model of the cortical map was 70 mm, thus the initial neighborhood width was 35 mm. The sigma then fell off linearly with each iteration of the algorithm to a final value of 2 mm of cortical distance.

In calculating the neighborhood function, the distances between nodes was defined as the geodesic distance across the curved cortical surface not the straight-line distance through the cortical volume or the distance across the flattened map. The algorithm therefore optimized 2-D smoothness across the curved cortical surface.

Because the Kohonen algorithm begins with random variations seeded on the node array, repeated runs of the algorithm may produce slightly different map results. In testing each version of the information structure, we ran the algorithm ≥15 times and determined that the result was similar each time. The results were therefore robust in the face of initialization variance.

RESULTS

In the present study, we modeled the informational relationships among visual areas. Each attempted model was tested by flattening it onto the cortical sheet and asking whether it recreated the target extrastriate topography shown in Fig. 1. The first attempt was a two-stream model, the second attempt was a four-stream model, and the final attempt involved systematically optimizing the four-stream model until it reproduced the target topography.

The logic of the study was to use the target topography shown in Fig. 1 as an empirically derived data set and to fit the model to the data set. It should not be a surprise that a successful model can be obtained. By optimizing the parameters of the model, it should be possible to find a fit to the data. The purpose of the study was not merely to demonstrate that a fit could be obtained but to determine the specific parameters of the model needed to obtain that fit. How many hierarchical streams are needed in the model? How much informational overlap must there be between streams? What is the specific hierarchical ranking of visual areas necessary to fit the data set? All of this information can potentially be obtained by fitting the model to the data set. The iterative process of fitting the model to the topographic data set is described in the following sections.

Two-stream model

Ungerleider and Mishkin (1982) proposed an organizing principle for the mosaic of extrastriate areas. In their scheme, from a common starting point in the early visual areas, two visual streams emerge. A ventral stream emphasizes object recognition or “what” vision, and a dorsal stream emphasizes spatial processing or “where” vision. This scheme provided the springboard for our first model, the two-stream model.

The purpose of the two-stream model was to provide a first guess at the information structure that, when mapped onto the cortex, might result in the target topography shown in Fig. 1. As will be seen, the two-stream model did not succeed in recreating the topography, thereby suggesting that this initial model was too simple an account of the informational relationships among visual areas. The model reconstructed some aspects of the topography but failed to reconstruct other major features of the topography. By considering the ways in which this model succeeded and failed, we were able to build a four-stream model that was more successful at reconstructing the target topography.

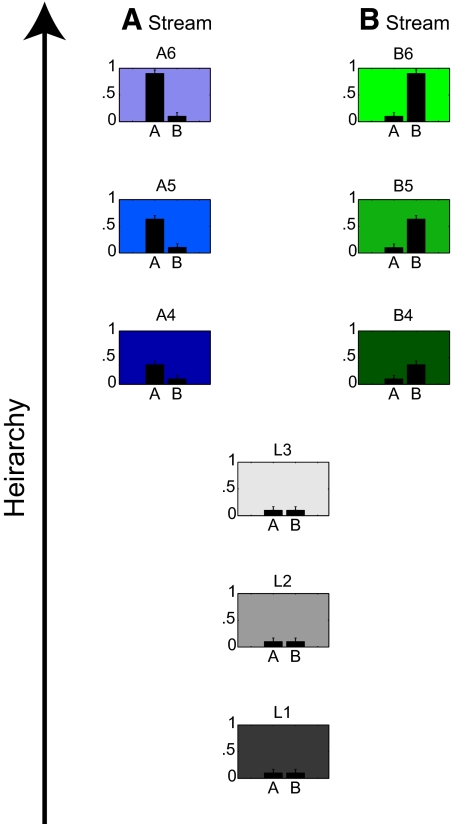
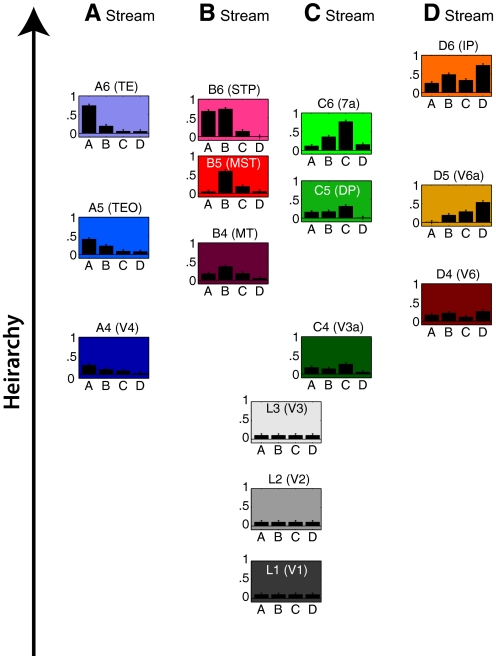
To embody the two-stream model, we constructed an information space defined by three dimensions: hierarchy, property A, and property B. Each dimension could vary from 0 to 1. This information space was populated by a data set that is shown in Fig. 2. Each graph in Fig. 2 represents a data cluster that was ultimately mapped to a region of the cortical sheet to form a visual area. Each data cluster was assigned a mean value for hierarchy (indicated by the height at which each graph is placed in Fig. 2) and mean values for properties A and B (indicated by the heights of the bars in each graph). Each data cluster contained 2,500 data points arranged in a spherical Gaussian distribution around its mean with a SD of 0.05. (The numerical values for the 2-stream model are provided in Table 1). The two streams overlapped in the first three levels of hierarchy (labeled L1–L3 in Fig. 2) and diverged in the subsequent three levels (labeled A stream and B stream). The A stream contained an increasing amount of property A with increasing hierarchy, whereas the B stream contained an increasing amount of property B.

Fig. 2. — The data set used for the 2-stream model. Each of the 9 data clusters is represented by a graph. The vertical position of the graph indicates the mean hierarchy value on a scale of 0 to 1. The 2 bars in the graph indicate the mean values of properties A and B on a scale of 0 to 1. The error bars indicate the SD (0.05) of the 2,500 points that comprised each data cluster. Numerical values are provided in Table 1. The 3 data clusters at the lowest hierarchical levels are labeled L1–L3. The higher hierarchical levels of the A stream are labeled A4–A6. The higher hierarchical levels of the B stream are labeled B4–B6.

Table 1.

Information structure that comprised the two-stream model

Cluster	n	Hierarchy	A	B
L1	2500	0.10	0.10	0.10
L2	2500	0.26	0.10	0.10
L3	2500	0.42	0.10	0.10
A4	2500	0.58	0.37	0.10
A5	2500	0.74	0.64	0.10
A6	2500	0.90	0.90	0.10
B4	2500	0.58	0.10	0.37
B5	2500	0.74	0.10	0.64
B6	2500	0.90	0.10	0.90

Open in a new tab

The same data set is shown graphically in Fig. 2. The data set consisted of 9 data clusters. The three data clusters at the lowest hierarchical levels are labeled L1–L3. The higher hierarchical levels of the A stream are labeled A4–A6. The higher hierarchical levels of the B stream are labeled B4–B6. The table indicates the number of data points (n) within each data cluster and the mean location of each data cluster in three dimensions (hierarchy and dimensions A and B). Each dimension could range from 0 to 1. Each data cluster was distributed around its mean location in a Gaussian manner with a SD of 0.05.

One could think of the A stream as the what stream and the B stream as the where stream. However, the specific type of information represented by A or B is actually irrelevant to the present model. The only relevant information is relational. The fact that the two streams overlap in information space at low hierarchical levels and diverge progressively at higher hierarchical levels is the critical information. The reason is that only relational information affects how the data clusters are projected onto the cortical sheet. According to the principle of optimal spatial continuity, if two data clusters are near each other in information space, then they should be mapped near each other on cortex.

In mapping this information structure onto the cortical sheet, the difficulty of rotations and reflections must be solved. Even if the Kohonen algorithm finds the correct map, the map might be flipped or rotated with respect to the cortex. To anchor the map, we fixed the location of the first hierarchical level in the following manner. The nodes within the known anatomical location of V1 were initialized at the lowest hierarchy value. The part of the data set that contained low hierarchy was therefore naturally mapped by the Kohonen algorithm to this anatomical location. The remainder of the cortical map was initialized with random values. For this reason, the model tested the organization of the extrastriate visual cortex only given a predefined V1. Without this anchoring, visual functions might be expected to coalesce in the correct relative positions but not in the correct orientation with respect to the cortical sheet. The map was therefore constrained in three ways. First, the physical structure of the cortical sheet was defined. Second, the location of V1 was defined. Third, the Kohonen method sought an optimization of continuity. From these constraints, the global map emerged.

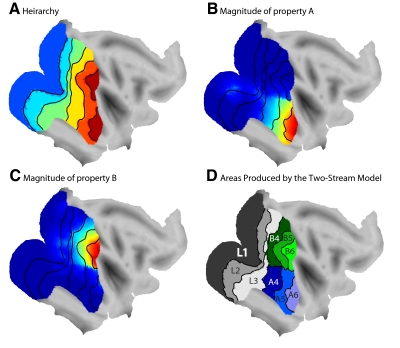
Figure 3 shows the result of mapping the data set onto the cortical surface. In Fig. 3A, different hierarchical levels are indicated in different colors. The first hierarchical level is of course an exact match to V1 because it was initialized in that location. The subsequent hierarchical levels show a spatial organization in some ways similar to the macaque visual cortex. Hierarchy is arranged in a set of bands progressing to higher levels in more anterior cortex. The second and third hierarchical levels show a characteristic pinching in the middle typical of the actual macaque monkey maps. The highest hierarchical level is divided between the temporal lobe and the parietal lobe.

The reason why hierarchy is mapped in this posterior-to-anterior manner is because low hierarchy was initialized to the posterior side of the map, and the optimization of continuity caused hierarchy to coalesce in a sequential manner such that similar hierarchical values were as physically near each other as possible. The result is a general progression of hierarchy from posterior to anterior cortex. There is nothing surprising about this initial result; it is merely a precise, mathematical demonstration of the principle of continuity.

It is difficult to trace back the specific reason for the pinching in the middle of the second and third hierarchical levels. When using the Kohonen method, the map self-organizes on the basis of local interactions, following the rule of optimal continuity. A large scale topography emerges, and the reasons for the emergent results are sometimes a matter of conjecture. In a simple case, with no cortical curvature and a perfectly square model cortex, on grounds of symmetry, one would expect the hierarchy bands to be straight and not pinched in the middle. The fact that they are pinched in the middle suggests that something about the curvature of the cortex, or the irregular outline of the cortical model, caused the hierarchy bands to obtain an irregular shape. It is an interesting result that the self-organizing map, following the principle of optimal continuity of function, re-created the idiosyncratic shape of V2 and V3.

Figure 3B shows that the magnitude of property A is largest in the ventral anterior region of the map, in the temporal lobe. Figure 3C shows that the magnitude of property B is largest in the dorsal anterior region of the map in the parietal lobe. The model therefore reconstructed the overall trend of two streams diverging and progressing into the temporal lobe and parietal lobe, respectively. Again this result is merely a mathematically precise demonstration of an intuitively obvious principle. If hierarchy is mapped in a posterior-to-anterior direction, then the other major variable, the division into functional streams, should be mapped in an orthogonal, dorsal-to-ventral manner to optimize cortical continuity.

In the two-stream model, properties A and B were defined in a symmetrical manner. The model had no basis for treating one differently from the other and therefore no basis for placing stream A in the ventral cortex and stream B in the dorsal cortex. As a result, when the mapping to the cortical sheet was repeated, on some runs, the locations were spatially reversed. This reversal was, in effect, only a reversal of labels. The spatial pattern was always the same as in Fig. 3 and was consistent across repeated runs of the algorithm.

Figure 3D shows a different way of displaying the results. Here the cortex was divided into areas showing where the nine different clusters in the original data set were mapped onto the cortex by the Kohonen algorithm. The result is a set of areas abutting each other. Some of the areas generated by the model appeared to match the locations of specific cortical areas in the macaque monkey cortex.

The data clusters labeled L1–L3 represented the lowest three levels of hierarchy and therefore corresponded to the three most posterior hierarchy bands. The fourth level of hierarchy was divided into two clusters, one emphasizing property A and one emphasizing property B. The resulting areas on the cortical sheet are labeled A4 and B4. The fifth and sixth level of hierarchy were similarly divided. For these reasons, the lowest three hierarchy levels formed single visual areas stretched in a ventral-to-dorsal manner, and the higher levels of hierarchy were divided into smaller, more tightly clustered areas.

In Fig. 3D, the higher hierarchical levels of the A stream, including A4–A6, approximately match the topographic locations of V4, TEO, and TE. The model therefore created an apparent functional stream marching down the ventral aspect of the cortex into the temporal lobe much like in the target topography shown in Fig. 1. The dorsal areas shown in Fig. 3D, however, do not show a specific correspondence between the model and the actual cortex. They show no obvious match to the real brain.

In summary, the first model incorporated two visual streams with six hierarchical levels each as a first guess at modeling the informational relationships among visual areas. The streams overlapped within the first three levels of hierarchy and diverged in information space at the higher levels of hierarchy. Despite the apparent simplicity of the model, it succeeded in capturing some of the overarching organization of the macaque extrastriate cortex. Hierarchy was mapped in a posterior-to-anterior direction, and the two streams were stacked in a dorsal-ventral direction such that one stream progressed into the temporal lobe and the other into the parietal lobe. The view that the visual system is divisible into two processing streams is a longstanding heuristic first introduced by Ungerleider and Mishkin (1982). The present two-stream model shows that this idea not only makes heuristic sense but when put to mathematical test, succeeds in explaining some of the main features of extrastriate organization. It is, however, an incomplete model. The map recreated by the model (Fig. 3D) is not accurate with respect to the dorsal areas. The following section describes how the model can be extended to improve its ability to reconstruct the known cortical topography.

Four-stream model

The major limitation of the two-stream, six-hierarchical-level model is that it produced too few visual areas to recreate the target topography. Only nine visual areas were defined in that model. How should new areas be added to the model to improve it? In the present framework of hierarchical streams, there are two ways to add areas to the model. One is to add more hierarchical levels to the two-stream model. The other way to add more areas is to add more streams, each stream with its own hierarchical sequence of areas.

In placing areas on the cortical surface, the principle of optimal continuity resulted in two patterns shown in Fig. 3. First, hierarchical levels were arranged in a posterior-to-anterior direction. Second, new streams, emphasizing distinct informational dimensions, were stacked in a more dorsal-ventral direction. By inspecting the results of the two-stream model (Fig. 3) and comparing them to the map from the macaque brain (Fig. 1), it becomes apparent that to properly account for the target topography the model does not need additional hierarchical levels. It does not need more areas crowded in the posterior-anterior direction. Instead it needs another two ranks of areas added in the dorsal-ventral direction. The addition of two more streams would add the correct number of areas in approximately the correct topographic relationships. There may be other distributions of information that can add areas in a dorsal-ventral direction. However, in the present study, we limited the model to conform to certain assumptions about visual streams: each visual stream is characterized by a stream-specific information category, and each stream contains a single hierarchical sequence of areas. Within a model of that type, on the basis of topographic considerations we were led to the hypothesis that the visual information mapped onto the cortex is roughly divisible into four major information types forming four functional streams.

The four-stream model is shown in Fig. 4. Each graph in Fig. 4 represents a data cluster. Each data cluster was assigned a mean value along five dimensions, each dimension ranging from 0 to 1. The dimensions included hierarchy (indicated by the height at which each graph is placed in Fig. 4) and the arbitrary dimensions A–D (indicated by the heights of the bars in each graph). (Numerical values for the 4-stream model are provided in Table 2.) In the four-stream model, the streams overlap in the first three levels of hierarchy (labeled L1–L3 in Fig. 4). They diverge in the subsequent three levels of hierarchy. In the A stream, property A increases with increasing hierarchy; in the B stream, property B increases with increasing hierarchy; and so on. This simple scheme represents a first pass at creating a four-stream description of the informational relationships among visual areas. This model of the visual information space was tested by rendering it onto the cortical sheet according to the principle of optimal continuity and assessing whether it succeeded in reconstructing the known extrastriate topography.

Table 2.

Information structure that comprised the four-stream model

Cluster	n	Hierarchy	A	B	C	D
L1	2500	0.10	0.10	0.10	0.10	0.10
L2	2500	0.26	0.10	0.10	0.10	0.10
L3	2500	0.42	0.10	0.10	0.10	0.10
A4	2500	0.58	0.37	0.10	0.10	0.10
A5	2500	0.74	0.64	0.10	0.10	0.10
A6	2500	0.90	0.90	0.10	0.10	0.10
B4	2500	0.58	0.10	0.37	0.10	0.10
B5	2500	0.74	0.10	0.64	0.10	0.10
B6	2500	0.90	0.10	0.90	0.10	0.10
C4	2500	0.58	0.10	0.10	0.37	0.10
C5	2500	0.74	0.10	0.10	0.64	0.10
C6	2500	0.90	0.10	0.10	0.90	0.10
D4	2500	0.58	0.10	0.10	0.10	0.37
D5	2500	0.74	0.10	0.10	0.10	0.64
D6	2500	0.90	0.10	0.10	0.10	0.90

Open in a new tab

The same data set is shown graphically in Fig. 4. The data set consisted of 15 data clusters. The three lowest hierarchical levels are labeled L1–L3. The higher hierarchical levels of the A stream are labeled A4–A6. Similar labeling indicates the data clusters within the B–D streams. The table shows the number of data points (n) within each data cluster and the mean location of each data cluster in five dimensions (hierarchy and dimensions A–D). Each dimension could range from 0 to 1. Each data cluster was distributed around its mean location in a Gaussian manner with a SD of 0.05.

The 15 graphs in Fig. 4 are color coded, and the regions of cortex to which they were mapped by the Kohonen algorithm are shown in the same color code in Fig. 5. Once again, just as for the two-stream model, the location of V1 was assigned the lowest hierarchy value, thereby pinning the orientation of the map. In this way the size, shape, and location of L1 in Fig. 5 was determined by the initialization. The remainder of the map was formed around this initial constraint. The map is the result of the Kohonen algorithm tiling the cortex with the data set shown in Fig. 4 while optimizing the similarity of neighboring points on the cortex.

As shown in Fig. 5, the four-stream model recreated some basic aspects of the extrastriate cortical topography, including three areas with low hierarchy stretching in medial-lateral bands, roughly corresponding to V1–V3, and a set of higher-order areas arranged in a mosaic anterior to the lower-order areas. The reasons for this arrangement are similar to the reasons described for the two-stream model. Hierarchy was pinned at a low value in V1, and therefore to optimize continuity, the Kohonen algorithm arranged hierarchy in an increasing sequence progressing from V1 outward to more anterior cortex. The other major variable, the division into four functional streams, was mapped in a roughly orthogonal direction, once again optimizing cortical continuity. These two trends account for the main organization shown in Fig. 5.

The topography produced by the four-stream model, however, had two main inaccuracies. By addressing these inaccuracies, we were able to construct the final, optimized model.

First, the areas produced by the four-stream model were not sized correctly. This error in size is most obvious in the case of L2 and L3 (see Fig. 5), which were too small when compared with V2 and V3 in the actual macaque brain. In the Kohonen method, the size of a cortical area is determined by many interacting influences. One major influence is the number of data points in the input data. The more data points that are mapped to an area of cortex, the larger that area of cortex will become although the relationship is not linear or simple. Other factors, such as the shape and size of surrounding cortical areas, will also play a role. The size error in Fig. 5 suggests that the number of data points in each data cluster needed to be adjusted. In particular, L2 and L3 needed to be represented by more data points relative to other areas, giving them a bigger representation on cortex. The reason why this undersizing of L2 and L3 is apparent in the four-stream model and not apparent in the two-stream model is that in the four-stream model, there were more visual areas competing for cortical space, and therefore each visual area covered a smaller region of cortex. The size of L1, in contrast, was relatively resistant to these modifications to the model because L1 was initialized to the topographic region of V1.

The second way in which the four-stream model failed is that because the four streams were defined in a symmetric manner, there was no reason for the Kohonen algorithm to place them on the cortex in any specific order. The order was arbitrary. In Fig. 5, the C stream was mapped to the most ventral locations, the A stream was mapped to a region just dorsal to the C stream, and so on. The reason for this lack of a coherent spatial ordering to the streams is that they did not have any specific informational relationships to each other. To cause the A stream to map consistently adjacent to the B stream would require some informational overlap between the two streams. For example, if the B stream contained an elevated value of property A in addition to property B, then it would contain some informational similarity to the A stream, and the two streams would tend to be mapped next to each other. The initial four-stream model was so schematic that it lacked any of these details of informational overlap among streams.

Both of these failures of the four-stream model suggest that the model needs extensive adjustment to its details to better account for the known cortical topography. Some areas may need to be represented by fewer or by more data points, the exact hierarchical relationships among areas may need to be adjusted, and each area may need to contain complex mixtures of properties A–D, allowing the areas to have idiosyncratic similarities and differences with respect to each other. The optimization of the four-stream model is described in the next section.

Optimized four-stream model

The goal of the present study was to find the information structure that when mapped onto the cortex, would correctly reconstruct the target cortical topography. Although the four-stream model shown in Fig. 4 captures some aspects of the target topography, the details are incorrect. The difficulty is essentially one of data fitting. We know the topography that the information structure should produce. To find the correct solution is therefore a matter of systematically adjusting the parameters of the information structure until it optimally fits the topography.

The information structure shown in Fig. 4 was improved through a series of iterations using a genetic search algorithm. The genetic search algorithm is described in the supplementary material.¹ The mean hierarchical value, and the mean values of dimensions A–D, were adjusted for each visual area. The number of data points representing each visual area was also adjusted. Each altered version of the information structure was used to produce a map of visual areas on the cortical surface, the map was correlated to the target map of visual areas (shown in Fig. 1), and the genetic algorithm adjusted the information structure between iterations to maximize the correlation value. In total, 360,000 versions of the information structure were tested in this iterative manner to obtain a best fit to the target topography shown in Fig. 1.

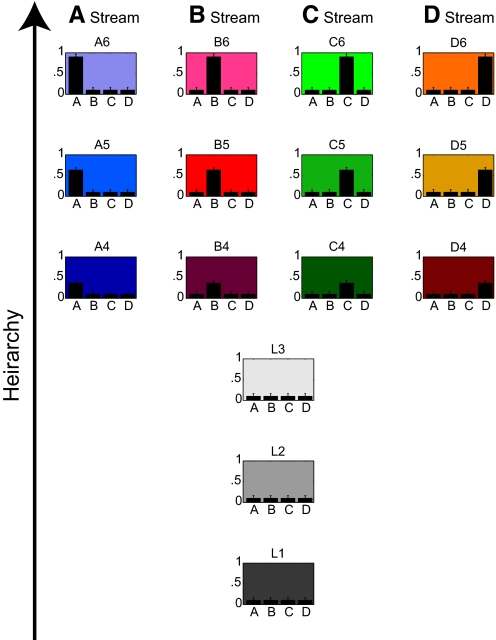
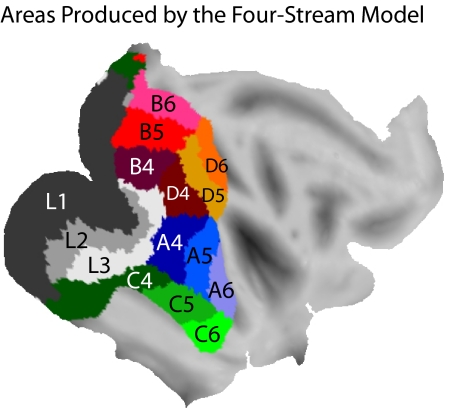
The best-fit solution (the information structure that, when mapped onto the cortex, best reconstructed the target topography) is shown in Fig. 6. Again each graph represents a data cluster. The vertical location of each graph represents the mean hierarchical value for that data cluster, with higher positions indicating higher values on a scale from 0 to 1. The four bars in each graph show the mean values for dimensions A–D. (The numerical values for this graph are provided in Table 3.)

Table 3.

Information structure that was obtained by a genetic search algorithm to form the optimized four-stream model

Cluster	Area	n	Hierarchy	A	B	C	D
L1	V1	3150	0.10	0.10	0.10	0.10	0.10
L2	V2	3203	0.21	0.10	0.10	0.10	0.10
L3	V3	1235	0.35	0.10	0.10	0.10	0.10
A4	V4	1315	0.45	0.23	0.10	0.13	0.03
A5	TEO	966	0.64	0.41	0.09	0.23	0.07
A6	TE	1251	0.84	0.74	0.05	0.19	0.05
B4	V3A	346	0.45	0.17	0.26	0.13	0.05
B5	DP	404	0.70	0.16	0.31	0.17	0.01
B6	7A	626	0.81	0.12	0.77	0.36	0.15
C4	MT	362	0.60	0.17	0.18	0.36	0.05
C5	MST	554	0.74	0.03	0.17	0.59	0.04
C6	STP	934	0.83	0.68	0.14	0.73	0.00
D4	V6	374	0.53	0.16	0.11	0.21	0.26
D5	V6A	464	0.69	0.01	0.29	0.19	0.53
D6	IP	693	0.90	0.23	0.33	0.48	0.73

Open in a new tab

The same data set is shown graphically in Fig. 6. The data set consisted of 15 data clusters. The three lowest hierarchical levels are labeled L1–L3. The higher hierarchical levels of the A stream are labeled A4– A6. Similar labeling indicates the data clusters within the B–D streams. When these data clusters were mapped to the cortical sheet, they occupied cortical locations that corresponded to known visual areas. These correspondences are indicated by the labels listed under “area.” The table shows the number of data points (n) within each data cluster and the mean location of each data cluster in five dimensions (hierarchy and dimensions A–D). Each dimension could range from 0 to 1. Each data cluster was distributed around its mean location in a Gaussian manner with a SD of 0.05.

Note the differences between the optimized model (Fig. 6) and the initial, unoptimized, four-stream model (Fig. 4). In the optimized model, the four streams are no longer informationally symmetric. Instead each stream has taken on its own complex, idiosyncratic mixture of properties. For example, one area in the B stream, B6, contains elevated values of property A in addition to property B. An area in the C stream, C6, contains elevated values of property B in addition to property C. The D stream contains elevated values of all four properties. Likewise, the hierarchical ordering of areas no longer forms six equal hierarchical steps. Instead each area has taken on its own, nuanced hierarchical value. The search algorithm converged on this particular quirky distribution of information across visual areas because when mapped to the cortex according to the principle of optimal continuity, it resulted in an accurate reconstruction of the target extrastriate topography. The optimal model shown in Fig. 6 therefore represents functional relationships among visual areas extracted by means of an analysis of topography.

An important aspect of the optimized model concerns the relative weighting of the dimensions. A dimension becomes less weighted if its range becomes smaller relative to other dimensions. It then has less impact on the final topography. In the extreme, a dimension in which the data have no variance at all would have no impact on the resulting map. Because we assigned all dimensions an initial range from 0 to 1, all dimensions were initially equally weighted. However, during the optimization, it is possible for the data distribution to be altered such that the data span a greater range in some dimensions and a lesser range in other dimensions, thereby effectively weighting the dimensions differently. Indeed this turned out to be the case. As indicated in Table 3, after optimization, the full range for hierarchy was ∼25% larger than the full range of any of the A–D dimensions. In this way, the optimization obtained a result in which hierarchy was weighted more heavily, and the individual dimensions A–D were weighted less, to optimally fit the topography. Dimensions A–D covered approximately the same range as each other and therefore were approximately equally weighted.

Figure 7 shows the resulting cortical map. It is nearly identical to the target topography based on the literature from the macaque visual cortex (see Fig. 1).

Fig. 7. — The topographic results of arranging the optimized 4-stream model on the cortical surface. The functional areas are labeled based on their topographic similarity to real areas in the macaque monkey brain. The optimized 4-stream model was able to reconstruct the organization of the macaque extrastriate visual cortex with great accuracy.

One potential concern with the optimized four-stream model is that it was, after all, optimized. The model was fit to the topography by means of an iterative search. Therefore how could the model fail to accurately reconstruct the topography? Is this merely an example of circularity? The result is not circular, once the purpose of the optimization is understood. Consider the case of an ordinary, linear curve fit. Suppose that one collects data on variable X and variable Y, and computes a regression line for the data. The regression is mathematically computed to optimize the closeness of the line fit. Yet if, in the end, the line fits the data well, one does not dismiss the result as mere circularity or as merely the result of an optimization routine. Instead two outcomes of value are obtained. First, if the linear fit performs well, capturing much of the data pattern, then one can infer that a linear model is indeed a reasonable model for the data. Second, specific parameters can be determined from the linear fit, including the slope and intercept, that may have practical importance. A similar type of outcome was obtained in the present study. We used an optimization routine to fit the information structure to the extrastriate topography. Two valuable outcomes were obtained. First, the fit performed well—the optimized four-stream model was able to reconstruct the topography correctly—suggesting that a four-stream, six-hierarchical-level model is indeed a reasonable model to capture at least the overarching topographic pattern. Second, the optimization supplied us with the specific parameter settings of the model that allowed it to correctly fit the topography. The optimization determined the relative hierarchical ranking of visual areas, and the pattern of informational overlap among areas, necessary to fit the visual areas to their target cortical locations. Figure 6 shows this optimized parameter set and represents the main result of the present study. The data set shown in Fig. 6 supplies a rich information set about cortical function extracted by a novel analysis of cortical topography. The discussion examines the accuracy of this data set with respect to physiological findings.

DISCUSSION

The present study used an analysis of topography to build up a model of the informational relationships among visual areas. Through a series of iterations, we obtained an optimized model that when flattened onto the cortical surface, correctly reconstructed main features of the macaque extrastriate topography. In the optimized model, visual processing was divided into four general information types. Each information type was emphasized within a functional stream, each stream incorporating six levels of hierarchy. The streams overlapped and diverged in a complex pattern in information space. When this complex informational pattern was flattened onto the cortical sheet according to the principle of continuity of function, it resulted in a topographic map that closely resembled the actual map in the macaque brain. Essentially, by using topography as a guide, we worked backward to infer a model of the functional relationships among areas that was consistent with that topography.

How well does this optimized model, derived by topographic analysis, reflect the actual functional properties of the macaque visual system?

Overlap between the object recognition stream and the motion stream

In the optimized model, property A is emphasized in areas that map to the cortical locations of V4, TEO, and TE (see Figs. 6 and 7). Within these visual areas, property A increases progressively with increasing hierarchy. Property B is emphasized in cortical areas that spatially correspond to MT, MST, and STP. Within these visual areas, property B increases progressively with increasing hierarchy. In comparison, in the macaque brain, areas V4, TEO, and TE emphasize information about object identity, with increasingly sophisticated information present at higher hierarchical levels. Areas MT, MST, and STP emphasize information about visual motion, again with increasingly sophisticated information present at higher hierarchical levels. Given this comparison, property A could be thought of as corresponding to information about object identity and property B as corresponding to information about visual motion.

In the optimized model, as can be seen in Fig. 6, area STP (area B6) contains a high magnitude of property A and of property B. In this way, the model implies that given the known cortical location of STP relative to its surrounding areas, it should combine information from object identity and object motion and should do so in roughly equal proportion. This mixing of properties in area STP matches the known physiology, in which STP contains a mixture of information about object motion and object identity (e.g., Anderson and Siegel 2005; Bruce et al. 1981; Oram and Perrett 1996; Perrett et al. 1984). This combination of information in STP can be understood heuristically by considering the location of STP between MST (emphasizing motion information) and TEO and TE (emphasizing object identity information). To cause STP to map to the correct cortical location, the present model settled on a result in which STP was given informational properties combining that of its neighboring areas.

In the optimized model (Fig. 6), in the A stream, property A increases gradually from V4 to TEO to TE. The other properties have low magnitude. The model therefore indicates that the A stream is a relatively informationally pure stream, focused mainly on one type of information, also matching the general pattern to emerge in the physiological literature.

Overlap between the motion stream and the object location stream

In the optimized model (Fig. 6), property C is emphasized in cortical areas corresponding to V3a, DP, and 7a. Among these areas, property C increases in magnitude with increasing hierarchy. In the macaque brain, areas V3A and 7a are known to contain information about the locations of objects in a variety of potentially useful spatial coordinate frames. These coordinate frames are believed to be encoded by neurons that have retinal receptive fields that are subject to gain fields based on nonvisual information such as eye position (Andersen et al. 1985, 1990; Galletti and Battaglini 1989). One could therefore consider property C as corresponding to information about useful spatial coordinates. The optimized model predicts that there exists an orderly progression, a processing stream in which this type of spatial information becomes increasingly expressed among areas V3a, DP, and 7a. Little is known about the physiology of area DP, and therefore the linking of these areas into a processing stream focused on computing spatial coordinates represents a novel prediction of the model.

In the optimized model (Fig. 6), area 7a contains an elevated magnitude of properties B and C. The model therefore implies that to place the areas in their known topographic locations, not only should a distinct stream exist for computing spatial coordinate frames, but at its hierarchical peak, within area 7a, information about object motion should also be represented. In this respect again, the model accurately reflects the physiological literature. The presence of motion information in area 7a is well established (e.g., Motter and Mountcastle 1981; Motter et al. 1987; Read and Siegel 1997; Steinmetz et al. 1987).

In the optimized model (Fig. 6), the areas of the B stream also contain some of property C. The model indicates that on topographic grounds, we should expect at least some information about spatial coordinate frames to be present in areas MT, MST, and STP. In the actual macaque brain, just as in the model, areas MT and MST emphasize motion processing while also containing neurons with spatial gain fields (Bremmer et al. 1997). Whether area STP also contains neurons with gain fields is yet to be determined.

The optimized model therefore reconstructed the informational overlaps and divergences between one set of areas (MT, MST, and STP) and another set (V3a, DP, and 7a). Many of these relationships are known to be correct from the physiological literature, and some have not been tested and therefore represent novel predictions of the model.

Vision-for-action stream

The optimized model incorporated a fourth functional stream, the D stream, that was mapped onto cortical areas corresponding to V6, V6a, and the intraparietal sulcus. Emerging evidence suggests that the dorsal-most areas in the primate brain may be best described as emphasizing sensory-motor integration (e.g., Cooke et al. 2003; Fattori et al. 2001, 2004; Goodale and Milner 1992; Kutz et al. 2003; Mountcastle et al. 1975; Sakata et al. 1995; Snyder et al. 1997; Stepniewska et al. 2005). On the basis of connectivity and functional properties, it has been proposed that these medial visual areas form a distinct stream for visuo-motor functions (Caminiti et al. 1999; Fattori et al. 2001, 2004; Kutz et al. 2003; Rizzolatti and Matelli 2003; Shipp et al. 1998). On these grounds, one could consider property D in the present model as corresponding to sensory-motor processing.

In the macaque brain, the medial areas have not been as extensively studied as lateral areas and different groups have defined them differently. Therefore there is some ambiguity and room for disagreement with our interpretation. Alternative naming schemes include area PO, MDP, V6, V6A, and PIP (Colby et al. 1988; Felleman and Van Essen 1991; Galletti et al. 1999, 2005 Lewis and Van Essen 2000). Galletti et al. (2005) mapped these medial areas in greater detail than had been done previously, and we used their designations of V6 and V6A.

As can be seen in Fig. 6, in the optimized model, the D stream is not focused exclusively on one type of visual information. Instead of all four streams, the D stream contains the most informational mixture. For example, IP, at the highest level of hierarchy in the D stream, contains an elevated value of properties A–D. The model suggests that for this area to be mapped to its known cortical location, it should be expected to contain information on object identity (property A), on object motion (property B), on spatial coordinate frames (property C), and on action control (property D). Exactly this mixture of properties has been reported in the physiological literature. In particular, a growing number of studies finds that IP contains information on object shape (Goodale and Milner 1992; Graziano et al. 2000; Murata et al. 2000; Sereno and Maunsell 1998). Object shape is traditionally in the province of ventral areas, and therefore the presence of this information in IP was considered to be surprising. The present analysis demonstrates that on the basis of the topographic relationships among areas, IP is expected to contain information on object identity.

Hierarchical relationships among areas

In Fig. 6, each data cluster has a hierarchical value indicated by the vertical position of the graph in the figure. Some of the hierarchical structure was built into the model at the outset. The model was based on the hypothesis of hierarchical processing streams, each stream with six stages of hierarchy. However, the initial, schematic structure of six equal hierarchical steps within each visual stream (see Fig. 4) was modified by the optimization algorithm to form the highly irregular, idiosyncratic pattern of hierarchy shown in Fig. 6. How well did the optimized model reconstruct the known hierarchical relationships among visual areas?

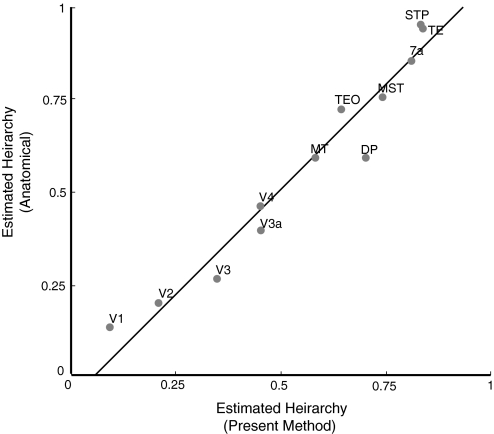
Previous studies ranked the hierarchies of visual areas through two means. First, the physiological properties of areas suggested a rough hierarchical ranking. Second, the laminar pattern of connectivity between areas was used to assign quantitative hierarchy values to areas (Felleman and Van Essen 1991; Hilgetag et al. 1996, 2000). In Fig. 8, the y axis shows the hierarchical ranking of visual areas according to a recent use of the analysis of connectivity (Hilgetag et al. 2000). These rankings are placed on a normalized scale from 0 to 1. The x axis shows the hierarchical ranking of visual areas as inferred by the present method based on the topographic locations of visual areas. The two methods correlate closely (r² value of 0.95).

Fig. 8. — Hierarchical ranking of visual areas. x axis represents relative hierarchical ranking based on the data set in Fig. 6. y only axis represents relative hierarchical ranking as determined by a previous study (Hilgetag et al. 2000) based on anatomical connectivity. Visual areas were equated between studies as follows: MST (from present study) = MSTd + MSTl (from Hilgetag et al. 2000). TEO = VOT + PITv + PITd. TE = CITv + CITd + AITv. STP = STPa + STPp. Dorsal areas V6, V6A, and IP were not included in the plot for 2 related reasons. First, it was not clear how to match these areas between the present study and Hilgetag et al. (2000). Second, the areal boundaries and connectivity of these dorsal areas (Galletti et al. 2005) were detailed mainly after the publication of Hilgetag et al. (2000).

It is important to note that the nonoptimized four-stream model (shown in Fig. 4) contains some of the hierarchical structure built into it. It therefore also has a correlation to the Hilgetag et al. result (r² value of 0.82). However, in specific ways, the nonoptimized version deviates from the correct hierarchical structure. For example, in the nonoptimized four-stream model, area MT and V4 are assigned the same hierarchical value. In the optimized version, to cause MT to map to the correct location relative to V4, the method converged on a solution in which MT had a higher hierarchical value than V4. This hierarchical difference between MT and V4 matches the previous estimates based on connectivity (Hilgetag et al. 2000).

As another example, in the nonoptimized four-stream model (Fig. 4), TE, STP, and 7A are assigned the same hierarchical value. In the optimized version, to cause these areas to map to their correct locations, the method converged on a solution in which TE and STP have similar hierarchical values and 7A has a lower hierarchical value. Again, this hierarchical arrangement matches the estimates based on connectivity (Hilgetag et al. 2000).

Thus in the present study, without considering how one area is connected to another and without considering the specific physiological properties of areas or the complexity of visual features encoded in visual areas, indeed considering nothing more than the sizes, shapes, and relative locations of areas on the cortical surface, the present method was able to read out the details of the hierarchical interrelationships among areas in a manner that matched previous estimates.

This example of hierarchy shows the power of the present approach. Based on the spatial relationships among areas, it is possible to deduce detailed information about their functional relationships.

Limitations of the present model

SUBAREAS, IN-BETWEEN AREAS, AND MAPS WITHIN AREAS.

The present model of four streams and six hierarchical levels, for all its success in capturing some of the main features of the extrastriate topography, is nonetheless a schematic model that leaves behind many details. It accounts for the approximate locations and sizes of 15 main visual areas. Yet the parcellation of visual cortex into 15 areas, shown in Fig. 1, is a simplified account. The macaque extrastriate cortex contains much greater complexity, and many of the areal divisions are in debate. Among the divisions not represented in our model are the subdivisions of the intraparietal sulcus including LIP, MIP, VIP and so on, the subdivisions of MST into MSTl and MSTd, the many proposed subdivisions of TE and TEO, and the proposed subdivisions of almost every other visual area. It also leaves out many proposed areas that are less well established such as V4t that might lie between MT and V4 or FST located between MST and TEO. It is important to note that these omissions are not the result of any intrinsic failure of the concept. One could build a model with greater detail and thereby account for more of these topographic features. The model contains only as many visual areas as one builds into it. The information structure in Fig. 6 contains 15 data clusters, and therefore 15 visual areas were mapped to the cortex by the Kohonen algorithm. To add more visual areas to the model, it would be necessary to add more data clusters to the information structure. The methods used here would then be able to determine the informational relationships among the expanded set of visual areas that allows them to be mapped to their correct cortical locations.

For example, consider visual area FST that lies between area MST and area TEO. The present model does not include this cortical zone. Yet by considering the model, and the principle of optimal cortical continuity of function, it is not difficult to infer the addition to the model that would be needed to produce FST. The model would need a new data cluster the mean of which in the five dimensional information structure is geometrically between that of MST and of TEO. The new data cluster would need a hierarchy value between that of MST and TEO, and a blended mixture of property A (elevated in TEO in the model) and property B (elevated in MST in the model). With these properties, the new data cluster is likely to be mapped by the Kohonen algorithm into the approximately correct location, forming a zone between MST and TEO. These guesses would presumably then require optimization to adjust the topography and shift the areas to their ideal target locations.

Consider the subdivisions of the intraparietal sulcus. In the optimized model, the intraparietal sulcus was rendered as a single area, labeled IP, at the highest hierarchical level of the action stream. In the actual macaque brain, the intraparietal sulcus is divisible into a complex mosaic of subregions that may partly emphasize different action types such as eye movement, reaching, grasping, and flinching (Cooke et al. 2003; Fattori et al. 2001, 2004; Kutz et al. 2003; Nakamura et al. 1999; Sakata et al. 1995; Snyder et al. 1997). The proposal that the intraparietal area is subdivided by ethologically relevant sensory-motor functions was emphasized recently in a study using electrical stimulation to evoke different complex movements from different areas of the parietal cortex of prosimians (Stepniewska et al. 2005). These divisions of the intraparietal sulcus could in principle be incorporated into an elaborated model, simply by removing the current data cluster that maps to the IP (data cluster D6 in Fig. 6) and replacing it with a set of smaller data clusters, all with similar means in the information structure, yet all differing from each other in some new set of dimensions, causing them to be mapped beside each other. In this way, by adding dimensions and data clusters, it is possible to add finer topographic divisions.

In principle, the model could be extended to include topography within each visual area. For example, V1 is represented in the present model by a single data cluster with no internal structure. It therefore maps to the cortex as a uniform area with no internal topography. One could supply an internal structure by defining the two new dimensions of retinotopic position and assigning different retinotopic locations to different data points within that cluster. The Kohonen algorithm would then not only map V1 to a particular cortical location but also create an internal map within V1 to reflect the internal structure in the data cluster. In a similar way, by adding dimensions such as line orientation or motion direction, it might be possible to reconstruct the known topographic and columnar features within many visual areas including the stripes in V2 (Tootell et al. 1983) and the direction columns in MT (Albright et al. 1984).

The present model, with its four overarching information streams, six hierarchical levels per stream, and lack of any internal structure within each visual area, is obviously a simplification. It captures, to first order, the extrastriate topography. There are three reasons why we did not extend the present model to include more topographic details. First, the topographic details are known for some areas but not for others. Whereas the retinotopy and columnar organization in V1 is well understood and has been modeled before as an example of optimal continuity of function (Chklovskii 2000; Durbin and Mitchison 1990; Kohonen 1982; Koulakov and Chklovskii 2001), the columnar organizations within V3, or TEO, or DP, for example, are not well known. In the Kohonen method for self-organizing maps, if one visual area is provided with detailed internal structure and another is not, the one with the greater informational detail will outcompete the other and take more cortical area. Therefore it is necessary to treat all the areas in the same way to provide an even field for the global map to develop properly. For this reason, though in principle we could model the details of some areas, we would not be able to adequately model the global extrastriate topography unless a similar level of detail was supplied for all areas.

A second reason why we did not pursue all details of extrastriate topography is the computational difficulty of the task. In theory a complete model, containing all dimensions necessary to capture the complexity of visual processing, might some day be possible to construct. Such a model, when rendered onto the cortical surface, should be able to accurately reconstruct all features of visual topography between and within visual areas. A model at that level of completeness, incorporating perhaps hundreds of informational dimensions, is prohibitively computationally complicated at this time. The amount of computation necessary for the present method increases exponentially with the number of dimensions and the problem becomes unsolvable in a practical amount of time. In the present study, in the optimized four-stream model, 15 visual areas were included, each of which was described by means of 5 dimensions (hierarchy and dimensions A–D), totaling 75 dimensions. Even a modest increase in the number of visual areas or subclusters within areas would make the computational process unmanageable.

The third and most important reason why we focused on a simple schematic model was to try to understand the general principles of extrastriate organization rather than the details. The fact that a simple five-dimensional data structure, containing hierarchy and four processing streams, was sufficient to reconstruct the main features of the extrastriate topography, is itself telling. It suggests that relatively few informational dimensions are responsible for the large-scale organization of the visual areas.

MINIMIZING WIRE LENGTH OR OPTIMIZING CONTINUITY?

The idea that the brain is organized to minimize wire length dates back at least to Cajal (1899). It has been invoked to explain the organization within cortical areas, such as cortical maps and cortical columns (Chklovskii 2000; Durbin and Mitchison 1990; Kaas and Catania 2002; Kohonen 1982; Koulakov and Chklovskii 2001; O'Leary and McLaughlin 2005; Saarinen and Kohonen 1985). It has also been invoked to explain the spatial organization among cortical areas (Klyachko and Stevens 2003; Kolster et al. 2009; Young 1992). These previous studies helped to establish the principle of the economy of wiring.

The economy of wiring does not necessarily translate directly into a rule of optimal continuity of function across the cortical surface. One reason is that connectivity passes not only tangentially through the cortex, connecting neighboring regions, but also passes through the white matter to connect more distant cortical locations. It has been suggested that the folding of the macaque visual cortex is shaped by the tension of axons passing from one visual area to another (Van Essen 1997). To the extent that local, lateral connections in cortex dominate information processing, then local continuity of function should result from wire-minimization. To the extent that more distant projections influence information processing, the local continuity of function should be modified in complicated ways.

It has been suggested that local continuity of function tends to dominate the organization of cortex rather than solely a global minimization of wiring length (Durbin and Mitchison 1990; Kaas and Catania 2002; Kohonen 1982; Rosa and Tweedale 2005). In this view, nearest neighbor relationships tend to be of greater weight than long range connectivity.

A compromise view is that several similar but nonidentical principles of organization combine, including the global minimization of wiring, the consequence of local correlative learning rules, and the inevitable result of chemical gradients that guide axonal development. All of these processes might combine to produce a like-attracts-like organization that is relatively but not entirely weighted toward local continuity.

In the present study, we chose to use the Kohonen (2001) algorithm, which optimizes continuity mainly at the local scale and which was previously successful in explaining some aspects of cortical organization (Kohonen 1982; Saarinen and Kohonen 1985). We recognize that this algorithm might provide only an approximate way to model cortical organization. For example, the Kohonen algorithm, at least as we applied it, considered only tangential distances across the cortical sheet. It did not consider short-cut distances through the white matter from one gyral wall to another. In this way, it maximized local continuity across the cortical surface rather than minimizing wiring. A better model might consider both types of distances, although it is not clear how to titrate the two. Yet another method might use the sign of the cortical curvature to weight the distance. A negative curvature implies neighboring points in cortex that cannot be connected via straight axons through the white matter, whereas a positive curvature implies neighboring points in cortex that can be connected via straight axons. A distance metric that explicitly includes cortical curvature may therefore be useful. It is always possible that an improved algorithm will be found to more accurately model the principle of spatial contiguity in cortical organization. The method that we used, however, despite its approximate nature, was apparently sufficient for the present purpose. With a relatively simple hypothesis about the set of visual functions, we were able to reproduce the essential features of the extrastriate cortical topography and infer informational relationships among visual areas. The inferred informational relationships at least qualitatively match the pattern of results obtained from physiological studies.

INFLUENCES FROM OUTSIDE THE EXTRASTRIATE CORTEX.

The present model considered the topography of the extrastriate cortex in isolation. Yet cortical areas outside the extrastriate system presumably influence the visual topography via the same principles. For example, the somatotopic map of the body in S1, in which the face is represented ventrally, might have some influence on the overarching trend in the extrastriate cortex in which foveal representations are emphasized in ventral areas. As a second example, area STP contains auditory responses (Bruce et al. 1981) perhaps partly explaining its proximity to the auditory cortex. In these ways, the present model in its focus on the visual system is approximate and incomplete. Ideally in understanding the cortical topography, one would model the entire cortex to take into account interactions among all possible areas. Such a brain-wide model may be a next useful step. However, at the present time, enough may not be known about the cortical topography to model it effectively using the current technique. Some cortical systems, such as the visual, somatosensory, and motor systems, have been mapped in at least some detail, whereas other cortical systems are still poorly understood topographically. Even within the extrastriate visual cortex, arguably the most thoroughly mapped of all the cortical systems, the ambiguities and disagreements are considerable. Perhaps at some future time the technique could be applied in a brain-wide fashion.

Two visual streams?

Ungerleider and Mishkin (1982) proposed that the task of vision could be divided into two major subtasks, including the processing of object identity and of object location. Object identity was hypothesized to be represented in a hierarchical manner in ventral extrastriate areas. Object location was hypothesized to be represented in a hierarchical manner in dorsal areas. As more physiological and anatomical data accumulated about the macaque visual system, this original hypothesis came under some criticism and re-interpretation (e.g., Goodale and Milner 1992; Merigan and Maunsell 1993; Sereno and Maunsell 1998). The two visual systems hypothesis remained influential but now tends to be interpreted in increasingly flexible ways. The current popular view could be put this way: the macaque visual system is divisible into a ventral stream for object recognition and a dorsal miscellany.

In the present study, we first tested a strict two-stream model in which vision was divisible into two broad types of information processing, each requiring a series of hierarchical steps. Our two-stream model was therefore in some ways comparable to the original Ungerleider and Mishkin model (1982). As described in results, the two-stream model captured the basic organization of the ventral stream but failed to reconstruct the organization of the dorsal areas. This success of the model in ventral areas and its failure in dorsal areas underscores the strengths and weaknesses of the original Ungerleider and Mishkin model. The hypothesis of a ventral stream fits the data; the hypothesis of a dorsal stream does not.

By considering the results of the two-stream model and the manner in which streams and hierarchical levels can be optimally arranged on cortex to maximize continuity, we inferred that the visual organization would be better explained by a four-stream model. Our optimized four-stream model was successful at reconstructing much of the topography of the macaque visual system.

Arguably, our four-stream model is consistent with the common view of the two stream model. Our A stream maps onto the standard ventral stream. Our B–D streams map onto the current dorsal stream. We suggest, however, that our four-stream model has more descriptive validity. Lumping the B–D streams together and labeling them as one functional stream discards the explanatory advantage of the stream concept. At least in the present method, at least as inferred by topographic organization, the task of vision is better understood as roughly divided into four broad and partially overlapping subtasks, not two. As discussed in the previous sections, this division of information into object identity, motion, spatial coordinates, and motor control also has good correspondence to the physiological literature. The idea of a distinct stream in the dorsal-most cortex that emphasizes visually guided actions such as saccades, reaches, and grasps, has been proposed before on the basis of connectivity and physiological properties (Caminiti et al. 1999; Fattori et al. 2001, 2004; Kutz et al. 2003; Rizzolatti and Matelli 2003; Shipp et al. 1998).

Informational meaning of a cortical area

The present approach raises a philosophical question about the definition of the area as a unit of cortical organization. Visual physiologists traditionally think in terms of areas with internal maps. According to a strict application of the principle of continuity of function, a discrete area forms only when the relevant information set has a distinct cluster that is separate from other parts of the information set. To the extent that the cortex has separate areas, there must be separable chunks of information to be represented on the cortex. In cases where those chunks of information grade into each other in information space, the borders of areas will be gradients. To the extent that chunks of information have an overarching set of relationships among each other, the cortical areas will fit together into a larger, overarching topography. If the relevant information space is of low dimensionality, it may be mapped across cortex in a continuous fashion. If the information space is of high dimensionality, it may be mapped across cortex in a complex, fractured manner that is difficult to understand without the mathematical tools of dimensionality reduction. Whether we are talking about the large scale organization of the entire cortex, the organization of areas within the visual system, a map within a visual area, or the columns within a part of a map, the principle of organization appears to be the same. The cortex is, in a sense, one giant cortical area that contains a systematic map of the immense and complex information space relevant to the animal's behavior.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant NS-046407.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

Supplementary Material

Supplemental Material

supp_105_1_305__index.html^{(804B, html)}

ACKNOWLEDGMENTS

We thank R. Desimone, M. Fruita, S. Kastner, T. Mole, J. Reynolds, and K. Schneider for comments.

Footnotes

The online version of this article contains supplemental data.

REFERENCES

Aflalo TN, Graziano MSA. Possible origins of the complex topographic organization of motor cortex: reduction of a multidimensional space onto a 2-dimensional array. J Neurosci 26: 6288–6297, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
Albright TD, Desimone R, Gross CG. Columnar organization of directionally selective cells in visual area MT of the macaque. J Neurophysiol 51: 16–31, 1984 [DOI] [PubMed] [Google Scholar]
Andersen RA, Bracewell RM, Barash S, Gnadt JW, Fogassi L. Eye position effects on visual, memory, and saccade-related activity in areas LIP and 7a of macaque. J Neurosci 10: 1176–1196, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]
Andersen RA, Essick GK, Siegel RM. Encoding of spatial location by posterior parietal neurons. Science 230: 456–458, 1985 [DOI] [PubMed] [Google Scholar]
Anderson KC, Siegel RM. Three-dimensional structure-from-motion selectivity in the anterior superior temporal polysensory area, STPa, of the behaving monkey. Cereb Cortex 15: 1299–1307, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Baylis GC, Rolls ET, Leonard CM. Functional subdivisions of the temporal lobe neocortex. J Neurosci 7: 330–342, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]
Boussaoud D, Ungerleider LG, Desimone R. Pathways for motion analysis: cortical connections of the medial superior temporal and fundus of the superior temporal visual areas in the macaque. J Comp Neurol 296: 462–495, 1990 [DOI] [PubMed] [Google Scholar]
Bremmer F, Ilg UJ, Thiele A, Distler C, Hoffman KP. Eye position effects in monkey cortex. I. Visual and pursuit-related activity in extrastriate areas MT and MST. J Neurophysiol 77: 944–961, 1997 [DOI] [PubMed] [Google Scholar]
Bruce C, Desimone R, Gross CG. Visual properties of neurons in a polysensopry area in the superior temporal sulcus of the macaque. J Neurophysiol 46: 369–384, 1981 [DOI] [PubMed] [Google Scholar]
Cajal SR y. Texture of the Nervous System of Man and the Vertebrates, translated by Passik P, Passic T. New York:, Springer, 2000. (original published in 1899) [Google Scholar]
Caminiti R, Genovesio A, Marconi B, Mayer AB, Onorati P, Ferraina S, Mitsuda T, Giannetti S, Squatrito S, Maioli MG, Molinari M. Early coding of reaching: frontal and parietal association connections of parieto-occipital cortex. Eur J Neurosci 11: 3339–3345, 1999 [DOI] [PubMed] [Google Scholar]
Cherniak C. Component placement optimization in the brain. J Neurosci 14: 2418–2427, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chklovskii DB. Binocular disparity can explain the orientation of ocular dominance stripes in primate primary visual area (V1). Vision Res 40: 1765–1773, 2000 [DOI] [PubMed] [Google Scholar]
Colby CL, Gattass R, Olson CR, Gross CG. Topographical organization of cortical afferents to extrastriate visual area PO in the macaque: a dual tracer study. J Comp Neurol 269: 392–413, 1988 [DOI] [PubMed] [Google Scholar]
Cooke DF, Taylor CS, Moore T, Graziano MS. Complex movements evoked by microstimulation of the ventral intraparietal area. Proc Natl Acad Sci USA 100: 6163–6168, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Desimone R, Ungerleider LG. Neural mechanisms of visual processing in monkeys. In: Handbook of Neuropsychology, edited by Boller F, Grafman J. Amsterdam: Elsevier, 1989, vol. 2, p. 267–299 [Google Scholar]
Durbin R, Mitchison G. A dimension reduction framework for understanding cortical maps. Nature 343: 644–647, 1990 [DOI] [PubMed] [Google Scholar]
Fattori P, Breveglieri R, Amoroso K, Galletti C. Evidence for both reaching and grasping activity in the medial parieto-occipital cortex of the macaque. Eur J Neurosci 20: 2457–2466, 2004 [DOI] [PubMed] [Google Scholar]
Fattori P, Gamberini M, Kutz DF, Galletti C. “Arm-reaching” neurons in the parietal area V6A of the macaque monkey. Eur J Neurosci 13: 2309–2313, 2001 [DOI] [PubMed] [Google Scholar]
Felleman DJ, Van Essen DC. Distributed hierarchical processing in primate cerebral cortex. Cereb Cortex 1: 1–47, 1991 [DOI] [PubMed] [Google Scholar]
Galletti C, Battaglini PP. Gaze-dependent visual neurons in area V3A of monkey prestriate cortex. J Neurosci 9: 1112–1125, 1989 [DOI] [PMC free article] [PubMed] [Google Scholar]
Galletti C, Fattori P, Gamberini M, Kutz DF. The cortical visual area V6: brain location and visual topography. Eur J Neurosci 11: 3922–3936, 1999 [DOI] [PubMed] [Google Scholar]
Galletti C, Gamberini M, Kutz DF, Baldinotti I, Fattori P. The relationship between V6 and PO in macaque extrastriate cortex. Eur J Neurosci 21: 959–970, 2005 [DOI] [PubMed] [Google Scholar]
Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends Neurosci 15: 20–25, 1992 [DOI] [PubMed] [Google Scholar]
Graziano MSA, Aflalo TN. Mapping behavioral repertoire onto the cortex. Neuron 56: 239–251, 2007 [DOI] [PubMed] [Google Scholar]
Graziano MS, Cooke DF, Taylor CS. Coding the location of the arm by sight. Science 290: 1782–1786, 2000 [DOI] [PubMed] [Google Scholar]
Hilgetag CC, O'Neill MA, Young MP. Indeterminate organization of the visual system. Science 271: 776–777, 1996 [DOI] [PubMed] [Google Scholar]
Hilgetag CC, O'Neill MA, Young MP. Hierarchical organization of macaque and cat cortical sensory systems explored with a novel network processor. Philos T Roy Soc B Biol Sci 355: 71–89, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kaas JH. Why brain size is so important: design problems and solutions as neocortex gets bigger or smaller. Brain Mind 1: 7–23, 2000 [Google Scholar]
Kaas JH, Catania KC. How do features of sensory representations develop? Bioessays 24: 334–343, 2002 [DOI] [PubMed] [Google Scholar]
Klyachko VA, Stevens CF. Connectivity optimization and the positioning of cortical areas. Proc Natl Acad Sci USA 100: 7937–7941, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kohonen T. Self-organizing formation of topologically correct feature maps. Biol Cybern 43: 59–69, 1982 [Google Scholar]
Kohonen T. Self-Organizing Maps. Berlin: Springer, 2001 [Google Scholar]
Kolster H, Mandeville JB, Arsenault JT, Ekstrom LB, Wald LL, Vanduffel W. Visual field map clusters in macaque extrastriate visual cortex. J Neurosci 29: 7031–7039, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Koulakov AA, Chklovskii DB. Orientation preference patterns in mammalian visual cortex: a wire length minimization approach. Neuron 29: 519–527, 2001 [DOI] [PubMed] [Google Scholar]
Kutz DF, Fattori P, Gamberini M, Breveglieri R, Galletti C. Early- and late-responding cells to saccadic eye movements in the cortical area V6A of macaque monkey. Exp Brain Res 149: 83–95, 2003 [DOI] [PubMed] [Google Scholar]
Lewis JW, Van Essen DC. Architectonic parcellation of parieto-occipital cortex and interconnected cortical regions in the macaque monkey. J Comp Neurol 428: 79–111, 2000 [DOI] [PubMed] [Google Scholar]
Lyon DC, Kaas JH. Evidence for a modified V3 with dorsal and ventral halves in macaque monkeys. Neuron 33: 453–461, 2002 [DOI] [PubMed] [Google Scholar]
Merigan WH, Maunsell JH. How parallel are the primate visual pathways? Annu Rev Neurosci 16: 369–402, 1993 [DOI] [PubMed] [Google Scholar]
Motter BC, Mountcastle VB. The functional properties of the light-sensitive neurons of the posterior parietal cortex studied in waking monkeys: foveal sparing and opponent vector organization. J Neurosci 1: 3–26, 1981 [DOI] [PMC free article] [PubMed] [Google Scholar]
Motter BC, Steinmetz MA, Duffy CJ, Mountcastle VB. Functional properties of parietal visual neurons: mechanisms of directionality along a single axis. J Neurosci 7: 154–176, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]
Mountcastle VB, Lynch JC, Georgopoulos A, Sakata H, Acuna C. Posterior parietal association cortex of the monkey: command functions for operations within extrapersonal space. J Neurophysiol 38: 871–908, 1975 [DOI] [PubMed] [Google Scholar]
Murata A, Gallese V, Luppino G, Kaseda M, Sakata H. Selectivity for the shape, size, and orientation of objects for grasping in neurons of monkey parietal area AIP. J Neurophysiol 83: 2580–2601, 2000 [DOI] [PubMed] [Google Scholar]
Nakamura K, Chung HH, Graziano MS, Gross CG. Dynamic representation of eye position in the parieto-occipital sulcus. J Neurophysiol 81: 2374–2385, 1999 [DOI] [PubMed] [Google Scholar]
O'Leary DD, McLaughlin T. Mechanisms of retinotopic map development: Ephs, ephrins, and spontaneous correlated retinal activity. Prog Brain Res 147: 43–65, 2005 [DOI] [PubMed] [Google Scholar]
Oram MW, Perrett DI. Integration of form and motion in the anterior superior temporal polysensory area (STPa) of the macaque monkey. J Neurophysiol 76: 109–129, 1996 [DOI] [PubMed] [Google Scholar]
Perrett DI, Smith PA, Potter DD, Mistlin AJ, Head AS, Milner AD, Jeeves MA. Neurons responsive to faces in the temporal cortex: studies of functional organization, sensitivity to identity and relation to perception. Hum Neurobiol 3: 197–208, 1984 [PubMed] [Google Scholar]
Read HL, Siegel RM. Modulation of responses to optic flow in area 7a by retinotopic and oculomotor cues in monkey. Cereb Cortex 7: 647–661, 1997 [DOI] [PubMed] [Google Scholar]
Rizzolatti G, Matelli M. Two different streams form the dorsal visual system: anatomy and functions. Exp Brain Res 153: 146–157, 2003 [DOI] [PubMed] [Google Scholar]
Rosa MG, Tweedale R. Brain maps, great and small: lessons from comparative studies of primate visual cortical organization. Philos Trans R Soc Lond B Biol Sci 360: 665–691, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Saarinen J, Kohonen T. Self-organized formation of color maps in a model cortex. Perception 14: 711–719, 1985 [DOI] [PubMed] [Google Scholar]
Sakata H, Taira M, Murata A, Mine S. Neural mechanisms of visual guidance of hand action in the parietal cortex of the monkey. Cereb Cortex 5: 429–438, 1995 [DOI] [PubMed] [Google Scholar]
Sereno AB, Maunsell JH. Shape selectivity in primate lateral intraparietal cortex. Nature 395: 500–503, 1998 [DOI] [PubMed] [Google Scholar]
Shipp S, Blanton M, Zeki S. A visuo-somatomotor pathway through superior parietal cortex in the macaque monkey: cortical connections of areas V6 and V6A. Eur J Neurosci 10: 3171–3193, 1998 [DOI] [PubMed] [Google Scholar]
Snyder LH, Batista AP, Andersen RA. Coding of intention in the posterior parietal cortex. Nature 386: 167–170, 1997 [DOI] [PubMed] [Google Scholar]
Steinmetz MA, Motter BC, Duffy CJ, Mountcastle VB. Functional properties of parietal visual neurons: radial organization of directionalities within the visual field. J Neurosci 7: 177–191, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]
Stepniewska I, Fang PC, Kaas JH. Microstimulation reveals specialized subregions for different complex movements in posterior parietal cortex of prosimian galagos. Proc Natl Acad Sci USA 102: 4878–4883, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Tootell RBH, Silverman MS, De Valois RL, Jacobs GH. Functional organization of the second cortical visual area in primates. Science 220: 737–739, 1983 [DOI] [PubMed] [Google Scholar]
Ungerleider LG, Mishkin M. Two cortical visual systems. In: Analysis of Visual Behavior, edited by Ingle DJ, Goodale MA, Mansfield RJW. Cambridge, MA: MIT Press, 1982 [Google Scholar]
Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 385: 313–318, 1997 [DOI] [PubMed] [Google Scholar]
Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analysis of cerebral cortex. J Am Med Inform Assoc 8: 443–459, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wandell BA, Dumoulin SO, Brewer AA. Visual field maps in human cortex. Neuron 56: 366–383, 2007 [DOI] [PubMed] [Google Scholar]
Young MP. Objective analysis of the topological organization of the primate cortical visual system. Nature 358: 152–155, 1992 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material

supp_105_1_305__index.html^{(804B, html)}

supp_00795.2010_jnsupmat.pdf^{(96.1KB, pdf)}

[B1] Aflalo TN, Graziano MSA. Possible origins of the complex topographic organization of motor cortex: reduction of a multidimensional space onto a 2-dimensional array. J Neurosci 26: 6288–6297, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] Albright TD, Desimone R, Gross CG. Columnar organization of directionally selective cells in visual area MT of the macaque. J Neurophysiol 51: 16–31, 1984 [DOI] [PubMed] [Google Scholar]

[B3] Andersen RA, Bracewell RM, Barash S, Gnadt JW, Fogassi L. Eye position effects on visual, memory, and saccade-related activity in areas LIP and 7a of macaque. J Neurosci 10: 1176–1196, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B4] Andersen RA, Essick GK, Siegel RM. Encoding of spatial location by posterior parietal neurons. Science 230: 456–458, 1985 [DOI] [PubMed] [Google Scholar]

[B5] Anderson KC, Siegel RM. Three-dimensional structure-from-motion selectivity in the anterior superior temporal polysensory area, STPa, of the behaving monkey. Cereb Cortex 15: 1299–1307, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] Baylis GC, Rolls ET, Leonard CM. Functional subdivisions of the temporal lobe neocortex. J Neurosci 7: 330–342, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] Boussaoud D, Ungerleider LG, Desimone R. Pathways for motion analysis: cortical connections of the medial superior temporal and fundus of the superior temporal visual areas in the macaque. J Comp Neurol 296: 462–495, 1990 [DOI] [PubMed] [Google Scholar]

[B8] Bremmer F, Ilg UJ, Thiele A, Distler C, Hoffman KP. Eye position effects in monkey cortex. I. Visual and pursuit-related activity in extrastriate areas MT and MST. J Neurophysiol 77: 944–961, 1997 [DOI] [PubMed] [Google Scholar]

[B9] Bruce C, Desimone R, Gross CG. Visual properties of neurons in a polysensopry area in the superior temporal sulcus of the macaque. J Neurophysiol 46: 369–384, 1981 [DOI] [PubMed] [Google Scholar]

[B10] Cajal SR y. Texture of the Nervous System of Man and the Vertebrates, translated by Passik P, Passic T. New York:, Springer, 2000. (original published in 1899) [Google Scholar]

[B11] Caminiti R, Genovesio A, Marconi B, Mayer AB, Onorati P, Ferraina S, Mitsuda T, Giannetti S, Squatrito S, Maioli MG, Molinari M. Early coding of reaching: frontal and parietal association connections of parieto-occipital cortex. Eur J Neurosci 11: 3339–3345, 1999 [DOI] [PubMed] [Google Scholar]

[B12] Cherniak C. Component placement optimization in the brain. J Neurosci 14: 2418–2427, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] Chklovskii DB. Binocular disparity can explain the orientation of ocular dominance stripes in primate primary visual area (V1). Vision Res 40: 1765–1773, 2000 [DOI] [PubMed] [Google Scholar]

[B14] Colby CL, Gattass R, Olson CR, Gross CG. Topographical organization of cortical afferents to extrastriate visual area PO in the macaque: a dual tracer study. J Comp Neurol 269: 392–413, 1988 [DOI] [PubMed] [Google Scholar]

[B15] Cooke DF, Taylor CS, Moore T, Graziano MS. Complex movements evoked by microstimulation of the ventral intraparietal area. Proc Natl Acad Sci USA 100: 6163–6168, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] Desimone R, Ungerleider LG. Neural mechanisms of visual processing in monkeys. In: Handbook of Neuropsychology, edited by Boller F, Grafman J. Amsterdam: Elsevier, 1989, vol. 2, p. 267–299 [Google Scholar]

[B17] Durbin R, Mitchison G. A dimension reduction framework for understanding cortical maps. Nature 343: 644–647, 1990 [DOI] [PubMed] [Google Scholar]

[B18] Fattori P, Breveglieri R, Amoroso K, Galletti C. Evidence for both reaching and grasping activity in the medial parieto-occipital cortex of the macaque. Eur J Neurosci 20: 2457–2466, 2004 [DOI] [PubMed] [Google Scholar]

[B19] Fattori P, Gamberini M, Kutz DF, Galletti C. “Arm-reaching” neurons in the parietal area V6A of the macaque monkey. Eur J Neurosci 13: 2309–2313, 2001 [DOI] [PubMed] [Google Scholar]

[B20] Felleman DJ, Van Essen DC. Distributed hierarchical processing in primate cerebral cortex. Cereb Cortex 1: 1–47, 1991 [DOI] [PubMed] [Google Scholar]

[B21] Galletti C, Battaglini PP. Gaze-dependent visual neurons in area V3A of monkey prestriate cortex. J Neurosci 9: 1112–1125, 1989 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B22] Galletti C, Fattori P, Gamberini M, Kutz DF. The cortical visual area V6: brain location and visual topography. Eur J Neurosci 11: 3922–3936, 1999 [DOI] [PubMed] [Google Scholar]

[B23] Galletti C, Gamberini M, Kutz DF, Baldinotti I, Fattori P. The relationship between V6 and PO in macaque extrastriate cortex. Eur J Neurosci 21: 959–970, 2005 [DOI] [PubMed] [Google Scholar]

[B24] Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends Neurosci 15: 20–25, 1992 [DOI] [PubMed] [Google Scholar]

[B25] Graziano MSA, Aflalo TN. Mapping behavioral repertoire onto the cortex. Neuron 56: 239–251, 2007 [DOI] [PubMed] [Google Scholar]

[B26] Graziano MS, Cooke DF, Taylor CS. Coding the location of the arm by sight. Science 290: 1782–1786, 2000 [DOI] [PubMed] [Google Scholar]

[B27] Hilgetag CC, O'Neill MA, Young MP. Indeterminate organization of the visual system. Science 271: 776–777, 1996 [DOI] [PubMed] [Google Scholar]

[B28] Hilgetag CC, O'Neill MA, Young MP. Hierarchical organization of macaque and cat cortical sensory systems explored with a novel network processor. Philos T Roy Soc B Biol Sci 355: 71–89, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] Kaas JH. Why brain size is so important: design problems and solutions as neocortex gets bigger or smaller. Brain Mind 1: 7–23, 2000 [Google Scholar]

[B30] Kaas JH, Catania KC. How do features of sensory representations develop? Bioessays 24: 334–343, 2002 [DOI] [PubMed] [Google Scholar]

[B31] Klyachko VA, Stevens CF. Connectivity optimization and the positioning of cortical areas. Proc Natl Acad Sci USA 100: 7937–7941, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] Kohonen T. Self-organizing formation of topologically correct feature maps. Biol Cybern 43: 59–69, 1982 [Google Scholar]

[B33] Kohonen T. Self-Organizing Maps. Berlin: Springer, 2001 [Google Scholar]

[B34] Kolster H, Mandeville JB, Arsenault JT, Ekstrom LB, Wald LL, Vanduffel W. Visual field map clusters in macaque extrastriate visual cortex. J Neurosci 29: 7031–7039, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B35] Koulakov AA, Chklovskii DB. Orientation preference patterns in mammalian visual cortex: a wire length minimization approach. Neuron 29: 519–527, 2001 [DOI] [PubMed] [Google Scholar]

[B36] Kutz DF, Fattori P, Gamberini M, Breveglieri R, Galletti C. Early- and late-responding cells to saccadic eye movements in the cortical area V6A of macaque monkey. Exp Brain Res 149: 83–95, 2003 [DOI] [PubMed] [Google Scholar]

[B37] Lewis JW, Van Essen DC. Architectonic parcellation of parieto-occipital cortex and interconnected cortical regions in the macaque monkey. J Comp Neurol 428: 79–111, 2000 [DOI] [PubMed] [Google Scholar]

[B38] Lyon DC, Kaas JH. Evidence for a modified V3 with dorsal and ventral halves in macaque monkeys. Neuron 33: 453–461, 2002 [DOI] [PubMed] [Google Scholar]

[B39] Merigan WH, Maunsell JH. How parallel are the primate visual pathways? Annu Rev Neurosci 16: 369–402, 1993 [DOI] [PubMed] [Google Scholar]

[B40] Motter BC, Mountcastle VB. The functional properties of the light-sensitive neurons of the posterior parietal cortex studied in waking monkeys: foveal sparing and opponent vector organization. J Neurosci 1: 3–26, 1981 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B41] Motter BC, Steinmetz MA, Duffy CJ, Mountcastle VB. Functional properties of parietal visual neurons: mechanisms of directionality along a single axis. J Neurosci 7: 154–176, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B42] Mountcastle VB, Lynch JC, Georgopoulos A, Sakata H, Acuna C. Posterior parietal association cortex of the monkey: command functions for operations within extrapersonal space. J Neurophysiol 38: 871–908, 1975 [DOI] [PubMed] [Google Scholar]

[B43] Murata A, Gallese V, Luppino G, Kaseda M, Sakata H. Selectivity for the shape, size, and orientation of objects for grasping in neurons of monkey parietal area AIP. J Neurophysiol 83: 2580–2601, 2000 [DOI] [PubMed] [Google Scholar]

[B44] Nakamura K, Chung HH, Graziano MS, Gross CG. Dynamic representation of eye position in the parieto-occipital sulcus. J Neurophysiol 81: 2374–2385, 1999 [DOI] [PubMed] [Google Scholar]

[B45] O'Leary DD, McLaughlin T. Mechanisms of retinotopic map development: Ephs, ephrins, and spontaneous correlated retinal activity. Prog Brain Res 147: 43–65, 2005 [DOI] [PubMed] [Google Scholar]

[B46] Oram MW, Perrett DI. Integration of form and motion in the anterior superior temporal polysensory area (STPa) of the macaque monkey. J Neurophysiol 76: 109–129, 1996 [DOI] [PubMed] [Google Scholar]

[B47] Perrett DI, Smith PA, Potter DD, Mistlin AJ, Head AS, Milner AD, Jeeves MA. Neurons responsive to faces in the temporal cortex: studies of functional organization, sensitivity to identity and relation to perception. Hum Neurobiol 3: 197–208, 1984 [PubMed] [Google Scholar]

[B48] Read HL, Siegel RM. Modulation of responses to optic flow in area 7a by retinotopic and oculomotor cues in monkey. Cereb Cortex 7: 647–661, 1997 [DOI] [PubMed] [Google Scholar]

[B49] Rizzolatti G, Matelli M. Two different streams form the dorsal visual system: anatomy and functions. Exp Brain Res 153: 146–157, 2003 [DOI] [PubMed] [Google Scholar]

[B50] Rosa MG, Tweedale R. Brain maps, great and small: lessons from comparative studies of primate visual cortical organization. Philos Trans R Soc Lond B Biol Sci 360: 665–691, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B51] Saarinen J, Kohonen T. Self-organized formation of color maps in a model cortex. Perception 14: 711–719, 1985 [DOI] [PubMed] [Google Scholar]

[B52] Sakata H, Taira M, Murata A, Mine S. Neural mechanisms of visual guidance of hand action in the parietal cortex of the monkey. Cereb Cortex 5: 429–438, 1995 [DOI] [PubMed] [Google Scholar]

[B53] Sereno AB, Maunsell JH. Shape selectivity in primate lateral intraparietal cortex. Nature 395: 500–503, 1998 [DOI] [PubMed] [Google Scholar]

[B54] Shipp S, Blanton M, Zeki S. A visuo-somatomotor pathway through superior parietal cortex in the macaque monkey: cortical connections of areas V6 and V6A. Eur J Neurosci 10: 3171–3193, 1998 [DOI] [PubMed] [Google Scholar]

[B55] Snyder LH, Batista AP, Andersen RA. Coding of intention in the posterior parietal cortex. Nature 386: 167–170, 1997 [DOI] [PubMed] [Google Scholar]

[B56] Steinmetz MA, Motter BC, Duffy CJ, Mountcastle VB. Functional properties of parietal visual neurons: radial organization of directionalities within the visual field. J Neurosci 7: 177–191, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B57] Stepniewska I, Fang PC, Kaas JH. Microstimulation reveals specialized subregions for different complex movements in posterior parietal cortex of prosimian galagos. Proc Natl Acad Sci USA 102: 4878–4883, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B58] Tootell RBH, Silverman MS, De Valois RL, Jacobs GH. Functional organization of the second cortical visual area in primates. Science 220: 737–739, 1983 [DOI] [PubMed] [Google Scholar]

[B59] Ungerleider LG, Mishkin M. Two cortical visual systems. In: Analysis of Visual Behavior, edited by Ingle DJ, Goodale MA, Mansfield RJW. Cambridge, MA: MIT Press, 1982 [Google Scholar]

[B60] Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 385: 313–318, 1997 [DOI] [PubMed] [Google Scholar]

[B61] Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analysis of cerebral cortex. J Am Med Inform Assoc 8: 443–459, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B62] Wandell BA, Dumoulin SO, Brewer AA. Visual field maps in human cortex. Neuron 56: 366–383, 2007 [DOI] [PubMed] [Google Scholar]

[B63] Young MP. Objective analysis of the topological organization of the primate cortical visual system. Nature 358: 152–155, 1992 [DOI] [PubMed] [Google Scholar]

PERMALINK

Organization of the Macaque Extrastriate Visual Cortex Re-Examined Using the Principle of Spatial Continuity of Function

T N Aflalo

MSA Graziano

Abstract

INTRODUCTION

METHODS

Model cortical sheet

Fig. 1.

Kohonen mapping algorithm

RESULTS

Two-stream model

Fig. 2.

Table 1.

Fig. 3.

Four-stream model

Fig. 4.

Table 2.

Fig. 5.

Optimized four-stream model

Fig. 6.

Table 3.

Fig. 7.

DISCUSSION

Overlap between the object recognition stream and the motion stream

Overlap between the motion stream and the object location stream

Vision-for-action stream

Hierarchical relationships among areas

Fig. 8.

Limitations of the present model

SUBAREAS, IN-BETWEEN AREAS, AND MAPS WITHIN AREAS.

MINIMIZING WIRE LENGTH OR OPTIMIZING CONTINUITY?

INFLUENCES FROM OUTSIDE THE EXTRASTRIATE CORTEX.

Two visual streams?

Informational meaning of a cortical area

GRANTS

DISCLOSURES

Supplementary Material

ACKNOWLEDGMENTS

Footnotes

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases