Reorganization of Finger Coordination Patterns During Adaptation to Rotation and Scaling of a Newly Learned Sensorimotor Transformation

Abstract

We examined how people organize redundant kinematic control variables (finger joint configurations) while learning to make goal-directed movements of a virtual object (a cursor) within a low-dimensional task space (a computer screen). Subjects participated in three experiments performed on separate days. Learning progressed rapidly on day 1, resulting in reduced target capture error and increased cursor trajectory linearity. On days 2 and 3, one group of subjects adapted to a rotation of the nominal map, imposed either stepwise or randomly over trials. Another group experienced a scaling distortion. We report two findings. First, adaptation rates and memory-dependent motor command updating depended on distortion type. Stepwise application and removal of the rotation induced a marked increase in finger motion variability but scaling did not, suggesting that the rotation initiated a more exhaustive search through the space of viable finger motions to resolve the target capture task than did scaling. Indeed, subjects formed new coordination patterns in compensating the rotation but relied on patterns established during baseline practice to compensate the scaling. These findings support the idea that the brain compensates direction and extent errors separately and in computationally distinct ways, but are inconsistent with the idea that once a task is learned, command updating is limited to those degrees of freedom contributing to performance (thereby minimizing energetic or similar costs of control). Second, we report that subjects who learned a scaling while moving to just one target generalized more narrowly across directions than those who learned a rotation. This contrasts with results from whole-arm reaching studies, where a learned scaling generalizes more broadly across direction than rotation. Based on inverse- and forward-dynamics analyses of reaching with the arm, we propose the difference in results derives from extensive exposure in reaching with familiar arm dynamics versus the novelty of the manual task.

INTRODUCTION

An important question in the study of goal-directed movement is how the brain learns to coordinate changes within the set of highly redundant control variables (e.g., motor cortical pyramidal cells, spinal stretch reflex thresholds, muscle forces, joint torques, etc.) to produce desired changes in the low-dimensional state of a controlled element (e.g., hand kinematics and/or kinetics). To capture a target with a single point-to-point movement, the brain must not only discriminate between control variables that influence task performance from those that do not, but it must also learn how much those task-relevant control variables should change to bring about a desired performance (an inverse Jacobian relationship; cf. Kaplan 1984). These two problems require “structural” and “parametric” learning, respectively (Braun et al. 2009, 2010). How does the brain learn the specific metric relationship between a desired change in task performance and control variable changes sufficient to realize that performance? How does it learn this motor representation of the “space” spanned by the task goals?

Many studies have focused on motor learning without considering redundancy by exploring how people adapt arm movements to kinematic visuomotor transformations such as those encountered when donning prism glasses (cf., among others, Held and Freedman 1963; Kitazawa et al. 1997; Martin et al. 1996; Redding and Wallace 1988, 1992, 1996; Rosetti et al. 1998) or when exposed to a rotation of the usual relationship between hand displacement and cursor motion on a computer screen (cf. Pine et al. 1996; Wigmore et al. 2002). In one such study, Krakauer and colleagues (2000) asked subjects to reposition the cursor from a common central origin to a series of eight peripheral targets by moving a handheld stylus across the surface of a horizontal digitizing tablet. After practicing the task, the baseline map between hand position and cursor position was distorted by either a rotation or scaling transformation. Subjects practiced the altered target capture task by reaching to 1, 2, 4, or 8 targets. Interestingly, the rate of adaptation to the rotation transformation depended on the number of training targets, whereas adaptation to the scaling transformation did not (see also Paz et al. 2005). The experimenters also evaluated how well adaptations generalized to unpracticed movement directions and extents: they found that learning of a scaling distortion generalized across all movement directions and extents but rotations generalized across distance only. The authors concluded that the brain processes errors in movement direction and extent separately and in computationally distinct ways during motor learning (Krakauer et al. 2000): extent errors experienced in moving to a single spatial target induce learning of a new “gain parameter” applied globally across all movement directions and extents, whereas direction errors induce learning of “rotation parameters” that do not generalize well across directions. Might direction and extent errors differentially influence updating of redundant motor control variables during goal-directed reaching?

Our experimental approach is similar to that first used by Mosier and colleagues (2005) to examine how the Euclidean (geometric) properties of space guide the development of coordination when learning a new motor task. In the current study as well as in that earlier study, each subject wore a data glove instrumented with a large number of bend sensors (defining the articulation space) and signals from these sensors drove the motion of a cursor on a computer screen (the task space, or simply “space” in the ordinary sense) via a linear hand-to-screen projection (or mapping). Each hand configuration projected onto one and only one screen location, although each screen location can be achieved using a virtually infinite number of different hand configurations. Subjects were to capture screen targets with the cursor. This task is unique in that it establishes a clear separation between those control degrees of freedom that contribute to kinematic performance and those that do not. Although the task is unlike anything subjects had previously experienced, it is similar to all other motor tasks in that a highly redundant set of control signals defines the motion of a controlled object in a low-dimensional workspace. Nearly all subjects learned to reduce cursor-positioning errors with practice within a single experimental session lasting 1 to 2 h. This learning generalized to unpracticed screen targets in trials performed without visual feedback, indicating that subjects learned how information about the relative distance between screen targets can constrain their choice of hand postures when presented with new targets. That is, subjects learned a motor representation of the Euclidean space onto which finger movements were mapped. Generalization developed along with a reduction of motion in those degrees of freedom not contributing to cursor motion (i.e., the task's null space). As recognized by Todorov and colleagues (Todorov 2004; Todorov and Jordan 2002) and others (Diedrichsen 2007; Latash et al. 2007; Müller and Sternad 2009; Scheidt et al. 2000; Scholz and Schöner 1999; Smith et al. 2006), examining the evolution of behavior within the null space of the task provides insight into how the nervous system organizes and reorganizes patterns of coordination as it learns. In Mosier's study, reduction in the extent and variability of null-space motion may have reflected a minimization of task energetics or an optimization of some other measure of efficiency, an interpretation consistent with the view that motor planning and control can be understood as resulting from an interplay between competing kinematic, energetic, and/or other “costs of control” (Shadmehr and Krakauer 2008).

Here, groups of subjects captured screen targets with a cursor in three experimental sessions performed on separate days. After becoming proficient in the task on day 1, we examined how one group would adapt to a rotation of the nominal hand-to-screen mapping when the distortion was imposed either stepwise or randomly over trials (days 2 and 3, respectively). Another group experienced a scaling on days 2 and 3. This allowed comparison of learning rates and the extent of reorganization of control induced by the two distortion types as well as a comparison of the role of direction and extent errors in driving adaptation of a newly learned, kinematic, sensorimotor transformation. Subjects in a third group performed experiments exploring how adaptations to rotational and scaling distortions acquired while moving to a single target generalize across space. We revisit the hypothesis that the brain processes errors in movement direction and extent separately and in computationally distinct ways during learning (Krakauer et al. 2000; Vindras et al. 2005), specifically testing whether extent errors induce learning of a single gain factor applied globally across all movement directions and extents, whereas direction errors induce learning of “rotation parameters” that generalize only to movements of different extent in the trained direction. We also test the hypothesis that adaptations to rotational and scaling distortions of task space both induce structural learning, such that after subjects identify those degrees of freedom that contribute to task performance (i.e., once they have learned an inverse hand-to-screen mapping; cf. Liu and Scheidt 2008a), motor command updating will be limited to only those degrees of freedom that contribute to task performance, thereby minimizing “costs of control” (cf. Shadmehr and Krakauer 2008). Portions of this work were previously presented in abstract form (Liu and Scheidt 2008b).

METHODS

Thirty subjects (19 female, 11 male) with no known neuromotor deficits provided written informed consent to participate in this study. All procedures were approved by Marquette University's Institutional Review Board in accord with the Declaration of Helsinki. All subjects (23.5 ± 4 yr of age; mean ± SD) reported to be right-hand dominant and naïve to the purposes of this study. Each wore a right-handed CyberGlove (Immersion, San Jose, CA). Nineteen joint angle measurements were recorded from flexion/extension of the phalangeal joints (proximal, middle, and distal), as well as abduction of the thumb and fingers. Glove signals encoding the configuration of fingers were sampled at 50/s. As described previously (Liu and Scheidt 2008a; Mosier et al. 2005), the glove's 19-dimensional (19-D) signal vector was mapped onto the 2-dimensional (x, y) coordinates of a cursor on a computer screen using a linear kinematic transformation

$$\begin{array}{c}P=\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{llll}{a}_{x,1}\hfill & a_{x,2}\hfill & \cdots \hfill & a_{x,19}\hfill \\ a_{y,1}\hfill & a_{y,2}\hfill & \cdots \hfill & a_{y,19}\hfill \end{array}\right]{\left[\begin{array}{llll}{h}_1\hfill & h_2\hfill & \cdots \hfill & h_{19}\hfill \end{array}\right]}^T+\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right]\\ =AH+P_0\end{array}$$ (1)

where P = [x, y]^T is the cursor location on the monitor (the task space), H = [h₁, h₂, …, h₁₉]^T is the glove signal vector (the articulation space), and A is a matrix of mapping coefficients [a_i,j] (the hand-to-screen map). P₀ = [x₀, y₀]^T is a constant-valued offset that aligns the hand's resting posture to the origin of task space (Fig. 1A, center hand configuration). Articulation degrees of freedom contributing to cursor motion comprise the “task-relevant” subspace of H

$$H_T=A^{+}AH$$ (2a)

where A⁺ = A^T(AA^T)⁻¹ is the Moore–Penrose pseudoinverse of A. The matrix (I₁₉ −A⁺A) projects H onto the complementary null space (thereby identifying articulation degrees of freedom that do not contribute to cursor motion; Mosier et al. 2005)

$$H_N=\left(I_{19}-A^{+}A\right)H$$ (2b)

where I₁₉ is the 19-D identity matrix.

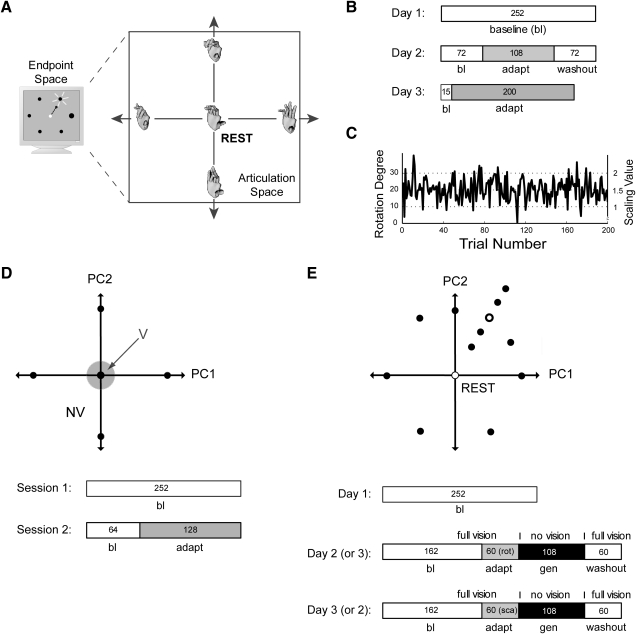
Fig. 1.

A: hand configuration was mapped onto a computer screen (the 2-dimensional task space) through a smooth and linear mapping. Representative hand postures at the center (rest) and boundaries of a planar slice through the 19-dimensional (19-D) articulation space are shown to the right, as are the corresponding locations of the 6 Test Session 1 targets. B: sequence of trials performed by both the Rotation and Scaling groups of Test Subjects. Shading indicates blocks of trials wherein visual distortions were imposed. C: pseudorandom sequence of visuomotor distortion magnitudes presented to Test Subjects during the adaptation block of Test Session 3. D: task space target locations for the group of Control Subjects. Note that real-time visual feedback was presented within only a small neighborhood of the Rest target for both the Rotation and Scaling groups. Control Subjects performed 2 experimental sessions on the same day (bottom). PC1, principal component 1; PC2, principal component 2; V, vision; NV, no vision. E: representative task space target locations for one subject from the Generalization group. The open circle target was the only target trained during adaptation blocks of trials (Generalization Sessions 2 and 3; bottom). This pattern of target locations was aligned with a different target direction for each different subject. Generalization block movements (gen) were performed entirely without real-time visual feedback or knowledge of results, although periodic “refresher” trials were made to the trained target with distorted visual feedback. rot, rotation; sca, scaling.

The primary experiments described in the following text were conducted in three sessions performed on separate days. In session 1, subjects learned to manipulate the cursor using coordinated motions of the fingers in a series of center-out, goal-directed cursor movements. In later sessions, we transformed the nominal hand-to-screen projection using either a rotation θ of cursor motion about the origin within task space

$$P_T=\left[\begin{array}{c}{x}_{rotated}\\ y_{rotated}\end{array}\right]=T_{R}P=\left[\begin{array}{cc}\cos \left(\theta \right)& -\sin \left(\theta \right)\\ \sin \left(\theta \right)& \cos \left(\theta \right)\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$ (3)

or a scaling k of cursor motion in task space

$$P_T=\left[\begin{array}{c}{x}_{scaled}\\ y_{scaled}\end{array}\right]=T_{S}P=\left[\begin{array}{cc}k& 0\\ 0& k\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$ (4)

By controlling how θ and k varied from one trial to the next, we sought to characterize how subjects use information about performance errors in a low-dimensional task space to update patterns of coordination within a high-dimensional set of control variables as they adapt to a rotational (T_R) or scaling (T_S) distortion of a recently learned relationship between motor output and its behavioral consequence.

Defining the hand-to-screen mapping and target locations

All subjects used the same calibration procedure (Liu and Scheidt 2008a), which was based on the observation that during object manipulation, the vast majority of kinematic variance between static hand postures can be captured by a small number of independent principal components (PCs) (Jerde et al. 2003b; Santello et al. 1998, 2002). Briefly, subjects donned the data glove and performed three repetitions of a random sequence of 24 hand postures corresponding to the static finger spelling characters of the American Manual Alphabet (AMA). [The AMA is a skill to which most individuals are naïve and it is well suited for studying how the brain learns novel motor coordination patterns in that its kinematic demands have been well characterized (Jerde et al. 2003a,b).] Subjects were provided photographic images of the desired hand postures as formed by a skilled AMA instructor. Gesture formation was coached by the investigator who ensured that there were no perceivable differences between the desired and realized gestures at the moment of data sampling.

Glove recordings were averaged across repetitions for each character. A data matrix H was constructed by appending, side-by-side, the column vectors of average signals h from each AMA character. Principal component analysis (PCA) was used to derive an ordered set of orthogonal bases spanning the space of AMA hand postures (cf. Johnson and Wischern 1998). The hand-to-screen mapping matrix A was constructed by stacking the resulting first two PCs on top of each other as row vectors (Eq. 1). Consequently, any screen location could be reached by superimposing motion along the two finger coordination patterns reflecting the greatest postural variation within a set of static AMA hand postures (Fig. 1A).

Six goal targets were distributed around a circle (8-cm radius) centered at the origin of the task space (Fig. 1A). Although the hand-to-screen map varied slightly from subject to subject due to differences in hand size, this configuration of targets ensured that all subjects could maneuver the cursor directly from its resting location to any target without finger collisions.

Experimental protocols

Subjects were seated 0.6 m in front of a computer monitor that served as the space in which cursor motion might occur. Subjects were provided no details of the relationship between hand configuration and cursor/target screen location. Subjects were randomly assigned either into a test group (n = 10), a control group (n = 14), or a generalization group (n = 6).

TEST GROUP.

Subjects participated in three experimental sessions conducted on three separate days.

Test Session 1 examined how subjects coordinate redundant kinematic control variables as they learn to maneuver a virtual object (a 5-mm-diameter cursor) between targets embedded within a low-dimensional workspace. Subjects practiced acquiring screen targets by maneuvering the cursor between a common resting position and each of six, 10-mm-diameter goal targets (Fig. 1A, left) in a series of 252 trials (Fig. 1B, top). Each target was presented once in pseudorandom order within each cycle of six trials. Each cycle included five training trials with ongoing visual feedback of cursor motion and one test trial wherein cursor feedback was suppressed. This was done to assess the time course and extent of learning without confounding influence from online feedback corrections. Each of the six targets was presented as a test trial once in pseudorandom order within each block of six consecutive cycles. No cursor was visible between trials such that subjects received information about the hand-to-screen mapping only during training trials.

Trials began with the appearance of the resting target. To assist in capturing the resting target without cursor feedback, we provided information about the distance between the desired resting configuration and the hand's actual configuration using a secondary display element, a variably sized circle centered at the origin. The circle's diameter was proportional to the Euclidean distance (measured in glove signal units [GSUs]) between the instantaneous hand configuration and the resting posture. Subjects were given unlimited time to minimize the circle's size so that each trial started from a consistent posture. Once the resting posture was held for 200 ms, one of six goals appeared, prompting movement. Test subjects were instructed to form hand gestures so that the cursor acquired the target as quickly and accurately as possible (within a 3.0-s time limit) and to hold the final gesture throughout a 2.0-s feedback interval wherein the final cursor position was displayed statically (for training but not test trials). Afterward, subjects were prompted to recapture the resting target. Subjects could rest at any time during the nearly 1-h session by choosing not to reduce the resting target circle size between trials.

Test Session 2 compared how subjects reorganize redundant kinematic control variables in response to a stepwise rotation or dilation of the recently learned hand-to-screen map. Subjects first reacquainted to the hand-to-screen transformation learned in Session 1 (the baseline map) by practicing the target-capture task for 20 min. After a 10-min rest, subjects then performed another set of 72 baseline trials before experiencing either a stepwise rotational (θ = 45°; five subjects) or scaling (k = 1.8; five subjects) distortion of visual performance feedback in a set of 108 adaptation trials (Fig. 1B, middle). (These particular distortion values were chosen to induce equivalent cursor deviations.) During adaptation trials, both groups of subjects had to modify finger coordination if they were to recover the desired initial performance. Finally, subjects performed 72 trials with the baseline mapping to wash out any learning acquired during the adaptation block.

Pilot experiments revealed that subjects in the scaling group could readily (i.e., within a single trial) compensate for a step change in movement amplitude using continuous visual feedback. We therefore modified cursor feedback for this group to eliminate cues necessary for feedback corrections to occur, encouraging subjects to rely on adaptation of feedforward motor commands to minimize performance errors. Whereas continuous feedback was provided throughout the targeting phase of training trials for the rotation group, scaling group subjects received feedback of cursor motion only within a small neighborhood of the central resting target (i.e., when the cursor was less than one fifth of the goal distance). This provided a glimpse of initial movement direction and extent without promoting online visual feedback corrections later in the trial. Subjects in both groups received a 2-s snapshot of final cursor location after each training trial.

Test Session 3 characterized how Test subjects use information about errors in the extent and direction of cursor motion to update patterns of coordination in redundant kinematic control variables from trial to trial. Both subsets of Session 2 Test subjects performed a series of 215 cursor movements directed from the central resting target to a single goal located in the upper right-hand quadrant of the screen (see Fig. 1A). The first 15 trials were performed with the baseline hand-to-screen mapping (Fig. 1B, bottom). Subjects then performed 200 adaptation trials wherein they experienced either a variable rotation (rotation group: 20 ± 6.7°; mean ± 1SD both here and elsewhere) or scaling (scaling group: ×1.5 ± 0.4). The disturbance sequence in both cases had nonzero mean values and both were drawn from a Gaussian distribution. The disturbance magnitude remained constant for the duration of each movement, changing only between trials (Fig. 1C). By design, the pseudorandom sequence was constructed to ensure insignificant correlation between perturbation magnitudes on consecutive trials. (The significance of each correlation term was evaluated by comparing the correlation magnitude at each integer lag value to an estimate of the 95% confidence interval bounding zero correlation: 2σ ≈ 2/√N; Box et al. 1994.) Each subject in each group experienced the same perturbation sequence during training.

CONTROL GROUP.

Because visual cursor feedback conditions differed between the two Test Groups in Sessions 2 and 3, differences in learning might simply reflect differential engagement of feedback mechanisms during movement. We therefore recruited a new set of subjects who participated in two sessions on a single day.

Control Session 1: Subjects trained under the baseline mapping with full visual feedback on a reduced set of training targets (Fig. 1D, top) for a minimum of 60 min (not less than 252 trials). As described in the following text, all subjects reached asymptotic levels of kinematic performance measured in terms of reaching error and cursor path linearity. Each target was presented once in pseudorandom order within each cycle of four trials. After a 15-min rest, subjects were then assigned randomly to either a rotation or scaling group (7 subjects each). All of them made center-out cursor movements in a second session wherein cursor feedback was limited to the same small neighborhood of the central resting target as described earlier for the scaling group of Test subjects.

Control Session 2: The first 64 trials were performed with the baseline hand-to-screen mapping. Subjects then performed 128 adaptation trials wherein they experienced either a stepwise 45° rotation or ×1.8 scaling distortion of visual performance feedback (Fig. 1D, bottom). As with Test subjects, Control subjects also received knowledge of results in the form of a 2-s snapshot of the final cursor location after each trial.

GENERALIZATION GROUP.

These experiments explored how adaptation to rotation and scaling generalize across space. Subjects participated in three experimental sessions conducted on three consecutive days (Fig. 1E, bottom).

Generalization Session 1: Subjects trained under the baseline mapping by moving the cursor in center-out movements to six targets exactly as during Test Session 1.

Generalization Session 2: Subjects reinforced the learned baseline mapping by performing 162 trials identical to those made in the first session. Subjects then were assigned to one of two groups (three subjects each). One group was exposed to a 45° rotational distortion of the baseline map while performing 60 trials toward just one of the six targets (the training targets were counterbalanced across subjects), whereas the other group was exposed to the ×1.8 scaling distortion during these trials. As in Test Session 1, full feedback of cursor motion was available throughout these trials regardless of distortion type. Subjects then performed a block of 108 generalization trials, the majority of which were performed entirely without visual or other performance feedback (feedback scheduling described in the following text). Subjects were instructed to “make hand gestures bringing an invisible cursor to the cued target locations.” For all subjects, generalization targets included the trained target as well as targets at ±30, ±60, ±120, and 180° relative to the trained target on the 8-cm-radius goal circle (cf. Fig. 1E, top). Additional generalization targets included targets located along the same radial direction as the trained target, but at 4-, 6-, 10-, and 12-cm screen distances. Target presentation order was pseudorandomized within cycles of 18 trials. Each cycle included the 12 generalization targets (presented one time each, without cursor feedback) and three sets of two “refresher” trials made to the trained target with distorted visual feedback. Refresher trials were included to maintain adaptation throughout generalization testing. The last 60 trials in Generalization Session 2 were made under the baseline hand-to-screen mapping to wash out adaptations acquired during training.

Generalization Session 3: Experiments were conducted using the same protocol as that in Generalization Session 2 except subjects who adapted the rotational distortion in Session 2 adapted the scaling distortion in Session 3 and vice versa. This was done to minimize crossover effects.

Data analysis

We analyzed seven aspects of kinematic performance to quantify learning-related changes in cursor manipulation. Spatial or Endpoint Error ε was the Euclidean distance between the target location on the computer screen and the cursor location (irrespective of whether visible or not visible) at the end of each trial. Endpoint error was computed separately for training trials (wherein cursor feedback was provided) and generalization trials (wherein cursor feedback was withheld). Aspect ratio, a measure of cursor path linearity, was defined as the ratio of maximum lateral cursor excursion to the distance between start and end positions of the cursor. A straight segment has zero aspect ratio. The instantaneous cursor vector direction was computed as the interior angle formed between two vectors: the first connecting each consecutive pair of sampled cursor positions during movement (i.e., where cursor speed exceeded 10% of its maximum) and the second joining the first position in that pair and the target location. The hand's peak speed configuration was the glove signal vector recorded at the moment of peak cursor speed. We evaluated performance changes in degrees of freedom that did not contribute to cursor motion using the across-trial, task- and null-space variabilities defined as the SD of the task- and null-space projections of the final hand postures (cf. Eqs. 2a and 2b). These variability measures were computed for each target within pairs of trial blocks (i.e., 10 training trials per movement direction) and then averaged across direction. Adaptation rate was evaluated by fitting an exponential function, ε = a exp(−t/λ) + c, to the behavioral performance data: a is a gain factor, λ is the time constant of error reduction, and c is the steady-state residual error at the end of training. Generalization of learning to untrained targets was quantified on a per-target basis using the generalization ratio: (ε₀ − c)/ε₀, where ε₀ is the initial uncompensated Euclidean error induced by the distortion and c is the steady-state residual error at each generalization target after training. If after training a subject moves to a target with an endpoint error of only 6 screen units, whereas the distortion induces 60 units of error, then the generalization ratio would be 0.9 (quite large). If instead the subject persists in making 54 units of error after training, the generalization ratio for that target would be 0.1.

We also sought to characterize how the complexity of within-trial patterns of finger coordination changes with learning. We used principal component analysis (PCA) to compute for each trial an ordered set of orthogonal eigenvectors [kinematic principal components (KIN_pc), called eigenpostures by Ebner and colleagues (Mason et al. 2001)] and a set of temporal weighting vectors KIN_wv(t) that together represent patterns of kinematic coordination emergent during movement as a result of the adaptive planning and execution of finger motion. Note that because PCA is recomputed for each movement, the resulting PCs are not the same as those used to define the hand-to-screen mapping. Briefly, a data matrix T was constructed by appending, side-by-side, the column vectors of hand signal time series from each signal h_i, where i ∈ {1, 2, …, 19}. PCA was performed and patterns of covariation between finger joints within the trial were identified. Thus if H_n is the matrix time series of 19-D hand signal vectors from a particular trial n, each hand signal vector can be reconstructed by multiplying the temporal weighting vectors [the 19 KIN_wv(t)] by the eigenpostures (the 19 KIN_pc) and adding

$$H_n\left(t\right)=H_{avg,n}+\left[{\text{KINwv}}_{\text{1,}n}\left(t\right)\cdot {\text{KINpc}}_{1,n}\right]+\left[{\text{KINwv}}_{2,n}\left(t\right)\cdot {\text{KINpc}}_{2,n}\right]\cdots +\left[{\text{KINwv}}_{19,n}\left(t\right)\cdot {\text{KINpc}}_{19,n}\right]$$ (5)

The total 19-D pattern for each hand trajectory can therefore be thought of as a time-varying sum of the average hand shape (H_avg,n) plus the weighted combination of 19 different eigenpostures. Because the PCs are ordered such that the first PC captures the greatest amount of signal variation within the data set, whereas the 19th PC captures the least, we were particularly interested in quantifying the distribution of data variance accounted for by the first few PCs as a function of learning and adaptation across trials. We computed variance accounted for as: VAF = {1 − [var (ε_n)/var (H_n)]} × 100%, where H_n is the matrix containing the glove signal recordings for a given trial and ε_n is the difference between the matrix H_n and the hand signal matrix obtained by considering only specific (e.g., the first three) eigenpostures. As revealed by examining the weighting vectors, the contributions of the different PCs range from simple monotonic changes in hand configuration (KIN_pc,1) to increasingly complex polyphasic changes (higher-order PCs). This analysis therefore characterizes how within-trial movement variability is distributed across coordination patterns of increasing temporal complexity and how this distribution changes with learning.

We next sought to quantify the extent to which stepwise application of rotation and scaling distortions induce reorganization of the “motor representation” of the Euclidean space onto which finger movements are mapped. We did this by evaluating changes in articulation-space coordination occurring after adaptation in Control Session 2. We computed the change in hand configuration (ΔH) and cursor position (ΔP) between the starting (rest) and final positions for each of 32 trials at the end of the adaptation trial block (ADAPT) as well as at the beginning (BL1) and end (BL2) of baseline trials in that session (i.e., trials recorded after 20 min reacquaintance with the baseline task). We estimated the inverse hand-to-screen transformation B_est used to solve the target acquisition problem during each of these three sets of trials

$$H=B{\text{}}_{est}P$$ (6)

by a least-squares fit to the data

$$B_{est}=HP{P}^T{\left(P{P}^T\right)}^{-1}$$ (7)

We evaluated how well the B_est obtained after adaptation (B_ADAPT) was predicted by rotation (T_R) or scaling (T_S) of the B_est obtained at the end of baseline practice (B_BL2) by computing the difference magnitude ΔB_ADAPT

$$\Delta B_{ADAPT}=\Vert B_{ADAPT}-B_{BL2}{T}^{-1}\Vert$$ (8)

We evaluated the significance of this difference by comparing it with the difference magnitude obtained from the beginning (B_BL1) to the end (B_BL2) of baseline training (wherein T⁻¹ of Eq. 8 is assumed to be the identity matrix)

$$\Delta B_{NOISE}=\Vert B_{BL1}-B_{BL2}\Vert$$ (9)

A difference magnitude ΔB_ADAPT exceeding ΔB_NOISE would strongly suggest that adaptation induced changes in the motor representation of the task space. Such changes would be inconsistent with a simple scaling or rotation of the effective target location within task space and the retention of the nominal (baseline) inverse hand-to-screen map.

Characterizing adaptation to rotation and scaling distortions of a novel kinematic mapping

We used systems identification techniques to characterize how Test Session 3 subjects use information about past kinematic performance to update motor commands on upcoming trials. We modeled trial-by-trial performance in the presence of variable rotations and scalings using a family of limited-memory, autoregressive models with external input

$$E_n={\displaystyle \sum _{j=1}^L{a}_j{E}_{n-j}+b_0{K}_n}$$ (10)

where n is the trial index, the a terms and b₀ are constant coefficients weighting the influence of performance errors from the prior j trials (E_n−j), and K_n is the magnitude of feedback distortion from the current trial. The error E is effectively a state variable and the number of elements in the sum specifies the order of the underlying learning dynamics [i.e., the constant L corresponds to the minimum number of memory elements (states) needed to describe the trial-by-trial evolution of errors]. Since we designed the sequence of perturbations to be uncorrelated from one trial to the next, trial-by-trial correlations in a subject's motor performance could not originate from the perturbation sequence itself but, rather, must originate from the processing of sensorimotor memories within the neuromotor controller. The family of models described by Eq. 10 can represent not only processes having very limited memory requirements (e.g., when L is small), but also processes having more complex dynamics. Note that for visuomotor transformations such as those applied in our study, the subject has no way to differentiate between errors induced by manipulation of task space and those induced by internal sources of variability (such as by motor execution noise). What they see is kinematic performance information without independent information about perturbation strength. Therefore the family of models described by Eq. 10 does not explicitly include memories of prior perturbation, as is proper for visuomotor distortions.

To select the most parsimonious model structure for the Rotation and Scaling subgroups, we first averaged movement error across subjects within each group on a trial-by-trial basis, thereby reducing the effect of intersubject execution variability on the structure estimation procedure. We used the Matlab computing environment (arxstruc function of the Systems Identification Toolbox) to fit all model structures of moderate complexity (L < 10) to one half of the resulting (perturbation, error) time series data under consideration and evaluated their ability to predict the sequence of errors in the other half. We used the minimum descriptor length (MDL) criterion (Ljung 1999) to identify the structure most consistent with the information filtering manifest in the trial series of errors we observed during adaptation (selstruc function of the Systems Identification Toolbox). [Of all models considered, the MDL model is the one that minimizes a modified mean-square-error (MSE) function: MSE_MDL = MSE [1 + m log (k)/k], where m is the total number of parameters in the model being considered (L + 1) and k is the number of data points in the estimation data set. Thus the MDL criterion offers an efficient compromise between model complexity and the quality of fit to the data.] We then refit the resulting model to each subject's original time series (MATLAB arx function of the System Identification Toolbox) to obtain individualized estimates of the model coefficients.

We sought to determine whether stochastic application of rotation and scaling distortions induce reorganization within the motor representation of space in a manner consistent with stepwise application of the distortions. We did so by evaluating the influence of task-space performance errors on null-space control variable changes in Test Session 3. For each of the 200 random perturbation trials, we selected the hand configuration vector at the moment of peak cursor speed during target capture. We decomposed this collection of vectors into independent task- and null-space components before computing the total signal variance within each subspace. We then computed the normalized variance [i.e., variance per degree of freedom (DOF)] by dividing the two subspace variances by the dimensionality of their respective subspaces.

Inverse- and forward-dynamics analyses of a more common reaching task

Finally, we performed a set of inverse- and forward-dynamics analyses of horizontal planar arm movements (see Appendix) to facilitate an understanding of how the current study of manual goal-directed reaching relates to an everyday reaching task. The purpose of the analysis was to examine patterns of kinetic coordination at the shoulder and elbow joints of a two-joint arm and to determine how these patterns would change during compensation for an imposed visuomotor rotation or scaling. Specifically, we compared the patterns of generalized muscle torques (Sainburg et al. 1995) needed to move the hand from a central origin to eight targets distributed around a 20-cm-diameter circle, before and after application of a visuomotor rotation (45° counterclockwise) or scaling (×2). The limb model we used for the analysis was the same as that used previously to simulate the adaptive response to mechanical force-field perturbations both in the presence and absence of ongoing visual feedback (Scheidt et al. 2005).

Statistical hypothesis testing

Statistical testing was carried out within the Minitab computing environment (Minitab, State College, PA). Error bars in figures represent ±1SD. Mixed-model, repeated-measures ANOVA and subsequent post hoc tests compared performance measures across training periods, across visual distortion types, and eigenposture number. Planned paired t-tests were used to compare the adaptive change in finger coordination resulting from prolonged exposure to rotation and scaling of the nominal hand-to-screen map. Planned two-sample t-tests were used to compare the normalized variability in task space and null space resulting from exposure to random rotations and scalings of the nominal hand-to-screen map. Effects were considered significant at the α = 0.05 level.

RESULTS

Session 1: baseline performance (test, generalization, and control groups)

Subjects gained proficiency in controlling the cursor with practice. Initial training trials were dominated by exploratory behavior that required ongoing cursor feedback to acquire targets (shown for a representative Test Group subject; Fig. 2A, top left); task-space projections of hand configuration during initial test trials performed without cursor feedback showed little directional selectivity (Fig. 2A, bottom left). Terminal accuracy of both training and test trials greatly improved with practice during Session 1 (Fig. 2A, middle) and by the end of training (Fig. 2A, right), task-space trajectories were generally straight and terminated in close proximity to the goal regardless of visual feedback condition. Trajectory rectilinearity developed progressively; whereas instantaneous cursor vector direction was unlikely to point toward the goal early on (Fig. 2B, left), this likelihood increased throughout the middle and late phases of training (Fig. 2B, middle and right, respectively).

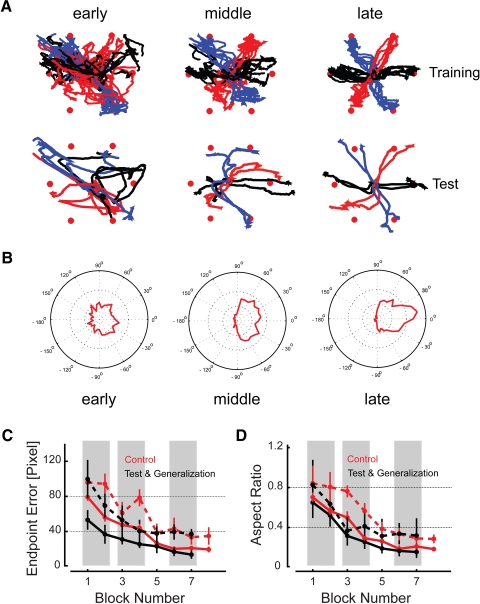
Fig. 2.

Analysis of kinematic performance in task space during Session 1. A: hand paths from a representative Test Group subject: Training trials (top) were performed with real-time visual feedback, whereas Test trials (bottom) were performed without any performance feedback. All trials recorded during the early, middle, and late thirds of training are displayed (left to right). B: polar histograms of instantaneous movement directions relative to the target computed across all subjects. The outer circle corresponds to 4% of all instantaneous movement directions and the innermost circle represents 1%. Bin width: 10°. Separate histograms are presented for early, middle, and late thirds of training (left to right). C and D: Endpoint Error and Aspect Ratio measures as a function of trial block number during both training (solid) and test (dashed) trials for Control Group subjects (red) and for the Test Group and the Generalization Group subjects (collapsed and shown in black). Shading corresponds to trial blocks (early, middle, late) used to create A and B.

Task-space error decreased in both training and test trials from the first to last block for each subject group (one-sided Tukey t-test: P < 0.001 in each case) (Fig. 2C, left). We also found practice-related reduction in the aspect ratio of cursor trajectories in both training and test trials for each group (P < 0.002 in each case) (Fig. 2D). Despite the difference in number of training trials per cycle in the Control Group (four) versus the other two groups (six), subjects in all three groups attained equivalent levels of performance by the end of training. Separate two-way, mixed-model, repeated-measures ANOVA found no main effect of training group on final endpoint error [F_(2,27) = 1.28; P = 0.298] or aspect ratio [F_(2,27) = 0.14; P = 0.871], although a main effect of trial type (training vs. test) was apparent [Error: F_(1,27) = 174.14; P < 0.0005; Aspect Ratio: F_(1,27) = 17.60; P < 0.0005]: not unexpectedly, subjects performed better with ongoing visual feedback than without.

Learning was accompanied by an increase in regularity of final finger configurations attained during target capture (Fig. 3A). As shown for the combined Session 1 data from all subjects trained on six targets (Test and Generalization subjects; solid traces) and for subjects trained on four targets (Control subjects; dashed traces), variability in hand posture at trial's end decreased throughout training for those degrees of freedom contributing to cursor motion (thick traces) as well as for those that did not (thin traces). Average task-space variability decreased from beginning to the end of training (i.e., from blocks 1 and 2 to blocks 6 and 7; Fig. 3A, shading) (paired Tukey t-test: P < 0.0005) as did average null-space variability (P < 0.0005). In all cases, performance appeared to reach steady state by block 5 or block 6.

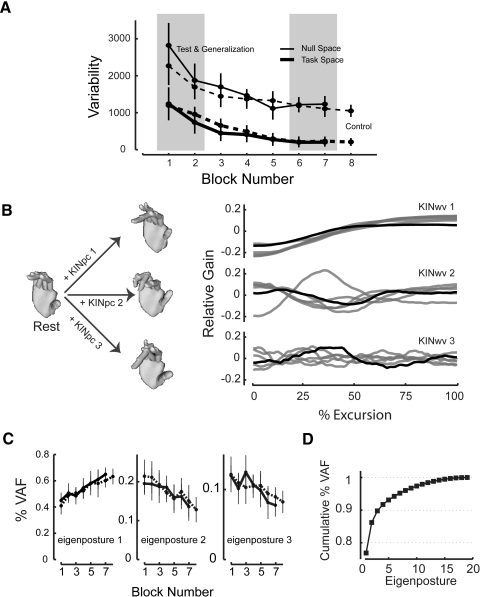
Fig. 3.

Analysis of kinematic performance in articulation space during Session 1. A: postural variability as a function of block number in task space (thick traces) and null space (thin traces) measured in glove signal units (GSU²) for Control Group (dashed) and combined Test and Generalization groups (solid). Shading corresponds to trial blocks included in the statistical analysis (see text). B: analysis of finger coordination from a representative Test Group subject. The first 3 sets of eigenpostures and temporal weighting time series computed from the measured changes in finger configuration. C: percentage of data variance accounted as a function of trial block number for the first 3 eigenpostures for Control Group subjects (dashed) and the combined Test and Generalization group subjects (solid). D: cumulative percentage data variance accounted for as a function of eigenposture number for the ordered set of eigenpostures and temporal weighting time series.

Training also induced a systematic decrease in the complexity of finger joint motion during the trials. Figure 3B shows the first three eigenpostures (left) and temporal weighting time series (right) from a representative subject computed from movements in the final trial block (bold traces) made from the central resting location to the screen target directly to its right (Fig. 1A, target drawn with a boldface line). Temporal weightings computed from movements made to the other targets are shown in gray. Across movement directions and subjects, the first eigenposture consistently displayed a simple, monotonically increasing temporal weighting. The second and third eigenpostures displayed a systematic increase in the number of oscillations in their contribution to the realized sequence of hand postures and thus their contributions had greater spatiotemporal complexity than did the first eigenposture. Group analysis found that control of redundant degrees of freedom decreased in complexity with practice (Fig. 3C): paired Tukey t-tests revealed a significant increase in the amount of data variance accounted for by the first eigenposture early to late in training (Fig. 3C, left), both for the combined Test and Generalization subjects (P < 0.0005) as well as for Control subjects (P < 0.0005). In contrast, the amount of data variance accounted for by the second and third eigenpostures decreased with practice (Fig. 3C, middle and right, respectively). Paired t-tests found a significant decrease in %VAF for eigenpostures 2 and 3 generated by both the Test/Generalization and Control groups (P < 0.002 in all cases). Thus as subjects practiced the target-capture task, they increasingly invoked monotonic changes in finger postures while decreasing use of patterns with higher spatiotemporal complexity. In contrast to the variability data shown in Fig. 3A, this simplification of coordinated control progressed steadily throughout training and did not asymptote even after hundreds of trials. Approximately 90% of articulation data variance was accounted for by the first three eigenpostures by the end of training (Fig. 3D).

Session 2: adaptation to stepwise rotation and scaling of the hand-to-screen mapping (Test and Control groups)

Representative Rotation and Scaling subjects readily learned to compensate for a stepwise introduction of distortion applied to the newly acquired hand-to-screen mapping (Fig. 4A). During preadaptation practice with the baseline map, cursor trajectories were well directed to the target, indicating that subjects had become proficient in the target-capture task during Session 1. Imposing the stepwise counterclockwise (CCW) rotation caused cursor trajectories to deviate CCW initially but later “hook back” to the desired final position (Fig. 4A, top). With practice under the altered mapping, trajectories regained their original rectilinearity. When the baseline map was suddenly restored, initial trajectories deviated clockwise (CW) relative to trajectories made at the start of Session 2, indicating that subjects used an adaptive feedforward strategy to compensate for the rotation. These aftereffects were eliminated by the end of the washout period. Similarly, initial exposure to a stepwise increase in the gain of the hand-to-screen mapping resulted in cursor trajectories that far overshot their goal (Fig. 4A, bottom). Further practice under the altered mapping reduced these extent errors. Restoration of the baseline mapping resulted in initial cursor movements that undershot their goal. These targeting errors were virtually eliminated by the end of the washout period. These findings were replicated across all subjects in both the Test and Control groups.

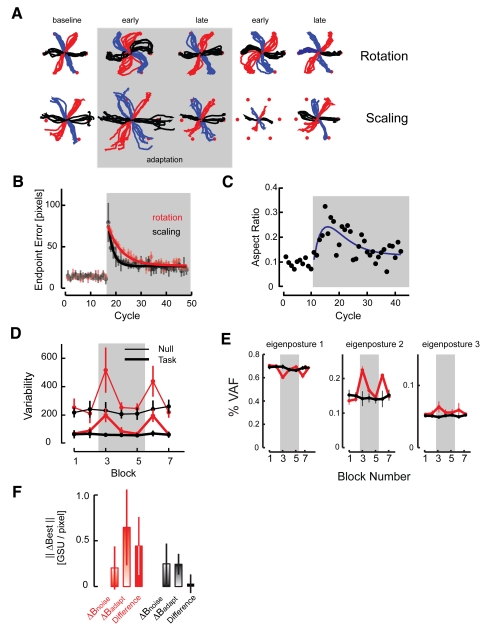
Fig. 4.

Analysis of kinematic performance during Test Session 2. A: hand paths from representative subjects from the Rotation (top) and Scaling (bottom) groups during baseline (left) adaptation (early and late) as well as washout (early and late) blocks of trials. Shading indicates the adaptation block of trials. B: group analysis: Euclidean task space error for the Rotation and Scaling groups of Control Group subjects. C: Aspect Ratio for Rotation subjects in the Control Group as a function of cycle number. As in the other panels, shading indicates the adaptation block of trials. D: postural variability as a function of block number in task space (dashed) and null space (solid) for Rotation Group subjects (red) and Scaling Group subjects (black). E: percentage of data variance accounted as a function of trial block number for the first 3 eigenpostures for Rotation Group subjects (red) and Scaling Group subjects (black). Note the differences in scale across the 3 panels. F: ΔB_est, our measure of reorganization within the redundant articulation space, for rotation (red) and scaling (black) Control Group subjects both before (solid bars) and after (unfilled bars) visuomotor adaptation.

We computed adaptation rates using spatial Endpoint Error as a performance measure for Control group subjects (who received a glimpse of cursor motion at movement onset and feedback of final cursor position after movement ceased; Fig. 4B). On imposing the distortion, subjects in the rotation and scaling subgroups decreased Endpoint Errors at decidedly different rates (λ_ROT: 5.5 ± 0.8 cycles; λ_SCA: 2.1 ± 0.5 cycles; two-sample t-test: P < 0.0005) in a manner well characterized using a single exponential function of cycle number (data variance accounted for = 77 ± 9%). This difference was not caused by differences in the magnitude of initial error, which averaged 74 ± 5 pixels for rotation subjects and 79 ± 24 pixels for scaling subjects (P = 0.61). In contrast, the time course of changes in Aspect Ratio for the rotation subjects first increased and then decreased in a pattern better fit using a dual-exponential function than a simple falling exponential (Fig. 4C, blue trace).

Across-trial task- and null-space variability depended on training phase during exposure to and recovery from rotation but not scaling distortions of the baseline hand-to-screen map (Fig. 4D). An initial two-way MANOVA found significant interaction between Test Group distortion type (rotation, scaling) and training phase (baseline, early and late adaptation, early and late recovery: blocks 2, 3, 5, 6, and 7, respectively) [Wilk's F_(10,114) = 7.31; P < 0.0005]. We therefore performed separate one-way, repeated-measures ANOVAs to examine how training influences task- and null-space variability for the rotation and scaling groups. Rotation subjects exhibited main effects of training phase for both task-space [F_(5,25) = 35.38; P < 0.0005] and null-space variability [F_(5,25) = 14.09; P < 0.0005]. In contrast, scaling subjects exhibited no main effects of training phase on either measure [task: F_(5,25) = 1.79; P = 0.152; null: F_(5,25) = 0.62; P = 0.683]. Specifically, performance variability increased transiently after both imposing and removing the rotation (but not the scaling) distortion.

Within-trial variations in coordination also depended on training phase for rotation but not scaling subjects (Fig. 4E). An initial MANOVA revealed significant interaction between distortion type and training phase for the contribution of the first three eigenpostures to overall hand-shape [Wilk's: F_(12,100) = 12.72; P < 0.0005]. Separate one-way, repeated-measures ANOVAs found that rotation subjects exhibited a marked effect of training phase for all three eigenpostures [Eigenposture 1: F_(4,24) = 219.43, P < 0.0005; Eigenposture 2: F_(4,24) = 106.92, P < 0.0005; Eigenposture 3: F_(4,24) = 3.35, P = 0.036]. Post hoc t-tests found that for Eigenposture 1, %VAF decreased at rotation onset but recovered to baseline levels by the end of adaptation (Fig. 4E, left). A similar %VAF decrease and subsequent recovery occurred on removal of the rotation. Eigenpostures 2 and 3 increased %VAF at rotation onset and, for Eigenposture 2, on its removal (Fig. 4E, middle and right). Onset and offset of the scaling distortion induced no systematic change in %VAF for the first three finger coordination patterns.

We next examined the extent to which B_est (the least-square estimate of each Control Group subject's learned inverse map) changed during adaptation to the rotation and scaling distortions. For the subjects exposed to the rotation distortion, B_est after adaptation could not reasonably be characterized as a rotated version of the baseline mapping because ΔB_ADAPT (Eq. 8) far exceeded ΔB_NOISE for these subjects [0.64 ± 0.41 glove signal unit (GSU) per pixel vs. 0.20 ± 0.19 GSU/pixel, respectively; Fig. 4F, red gradient bars] (paired t-test comparing ΔB_ADAPT to ΔB_NOISE: P = 0.010). The within-subject difference between ΔB_ADAPT and ΔB_NOISE was 0.44 ± 0.32 GSU/pixel (Fig. 4F, red solid bar). Thus the rotational distortion induced these subjects to form a new inverse hand-to-screen mapping during adaptation. In contrast, ΔB_ADAPT did not exceed ΔB_NOISE for scaling subjects (0.24 ± 0.11 vs. 0.25 ± 0.22 GSU/pixel, respectively; Fig. 4F, black gradient bars) (P = 0.942), yielding an average within-subject difference between ΔB_ADAPT and ΔB_NOISE of 0.03 ± 0.10 GSU/pixel (Fig. 4F, black solid bar). We therefore found no compelling reason to reject the hypothesis that after adaptation, scaling subjects simply contracted their baseline inverse map to compensate for the imposed scaling distortion. Taken together, the results shown in Fig. 4 demonstrate that applying a rotational distortion to cursor motion initiated a search within redundant degrees of freedom for a new solution to the target-capture task, whereas application of the scaling distortion did not. For rotation subjects, the effect of this search was the formation of a new inverse hand-to-screen map, one that differed significantly from the one established during baseline training.

Session 3: adaptations to pseudorandom rotation and scaling distortions (Test group)

As shown for representative Rotation and Scaling subjects (Fig. 5A), subjects learned to compensate for the approximate mean distortion when the effective mapping varied pseudorandomly from trial to trial. When the rotation or scaling distortion was less than average, movements exhibited overcompensation in that they either initially deviated to the target's left and then curved CW (Fig. 5A, top left) or undershot the goal (Fig. 5A, bottom left). In contrast, trials with distortions greater than average exhibited undercompensation (Fig. 5A, right panels). Movements made in trials with the approximate mean distortion were directed straight to the target and terminated in its close proximity. The presence of mirror-symmetric trajectory deviations early in the movement for both subject groups provides strong evidence that subjects used an adaptive, feedforward strategy to plan and execute target capture regardless of distortion type.

Fig. 5.

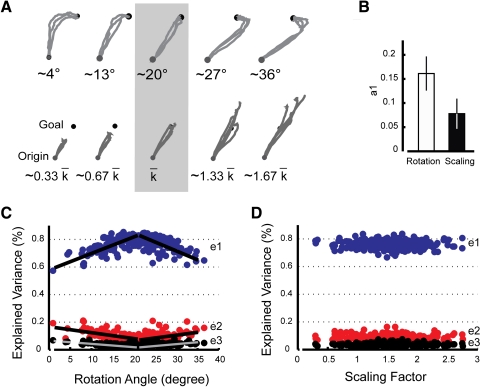
Analysis of kinematic performance during Test Session 3. A: hand paths from representative subjects from the Rotation (top) and Scaling (bottom) groups. Three trials are displayed for the average distortions (∼20° top, ×1.5 bottom; shading) as well as for 2 sets of weaker (left) and stronger (right) distortions. B: group analysis of coefficient a₁ values from both groups of Test subjects (see Eq. 10). C and D: percentage data variance accounted by the first 3 eigenpostures (e1 through e3) as a function of rotational distortion strength (Rotation group) or scaling distortion strength (Scaling group).

These findings were replicated across all Test Group subjects. The across-subject average performance (quantified by Aspect Ratio for the rotation subgroup and by Endpoint Error for the scaling subgroup) was reasonably characterized as a linear function of distortion magnitude (rotation: r² = 73.7; scaling: r² = 67.5), although analysis of residuals found significant deviations from normality such that the realized distributions favored extrema (Ryan–Joiner W-test: P < 0.023 in both cases). Because this can indicate the influence of unmodeled factors on subject performance, we explored how past performances might have informed the selection of motor commands on subsequent trials. Specifically, we evaluated whether subjects would use common or differential strategies of sensorimotor information processing when adapting to rotation and scaling distortions of a baseline hand-to-screen mapping.

Of all candidate models of moderate complexity having the form of Eq. 10, the model of Eq. 11 was identified as the minimum descriptor length (MDL) model that best predicts the evolution of trial-by-trial performance for the rotation (Aspect Ratio) and scaling (Endpoint Error) subgroups of Test Session 3. This model includes a single memory term

$$E_n=a_1{E}_{n-1}+b_0{K}_n$$ (11)

showing that limited-memory adaptive processes drive motor command updating in both cases. We then refit the model of Eq. 11 to each subject's original time series to obtain individualized estimates of coefficients a_i and b₀ (Table 1). The percentage of data variance-accounted-for (VAF) by the model averaged 71 ± 7% across both subgroups (with no difference between groups; P = 0.126). We sought to determine whether subjects use sensorimotor memories differentially to adapt to rotation and scaling distortions and therefore performed a single two-sample t-test to compare model coefficient a₁ across training conditions (Fig. 5C). Because the sequence of perturbations had negligible trial-to-trial correlation, a₁ quantifies the relative influence of the most recent sensorimotor memory on subsequent performance. Our analysis found a₁ to vary with distortion type (P = 0.012) with the influence of a prior error for Rotation subjects (0.15 ± 0.04) substantially exceeding that for Scaling subjects (0.08 ± 0.03) by a factor of nearly 2. Thus motor compensations for extent errors are much more efficacious than those for directional errors in this task.

Table 1.

ARX model coefficients by test subject group (day 3)

Subject	Group	a1	b0	%VAF
T01	Rotation	0.17	−0.77	63.91
T02	Rotation	0.12	−0.90	70.53
T03	Rotation	0.11	−0.82	63.57
T04	Rotation	0.19	−0.63	65.87
T05	Rotation	0.17	−0.72	72.07
Rotation avg (±SD)		0.15 ± 0.04	−0.77 ± 0.10	67.19 ± 3.89
T06	Scaling	0.04	−0.77	76.01
T07	Scaling	0.11	−0.74	73.08
T08	Scaling	0.11	−0.70	79.87
T09	Scaling	0.07	−0.82	60.96
T10	Scaling	0.08	−0.77	78.64
Scaling avg (±SD)		0.08 ± 0.03	−0.76 ± 0.04	73.71 ± 7.59

Consistent with the results of Test Session 2, the complexity of articulation-space corrections during movements in this session differed for the two subject groups. For Rotation subjects, the contribution of Eigenposture 1 to the overall performance decreased as the rotational distortion deviated from its nominal value, whereas Eigenpostures 2 and 3 both increased %VAF with increasing deviations (Fig. 5C). These relationships could reasonably be described as being piecewise linear about the adapted distortion strength and the slope of this relationship was significantly different from zero (P < 0.001 in each case). In contrast, Scaling subjects demonstrated no systematic variation in %VAF for any of the first three eigenpostures with variation in scaling distortion (P > 0.395 in each case) (Fig. 5D). The observation of curved trajectories when rotational distortions deviated from the norm (Fig. 5A), along with the fact that higher-order eigenpostures reflect coordination patterns having progressively greater temporal and spatial complexity (Fig. 3B), mean that subjects invoked increasingly complex coordination patterns to correct for larger targeting errors that arose during rotational (but not scaling) distortions.

Finally, we analyzed the across-trial variations in peak-speed hand configurations during target capture to determine whether exposure to random rotations and scalings might, like stepwise perturbations, lead to categorically different reorganizations of control. For rotation subjects, the variance per DOF in the null space (34 ± 18 GSU/DOF) was nearly as large as that for the (experimentally perturbed) task-space DOFs (48 ± 33 GSU/DOF); the ratio of these variances (0.8 ± 0.3) was not significantly different from unity for Rotation subjects (one-sample t-test: T = −1.62, P = 0.18) and thus adaptive responses to direction errors demonstrated no bias toward the learned inverse hand-to-screen map. By contrast, Scaling subjects generated much less null-space variance (14 ± 11 GSU/DOF) compared with the task space (62 ± 53 GSU/DOF), resulting in a variance ratio of 0.2 ± 0.1, which was much less than unity (one-sample t-test: T = −45.5, P < 0.0005), demonstrating that adaptive responses to extent errors were, in fact, biased toward the learned inverse map. The variance ratios differed significantly across groups (two-sample t-test: T = 3.76, P = 0.02), supporting the idea that in our task, directional errors induce substantial reorganization of coordination within redundant control DOFs, whereas extent errors do not.

Generalization study: spatial generalization of adaptations to rotation and scaling distortions

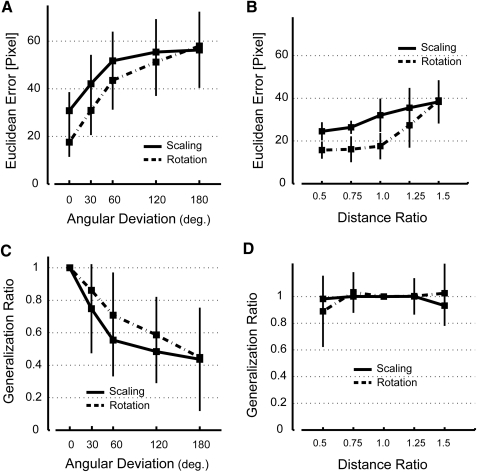
For both subject groups, accuracy decreased and the average endpoint error increased as a function of the angular difference between the trained target direction and the generalization target direction (Fig. 6A). Although both subject groups tended to overshoot the target somewhat—even in generalization trials made to the trained target (i.e., at a distance ratio of 1.0, Fig. 6B)—this overshoot scaled in approximate proportion to the difference in cued extents between the generalization and trained targets for both subject groups.

Fig. 6.

Analysis of kinematic performance in task space during Generalization Testing. A: Euclidean Error as a function of angular deviation from the trained target direction for the Rotation (dashed trace) and Scaling (solid trace) group subjects. B: Euclidean error as a function of distance deviation (scaling) from the trained target distance for the Rotation and Scaling group subjects. C: Adaptation Ratio as a function of Angular Deviation for the 2 generalization subject groups. D: Adaptation Ratio as a function of distance deviation for the 2 generalization subject groups.

To compare the effectiveness of generalization across training conditions, we normalized within each subject the generalization ratio computed for each target by the ratio computed for generalization trials made to the trained target. We used a two-way, repeated-measures ANOVA to compare generalization ratio across angular deviations and found a main effect of both the angular difference between trained and target movement directions [F_(4,59) = 18.06, P < 0.0005] and distortion type [F_(1,59) = 6.26, P = 0.016]. The generalization function for a newly learned scaling transformation was somewhat narrower than that for a rotation transformation (Fig. 6C). In contrast, a second two-way repeated-measures ANOVA found no difference in generalization across movement extents for both types of learned transformations [main effect of cued extent: F_(4,59) = 0.65, P = 0.632; training group: F_(1,59) = 0.25, P = 0.618] (Fig. 6D). Thus adaptations to rotation and scaling transformations generalized effectively and equally across movement extents in the trained direction, whereas both failed to generalize well across directions. In contrast to the observation in whole-arm reaching that a learned scaling generalizes across all movement directions (Krakauer et al. 2000), a learned scaling in our completely novel task generalizes poorly across directions, even less effectively than does a learned rotation.

Supplemental analysis: horizontal planar reaching with the arm

We performed a set of inverse- and forward-dynamics analyses to determine whether observed differences between the extent generalization results of Krakauer et al. (2000) and those presented here might have a biomechanical, rather than a neurocomputational, basis (see Appendix). The analysis reveals a fundamental asymmetry in the dynamics of compensation for visuomotor scaling and rotation during arm movements: regardless of movement direction, compensation for a novel scaling requires learning just one gain factor that can be used to scale existing patterns of coordination between the shoulder and elbow joints. Doing so yields similarly scaled and accurate movements in all directions. In contrast, we found no simple magnitude or phase transformation of interjoint coordination that could be applied commonly across directions to produce a common learned rotation.

DISCUSSION

This study is the third in a series examining how people form patterns of coordination within a highly redundant set of kinematic control variables (finger joint configurations) as they learn to move a virtual object (a cursor) within a low-dimensional task space (a computer screen) (Liu and Scheidt 2008a; Mosier et al. 2005). Here, we examined how people compensate for rotational and scaling visuomotor distortions that induce spatial errors of equivalent magnitude. Although others have asked whether visuomotor rotation and scaling are differentially compensated within the context of whole-arm reaching and pointing (Bock 1992; Krakauer et al. 2000, 2004; Pine et al. 1996; Vindras and Viviani 2002), conclusions based solely on studies of arm movement may be influenced (and thus limited) by the fact that those movements have been overlearned through years of practice. Indeed, inverse- and forward-dynamics analyses of horizontal planar reaching with the arm reveal that to compensate a visuomotor scaling in all directions, it is necessary to learn only a single gain factor that can then be applied to patterns of interjoint muscle coordination (the generalized muscle torques of Sainburg et al. 1995) appropriate for movements in other directions. Doing so will yield satisfactory results with only small trajectory deviations from the ideal. In contrast, no simple magnitude or phase transformation of learned net muscle torques was found capable of producing a common learned rotation. This represents a fundamental asymmetry in the dynamics of compensation for visuomotor scalings and rotations in reaching with the arm, one that the brain might learn to exploit with years of practice in reaching for objects.

Our study avoids this potential confound by defining a redundant target-capture task quite unlike anything most people have previously encountered, one in which the spatial relationship between task-space targets and the change in motor output required to attain them is completely under experimental control. The task subjects were to learn was a kinematic task and we intentionally ignored the dynamics of finger and/or cursor motion because doing so facilitates the subdivision of redundant control variables into task- and null-subspaces using simple linear algebra (a computational tractability absent from most other studies of redundant control of reaching). Our findings extend those previously reported by Mosier et al. (2005) and Liu and Scheidt (2008a): although initial task performance was dominated by exploratory behavior, learning of the kinematic mapping between hand and object motion progressed rapidly and resulted in increased object trajectory linearity and a reduction in target acquisition error. Subjects also reduced complexity in the overall coordination of finger motions during initial learning, as evidenced by a reduction in both task- and null-space movement variability. On imposing stepwise rotation and scaling distortions of the baseline hand-to-screen mapping, task-space errors transiently increased, although we again found recovery of rectilinear (straight) cursor trajectories and accurate target capture performance as often seen in studies of reaching with the arm in the horizontal plane (Scheidt and Ghez 2007; Scheidt et al. 2005; Shadmehr and Mussa-Ivaldi 1994; Wolpert et al. 1995). Likewise, random rotations or scalings of the baseline mapping induced limited-memory compensations similar to those observed in reaching with the arm (Scheidt et al. 2001). Importantly, direction and extent errors induced categorically different compensatory responses in control degrees of freedom not contributing to task performance. As discussed in greater detail in the following text, these findings are inconsistent with the general proposition that once the “structure” of a redundant task is learned, such dimensionality reduction is used to improve the efficiency of learning in tasks sharing a similar structure (Braun et al. 2010).

As shown previously (Liu and Scheidt 2008a), subjects in the current study had more than enough practice capturing targets in Session 1 for them to learn geometric relationships between target locations in task space. Subjects in our previous study used a hand-to-screen projection matrix virtually identical to the one used here and, if provided visual feedback of cursor motion, reached asymptotic levels of generalization in less than half the number of baseline trials performed by current Test and Control subjects. In contrast, subjects shown pictures of desired hand postures at specific screen locations learned to associate those locations with the desired postures, but were unable to generalize learning beyond the trained target set. Consequently, the ability to capture screen targets and to generalize beyond the region of task space spanned by the training targets requires subjects not only to learn stimulus/response associations between screen target locations and appropriate hand postures, but also that they learn how finger configuration should change given an arbitrary, untrained, desired change in cursor position (i.e., they learn an inverse hand-to-screen mapping: a motor representation of task space). Our approach therefore allows us to address a fundamental question that cannot be addressed by analyzing hand kinematics in a standard reaching experiment: if a geometrical transformation T is imposed on the geometry of cursor motion, do subjects preserve their original (baseline) inverse map or do they interpret the transformed environment as a whole new condition? Subjects in the current experiments had two choices after we applied a rotation or scaling to the task space: 1) to maintain their baseline model of the map and apply the inverse transformation T⁻¹ to the targets or 2) to create a whole new model of the map. The first case requires subjects to interpret the new map as a transformation of the old one (as indeed implemented by the experimenters). In the second case, subjects learn the new map de novo, without any particular reference to the old one. Both choices are perfectly legitimate and both effectively deal with the new environment. This is because the subject's model is functionally a right-inverse of the hand-to-screen map and there are infinitely many right-inverses equally capable of capturing the screen targets.

In more precise mathematical terms, if the map from hand gesture (h) to cursor (x) is implemented by a rectangular, 2 × 19 matrix (A) as in Eq. 1, subjects learn to generate an inverse map from the position of the target to the corresponding hand gesture by learning something equivalent to a 19 × 2 matrix B, where H = BP (Eq. 6). To capture targets with the cursor, one must have (at the target locations) P = ABP, where AB = I₂. Because A is a rectangular matrix (more columns than rows), the right inverse B is not unique: There exists an infinite number of B matrices that would work equally well in identifying hand gestures corresponding to the same cursor targets. If one applies a transformation (T) to the original map, the hand-to-screen map becomes P = TAH (Eqs. 3 and 4). One way to compensate for this change is to create a new inverse B′ = BT⁻¹. This would still satisfy the target-capture requirement since TABT⁻¹ = TI₂T⁻¹ = I₂. This solution corresponds to the first choice in the preceding paragraph. Again, however, there exists an infinite number of other right inverses B′, any of which would correspond to the choice of creating a whole new inverse map. One can readily see that the first choice is most economical from a computational perspective, since the transformation T has a small number of parameters, whereas a whole new right inverse has 19 × 2 = 38 components. Indeed, the first choice corresponds to subjects understanding that the experimenter changed the game by introducing a rotation or scaling and canceling this trick by applying its inverse.

Under the assumption that the brain minimizes kinematic and energetic (or similar) motor costs, subjects in the current study should have used their baseline inverse map to constrain command updates to only those degrees of freedom contributing to task performance. This corresponds to the brain exploiting knowledge of the “structure” of the task acquired in Session 1 (including, importantly, the learned inverse map), to minimize changes in control variables that have no impact on kinematic performance during adaptation in later sessions. Although the behaviors of scaling group subjects in Control Session 2 conform to this prediction, rotation group performances do not because motor command updating was not limited to task-space performance changes (null-space contributions to command updating increased significantly on imposing the task-space rotation; Fig. 4D) and resulted in new learned inverses (Fig. 4F). Moreover, the scaling group subjects in Test Session 3 demonstrated a clear bias toward updating motor commands within task-relevant control degrees of freedom, whereas we found no evidence that rotation group subjects exhibited such a bias. Instead, our results provide compelling evidence that correction for directional errors stimulated learning a new inverse map (or motor representation) of the Euclidean space onto which finger motions were projected, as well as evidence that extent errors did not. What factors could contribute to this difference in behavior?

In Test Session 2, the magnitudes of initial exposure reaching errors were similar for the two types of visuomotor distortion and so discrimination cannot have been made on the basis of error magnitude. It is also hard to see how our observations can be reconciled with theories of sensorimotor control wherein the brain balances competing optimizations of kinematic performance and the expenditure of effort or similar “costs of control” (see Liu and Todorov 2007; for a review see Shadmehr and Krakauer 2008). The typical formulation of an optimal motor control problem defines a cost function (to be minimized) that is quadratic in kinematic error and effort; this establishes a unique, globally optimal solution that can be found using gradient descent, related approaches, or even trial and error. Theory and simulations agree that using memory of recent performances to guide updating of the control solution is far more effective than not doing so and, indeed, subjects do use a limited-memory strategy to update their performance in our task (shown by Test Session 3 experiments). However, because subjects in our experiments learned to solve the inverse hand-to-screen mapping problem in Session 1, there was no kinematic or energetic need for intermediate solutions to the rotation problem to move up the energetic (null-space motion) cost curve in Test Sessions 2 and 3; a simple mental counterrotation or counterscaling of target location in task space and a reweighting of existing kinematic coordination patterns would have sufficed. Moreover, a trade-off between accuracy and energetic efficiency should not have yielded differential adaptive behaviors (Fig. 4, D and F) in response to visuomotor distortions that cause similar task-space error magnitudes. One possible explanation for the curious behavior we observed is that the cost function is incomplete as usually formulated—that it requires an additional term that would cause effort (null-space motion) to increase if a simultaneous decrease in this other (unspecified) cost term were greater in magnitude. Another possibility is that the online optimization of quadratic performance costs simply fails to describe how people modify performance based on prior experience. An alternative approach—reinforcement learning—would allow the possibility of increasing performance cost in the short term if long-term rewards are thereby maximized (Sutton and Barto 1998). In any case, our findings refute the idea that once a kinematic task is learned, motor command updating is limited to only those degrees of freedom contributing to task performance (e.g., Braun et al. 2009), thus minimizing energetic or similar costs of control including control variable change (Emken et al. 2007; Nakano et al. 1999; Uno et al. 1989) and intervening control actions (Todorov and Jordan 2002) within the time period (days) spanned by our experiments. Indeed, the difference between extent generalization reported here and that reported by Krakauer et al. (2000) suggests that structural learning may be important for performance optimization over much longer timescales than those examined here. Just what factors trigger a rescaling of existing coordination patterns during adaptation to a visuomotor scaling and exploration throughout the larger control space for new coordination patterns in response to a rotation is an intriguing question for future study.

Separate neural channels encoding movement direction and extent

Support for the idea that distinct adaptable mechanisms specify the intended direction and extent of arm movements come primarily from studies of reaching in the horizontal plane (Vindras et al. 2005; see also Bock 1992; Bock and Eckmiller 1986; Gordon et al. 1994; Krakauer et al. 2000, 2004; Lemay and Stelmach 2005; Messier and Kalaska 1997; Pine et al. 1996; Seidler 2006; van den Dobbelsteen et al. 2003; Vindras and Viviani 1998). Experimental evidence includes the patterns of constant and/or variable errors observed at the end of movement (cf. McIntyre et al. 1997, 1998; Vindras et al. 2005) as well as differences in the rate and generalizability of adaptations to rotational and scaling distortions of the nominal transformation between motion of the hand and motion of the viewed endpoint (Krakauer et al. 2000, 2004; Paz et al. 2004; Pine et al. 1996). These later results were suggested to support the idea that adaptation to rotational distortions places greater demands on short-term working memory (i.e., errors from multiple successive movements in different directions must be stored and interpreted to resolve directional errors) as compared with adaptation under gain alterations (which may make more modest demands on short-term memory to recalibrate a visuomotor scaling factor) (Pine et al. 1996). Details regarding the computational demands in both cases were not elucidated.

Ghez and colleagues concluded that adaptations to scaling and rotation of a previously learned visuomotor transformation are mediated by separate adaptable mechanisms because they had observed differences in generalization function shape and learning rate (Gordon et al. 1994; Krakauer et al. 2000, 2004; Pine et al. 1996). The results our generalization study do affirm this conclusion but, in contrast to Krakauer et al. (2000, 2004) and others (Bock 1992; Vindras and Viviani 2002), we found that adaptation to a scaling transformation in our task generalized somewhat less broadly across movement directions than did adaptation to a rotation and thus our results do not support the idea that extent errors induce learning of a single gain factor applied globally across all movement directions and extents (Krakauer et al. 2000). Based on an inverse-dynamics analysis of arm movements (Appendix), we suggest instead that the discrepancies between our findings and those previously reported (Bock 1992; Krakauer et al. 2000; Vindras and Viviani 2002) arise from experience-dependent changes in the adaptive mechanisms mediating gain learning, given that initial learning in our task required formation of completely novel patterns of coordination, whereas target capturing with the arm is a task in which adult subjects have had copious practice. It is possible that the narrow generalization functions we report here for a novel manual reaching task are more representative of the generalization curves for the neural mechanisms mediating visuomotor spatial learning than those previously identified in reaching with the arm. Broad gain generalization as observed in arm adaptation studies could well arise from structural learning of the simple relationship between movement extent and the gain of fundamental patterns of interjoint coordination enforced by the biomechanics of the arm (i.e., the “learning to learn” of Braun et al. 2010).

Because the hand-to-screen mapping was linear, monotonic changes in control variables contributing to task-space motion cause monotonic displacements of the endpoint, whereas synchronous, monotonic changes in any set of control variables contributing to task-space motion yield rectilinear cursor trajectories within that space. This property confers particular advantage to the generation of straight cursor trajectories, a fact that our subjects may have sought to capitalize on (Fig. 2D). Knowledge of the geometric properties of task space allows the decomposition of task-space errors into a component lying along the desired straight-line path (and thus correctable via rescaling of already learned coordination patterns) and a component lying off that path (and thus requiring, at minimum, a reweighting of the two articulation space basis vectors defining the cardinal axes of task space). Figure 4, D and F provides compelling evidence that subjects do indeed differentiate between direction and extent errors because they engage in very different behaviors in response to scaling and rotation distortions of task space. Under our experimental conditions, there is a clear benefit to making straight cursor trajectories: doing so allows one to reduce the complexity of adaptive compensation for extent errors. However, it is also possible that generation of corrective submovements in a direction perpendicular to the desired rectilinear path—such as those that may be required in response to persistent kinematic errors—may trigger a restructuring of the coordination of redundant control variables (cf. Fagg et al. 1998; Fishbach et al. 2007). Additional studies should examine the necessary conditions triggering exploratory behavior and reorganization of redundant control, those that instead foster updating of existing coordination patterns, and the neural mechanisms subserving both responses.

The current study also advances understanding of the computational demands placed on short-term working memory as subjects adapt to rotational and scaling distortions of a nominal visuomotor map. Although sensorimotor adaptation required very limited memory to compensate for both types of distortion (Eq. 11), differences in the relative influence of prior errors on subsequent movement attempts (Table 1 and Fig. 5C) reflect differences in the efficacy of error compensation in the two cases and predict differences in learning rates (Fig. 4B; see also Scheidt et al. 2001). Moreover, whereas task-space errors decreased exponentially on imposing both distortions, the aspect ratio for rotation subjects first increased then decreased (Fig. 4C), suggesting that rotational errors first induced corrective actions that took a few trials to develop before being integrated into the primary movement. These corrections were not driven by ongoing visual feedback because they were present in Control Session 2 subjects who, like scaling subjects in the Test Sessions, received only initial cursor feedback and a static representation of the cursor's final position attained at the end of the trial. The learning rate advantage of scaling over rotation in our study cannot be due to a broader generalization function for scaling as suggested in Krakauer et al. (2000), but rather must reflect the benefits of reweighting existing coordination patterns as opposed to searching through redundant control space for a new set of viable coordination patterns (a process likely to place greater demands on recent motor memory; cf. Fig. 5C).

Separate neural substrates encoding movement direction and extent

Several primate single-unit recording studies have sought to identify independent neural correlates of movement direction and extent in primary motor cortex M1 (Riehle and Requin 1989) and dorsal premotor cortex PMd (Messier and Kalaska 2000; see also Fu et al. 1993; Kurata 1993). By controlling the timing and nature of cues about upcoming intended movements, these studies have found evidence that the temporal dynamics of processing of movement direction and extent in these cortical regions are sequential and independent in preparation for reaching. Notably, although many neurons appear to encode both the direction and extent of an upcoming movement and some encode for just direction, very few neurons in PMd and M1 encode exclusively for movement extent. This has led to the suggestion that if an independent channel for amplitude exists, it most likely resides outside of PMd (Messier and Kalaska 2000) and M1 (Riehle and Requin 1989).

Although current neuroimaging techniques lack the spatial and temporal resolution of single-unit recordings, they do permit whole-brain monitoring of signals thought to correlate with neural activity. Krakauer and colleagues (2004) used positron emission tomography (PET) to compare brain activities during both rotation and gain learning. In that study, right-handed subjects underwent neuroimaging while moving a stylus on a digitizing tablet with their dominant hand. Subjects had real-time cursor feedback of relative hand position as they moved fluidly out and back between a common starting location and eight spatial targets in successive cued motions. Rotational and scaling distortions were imposed in separate blocks of trials. Rotation adaptation induced greater rCBF signal in right posterior parietal cortex, right ventral premotor cortex, left pre-SMA, and left lateral cerebellum, areas thought to be involved in the visuospatial computations supporting sensorimotor integration for visually guided reaching (see also Burnod et al. 1999; Inoue 2000; Tseng et al. 2007) and in representing the dynamics of the limb and handheld tools (Diedrichsen et al. 2005; Imamizu 2000, 2003; Shadmehr and Holcomb 1997). In contrast, Krakauer et al. (2004) found that adaptations to changes in visuomotor gain induced only a subtle increase in rCBF signal in a subset of subcortical motor areas activated in their control task (left insula/putamen, left medial cerebellum, and right putamen) and no significant activation outside of the regions active during the control task. These results are consistent with the proposed role of basal ganglia in scaling the magnitude and rate of increase of muscle activity during movement (Horak and Anderson 1984) and thus in controlling movement extent and velocity (Anderson and Horak 1985; Desmurget et al. 2003, 2004; Mazzoni et al. 2007; Turner and Anderson 1997; Turner et al. 2003). Indeed, inactivation of basal ganglia output pathways in animal models reduces the extent of goal-directed movements but alters neither reaction times (Mink and Thach 1991) nor the normal activation sequence seen during reaching prior to inactivation (Horak and Anderson 1984). These considerations—and our own finding that extent errors in planar goal-directed endpoint motions elicit only rescaling of existing coordination patterns rather than an extensive search through control space to derive a new inverse hand-to-screen map (Fig. 4, D–F)—suggest that motor learning accomplished by the basal ganglia involves the selection and scaling of existing motor coordination patterns. By combining the current experimental approach (wherein distinct behavioral adaptations to rotational and scaling visuomotor distortions are observed) with neuroimaging techniques, it may be possible to gain new insight into the mechanisms mediating adaptive compensation for errors in movement direction and extent as well as the differential role of the cerebellum and basal ganglia in those adaptations.

Conclusions

Visuomotor adaptations in our novel target-capture task were similar to those observed during reaching with the arm: errors transiently increased after imposing stepwise rotation or scaling distortions but recovery of rectilinear task-space trajectories and accurate target capturing rapidly ensued. As with whole-arm reaching, compensation for scaling was faster than that for rotation. This could not be explained by a broader generalization function for gain versus rotation learning because generalization was narrower for gain learning than that for rotation learning in our subjects. Instead, we found that directional errors stimulated a search through the space of control variable changes to re-solve the target-capture task, whereas extent errors did not. The learning rate advantage of scaling over rotation likely results from a rescaling of existing coordination patterns as opposed to a search for a new set of viable patterns. These findings are inconsistent with the idea that once a kinematic task is learned, motor command updating is limited to only those degrees of freedom contributing to task performance (thereby minimizing energetic or similar costs of control), but instead highlight limitations of recent experience in guiding adaptive responses in a newly learned motor task.

GRANTS

This work was supported by National Science Foundation Grant BES 0238442 and National Institutes of Health Grants NS-053581 and HD-053727.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

APPENDIX

We performed a set of inverse dynamics analyses and forward dynamic numerical simulations of goal-directed reaching with the arm to: 1) explore patterns of kinetic coordination at the shoulder and elbow joints during a common reaching task and 2) determine how these patterns change during compensation for an imposed visuomotor rotation or scaling. Eight standard template movements were created within the MATLAB computing environment (The MathWorks, Natick, MA). These were straight-line reaching movements of 10 cm length and 0.5 s duration in the horizontal plane (Fig. A1, A and B, top). Movements originated from a position 0.4 m in front of the subject and 0.05 m to the left of the shoulder center of rotation. The movements were directed outward from this origin to eight targets equally distributed across directions in the horizontal plane. A movement to the subject's right was considered a 0° movement, with positive angles corresponding to counterclockwise (CCW) deviations. An additional set of “short” (0.05 m long) template movements was implemented from the same origin with the same 0.5 s duration.

Fig. A1.

A: simulated movement scenario. The blue trajectory is half the extent of the black trajectory. B: hand displacement (d) and hand speed (s) profiles for the 0° movement shown in A. The elbow (Te) and shoulder torques (Ts) for the 3 highlighted trajectories in A are also shown. Color coding as in A. Vertical scale: 2.5 Nm; horizontal scale: 0.5 s. C: interjoint coordination as revealed by plotting Te vs. Ts. Color coding as in A. The light blue trace is a scaled (×2) version of the dark blue trace. Vertical and horizontal scales both represent 1 Nm. D: comparison of shoulder (left) and elbow torques (right) estimated from each of the baseline (black) and short (dark blue) template movements. The light blue traces are scaled (×2) versions of the dark blue traces and they closely approximate the black traces for each movement direction at both joints. (In some cases, the black traces are completely hidden by the light blue traces.) Scale bars as in B. E: comparison of shoulder (left) and elbow torques (right) estimated from each of the baseline (black) and rotated (red) template movements. Note that there is no simple scaling or staggering of joint torques that could transform the red traces into the black traces across movement directions and joints. Scale bars as in B. F: light blue traces correspond to forward dynamics simulations of 10 cm reaches driven by scaled (×2) versions of the torques estimated from the shorter template movements. Black traces represent simulations of 10 cm reaches driven by torques derived from the baseline templates. Terminal accuracy is degraded only slightly if baseline torques are instead approximated by applying a direction-independent scaling rule to joint torques suited for a different movement extent, but in the same movement direction. The results are generally insensitive to the particular choice of V used in the inverse- and forward-dynamic computations. Scale bars: 0.05 m.

The analysis was conducted in four stages. First, inverse kinematic calculations were performed to calculate shoulder and elbow joint excursions required to perform each template movement. The anthropometric parameters used for joint motions for a typical subject were based on previously published simulations of reaching and adaptation to velocity-dependent force fields (Shadmehr and Mussa-Ivaldi 1994) and were modified to attain a limb-damping factor within the physiological range (cf. Perreault et al. 2004) (Table A1; see also Scheidt and Ghez 2007).

Table A1.

Anthropometric and joint mechanical properties used to simulate arm movements

Parameter	Value
Upper arm length	0.33 m
Upper arm mass	2.62 kg
Upper arm center of mass	0.165 m
Upper arm inertia	0.0231 kg · m2
Forearm/hand length	0.34 m
Forearm/hand mass	1.52 kg
Forearm/hand center of mass	0.19 m
Forearm/hand inertia	0.0372 kg · m2
Joint viscosity	$V=\left[\begin{array}{cc}2.1& 0.8\\ 0.8& 2.2\end{array}\right]\mathrm{N}\cdot \mathrm{m}\cdot \mathrm{s}/\mathrm{rad}$

Second, the shoulder (τ_s) and elbow (τ_e) joint torques required to drive the simulated limb through the template trajectories (i.e., the generalized muscle torques of Sainburg et al. 1995) were estimated using inverse dynamics equations of motion, expressed as

$$\left[\begin{array}{c}{\tau }_s\\ {\tau }_e\end{array}\right]=\left[\begin{array}{cc}{I}_s+I_e+m_s{r}_s^2+m_e{r}_e^2+m_e{l}_s^2+2l_s{m}_e{r}_e\cos \left({\theta }_e\right)& I_e+m_e{r}_e^2+l_s{m}_e{r}_e\cos \left({\theta }_e\right)\\ I_e+m_e{r}_e^2+l_s{m}_e{r}_e\cos \left({\theta }_e\right)& I_e+m_e{r}_e^2\end{array}\right]\left[\begin{array}{c}{\ddot{\theta }}_s\\ {\ddot{\theta }}_e\end{array}\right]+\left[\begin{array}{ccc}0& -l_s{m}_e{r}_e\sin \left({\theta }_e\right)& -2l_s{m}_e{r}_e\sin \left({\theta }_e\right)\\ l_s{m}_e{r}_e\sin \left({\theta }_e\right)& 0& 0\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_s^2\\ {\dot{\theta }}_e^2\\ {\dot{\theta }}_s{\dot{\theta }}_e\end{array}\right]+\left[\begin{array}{cc}{V}_{11}& V_{12}\\ V_{21}& V_{22}\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_s\\ {\dot{\theta }}_e\end{array}\right]$$ (A1)

Here, the arm was modeled as a two-segment link in the horizontal plane (cf. Scheidt et al. 2005). Each segment was modeled as a homogeneous rigid body with mass m_i, length l_i, moment of inertia I_i, and center of mass located at distance r_i from the proximal joint. θ_i are the joint angles, where the index i = s corresponds to the shoulder joint and i = e corresponds to the elbow joint. Because we were interested in kinetic coordination across joints, we ignored the possible influence of limb postural stabilization about the goal target at the end of movement (for an analysis of those effects in horizontal planar reaching, see Scheidt and Ghez 2007). Note also that we make no assumption regarding how the nervous system produces generalized muscle torques, whether by modulating motor neuron threshold potentials as in equilibrium trajectory models or by simply specifying a time series of muscle activations. Both approaches yield the same feedforward joint torques in the absence of environmental perturbations (as in the case with the visuomotor perturbations studied in Krakauer et al. 2000).

Third, we compared coordination between joints within single movements by plotting elbow torque as a function of shoulder torque at each moment in time (e.g., Fig. A1C). We also compared how patterns of coordination within joints would have to change to compensate for either a twofold scaling of cursor motion relative to hand motion or a 45° CCW rotation of cursor motion about the common movement origin. We did so by plotting elbow and shoulder torques as a function of time for the standard template movements and their shortened (Fig. A1 D) or 45° clockwise-rotated versions (Fig. A1 E).

Finally, we conducted a set of forward dynamic simulations to evaluate the feasibility of altering the extent of straight-line hand movements by applying a common, direction-independent scaling factor to patterns of joint torques suited for moving to targets at a single, different distance. Movements were simulated by propagating the forward dynamic equations of motion forward in time (i.e., by solving Eq. A1 for θ at each moment in time), subject either to the torques calculated along the templates or to a scaled version of those torques. Because postural stabilization increases the restorative effects of limb viscoelasticity about the desired target configuration (Gomi and Osu 1998; Lacquaniti et al. 1993) and because the model of Eq. A1 ignores these effects, simulations based on Eq. A1 provide a worst-case analysis of the mechanical consequences of feedforward motor command planning errors introduced by application of a scaling factor to kinetic coordination patterns drawn from movements half the desired extent. We evaluated the sensitivity of simulation results to the particular values of effective joint viscosity specified in Table A1 by systematically varying matrix V over a ±10-fold range in both the inverse- and forward-dynamics computations.

Results

We simulated movements with monotonic displacements (Fig. A1 B, trace d) and smooth hand speed profiles (Fig. A1 B, trace s). Inverse dynamic joint torque estimates for the three highlighted trajectories in Fig. A1 A reveal that the two 0° trajectories required similarly shaped torque waveforms at both the shoulder and elbow joints, albeit with different magnitudes (Fig. A1 B; compare blue and black traces). In contrast, the torque waveforms needed to compensate for a CCW visuomotor rotation differed in both sign (elbow) and magnitude (shoulder) from those for the 0° baseline target (Fig. A1 B; compare red and black traces). These differences indicate that compensating for a rotation requires a dramatic change in the temporal phasing of interjoint coordination (Fig. A1 C; compare black and red traces from the 0 and 315° trajectories, respectively), whereas compensating for a scaling of movement does not (Fig. A1C; compare black and small dark blue traces). Importantly, by multiplying both of the shorter movement's joint torques by a common scaling factor\?\195 the ratio of desired versus original movement extents or twofold in these simulated movements\?\195 the pattern of interjoint coordination observed in the baseline trajectory is largely recovered. We obtain similar results when this same scaling relationship is applied to the short template movements in each of the other directions (Fig. A1 D).

It is not as easy to see how interjoint coordination should be reorganized to induce a common rotation of point-to-point reaches. Compare, for example, traces a, b, and c in Fig. A1 E, which correspond to intended movements in the 45, 135, and 225° directions. For both the 45 and 225° movements, elbow torque profiles were very similar before (black traces) and after (red traces) compensating for the visuomotor rotation. In contrast, shoulder torques were oppositely directed and had different magnitude ratios before and after rotation in these two cases. For the 135° target direction, the pattern was reversed. Here, shoulder torques were similar before and after compensating for the rotation, whereas the elbow torques differed in sign. In other directions (e.g., 0°), other different patterns were observed. No simple scaling or staggering of joint torques can be commonly applied across movement directions to induce a common rotation of point-to-point reaches.

Results of the forward-dynamics simulations reveal that only small movement errors would be introduced by applying a common kinetic scaling rule across movement directions (Fig. A1 F, left). These errors result from neglecting extent-related differences in interaction torque magnitudes, which do not scale in direct proportion to the visuomotor scaling factor but rather scale as the square of this factor. The results of a sensitivity analysis on the effects of joint viscosity magnitude established that our findings were robust over a 100-fold range of V (Fig. A1 F, center and right).

Conclusions

This analysis has revealed a fundamental asymmetry in the dynamics of compensation for a visuomotor scaling and rotation: It is a simple matter to compensate for a visuomotor scaling because a single gain factor can be applied across joints and movement directions to adjust movement extent. The striking simplicity of this approximate scaling relationship derives from Newton's second law for rotational systems (τ = Iθ¨), from the fact that the limb's mechanical response to application of muscle torque is largely dominated by the limb's inertia (i.e., the effects of interaction torques are modest in point-to-point reaching) and from the fact that the nonlinearities inherent to multijoint limb motion are smooth. In contrast, the reorganization of interjoint coordination needed to compensate a visuomotor rotation is complex and direction-dependent. An adaptive system capable of distinguishing extent from direction errors could learn to capitalize on this inherent asymmetry by adjusting only the gain of existing coordination patterns in inverse proportion to the amount of target overshoot or undershoot if the movement error was primarily one of extent. Compensating for direction errors would require a more complicated reorganization of coordination patterns, a reorganization that may well take longer to learn.