Linear Hypergeneralization of Learned Dynamics Across Movement Speeds Reveals Anisotropic, Gain-Encoding Primitives for Motor Adaptation

Abstract

The ability to generalize learned motor actions to new contexts is a key feature of the motor system. For example, the ability to ride a bicycle or swing a racket is often first developed at lower speeds and later applied to faster velocities. A number of previous studies have examined the generalization of motor adaptation across movement directions and found that the learned adaptation decays in a pattern consistent with the existence of motor primitives that display narrow Gaussian tuning. However, few studies have examined the generalization of motor adaptation across movement speeds. Following adaptation to linear velocity-dependent dynamics during point-to-point reaching arm movements at one speed, we tested the ability of subjects to transfer this adaptation to short-duration higher-speed movements aimed at the same target. We found near-perfect linear extrapolation of the trained adaptation with respect to both the magnitude and the time course of the velocity profiles associated with the high-speed movements: a 69% increase in movement speed corresponded to a 74% extrapolation of the trained adaptation. The close match between the increase in movement speed and the corresponding increase in adaptation beyond what was trained indicates linear hypergeneralization. Computational modeling shows that this pattern of linear hypergeneralization across movement speeds is not compatible with previous models of adaptation in which motor primitives display isotropic Gaussian tuning of motor output around their preferred velocities. Instead, we show that this generalization pattern indicates that the primitives involved in the adaptation to viscous dynamics display anisotropic tuning in velocity space and encode the gain between motor output and motion state rather than motor output itself.

INTRODUCTION

In motor adaptation, generalization describes the extent to which learned changes in motor output transfer to conditions other than those experienced during training. One readily learned motor adaptation involves predictive compensation for changes in the physical dynamics of the environment. These dynamics result in time-varying physical perturbations that are a function of the motion state (Conditt et al. 1997, 1999; Diedrichsen et al. 2007; Sing et al. 2009). Several recent studies have focused on the generalization of this type of motor adaptation in reaching arm movements. A number of different types of conditions have been studied, including limb position (Gandolfo et al. 1996; Hwang et al. 2003; Malfait et al. 2002; Shadmehr and Moussavi 2000; Shadmehr and Mussa-Ivaldi 1994), movement direction (Donchin et al. 2003; Hwang et al. 2006; Sainburg et al. 1999; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005), and trajectory shape (Conditt et al. 1997, 1999).

Because of the high dimensionality of the space of possible actions (Vetter et al. 2002), the ability to generalize learning to different conditions shows properties of the mechanisms that underlie the acquisition and storage of motor adaptation. Specifically, it has been suggested that the pattern of generalization shows properties of neural basis functions for adaptation (Poggio and Bizzi 2004; Shadmehr 2004). Although the relationships that determine the physical dynamics for the limb are mathematically complex (Schaal and Schweighofer 2005), these dynamics are often locally smooth, implying that local basis functions with appropriate widths could provide a flexible yet efficient substrate for learning (Haruno et al. 1999; Kawato et al. 1987; Wolpert and Kawato 1998). The width of these basis elements would be a key property of such an architecture: larger widths allow for faster initial adaptation to new environments because of broader generalization across neighboring contexts, whereas smaller widths allow for finer mapping of context specificity and limit overgeneralization.

Previous computational models of adaptation to physical dynamics have assumed that these neural basis elements represent motor output (such as force or torque) as a function of the movement velocity and that the widths of these basis elements are isotropic in velocity space—i.e., identical across movement directions and speeds (Donchin et al. 2003; Shadmehr 2004; Thoroughman and Shadmehr 2000). That is, the ability to apply adaptation from one context (e.g., a from a trained velocity) to another is the same for equal magnitude changes in the velocity vector, regardless of whether these changes correspond to changes in the magnitude or direction of the velocity vector.

Although several studies have focused on determining the width of these neural basis functions across neighboring movement directions (Bedford 1993; Darainy et al. 2009; Donchin et al. 2003; Gandolfo et al. 1996; Ghilardi et al. 1995; Huang and Shadmehr 2007; Krakauer et al. 2000; Mattar and Ostry 2007; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005; Vetter et al. 1999), few studies have examined the width across neighboring movement speeds (Francis 2008; Goodbody and Wolpert 1998; Mattar and Ostry 2010). Generalization across movement directions has generally been shown to decay in a bell-shaped, Gaussian-like pattern, with width estimates for the neural basis functions ranging from 0.12 to 0.16 m/s in velocity space (Donchin et al. 2003; Thoroughman and Shadmehr 2000). In contrast, Goodbody and Wolpert (1998) found that the generalization of force-field adaptation to novel movement speeds was between level and linear extrapolation transfer and closer to linear. That is, they reported that forces exerted by subjects increased with the magnitude of the velocity vector in an almost linear fashion whether or not target distance was increased for high-speed movements. This result suggests that basis functions for motor adaptation might encode motor output gain rather than raw motor output itself and that these basis elements may be highly anisotropic in velocity space, because isotropic basis elements compatible with the relatively narrow pattern of generalization observed across movement directions (σ = 0.12–0.16 m/s) would fail to show substantial generalization across the 0.3 m/s difference between the low- and high-speed movements studied (see Fig. 2 for an illustration).

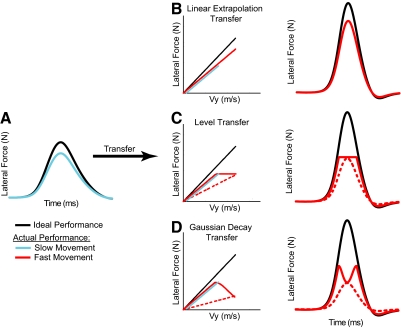
Fig. 2.

Comparison of predicted generalization patterns for different mechanisms of transfer. The traces in the 1st and last column represent lateral force profiles (lateral force vs. time) associated with force-field adaptation during point-to-point movements: ideal (black) and predicted (colored). The middle column plots the same lateral forces vs. movement velocity. A: typical performance during slow movements after training. Subjects typically produced force patterns that were close to 80% of the ideal patterns, which would fully compensate the force field. We compared several possible mechanisms for transfer of adaptation from slow (blue trace) to fast (red traces) movements. B: linear extrapolation transfer: adaptation remains at 80% of the ideal pattern and the amount of exerted force increases with movement velocity in the same relationship learned during training; C: level transfer: force-level levels off (solid line) or is scaled (dashed line) so that the maximum exerted force at the maximum movement velocity is the same as the force exhibited during adaptation; D: Gaussian decay transfer: force-level decays (solid line) or is scaled (dashed line) in a Gaussian manner for movement velocities beyond those experienced during training. Note that the blue lines in the 2nd column have been shifted slightly to the right to allow the red traces beneath them to be more visible.

However, there were two issues with the study of Goodbody and Wolpert that make it difficult to be certain about the actual pattern of transfer across movement speeds. First, transfer of adaptation was assessed indirectly by measuring performance in force-fields compatible with specific types of generalization patterns to faster movement speeds, rather than by directly measuring the force patterns that subjects exerted during high-speed movements. Second, and more importantly, because the transfer pattern was estimated during a block of nearly 400 trials including nearly 100 high-speed force-field trials in a mix of different test fields, the average content of these test fields would be likely to affect the results; the average transfer pattern observed may have reflected the average of the tested high-speed transfer patterns rather than pure transfer of adaptation from low-speed to high-speed movements. The specifics of this effect are detailed in the discussion section and Fig. 8.

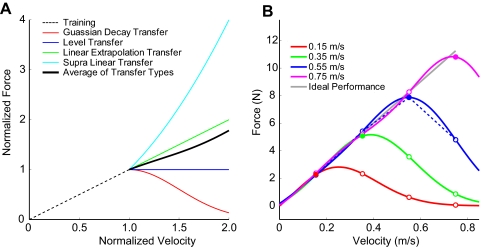
Fig. 8.

Issues with previous work. A: illustration of the test-period force-fields in Goodbody and Wolpert (1998). During the 384-trial test period of experiment 1 in this study, 75% of trials called for slow movements in a linear viscous force-field with a force-velocity relationship depicted by the black dashed line. The remaining trials consisted of 24 high-speed (double speed) test movements in each of 4 force-fields. These 4 force-fields shared the same linear force-velocity relationship depicted by black dashed line at low speeds but diverged according to the force-velocity relationships shown in the colored traces. The mean of these force-fields is represented by the thick black curve. If experience with the 96 high-speed test trials affected estimated generalization pattern, the effect should reflect the mean force-fields experienced, which is just below linear transfer. B: simulated transfer patterns with the isotropic basis elements used in Francis (2008). The various colored traces show simulated generalization from trained movement speeds 0.15, 0.35, 0.55, and 0.75 m/s. ●, maximum movement speed during training for each trace; ○, generalization to each of these cardinal speeds. Francis (2008) presents simulation of generalization only from 0.55 m/s to the other cardinal speeds—represented here by the blue dashed line. This single simulation matches the experimentally estimated transfer results in Francis (2008) from all 4 movement speeds. However, the simulations of generalization from the other movement speeds, which were not presented in Francis (2008), yield very different transfer patterns, inconsistent with the experimentally estimated transfer results.

Interestingly, Mattar and Ostry (2010) have recently found that viscous force-field adaptation shows essentially level transfer when the velocity and target distance are simultaneously doubled. This is at odds with part of the results of Goodbody and Wolpert and with the idea of linear transfer across speeds. However, target distance is likely to have a contextual effect on motor adaptation (see discussion) that might obscure the velocity-dependent transfer if not controlled.

Here we studied how adaptation to velocity-dependent dynamics generalizes across different movement speed contexts by directly measuring how adaptation transfers to untrained movement speeds using lateral error-clamp trials (Joiner and Smith 2008; Scheidt et al. 2000; Sing et al. 2009; Sing and Smith 2010; Smith et al. 2006; Wagner and Smith 2008) when movement extent is controlled. Specifically, we studied the amount of transfer from low-speed to high-speed movements immediately after training, the shape of the force pattern associated with this transfer, and how fast this transfer decays relative to the decay of the primary adaptation. We combined these empirical observations about the pattern of transfer with computational modeling of how motor primitives could learn velocity-dependent dynamics to determine 1) whether these basis elements for motor adaptation show different responses with respect to the magnitude and direction of the velocity vector and 2) whether learned motor adaptations represent motor output itself or the gain between motor output and motion state.

METHODS

Participants

Twenty-two healthy subjects without known neurological impairment were recruited from the Harvard University community to participate in the study. All participants were right handed and used their dominant hands. The study protocol was approved by the Harvard University committee on the use of human subjects and all participants gave informed consent.

Task

The experimental paradigm was patterned after the standard force-field adaptation paradigm (Shadmehr and Mussa-Ivaldi 1994). Subjects sat in an adjustable chair in front of a robot manipulandum facing a computer display (Fig. 1A). Their right arms were supported by a ceiling-mounted sling so that the forearm and upper arm were both parallel to the floor (in the horizontal plane). The manipulandum measured hand position, velocity, and force, and its motors were used to apply forces to the hand, all at a sampling rate of 200 Hz. The position of the hand was shown as a small round cursor (3 mm diam) on a vertically oriented computer monitor in front of the participant (refresh rate of 75 Hz). Subjects made point-to-point reaching movements between two circular targets 1 cm in diameter that were placed in the midline and spaced 10 cm apart (30 and 40 cm from the sternum). Thus all movements were oriented along the y-axis in the midline, toward or away from the sternum—with alternating inward and outward movements.

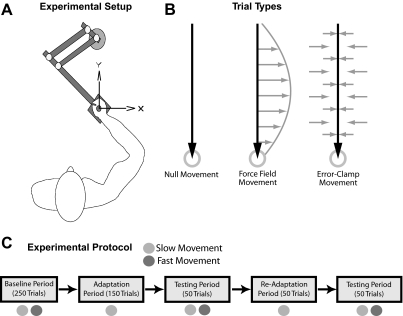
Fig. 1.

Experimental setup and protocol. A: subjects sat in front of a computer display and made reaching movements toward and away from the body while holding the handle of a robotic manipulandum that applied forces to the hand. B: there were 3 trial types: null trials, force-field trials, and error-clamp trials. The motors of the manipulandum were turned off for null trials. During force-field trials, the motors were used to produce forces on the hand (gray arrows) that were proportional in magnitude and perpendicular in direction to the velocity of hand motion (black arrow). Forces were determined as a function of hand velocity: f = Bv. During error-clamp trials, the robot motors were used to constrain movements in a straight line toward the target by counteracting any motion perpendicular to the target direction. C: timeline of the experiment. Only slow movements were cued during the adaptation periods, whereas a mixture of both fast and slow movements was cued during the baseline and testing periods.

We trained subjects to make movements at two different speeds (slow and fast) based on the color of the target (Fig. 1C). When the target was colored blue, subjects were cued to move slowly (desired peak speed of 0.3 ± 0.05 m/s). When the target was colored green, subjects were cued to move fast (desired peak speed of 0.6 ± 0.05 m/s). The subjects received visual and auditory feedback on performance (whether the movement was slower, faster, or within the cued speed range) after each trial.

Three trial types were used: null trials, error-clamp trials, and force-field trials (Fig. 1B). During null-field trials, the robot motors were turned off. These null trials were used for initial practice and to assess baseline, preadaptation performance. During force-field trials, the robot motors were used to produce forces on the subject's hand proportional in magnitude and perpendicular in direction to the instantaneous velocity of hand motion. The relationship between force (f) and velocity (v) vectors in the force-field trials was determined by the matrix B = [1 15; −15 0] Ns/m via the relationship f = Bv. During error-clamp trials, the robot motors were used to constrain movements in a straight line with a “force channel” directed toward the target, which effectively counteracted any motion perpendicular to the target direction (Joiner and Smith 2008; Scheidt et al. 2000; Smith et al. 2006). This was achieved by applying a stiff one-dimensional spring (6 kN/m) and damper (150 Ns/m) in the axis perpendicular to the target direction. In these trials, the average perpendicular displacement from a straight line to the target was 0.48 mm in magnitude.

The experiment was divided into baseline, adaptation, and testing periods with a total of 550 trials in each of the two movement directions (Fig. 1C). During training, all outward movements were error-clamp trials and were cued to be made at the slow movement speed. The experiment began with a baseline period consisting of 250 null trials in each direction with fast and slow speed trials interspersed. This was followed by the adaptation period, in which subjects performed 150 low-speed trials in each direction. As shown in Fig. 1, we applied the force-field only on inward movements, and correspondingly, only inward movements were analyzed. The force-field was applied on 125 of the adaptation period trials, with 25 error-clamp trials randomly interspersed (∼17% of trials) to provide estimates of the learned feedforward changes in lateral force profiles (see Fig. 1B). Subjects completed a testing period (contiguous with the end of the adaptation period) of 50 consecutive inward error-clamp trials evenly split between randomly ordered fast and slow movements. These trials tested the generalization of adaptation to the faster movement speed randomly intermixed with the decay of adaptation for the slow movement speed. As in the adaptation period, all outward trials were slow error-clamp movements. The testing period was followed by a readaptation period of 50 trials and then another testing period (50 trials). In the testing periods, movements were classified by actual speed rather than the trial cue. For example, if a subject, by mistake, made a low-speed movement on a trial that was cued to be high-speed, this movement was classified as a low-speed trial (cut-off at 0.4 m/s) rather than a high-speed trial. In addition, the data were combined between the two adaptation and testing periods; i.e., the first trials of the first and second testing periods were grouped together as the first test trials.

Analysis of force profiles

Because the environmental perturbations applied during this experiment consisted of forces exerted by the robot manipulandum onto the participant's hands perpendicular to the direction of hand motion, we focused our analysis on the temporal profiles of the lateral (perpendicular) forces that participants generated during movement. In general, during a force-field trial, lateral force could reflect an adaptive compensation of expected lateral force or an on-line corrective response to errors detected during the course of movement. To isolate feedforward (predictive) adaptive compensation of the force-field environment from on-line corrective responses, we looked at the progression of lateral force profiles during error-clamp trials in the baseline, adaptation, and testing periods of the experiment. During these trials, lateral errors were kept small (the peak magnitude of the lateral error was <0.48 mm on average), so lateral force profiles essentially reflected adaptive compensation of the force-field perturbations. A typical example of a lateral force exerted late in the training epoch is presented in Fig. 3C (black trace-ideal force profile, blue trace-measured lateral force profile). (A detailed explanation of this figure appears below.) These force profiles were aligned to peak movement speed and, for each subject, the average force profile exerted during the baseline period was subtracted from the force profiles obtained in the adaptation and testing periods for slow and fast movements, respectively.

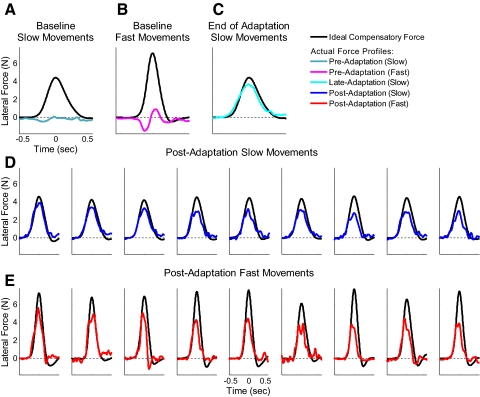
Fig. 3.

Evolution of force profiles associated with motor adaptation during the baseline, training, transfer, and decay periods of the experiment. Lateral force patterns for (A) slow movements and (B) fast movements before the adaptation period and (C) late in the adaptation period after adaptation levels had reached asymptote of ∼80% of the ideal force. Lateral force patterns for (D) the 1st 9 slow trials and (E) the 1st 9 fast trials during the postadaptation period are displayed in the bottom 2 rows. The black trace in each panel is the ideal compensatory force pattern based on the force field perturbation that we applied, whereas the actual lateral force patterns we measured in each condition are represented by colored traces. Note the substantial transfer of adaptation to the fast movements in the postadaptation block and the parallel patterns of decay for the slow and fast movements during this block.

Because full compensation of the force-field perturbation on a particular trial required a lateral force profile proportional to the velocity profile shown on that same trial (and this velocity profile varied from 1 trial to another), we assessed the relative amount of adaptation on each error-clamp trial by computing a velocity-normalized adaptation coefficient found by linear regression of the measured lateral force profile on each error-clamp trial onto the ideal compensatory force profile required for full force-field compensation on that trial. Each regression coefficient thus characterizes the overall amount of force-field compensation (adaptation) in a given trial. Note that this measure represents the gain between the exerted force and the velocity-dependent ideal force. Independent of movement speed, if the applied force and the ideal force perfectly coincide, this learning metric is 1; if they are directly opposed, the metric is −1; and if they are unrelated it will be 0. As an example, the lateral force profile for the slow movement presented in Fig. 2A represents an adaptation level of ∼0.8.

To quantify the level of generalization, we computed two additional metrics based on these force patterns. The mid-movement force was computed as the average lateral force in a window extending from 70 ms before to 70 ms after the peak speed point of the movement. This mid-movement force is a reasonable measure of the level of adaptation and transfer of motor output because it estimates the force output at the time when the learned change should be maximal. If the force patterns in most individual force profiles are similar in shape to the ideal force profile, a more robust measure can be created by regressing the force profile measured on each trial onto the shape of the ideal force profile. This would allow the adaptation metric to take the entire force profile into account, rather than just a portion of it. We computed raw adaptation coefficients by regressing measured force profiles from each error-clamp trial onto a normalized version of the corresponding ideal force profile scaled to a max height of 1 unit, which normalizes the values of the peak speed and the force-field magnitude out of the ideal force profile. Note that this is equivalent to scaling the velocity-normalized adaptation coefficients by the product of the peak speed and the force-field magnitude, 15 Ns/m. For example, the lateral force profiles in Fig. 2, A and B, exhibit the same velocity-normalized adaptation coefficients (0.8) despite doubled force levels for the faster movement. However, the raw adaptation coefficients (3.6 and 7.2 N for the slow and fast movements, respectively) reflect the 2 to 1 ratio between the raw forces associated with these trials indicating the linear transfer of adaptation that is being shown in Fig. 2B. Note also that the value of each raw adaptation coefficient loosely indicates an estimate of the peak force consistent with each particular force profile.

We used the raw adaptation coefficient and movement velocity shown late in adaptation to simulate the amount of adaptation transferred to faster movement speeds if the mechanism of transfer was linear, level, or a Gaussian-decay (as shown in Fig. 2). The simulated data for these three different mechanisms was determined by scaling the raw adaptation coefficient for all subjects by the respective adaptation-velocity relationship. The predicted values were the mean and SE of this scaled data (represented in Fig. 4C).

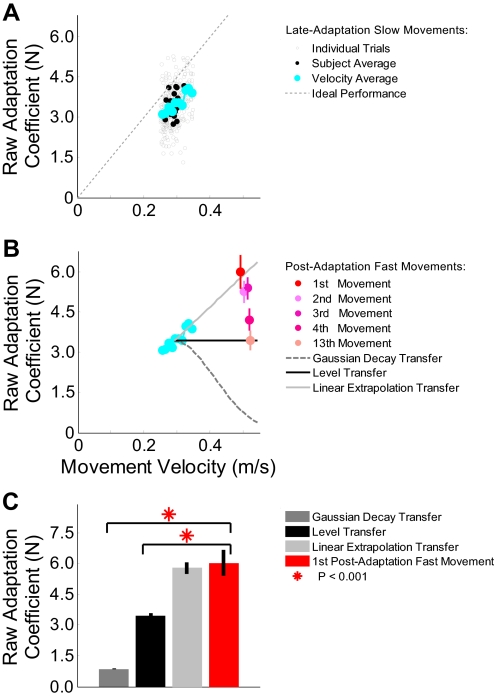
Fig. 4.

Raw adaptation coefficients during training and transfer. A: the unfilled gray circles represent the raw adaptation coefficients for the final 5 movements during the adaptation period for all subjects. The filled black circles indicate the average raw adaptation coefficient and movement velocity for each subject. The blue circles are the average raw adaptation coefficients binned by movement velocity. Ten velocity bins are shown, ranging from 0.25 and 0.35 m/s. B: the blue circles display the same data shown in A. The 3 different lines represent different generalization functions: linear extrapolation transfer (light gray), level transfer (black), and Gaussian decay transfer (dark gray, dashed). The red and pink circles show the mean raw adaptation coefficient and velocity for fast movements made during the postadaptation period. The vertical lines represent SE. C: comparison of the raw adaptation coefficient for the 1st fast movement postadaptation with predictions for 3 different mechanisms for generalization. The error bars show SE.

Modeling of generalization to novel movement speeds

To understand how motor adaptation learned over one range of movement speeds would generalize to untrained movement speeds, we considered three different ways in which the basis elements for motor adaptation could encode the mapping between limb motion and motor output. In the first model, basis elements show isotropic (circular) tuning in velocity space (σ_XY = 0.12 m/s) and directly code for force output as suggested in previous work (Donchin et al. 2003; Shadmehr 2004; Thoroughman and Shadmehr 2000). The primitives were tiled across velocity space with a spacing of σ/2 in each direction (spacing = 0.06 m/s) to assure uniform coverage of the space. For these isotropic force-encoding primitives, we chose the value of 0.12 m/s for the width based on this same previous work that examined the generalization of adaptation across different movement directions.

In the second model, the basis elements also code for force output but show anisotropic tuning in velocity space. These primitives are defined in terms of separate widths for the magnitude and direction of the velocity vector (σ_r = 0.5 m/s, σ_θ = 0.4 radians). Note that we chose the value of σ_θ for these anisotropic force-encoding primitives such that the circumferential width would be similar to that for the isotropic primitives at a speed of 0.3 m/s, which is similar to the average speed associated with the data on which σ_XY was based: arctan(0.12/0.3) ≅ 0.4rad. The value of 0.5 m/s for σ_r was chosen so that σ_r ≫ σ_XY, but its exact size is somewhat arbitrary. (Note that Figs. S4–S6 and S8 in the Supplementary Materials assesses effects of choosing larger or smaller values for σ_r).

In the third model, the basis elements display the same anisotropic tuning for the magnitude and direction of the velocity vector as the anisotropic force-encoding primitives, (σ_r = 0.5 m/s, σ_θ = 0.4 radians), but instead code for the gain between force output and speed of movement. These anisotropic gain-encoding primitives and the other two primitives are shown in Fig. 7 (which is fully described in results). As shown in this figure, the anisotropic primitives are wedged-shaped and tiled across velocity space in magnitude and direction with a spacing of about σ/2 in each direction (spacing = 0.25 m/s in magnitude and 0.2 radians in direction). (In Fig. 7, the contours for the basis elements are shown at the 1-sigma point and only one fourth are shown to reduce visual overcrowding. The spacing in the circumferential direction was chosen to remain consistent with model 1. Additionally, the radial spacing was selected to ensure that the degree of overlap in the radial direction was consistent with the overlap in the circumferential direction. Figure S7 in the Supplementary Materials examines the effects in the radial spacing for the anisotropic force encoding primitives.) Note that within a given model, all basis elements g_k(v), share the same basic shape (with respect to radial symmetry in velocity space).

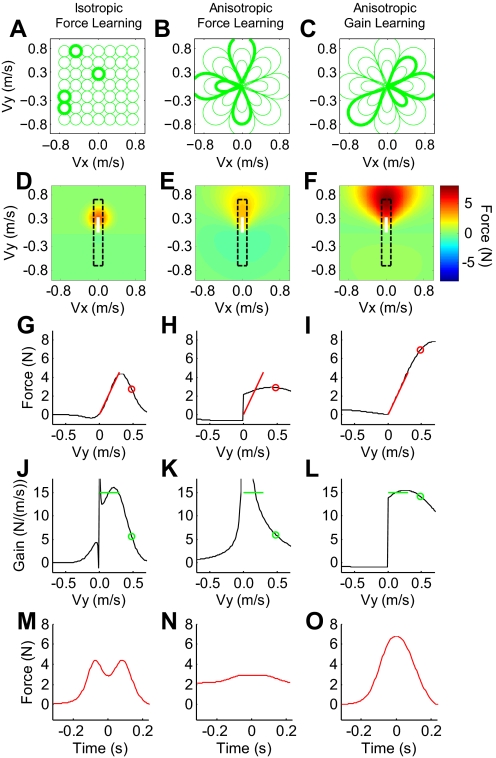
Fig. 7.

Comparison of adaptation generalization for different motor primitive coding schemes. Shown is the comparison of the 3 different hypothetical configurations of the neural bases (each column) used to simulate the generalization of adaptation to novel movement speeds. The configurations were different in the relationship learned between movement speed and force during adaptation [either an absolute force-velocity (A and B) or force gain-velocity relationship (C)] and arrangement in movement velocity space [either isotropic (A) or anisotropic with differential tuning across magnitude vs. direction (B and C)]. (Note that the basis element illustrations in A–C show contours at the 1-sigma point and only a 4th of the elements are shown to reduce visual overcrowding. The 1-sigma point for the basis elements in both anisotropic primitive simulations was at the origin. Selected bases are highlighted to clarify their shape in velocity space.) In all cases, the relationship learned by the bases during adaptation decayed in a Gaussian manner as the movement velocity moved away from the center of the tuning curve. D–F: the pattern of adaptation (amount of mid-movement force) generalization to different movement velocities for the 3 configurations. The heat map represents the generalization of adaptation in terms of lateral force (N). Note that the color bar alongside F applies to the entire row. The white lines represent the region of velocity space over which the force-field is trained for each model (v_X = 0 ms, v_Y = 0–0.3 m/s). The next 2 rows show the learned force-velocity (G–I) and force gain-velocity relationships (J–L) along the slice of velocity space corresponding to the movement direction experienced during the training (v_X = 0, v_Y = −0.7 to 0.7 m/s, the range enclosed by the black dashed-line rectangle). The red and green lines in these panels highlight the relationships between force and velocity, or force gain and velocity that were trained, corresponding to the white line regions in D–F. Note that the red lines extend from the origin with a slope of 15 Ns/m = B, whereas the green lines have a constant value of 15 Ns/m over the range of 0–0.3 m/s for v_Y. The red and green circles show the extent to which the learning predicted by each model would generalize to the untrained, high-speed movements, we observed during the initial high-speed testing trial (v_Y = 0.49 m/s) to facilitate comparison of these modeling results with the data shown in Fig. 4. The spikes in the black trace in J and K are the result of division by 0 in determining the force gain (F/v_Y) at movement speeds near 0. The bottom row (M–O) shows the resulting lateral force patterns for the 3 different primitive configurations at the initial transfer speed (v_Y = 0.49 m/s).

For the first two models (isotropic and anisotropic force-learning primitives), the net force exerted at a given speed is represented by

$$F_{\text{output}/v}={\displaystyle \sum w_{\text{k}}\cdot g_{\text{k}}\left(v\right)}$$ (1)

where w_k is the weight applied to a given basis element, g_k(v), in movement velocity space. During adaptation, the change in weights is determined by

$$\Delta w_{\text{k}}=-\alpha \cdot g_{\text{k}}\left(v\right)\cdot \left[F_{\text{output}}-\left(-Bv\right)\right]$$ (2)

Here (−Bv) represents the ideal exerted force (recall that B is the matrix (B = [0 15; −15 0] Ns/m) that defines the relationship between movement velocity, v, and the force exerted by the manipulandum, f = Bv). Hence, the weights change as a function of the difference between the exerted and the ideal force at each time point in the movement. Each simulation was discretized into 10 ms intervals, and the weight changes associated with each interval were summed.

For model 3 (anisotropic gain-learning primitives), the net force exerted at a given speed is scaled by the movement speed

$$F_{\text{output}}={\displaystyle \sum w_{\text{k}}\cdot g_{\text{k}}\left(v\right)\cdot v}$$ (3)

and the change in weights for the primitives is determined by

$$\Delta w_{\text{k}}=-\alpha \cdot g_{\text{k}}\left(v\right)\cdot \left[F_{\text{output}}-\left(-B\right)\right]$$ (4)

Here, the weights change as a function of the difference between the exerted force-velocity relationship and the ideal force-velocity relationship (B). In all models α (0.00045) is the intrinsic learning rate. (This value of α was used to insure that the learning for the 3 models was biologically plausible—no instability or oscillatory behavior of motor output from one trial to the next. See the Supplementary Materials for a detailed discussion.)

In model 1 (isotropic force-learning primitives), each basis element, G_k(v), is a function of velocity represented in Cartesian coordinates

$$g_{\text{k}}\left(v\right)=e^{-\left\{\left[\frac{{\left(v_{\text{X}}-v_{\text{centerX}}\right)}^2}{2{\sigma }^2}\right]+\left[\frac{{\left(v_Y-v_{\text{centerY}}\right)}^2}{2{\sigma }^2}\right]\right\}}$$ (5)

Here v_X and v_Y represent the movement velocity, v_centerX and v_centerY represent the center of the primitive in velocity space, and σ is the width of tuning.

In models 2 and 3 (the anisotropic force- and gain-learning primitives, respectively), each basis element is also a function of the velocity vector, but its tuning function is expressed in terms of the magnitude, r_V, and direction, θ_V, of the velocity vector

$$g_{\text{k}}\left(v\right)=e^{-\left\{\left[\frac{{\left({\text{r}}_{\text{V}}-v_{\text{centerR}}\right)}^2}{2{\sigma }_{\text{r}}^2}\right]+\left[\frac{{\left({\theta }_{\text{V}}-v_{\text{center}\theta }\right)}^2}{2{\sigma }_{\theta }^2}\right]\right\}}$$ (6)

In this case, v_centerR and v_centerθ represent the center of each primitive in velocity space. σ_θ and σ_r are the widths of the basis functions across the magnitude and direction of the velocity vector.

In these simulations, point-to-point reaching movements with bell-shaped minimum-jerk velocity profiles (Flash and Hogan 1985) oriented along the y-axis were planned, so that

$$\begin{array}{c}{v}_{\text{Y}}=\left[{\left(\frac{30t}{t_{\text{f}}}\right)}^4-{\left(\frac{60t}{t_{\text{f}}}\right)}^3+{\left(\frac{30t}{t_{\text{f}}}\right)}^2\right]\cdot \left(\frac{x_{\text{f}}}{t_{\text{f}}}\right)\\ v_{\text{X}}=0\end{array}$$ (7)

were x_f = 10 cm and t_f = 0.6 s. The peak movement speed was 0.3 m/s, and the model was adapted for 125 trials.

Reassessing previous studies of generalization to novel movement speeds

Two previous studies (Goodbody and Wolpert 1998 and Francis 2008) examined the generalization of learned dynamics across movement speeds. Goodbody and Wolpert (1998) tested the transfer of adaptation to high-speed movements in different force-fields consistent with decay, level, linear, or quadratic transfer of the trained adaptation. In their study, the high-speed movements were approximately twice the speed of trained movements. During the transfer phase of the experiment, they intermixed low-speed training trials with high-speed testing trials for the four test fields, and the results over the entire 400-trial transfer phase were averaged. Because this transfer phase contained nearly 100 high-speed force-field trials, subjects performance after the first few of these trials might have depended on the fields experienced on previous high-speed trials, either instead of or in addition to the transfer across movement speeds that was studied. Subsequent work has shown that when force-fields are applied with randomly varying magnitudes from one to the next, an overall adaptation level is rapidly achieved which approximates the average of these force-fields (Scheidt et al. 2001).

To understand how the high-speed trials experienced might affect other high-speed trials in the study of Goodbody and Wolpert, we computed the average of the force-fields experienced during the transfer phase. For generality, we normalized the exerted force and movement speed during the low-speed training movements to 1. The normalized force, F_N, transferred as a function of normalized velocity, v, for each force-field was represented by:

• Decay transfer: $F_N=e^{\left(\frac{-{\left(v-1\right)}^2}{2{\sigma }^2}\right)}$

• Level transfer: F_N = 1

• Linear transfer: F_N = v

• Quadratic transfer: F_N = v²

In our simulation, the normalized speed, v, went from 0 to 2 (twice the speed of trained movements) in steps of 0.01 m/s with σ for the “decay transfer” field set to 0.5 m/s to match Goodbody and Wolpert (1998). Because these four fields were mixed in equal proportions, we computed the simple average of F_N across the different force-field types for v > 1.0.

Francis (2008) also claimed adaptation transfer across movement speeds (0.15, 0.35, 0.55, and 0.75 m/s) that was between level and linear. This study claimed that the experimental findings could be explained by the model of learning proposed by Donchin et al. (2003), which used isometrically tuned basis elements that encoded raw motor output (as in model 1 described above). However, the author simulated transfer from only one movement speed (0.55 m/s) to the other four, even though the experimental transfer data from all four movement speeds were presented. We ran simulations of generalization from all four movement speeds (0.15, 0.35, 0.55, and 0.75 m/s) to facilitate a full comparison between modeling results and experimental results. Following the Francis simulations, we used motor primitives and a learning rule identical to those in model 1, but assigned a value of 0.14 rather than 0.12 m/s to σ_XY. The model was simulated for 200 trials per movement speed to approximately match the experimental conditions in the Francis paper.

RESULTS

Analysis of the initial motor adaptation

Before testing for generalization across movement speeds, we familiarized subjects with the task and trained adaptation to novel velocity-dependent dynamics. The experiment began with 250 baseline trials during which low-speed and high-speed cued trials were interspersed to ensure that subjects were fully comfortable with the speed cueing and collect baseline data. During the last 50 trials of this baseline period, subjects showed peak speeds of 0.30 ± 0.01 (SE) m/s (across subjects; the average within-subject SD was 0.03 m/s) on low-speed trials and 0.47 ± 0.02 m/s (across subjects; the average within-subject SD was 0.05 m/s) on high-speed trials. Note that in the remainder of this study, we loosely refer to movement speed as the peak speed achieved on a trial. After the baseline period, subjects were exposed to an adaptation period of 150 trials during which a 15 Ns/m velocity-dependent curl force-field was applied to subjects' hands by the robotic manipulandum (see methods). During this training period, 25 error-clamp measurement trials were randomly interspersed—a frequency of one in six trials. By the end of the adaptation period (during which subjects were cued to only make slow movements), subjects had learned to adapt their reaching movements in the velocity-dependent force field. On average, subjects learned ∼80% of the force-field (a velocity-normalized adaptation coefficient of 0.80 ± 0.04; see methods) with a mid-movement force of 3.07 ± 0.13 N (Fig. 3C), corresponding to ∼70% of what would be ideal.

Amount of postadaptation generalization to high-speed movements

There are several ways that the learned force profiles for slow movement speeds could generalize to fast movement speeds. Three types of transfer are shown in Fig. 2. On the left, Fig. 2A shows the adaptation learned during low-speed movements. For each of the three transfer types, the middle column shows the force-velocity relationship (lateral forces vs. movement velocity) that would be predicted during high-speed movements, and the right column shows the corresponding lateral force profiles (lateral force vs. time). The generalization could reflect linear extrapolation transfer (Fig. 2B). In this case, the gain between the exerted lateral force profile and movement velocity during adaptation is preserved between low-speed and high-speed movements such that the learning-related forces produced during the faster movements increase with the same ratio as the movement speed. Another possible generalization pattern is level transfer (Fig. 2C). For this type of transfer, the maximum force exerted for the fast movement is capped, or the force profile is scaled so that the maximum force only reaches the maximum force trained during adaptation. Thus the maximum exerted lateral force during high-speed movements would be the same as the force exhibited during adaptation. A third possibility (Donchin et al. 2003; Shadmehr 2004; Thoroughman and Shadmehr 2000) is Gaussian decay transfer (Fig. 2D). This transfer would result in the force-level decaying in a Gaussian manner once the movement velocity surpasses the maximum velocity exhibited during adaptation or the force profile is scaled in a Gaussian manner. [Note that the alternate transfer types represented by the dashed lines in Fig. 2, C and D, violate the learned force-velocity relationship (blue line) and are therefore unlikely to occur.] We used σ = 0.12 m/s for Gaussian decay transfer in the illustration in Fig. 2.

The lateral force profiles we measured during the course of the experiment are shown in Fig. 3. The average profiles during the baseline and adaptation periods are shown as the colored traces in the first row, and the bottom two rows of Fig. 3 show the lateral force profiles averaged across all subjects for the first nine consecutive postadaptation trials for slow (Fig. 3D) and fast movements (Fig. 3E). The black trace in each panel is the corresponding ideal lateral force profile (based on the average movement velocity profile). Inspection of these postadaptation force profiles reveals two key observations. First, the force profiles for the first slow and fast reaching movements in the transfer period (1st column of Fig. 3, D and E, respectively) are clearly different from one another. Although adaptation of the lateral force profile was trained solely at the slower movement speed, the force profile for the first fast movement after adaptation does not resemble the force profile for the first slow movement, but instead closely matched the ideal force required at the faster movement speed. The clear increase in lateral force that parallels the increase in velocity shows that, although the subjects were not trained at the higher speed, they extrapolated the required force-velocity relationship to it. Note that this effect is quantified in Fig. 4, which is detailed below (and in Figs. S1 and S2 in the Supplementary Materials). The second observation was that the force patterns exerted by the subjects decreased for both movement speeds as the adaptation decayed. This is most apparent when comparing the peak of the ideal and exerted force profile across Fig. 3, D and E. This difference between these peaks increases in a parallel fashion for low-speed and high-speed movements as the postadaptation trial number increases. A detailed analysis of this effect is presented in Fig. 6.

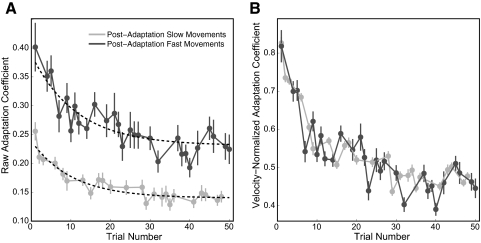
Fig. 6.

Parallel decay of performance in the postadaptation period for fast and slow movements. A: decay of raw adaptation coefficients as a function of trial number. The black dashed lines are the exponential fits to the data (with time constants of 11.4 and 10.3 trials for fast and slow movements, respectively). B: velocity-normalized adaptation coefficients for the same data presented in A. Data for fast movements are shown in dark gray and slow movements in light gray. The error bars represent SE across subjects.

We quantified the level of motor adaptation by computing the regression between the lateral force that subjects exerted and the normalized ideal force on each error-clamp trial (see methods). This normalized ideal force profile was scaled to have a maximum value of unity and thus reflected the shape but not the magnitude of the longitudinal velocity profile shown on each trial (see methods). At the end of the adaptation period, the average value the “raw adaptation coefficient” obtained from this regression was 3.45 ± 0.11 N at an average movement velocity of 0.29 ± 0.01 m/s (across subjects; the average within-subject SD was 0.02 m/s). This corresponds to a velocity-normalized adaptation coefficient of 0.80 ± 0.04 (see Fig. S2). The raw adaptation coefficients for the final 5 of the 25 error-clamp trials in the adaptation period are plotted against the corresponding movement velocity on that trial for all subjects in Fig. 4A (unfilled gray circles). In addition, the average raw adaptation coefficient is plotted against the average movement velocity over these same trials for each subject (filled black circles, subject average). Note that, on average, the adaptation levels are ∼80% of the ideal adaptation level depicted by the gray diagonal line. To determine whether the raw adaptation coefficient significantly varied with movement velocity during the adaptation period, we pooled the data from all subjects and binned this group data (bin width, 0.01 m/s) between the movement velocities of 0.25 and 0.35 m/s. We calculated the average raw adaptation coefficient and movement velocity within each bin (velocity average). These averages are represented by the filled cyan circles in Fig. 4A and B. As illustrated in these panels, the raw adaptation coefficient increased in a linear manner with movement velocity during adaptation (slope = 0.72 ± 0.27, F_2,9 = 38.6, R² = 0.83, P = 0.0003). Note that the slope of this relationship is not significantly different from the mean velocity-normalized adaptation coefficient, suggesting trial-to-trial variations in speed resulted in matched modulations in lateral force.

We were primarily interested in the ability of the subjects to extrapolate adaptation to novel movement speeds not experienced during the adaptation. To determine how the pattern of experimental generalization might relate to the three types of adaptation transfer shown in Fig. 2, we plotted the expected relationship between the raw adaptation coefficient and movement speed for each. To represent linear extrapolation transfer, we extrapolated a line (light gray trace in Fig. 4B) passing through the origin (which represents a raw adaptation coefficient and a movement velocity of 0) and the average raw adaptation coefficient and average movement velocity shown during adaptation (3.45 N and 0.29 m/s, respectively). Note that this line has a slope of ∼12 Ns/m, corresponding to the product of the force-field amplitude (15 Ns/m) and the mean velocity-normalized adaptation coefficient (0.80) that subjects displayed late in the training period. This slope also corresponds to the ratio between the average raw adaptation coefficient (3.45 N) and the average movement speed (0.29 m/s). For Gaussian decay transfer (dark gray dashed trace in Fig. 4B), the raw adaptation coefficient would decay in a Gaussian manner (σ = 0.12 m/s) around the trained movement velocity (0.29 ± 0.01 m/s). Finally, for level transfer (black trace), the raw adaptation coefficient would remain the same (3.45 N) at faster movement speeds.

The mean raw adaptation coefficient is plotted against the mean movement velocity across all subjects for the fast postadaptation movements for select trials in the testing period (trials 1–4 and 13) in Fig. 4B (colored circles in the top right). The error bars represent SE. The first postadaptation fast movement displayed an average speed of 0.49 m/s and a raw adaptation coefficient of 6.0 ± 0.6 N. This raw adaptation coefficient, which is 74% greater than the end of the low-speed training period, closely matches the 69% increase in speed we observed, consistent with linear extrapolation transfer. Correspondingly, the red-colored data point that represents this movement lies almost on top of the light gray trace that represents linear extrapolation transfer in Fig. 4B. The mean raw adaptation coefficient for this movement (6.0 ± 0.6 N) closely matches the value predicted by linear extrapolation transfer (5.85 N) but does not match the values predicted by either the Gaussian decay (0.87 N) or level transfer (3.45 N) patterns. Correspondingly, the velocity-normalized adaptation coefficient for this trial is essentially equal to that seen late in the training period and on the first postadaptation low-speed trial (0.83 vs. 0.78 and 0.82, respectively), consistent with a constant force-gain, which would be expected from linear extrapolation transfer. Note that the average mid-movement force associated with this trial (5.2 N) is also 70% greater than during training (Supplementary Fig. S1), further supporting linear extrapolation transfer.

Alternate versions of Fig. 4 that show mid-movement force or the velocity-normalized adaptation coefficients are included in the supplementary materials (Supplementary Figs. S1 and S2). All three metrics are consistent with linear extrapolation transfer. Note that a small difference between the actual values of our raw adaptation coefficient and mid-movement force measures is to be expected because our mid-movement force measure operates in a window of 70 ms on either side of the peak speed, and thus by averaging, slightly underestimates the expected value of the peak force. Nevertheless, it provides a self-consistent measure of adaptation. Also note that, after the 1st postadaptation trial, the adaptation level appears to steadily decay such that, by the 13th postadaptation high-speed trial, the raw adaptation coefficient has descended to the level observed in the low-speed trials during late adaptation. The time course of this decay is also apparent in Fig. 3 and is examined in detail in Fig. 6 below.

Figure 4C shows a direct comparison of the generalization levels we measured on the first postadaptation high-speed movement and those predicted by the three types of transfer illustrated in Fig. 2. We found no significant difference between the experimental data and generalization levels predicted by Linear Extrapolation Transfer (P > 0.2), however our data show significantly higher generalization than predicted by either Gaussian Decay Transfer or Level Transfer (1-tailed t-test, P < 0.001 in both cases).

Temporal profile of postadaptation generalization to high-speed movements

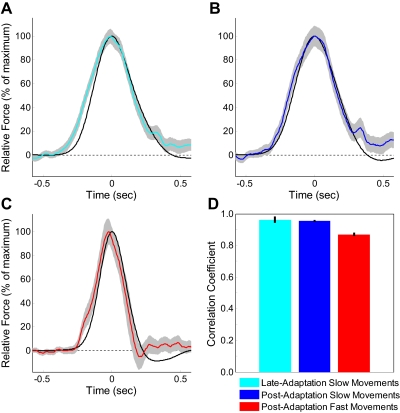
In addition to determining the type of generalization to faster novel movement velocities, we also quantified how accurately the shape of the exerted force profile matched the shape of the ideal compensatory force, because faster movements result in not only faster but narrower velocity profiles, corresponding to narrower ideal compensatory force patterns. To examine the shape of these force patterns independently of their magnitudes, we normalized the lateral force profiles we measured during error-clamp trials by the peak force exerted. Figure 5 shows these normalized force profiles for the ideal compensatory and actual force at the end of adaptation and for slow and fast movements after adaptation. Inspection of Fig. 5, A–C, shows that the normalized actual force profile closely matches the shape of the normalized ideal compensatory force profile. This is a key finding because the narrower force profile for the fast postadaptation movements (Fig. 5C) was never trained. To quantify this result, we determined the correlation coefficient between the ideal and actual force profiles (Fig. 5D). We found that, for all movement speeds, the correlation was extremely high (r > 0.86 in all cases), indicating that subjects did not just increase the output force at the faster movement speeds but instead closely matched the extrapolated pattern of force at these speeds.

Fig. 5.

Comparison of the shapes of actual and ideal force profiles for slow and fast movements. To examine the shape of each force profile independent of its magnitude, we normalized each by its maximum. Force profiles shapes are shown for (A) slow movements near the end of the adaptation period and (B) slow and (C) fast movements in the postadaptation period. In each panel, the black trace is the ideal compensatory force, the colored traces represent the actual force produced by subjects, and the gray shaded region represents the SE around the latter. D: correlation coefficients for the data presented in A–C. The vertical black bars represent SE.

Decay of generalization parallels the decay of adaptation

Figure 4B shows that the raw adaptation coefficients for the fast postadaptation movements decreased with trial number and only reached the average level achieved during adaptation by the 13th movement. This same decay pattern is also apparent in Fig. 3, D and E. The data in Fig. 3 suggest a constant amount of generalization from low-speed to high-speed movements because the force profiles associated with the low-speed and high-speed movements seem to decrease in parallel after training. To quantify this decay, we analyzed the change in the raw adaptation coefficient as a function of postadaptation trial number. This data are plotted in Fig. 6A. The circles represent the mean raw adaptation coefficient across subjects for fast (dark gray circles) and slow (light gray circles) postadaptation movements. The error bars represent SE. We fit a single exponential to each data set (black dashed line) and found time constants (11.4 and 10.3 trials for fast and slow movements, respectively) that were not significantly different from one another (P > 0.5). When velocity-normalized adaptation coefficients (Fig. 6B) are examined instead for the same data sets, the similarity between the decay patterns in the postadaptation period for high-speed and low-speed trials is even more readily apparent, because the two curves essentially lie on top of one another. This indicates that the generalization to faster movement speeds decays at the same rate as the adaptation itself, suggesting that a constant linear extrapolation transfer across movement speeds was maintained during the entire decay period as adaptation levels were reduced.

Patterns of generalization predicted by different types of motor primitives

The ability of subjects to linearly extrapolate reaching adaptation to novel movement speeds may provide information about the shape of the neural basis elements that underlie motor adaptation. In general, basis elements with large widths would allow for faster initial adaptation to new environments because of broad generalization between neighboring conditions, whereas smaller widths would allow for a finer mapping of condition specificity and limit overgeneralization. We simulated adaptation and generalization for different types of neural basis elements to examine two issues. 1) Whether the widths of these adaptive motor primitives might be anisotropic in velocity space when learning velocity-dependent dynamics. In particular, are the widths of these primitives in velocity space identical laterally (i.e., across movement directions) versus radially (i.e., across speeds) as several computational models have assumed (Donchin et al. 2003; Shadmehr 2004; Thoroughman and Shadmehr 2000)? 2) Whether the learned adaptation directly represents motor output (such as force or torque), as often assumed, or the gain between motor output and motion state.

To investigate these issues, we simulated the adaptation and generalization of our motor task to novel movement speeds with three different models (Fig 7, each column is a different model). The models differed 1) in the relationship learned between movement speed and primitive output during adaptation [either an absolute force-velocity relationship (models 1 and 2)] or a force gain-velocity relationship (model 3), and 2) in the shape of the basis elements in movement velocity space [either isotropic (model 1) or anisotropic across the magnitude and direction of the velocity vector (models 2 and 3)]. For all models, the basis functions show Gaussian tuning for the respective relationship learned between motion state and the motor primitive output during adaptation (see methods for details). Model 1, depicted in Fig. 7A, assumes that the basis elements learn an absolute force-velocity relationship and that the widths are isotropic in the velocity space. That is, the output of each basis element represents a contribution to the learned force at a particular movement speed, and this contribution decays in a Gaussian manner as the movement speed moves away from the center of the primitive in velocity space. By isotropic width, we mean that these basis elements are radially symmetric with respect to their own centers such that the decay across changes in the magnitude and direction of the velocity vector are identical. As noted above, this has been assumed in previous modeling work. Model 2 (Fig. 7B) considers basis elements that code directly for motor output (force), but with widths that are anisotropic in the velocity space. We considered a radical pattern of anisotropy (as shown in Fig. 7B) in order to reconcile our finding of broad generalization across the magnitude of the velocity vector with previous work showing relatively narrow generalization as the direction of the velocity vector was changed (Darainy et al. 2009; Gandolfo et al. 1996; Mattar and Ostry 2007; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005). The widths of these basis elements are elongated in the direction of the velocity vector. Model 3, shown in Fig. 7C, features radially anisotropic basis elements shaped identically to those in model 2, but here, the motor primitives learn the gain between force and velocity rather that force itself.

Following a simulated adaptation period in which the models were trained with movements that had minimum-jerk velocity profiles and peak speeds of 0.3 m/s (see methods for additional details), we determined the amount of adaptation that would transfer to other novel movement velocities for each model. We found that the pattern of this generalization (shown in Fig. 7, D–F) was different for the three models. The generalization was most localized to the movement velocities experienced during adaptation (0–0.3 m/s in the y-direction) for model 1 and broadest for model 3, in which anisotropically shaped motor primitives learned the relationship between gain and velocity. The differences are more apparent by examining the force-velocity (Fig. 7, G–I) and force gain-velocity relationships (Fig. 7, J–L) along the slice of velocity space, corresponding to the movement direction experienced during the training, denoted by the black rectangle in Fig. 7, D–F. The anisotropic primitive models generalize more broadly to high-speed movements than the isotropic primitive model because the basis element widths across movement speed are wider (0.5 vs. 0.12 m/s in our simulations). Note that, although the anisotropic gain-encoding primitive model generalizes somewhat more broadly than the anisotropic force-encoding primitive model, both show clear extrapolation of the force level acquired during training. In contrast, the isotropic force-encoding primitive model shows a transfer pattern that falls off sharply beyond 0.3 m/s.

Interestingly, unlike the other two models, the anisotropic force-encoding primitive model is unable to fully learn the adaptation trained at low speeds—this model learns so slowly that 125 force-field training trials (the number of training trials we use in our experiment) is not enough for asymptotic performance to be achieved. This model is quickly able to learn the mean force level experienced during training but has trouble learning the specific (linear) force-velocity relationship. Thus the incomplete adaptation is manifested in the reduced slope of the learned force-velocity relationship (black line) shown in Fig. 7H, which is only about one third the slope of the ideal force-velocity relationship (red line). The incomplete initial adaptation produced by the anisotropic force-encoding primitive model is particularly surprising because this model is intermediate in its architecture between the other two. Note that, because the trained force-velocity relationship is linear, whereas the trained force-gain relationship is constant, force-encoding primitives must learn a ramp-like input-output function, whereas gain-encoding primitives need only learn a constant-value input-output function. Further analysis (see the Supplementary Materials) reveals that the anisotropic force model learns slowly because wide Gaussian primitives have trouble learning ramp-like functions but can readily learn constant-value functions. In contrast, narrow Gaussian basis elements can readily learn both ramp-like and constant-value input-output functions. Note that narrow versus wide would be defined here in terms of the ratio between the basis element width (0.12 or 0.5 m/s) and the width of the trained function (0.3 m/s in our case).

One might conjecture that the slow learning showed by the anisotropic force-encoding primitive model could be overcome by simply increasing the value of the learning rate parameter (α). However, this is not the case. Although some improvement in performance can be achieved by increasing the learning rate, model 2 becomes unstable well before it can match the performance of the other two models (see Supplementary Materials, Figs. S4–S6). Consequently, only the anisotropic gain-encoding primitive model can reproduce our experimental results: a linear extrapolation of the trained adaptation to short-duration higher-speed movements (Fig. 7O). The isotropic force-encoding primitive model can learn the initial adaptation but shows poor transfer to high-speed movements, whereas the anisotropic force-encoding primitive model can extrapolate what it does learn to high-speed movements but cannot learn the initial adaptation well. Thus the transfer of adaptation to higher-speed movements for both force encoding models (models 1 and 2) results in force profiles that do not resemble the force pattern shown by subjects (Fig. 3E). The isotropic model results in a Gaussian-like decay of force-level for movement velocity beyond the maximum velocity exhibited during adaptation (Fig. 7M) and the anisotropic model results in a plateauing of the force-level (Fig. 7N). (Note that the offset in force level in Fig. 7N is caused by the anisotropic force encoding primitives readily learning the mean force during training, but not the force-velocity relationship. See Supplementary Materials for details.)

DISCUSSION

In this study, we quantified the generalization of motor adaptation to movement speeds beyond those experienced during training. Our results showed that this generalization shows linear extrapolation across velocity space from low-speed to high-speed movements. When subjects moved at speeds that were ∼70% faster than the speed experienced during adaptation, the exerted force pattern also increased by ∼70%. In addition, the force profiles for low-speed and high-speed movements decayed in parallel during the transfer period, indicating that a constant linear extrapolation transfer across movement speeds was maintained as adaptation levels were reduced. Our simulation results showed that the linear hypergeneralization of adaptation is the result of anisotropic gain-encoding motor primitives rather than an isotropic or anisotropic force-encoding scheme. Taken together, our experimental data and modeling results indicate that the basis elements for adaptation display broader tuning for movement speed than for movement direction and encode the gain between motor output and motion state rather than motor output itself.

Comparison to previous computational models

Recent models of the trial-to-trial dynamics during adaptation assume that subjects learn novel velocity-dependent dynamics for reaching arm movements through a flexible combination of primitives that are isotropic in velocity space with Gaussian-like tuning functions (Donchin et al. 2003; Hwang et al. 2003; Shadmehr 2004; Thoroughman and Shadmehr 2000). That is, these primitives encode motor output, the exerted force, at a preferred movement velocity (speed and direction of the velocity vector) that decays as the speed or movement direction moves away from the preferred velocity. However, direct evidence for the existence of isotropically shaped primitives is sparse. Through simulation, we showed that this coding scheme cannot account for these results (Fig. 7), because it predicts decreased learning-related motor output during high-speed movements if the primitive width determined from studying the direction of the velocity vector is applied to the velocity magnitude. In contrast, we observe increases in motor output in the transfer of adaptation to high-speed movements. Interestingly, we were only able to match the observed increases in learning-related motor output with movement speed in combination with the ability to readily learn the dynamics of the trained field in a model with anisotropic basis elements that encode motor output gain. (This model was also able to reproduce the generalization of adaptation across movement directions the isotropically shaped primitives were originally derived to describe; see Supplementary Fig. S3.) Both isotropic and anisotropic force-encoding primitives are unable to reproduce our experimental findings, with the former failing to show extrapolation and the latter failing to show the ability to readily learn the initial adaptation. (see the Supplementary Materials for a detailed discussion).

Linear extrapolation of adaptation to novel movement speeds

Two previous studies have looked at the generalization of learned dynamics across movement speeds when target distance was held constant. Like this study, both examined orthogonal velocity-dependent dynamics—i.e., viscous curl force-fields. Goodbody and Wolpert (1998) tested the transfer of adaptation to high-speed movements in force-fields that showed either decay, level, linear, or quadratic transfer of the trained adaptation. Because the high-speed movements were approximately twice the speed of trained movements, perfect performance on each field corresponded to generalization at the maximum speed with zero, equal, double, or quadruple the trained force level, respectively, as shown in Fig. 8. The pattern of transfer observed by the authors suggested that transfer was between level and linear, but closer to linear extrapolation. Unfortunately, the transfer phase of the experiment was lengthy (it lasted for 384 trials including 96 high-speed trials; 24 of each type of generalization force-field), and only results averaged over the entire transfer phase were presented. The high-speed movements during the transfer phase were randomly ordered between the four test force-fields. Subsequent work has shown that when force-fields are applied with randomly varying magnitudes from one to the next, an overall adaptation level is rapidly achieved that approximates the average of these force-fields (Scheidt et al. 2001). This finding bears directly on Goodbody and Wolpert's results because the force profile for the linear field is near the average force profile across all fields tested as shown in Fig. 8A (see methods for details). In particular, at a velocity twice the speed of trained movements, the average of the tested force-fields would be 1.75 times the maximum force trained during low-speed movements, corresponding to the finding of transfer between level (1 time) and linear (2 times), but closer to the linear that Goodbody and Wolpert reported. Thus it is not clear as to how much of the apparent transfer to high-speed trials observed in this study resulted from generalization of the adaptation learned in low-speed movements because direct adaptation to the mix of force-fields experienced on other high-speed testing trials can also account for the results. It is possible that this issue could have been resolved by the analysis of the very first trials for each test field, analogous to the first-trial analysis presented here.

Francis (2008) also claimed adaptation transfer across movement speeds (0.15, 0.35, 0.55, and 0.75 m/s) that was between level and linear: in this case, more level at high speeds and more linear at lower speeds. In particular, the results claimed a somewhat linear extrapolation of adaptation from each of the four speeds studied up to a speed of 0.55 m/s and a leveling off of transfer from 0.55 to 0.75 m/s. However, the velocity profiles themselves for the high-speed movements appeared to display considerable variability from one trial to the next, suggesting that the apparent leveling off might be caused by overlap between the actual speeds shown for the 0.55 and 0.75 m/s trials. This effect could potentially be ameliorated by classifying movements based on actual rather than cued movement speed. There are two issues with this study. The first involves the robustness of the experimental results and the second involves the modeling work that was presented. This study used trial-by-trial modeling of the adaptation process to estimate the learning rates associated with the four different movement speeds. Unfortunately, in this model, the 16 learning rate parameters that were fitted explained, in aggregate, only ∼40% of the variance in trial-by-trial performance that remained after the effects of arm stiffness were taken into account, even after the data to be fitted were averaged across subjects to reduce noise. This suggests that the estimates obtained for the learning rate parameters may not have been robust, consistent with the fact that the initial conditions used in the procedure for parameter estimation had a noticeable effect on the learning rate estimates. Interestingly, this study claimed that the experimental findings that included linear extrapolation could be explained by the isotropic force-encoding primitive model proposed by Donchin et al. (2003). This is at odds with the modeling results presented here, which showed that such a model will not display linear extrapolation. How could this be? Although the Francis study reported similar patterns of transfer from each of the four speeds that were studied, the isometric basis element model was only used to simulate generalization from one of the four speeds (the 0.55 m/s trials) to the other three speeds. This single simulation appeared to reproduce the pattern of transfer matching the experimental findings from all four movement speeds. Unfortunately, simulations of the generalization from the other three movement speeds were not presented. We ran simulations of generalization from all four movement speeds with the isometric primitives used in Francis (2008) (see methods for details), and the results are shown in Fig. 8B. Because the isometric primitive model cannot account for linear extrapolation, these simulation results do not show linear extrapolation and thus do not match the parameter-fit experimental results from the same paper, suggesting linear extrapolation from 0.35 to 0.55 m/s (or from 0.15 m/s to both 0.35 and 0.55 m/s).

Previous studies on other adaptation paradigms have shown linear hypergeneralization of movement adaptation to novel speed contexts. For example, Krakauer et al. (2000) examined the generalization of visuomotor rotation to targets with different extents and found near-perfect extrapolation to larger extents and speeds. Although learning a visuomotor rotation and a force-field perturbation are likely to involve different neural processes (Tanaka et al. 2009), this similarity suggests that the transfer of adaptation to novel movement speeds may be a general feature of motor adaptation. Similar results have been reported for saccade adaptation (Noto et al. 1999): following a gain decrease adaptation for horizontal saccades to 15° target steps, saccades to horizontal target steps of different amplitudes (5–25°) were tested for generalization. Larger saccades showed greater learning-related changes in saccade amplitude. However, saccadic gain was found to be reduced for the largest saccades, suggesting local transfer of the gain associated with saccadic adaptation, i.e., linear extrapolation that is locally tuned. In both the visual rotation and the saccade adaptation studies, the adaptation affected novel states (untrained movement velocities or saccade amplitudes) in a manner beyond level transfer. That is, the data presented in these two studies were suggestive of the linear hypergeneralization we found to faster movement speeds following adaptation to novel velocity-dependent dynamics. Combined with the results presented here, these findings suggest that similar neural computations may underlie the learning and adaptation of arm dynamics and visuomotor transformations for arm and eye movements. The adaptation observed in these tasks may represent the gain between motor output and movement velocity or extent rather that the learning of motor output itself.

Evidence for anisotropic, gain-encoding motor primitives

Previous work has shown anisotropic tuning in the representation of the movement parameters encoded by the neural circuits that underlie the motor action. For example, several single unit studies have examined how the extent and direction of point-to-point reaching arm movements correlate with activity in premotor and primary motor cortex. When movement direction and extent are considered independently, extent by itself correlates poorly with firing rates (Fu et al. 1993). Correspondingly, cells that code for extent generally do so in combination with direction (Messier and Kalaska 2000), consistent with the tuning in our models. For movements in the preferred direction, firing rates, on average, extrapolate with extent, however, in a sublinear manner; a 200% increase in extent (2.5–7.5 cm) leads to only a 15% increase in firing rate, on average, and only a 30% increase for the subset of cells whose firing rates show a significant positive regression onto extent (Messier and Kalaska 2000). However, speed was not specifically controlled in these studies and was thus highly correlated with extent as expected from Fitts Law (Fitts 1954). Therefore it is difficult to know the degree to which the positive, but sublinear, effects observed in these studies reflect the coding of speed versus extent or a combination thereof.

A pair of recent studies has focused on the neural coding of velocity in continuous movements for which the effects of velocity and position could be readily disambiguated and in which extent is not that relevant of a parameter. Interestingly, these studies showed that speed primarily acts in such a way as to linearly scale the responses for both neurons in primary motor cortex (Paninski et al. 2004) and Purkinje cells in the cerebellum (Roitman et al. 2005). These neural responses are consistent with the fully linear extrapolation of motor output with velocity that we observe experimentally and with the anisotropic gain-encoding model that our data support. If motor adaptation modulates the activity of these cells, the linear scaling of their responses would provide the velocity gain for our gain-encoding model. Thus their activity, which already reflects this gain, would relate directly to motor output itself. In line with this idea, Moran and Schwartz (1999) found that velocity acts in real time as a gain factor on directionally modulated responses in primary motor cortex for point-to-point reaching movements.

Movement-related neurons in the neural areas involved in the generation of motor commands for saccadic eye movements also show anisotropic tuning, responding over a larger set of movement amplitudes than movement directions [superior colliculus (SC), Sparks et al. 1976; frontal eye field (FEF), Bruce and Goldberg 1985; Bruce et al. 1985]. Furthermore, the activity of these neurons decreases more rapidly when the movement amplitude is less than the preferred amplitude and more slowly when the amplitude exceeds it, as would be expected for a gain-encoding cell without extremely broad tuning. The activity related to movement direction, on the other hand, decreases even more rapidly and in a symmetric Gaussian-like manner as the saccade direction moves away from the preferred direction. These findings are consistent with narrower tuning across movement direction versus speed and a symmetric representation of gain rather than motor output. However, as with the studies of arm movement amplitude mentioned above, one cannot be certain about the degree to which the results reflect the coding of velocity versus extent, because of the high level of covariation between them. The asymmetric tuning observed in SC and FEF is also consistent with the compressive, log-like, coding of space that is displayed in these areas (Ottes et al. 1986; Sommer and Wurtz 2000; Van Gisbergen et al. 1987). However, it could be pointed out that, in general, local Gaussian tuning acting in combination with compressive coding may be a mechanism for generating responses similar to the Gaussian modulation of a linear gain function that is represented in our modeling work.

Contextual effects

Churchland et al. (2006) found that speed and extent strongly and independently modulated firing rates in the vast majority of motor cortical cells they studied both during movement time (in agreement with previous work) and in the preparatory activity. However, it should be pointed out that the degree of heterogeneity in the neural responses they recorded was tremendous. There was a general trend for higher firings rates with larger extents and velocities; however, as many as 30–40% of the significantly modulated cells displayed higher firing rates when velocity or extent was reduced rather than increased. Furthermore, these negative effects could occur either in combination or in isolation. This is in line with the idea that individual motor cortical cells might, at least partially, code for different movement contexts. In contrast with these results, Mattar and Ostry (2010) recently reported approximately level extrapolation for force-field adaptation to reaching movements that were simultaneously faster and of greater extent than trained movements. The reduction in transfer compared with these findings may arise from the contextualization of movements based on extent. If so, the linear effect of gain-encoding primitives would be mitigated by contextual differences between short-slow and long-fast movements. The composition of these linearly extrapolating and locally decaying effects might result in the near-level transfer that was reported. This is line with the saccade adaption results mentioned above for which velocity and extent increased together (Noto et al. 1999); however, further work will be necessary to determine whether this is indeed the case.

Implications for neurorehabilitation

Understanding the properties of these neural circuits and how they guide the generalization of motor adaptation to novel motions may be valuable in developing devices that interact or decode the output of these neural mechanisms (Lebedev et al. 2005; Shenoy et al. 2006) and for developing improved paradigms for rehabilitation therapy (Bastian 2008; Huang and Krakauer 2009). If primitives were isotropically narrow as had previously been assumed, complete generalization of adaptation within a novel environment would require training that densely sampled the entire velocity space—with all combinations of magnitude and direction. However, these results suggest that near-complete generalization can be achieved with training that densely samples different movement directions, but only coarsely samples different speeds. This could improve the efficiency of training and may have practical ramifications for rehabilitation. When retraining limb movements after injury or disease, patients may initially only be able to perform motor tasks at low speed. However, according to these results, the properties of the underlying motor primitives should allow low-speed training to smoothly transfer to high-speed movements.

GRANTS

This work was supported by the Sloan Research Fellowship from the Alfred P. Sloan Foundation and a Scholar Award from the McKnight Endowment for Neuroscience to M. A. Smith.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.