Abstract
In the companion paper we show that GAD67-GFP+ (GFP+) inhibitory neurons located in the Nucleus of Roller of the mouse brain stem can be classified into two main groups (tonic and phasic) based on their firing patterns in responses to injected depolarizing current steps. In this study we examined the responses of GFP+ cells to fluctuating sinusoidal (“chirp”) current stimuli. Membrane impedance profiles in response to chirp stimulation showed that nearly all phasic cells exhibited subthreshold resonance, whereas the majority of tonic GFP+ cells were nonresonant. In general, subthreshold resonance was associated with a relatively fast passive membrane time constant and low input resistance. In response to suprathreshold chirp current stimulation at a holding potential just below spike threshold the majority of tonic GFP+ cells fired multiple action potentials per cycle at low input frequencies (<5 Hz) and either stopped firing or were not entrained by the chirp at higher input frequencies (= tonic low-pass cells). A smaller group of phasic GFP+ cells did not fire at low input frequency but were able to phase-lock 1:1 at intermediate chirp frequencies (= band-pass cells). Spike timing reliability was tested with repeated chirp stimuli and our results show that phasic cells were able to reliably fire when they phase-locked 1:1 over a relatively broad range of input frequencies. Most tonic low-pass cells showed low reliability and poor phase-locking ability. Computer modeling suggested that these different firing resonance properties among GFP+ cells are due to differences in passive and active membrane properties and spiking mechanisms. This heterogeneity of resonance properties might serve to selectively activate subgroups of interneurons.
INTRODUCTION
Traditionally the input–output properties of neurons have been studied by examining their spike firing discharge pattern in response to long depolarizing current (DC) steps. The firing pattern of neurons to DC current steps gives only limited information about the input–output properties of neurons and cannot accurately predict the response to more complex stimuli as likely occur in vivo. The nature of the stimuli that drive neurons in vivo during specific behaviors is often not known. An exception are hypoglossal motoneurons (HMs) whose synaptic input received during inspiration is composed of a slow depolarizing envelope, which brings these cells close to firing threshold, on top of which a fluctuating input is superimposed, which triggers spikes when the positive-going voltage fluctuations exceed threshold (Funk et al. 1993). During inspiration HMs therefore operate in the fluctuation-driven regime where the mean of the synaptic driving current is below spike threshold and spiking occurs only when the superimposed fluctuations exceed threshold (Schreiber et al. 2009; Tiesinga and Sejnowski 2009).
Membrane voltage fluctuations are not only important to bring neurons to firing threshold but they also improve spike timing reliability. Mainen and Sejnowski (1995) have shown that spike timing in cortical pyramidal cells is highly unreliable when they are stimulated with a DC input and that reliability and precision are improved when a fluctuating current input is used as stimulus. Spike timing precision depends on the ability of neurons to phase-lock to the stimulus (Tiesinga et al. 2008). By using sinusoidal current stimuli of varying frequency (chirp or ZAP stimulus) it has been shown that neurons phase-lock 1:1 to the stimulus over a relatively narrow range of preferred input frequencies. Cortical pyramidal cells (Brumberg and Gutkin 2007; Nowak et al. 1997), hippocampal CA1 neurons (Leung and Yu 1998; Pike et al. 2000), and HMs (van Brederode and Berger 2008) prefer sinusoidal inputs in the 2- to 20-Hz range, although certain types of interneurons prefer much higher input frequencies (Fellous et al. 2001; Pike et al. 2000). In the fluctuation-driven firing regime the most reliable spiking occurs when the cell phase-locks 1:1 to the stimulus (Beierholm et al. 2001; Fellous et al. 2001; van Brederode and Berger 2008), thus endowing these cells with mechanisms to respond best to stimuli within a specific frequency band; i.e., they show firing resonance for these frequencies. Spiking with high reliability and precision in response to a fluctuating input is important to produce synchronous firing in a group of neurons (Tiesinga et al. 2008).
In the fluctuation regime the firing resonance properties of a neuron are to a large extent determined by subthreshold resonance properties (Engel et al. 2008; Schreiber et al. 2004a, 2009). When the subthreshold membrane impedance profile of a neuron shows a peak at nonzero input frequency a neuron is said to be resonant; if a neuron has an impedance profile that decays monotonically from a maximum at zero frequency it is said to be nonresonant (Hutcheon and Yarom 2000). When stimulus amplitude is increased to elicit spike firing, resonant neurons fire most reliably when the stimulus frequency matches the preferred frequency of their subthreshold impedance profile (Fellous et al. 2001; Hutcheon et al. 1996b). Neurons with subthreshold resonance have been described in the entorhinal cortex (Erchova et al. 2004; Haas and White 2002), prefrontal cortex (Fellous et al. 2001), hippocampus (Leung and Yu 1998; Pike et al. 2000), trigeminal root ganglion cells (Puil et al. 1986), vestibular neurons (Beraneck et al. 2007), and HMs (Nguyen et al. 2004). Subthreshold resonance is due to the low-pass filtering of high-frequency input by the cells' passive membrane properties in combination with high-pass filtering by slow, voltage-activated conductances that oppose changes in membrane potential (reviewed by Hutcheon and Yarom 2000). It has been suggested that the relative importance of subthreshold resonance properties in firing resonance is dependent on the mean depolarization level of a cell (Richardson et al. 2003; Schreiber et al. 2009).
In the companion paper (van Brederode et al. 2011) we have identified a population of GAD67-GFP+ GABAergic interneurons (GFP+ cells) located in the Nucleus of Roller (NR) that provides synaptic inhibition to HMs. These GFP+ cells are morphologically and electrophysiologically heterogeneous. The firing responses to DC pulses of these cells suggest that one group (tonic cells) are best suited to decode slowly varying stimuli, whereas another group, composed of phasic cells, will respond best to a fluctuating stimulus. Different types of GFP+ cells also differed in the magnitude and time course of spike afterpotentials, suggesting different ionic currents underlying spike repolarization in these cells. Interestingly, many of the GFP+ cells are spontaneously active due to intrinsic autorhythmicity and they would therefore operate mainly in the mean-driven regime where neurons are in a continuous firing mode (Hunter et al. 1998; Schreiber et al. 2009). Furthermore, the firing rate of spontaneously active GFP+ neurons was not modulated by ongoing inspiratory drive (van Brederode et al. 2011). In the mean-driven regime firing resonance is less dependent on subthreshold resonance properties and instead relies more on the spiking mechanism of the neurons (Engel et al. 2008; Hunter et al. 1998; Richardson et al. 2003).
Inspiratory activity in the hypoglossal nerve is characterized by high-frequency synchronous oscillatory activity. It has been shown that the power and frequency of these oscillations are controlled by GABAergic synaptic inhibition (Sebe and Berger 2008; Sebe et al. 2006). In addition, the gain of the HMs during the inspiratory drive is controlled by GABAergic synaptic inhibition (Sanchez et al. 2009). Modeling studies have suggested that the synchronicity and gain of a population of excitatory neurons in a network to other inputs can be modified by the degree of synchronicity of the inhibitory inputs (Tiesinga et al. 2008). In the neocortex it has been demonstrated that a subgroup of inhibitory interneurons—the fast-spiking interneurons—are responsible for generating gamma-oscillatory activity based on their firing resonance properties that lie within the gamma-band frequency range (reviewed by Tiesinga and Sejnowski 2009). It is not known whether GFP+ inhibitory interneurons in the NR are involved in generating synchronous discharges in HMs, but, if they are, it would be of interest to know their firing resonance properties and specifically whether some or all GFP+ interneurons have the ability to generate precisely timed spikes in response to fluctuating synaptic inputs. In addition to examining the subthreshold and firing resonance properties of GFP+ cells in the NR our study compares interneuron properties to those of HMs, a population of cells whose firing resonance properties we have described in a previous paper (van Brederode and Berger 2008). The differences in firing resonance properties that we describe herein might have important consequences for the roles that different types of GABAergic interneurons play in determining the synchronized output and gain of HMs during inspiration and orofacial behaviors.
METHODS
Experimental procedures
In vitro experiments were performed on medullary slices derived from heterozygous neonatal (P5 to P15) GAD67-GFP knock-in mouse pups (Tamamaki et al. 2003). Details of the experimental procedures are given in the companion paper (van Brederode et al. 2011). All animal and experimental procedures were approved by the University of Washington Institutional Animal Care and Use Committee. After the whole cell recording configuration was established we “typed” the cells at resting membrane potential based on their firing patterns in response to long depolarizing current pulses and membrane voltage responses to hyperpolarizing steps as described in the companion paper (van Brederode et al. 2011). The negative current pulses were used to calculated passive membrane properties of the neurons. Input resistance (Rn) was calculated from the steady-state voltage (Vss) response to small (maximum voltage deflection of between −5 and −10 mV) hyperpolarizing DC current pulses: Rn = Vss/I. The membrane time constant (τm) was calculated from exponential curve fits to the initial 50–100 ms of the same membrane voltage traces.
Subthreshold resonance properties
For recording of subthreshold resonance properties individual slices were transferred from a holding chamber to a heated perfusion-recording chamber bathed in carbogen-gassed artificial cerebrospinal fluid (ACSF; 26 ± 1°C). The ACSF contained blockers of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA)–mediated glutamatergic [6,7-dinitroquinoxaline-2,3-dione (DNQX), 10 μM], GABAergic [2-(3-carboxypropyl)-3-amino-6-methoxyphenyl-pyridazinium bromide (SR95531), 0.5 μM], and glycinergic (strychnine, 1 μM) synaptic transmission. Subthreshold membrane impedance was calculated from membrane voltage responses to injected sinusoidal currents of linearly varying frequency (chirp or ZAP current). The time-dependent frequency of the current f(t) was increased from f0 = 0 Hz to fm = 40 Hz (forward chirp) or decreased from 40 to 0 Hz (reverse chirp) for a total duration (T) of the chirp stimulus of 20 s (chirp rate ±2 Hz/s). The total injected current was
In quiescent cells (see van Brederode et al. 2011) the amplitude of the sine wave (I0) was increased in steps up to a maximum value where the depolarizing half-cycles remained just-subthreshold for action potential (AP) generation; the resultant depolarizing voltage excursions from the resting membrane potential at this current stimulus amplitude were between 20 and 30 mV. In spontaneously active GFP+ cells a steady hyperpolarizing DC current was injected such that the resting membrane potential and maximum voltage excursions were similar to those of quiescent cells (see results). The impedance was calculated from the real parts of the fast Fourier transform (FFT) of the voltage response divided by the injected chirp current
Impedance curves were analyzed with IGOR Pro (WaveMetrics) software. Values of impedance magnitude generally were noisy at the boundary of the chirp below a stimulus frequency of 1 Hz due to the discrete FFT procedure that we used (see Gutfreund et al. 1995) and thus we only analyzed frequencies >1 Hz. For each cell we determined fres = the frequency at which impedance reaches its peak value Zres (for low-pass cells fres = 1 Hz; see results). In neurons with a depolarizing “hump” in their subthreshold impedance profiles (see results) we also determined the upper resonance frequency (fupp), calculated as the chirp frequency at which the positive membrane voltage deflection reached its peak (see also Schreiber et al. 2009). The sharpness of the resonance peak Q was calculated as the ratio of the impedance at the resonance frequency (Zres) and impedance at 1 Hz (Z1). A damping factor D that described the high-frequency impedance decay was calculated as the ratio of the impedance at 40 Hz (Z40) and Z1. The half-decay frequency (fHD) is the frequency at which impedance equals Z1/2.
Suprathreshold resonance properties
After subthreshold resonance properties were assessed we tested the firing resonance characteristics of individual cells with chirp stimuli. First, we depolarized all cells with a tonic DC current until the neurons started to spike and then we reduced the amplitude of the DC current such that the cells just stopped spiking. Superimposed on this DC offset current we injected a 20-s chirp current stimulus of linearly varying frequency. The frequency of the chirp current was increased from 0 to 40 Hz (forward chirp) or decreased from 40 to 0 Hz (reverse chirp) at a chirp rate of 2 Hz/s. The chirp current amplitude was adjusted from the minimum current that elicited firing (1T) in subsequent trials, such that their amplitude were multiples of the threshold current (2T, 3T, etc.). Maximum stimulus amplitude was reached when no further increases in the number of spikes during the chirp stimulus was observed, or when the maximum negative voltage excursion reached about −30 to −35 mV to avoid cell damage. Using this protocol all cells fired only during the depolarizing half-cycle of the chirp stimulus. Firing resonance in response to chirp stimuli was studied by plotting either the number of spikes or the instantaneous firing frequency as a function of time or sine wave cycle number as described in results. To quantify the regularity of firing we adopted the modified coefficient of variation (CV2) proposed by Holt et al. (1996): CV2 = 2 × abs [(Ii +1 − Ii)]/(Ii +1 + Ii). This measure of variability for an interval at t = i seconds compares only two adjacent spike intervals Ii+1 and Ii. A perfectly regular spike train has a CV2 of 0, whereas spikes occurring randomly (Poisson process) have a CV2 of 1.
Measurement of reliability and spike timing precision
Reliability and spike timing precision analyses were performed as described in a previous paper (van Brederode and Berger 2008). Briefly, to quantify the reliability of firing (i.e., the likelihood that a cell will fire an AP at a certain time relative to the onset of the stimulus), the cells were stimulated with the same repeated chirp current stimuli (10 trials, >10 s between trials). The times of occurrence of spikes from the start of the stimulus (T = 0) were collected in 3-ms-wide bins and a peristimulus time histogram (PSTH) was constructed from the number of spikes that fell within each bin. Reliability was expressed as the number of spikes/bin divided by the number of trials (10). Highest reliability (1 spike · bin−1 · stimulus−1) was obtained if the cell always fired a spike at the same latency (i.e., fell within the same bin) at each trial. This reliability measure is sensitive to both the presence of a spike (i.e., firing probability) and spike timing precision (see Schreiber et al. 2009).
Chirp stimuli were always injected in combination with positive and negative step current pulses at the same half-amplitude as that of the chirp stimulus (250–500 ms in duration) to be able to compare passive and active properties during step stimulation to those obtained with chirp stimulation. In all neurons chirps were run in forward and reverse modes to check for time-dependent nonlinearities in the chirp responses. No qualitative differences between forward and reverse stimuli were observed and only the results of forward chirp stimulation are shown.
Numerical methods
The details of the model cells are described in the appendix. Numerical calculations were performed with custom software procedures written for IGOR Pro 6 (WaveMetrics). The differential equations that describe the mathematical model were solved using forward Euler integration, with an integration step interval of 0.05 ms. As a control for accuracy of the integration method we also ran simulations with a step size of 0.01 ms. No discernible differences between the step sizes were observed. Impedance of simulated voltage and current traces was calculated in the same way as the impedance curves of actual experimental current and voltage traces as described earlier.
Statistics
Statistical comparisons were performed using the t-test (paired comparisons) or ANOVA. If a significant difference between group means was found with an ANOVA, a post hoc Tukey test was performed to determine which groups differed from each other. Statistical correlations were performed using linear regression techniques and Pearson's correlation coefficient. Results are expressed as mean ± SE unless otherwise noted. For statistical comparisons we used a P < 0.05 as the threshold for significance.
RESULTS
In the companion paper (van Brederode et al. 2011) we have identified several types of GFP+ interneurons located in the NR based on differences in firing patterns in response to injected square current pulses at resting membrane potential. We classified these neurons into two broad groups— phasic and tonic cells—based on the ability to fire a train of spikes throughout the pulse at just-suprathreshold current strength. In this study we examine whether interneurons in the NR can be functionally subdivided based on their responses to time-varying inputs. To compare results in GFP+ interneurons with previous data on the frequency preferences of HMs (van Brederode and Berger 2008) we performed similar experiments under identical conditions in a group of HMs located in the genioglossus region of the XII nucleus.
Subthreshold responses of GFP+ interneurons and HMs to step and chirp stimulation
In all experiments the tested neurons were stimulated, in whole cell current-clamp, by a positive and negative square pulse (250–500 ms long; 1–2 s between pulses) followed by a 20-s-long sine wave stimulus of continuously varying frequency from 0 to 40 Hz but constant amplitude (forward chirp stimulus; see methods). The amplitude of the step stimuli was always the same as the half-amplitude of the chirp stimulus. We used this stimulus to characterize, in the same trial, the firing response of the neuron to depolarizing step stimulation, passive membrane properties such as time constant and input resistance (from the hyperpolarizing pulse), and membrane resonance (from the chirp stimulus). The cells were recorded at resting membrane potential for quiescent GFP+ cells and at a membrane potential where the cells just stopped spiking by the injection of hyperpolarizing DC current for spontaneously spiking GFP+ cells (see van Brederode et al. 2011). The mean values for the holding potentials for subthreshold resonance studies are given in Table 1. The amplitude of the stimulus was gradually increased from zero until APs were evoked by the current stimulus. To study and compare subthreshold impedance profiles the stimulus amplitude was set at the maximum value at which the chirp stimulus remained just subthreshold, since spiking distorted the impedance curves (see for instance Fig. 1B2). At this amplitude the membrane voltage change resulting from step stimulation was between 20 and 30 mV. All experiments were performed in the presence of blockers of excitatory and inhibitory synaptic neurotransmission (see methods).
Table 1.
Subthreshold impedance characteristics of GAD67-GFP+ neurons and HMs
| Cell Type | Vhold, mV | Z1, MΩ | Z40, MΩ | Q | D | fres, Hz | fHD, Hz | fupp, Hz | Rr |
|---|---|---|---|---|---|---|---|---|---|
| GFP+ | |||||||||
| Nonresonant (n = 13) | −77.9 (2.3) | 744.2* (114.4) | 108.7 (7.0) | 1.0†* | 0.17* (0.02) | 1.0‡* | 8.2* (1.1) | 1.0§* | 1.31* (0.03) |
| Resonant (n = 8) | −75.8 (2.5) | 332.3 (40.7) | 105.3 (23.0) | 1.06 (0.02) | 0.36 (0.06) | 2.2 (0.33) | 20.3 (3.8) | 4.1 (0.8) | 0.89 (0.005) |
| HMs (n = 5) | −75.4 (1.0) | 77.6 (10.8) | 54.2 (8.0) | 1.16 (0.02) | 0.71 (0.05) | 2.8 (0.3) | >40.0 | 4.3 (0.5) | 0.98 (0.007) |
Values are means, with the corresponding SE given in parentheses. Vhold, holding potential; Q, sharpness of the resonance peak; the ratio of peak impedance and impedance at 1 Hz (Zres/Z1); D, high-frequency decay; ratio between impedance at 40 Hz (Z40) and that at 1 Hz (Z1); fHD, half-decay frequency; frequency at which impedance equals Z1/2. In two interneurons and for all HMs this value was larger than the highest tested frequency (40 Hz) and was left undefined. fupp, upper-resonance frequency; fres, frequency at which impedance curve reaches its peak value (Zres); Rr, rectification ratio determined from depolarizing and hyperpolarizing step current pulses.
Indicates significant difference between the means of the two groups of GFP+ cells.
Nonresonant neurons were all assigned a Q value of 1.
Nonresonant cells displayed peak impedance at the start frequency of 1 Hz.
Fig. 1.
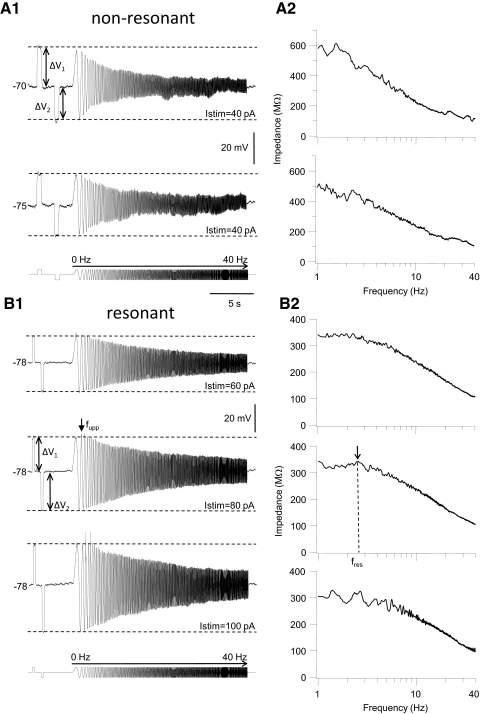
Subthreshold impedance and resonance in GAD67-GFP+ (GFP+) interneurons. A1: membrane voltage traces recorded in a representative example of a nonresonant GFP+ cell. The cell was stimulated with a sequence of current steps followed by a chirp function (0–40 Hz, 2 Hz/s chirp rate). The stimulus is shown schematically at the bottom of the panel. Stimulus amplitude (Istim) was 40 pA. Voltage traces were recorded at a membrane potential of −70 mV (top) or −75 mV (bottom) in the same neuron by injection of DC current. The rectification ratio (Rr), calculated as the ratio of the of the steady-state membrane voltage response to depolarizing (ΔV1) and hyperpolarizing (ΔV2) current steps (indicated by dashed horizontal lines), was 1.13 at −70 mV and 1.05 at −75 mV. Note the depolarizing membrane voltage “sag” in response to hyperpolarizing current pulses. A2: corresponding impedance curves of this cell. Impedance magnitude (see methods) is plotted against chirp frequency (1 to 40 Hz) for the 2 chirp stimuli shown in A1. Membrane impedance decays monotonically in both cases from a maximum at the minimum chirp frequency of 1 Hz, with increasing chirp frequency up to 40 Hz. B1: membrane voltage traces recorded in a representative example of a resonant GFP+ cell. This cell was stimulated with a sequence of current steps (250 ms long in this cell) followed by a chirp function (0–40 Hz; current stimulus is shown schematically at the bottom). Stimulus amplitude was 60 pA (top trace), 80 pA (middle trace), or 100 pA (bottom trace), all at the same resting membrane potential (−78 mV). Action potentials (APs, clipped at the top) were evoked during the depolarizing half of the third and fifth sine wave cycle of the chirp at stimulus strength 100 pA, but note the lack of spiking during the preceding depolarizing step current pulse of the same amplitude as the chirp. In this cell, and all other resonant GFP+ cells, there was a “hump” in the depolarizing voltage envelope when the stimulus amplitude was just below the amplitude necessary to evoke spiking with a maximum amplitude at the upper resonance frequency (middle trace, arrow labeled fupp). When amplitude was increased to evoke spiking, APs preferentially occurred in cycles at fupp (compare middle and bottom voltage traces). Note the asymmetry in the membrane voltage response to positive and negative current steps and the asymmetry in the depolarizing and hyperpolarizing voltage envelope during chirp stimulation (Rr was 0.90 in this cell). B2: corresponding impedance curves for the voltage traces shown on the left. Arrow points to a peak in impedance magnitude at the resonant chirp frequency fres. In this cell fres was found at 3.7 Hz. Note the “noise” in the impedance curve when spikes were evoked (bottom panel).
We found two basic types of impedance profiles, resonant and nonresonant, in GFP+ cells. In nonresonant cells (NR cells; Fig. 1A) the amplitude of the membrane voltage excursions in response to chirp stimulation (0–40 Hz; chirp rate = 2 Hz/s) decreased steadily from a maximum during the first sine wave cycle to a minimum during the last cycle when sine wave frequency was increased from 0 to 40 Hz (Fig. 1A1). The majority of GFP+ interneurons (13 of 21 cells tested) was nonresonant and showed this type of voltage profile at resting membrane potential. In agreement with other studies (Erchova et al. 2004; Hu et al. 2002; van Brederode and Berger 2008) we found that reversing the direction of the chirp stimulus (from 40 to 0 Hz, chirp rate = −2 Hz/s) did not alter the subthreshold resonance profile (data not shown). Note that the membrane voltage response to a depolarizing step (ΔV1) is larger than the voltage response to a hyperpolarizing step (ΔV2) and that amplitude of the membrane voltage response to step depolarization is larger than the amplitude of the voltage response during the depolarizing half of the chirp stimulus at any frequency (Fig. 1A1). We quantified this observation by calculating the rectification ratio Rr according to
where ΔV1 is the absolute value of the amplitude of the steady-state voltage response to a positive step and ΔV2 is the absolute value of the amplitude of the response to a negative step. The cells show inward rectification if Rr > 1 and outward rectification of Rr < 1. The amount of rectification was dependent on the holding potential, as illustrated by the two voltage traces in Fig. 1A1. Membrane impedance (Z) was calculated by dividing the magnitude of the fast Fourier transform of the membrane voltage [FFT(V)] by that of the chirp current [FFT(I)] according to: Z = FFT(V)/FFT(I) (see methods). Subthreshold impedance curves, constructed by plotting impedance magnitude against chirp frequency, showed a monotonic decay from a maximum at 1 Hz in nonresonant GFP+ cells irrespective of the holding potential (Figs. 1A2 and 3A1).
Fig. 3.
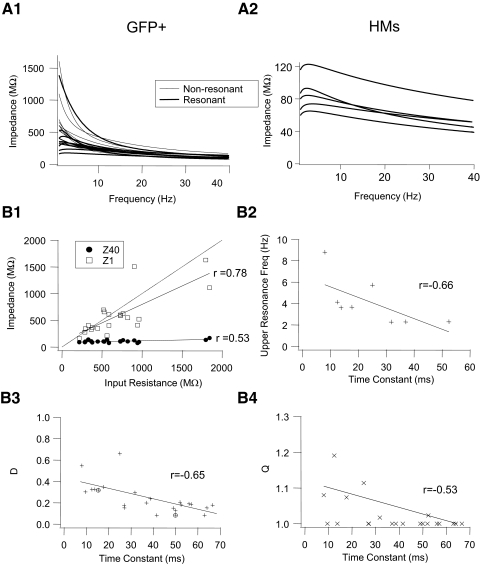
Impedance profiles among GFP+ cells are heterogeneous, whereas those in HMs are similar. A: superimposed impedance curves for GFP+ cells (A1; n = 21 cells) and HMs (A2; n = 5 cells). Impedance curves were derived from fits to individual raw impedance curves. Bold curves were fit to the impedance curves of resonant GFP+ cells and resonant HMs and thin curves to nonresonant GFP+ cells. Note the difference in scale for the y-axis between A1 and A2. B1: values for impedance at an input frequency of 1 Hz (Z1) and 40 Hz (Z40) for individual GFP+ cells plotted against their input resistance calculated from rectangular hyperpolarizing current pulses (see methods). Dashed line is unity line. B2: values for upper resonance frequency (fupp) for GFP+ cells, with asymmetric impedance profiles plotted against their membrane time constant derived from rectangular hyperpolarizing current pulses (see methods). B3 and B4: values for the damping coefficient D (D = Z40/Z1) and the resonance quality (Q) of individual GFP+ cells plotted against their membrane time constant. Relationships between parameters in B were fit with straight lines and correlation coefficients (r) were calculated from linear regression applied to these straight-line fits. Circled symbols in B3 represent the D values for the slow and fast τm model cells (see Modeling results) and were not included in the regression analysis.
All but one GFP+ interneuron in the nonresonant group of GFP+ cells (n = 13) were tonic firing cells based on their firing response during the step depolarization at resting membrane potential (all the cells in the present study were also part of the data sets in the companion paper, which describes in more detail the firing patterns of GFP+ interneurons in the NR; see van Brederode et al. 2011). Tonic cells fired a regular train of APs during a just-suprathreshold step stimulus. One GFP+ neuron in this group fired irregularly during the step stimulus (data not shown). The pattern or degree of spike frequency adaptation during tonic firing evoked by a step stimulus (see van Brederode et al. 2010) in these nonresonant GFP+ cells was variable, ranging from no adaptation (n = 2 cells), spike-frequency adaptation (n = 8), or spike-frequency acceleration (n = 3). Seven of 13 nonresonant GFP+ neurons fired spontaneously at rest in the absence of any holding current (see van Brederode et al. 2011).
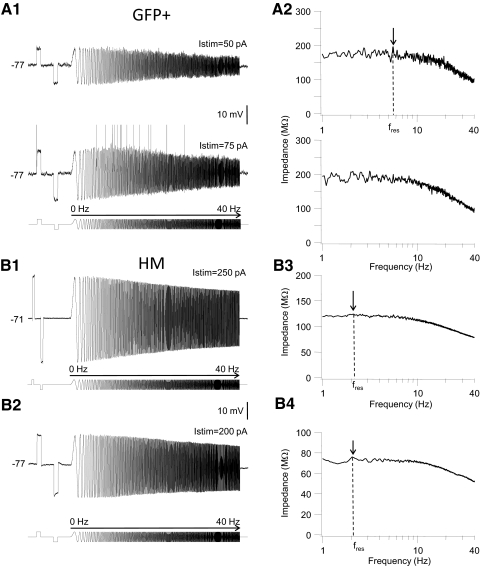
The remaining GFP+ cells (n = 8 cells) showed one of two forms of subthreshold resonance. Figure 1B shows a representative example of the most prevalent impedance profile (7 of 8 cells). In this group of cells the amplitude of the positive membrane voltage oscillations first increased and reached a peak at a sine wave cycle other than the first cycle before decreasing again with increasing chirp frequency (Fig. 1B). The “hump” in the depolarizing voltage envelope was most prominent when the voltage response was just below threshold for spike generation (Fig. 1B1, middle trace). When stimulus strength was gradually increased to evoke spiking during the chirp stimulus cells in this group spiked first during depolarizing half-cycles associated with subthreshold membrane resonance (compare middle and bottom voltage traces in Fig. 1B1). The envelope of the voltage response to chirp stimulation in this group of cells was asymmetrical; the “hump” in the depolarizing response was not mirrored by a similar “hump” in the hyperpolarizing response. Instead the hyperpolarizing envelope decreased steadily from a peak during the first hyperpolarizing half-cycle to the last cycle (Fig. 1B1). Impedance graphs in this group of cells often showed a modest peak at the resonant frequency fres (Fig. 1B2, middle graph), but in other cells with asymmetric voltage profiles there was no clear peak visible in the impedance curve; in these cells the calculated impedance decreased monotonically from a frequency of 1 Hz (Fig. 3A1). Similar observations regarding asymmetric voltage profiles and the lack of a peak in the impedance curve have recently been reported by Schreiber et al. (2009). These authors proposed to use a different measure of the resonance frequency, i.e., the sine wave frequency corresponding to the peak in the upper envelope of the impedance profile fupp (Fig. 1B1). When stimulus amplitude was increased to evoke spike discharge during sine wave stimulation, spikes were first evoked at input frequencies corresponding to fupp (Fig. 1B1, bottom trace). In one GFP+ interneuron the voltage envelope in response to chirp stimulation was symmetrical with a peak in both the depolarizing and hyperpolarizing voltage envelope at cycles other than the first cycle (Fig. 2A). The corresponding impedance curve showed a broad peak and relatively small decay in impedance with increasing chirp frequency (Fig. 2A2). When stimulus amplitude was increased to evoke spiking, APs were evoked over a relatively wide band of input frequencies (Fig. 2A1, bottom trace).
Fig. 2.
Subthreshold impedance and resonance in a GFP+ interneuron (A) and hypoglossal motoneurons (HMs, B). A1: membrane voltage traces recorded in an example of a resonant GFP+ cell with a symmetrical voltage envelope (top trace). Stimulus amplitude was 50 pA in the top trace and 75 pA in the bottom trace. The stimulus is shown schematically at the bottom of the panel. Both voltage traces were recorded at a membrane potential of −77 mV. Note that at a just-suprathreshold stimulus amplitude of 75 pA one spike was evoked during the depolarizing step stimulus (500 ms long) and several spikes during depolarizing half-cycles of the chirp stimulus at a broad range of intermediate input frequencies. APs are clipped at the top. The rectification ratio (Rr), calculated as the ratio of the steady-state membrane voltage response to depolarizing and hyperpolarizing current steps was 0.93 in this cell. A2: corresponding impedance curves of this cell. Impedance magnitude (see methods) is plotted against chirp frequency (1 to 40 Hz) for the 2 chirp stimuli shown in A1. Arrow points to the peak in impedance magnitude at the resonance frequency. B1: membrane voltage traces recorded in 2 representative examples of resonant HMs. The cell in B1 showed resonance in the depolarizing voltage envelope in response to chirp stimulation (fupp = 5.4 Hz), whereas the cell in B2 showed resonance in both the depolarizing and hyperpolarizing voltage envelopes (current stimuli are shown schematically at the bottom of each panel). Stimulus amplitude was 250 pA (B1) or 200 pA (B2). Rr values were 0.99 for the cell in B1 and 0.98 for the cell in B2. B3 and B4: corresponding impedance curves for the voltage traces shown on the left. Arrows points to a peak in the impedance magnitude corresponding to the location of fres.
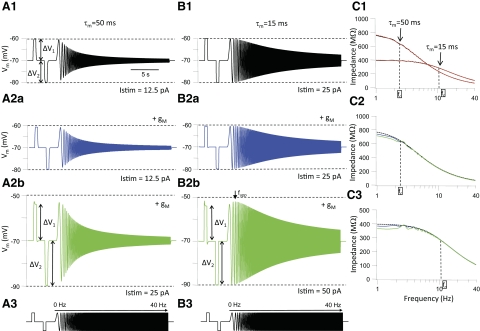
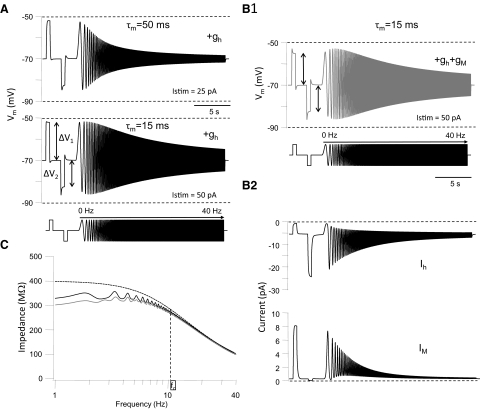
Since the amount of rectification depended on holding potential and stimulus amplitude (Fig. 1) we compared Rr values in cells at similar holding potentials when stimulated with just-subthreshold current steps. Nonresonant GFP+ cells had a mean Rr value of 1.31 ± 0.03 (n = 13, range: 1.03–2.46; see Table 1), indicating a marked inward rectification of the current–voltage relationship in the subthreshold membrane voltage range (−100 to −50 mV) in this group of cells. The average value for Rr in resonant GFP+ neurons was 0.89 ± 0.005 (range: 0.60–1.03), demonstrating outward rectification in the subthreshold voltage range in these cells. The mean Rr in resonant GFP+ cells was significantly different from the Rr in nonresonant GFP+ cells (Student's t-test, P < 0.05). In addition resonant and nonresonant GFP+ cells differed both in their input resistance (469 ± 84 vs. 833 ± 133 MΩ, determined from hyperpolarizing current step, P < 0.05) and their membrane time constant (24.8 ± 5.3 vs. 46.3 ± 4.7 ms, determined from hyperpolarizing current step, P < 0.05), respectively. These results indicate that differences in subthreshold resonance profiles are the result of differences in the expression of voltage-activated conductances responsible for subthreshold membrane rectification and passive membrane properties among GFP+ cells. These observations are further explored in the modeling section that follows.
The firing patterns of resonant GFP+ cells in response to step stimulation at rest were variable. Three cells were tonic cells, three cells showed a characteristic long delay to the first AP (delayed onset phasic cells; see companion paper), and two cells were phasic cells that fired fewer than four APs only at the start of the current pulse. These results suggest that the phasic and delayed onset phasic firing patterns are associated with subthreshold membrane resonance, whereas tonic firing can be associated with either resonant or nonresonant subthreshold properties. None of the eight resonant GFP+ cells fired spontaneously at rest.
The amplitude of the steady-state voltage responses to step depolarizing and hyperpolarizing currents in HMs lacked the prominent rectification in response to step current stimuli evident in GFP+ cells (Rr = 0.98 ± 0.007; range: 0.95–0.99, n = 5). In HMs we found two main types of impedance profiles in response to chirp stimulation, i.e., depolarizing resonance only (n = 3 cells; Fig. 2B1) and resonance in both the depolarizing and hyperpolarizing voltage envelope (n = 2 cells; Fig. 2B2). HMs had significantly shorter membrane time constants (5.9 ± 0.8 ms, n = 5) and lower input resistances (63 ± 8.3 MΩ, n = 5) than those of either resonant or nonresonant GFP+ cells (t-test, P < 0.05). The impedance graphs of HMs showed a modest peak in impedance at the resonance frequency, whereas the drop-off in impedance with increasing sine frequency was smaller than that in GFP+ interneurons (Fig. 2, B3 and B4).
We quantified the strength of subthreshold resonance by calculating the Q-value (Hutcheon et al. 1996b). The Q-value defines the quality or sharpness of the resonance as the ratio of the impedance at the peak in the impedance curve (Zres) and the impedance at 1 Hz (Z1). Nonresonant cells have a Q-value of 1.0 (Zres = Z1; see Table 1). Subthreshold membrane resonance in our study was modest, with no resonant GFP+ cells showing a Q-value >1.2 and only two HMs with a Q-value >1.2. Average Q-values for resonant interneurons (Q = 1.06 ± 0.02) and HMs (Q = 1.16 ± 0.02) were not significantly different (Table 1; t-test, P > 0.05). The impedance at chirp frequency of 1 Hz (Z1) was smaller in HMs than that in either nonresonant or resonant GFP+ cells (ANOVA; Tukey test; P < 0.05, Table 1). Z1 in resonant GFP+ cells was smaller than that in nonresonant GFP+ cells (ANOVA; Tukey test; P < 0.05, Table 1). Mean impedance at a chirp frequency of 40 Hz (Z40) was not significantly different between resonant and nonresonant GFP+ cells, but values for Z40 in both groups of GFP+ cells were larger than those in HMs (ANOVA; Tukey test; P < 0.05, Table 1). These differences in the frequency dependence of membrane impedance among GFP+ cells are further illustrated in Fig. 3A1. The magnitude of the drop-off in impedance with increasing sine frequency is a measure of the low-pass filter behavior of the neurons, defined as D = Z40/Z1. A smaller D-value reflects more low-pass filtering by the cell membrane of high-frequency input. The mean D-value is significantly smaller in nonresonant interneurons than that in resonant interneurons and the D-values of both groups of interneurons are smaller than the mean D-value in HMs (ANOVA; Tukey test; P < 0.05, Table 1). Reflecting these differences in membrane filtering properties the impedance had decayed to half its original value at Z1 at a half-decay chirp frequency (fHD) of 8.2 Hz in nonresonant interneurons, which was lower than the mean value for fHD of 20.3 Hz found in resonant interneurons (Table 1; t-test, P < 0.05). In HMs fHD was always greater than the highest chirp frequency tested (i.e., >40 Hz). In general, the impedance curves for HMs showed less cell-to-cell variability than those of GFP+ cells (compare Fig. 3, A1 and A2; notice the difference in scale between the two graphs). Mean resonance frequency in resonant GFP+ cells (2.2 ± 0.3 Hz) was not different from the mean fres in HMs (2.8 ± 0.3 Hz) and also the values for fupp (4.1 and 4.3 Hz, respectively) in these two groups were not significantly different (Table 1; t-test, P > 0.05).
How do the impedance profiles for GFP+ cells compare with their passive membrane properties measured with step currents? There was a good correlation (determined from the Pearson's correlation coefficient) between steady-state input resistance Rn measured from step pulses (see methods) and Z1 measured with chirp stimuli (r = 0.78, n = 21, P < 0.05, Fig. 3B1). Although there was a significant positive correlation between Rn and high-frequency impedance Z40 (Fig. 3B1; r = 0.53, P < 0.05), the slope of this relationship was much smaller than that for the linear fit to the Rn versus Z1 graph, suggesting that for high-frequency inputs all GFP+ interneurons have low subthreshold impedance, irrespective of their impedance at zero frequency. Interneurons with a short membrane time constant (τm) had less of a decline in impedance with increasing chirp frequency than that of cells with a long τm, as indicated by the inverse correlation between the damping factor D and τm (Fig. 3B3; r = −0.65, P < 0.05). A similar inverse correlation was found between D and Rn (data not shown; r = −0.52, P < 0.05). There was a modest but significant inverse correlation between the upper resonance frequency fupp and τm (Fig. 3B2; r = −0.66, P < 0.05). The magnitude of the resonance, as expressed by the Q-value, was also inversely correlated with the τm (Fig. 3B4; r = −0.53, P < 0.05).
As explained by Hutcheon and Yarom (2000) subthreshold membrane resonance is the result of a combination of the passive properties of the cell membrane, i.e., a leak conductance (gL) and capacitance (Cm) in parallel, which attenuate the voltage responses to high-frequency inputs, and voltage-activated conductances, which attenuate responses to low-frequency inputs. Our results indicate that the likelihood that GFP+ cells show subthreshold resonance depends strongly on the relative importance of passive and active membrane properties in a particular cell. In cells with a long membrane time constant low-pass filtering is the main factor controlling the membrane voltage envelope to sine wave stimulation and these cells tend not to show resonance. Low-pass filtering is less dominant in cells with a fast time constant and this allows the expression of high-pass filtering of low-frequency inputs. These issues are further explored later in the modeling section (see following text).
Suprathreshold responses to step and chirp stimulation
Since subthreshold responses to sine wave current stimuli were clearly heterogeneous among GFP+ neurons we next examined whether this heterogeneity influenced the spike firing response to suprathreshold sine wave stimuli in different types of GFP+ neurons. Specifically, we wanted to test whether the different subthreshold properties described earlier were associated with different types of firing resonance. To compare the spike firing response to sine wave stimulation among neurons, all cells were held at a membrane potential just below the threshold for AP generation by DC current injection. By holding the cells just below firing threshold we were able to elicit firing with relatively small amplitude current stimuli since the large current stimuli necessary to elicit firing from rest tended to damage the neurons. We found that the firing pattern in response step depolarization at these depolarized membrane potentials sometimes differed from the firing patterns at rest, specifically the number of spikes in the initial burst was increased in phasic neurons (but always remained fewer than four) and the delay to the first spike in delayed onset cells was decreased by depolarization (data not shown; also see Prescott and De Koninck 2002). At depolarized membrane potentials it was difficult to discriminate between delayed onset and tonic GFP+ cells, although the characteristic irregular firing of delayed onset cells remained even at depolarized potentials. The sine wave stimulus used to examine firing resonance consisted of a chirp current of linearly varying frequency (0–40 Hz, chirp rate = 2 Hz/s) superimposed on the maximum injected DC current which did not elicit spike firing by itself. In all cells we also injected step current stimuli in combination with chirp stimuli to examine the firing responses (from the depolarizing step) and passive membrane properties (from the hyperpolarizing step). The smallest step stimulus amplitude that elicited firing in individual cells was the threshold current (1T). In subsequent trials amplitude was varied in multiples of this threshold current (2T, 3T, 4T, etc.) until no substantial further increases in the number of spikes per trial were found. In all cells we also tested the responses to reverse chirp stimuli (40–0 Hz). These responses were qualitatively similar to the forward chirp stimuli (data not shown), in agreement with our previous studies (van Brederode and Berger 2008).
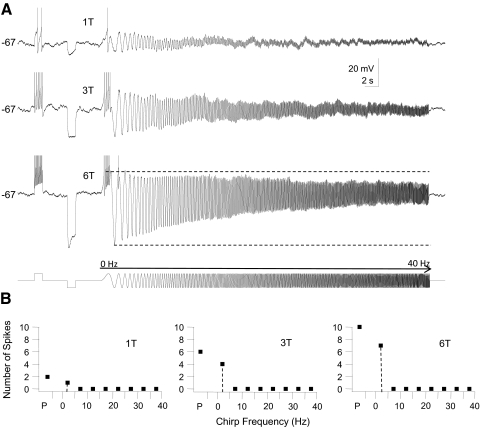
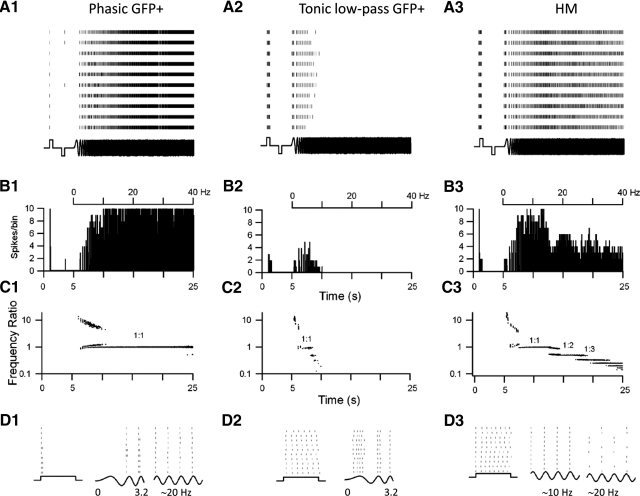
In GFP+ cells (n = 33 cells) we were able to distinguish three different responses based on the firing responses to step and chirp current stimuli. The first group (n = 24) consisted of GFP+ neurons that fired multiple spikes during a step DC depolarization at just-suprathreshold current strength (1T) (Fig. 4A). This group of neurons fired spikes during the first few depolarizing half-cycles of a forward chirp current stimulus at 1T stimulus strength, but after the first few sine wave cycles the amplitude of the voltage response decreased and spike firing either ceased abruptly (Fig. 4, top trace) or spike firing continued at a low rate without being entrained by the chirp stimulus at intermediate and high chirp frequencies (data not shown). When stimulus amplitude was increased beyond threshold the depolarizing step generated more spikes and the number of spikes per sine wave cycle at low chirp frequency was also increased, but it was difficult to elicit spike firing or entrain firing in this group of cells beyond chirp frequencies of 5–10 Hz even at current strengths that elicited steady-state voltage deflections in the hyperpolarizing direction of ≥30 mV (Fig. 4A, middle and bottom traces). We quantified these responses by calculating the number of spikes that were fired at different frequency ranges in 5-Hz bins (Fig. 4B). At a stimulus strength of 3T the peak number of spikes fired during the chirp stimulus typically occurred in the frequency range between 0 and 5 Hz (n = 17 cells) or between 5 and 10 Hz (n = 7 cells, summarized in Fig. 9A1). This group of GFP+ interneurons responded with the most spikes to steady-state or low-frequency inputs and we classified them as low-pass cells. All of the cells in this group fired regular trains of APs in response to step depolarization both at rest and at depolarized potentials and all neurons in this group were thus tonic low-pass GFP+ cells. In many cells in this group there was a marked asymmetry in the envelope of the impedance profile when large-amplitude chirp stimuli were used; subthreshold depolarizing voltage deflections were smaller than the corresponding hyperpolarizing membrane voltage excursions (Fig. 4A, bottom trace). This type of asymmetry suggests that depolarizing currents activate/inactivate ionic currents that, together with low-pass filter properties of the cell membrane, prevent the cell from reaching firing threshold at higher sine wave frequencies.
Fig. 4.
Example of firing response of a tonic-firing low-pass GFP+ cell to step and sine wave stimuli. This cell is a representative example for a group of GFP+ cells (n = 24) that fired trains of spikes during the step stimulus (tonic firing), but stopped firing early or failed to be entrained by the chirp stimulus at intermediate- or high-input frequencies. A: 3 membrane voltage traces recorded in response to a just-suprathreshold stimulus (10 pA = 1T, top trace), 30 pA (3T, middle trace), and 60 pA (6T, bottom trace), all at the same holding potential (−67 mV in this cell). Cell was depolarized to just below the threshold for spiking by DC current injection and then stimulated sequentially with a step (500 ms) depolarization, a step (500 ms) hyperpolarization, and a chirp stimulus (0–40 Hz, chirp rate 2 Hz/s; stimulus shown schematically in the bottom trace). Note the marked asymmetry in the membrane potential envelope at 6T; the amplitude of the membrane potential changes during the hyperpolarizing half-cycle was much larger than the amplitude during the depolarizing half-cycle at low chirp frequency, but this difference disappeared with increasing chirp frequency. B: for each of the stimuli in A (1T, 3T, and 6T) we plotted the number of spikes during the step pulse (P) and during the chirp stimulus (grouped into 5-Hz bins). Note the increase in the number of spikes during the step and in the 0- to 5-Hz bin when stimulus amplitude was increased. This cell failed to fire spikes beyond a chirp frequency of 5 Hz at all stimulus strengths. At all 3 stimulus amplitudes the peak number of spikes (i.e., the preferred input frequency, dashed line) during the chirp stimulus was found in the 0- to 5-Hz frequency bin.
Fig. 9.
Summary of firing resonance data. A1: composite graph for the average number of spikes per frequency bin for the 3 groups of GFP+ cells and HMs. All cells were stimulated with step and chirp currents at 3T amplitude and were depolarized to just below spiking threshold by injection of DC current. Bars represent SE. T-LP = tonic low-pass (n = 24); T-BP = tonic band-pass (n = 5); Ph = phasic GFP+ cells (n = 4); and HMs (n = 7). Note the differences in the peak number of spikes and the input frequency range where this peak occurs among the 4 cell types. Statistical comparisons are given in the results. A2: comparison of the mean firing frequency during the step current pulse, the minimum (Fmin) and maximum (Fmax) firing rate for the 1:1 phase-locking region, and the width of the 1:1 phase-locking region (Range) in the 4 groups of cells indicated by the vertical bars (error bars indicated are SE). All values were calculated for a 3T stimulus strength. Asterisks indicate statistically different values between groups (details of statistical comparisons are given in the results). B: relationship between Fmin, Fmax, and 1:1 phase-locking range of individual GFP+ cells plotted against the membrane time constant determined from hyperpolarizing square current pulses (B1) or plotted against the impedance ratio D (D = Z40/Z1) calculated from subthreshold impedance curves at rest (B2) as in Fig. 3. Straight lines were determined from best-fit linear regression to the data points. Regression coefficients were significant for all relationships shown (Spearman correlation coefficients are given in the results). Data points surrounded by circles in B1 and B2 are the values for Fmin, Fmax, and range for the slow (τm = 50 ms) and fast (τm = 15 ms) passive model cells (see Modeling results).
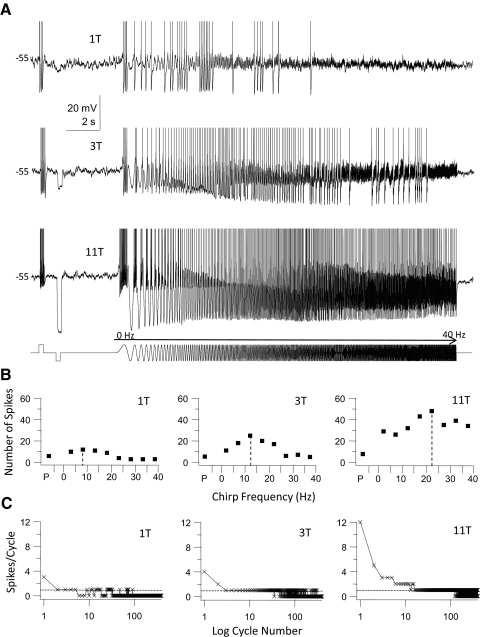
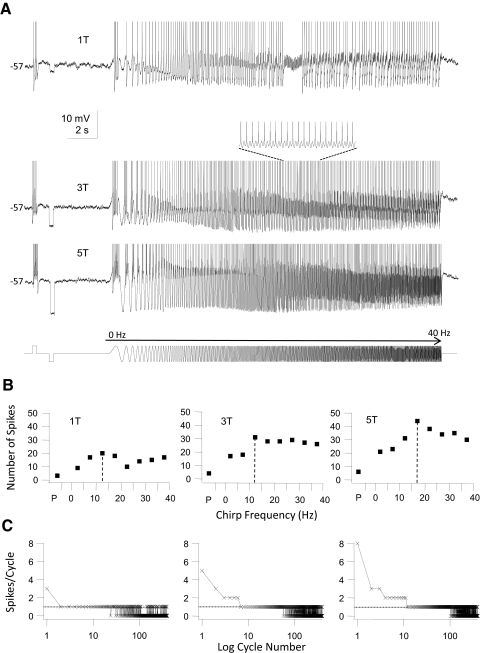
A second group of GFP+ cells (n = 5) fired trains of spikes in response to step current stimuli, but at just-suprathreshold stimulus strength these cells fired irregularly during the chirp stimulus with regions of entrainment alternating with cessation of firing (Fig. 5A, top trace). When stimulus amplitude was increased beyond 1T the chirp regions over which entrained firing was elicited were increased until cells fired throughout the entire chirp stimulus (Fig. 5A, bottom). At intermediate stimulus amplitudes these cells typically fired irregular clusters of spikes during the chirp stimulus, with regions of spike firing interrupted by regions where the cells failed to fire (Fig. 5A, middle trace). Increasing current stimulus amplitude elicited more spikes both during the depolarizing step and chirp stimulus and shifted the resonance frequency (i.e., the frequency where the cell fired the maximum number of spikes/frequency bin) to higher values (Fig. 5B). This group of cells was able to phase-lock 1:1 to the chirp stimulus, whereas at the highest stimulus amplitudes additional phase-locking regimes (i.e., 3:1 or 2:1 phase-locking; see Fig. 5C) often became apparent. Beyond the maximum chirp frequency of the 1:1 phase-locking range the number of spikes started to decline due to cycle skipping (Fig. 5, B and C). The responses of these cells are band-pass in nature and cells in this group were classified as tonic band-pass cells (group data are summarized in Fig. 9A1). Even though neurons in this group fired tonically to step depolarization at depolarized membrane potential, three of the cells showed delayed onset firing and one phasic firing when stimulated with long depolarizing pulses at resting membrane potential.
Fig. 5.
Firing response of a tonic-firing band-pass GFP+ cell to step and sine wave stimuli. This cell is a representative example for a group of GFP+ cells (n = 5) that fired trains of spikes during the step stimulus (tonic firing), but was also able to fire throughout the chirp stimulus. A: 3 membrane voltage traces recorded in response to a just-suprathreshold stimulus (10 pA = 1T, top trace), 30 pA (3T, middle trace), and 110 pA (11T, bottom trace), all at the same holding potential (−55 mV in this cell). Cell was depolarized to just below the threshold for spiking by DC current injection and then stimulated sequentially with a step (250 ms) depolarization, a step (250 ms) hyperpolarization, and a chirp stimulus (0–40 Hz, chirp rate 2 Hz/s; stimulus shown schematically in the bottom trace). Note the irregular spiking during the chirp stimulus at just-suprathreshold amplitude and the increase in input frequency range to which the cell responded with spike firing when stimulus amplitude was increased. At the largest stimulus amplitude the cell was able to respond with spike firing to all chirp frequencies. APs have been clipped at the top. B: for each of the stimuli in A (1T, 3T, and 11T) we plotted the number of spikes during the step pulse (P) and during the chirp stimulus (grouped into 5-Hz bins). Note the increase in the peak number of spikes and the shift of the preferred input frequency (dashed lines) to higher frequencies when stimulus amplitude was increased. Past the preferred frequency the number of spikes decreased due to cycle skipping, indicating a band-pass firing resonance. C: the number of spikes/cycle plotted against the logarithm of the cycle number of the chirp stimulus (400 cycles total, 0–40 Hz) for the responses shown in A. Dotted horizontal line indicates the firing of exactly 1 spike/cycle (1:1 phase-locking). At 1T there were brief runs of 1:1 phase-locking alternating with cycle skipping, whereas at 3T and 11T there were extended runs of 1:1 phase-locking to individual cycles before cycle skipping occurred at high-input frequencies. The cell was able to fire multiple spikes per cycle during consecutive cycles and phase-lock in this mode (2 and 3 spikes/cycle) to low chirp frequencies at a stimulus strength of 11T.
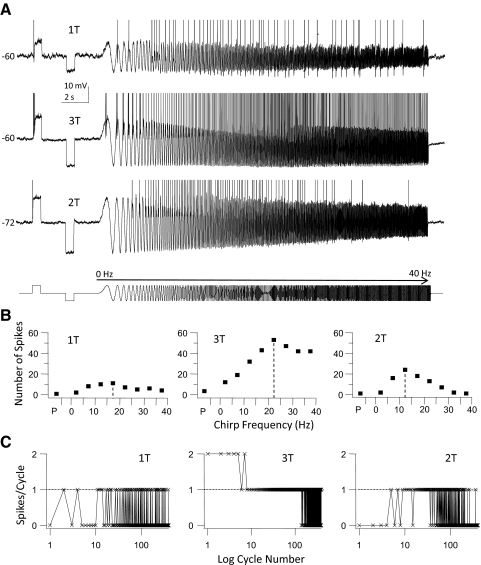
A third group of GFP+ cells fired a single spike or fewer than four spikes during the initial part of a step DC depolarization and they were classified as phasic cells (n = 4, Fig. 6). At just-suprathreshold current (1T) these cells fired a single spike during step depolarization and single spikes during the depolarizing half of the sine wave stimulus during the entire chirp stimulus, except for the first cycle of the chirp stimulus (Fig. 6A, top trace). Firing during the chirp was irregular with periods of spiking interrupted by cycle skipping. When stimulus strength was increased beyond 1T several phase-locking regions became evident where cells fired two (2:1) or one (1:1) spike/cycle on consecutive cycles (Fig. 6, A, middle trace, and C). The number of spikes/frequency bin gradually increased from the start of the chirp up to a critical input frequency after which the number of spikes started to decline because spikes started to “drop out” due to cycle skipping (Fig. 6, B and C). The responses of these cells were therefore band-pass in nature (group data are summarized in Fig. 9A1). At the highest stimulus strength and low chirp frequency these cells fired multiple spikes (but always ≤2 spikes) per cycle. When the cells were hyperpolarized the “band-pass” characteristic of this cell type became more obvious (Fig. 6; compare traces at −60 and −72 mV). Now the cells failed to fire at low and high chirp frequencies, but fired spikes at intermediate chirp frequency (5–25 Hz in this example). Membrane hyperpolarization also shifted the resonant frequency to lower values. All four neurons in this group showed phasic firing patterns when stimulated with long depolarizing current pulses at resting membrane potential.
Fig. 6.
Firing response of a phasic-firing GFP+ cell to step and sine wave stimuli. This cell is a representative example for a group of cells (n = 4) that fired <4 spikes during the step stimulus (phasic firing), but were able to fire throughout the chirp stimulus. A: 2 membrane voltage traces recorded in response to a just-suprathreshold stimulus (50 pA = 1T, top trace) and 150 pA (3T, middle trace) at a holding potential of −60 mV and the response of the same cell when hyperpolarized to −72 mV by DC current injection (2T stimulus amplitude, bottom trace). Stimulus consisted of a step (500 ms) depolarization, a step (500 ms) hyperpolarization, and a chirp stimulus (0–40 Hz, chirp rate 2 Hz/s; stimulus shown schematically in the bottom trace). At just-suprathreshold amplitude (1T) the cell responded with one spike during the step and a series of spikes throughout most of the chirp stimulus, but note that the cell failed to fire during the first depolarizing half-cycle of the chirp. Increasing the stimulus amplitude entrained firing during the entire chirp, but note that the cell failed to fire a train of APs during the preceding step stimulus (middle trace). Hyperpolarization demonstrated that this cell fired preferentially at intermediate input frequencies (bottom trace). APs have been clipped at the top. B: for each of the stimuli in A we plotted the number of spikes during the step pulse (P) and during the chirp stimulus (grouped into 5-Hz bins). Note the increase in the peak number of spikes and the shift of the preferred input frequency (dashed lines) to higher frequencies when stimulus amplitude was tripled, whereas membrane hyperpolarization shifted these parameters in the opposite direction. This cell showed band-pass firing resonance. C: the number of spikes/cycle plotted against the logarithm of the cycle number of the chirp stimulus (400 cycles total, 0–40 Hz) for the responses shown in A. Dotted horizontal line indicates the firing of exactly 1 spike/cycle (1:1 phase-locking). At 1T there were only brief runs of 1:1 phase-locking alternating with cycle skipping (left panel), but at 3T (at −60 mV) there were extended runs of 1:1 phase-locking to individual cycles before cycle skipping occurred at high-input frequencies (middle panel). At this stimulus amplitude the cell was able to fire 2 (but not more) spikes per cycle at low chirp frequencies. Membrane hyperpolarization decreased the input frequency range over which 1:1 phase-locking to the stimulus occurred (right panel).
In comparison with the three groups of GFP+ interneurons HMs (n = 5, Fig. 7) fired trains of spikes during step stimulation. At just-suprathreshold current (1T) 1:1 phase-locking regions were already evident in this group of cells (Fig. 7A, top trace), flanked by regions of entrainment where the cells fired multiple spikes/cycle (low chirp frequencies) and regions where the cells phase-locked to subharmonics of the chirp stimulus (at high chirp frequencies; also see van Brederode and Berger 2008). The frequency range for 1:1 phase-locking was shifted to higher frequencies when chirp amplitude was increased and beyond the critical frequency the number of spikes/frequency bin started to decline due to cycle skipping (Fig. 7, B and C). HMs were able to fire every other cycle (1:2 phase-locking; see inset in Fig. 7A) or every third cycle (1:3 phase-locking; data not shown) when the chirp frequency exceeded the critical frequency (see also van Brederode and Berger 2008).
Fig. 7.
Firing response of an HM to step and sine wave stimuli. This cell is a representative example for this group of cells (n = 7). All HMs tested fired trains of APs during a step stimulus and were able to fire throughout the entire chirp stimulus. A: 3 membrane voltage traces recorded in response to a just-suprathreshold stimulus (30 pA = 1T, top trace), 90 pA (3T, middle trace), and 150 pA (5T, bottom trace), all at a holding potential of −57 mV. Stimulus consisted of a step (250 ms) depolarization, a step (250 ms) hyperpolarization, and a chirp stimulus (0–40 Hz, chirp rate 2 Hz/s; stimulus shown schematically in the bottom trace). At just-suprathreshold amplitude (1T) the cell responded with a train of spikes during the depolarizing step and a series of spikes throughout most of the chirp stimulus. Increasing the stimulus amplitude entrained firing during the entire chirp. Inset in the middle trace shows an extended run of 1:2 phase-locking. APs have been clipped at the top. B: for each of the stimuli in A we plotted the number of spikes during the step pulse (P) and during the chirp stimulus (grouped into 5-Hz bins). Note the increase in the peak number of spikes and the shift of the preferred input frequency (dashed lines) to higher frequencies when stimulus amplitude was increased. This cell showed band-pass firing resonance. C: the number of spikes/cycle plotted against the logarithm of the cycle number of the chirp stimulus (400 cycles total, 0–40 Hz) for the responses shown in A. Dotted horizontal line indicates the firing of exactly 1 spike/cycle (1:1 phase-locking). At 1T there was already an extended run of 1:1 phase-locking at low chirp frequencies. At higher stimulus strengths the 1:1 phase-locking range shifted to higher input frequencies (higher cycle numbers) and the cell was able to phase-lock 2:1 to the stimulus at low chirp frequencies, whereas cycle-skipping occurred at high-input frequencies.
The spike firing resonance profiles described earlier show that the responses to time-varying current inputs are dependent not only on the frequency of the stimulus, but also on the holding potential (varied by injecting DC current) and the stimulus amplitude (see also Beierholm et al. 2001; Brumberg 2002; Fellous et al. 2001; Hunter et al. 1998). To allow for a comparison between spike firing resonance responses between groups of GFP+ interneurons and HMs we compared responses at the same relative stimulus strength (threefold the threshold current, or 3T) with all cells depolarized to just below firing threshold by the injection of DC current. At this stimulus strength tonic low-pass GFP+ cells either failed to phase-lock to the stimulus or phase-locked only for a few sine wave cycles (data not shown; see Fig. 9A1). Tonic band-pass GFP+ cells did show a 1:1 phase-locking region of input frequencies flanked by regions of multiple spikes/cycle firing and irregular firing (Fig. 8A1). When instantaneous firing frequency was plotted against time, the resulting f–t plots during the chirp stimulus showed a “devil's staircase” shape (see also Brumberg 2002; Brumberg and Gutkin 2007; van Brederode and Berger 2008). For phasic GFP+ cells we found a relatively broad 1:1 phase-locking region (Fig. 8A2). Usually there were additional regions of phase-locking at higher chirp frequencies (1:2 in the example shown in Fig. 8A2). To measure the intrinsic variability or “jitter” of the spike responses we plotted the “local” spike rate variability or CV2 against time (Holt et al. 1996). The CV2 variable was lowest (close to zero) when the cell phase-locked 1:1 or to one of the subharmonics of the fundamental chirp frequency (Fig. 8). The characteristic irregularity in the spike discharge of the tonic band-pass GFP+ cell is reflected in a “noisier” f–t plot and higher CV2 values than those of phasic GFP+ cells or HMs (Fig. 8B1). Note that the CV2 was higher in the 1:1 phase-locking range in tonic band-pass GFP+ cells than that in either phasic GFP+ cells or HM neurons (Fig. 8B). This observation suggests that there is more “jitter” in the spike timing of tonic band-pass cells even when they phase-lock 1:1 to the stimulus. Note that even though the example tonic band-pass cell in Fig. 8, A1 and B1 fired tonically at depolarized membrane potentials it had delayed onset characteristics with the associated irregularity of firing (see companion paper) when stimulated with long depolarizing current pulses at more hyperpolarized potentials. As we have shown in a previous study (van Brederode and Berger 2008) HMs are readily entrained by sine wave stimuli and multiple intermediate phase-locking regimes (for example, 3:4 and 2:3) could be discerned when these cells transitioned from 1:1 to 1:2 phase-locking at sine frequencies higher than the critical input frequency (Fig. 8C2). Phasic GFP+ cells, in contrast, typically transitioned from phase-locking to every cycle (1:1) to every other cycle (1:2) by runs of 1:1 phase-locking interrupted by irregular cycle skipping (Fig. 8C1).
Fig. 8.
Phase-locking properties in GFP+ cells and HMs differ. Top row (A1–A3): instantaneous firing frequency (f) plotted against time (t) for a tonic band-pass GFP+ cells (A1); a phasic GFP+ cell (A2); and an HM (A3) stimulated sequentially with a step (500 ms) depolarization, a step (500 ms) hyperpolarization, and a chirp stimulus (starting at t = 5 s and ending at t = 25 s, chirp rate 2Hz/s), all at the same amplitude (stimulus shown schematically at the bottom). Stimulus amplitude was 3-fold the threshold amplitude (3T) for all 3 neurons. Straight line is the chirp frequency (0–40 Hz) plotted against time. The 1:1 and 1:2 phase-locking regimes are indicated by the vertical dashed lines. Middle row (B1–B3): the local interspike variability as measured by the Holt coefficient of variation (CV2; see methods) plotted against time for the corresponding f–t plots above. Phase-locking (1:1 or 1:2) regions have the lowest CV2 values. The CV2 in B1 in the 1:1 region is higher than that in the cells in B2 and B3, indicative of more irregular firing even during phase-locking in this cell type. Even though it fired tonically at depolarized membrane potentials the cell in B1 had delayed onset characteristics when stimulated at resting membrane potential. C: membrane voltage traces shown on an expanded timescale taken from the transition region between 1:1 and 1:2 phase-locking, as indicated by the double-ended arrows in A2 and A3. The trace in C1 was taken from the phasic GFP+ cell in A2 and the trace in C2 from the HM in A3. Note the regions of 3:4 and 2:3 firing during the transition between 1:1 and 1:2 phase-locking in the HM (C2) and the irregular firing during this transition in the phasic GFP+ cell (C1). APs are clipped at the top.
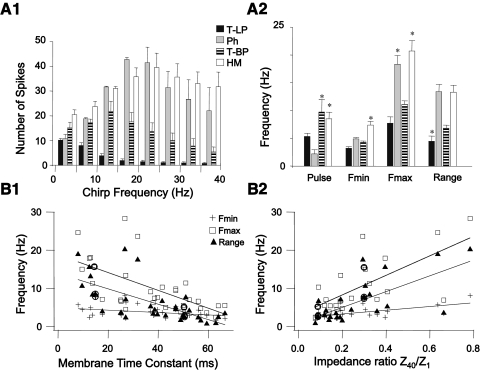
Our findings regarding the phase-locking and firing resonance properties of GFP+ interneurons and HMs at normalized stimulus strength are summarized in Fig. 9. The peak number of spikes fired during a chirp stimulus at 3T stimulus strength was significantly higher in phasic GFP+ cells and HMs than that in either group of tonic GFP+ interneurons (Fig. 9A1; ANOVA, Tukey test, P < 0.05). The peak number of spikes occurred on average between a chirp frequency of 0–5 Hz for tonic low-pass GFP+ cells, between 10 and 15 Hz for tonic band-pass cells, between 15 and 20 Hz for phasic GFP+ cells and between 20 and 25 Hz in HMs (Fig. 9A1; ANOVA, Tukey test, P < 0.05). HMs and tonic band-pass GFP+ neurons fired on average significantly more spikes during the step pulse current stimulus than phasic GFP+ neurons (ANOVA, Tukey test, P < 0.05), but the average number of spikes during the step pulse for tonic low-pass and phasic GFP+ cells (5.4 and 2.3 spikes, respectively) was not significantly different. HMs had a 1:1 phase-locking region whose frequency range was of similar width as the range in phasic GFP+ cells (Fig. 9A2, ANOVA P > 0.05), whereas tonic low-pass GFP+ cells had the smallest 1:1 phase-locking range of cell groups tested; the difference between tonic low-pass GFP+ cells with phasic GFP+ cells and HMs was significant (ANOVA, P < 0.05). The critical resonance frequencies (Fmax) of phasic GFP+ cells and HMs were significantly higher than those of tonic GFP+ cells (ANOVA, P < 0.05). The minimum frequency for 1:1 phase-locking (Fmin) was higher in HMs than that in GFP+ cells (ANOVA, P < 0.05), a reflection of the tendency of HMs to fire multiple spikes/cycle at low chirp frequencies (Fig. 8A3).
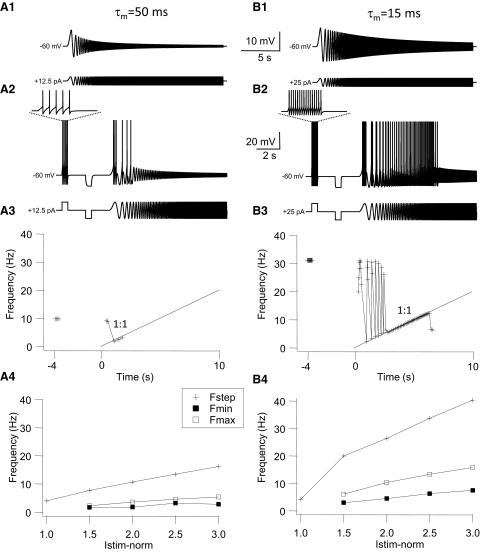
The critical resonance frequency Fmax is a function of the stimulus (Brumberg 2002; van Brederode and Berger 2008). We quantified this relationship by measuring the change in Fmax as a function of stimulus amplitude (normalized by expressing it in multiples of the threshold current 1T). The slope of this relationship was steeper (almost fourfold) in phasic than that in tonic low-pass and band-pass GFP+ cells (data not shown; ANOVA, P < 0.05). The minimum frequency for 1:1 phase-locking (Fmin) was much less sensitive to stimulus current amplitude; the slope of the relationship between Fmin and normalized stimulus current amplitude was on average fivefold smaller than the slope of the relationship between Fmax and normalized current amplitude in the same cell group and was not different between groups (data not shown; ANOVA, P > 0.05). These data demonstrate that 1:1 phase-locking range (i.e., Fmax–Fmin) can be expanded when stimulus current amplitude is increased in phasic GFP+ cells mainly through an increase in the critical frequency Fmax, but that the 1:1 phase-locking range in tonic GFP+ cells is less sensitive to stimulus amplitude.
The results just presented demonstrate that the ability of GFP+ cells to encode time-varying signals is correlated with their firing properties. It has been suggested that the suprathreshold resonance properties of a neuron are largely determined by their subthreshold impedance profiles (Gutfreund et al. 1995; Pike et al. 2000; Schreiber et al. 2004a). In our study we found that there were significant inverse correlations—as determined by calculating Pearson's correlation coefficient (r)—between the passive membrane time constant τm and Fmin (r = −0.36), τm and Fmax (r = −0.62), and τm and the range of the 1:1 phase-locking region (r = −0.64) in GFP+ neurons (n = 31 cells; Fig. 9B1; P < 0.05). A significant inverse correlation was also found between input resistance Rn and Fmax and between Rn and the 1:1 phase-locking range (n = 30, P < 0.05). These data demonstrate that GFP+ neurons with a slow passive membrane time constant and high-input resistance tend have a narrow 1:1 phase-locking range and low critical input frequency. Conversely, cells with a fast τm and low Rn tend to have the broadest phase-locking range and highest critical input frequency. The subthreshold resonance quality Q was not correlated with Fmin, Fmax, or the phase-locking range (P > 0.05), but the damping factor D (Z40/Z1) showed a significant (P < 0.05) positive correlation with all three suprathreshold resonance parameters (n = 21; Fig. 9B2). This result indicates that cells that have a large drop in subthreshold impedance with increasing sine frequency (i.e., small D values) tend to have the smallest phase-locking range (r = 0.67) and lowest Fmin (r = 0.59) and lowest Fmax (r = 0.68). The low-pass filtering of time-varying inputs by passive membrane properties therefore plays a significant role in determining the firing resonance properties of GFP+ interneurons.
Spike timing reliability
In this study spike timing reliability was tested with repeated (10 trials) chirp current stimuli. Individual spikes from each trial were binned and a PSTH was constructed from the binned (3-ms bin width) values of spike time occurrence (see methods). This measure of reliability includes both spike probability (i.e., the probability that the cell fired a spike during the depolarizing half-cycle at a given chirp frequency in each trial) and timing precision (the cell fired at the same point in time in a cycle in each trial). Thus spike timing reliability measures the ability of a neuron to produce identical neuronal output (e.g., spike firing) given repeated presentations of the same input with 1.0 spikes · bin−1 · trial−1 being the maximum value (high precision) and a value of 0 spikes · bin−1 · trial−1 the minimum (low precision).
As described in a previous paper (van Brederode and Berger 2008) we found that spike timing reliability in HMs was highest when these cells phase-locked 1:1 to the stimulus (Fig. 10, A3 and B3). When the cells phase-locked 1:1 to the stimulus they coded the frequency of the chirp current with high precision and the frequency ratio (output frequency/input frequency) was 1 (Fig. 10C3). Peak reliability was on average 0.86 ± 0.06 spikes · bin−1 · trial−1 in HMs (n = 5 cells) and peak reliability was found at a mean chirp frequency (the preferred input frequency) of 13.0 ± 0.7 Hz. Besides the dominant reliability peak in the 1:1 mode several additional but lower reliability peaks were often seen at higher chirp frequencies that were multiples of the preferred input frequency (Fig. 10B3). These additional peaks coincided with phase-locking modes in which the cells fired every second (1:2 mode) or every third cycle (1:3 mode), corresponding to coding of subharmonics of the chirp frequency. When the cell phase-locked 1:2 or 1:3 to the sine wave the cells fired with high timing precision, but with lower probability, since the cells did not always fire during the same cycle from trial to trial (Fig. 10D3), resulting in lower peak reliability (see van Brederode and Berger 2008 and the modeling study of Brette and Guigon 2003 for more detailed descriptions of this phenomenon). In these subharmonic phase-locking regions spike timing was reliable, but it depended on the initial state of the neuron. Reliability was lowest during the transition between phase-locking modes. For instance, when the cells transitioned from 1:1 to 1:2 phase-locking they often went through a brief period of 2:3 firing, although the spiking did not always occur in the same cycle of the chirp stimulus from trial to trial, resulting in low reliability. Spike timing reliability during a square depolarizing current pulse was high for only the first spike in the train in these cells (Fig. 10B3). Peak reliability for the first spike in this train (0.86 ± 0.08 spikes · bin−1 · trail−1) was not significantly different from peak reliability during the 1:1 mode (P > 0.05) An accumulation of spike jitter of subsequent spikes lowered reliability values for spikes that occurred later in the train, such that overall reliability during the square pulse stimulus was low. At low chirp frequencies (<10 Hz) HMs fired multiple spikes/cycle (Fig. 10C3) and spike timing reliability was low and similar to values during a step depolarization.
Fig. 10.
Spike-timing precision is a function of the stimulus frequency and cell type. A1–A3: rasterplots of the occurrence of spikes of 3 different cell types in response to repeated intracellular current stimuli (stimulus shown schematically at the bottom). Cell on the left (A1) is a phasic GFP+ cell; cell in A2 is a tonic low-pass GFP+ cell; and A3 shows an example of an HM. Cells were stimulated repeatedly (10 trials, >10 s between individual trials) with a step (500 ms) depolarization and a step (500 ms) hyperpolarization followed by a chirp current stimulus (20 s, chirp rate 2 Hz/s), all at the same amplitude (stimulus shown schematically on the bottom). Stimulus amplitude was adjusted such that the negative steady-state voltage deflection in response to the hyperpolarizing DC pulse was −20 mV. Stimulus strength was 150, 40, and 250 pA, respectively, for the cells in A1, A2, and A3. B1–B3: corresponding peristimulus time histograms (PSTHs) for the responses shown in A. Spikes were binned in 3-ms-wide bins. The phasic GFP+ cell in B1 fired a single spike or 2 spikes at the start of the depolarizing step (see D1), only the first one of which was a high-precision event (i.e., 10 spikes/bin). Note the absence of firing in this cell during the first cycle of the chirp in any of the trials. The tonic low-pass GFP+ cell (B2) and the HM (B3) fired a train of spikes in response to DC current (see D2 and D3) but only the first spike of the phasic cells and the first spike in the train of the HM cell were high-precision events. During the chirp stimulus (from 5 to 25 s) the phasic cell (B1) fired spikes with high-precision beyond a chirp frequency of 10 Hz (frequency of chirp shown at the top). The tonic cell fired only low-precision spikes with a chirp frequency <10 Hz and stopped firing all together at higher chirp frequency (B2). The HM fired high-precision spikes between 5 and 10 Hz and medium-precision spikes at higher chirp frequency (B3). C1–C3: the logarithm of the frequency ratio (spike frequency/chirp frequency) plotted against time for the corresponding spike trains shown in A1–A3 at the same timescale as in A and B. When the frequency ratio = 1 the cell fired exactly 1 spike/sine wave cycle. In all 3 cell types (C1–C3) the highest spike-timing precision was achieved when the cell fired 1:1 (compare B and C). In the HM additional phase-locking regions (1:2) and (1:3) were evident during the chirp stimulus. D1–D3: selected regions of the rasterplot in A and the corresponding current stimulus (bottom) shown on an expanded timescale. For the phasic cell (D1) are shown the DC depolarizing pulse, the first 3 cycles of the chirp stimulus, and a 4-cycle segment around a stimulus frequency of 20 Hz (chirp segments have been scaled to the same width and do not represent actual time). Note the 1:1 phase-locking at 20 Hz and high repeatability and spike timing precision at this frequency. For the tonic cell (D2) the DC step and the first 3 cycles of the chirp are shown on an expanded timescale. Notice the trial-to-trial “jitter” in the occurrence of individual spikes with respect to the phase of the sine wave cycle. For the HM (D3) are shown (from left to right) the DC step, 1:1 phase-locking around 10 Hz (4 cycles), and 1:2 phase-locking at 20 Hz (4 cycles). Note that the cell does not always fire a spike in the same cycle from trial to trial during 1:2 phase-locking, but spike “jitter” for a given cycle is low.
Compared with HMs, GFP+ neurons as a group (n = 13 cells) had lower mean values for peak reliability (0.60 ± 0.06 spikes · bin−1 · trial−1) and preferred frequency (7.9 ± 1.7 Hz) than those of HMs (Student's t-test, P < 0.05). However, reliability and preferred input frequency were highly variable between cell types within this group. As an example the response recorded in a representative tonic low-pass interneuron is shown in Fig. 10A2. These cells typically fired spikes only at the beginning of the chirp, phase-locked 1:1 to the stimulus for a few cycles, and only at low sine frequency. When tonic low-pass cells phase-locked 1:1 to the chirp stimulus (frequency ratio = 1 in Fig. 10C2) spiking probability was high (the cells fired a spike during every trial for a given cycle) but reliability was low because spike time occurrence varied from trial to trial (Fig. 10D2). Tonic low-pass cells (n = 8) showed on average low values for peak reliability during the square pulse (0.36 ± 0.05 spikes · bin−1 · trial−1) and peak reliability during the chirp stimulus (0.48 + 0.06 spikes · bin−1 · trial−1). Peak spike timing reliability was found at a preferred input frequency of 4.6 ± 0.9 Hz.
On the other extreme we encountered two phasic GFP+ cells that phase-locked 1:1 to the chirp stimulus over a wide range of input frequencies with high reliability resulting from both a high spike probability and high timing precision (Fig. 10, A1–D1). Characteristically, these cells did not fire during the first cycle of the chirp and spike timing precision was high during 1:1 phase-locking (Fig. 10D1). Spike timing precision and phase-locking in tonic band-pass GFP+ cells (n = 3) fell in between the characteristics for tonic low-pass and phasic GFP+ cells (data not shown). In many ways their responses to repeated step and chirp stimuli resembled those of HMs. Responses in tonic band-pass GFP+ neurons were characterized by moderately high peak reliability during the step (0.77 ± 0.19 spikes · bin−1 · trial−1) and chirp (0.73 ± 0.09 spikes · bin−1 · trial−1) stimuli and relatively high preferred input frequency (9.0 ± 1.9 Hz).
In summary, tonic low-pass GFP+ cells are best suited to decode DC stimuli with high probability but low precision (“integrator” cells), whereas phasic/single spike GFP+ cells function optimally to decode time-varying stimuli (“coincidence detector” cells). Tonic band-pass GFP+ neurons fall somewhere in between these two extremes and, like HMs, have input–output characteristics that allow them to encode both DC and time-varying input signals.
Modeling results
We investigated the mechanisms underlying the differences in firing resonance properties among GFP+ interneurons using a single-compartment mathematical model of NR interneurons. Through computer simulations of this neuron model we were able to qualitatively examine the roles played by passive membrane properties and voltage-activated conductances in determining firing and phase-locking properties of different types of GFP+ interneurons encountered in our experimental studies (also see van Brederode et al. 2011). Since the ionic currents and biophysical properties of GFP+ interneurons have not been described in detail we chose a simple nonlinear exponential integrate-and-fire (EIF) model (Fourcaud-Trocme et al. 2003) to model these neurons. In this model the threshold-and-reset spiking mechanism of the standard leaky integrate-and-fire (LIF) model has been replaced by an exponential term to better capture the spiking mechanisms of real neurons (Badel et al. 2008). In addition, we used a modification of the EIF model introduced by Richardson (2009) who used a deterministic voltage-spike template instead of the usual abrupt reset after membrane voltage reaches a spike threshold to better describe spike shape. In the standard LIF model the voltage trajectory between spikes is determined solely by the membrane capacitance (Cm) and “leak” conductance (gL), resulting in linear filtering of input currents. By adding voltage-activated conductances with nonlinear voltage-activation and time constants subthreshold resonance and spike frequency adaptation can be modeled with the EIF model (Richardson 2009). Details of the modified EIF model that we used are given in the appendix. The standard parameters of the EIF model were adjusted where necessary to give a better qualitative description of the passive and active properties of GFP+ interneurons (this study; see also van Brederode et al. 2011). In particular we adjusted the values for Cm and gL to reflect the high-input resistance and relatively slow membrane time constant of GFP+ interneurons (this study; see also van Brederode et al. 2011). We used descriptions of nonlinear voltage-gated conductance derived from recordings in other neuron types or used in other models to describe the active properties of GFP+ neurons (see the appendix for details). Where necessary we adjusted the magnitude of the conductance values or activation kinetics of these nonlinear conductances to better describe the active properties of GFP+ neurons (see following text). For each simulation result we varied the main parameters for passive and active conductances around the chosen value as described in the following text to verify that our modeling results were consistent over a range of values and not unique to a single value.
Our experimental observations indicated that the passive membrane time constant, which determines how fast the membrane potential can change in response to a current input, varied considerably among GFP+ interneurons (Fig. 3, B3 and B4). Furthermore, this membrane time constant is an important determinant of the subthreshold resonance properties of GFP+ interneurons (Fig. 3, B3 and B4). We used two model cells, one with a slow passive membrane time constant (τm = 50 ms) and one with a relatively fast membrane time constant (τm = 15 ms) to explore the effects of differences in τm on subthreshold resonance properties. For the slow τm model we set the value of the membrane capacitance and leak conductance to 62.5 pF and 1.25 nS, respectively, according to: τm = Cm/gL. For the fast τm model the values for Cm and gL were 37.5 pF and 2.5 nS. With this choice of parameters the input resistance (Rn) values of the passive slow and fast τm models were 800 and 400 MΩ, respectively. With these sets of parameters for Cm, Rn, and τm the passive membrane properties of the slow τm model are similar to those of tonic firing GFP+ cells, whereas the fast τm model has passive properties similar to those of phasic GFP+ cells (see Table 1; van Brederode et al. 2011).
We stimulated the two purely passive model cells (all voltage-activated conductances and spike current Ispike were set to zero; see the appendix), with a sequence of step depolarizing and hyperpolarizing current stimuli followed by a 20-s-long chirp (0–40 Hz), all at the same amplitude at a membrane potential of −70 mV. The stimulus strength was adjusted to give the same voltage amplitude to the step stimulus (10 mV) in the slow and fast τm model (Fig. 11, A1 and B1). We found that the voltage response behaved according to what would be expected for a cell membrane consisting of only a membrane resistance (Rm = 1/gL) and capacitance in parallel. The voltage response to step currents rose and decayed with a time constant τm determined by the values for Cm and Rm and the rise and decay time of step voltage responses was slower in the slow compared with that in the fast τm model (Fig. 11, A1 and B1). The amplitude of the voltage excursions during chirp stimulation decreased monotonically with increasing chirp frequency in both model cells, but the decrease in amplitude was more pronounced in the slow τm model cell. The strong low-pass filtering of the slow τm model cell also causes the voltage response of the depolarizing half-cycle to be larger than that of the following hyperpolarizing half-cycle (which has a higher sine frequency due to the linear nature of the forward chirp), but this effect was negligible in the fast τm model.
Fig. 11.
Effects of membrane time constant on resonance profiles of the passive model cells and the effects of adding the muscarine-sensitive conductance gM. A1: membrane voltage response of a purely passive model cell with a slow passive membrane time constant (τm = 50 ms) stimulated with a current stimulus consisting of a step depolarization and hyperpolarization followed by a 20-s-long chirp (shown schematically in A3). The stimulus current amplitude (Istim = 12.5 pA) was set to give a 10-mV step membrane polarization (dashed horizontal lines). The model cell consisted of a leak conductance (gL = 1.25 nS) and membrane capacitance (Cm = 62.5 pF) in parallel. Vertical arrows show the steady-state membrane voltage change in response to the depolarizing (ΔV1) and hyperpolarizing (ΔV2) step current pulses. For this purely passive cell the rectification ratio (Rr = ΔV1/ΔV2) equaled 1. B1: response of a purely passive model cell with fast membrane time constant (τm = 15 ms) to the current stimulus shown schematically in B3. Values for gL and Cm were 2.5 nS and 37.5 pA, respectively. The stimulus current amplitude (Istim = 25 pA) was set to give a 10-mV step depolarization. C1: impedance graphs calculated from the fast Fourier transform (FFT) of Istim and Vm (see methods) plotted against log chirp frequency for the corresponding chirp responses in A1 and B1. Superimposed dashed red lines are the theoretical impedance curves of a resistor–capacitor (RC) circuit with R = 800 MΩ and C = 62.5 pF (slow τm model) or an RC circuit with R = 400 MΩ and C = 37.5 pF (fast τm model). The calculated cutoff frequency (fc) for a slow τm model cell was 3.2 Hz and the high-frequency decay D (D = Z40/Z1) was 0.08. Values for the fast τm model were fc = 10.6 Hz and D = 0.32, respectively. A2a: response of the slow τm model cell to the same current stimulus as in A1 after we added gM (gM = 80gL) to the passive model cell. Note the smaller amplitude of ΔV1 compared with the response in A1 corresponding to a step rectification of Rr = 0.93. A2b: just-subthreshold response of the slow τm model cell with gM when the stimulus amplitude was doubled to 25 pA. Note the increase in asymmetry of the step responses compared with A2a (Rr = 0.80). B2a: response of the fast τm model cell to the current stimulus after we added gM (at gM = 80gL) to the passive model cell of B1. B2b: response of the fast τm model with gM added when we doubled the stimulus amplitude. The rectification ratios for the step responses were 0.93 (B2a) and 0.80 (B2b). Note the resonance only in the depolarizing voltage envelope with an upper resonance frequency (fupp) of 3.0 Hz in B2b. C2: impedance curves for the responses of the slow τm model cell with gM added stimulated at a current amplitude of 12.5 (A2a, blue trace) or 25 pA (A2b, green trace). Dashed line is the theoretical impedance curve of an RC circuit with R = 800 MΩ and C = 62.5 pF. C3: same as in C2 but for the chirp responses of fast τm model cell in B2a (blue) and B2b (green). Note the “oscillations” at low chirp frequency that are the result of asymmetrical voltage envelopes.
The impedance curves, calculated from Z(f) = FFT(V)/FFT(I), of both passive cell models (Fig. 11C1), were well fit by the theoretical impedance function for a parallel resistor–capacitor (RC) circuit
which describes a low-pass filter with cutoff frequency fc = 1/(2πτm). At fc the capacitive reactance equals the resistance component of the circuit. Below fc the behavior is dominated by the resistance and above fc by the capacitance. For the slow τm model cell the value for fc was 3.2 Hz and for the fast τm model cell fc equaled 10.6 Hz (Fig. 11C1). The high-frequency decay of membrane impedance was greater in the slow compared with the fast τm model cell (D = Z40/Z1 values were 0.08 and 0.32, respectively). These values are within the range of D-values obtained in GFP+ interneurons with similar time constants as the fast and slow τm model cells (Fig. 3B3; model cell values indicated by circled symbols). The similarity between the high-frequency decay of membrane impedance of GFP+ interneurons and that of the passive model cells would suggest that low-pass filtering by passive membrane properties is a major determinant of the voltage profiles during chirp stimulation, especially in nonresonant interneurons (compare the chirp responses in Figs. 1A and 11A1). GFP+ interneurons with a slow passive membrane time constant generally showed a lack of subthreshold resonance (Fig. 3B4) and in these cells the membrane acts as a low-pass filter, with the cutoff frequency determined by the membrane time constant.
To simulate asymmetrical subthreshold resonance (Fig. 1B1) we had to add nonlinear voltage-gated conductances to the purely passive model cells. It has been shown experimentally and using mathematical modeling that two main currents responsible for the generation of slow subthreshold resonance at frequencies <10 Hz are the M-current IM and the h-current Ih (Hu et al. 2002). Both currents are active in the subthreshold voltage range and activate and deactivate slowly, but differ in voltage dependence (IM is activated by membrane depolarization, whereas Ih is activated by hyperpolarization) and direction (IM is an outward current carried by potassium ions and Ih is a mixed cation inward current). It is not known whether interneurons in the NR possess IM and Ih, but the presence of undershoot and overshoots and “sag” in the membrane response to step currents (see Fig. 5 in van Brederode et al. 2011) suggests that one or both currents might be active near resting membrane potential in these cells. In addition, the asymmetry in the response to step depolarizing and hyperpolarizing currents (step rectification) and chirp currents at rest suggests that these stimuli activated or deactivated slow subthreshold voltage-dependent currents in some GFP+ interneurons (Fig. 1B1).
Our description of the M-current is based on the well-known Traub–Miles model, as modified by Benda and Herz (2003) and incorporated into the EIF model by Richardson (2009). In this model very little M-current is activated below −65 mV, but it activates rather steeply near spike threshold (see the appendix for details). The modified Traub–Miles model gives a good approximation to the spike-frequency adaptation and f–I curves of real neurons when the magnitude of the steady-state M-conductance (gM) is 80 times the value of the leak conductance (Benda and Herz 2003). Adding the M-conductance (at gM = 80gL) to the passive model cell with slow τm resulted in rectifying responses to depolarizing and hyperpolarizing step currents (Fig. 11A2a). The amplitude of the steady-state depolarizing voltage change (ΔV1) was smaller than the hyperpolarizing voltage change (ΔV2) with an Rr value of 0.93. When we doubled the stimulus amplitude to just below the threshold for spiking the rectification of the depolarizing step response became more pronounced (Rr = 0.80) and now small over- and undershoots at the beginning and end of the depolarizing step were seen, indicating that activation of gM by the depolarizing step opposed membrane depolarization (Fig. 11A2b). Although the amplitude of the depolarizing envelope of the response to chirp stimulation was generally smaller than the hyperpolarizing envelope, the chirp responses of the slow τm model with gM did not show subthreshold resonance (Fig. 11A2b). In contrast, the fast τm model cell with gM (gM = 80gL) showed asymmetrical subthreshold resonance of the type found in some GFP+ interneurons, but only with a large-amplitude chirp stimulus (compare Fig. 11, B2a and B2b; also see Fig. 1B1). With this stimulus amplitude the depolarizing envelope showed resonance at a local maximum voltage at fupp at 3.0 Hz, whereas the hyperpolarizing envelope decreased monotonically with increasing chirp frequency (Fig. 11B2b). This value for fupp is within the range that we found experimentally for resonant GFP+ neurons (average fupp was 4.1 Hz; see Table 1). Note that the amount of rectification in response to step responses for the simulations in Fig. 11, A2b and B2b was the same (Rr was 0.80 in both cases), but that only the fast τm model cell showed resonance. We achieved the same amount of step rectification in these simulations because the magnitude of gM was scaled to the magnitude of gL in both the slow and fast τm model cells to give a comparable level of M-conductance, despite a difference in the cells' leakage conductance. We also ran simulations in which the value of gL was the same, which eliminated the need to scale active conductances, but varied the effective membrane capacitance to make an alternative slow (gL = 2 nS, Cm = 100 pF, τm = 50 ms) and fast (gL = 2 nS, Cm = 30 pF, τm = 15 ms) τm model cell. These alternative fast and slow τm model cells behaved the same with respect to the effect of adding gM on subthreshold resonance as the standard model cells, with identical membrane time constant (data not shown), suggesting that it is the membrane time constant and not input resistance alone that determines whether resonance is expressed. Asymmetric resonance of the depolarizing voltage envelope in response to large-amplitude chirp stimulation of the standard fast τm model cell was still observed when we reduced the magnitude of gM by half (gM = 40gL), but the magnitude of the resonance and upper resonance frequency were reduced compared with the model cell with the standard value of gM (data not shown). It was possible to create subthreshold resonance in the depolarizing voltage envelope of the slow τm model in response to large-amplitude chirp response, but only when we increased the amount of M-conductance to at least threefold the standard gM conductance value (data not shown). However, with this magnitude of M-conductance (gM = 240gL) the response to step current stimulation in the slow τm model cell showed a large amount of rectification (Rr = 0.69), which was beyond the range of Rr values found experimentally in GFP+ interneurons (Table 1). The upper resonance frequency in these simulations with gM = 240gL was lower in the slow (fupp = 2.3 Hz) compared with that in the fast (fupp = 3.6 Hz) τm model cell with gM = 240gL.
The effects of chirp stimulus amplitude and the role played by gM to create asymmetrical subthreshold resonance were also reflected in the corresponding impedance curves for the slow and fast τm model cells (Fig. 11, C2 and C3). At small chirp amplitude the amplitude of the depolarizing voltage excursions was slightly smaller than that of the corresponding purely passive model at low chirp frequency (Fig. 11, A2a and B2a) and this resulted in a small decrease of the calculated impedance from the theoretical passive impedance graph at these frequencies (Fig. 11, C2 and C3; compare black and blue curves). This smaller impedance at low chirp frequencies (i.e., below the passive cutoff frequency) of the model cells with gM compared with the purely passive model cells was more obvious with a large-amplitude chirp stimulus (Fig. 11, C2 and C3, green traces). The higher passive cutoff frequency in the fast τm model and larger “flat” region of the impedance curve at low-input frequency allowed for a more pronounced counteracting of the depolarizing voltage response to chirp stimulation by gM at low input frequency (compare Fig. 11, C2 and C3). The “oscillations” in impedance curves at low frequency are characteristic of asymmetric voltage responses to low-frequency chirp stimulation. The amount of resonance, as quantified by the Q-value obtained from a log-normal fit to the impedance curve (fit not shown) for the chirp response in Fig. 11B2b, was 1.05, which is in the same range as that found experimentally in resonant GFP+ neurons (Table 1). Similar voltage profiles and impedance curves were obtained in the model when we ran the chirp stimulus in forward (0–40 Hz) or reverse (40–0 Hz) mode (data not shown), confirming our experimental observation that the direction of the chirp stimulus does not substantially alter subthreshold resonance profiles.
In summary, adding gM to the passive model cell predominantly depressed the depolarizing amplitude of low-frequency sine wave stimuli and caused asymmetrical resonance profiles. At high-input frequencies this current is too slow to oppose membrane depolarization and the behavior of the cell is dominated by its passive membrane properties instead, more specifically by its passive membrane time constant. The cutoff frequency of cells' passive membrane determines the relative importance and frequency range of the resonance effect of gM. The effects of gM are more pronounced with large depolarizing steps because more of the current is activated at depolarized voltages.
The simulations of the effects of adding gM to the two model cells are in agreement with several of our experimental findings in GFP+ interneurons. First, we found asymmetric resonance mainly in neurons with a relatively fast τm and neurons with the fastest τm had the highest upper resonance frequency (Fig. 3B2). Second, we saw depolarizing step rectification in our recordings from resonant GFP+ cells (Fig. 1B1; Table 1) that was similar in nature and magnitude as in the model cell with gM. Last, we found experimentally that asymmetric voltage profiles in response to chirp stimulation were observed for large-amplitude stimuli only (Fig. 1B1). These observations suggest that gM (or a similar type of current) plays a role in shaping subthreshold responses at rest in response to large-amplitude sine wave stimuli in resonant GFP+ cells.
Adding gh to the passive model cells (see the appendix for details on the h-current parameters) resulted in the characteristic depolarizing membrane “sag” in response to hyperpolarizing step current pulses (Fig. 12A). We set gh = 0.5gL to create a depolarizing sag ratio (the sag ratio = peak voltage/steady-state voltage) of 1.31, which was similar to that found in GFP+ interneurons with the largest sag (see Table 1 in the companion paper, van Brederode et al. 2011). Adding gh resulted in asymmetric voltage responses to step and chirp current stimuli when we stimulated the model cells with just-subthreshold current stimuli (Fig. 12A). Hyperpolarizing step responses were reduced more than depolarizing step responses by adding gh, resulting in an Rr value of 1.44. As with gM the effects of the h-current on chirp responses were more pronounced in the fast compared with the slow τm model cell, even though the amount of rectification and the sag ratio were the same in the fast and slow model cells (gh = 0.5gL in both model cells; compare top and bottom traces in Fig. 12A). In contrast to the effects of gM, activation of the h-conductance by a large-amplitude chirp stimulus resulted in a resonance peak in the hyperpolarizing voltage envelope, but again only in the fast τm model cell (Fig. 12A). Similar to the effect of IM the h-current decreased the impedance of the fast τm model cell for chirp frequencies below fc (Fig. 12C). Hyperpolarizing asymmetric resonance of the type shown in the bottom trace of Fig. 12A was not seen experimentally in GFP+ neurons and the hyperpolarizing step rectification ratio values were also larger than those found experimentally (see Table 1). When we added both gM and gh to the fast τm model cell we observed a more symmetric resonance profile of the type shown in Fig. 12B1. The amount of step rectification (Rr = 1.21) was reduced in the model with gM and gh compared with the model with gh alone (compare Fig. 12, A and B1) and both the depolarizing and hyperpolarizing voltage envelopes during chirp stimulation showed resonance. The opposite effects of gh and gM on the voltage responses to step and chirp current stimuli are the result of the differences in voltage-activation between the two currents. There is some activation of Ih at rest in our model but little activation of IM (Fig. 12B2). During step or chirp depolarization, Ih is turned off whereas IM is turned on; the opposite effect is seen during the hyperpolarizing phases of the current stimulus (Fig. 12B2). At high-input frequencies both currents are too slow to oppose changes in membrane potential. The impedance curves for the fast τm model with gh alone and with gM and gh show a decreased impedance at frequencies below fc compared with the purely passive model (Fig. 12C). The model cell with gM and gh showed a resonance peak (Q = 1.14) at a chirp frequency of 3.6 Hz. These values fupp and Q are within the range found experimentally in resonant GFP+ interneurons (see Table 1 and Fig. 3, B2 and B4).
Fig. 12.
The effects of adding the hyperpolarization-activated conductance gh on subthreshold resonance properties. A: effects of adding the conductance for the h-current (gh = 0.5gL) to the responses of a passive model cell with a slow (top trace, τm = 50 ms) or fast (bottom trace, τm = 15 ms) membrane time constant. Hyperpolarizing DC current was used to set Vm to −70 mV in the models with gh. Dashed horizontal lines show the magnitude of the membrane depolarization and hyperpolarization elicited by a step stimulus of this amplitude in the purely passive model cell. Note the asymmetry in the voltage responses to step currents. Vertical arrows show the steady-state membrane voltage change in response to depolarizing (ΔV1) and hyperpolarizing (ΔV2) step current pulses (current stimulus shown schematically at the bottom). Activation of Ih by the hyperpolarizing step resulted in a depolarizing membrane voltage “sag” toward rest (the sag ratio = peak voltage/steady-state voltage, was 1.31; see companion paper) and a decrease in the amplitude of ΔV2. The rectification ratio of the step responses was 1.44. The conductance gh caused resonance of the lower voltage envelope of the large-amplitude chirp response in the fast τm but not in the slow τm model cell. B1: combined effects of adding gh (gh = 0.5gL) and gM (gM = 80gL) to the fast τm model cell. The amount of asymmetry of the step responses was decreased compared with the trace in A, whereas the chirp response now showed resonance in both the upper and lower voltage envelopes, resulting in a more symmetrical impedance profile (fres = 3.6 Hz). B2: traces showing the magnitude and time course of Ih (top) and IM (bottom) during the voltage response shown in B1. C: superimposed impedance graphs for the purely passive model cell (dashed line), the model cell with gh (black line), and the model cell with both gh and gM (gray line).
In summary, these modeling results suggest that the presence of currents such as Ih and IM, either alone or in combination, in neurons with passive properties similar to GFP+ interneurons in the NR can create subthreshold resonance. Whether these resonance profiles are symmetric or asymmetric depends on the relative balance between these two currents. Due to the voltage-dependent activation characteristics of Ih and IM, membrane potential and stimulus amplitude influence the resonance profiles, whereas the low-pass filtering properties of the cells influence whether subthreshold resonance is expressed or not in these neurons.
We next examined the effects of passive and active membrane properties on the firing resonance properties of the EIF model. As in our experimental studies we studied firing resonance at a depolarized membrane voltage just below spike threshold. To achieve this, the slow and fast τm model cells were first depolarized to a holding potential of −60 mV by injection of steady DC current. We then injected them with the same sequence of step and chirp current stimuli that we used experimentally in GFP+ neurons (Fig. 13). To study firing resonance we added a spike-generating mechanism to the passive slow and fast τm model cells as described earlier (see the appendix for details; also see Richardson 2009). Chirp stimulation at −60 mV at just-subthreshold stimulus amplitude resulted in a voltage envelope that decreased monotonically with increasing sine wave frequency when the model cells consisted of a passive RC circuit and spiking mechanism (Fig. 13). The amount of low-pass filtering of the input signal depended on the time constant of the cell membrane; the amplitude of the voltage envelope decreased more with increasing chirp frequency in the slow (Fig. 13A) compared with the fast (Fig. 13B) τm model with D-values of 0.07 and 0.24, respectively. The slight difference in voltage envelopes and D-values between simulations at −70 (Fig. 11) and −60 mV (Fig. 13) is explained by the fact that at −60 mV with just-subthreshold chirp stimulus amplitude there is already some activation of the spike-generating current of the model (see the appendix). When stimulus current amplitude was increased beyond firing threshold (the model cell generates a spike when the voltage crosses a spike-initiating threshold at −53 mV; see the appendix) both model cells fired a train of APs in response to a depolarizing step stimulus that did not show spike-frequency adaptation (Fig. 13, A2 and B2). Compared with the slow τm model the fast τm model fired more spikes in response to positive step current stimulation for an equivalent stimulus amplitude (stimulus amplitude was set to give the same amount of membrane hyperpolarization during the negative current step in each model cell; see Fig. 13, A2 and B2). The fast τm model also fired more spikes during chirp stimulation, showed a more pronounced firing of multiple spikes/cycle at low chirp frequency, and had an expanded 1:1 phase-locking range compared with the slow τm model (Fig. 13, A2 and B2). The relationship between average firing frequency during the step depolarization and injected current strength (normalized for the difference in absolute threshold current between the two model cells) was more nonlinear in the fast τm model and had a steeper initial normalized f–I slope (31.6 vs. 7.4 Hz; Fig. 13, A3 and B3). The slope of the relationship of Fmin and Fmax of the 1:1 phase-locking range of the chirp response as a function of stimulus strength was 0.9 and 2.1 (slow τm) and 3.1 and 6.4 (fast τm), whereas the width of the 1:1 phase-locking range at a stimulus strength of threefold threshold current amplitude (3T) was 2.6 Hz (slow τm) and 8.3 Hz (fast τm), respectively. At chirp frequencies beyond the 1:1 phase-locking range both model cells stopped firing abruptly (Fig. 13); when stimulus amplitude was further increased the cells were able to phase-lock to subharmonics of the input frequency, albeit for only a very limited input frequency range (data not shown). As a control we ran similar simulations for the alternative fast and slow model cells [in these models gL was the same (i.e., 2 nS) but different membrane time constants (50 and 15 ms) were achieved by adjusting the effective membrane capacitance; see description in preceding text]. The results for these alternative slow and fast model cells were very similar to what was found for the standard cells with the same membrane time constant (data not shown), suggesting that it is the membrane time constant and not input resistance or capacitance alone that determine firing resonance properties in the passive model. These computer simulations further illustrate the important role that passive membrane properties play in determining the firing resonance properties of GFP+ interneurons. The minimum and maximum firing frequencies and 1:1 frequency range of the slow and fast τm model cells were similar to what we found experimentally in GFP+ interneurons for cells with comparable passive membrane time constants (Fig. 9B1, model values indicated by circles) or subthreshold resonance profiles (Fig. 9B2, model values indicated by circles).
Fig. 13.
Effects of passive membrane properties on firing resonance properties of the exponential integrate-and-fire (EIF) model cell. We compared firing resonance in the model cells with slow (Cm = 62.5 pF, gL = 1.25 nS, τm = 50 ms, left) and fast τm (Cm = 37.5 pF, gL = 2.5 nS, τm = 15 ms, right). Slow and fast τm model cells were depolarized with DC current (+12.5 or +25 pA, respectively) to just below firing threshold at a holding potential of −60 mV prior to step or chirp current stimulation. Model cells consisted of a leak conductance, membrane capacitance, and spiking current Ispike (see the appendix). A1 and B1: membrane voltage traces (top) of the 2 model cells in response to just-subthreshold chirp stimulation. Chirp stimulus (20 s, 0–40 Hz) is shown schematically at the bottom. Actual stimulus current amplitude was 7.5 pA (A1) and 12.75 pA (B1). Note the absence of subthreshold resonance. A2 and B2: examples of membrane voltage traces (top) in response to suprathreshold step and chirp stimulation (stimulus shown schematically at the bottom) for the model cells shown in A1 and B1. Stimulus amplitude was 15 pA (A2) or 30 pA (B2), which gave the same amount of step hyperpolarization in both model cells. Only the first 10 s of the 20 s linear (0–40 Hz) chirp stimulus are shown. Insets show membrane voltage during the depolarizing step on an expanded timescale. A3 and B3: instantaneous firing frequency plotted against time for the step and chirp responses in A2 and B2. The dashed lines represent linear chirp frequency (cutoff in the graph at a frequency of 20 Hz). Chirp stimulation started at t = 0 s, step stimulation at t = −4 s. Phase-locking ranges are indicated on the graphs. Note the abrupt cessation of firing beyond the critical input frequency. A4 and B4: average firing frequency during the step depolarization (Fstep), and Fmax and Fmin of the 1:1 phase-locking range plotted against normalized stimulus amplitude (Istim-norm) for the slow (A4) and fast (B4) τm model cells. Stimulus current was normalized by dividing the actual current amplitude by the amplitude of the threshold current (= minimum current where cell fired 2 spikes during step stimulation). Values for threshold current were 8.1 pA (A4) and 12.9 pA (B4). Minimum firing frequency at threshold step current amplitude was 4.0 (A4) or 4.2 Hz (B4).
The influence of gh on firing resonance properties is small since this current is scarcely activated at voltages near spike threshold (data not shown; also see Hu et al. 2002) and therefore the role of this conductance was not studied further. The M-current, in contrast, is expected to make a larger contribution to membrane properties and firing because it is more activated at −60 than that at −70 mV. Adding gM to the passive model cell with spiking mechanism (at gM = 80gL) resulted in subthreshold resonance when the cells were stimulated with a just-subthreshold chirp current stimulus at a holding potential of −60 mV (Fig. 14A1; only the trace for the fast τm model cell is shown). The resonance quality was larger (Q = 1.22 vs. 1.02) and the upper resonance frequency was higher (fupp = 3.0 vs. 1.7 Hz) in the fast compared with the slow τm model cell. Since the effects of gM in the fast τm model cell were much more pronounced and since resonance was found experimentally mainly in neurons with a fast τm (see preceding text), only the firing resonance properties of this model are described here.
Fig. 14.
Effects of the muscarine-sensitive potassium conductance (gM, left) or a depolarization-activated potassium conductance (gKLT, right) on firing resonance properties of the EIF model. A1: firing response of the fast τm (Cm = 37.5 pF, gL = 2.5 nS, passive τm = 15 ms) model cell with gM (gM = 80gL) in response to step stimulation. The model cell was depolarized to a membrane potential of −60 mV by injection of DC current (+27.5 pA). At the threshold pulse amplitude (17.5 pA) the model cell fired a single spike (left) or a train of spikes when stimulus strength was increased to 40 pA (right). Note the progressive lengthening of spike intervals (adaptation ratio = the frequency of the first interval/frequency of the last interval = 1.21 for this trace; also see van Brederode et al. 2011). Arrow points to the afterhyperpolarization that followed the spike train. B1: similar experimental protocol as that in A1 but for the fast τm model cell with gKLT added (gKLT = 2gL; see the appendix). Note the increase in holding current (+36.7 pA) and threshold current (28.6 pA) compared with the model in A1. Arrow points to depolarizing “hump” after the initial burst of spike firing when stimulus amplitude was 40 pA. A2 and B2: responses of the fast τm model cells with either gM (A2) or gKLT (B2) to just-subthreshold chirp (0–40 Hz) current stimulation (chirp current stimulus shown schematically at the bottom). Model cells were depolarized to −60 mV by injection of DC current. Stimulus amplitude was 17.5 pA (A2) or 28.6 pA (B2). Both model cells show subthreshold resonance with an upper resonance frequency of 3.0 Hz (A2) and 5.0 Hz (B2), Q-values of 1.17 (A2) and 1.50 (B2) and D-values of 0.30 (A2) and 0.39 (B2), respectively. A3 and B3, top: examples of the responses of the model cells with gM (A3) or gKLT (B3) to suprathreshold current stimulation (current amplitude was 35 pA in both simulations). Step depolarization resulted in firing of a train of APs in A3 compared with the firing of a single spike at the beginning of the pulse in B3. Insets show membrane voltage during the depolarizing step at an expanded timescale. Hyperpolarizing current step caused depolarizing “sag” of the membrane potential back to the holding potential (sag ratio = 1.15) and a depolarizing overshoot at the end of the pulse in the model with gKLT (B3). Note the lack of firing of the model with gKLT at low chirp frequency. Only the first 10 s (0–20 Hz) of the chirp stimulus (shown schematically at the bottom) are shown. Bottom: instantaneous firing frequency plotted against time for the step and chirp responses shown in the top traces. The straight dashed line represents linear chirp frequency (cutoff at a frequency of 20 Hz). Phase-locking modes are indicated on the graphs. Note the prominent phase-locking to harmonics of the chirp frequency (e.g., 1:2, 1:3) in the model with gM, whereas the model with gKLT phase-locked exclusively in 1:1 mode at this stimulus amplitude. A4 and B4: frequency–current relationships for the model cell with gM (A4) and gKLT (B4) for the average firing frequency during the step pulse (Fstep) and the minimum and maximum frequency of the 1:1 phase-locking range (Fmin and Fmax, respectively). The model with gKLT fired exclusively single spikes during step and chirp stimulation at current amplitudes below 35.9 pA but was able to fire repetitively when amplitude was increased beyond this threshold.
Adding gM caused a decrease in average firing rate response to membrane depolarization compared with the fast τm model cell without gM (compare Figs. 13B and Fig. 14A). With the addition of gM the minimum step current amplitude to cause firing of a single AP was increased from 12.7 to 17.5 pA compared with the passive model (Fig. 14A1). A train of APs was evoked at suprathreshold step stimulus amplitudes, characterized by spike-frequency adaptation and a pronounced afterhyperpolarization (Fig. 14A1). The model with gM spiked first at the subthreshold upper resonance frequency and not at the first cycle as in the passive model when stimulus amplitude was increased from sub- to suprathreshold amplitude (data not shown). For the same suprathreshold chirp stimulus amplitude the model cell with gM fired fewer multiple spikes/cycle than the model cell without gM and the model cell was able to phase-lock to harmonics of the chirp stimulus (Fig. 14A3). The f–I curve for the EIF model was linearized after inclusion of gM and its normalized slope decreased to 4.0 Hz compared with an initial normalized slope of 31.6 Hz for the passive fast τm model cell (Fig. 14A4). Fmin and Fmax for the 1:1 phase-locking range were shifted to lower frequency values and the slopes of the Fmin and Fmax versus normalized current relationships were reduced to 1.6 and 3.0 Hz from their values of the fast τm model cell without gM (3.1 and 6.4 Hz, respectively). The hyperpolarizing M-current is substantially activated at a holding potential of −60 mV and this resulted in an increase in the minimum injected current necessary to cause repetitive firing from 12.9 to 23.6 pA, whereas the minimum firing frequency at threshold current amplitude was reduced to 2.6 Hz compared with 4.2 Hz for the passive model. At a stimulus amplitude of 3T the values of Fmin, Fmax, and 1:1 phase-locking range in this model cell were 4.4, 9.7, and 5.3 Hz, respectively, which is within the range found experimentally in GFP+ neurons (Fig. 9A2). In summary, inclusion of gM in the fast τm model cell enabled it to phase-lock to harmonics of the stimulus and it decreased the number of spikes fired at low-frequency input compared with the passive model, thereby extending the range of input frequencies where the model responded with well-timed spikes.
In our experimental studies we encountered a group of GFP+ interneurons that fired a single spike or a brief burst of a few spikes only at the beginning of a long step depolarization (“phasic” cells; also see van Brederode et al. 2011). Phasic spiking was found in interneurons with a relatively fast membrane time constant (15 ms on average; see van Brederode et al. 2011). We were able to create single spiking as a result of extreme spike-frequency adaptation in the fast τm model cell with gM (see preceding text) when we increased the value of gM from the standard value of 80gL, but at this magnitude of the conductance the size of the afterhyperpolarization became much larger than what we saw experimentally in phasic GFP+ interneurons (data not shown) and the overall firing rate became very low. Short-latency firing of a single spike during a long depolarizing current step has been attributed to activation of dendrotoxin (DTX)-sensitive, low-threshold potassium conductance in a variety of neurons (Barnes-Davies et al., 2004; Catacuzzeno et al., 2008). In these prior studies block of this type of conductance with DTX transformed single spiking to repetitive firing of multiple spikes in response to long depolarizing current pulses. Single and phasic spikings in our simulations were achieved by including a low-threshold, depolarization-activated potassium current IKLT in the fast τm model cell. This current, named Ix by Richardson (2009), activates at voltages positive to −80 mV, is half-activated at −50 mV, and has two voltage-dependent activation time constants (see the appendix for details). Adding this conductance (at gKLT = 2gL; see Richardson 2009) to the fast τm model cell resulted in firing of a single spike immediately at the beginning of the pulse at just-suprathreshold current pulse strength (see Fig. 14B1). Single spiking persisted until the current amplitude was increased from threshold to 35.9 pA, after which the cell fired a brief burst of spikes at the beginning at the pulse (i.e., “phasic” spiking; Fig. 14B1). Only at high current amplitude was this model cell able to fire a train of APs (data not shown). Spikes were followed by a brief, depolarizing hump, similar to what we saw experimentally in some phasic GFP+ interneurons at membrane potentials close to firing threshold (see Fig. 7A1; van Brederode et al. 2011). Adding gKLT also caused a depolarizing membrane voltage sag and overshoot at the end of a hyperpolarizing current pulse and induced a prominent subthreshold membrane voltage resonance in response to chirp stimulation at −60 mV (Fig. 14, B2 and B3; also see Richardson 2009). The upper resonance frequency of the fast τm EIF model with gKLT was 5.0 Hz, with a Q-value of 1.50 at a holding potential of −60 mV. Subthreshold resonance was also present in this model cell at a holding potential of −70 mV, but was much less pronounced than that at −60 mV with a Q-value of 1.08 and upper resonance frequency of 4.1 Hz. At −70 mV this model cell showed rectification of the depolarizing step current response with a rectification ratio (Rr) of 0.63 (data not shown). The model cell with gKLT fired spikes first during cycles corresponding to the maximum in the depolarizing subthreshold voltage envelope when stimulus amplitude was increased (data not shown). The model with gKLT was further characterized by the fact that it fired exclusively single spikes/cycle in response to intermediate chirp frequencies (Fig. 14B3). This band-pass behavior was most evident at moderate stimulus strength and was characterized by the absence of spike firing at low and high chirp frequencies. At high current amplitude the model cell with gKLT was able to fire multiple spikes/cycle during chirp stimulation at low input frequencies, but phase-locking to subharmonics of the input frequency at frequencies beyond Fmax was not seen until current amplitude was increased beyond twofold the threshold current to evoke spiking in this model (data not shown). The slope of the relationship between Fmax and normalized chirp stimulus amplitude was steeper in the model with gKLT than in any of the other models (15.2 Hz), but the slope of the Fmin versus normalized current amplitude relationship (3.0 Hz) was similar to that of the fast τm model cell without gKLT and the model with gM. Furthermore, the normalized slope of the f–I relationship for the average firing frequency during the step depolarization (Fstep) was steeper than that for the other EIF models and the threshold current for repetitive firing (35.9 pA) and minimum firing frequency (12.9 Hz) larger (Fig. 14B4). These properties of the model cell with gKLT compared with the model without gKLT are similar to what we found experimentally when we compared the firing resonance and phase-locking properties phasic to tonic GFP+ interneurons (see preceding text). When we reduced the magnitude of the conductance gKLT from its standard value by half (i.e., gKLT = gL) our main findings regarding the firing patterns in response to step and chirp current stimulation such as single/phasic spiking, large 1:1 phase-locking range, and the absence of spiking during high and low chirp frequency were qualitatively similar to the model with gKLT = 2gL (data not shown). Thus the presence of a current such as IKLT promotes both single and phasic spiking and extends the 1:1 phase-locking range associated with the firing of spikes with high reliability and precision (see preceding text).
In summary, our modeling studies suggest that firing resonance and phase-locking are functions of both the passive membrane properties and voltage-gated conductances active in the perithreshold membrane voltage range. Differences in membrane time constant and the relative expression of gM and gKLT are sufficient to explain the variety of the firing responses observed with step current pulses and firing resonance and phase-locking properties observed in response to sine wave stimulation that we encountered in our experimental studies of GFP+ interneurons.
DISCUSSION
Summary
In the companion paper (van Brederode et al. 2011) we describe the subthreshold and spike firing responses to long depolarizing injected current pulses of different classes of GAD67-GFP+ interneurons in the NR. Herein we extend this analysis to time-varying stimuli by examining the sub- and suprathreshold resonance properties of these neurons injected with sine wave current stimuli. Our results indicate that neurons with tonic or phasic firing patterns in response to step current pulses have different firing resonance properties and differ in their ability to phase-lock to sine wave current input. We used a mathematical model to simulate the firing resonance properties of different classes of GFP+ interneurons and found that differences in voltage-activated currents active in the perithreshold voltage range most likely contribute to different firing properties to step and sine wave current stimuli among interneuron classes. In addition we show that the passive membrane properties—and the associated low-pass filtering of time-varying inputs—are a major determinant of firing resonance and phase-locking properties in these neurons.
Responses of inhibitory interneurons to fluctuating current inputs
Although our study is, to our knowledge, the first to describe the responses of brain stem inhibitory interneurons to fluctuating current inputs, the responses of different classes of inhibitory interneurons to chirp current inputs have been investigated in the hippocampus (Pike et al. 2000). Horizontal, presumably inhibitory, interneurons in the stratum oriens had a preferred maximum firing frequency at input frequencies between 3 and 10 Hz, but most fast-spiking interneurons had a much higher preferred input (between 30 and 50 Hz). In addition, subthreshold resonance curves in horizontal interneurons showed a peak at a mean input frequency of 2.4 Hz, whereas fast spiking interneurons showed subthreshold resonance at frequencies between 10 and 50 Hz. Horizontal interneurons also had higher input resistance and longer time constants than those of fast-spiking interneurons. In our sample of inhibitory interneurons in the NR we did not find neurons with a “fast spiking” phenotype, such as described in the hippocampus (and neocortex). Although some tonic GFP+ cells showed little or no spike-frequency adaptation in response to long depolarizing currents pulses (van Brederode et al. 2011), these cells lacked the relatively fast membrane time constant and narrow AP width characteristics of fast-spiking interneurons in the hippocampus (Pike et al. 2000). Instead, the frequency preference and subthreshold resonance properties of tonic GFP+ cells in our study are in the same range as those of horizontal hippocampal interneurons.
The firing properties of GFP+ interneurons in our study resemble more closely those of neurons in lamina I of the spinal dorsal horn, including tonic, delayed onset, and single spike/phasic firing in response to long depolarizing current pulses (Prescott and De Koninck 2002). In their study, lamina I neurons with tonic and delayed onset firing properties responded best to slowly varying stimuli, whereas phasic and single spike neurons responded best to high-frequency stimulation. Furthermore, the slow time constant of tonic spinal neurons tended to promote temporal summation, allowing these cells to linearly transduce stimulus intensity into firing frequency, whereas the fast membrane time constant and high-threshold current of single spike neurons allowed for detection of coincident input (Prescott and De Koninck 2002). We found a similar functional division between neurons with these firing types in the NR based on their responses to step and chirp current stimuli. These distinct firing patterns (tonic, delayed onset, and single spike) have also been described in trigeminal ganglion neurons (Catacuzzeno et al. 2008) and thus might be a more general feature of heterogeneous populations of sensory neurons. In experimental and modeling studies of GABAergic neurons in the medial septum (Wang 2002) and cerebellar granule cells (D'Angelo et al. 2001) intermittent firing coupled with a long delay to the first spike when cells are made to fire from a relatively hyperpolarized membrane potential was due to a depolarization-activated potassium current IKS. We also saw this behavior in a subclass of GFP+ interneurons at just-suprathreshold current amplitude (van Brederode et al. 2011). IKS inactivates slowly and causes ramp depolarizations in response to a step depolarizing current pulse (the slow depolarization-activated potassium current IKLT in our model deactivated instantaneously and does not cause this type of firing behavior). Neurons that possess IKS respond better to phasic stimuli and can produce precisely timed spikes (Balu et al. 2004). In other cell types delayed firing is caused by a fast-inactivating A-type potassium current (Catacuzzeno et al. 2008). Although our sample was small, we observed that delayed-onset irregular firing GFP+ interneurons were band-pass in nature and we hypothesize that their firing and firing resonance properties are due to the presence of IKS and/or IA in these cells.
The nature of the synaptic stimulus that GFP+ interneurons located in the NR receive is not known, but it is possible that they are encoding different stimulus modalities that are then integrated at the HM level during various orofacial behaviors and respiration. In the cat, neurons in perihypoglossal regions just ventrolateral to the XII nucleus, which includes the NR, relay information carried by afferents in the trigeminal, hypoglossal, and vagal nerves and inhibit hypoglossal neurons during swallowing (Ono et al. 1998). We did not investigate whether different types of GFP+ interneurons are involved in these types of sensory processing, but based on their transduction properties most tonic GFP+ interneurons are best suited to control how fast HMs fire, whereas phasic/single spike GFP+ interneurons are best suited to control when HMs fire, thus functionally dividing inhibitory interneurons in the NR into different groups.
Mechanisms of subthreshold resonance
Many neurons in the brain show some form of subthreshold membrane resonance (Erchova et al. 2004; Gimbarzevsky et al. 1984; Hu et al. 2002; Hutcheon et al. 1996b; Manuel et al. 2009; Nguyen et al. 2004; Pike et al. 2000). Neurons that exhibit subthreshold resonance produce large membrane voltage responses when they are driven by inputs at their resonance frequency and smaller voltage deflections at other input frequencies (Hutcheon and Yarom 2000). Subthreshold resonance has been shown to be caused by a combination of low- and high-pass filtering of fluctuating inputs by the cells' membrane (reviewed by Hutcheon and Yarom 2000). The low-pass filtering is the result of the passive membrane properties (the combination of a leak conductance and capacitance in parallel), with the cutoff frequency set by the RC time constant. A purely passive RC circuit does not show resonance and in our study the majority of tonic GFP+ interneurons at rest behaved like such a circuit. The high-pass filtering is due to slow voltage-activated conductances such as Ih, IM, and IKLT that actively oppose changes in membrane potential. The published time constants for activation of Ih and IM are similar to the passive membrane time constant of many tonic GFP+ cells (see Hu et al. 2002) and in these cells there is no resonance, even though the rectification and “sag” in the membrane voltage responses to step depolarizing pulses and the voltage dependence of this rectification suggest that these conductances are present. Only when there is enough of a “gap” between the activation time constant of these conductances and the passive membrane time constant is there a “window” at intermediate frequencies where membrane resonance can occur (Hutcheon et al. 1996a). The faster membrane time constant of resonant GFP+ cells allows for such a “gap.” Consistent with this theory we found that, among GFP+ cells that showed resonance, the resonance frequency and quality increased with a decreasing membrane time constant. HMs, which had the fastest passive membrane time constant, all showed some form of membrane resonance. Similar relationships between membrane time constant, quality, and resonance frequency were recently described in mouse spinal motoneurons (Manuel et al. 2009). The resonance frequency in these neurons (17 Hz on average) was higher than that in any of the neurons in our study, attributable at least in part to the very fast membrane time constants in spinal motoneurons (2.5 ms on average; Manuel et al. 2009). The fact that their recordings were performed in vivo with sharp microelectrodes likely contributes to the fast membrane time constant reported in these studies.
Although both IM and Ih can cause subthreshold resonance, the resulting resonance profiles are not necessarily the same. M-current is turned on by the depolarizing half-cycle at low chirp frequency and turned off by the hyperpolarizing cycle, thus attenuating both the peak positive and negative voltage deflections (Hu et al. 2002). Our modeling results indicate that this attenuation is not always symmetrical, depending on the membrane potential and activation characteristics of this current. At resting membrane potential the cell operates near the bottom of the sigmoidal activation curve of IM and therefore the depolarizing half-cycle activates more IM than is deactivated by the hyperpolarizing half-cycle. As a result the depolarizing voltage excursions are always smaller then the hyperpolarizing voltage executions and the response to step and chirp stimulation shows outward rectification. Similarly, membrane hyperpolarization opens more h-channels than are closed by the depolarizing half-cycle, resulting in voltage profiles in response to step and chirp stimulation that show inward rectification. Since the conductances responsible for high-pass filtering are voltage dependent it is not surprising that subthreshold membrane resonance is also voltage dependent. In both experimental studies and through modeling Hu et al. (2002) demonstrated that the M-current is responsible for subthreshold membrane resonance at depolarized potentials just below spike threshold and that the h-current causes resonance at hyperpolarized potentials. Besides membrane potential and stimulus amplitude the relative expression and activation characteristics of each conductance also determine whether one or both forms of subthreshold resonance are found in a given neuron and whether resonance is asymmetric or symmetric. Asymmetric resonant voltage profiles in response to chirp stimuli have also been described using a single-compartment conductance-based model that included M-current (Schreiber et al. 2009). Their model showed resonance only on the depolarizing voltage envelope and only at large just-subthreshold chirp amplitude, similar to the experimental and modeling results described in our study. Furthermore, they showed that asymmetrical voltage profiles do not cause a peak in the calculated impedance curve using the fast Fourier transform of the current and voltage waveforms. The upper resonance frequency is not always equal to the resonance frequency as determined from impedance profiles and fupp is a better predictor than fres of the input frequency where spiking probability is highest (Schreiber et al. 2009).
In nonresonant, tonic GFP+ cells the amplitude of the depolarizing steps was larger than that of the corresponding hyperpolarizing steps (see Fig. 1A1). Many of these cells also showed rebound firing after membrane hyperpolarization and depolarizing membrane voltage “sag” in response to negative current steps (van Brederode et al. 2011), suggesting that h-current dominates the responses of these cells to subthreshold chirp stimulation at rest. Resonant GFP+ cells, in contrast, showed outward rectification in response to step stimulation, suggesting that an M-like current and/or a slow depolarization activated K+ current like IKLT dominate the subthreshold resonance profiles at rest in these cells. Our experimental results regarding subthreshold resonance profiles in GFP+ neurons show similarities to the findings in tonic and phasic firing vestibular neurons in the frog (Beraneck et al. 2007). In that study these authors describe asymmetrical subthreshold chirp responses of opposite polarity in these two cell types and differences in firing patterns in response to depolarizing current steps similar to our findings in tonic and phasic GFP+ cells. Subthreshold resonance and chirp asymmetry in phasic cells was reduced by low concentrations of 4-aminopyridine, which was attributed to blockade of a slow, depolarization-activated potassium current (Beraneck et al. 2007), similar to the IKLT current in our modeling study. This conductance was also thought to be responsible for the fast termination of spiking in response to step depolarizations in phasic cells. From these studies and our own results it appears likely that passive and active membrane properties both contribute to low-pass or band-pass transduction properties of neurons when they are stimulated with subthreshold fluctuating inputs.
Mechanisms of firing resonance
Many studies have shown that neurons show firing resonance—i.e., they spike preferentially at a given input frequency. This frequency preference is explained by the fact that at the firing resonance frequency the input frequency matches the subthreshold resonant frequency due to the amplification of membrane voltage responses at this frequency (Engel et al. 2008; Erchova et al. 2004; Gutfreund et al. 1995; Pike et al. 2000). In accordance with these studies we found in our experimental and modeling studies that neurons start to fire first at a chirp frequency where the depolarizing voltage amplitude is largest (i.e., at the upper resonance frequency). For nonresonant GFP+ neurons this was close to zero input frequency, whereas for resonant cells this chirp frequency matched the upper resonance frequency. The correlation between subthreshold and firing resonance is strong when the neuron operates in the fluctuation-driven regime or under conditions where the amount of membrane noise generated by synaptic bombardment is large, but much less so when the neuron operates in the mean-driven regime or the noise level is low (Richardson et al. 2003; Schreiber et al. 2009). Others have found that spike-induced ionic currents combined with subthreshold resonance properties determine the spiking patterns of neurons in response to fluctuating inputs (Engel et al. 2008), whereas phase-locking properties to time-varying signals have been reported to be dependent on the properties of the spike-generating currents (Brumberg and Gutkin 2007).
Spike timing reliability in real and model neurons is highest when neurons phase-lock 1:1 to a periodic input stimulus (Beierholm et al. 2001; Fellous et al. 2001; Schreiber et al. 2004b). In this study we show that this also holds true in GFP+ interneurons and HMs (also see van Brederode and Berger 2008). In their modeling studies Gutkin et al. (2003) discriminate between three different phase-locking regimes using a modified IF model. In the first n:1 regime, at low input frequency, the neurons fire n spikes per cycle and the output frequency reflects the amplitude of the stimulus. In this regime spike probability is high but spike timing precision is low due to the large amount of “jitter” in the spike times during the burst. In the second regime, at intermediate input frequencies, the model cells fired exactly 1 spike/cycle (1:1 regime) and output frequency reflected the frequency of the input. In this regime both spike probability and precision are high. In the third regime the output frequency is lower than the input frequency and the firing of the model cell was determined by either noise resulting in irregular firing or 1:n phase-locking where the cell fired at harmonics of the input frequency (1:2, 1:3, 1:4 phase-locking). When the firing is irregular, reliability is low but regions of enhanced reliability have been shown to exist in the 1:n phase-locking regime in modeling studies (Beierholm et al. 2001; Schreiber et al. 2004b) and experimentally in HMs (van Brederode and Berger 2008). The prominence or presence of each regime depends on stimulus amplitude, membrane depolarization, and the type of neuron studied (Fellous et al. 2001; van Brederode and Berger 2008). Our study indicates that the different phase-locking regimes are also dependent on the passive membrane properties of the cells, with cells that have a slow membrane time constant showing a narrow 1:1 phase-locking range. Tonic low-pass GFP+ cells, which constituted the majority of GFP+ cells in our sample, display prominent n:1 phase-locking at low input frequency characterized by high spike probability, large jitter and low spike timing precision, and only a narrow 1:1 phase-locking regime. These cells stopped firing altogether when input frequency was further increased or acted like they were stimulated with a noisy DC current, resulting in irregular firing, because they could not follow the time course of the chirp stimulus. Phasic cells showed a relatively narrow n:1 regime but a prominent 1:1 phase-locking regime and a wide range of input frequencies where firing was both reliably and precise. All three regimes were prominently present in HMs when they are stimulated with chirp stimuli from a just-subthreshold membrane potential.
Our study shows that nonresonant GFP+ cells are spontaneously active in the slice, whereas resonant GFP+ cells are generally quiescent (also see van Brederode et al. 2011). This suggests that nonresonant GFP+ cells operate mainly in the mean-driven regime. The tonic firing pattern and slow membrane time constant of nonresonant GFP+ cells make them ideally suited to encode the stimulus mean by their firing rate. For the (nonresonant) leaky integrate-and-fire model operating in the mean-driven regime the input frequency that induces maximum spike timing reliability is the mean spontaneous firing rate (Hunter et al. 1998). In agreement with these modeling studies our studies show that the input frequency where maximum reliability occurred in nonresonant GFP+ cells (∼5 Hz) is similar to the spontaneous firing rate of GFP+ cells in the slice (van Brederode et al. 2011). Resonant GFP+ neurons, in contrast, were generally not spontaneously active and therefore most likely operate in the fluctuation-driven regime. The phasic and delayed onset spiking patterns of these neurons together with a relatively fast membrane time constant are well suited to encode the timing of the stimulus. In the fluctuation-driven regime maximum reliability occurs at the subthreshold resonance frequency, allowing only certain frequencies to induce reliable spiking (Schreiber et al. 2009).
Ionic mechanisms influence spike timing precision and phase-locking. Spike-frequency adaptation caused by a slow noninactivating K+ current such as M-current (Madison and Nicoll 1984) influences spike timing probability and precision based on its activation properties (Prescott and Sejnowski 2008). Adaptation mediated by IM improves spike-time coding of high-frequency input signals but it does this at the expense of spike-rate coding (Prescott and Sejnowski 2008). The frequency of highest reliability for a given amplitude is very sensitive to the density of slow K+ conductances (Schreiber et al. 2004b). Introducing a slow K+ conductance into rat cortical neurons using the dynamic-clamp technique lowered the preferred frequency of these neurons and increased the reliability at that frequency (Schreiber et al. 2004b).
Our modeling experiments support these earlier studies showing that ionic mechanisms can influence phase-locking properties, but only in cells that have a membrane time constant that is faster than the time constants of voltage-gated currents active in the perithreshold voltage range. In our modeling studies the main effect of adding gM to the passive fast membrane time constant EIF model was to lower the frequency of the 1:1 phase-locking range, similar to what has been described experimentally (Schreiber et al. 2004b). Adding gM also improved phase-locking to harmonics of the input frequency (1:n phase-locking) compared with the purely passive model cell. We found that adding the low-threshold K+ current gKLT enhanced the 1:1 phase-locking ability of the EIF model cell to sine wave stimuli by suppression of the firing of multiple spikes per sine wave cycle at low input frequency (which leads to imprecise spiking in the n:1 regime) and suppression of phase-locking at the harmonics. Furthermore, gKLT led to an increase in the critical or phase-locking frequency (Fmax) and the expansion of the 1:1 phase-locking range where spike timing precision is highest. In addition, a larger stimulus amplitude was necessary to induce firing. As a result of these changes after adding gKLT the model cell became more “band-pass” in nature and increased its signal-to-noise ratio compared with the passive model cell. Single or phasic spiking is due to the fact that IKLT activates slowly enough to allow firing of a single or only a few spikes at the beginning of a just-suprathreshold depolarizing current pulse, but prevents or reduces generation of additional spikes when it is fully activated (Catacuzzeno et al. 2008). Whether or not subsequent spikes are generated depends on the balance between continued depolarization by the current pulse and membrane repolarization by IKLT. Functionally, these types of low-threshold K+ currents have been shown to enhance spike timing precision in auditory neurons (Barnes-Davies et al. 2004) and phase-locking to periodic stimuli in IF model cells (Svirskis and Rinzel 2003). These studies also suggest that the frequency preference of neurons can be “tuned” by neuromodulator substances that alter the activation and/or kinetic properties of slow K+ conductances.
Functional significance
Parkis et al. (1999) in phrenic motoneurons and Sanchez et al. (2009) in hypoglossal motoneurons have demonstrated that GABAergic inhibition reduces the gain of these cells during inspiration. Our studies indicate that the majority of GFP+ inhibitory interneurons are spontaneously active in the slice and that their firing rate is not modulated by respiration (van Brederode et al. 2011). These firing properties are well suited to generate a form of background tonic inhibition in HMs. The synaptic inputs of GFP+ inhibitory interneurons to HMs are probably located on their dendrites (van Brederode et al. 2011) and are possibly in the form of axodendritic or dendodendritic synapses. Modeling studies have shown that this type of dendritic inhibition reduces the firing rate gain of a neuron for excitatory drive arriving more distally than the inhibitory input, but not for inputs located more proximally (Capaday and van Vreeswijk 2006). Dendritic shunting inhibition reduces neuronal gain by attenuation of current flowing from dendrite to soma. This kind of spatial arrangement divides inhibitory synaptic input into two functional compartments. HMs have large dendritic trees that branch extensively not only within the hypoglossal motor nucleus but also in the lateral reticular formation of the brain stem. Since HMs are involved in a variety of orofacial behaviors in addition to their respiratory function, it might be advantageous to have a motoneuron that is functionally compartmentalized such that the gain for proximal excitatory inputs associated with one type of behavior is unaffected by dendritic inhibition, whereas more distal excitatory input associated with another type of behavior is prevented from reaching the soma by local dendritic shunting inhibition. In this way the level of shunting inhibition, controlled by the mean firing rate of GFP+ inhibitory interneurons, can act as a “gatekeeper” for certain types of inputs to the HM. Tonic inhibitory synaptic input from GFP+ neurons could also decrease the membrane time constant of HMs and our modeling studies indicate that this might increase the amount of subthreshold resonance and the resonance frequency. Enhanced membrane resonance functions to facilitate synchronous oscillations in populations of neurons (Buzsáki and Draguhn 2004). This hypothesis is consistent with the observation that both GABAergic and glycinergic inhibitions are important for synchronous discharge of HMs during inspiration (Bou-Flores and Berger 2001; Sebe et al. 2006). The morphology of GFP+ interneurons is such that their dendrites and axons are arranged perpendicularly to the dendrites of HMs (van Brederode et al. 2011). This anatomical arrangement might serve to synchronize the output of adjacent HMs to the firing of a single inhibitory interneuron. More studies are needed to determine whether the different subclasses of GFP+ interneurons (tonic and phasic) mediate different types of inhibition and whether this is related to differences in their firing resonance properties.
GRANTS
This work was supported by National Heart, Lung, and Blood Institute Grant HL-49657 to A. J. Berger and J. van Brederode.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
ACKNOWLEDGMENTS
We thank J. Numata for expert technical assistance and help with data analysis, running of computer models, and drawing of biocytin-filled cells and L.-S. Burton for drawing biocytin-filled cells and running of computer models.
APPENDIX
To understand the intrinsic membrane properties that determine the response of interneurons to steady-state and time-varying inputs we used the exponential integrate-and-fire (EIF) model developed by Forcaud-Trocme et al. (2003). This model is based on the standard leaky integrate-and-fire model but includes a nonlinear exponential term to more accurately represent the process of spike initiation (Badel et al. 2008). In this study we used the EIF model as modified by Richardson (2009) who added conductance-based gated ionic currents with nonlinear voltage-activation and time constants to the standard EIF model. These additional currents operate on a slower timescale and modify the subthreshold behavior and/or cause spike-frequency adaptation of the model cell. The membrane potential dynamics of this model are governed by
| (A1) |
The leak current is given by IL = gL(EL − V). The spike current is a current that increases exponentially with depolarization (Fourcaud-Trocme et al. 2003) and is given by
With a spike-initiation threshold VT = −53 mV and a spike slope factor ΔT = 2 mV. The value of ΔT controls the sharpness of the spike onset phase. The shape of the spike down swing is described by a linear repolarization from a threshold voltage Vth to a reset voltage Vre after a refractory period τref has elapsed. The deterministic spike trajectory during repolarization Vsp(t) is described by Richardson (2009)
with Vth = 0 mV, Vre = −70 mV, and τref = 2 ms.
The various ionic currents are described by equations of the form: Ix = gxx(t)(Ex − V). The gating variable x(t) depends on a voltage-dependent time constant τx(V) and steady-state activation variable x∞(V) defined by
| (A2) |
| (A3) |
where θx is the voltage at which the current is half-activated and Δx is a parameter that determines the steepness of the steady-state activation curve.
The additional ionic currents included in the modified EIF model are as follows:
The hyperpolarization-activated current Ih.
This current is governed by both fast and slow gating variables (Spain et al. 1987) according to
The fast (h1) and slow (h2) gating variables obey the dynamics given by Eqs. A2 and A3, where τ1 = 100 ms, τ2 = 1,000 ms, and θx = −82 mV. Eh was set to −20 mV and gh = 0.5gL.
The M-current IM.
This voltage-activated potassium current is described by
The gating variable w obeys the dynamics given by Eq. A2 with τw = 100 ms and w∞ is described by Eq. A3, with θw = −20 mV and Δw = 5 mV. EK was set to −100 mV and gM = 80gL.
The low-threshold depolarization-activated potassium current IKLT is described by (Richardson 2009)
with gKLT = 2gL. The gating variable n obeys the dynamics given by
where τn1 = 50 ms, τn2 = 20 ms, Vτ = −50 mV, and Δτ2 = 30 mV2. The gating variable n∞ was described by Eq. A3, with Vn = −50 mV, Δn = 5 mV.
REFERENCES
- Badel L, Lefort S, Berger TK, Petersen CC, Gerstner W, Richardson MJE. Extracting non-linear integrate-and-fire models from experimental data using dynamic I–V curves. Biol Cybern 99: 361–370, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balu R, Larimer P, Strowbridge BW. Phasic stimuli evoke precisely timed spikes in intermittently discharging mitral cells. J Neurophysiol 92: 743–753, 2004 [DOI] [PubMed] [Google Scholar]
- Barnes-Davies M, Barker MC, Osmani F, Forsythe ID. Kv1 currents mediate a gradient of principal neuron excitability across the tonotopic axis in the rat lateral superior olive. Eur J Neurosci 19: 325–333, 2004 [DOI] [PubMed] [Google Scholar]
- Beierholm U, Nielsen CD, Ryge J, Alstrom P, Kiehn O. Characterization of reliability of spike timing in spinal interneurons during oscillating inputs. J Neurophysiol 86: 1858–1868, 2001 [DOI] [PubMed] [Google Scholar]
- Benda J, Herz AVM. A universal model for spike-frequency adaptation. Neural Comput 15: 2523–2564, 2003 [DOI] [PubMed] [Google Scholar]
- Beraneck M, Pfanzelt S, Vassias I, Rohregger M, Vibert N, Vidal PP, Moore LE, Straka H. Differential intrinsic response dynamics determine synaptic signal processing in frog vestibular neurons. J Neurosci 27: 4283–4296, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bou-Flores C, Berger AJ. Gap junctions and inhibitory synapses modulate inspiratory motoneuron synchronization. J Neurophysiol 85: 1543–1551, 2001 [DOI] [PubMed] [Google Scholar]
- Brette R, Guigon E. Reliability of spike timing is a general property of spiking model neurons. Neural Comput 15: 279–308, 2003 [DOI] [PubMed] [Google Scholar]
- Brumberg JC. Firing pattern modulation by oscillatory input in supragranular pyramidal neurons. Neuroscience 114: 239–246, 2002 [DOI] [PubMed] [Google Scholar]
- Brumberg JC, Gutkin BS. Cortical pyramidal cells as non-linear oscillators: experiment and spike-generation theory. Brain Res 1171: 122–137, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science 304: 1926–1929, 2004 [DOI] [PubMed] [Google Scholar]
- Capaday C, van Vreeswijk C. Direct control of firing rate gain by dendritic shunting inhibition. J Integr Neurosci 5: 199–222, 2006 [DOI] [PubMed] [Google Scholar]
- Catacuzzeno L, Fioretti B, Pietrobon D, Franciolini F. The differential expression of low-threshold K+ currents generates distinct firing patterns in different subtypes of adult mouse trigeminal ganglion neurones. J Physiol 586: 5101–5118, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- D'Angelo E, Nieus T, Maffei A, Armano S, Rossi P, Taglietti V, Fontana A, Naldi G. Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow K+-dependent mechanism. J Neurosci 21: 759–770, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel TA, Schimansky-Geier L, Herz AVM, Schreiber S, Erchova I. Subthreshold membrane-potential resonances shape spike-train patterns in the entorhinal cortex. J Neurophysiol 100: 1576–1589, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erchova I, Kreck G, Heinemann U, Herz AVM. Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol 560: 89–110, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellous JM, Houweling AR, Modi RH, Rao RPN, Tiesinga PHE, Sejnowski TJ. Frequency dependence of spike timing reliability in cortical pyramidal cells and interneurons. J Neurophysiol 85: 1782–1787, 2001 [DOI] [PubMed] [Google Scholar]
- Forti L, Cesana E, Mapelli J, D'Angelo E. Ionic mechanisms of autorhythmic firing in rat cerebellar Golgi cells. J Physiol 574: 711–729, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fourcaud-Trocme N, Hansel D, van Vreeswijk C, Brunel N. How spike generation mechanisms determine the neuronal response to fluctuating inputs. J Neurosci 23: 11628–11640, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funk GD, Smith JC, Feldman JL. Generation and transmission of respiratory oscillations in medullary slices: role of excitatory amino acids. J Neurophysiol 70: 1497–1515, 1993 [DOI] [PubMed] [Google Scholar]
- Gimbarzevsky B, Miura RM, Puil E. Impedance profiles of peripheral and central neurons. Can J Physiol Pharmacol 62: 460–462, 1984 [DOI] [PubMed] [Google Scholar]
- Gutfreund Y, Yarom Y, Segev I. Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: physiology and modelling. J Physiol 483: 621–640, 1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutkin B, Ermentrout GB, Rudolph M. Spike generating dynamics and the conditions for spike-time precision in cortical neurons. J Comput Neurosci 15: 91–103, 2003 [DOI] [PubMed] [Google Scholar]
- Haas JS, White JA. Frequency selectivity of layer II stellate cells in the medial entorhinal cortex. J Neurophysiol 88: 2422–2429, 2002 [DOI] [PubMed] [Google Scholar]
- Holt GR, Softky WR, Koch C, Douglas RJ. Comparison of discharge variability in vitro and in vivo in cat visual cortex neurons. J Neurophysiol 75: 1806–1814, 1996 [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol 545: 783–805, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter JD, Milton JG, Thomas PJ, Cowan JD. Resonance effect for neural spike time reliability. J Neurophysiol 80: 1427–1438, 1998 [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Puil E. Models of subthreshold membrane resonance in neocortical neurons. J Neurophysiol 76: 698–714, 1996a [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Puil E. Subthreshold membrane resonance in neocortical neurons. J Neurophysiol 76: 683–697, 1996b [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci 23: 216–222, 2000 [DOI] [PubMed] [Google Scholar]
- Leung LS, Yu HW. Theta-frequency resonance in hippocampal CA1 neurons in vitro demonstrated by sinusoidal current injection. J Neurophysiol 79: 1592–1596, 1998 [DOI] [PubMed] [Google Scholar]
- Madison DV, Nicoll RA. Control of the repetitive discharge of rat CA1 pyramidal neurones in vitro. J Physiol 354: 319–331, 1984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science 268: 1503–1506, 1995 [DOI] [PubMed] [Google Scholar]
- Manuel M, Iglesias C, Donnet M, Leroy F, Heckman CJ, Zytnicki D. Fast kinetics, high-frequency oscillations, and subprimary firing range in adult mouse spinal motoneurons. J Neurosci 29: 11246–11256, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen QT, Wessel R, Kleinfeld D. Developmental regulation of active and passive membrane properties in rat vibrissa motoneurones. J Physiol 556: 203–219, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak LG, Sanchez-Vives MV, McCormick DA. Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb Cortex 7: 487–501, 1997 [DOI] [PubMed] [Google Scholar]
- Ono T, Ishiwata Y, Kuroda T, Nakamura Y. Swallowing-related perihypoglossal neurons projecting to hypoglossal motoneurons in the cat. J Dent Res 77: 351–360, 1998 [DOI] [PubMed] [Google Scholar]
- Parkis MA, Dong XW, Feldman JL, Funk GD. Concurrent inhibition and excitation of phrenic motoneurons during inspiration: phase-specific control of excitability. J Neurosci 19: 2368–2380, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pike FG, Goddard RS, Suckling JM, Ganter P, Kasthuri N, Paulsen O. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J Physiol 529: 205–213, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y. Four cell types with distinctive membrane properties and morphologies in lamina I of the spinal dorsal horn of the adult rat. J Physiol 539: 817–836, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, Sejnowski TJ. Spike-rate coding and spike-time coding are affected oppositely by different adaptation mechanisms. J Neurosci 28: 13649–13661, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puil E, Gimbarzevsky B, Miura RM. Quantification of membrane properties of trigeminal root ganglion neurons in guinea pigs. J Neurophysiol 55: 995–1016, 1986 [DOI] [PubMed] [Google Scholar]
- Richardson MJE. Dynamics of populations and networks of neurons with voltage-activated and calcium-activated currents. Phys Rev E 80: 021928, 2009 [DOI] [PubMed] [Google Scholar]
- Richardson MJE, Brunel N, Hakim V. From subthreshold to firing-rate resonance. J Neurophysiol 89: 2538–2554, 2003 [DOI] [PubMed] [Google Scholar]
- Sanchez A, Mustapic S, Zuperku EJ, Stucke AG, Hopp FA, Stuth EAE. Role of inhibitory neurotransmission in the control of canine hypoglossal motoneuron activity in vivo. J Neurophysiol 101: 1211–1221, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber S, Erchova I, Heinemann U, Herz AVM. Subthreshold resonance explains the frequency-dependent integration of periodic as well as random stimuli in the entorhinal cortex. J Neurophysiol 92: 408–415, 2004a [DOI] [PubMed] [Google Scholar]
- Schreiber S, Fellous JM, Tiesinga P, Sejnowski TJ. Influence of ionic conductances on spike timing reliability of cortical neurons for suprathreshold rhythmic inputs. J Neurophysiol 91: 194–205, 2004b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber S, Samengo I, Herz AV. Two distinct mechanisms shape the reliability of neural responses. J Neurophysiol 101: 2239–2251, 2009 [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Foehring RC, Stafstrom CE, Chubb MC, Crill WE. Multiple potassium conductances and their functions in neurons from cat sensorimotor cortex in vitro. J Neurophysiol 59: 424–449, 1988 [DOI] [PubMed] [Google Scholar]
- Sebe JY, Berger AJ. Inspiratory-phase short timescale synchrony in the brainstem slice is generated downstream of the pre-Bötzinger complex. Neuroscience 153: 1390–1401, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebe JY, van Brederode JFM, Berger AJ. Inhibitory synaptic transmission governs inspiratory motoneuron synchronization. J Neurophysiol 96: 391–403, 2006 [DOI] [PubMed] [Google Scholar]
- Spain WJ, Schwindt PC, Crill WE. Anomalous rectification in neurons from cat sensorimotor cortex in vitro. J Neurophysiol 57: 1555–1576, 1987 [DOI] [PubMed] [Google Scholar]
- Svirskis G, Rinzel J. Influence of subthreshold nonlinearities on signal-to-noise ratio and timing precision for small signals in neurons: minimal model analysis. Network 14: 137–150, 2003 [PMC free article] [PubMed] [Google Scholar]
- Tamamaki N, Yanagawa Y, Tomioka R, Miyazaki J, Obata K, Kaneko T. Green fluorescent protein expression and colocalization with calretinin, parvalbumin, and somatostatin in the GAD67-GFP knock-in mouse. J Comp Neurol 467: 60–79, 2003 [DOI] [PubMed] [Google Scholar]
- Tiesinga P, Fellous JM, Sejnowski TJ. Regulation of spike timing in visual cortical circuits. Nat Rev Neurosci 9: 97–109, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiesinga P, Sejnowski TJ. Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron 63: 727–732, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Brederode JFM, Berger AJ. Spike-firing resonance in hypoglossal motoneurons. J Neurophysiol 99: 2916–2928, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Brederode JFM, Yanagawa Y, Berger AJ. GAD-67-GFP+ neurons in the Nucleus of Roller: a possible source of inhibitory input to hypoglossal motoneurons. I. Morphology and firing properties. J Neurophysiol 105: 235–248, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ. Pacemaker neurons for the theta rhythm and their synchronization in the septohippocampal reciprocal loop. J Neurophysiol 87: 889–900, 2002 [DOI] [PubMed] [Google Scholar]