Evidence That Prestin Has at Least Two Voltage-dependent Steps

Abstract

Prestin is a voltage-dependent membrane-spanning motor protein that confers electromotility on mammalian cochlear outer hair cells, which is essential for normal hearing of mammals. Voltage-induced charge movement in the prestin molecule is converted into mechanical work; however, little is known about the molecular mechanism of this process. For understanding the electromechanical coupling mechanism of prestin, we simultaneously measured voltage-dependent charge movement and electromotility under conditions in which the magnitudes of both charge movement and electromotility are gradually manipulated by the prestin inhibitor, salicylate. We show that the observed relationships of the charge movement and the physical displacement (q-d relations) are well represented by a three-state Boltzmann model but not by a two-state model or its previously proposed variant. Here, we suggest a molecular mechanism of prestin with at least two voltage-dependent conformational transition steps having distinct electromechanical coupling efficiencies.

Introduction

Electromotility (1) of mammalian cochlear outer hair cells (OHCs)² is a rapid voltage-induced force-generating cell length change that is indispensable for the frequency selectivity and sensitivity of mammalian hearing (2). The membrane-based motor protein, prestin, which is a member of the solute carrier 26 anion transporter family (3), is known to be responsible for generating electromotility (4). Accompanying OHC electromotility, charge movement in the lateral membrane of the cell is observed. This charge movement is manifested in the bell-shaped voltage-dependent cell membrane capacitance, which is often referred to as nonlinear capacitance (NLC) (5, 6)).

The question of how prestin functions as a membrane-based molecular motor has received a great deal of attention; however, even some fundamental issues are still obscure. To understand the mode of operation of the molecule, the relationship between charge movement, which initiates conformational change, and motor function needs to be quantified. However, only minimal attempts have been made to this effect (6, 7). Under normal operating circumstances NLC data are usually well explained by the simple two-state Boltzmann model with an apparent valency of charge of less than unity. Interesting theoretical work suggested that three- or higher-state models might provide superior description of the process (8, 9). In some work three-state fits were dictated by the data (10). To explain some properties of NLC at extreme membrane voltages, a modified two-state model has also been proposed (11). However, those models have not been subjected to rigorous examination as to their generality under various experimental conditions. It is one purpose of the present work to provide such an examination. We find that a Boltzmann model with at least two voltage-dependent steps is required for explaining prestin function.

Since the discovery of prestin, assessments of effects of mutations and drugs on its function have become readily feasible using heterologous expression systems in which NLC measurement is easily performed, while motility measurements are difficult or impossible. NLC measurement has generally been accepted as a proper and sufficient substitute for directly measuring electromotility since its discovery and initial description (5, 6). This substitution has been made for the past 20 years even though sufficient quantitative proof for its validity has not been provided. Only very recently was it quantitatively and statistically demonstrated that the prestin-dependent charge movement and the resulting electromotility are indeed fully coupled under normal operating conditions (12). Because the observed charge movement should intimately relate to conformational change of the prestin molecule for generating motility, further detailed quantitative knowledge of the relation between charge movement and physical displacement is essential for better understanding the molecular mechanism of prestin. However, this fundamental knowledge is still largely missing.

In this study we used isolated murine OHCs for examining the electromechanical coupling of prestin. Isolated OHCs are the appropriate system for studying the relation between the charge movement and the motor activity of prestin for various reasons. First, because of the OHC quite regular cylindrical diameter, with restricted expression of prestin motor only in the lateral membrane, the overall motor activity of prestin molecules is effectively translated into longitudinal length-change of the cell. This permits the quantification of the relation between charge movement and mechanical displacement. Furthermore, because OHCs are the natural hosts of prestin, being the only mammalian cell that expresses the functional protein, any conclusion derived from the current study has potential physiological significance.

EXPERIMENTAL PROCEDURES

Adult mice were euthanized with euthasol, and OHCs were isolated in the same way as described before (13). Whole-cell recordings were performed at room temperature with holding potentials at 0 mV using the Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA). Recording pipettes were pulled from borosilicate glass to achieve initial bath resistances averaging 3–4 megaohms and were filled with an intracellular solution containing 140 mm CsCl, 2 mm MgCl₂, 10 mm EGTA, and 10 mm HEPES (pH 7.3). Cells were bathed during whole-cell recordings in an extracellular solution containing 120 mm NaCl, 20 mm triethylammonium chloride, 2 mm CoCl₂, 2 mm MgCl₂, 10 mm HEPES (pH 7.3). Osmolarity was adjusted to 310 mosmol liter⁻¹ with glucose. Sinusoidal voltage stimulus (1-Hz, 120-mV amplitude or 2 Hz, 100-mV amplitude) superimposed with two higher frequency stimuli (390.6 and 781.2 Hz, 5- or 10-mV amplitude) was used for measuring NLC and for simultaneously measuring NLC and OHC motility. The intracellular pressure was kept at 0-mm Hg. Current data were collected by jClamp (SciSoft C., New Haven, CT) for the fast Fourier transform-based admittance analysis for determining NLC (14). The NLC data were analyzed by Equations 3, 4, and 5 shown under “Results.”

OHC electromotility was captured by WV-CD22 digital camera (Panasonic), and the sequential images were analyzed using ImageJ. For measuring the OHC displacement, we analyzed the image density in an observation pixel window (5 × 5 pixels, 8-bit) positioned at the apical region of OHCs (supplemental Fig. S1). The motility data were analyzed by Equations 6 and 7 shown under “Results.” PRISM (GraphPad software) and Igor (WaveMetrics, Inc.) were used for the curve fitting analysis of both motility and NLC.

To test the identity of the describing parameters (α and V_pk) derived from NLC and motility measurements, the Deming linear regression analysis was employed (15). The average S.E. of curve-fitting derived from the NLC measurement and the motility measurement were used to determine the ratio of uncertainties associated with the two methods. The error ratio is required for calculating the sum of squared distances to be minimized in the Deming regression analysis (15). PRISM (GraphPad software) was used for the Deming regression analysis. The null hypothesis of identity was tested by the independent t tests, t = |a − 0|/S.E._a and t = |b − 1|/S.E._b, where a and b are the y intercept, and the slope (y = a + bx) is estimated by the Deming linear regression analysis. S.E._a and S.E._b are the S.E. of a and b, respectively. The p values were calculated from Student's t distribution (two-tailed) by using the t values defined above. Values smaller than 0.05 indicated rejection of the null hypothesis of identity. Akaike's information criterion was used for comparing the Boltzmann models (16).

RESULTS

Two-state and Three-state Boltzmann Models for Describing the Prestin Electromechanical Coupling Process

The voltage-dependent charge displacement of prestin is adequately explained by the simple two-state Boltzmann model in most cases (5, 6); however, deviation of NLC data from this model sometimes becomes evident, especially at very large positive or negative membrane potentials (±200 mV) (11). The deviation may indicate that there is more than one voltage-dependent processes associated with prestin. Thus, understanding the deviation would be a key for unraveling the relevant molecular process. In this study we describe the voltage-dependent charge movement and the resulting electromotility of prestin by using the following two-state and three-state Boltzmann models. The models are based on the following scheme with distinct conformational states (C_i).

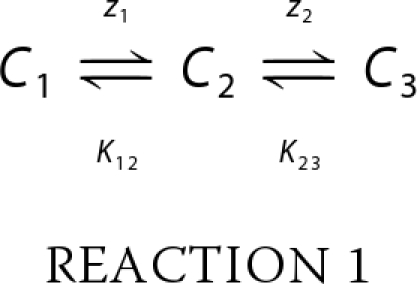z_i is the apparent valence of charge movement at each step, and K₁₂ and K₂₃ are equilibrium constants that are expressed as exp{α₁(V_m − V_pk1)} and exp{α₂(V_m − V_pk2)}, respectively. α_i (=z_ie/k_BT) is the slope factor of the voltage dependence of charge transfer, where e is electron charge, k_B is the Boltzmann constant, and T is absolute temperature. V_m is the membrane potential. V_pki is the voltage at which the maximum charge movement or motility response per voltage for each step is attained. If the C₃ state does not exist, then the scheme becomes a two-state Boltzmann model. Charge movement (q) is described as follows for the two-state (Equation 1) and three-state (Equation 2) models.

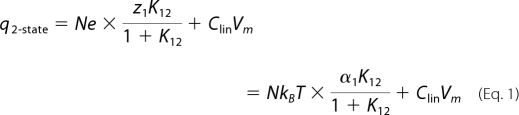N is the total number of functional prestin molecules. C_lin designates the linear, voltage-invariant capacitance of a cell. The maximum charge movement, Q_max, is calculated as Q_max = α₁Nk_BT for the two-state Boltzmann model, and Q_max = (α₁+α₂)Nk_BT is calculated for the three-state Boltzmann model. Differentiation of Equation 1 and Equation 2 in terms of V_m yields membrane capacitance (C_m),

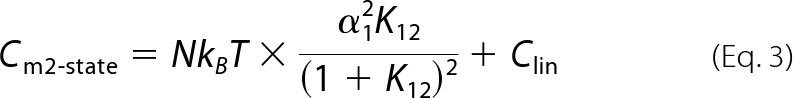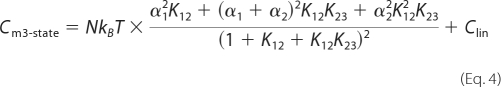The following modified two-state Boltzmann model was proposed previously to correct the deviation of NLC data observed at very large positive or negative membrane potentials (11), which is referred to as two-state-C_sa model in this study.

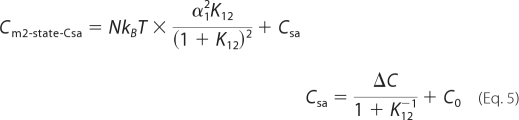where C₀ represents linear capacitance of a cell, and ΔC represents the combination of prestin-dependent changes in the membrane area and in either the dielectric constant or thickness of the cell membrane. The voltage-induced prestin-dependent charge movement is presumed to trigger physical change in the molecules with resultant length change of OHCs. If prestin had multiple voltage-dependent steps, the electromechanical coupling efficiencies at each step could be different from one another. We defined electromechanical coupling efficiency as m_i = d_i/z_ie, where d_i is a unitary displacement along the axial direction of an OHC induced at each voltage-dependent step. Thus, overall OHC displacement is described as follows for the two-state (Equation 6) and for the three-state (Equation 7) Boltzmann models.

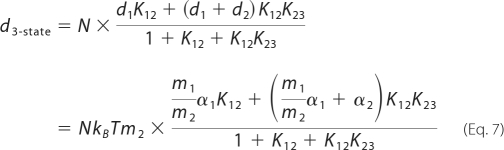Using the Prestin Inhibitor, Salicylate, to Unravel the Steps in Prestin Operation

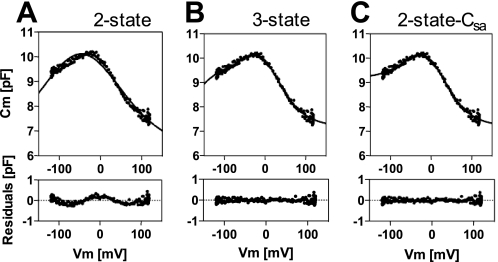
Salicylate is an inhibitor of OHC electromotility (7, 17, 18), which is thought to compete with anions such as chloride for the anion-binding site on prestin (19). Fig. 1 shows typical NLC recorded in the presence of salicylate. The NLC response is smaller than normal, and the voltage dependence is altered. Deviation of the NLC data from the simple two-state Boltzmann model (Equation 3) is obvious by examining the residues of the curve fitting process (Fig. 1A). Consequently, it is conceivable that there are more than two conformational states in prestin, which may not be distinguishable in a normal recording condition, e.g. in the absence of salicylate, or if extreme membrane potentials are not used. Therefore, salicylate could be a useful tool for dissecting the molecular mechanism of prestin. We tested the three-state Boltzmann model (Equation 4, Fig. 1B) together with the two-state-C_sa model that was used previously for analyzing salicylate-dependent NLC data (Equation 5, Fig. 1C, Ref. 11). Compared with the simple two-state Boltzmann model, both the three-state and the two-state-C_sa models drastically improved the fittings, which is obvious in examining the residual plots. For quantitatively evaluating the goodness-of-fit, we ran the Akaike's information criterion method, which is based on information theory for comparing one model to any other model (16). Use of the F-test is inappropriate because the two-state models are not nested in the three-state model. For the two-state models to be nested in the three-state model, one has to be able to choose the coefficient, α₂, such that K₂₃ is approximately 0 for all values of V_m. A calculated Akaike's weight, which provides the likelihood of one model to be superior to an alternative model, were >10¹³ times higher for the three-state and the two-state-C_sa fittings than that for the simple two-state fitting, strongly suggesting that the improvement of the fits was not due to the increased number of free fitting parameters. Akaike's weights were 0.19 ± 0.08 and 0.81 ± 0.08 (average ± S.D., n = 8) for the 3-state and 2-state C_sa models, respectively, suggesting that the 2-state C_sa model fits the data about 4 times better than the 3-state model. This seems reasonable because the two-state-C_sa model, with fewer free parameters, fits the data as well as the three-state model with more fitting parameters (five versus six). Because the three-state and the two-state-C_sa models fit the salicylate-dependent NLC data similarly, both models were used in the present study for comparison, whereas below we also evaluate the likelihood of their correctness.

FIGURE 1.

Deviation of NLC from the simple two-state Boltzmann model. NLC was measured in the presence of 0.5 mm salicylate. The NLC data were analyzed by the simple two-state Boltzmann model (Equation 3, A), the three-state model (Equation 4, B), and the two-state-C_sa model (Equation 5, C). Solid lines show the fitting curves. Improvements of the fits are visually obvious in the residual plots by the three-state fitting (B) and the two-state-C_sa fitting (C) compared with that by the simple two-state fitting (A). Indeed, >10¹³ times higher Akaike's weights were obtained for the three-state and the two-state-C_sa fittings over the simple two-state fitting. Akaike's weights for the three-state and two-state-C_sa were 0.19 ± 0.08 and 0.81 ± 0.08% (n = 8), respectively.

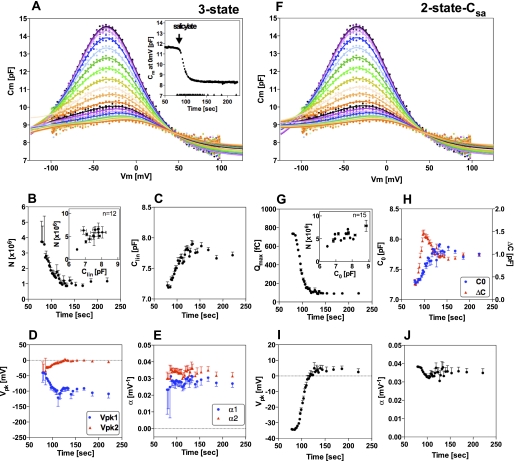
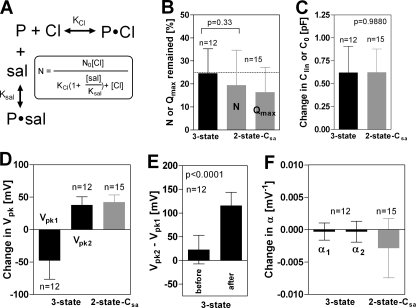
For examining the salicylate-dependent NLC in detail, we performed repeated NLC measurements on individual OHCs during the application of 1.5 mm salicylate in the extracellular solution. The time-dependent NLC data were then analyzed by the three-state and the two-state-C_sa models (n = 15). Fig. 2 shows a typical example of such recordings analyzed by either the three-state (Fig. 2, A–E) or the two-state-C_sa models (Fig. 2, F–J). At the beginning of the time course, before applying salicylate, the total number of functional prestin molecules was estimated to be ∼5 million by both models (insets of Fig. 2, B and G). As expected, application of salicylate reduced the prestin-dependent charge movement of isolated OHCs, and the inhibition was reversible (data not shown) as reported previously (7, 17, 18), suggesting that the reduction of the prestin-dependent charge movement was not a consequence of some damage caused by the repetitive voltage stimulation. We also performed separate experiments for confirming that neither NLC nor electromotility is affected by repetitive voltage stimulations (supplemental Fig. S2). Salicylate is known to block prestin function by competing for the anion binding site (Fig. 3A) (19). If we adopted the binding affinities of chloride and salicylate to prestin from the previous study (6.3 mm and 21 μm, respectively) (19), almost all prestin molecules in OHCs, ∼96% (computation, 140/(6.3 + 140) = 0.957), are estimated to be fully functional with 140 mm chloride at the beginning of each time course before the application of 1.5 mm salicylate. Application of 1.5 mm salicylate is expected to inhibit overall prestin activity ∼77% (computation, 1–140/(6.3(1 + 1.5/0.021) + 140) = 0.765). Thus, roughly 23 ∼ 25% (if prestin activity at 140 mm (∼96% of chloride-bound prestin) were defined as 100%) prestin activity (N or Q_max) would be expected to remain after the application of 1.5 mm salicylate. The fractions of active prestin remained after the application of 1.5 mm salicylate were very similar when computed with the three-state and the two-state-C_sa models and were reasonably close to the expected value of 25% (broken line in Fig. 3B).

FIGURE 2.

Salicylate-dependent change of NLC parameters determined by the three-state model (A∼E) and the two-state-C_sa model (F∼J). A and F, NLC was repetitively measured on an isolated OHC before and after applying 1.5 mm salicylate in the bath solution. Different colors represent different NLC recordings at different time points shown in the inset of A. The solid lines are fitting curves by the three-state model (Equation 4, A) or the two-state-C_sa model (Equation 5, F). A and F are the same NLC data set but with different data analyses. The six NLC parameters, N, C_lin, V_pk1/V_pk2, and α₁/α₂, for the three-state model (B∼E) and the five NLC parameters, Q_max, ΔC/C₀, V_pk, and α, for the two-state-C_sa model (G∼J) were determined for each NLC curve and were plotted against the recording time. The bars indicate the S.E. of fitting. The insets of B and G show the numbers of functional prestin molecules before application of salicylate, which are plotted against C_lin or C₀. Variation of the NLC parameters obtained from the three-state model before application of salicylate was large in some recordings. For this reason, 3 of 15 data sets were not included in the analysis for the three-state model (therefore, n = 12 for the three-state model analyses).

FIGURE 3.

Summary of the salicylate-dependent NLC measurements. The salicylate-dependent NLC recording exemplified in Fig. 2 was performed on 15 OHCs. The NLC parameters determined by the three-state and the two-state-C_sa models are summarized. All bars indicate the S.D. A, shown is a reaction scheme of chloride/salicylate binding to prestin according to the competitive inhibition model. P stands for prestin. Sal, salicylate. The fraction of functional prestin that remains after application of salicylate is calculated by the displayed equation. B, inhibition of prestin-dependent charge movement by 1.5 mm salicylate is shown. The broken line indicates the prestin activity that is expected to remain (25%, see “Results”). C, shown is a summary of the basal linear capacitance increment induced by salicylate. pF, picofarads. D and E, a summary of salicylate-induced V_pk shift is shown. F, a summary of salicylate-induced change in α is shown.

Increment in the basal linear capacitance was evident in all recordings, and both models found very similar values (C_lin for the three-state model and C₀ for the two-state-C_sa model; Figs. 2, C and H, and 3C and supplemental Fig. S3). This increment is prestin-dependent because the linear capacitance change was not observed in prestin-knock-out OHCs (supplemental Fig. S2). Similarly, no change in the linear capacitance of Deiters' cells was found (data not shown), which confirms previous studies (7, 11). The increment in basal linear capacitance may indicate fixation of prestin in a thinner/expanded conformational state (higher capacitance) by salicylate. Curiously, a non-monotonic change in ΔC with time (increasing salicylate concentration) was commonly derived when data fits were made with the two-state-C_sa model (Fig. 2H). If ΔC represented the combination of prestin-dependent changes in membrane surface area and in either the membrane dielectric constant or thickness as suggested in the previous study (11), gradual monotonic reduction in ΔC should be expected upon monotonic inhibition by salicylate (Fig. 2G). To exclude the possibility that the non-monotonic change in ΔC was falsely observed in our continuous NLC recordings during the gradual inhibition by salicylate, we measured NLC in the presence of various concentrations of salicylate under steady-state conditions with the same concentration of salicylate inside and outside OHCs (supplemental Fig. S3). The salicylate-dependent non-monotonic change of ΔC was also evident in the steady-state recording condition, when the data were fit with the two-state-C_sa model, suggesting that peculiar pattern is the consequence of the curve-fitting model.

The three-state model found separation of V_pk values (hyperpolarizing shift for V_pk1 and depolarizing shift for V_pk2), whereas the two-state-C_sa model found a depolarizing V_pk shift (Figs. 2, D and I, and 3D). The difference between V_pk1 and V_pk2 (defined as ΔV_pk = (V_pk2 − V_pk1) was small before applying salicylate but became significantly larger with salicylate application (Fig. 3E). This was observed in all recordings. The small difference in V_pk1 and V_pk2 values before applying salicylate would explain why the simple two-state model fits NLC data reasonably well in the absence of salicylate. The three-state fitting typically produced larger S.E., suggesting that multiple α/V_pk parameters are not essential for explaining the NLC data in the absence of salicylate (supplemental Fig. S4). The depolarizing V_pk shift observed for the two-state C_sa fitting seems to be consistent with the previous observation with the simple two-state model (17).

Τhe α₁ and α₂ values estimated by the three-state model were similar and were virtually constant throughout the time course, but there was a tendency of a slight transient decrement and recovery (Fig. 2E). On average, the α₁ and α₂ values were slightly smaller than the original values although the decrement is not significant (Fig. 3F). A similar tendency was much more obvious for the α values estimated by the two-state C_sa model (Figs. 2J and 3F). These transient changes of α values can be understood by the salicylate-induced V_pk shifts. An observed V_pk value is the average of V_pk values of many prestin molecules. During the inhibition by salicylate, V_pk values of some prestin molecules shift, whereas those of other prestin molecules do not. This would cause a transiently wider distribution of V_pk; thus, α would become smaller over the same time course.

The Electromechanical Coupling of Prestin

Quite recently, Wang et al. (12) measured NLC and electromotility simultaneously in OHCs and concluded that NLC and electromotility are fully coupled. This was based on their observation that the average α and V_pk values determined by the simple two-state Boltzmann model could not be discriminated statistically as obtained from the two different measurements (12). This is the most complete demonstration of full coupling between NLC and motility thus far available in the literature. However, some issues are unresolved. It is appreciated that NLC parameters differ from cell to cell, reflecting their different physiological conditions. Variability is especially large in V_pk among cells. Therefore, a more proper and rigorous way of testing the NLC motility coupling should be to compare individual α and V_pk values derived from the two different measurements obtained from the same cell instead of averaging data from multiple cells, as was done by Wang et al. (12).

We measured NLC and electromotility simultaneously to examine the relation between charge movement and the conformational change of prestin. In the present study we used a digital video camera (30 frames per second) for capturing low frequency OHC electromotility. The images were analyzed by the subpixel method (20–22) with 45 nm accuracy (supplemental Fig. S1). Inasmuch as no salicylate was used in these experiments, the two-state Boltzmann model was used to separately analyze both the NLC data (Equation 3, Fig. 4A) and the motility data (Equation 6, Fig. 4B). The fitting parameters (α and V_pk) that describe the voltage-dependent charge movement of prestin and the resultant motility, derived from the two different fits, were plotted against each other for comparison (Fig. 4, C and D). For both α and V_pk, most data points were found on or in the close vicinity of the line of identity defined as y = x (slope = 1 and intercept = 0, the diagonal broken lines). To quantitatively evaluate the identity, the Deming linear regression analysis (15) was performed (solid lines). Because α and V_pk derived from the two methods (the NLC measurement and the motility measurement) are independent and experimentally determined with uncertainties, the ordinary linear regression analysis should not be used for this purpose. Using the Deming's fitting parameters with the S.E. of the fittings, the null hypothesis of identity (y = x) was tested by t tests as described under “Experimental Procedures.” The p values calculated for the slopes and the y intercepts were 0.62 and 0.83 for the α-value comparison (Fig. 4C) and 0.40 and 0.32 for the V_pk-value comparison (Fig. 4D), respectively, which were significantly larger than the criterion value of p = 0.05. Thus, the null hypothesis of identity should not be rejected, suggesting that charge movement and motility of mammalian prestin are fully coupled in terms of α and V_pk under the two-state Boltzmann assumption.

FIGURE 4.

Simultaneous measurement of NLC and motility. NLC (A) and OHC displacement (B) were measured simultaneously as described under “Experimental Procedures” and in supplemental Fig. S1. The data were analyzed using the two-state Boltzmann model-based equations (Equations 3 and 6) shown under “Results.” The solid lines are the fitting curves derived from the equations. The simultaneous NLC and motility measurements were performed on 36 different OHCs, and α values (C) and V_pk values (D) were compared against each other for testing their identity. The error bars represent the S.E. of the curve-fitting analyses. The diagonal broken lines indicate exact match (y = x). Deming linear regression analyses (solid lines) followed by t tests were performed for quantitatively testing identity (see “Experimental Procedures”). The p values for the y intercept and the slope were 0.83 and 0.62 (C) and 0.33 and 0.39 (D), none of which disagreed with the null hypothesis of identity, i.e. a = 0, b = 1. E, Q_max and D_max were estimated from the curve fitting analyses shown in A and B. D_max values are plotted against the corresponding Q_max (n = 36). The error bars represent S.E. of the curve-fitting analyses. Alternatively, the observed maximum OHC displacement (d) is plotted against the observed prestin-dependent charge movement (q) that is determined by the area between NLC curves and the C_lin (E, inset). The Deming linear regression analysis was performed with the y intercept fixed at zero (y = ax). r² values for Q_max-D_max and q-d were 0.036 and 0.41, respectively. The NLC motility data (n = 36) were also analyzed by the three-state model, and the α₁ and α₂ values (F) and the V_pk1 and V_pk2 values (G) were compared against each other. Because the three-state fitting on NLC/motility data recorded in the absence of salicylate usually finds larger S.E., only data sets whose S.E. found in V_pk1/V_pk2 were less than 100 mV are shown, with bold symbols error bars, whereas others are shown with smaller pale symbols without error bars. The p values determined by Deming linear regression analyses (solid lines) followed by t tests for the y intercept (=0) and the slope (=1) were less than 0.05 for α₁, α₂, V_pk1, and V_pk2 comparisons, suggesting that α₁, α₂, V_pk1, and V_pk2 values are different between NLC and motility. H, shown are computer simulations of m₁/m₂-dependent OHC displacements using Equation 7. The parameters used were 0.0252 mV⁻¹, 0.0239 mV⁻¹, −85.7 mV, and −52.6 mV for α₁, α₂, V_pk1, and V_pk2, all of which were derived from the NLC measurements (F and G). The generated displacement data were analyzed by Equation 7 in which m₁/m₂ was fix at unity, and the resultant fitting parameters were plotted against m₁/m₂ for α₁ and α₂ (I) and V_pk1 and V_pk2 (J). The broken lines indicate the α and V_pk values used for generating the displacement data. K and L, NLC and OHC displacement were measured simultaneously as in A and B in the presence of 0.1∼1 mm salicylate. The NLC motility data (n = 15) were analyzed by the three-state model, and the α₁ and α₂ values (K) and the V_pk1 and V_pk2 values (L) were compared against each other. The p values determined by Deming linear regression analyses (solid lines) followed by t tests for the y intercept (=0) and the slope (=1) were all greater than 0.05 for α₁, α₂, V_pk1, and V_pk2 comparisons, suggesting that the NLC and motility are coupled in terms of α₁–α₂ and V_pk1–V_pk2.

The two-state Boltzmann model-based curve-fitting also gives estimates of maximum charge movement (Q_max) and maximum cell displacement (D_max). We plotted D_max against Q_max for determining the relation between charge movement and OHC length change (Fig. 4E). The data were also analyzed by the Deming linear regression. Because voltage-dependent cell displacement in prestin-ko OHCs is negligible (23), we fixed the y intercept of the regression line at zero. One might expect greater D_max for larger Q_max; however, a positive correlation was not obvious (r² = 0.036). It is possible that Q_max and D_max were over/under-estimated in the analysis because the accuracies of estimating Q_max and D_max highly depend on the accuracies of α and C_lin. Therefore, instead of estimating Q_max, we determined the charge movement that was actually observed with the ±120-mV stimulus. This charge displacement was determined from the area between the NLC curve and C_lin, and we defined this as q. Very similar q values were obtained by the two-state-C_sa model (data not shown). We then compared q to OHC displacement, d, that was actually observed with the ±120-mV stimulus (Fig. 4E, inset). Although the estimation of q still depends on C_lin, as determined by the two-state model, a positive correlation between charge movement (q) and motility (d) became clearer (r² = 0.41), the relation of which is likely to be linear. In other words, when actually measured charge movement (q) and motility (d) are compared, the relation between them is linear. When derived quantities (Q_max and D_max) are related, the linearity (if exists) is obscured, probably by propagated errors in the estimation of other parameters.

We also analyzed the NLC motility data using the three-state models, Equation 4 for NLC and Equation 7 for motility (Fig. 4, F and G). Because the three-state motility model with an additional free-fitting parameter, m₁/m₂, made fitting analysis very sensitive to initial values and usually found very large S.E. in the NLC parameters, the electromechanical coupling efficiencies at two steps were assumed to be the same (m₁/m₂ = 1) for the motility analyses. Deviations of the data points from the line of identity shown with the broken lines are obvious, especially for α₁ and V_pk2. Indeed, Deming linear regression followed by t tests found p < 0.05 for the null hypothesis of identity (slope = 1, y intercept = 0) for all α/V_pk parameters, suggesting either that NLC and motility are not fully coupled or that the electromechanical coupling efficiencies at two steps are not the same. To test the latter possibility, we computer-simulated the m₁/m₂-dependent motility response of prestin using Equation 7 with experimentally determined average α₁/α₂ and V_pk1/V_pk2 values derived from the NLC measurements (Fig. 4H). We analyzed the generated data using Equation 7 with m₁/m₂ fixed at unity and obtained α and V_pk values, which were then plotted against m₁/m₂ (Fig. 4, I and J). The results show that α₁/α₂ and V_pk1/V_pk2 values are exactly the same for NLC (shown with the horizontal broken lines) and motility at m₁/m₂ = 1 and that apparently larger values are computed for motility at m₁/m₂ < 1 with greater increments for α₁ and V_pk2 compared with those for α₂ and V_pk1, respectively. These deviations are caused by the discrepancy between the apparent α₁ (=α₁m₁/m₂) in the numerator of Equation 7 and the α₁ in the equilibrium constant, K₁₂, which is independent of m₁/m₂. The qualitative trends of the deviations from the line of identity shown in Fig. 4, F and G can be understood if, in fact, m₁/m₂ < 1. The ratio m₁/m₂ is roughly estimated to be in the range of 0∼0.6 by interpolation, using the average α/V_pk values derived from the motility measurement in Fig. 4, F and G.

To determine m₁/m₂, we measured NLC and motility simultaneously under fixed concentration of salicylate (0.1∼1 mm) to widely separate V_pk1/V_pk2 for a more accurate curve-fitting analysis with the three-state model. The motility response was analyzed by Equation 7 with a free parameter for m₁/m₂, and the resultant α/V_pk values were compared with those derived from the NLC measurement (Fig. 4, K and L). Deming linear regressions followed by t tests found p > 0.05 for the null hypothesis of identity (slope = 1, y intercept = 0) for all α/V_pk parameters, suggesting that the charge movement and the motility response are fully coupled at each voltage-dependent step of prestin. The ratio of the coupling efficiencies, m₁/m₂, was determined to be 0.54 ± 0.22 (average ± S.D., n = 15). Because the S.E. of fitting of the α/V_pk values derived from the motility measurements were usually very large due to the introduction of the additional free-fitting parameter, m₁/m₂, and because some fitting analyses were very sensitive to initial values, we also analyzed the motility data using Equation 7 where α₁/α₂ and V_pk1/V_pk2 values were fixed with the values derived from the corresponding NLC measurements (data not shown). A very similar m₁/m₂ value, 0.55 ± 0.21 (average ± S.D., n = 15), was obtained by this analysis. These results indicate that the electromechanical coupling efficiency at the K₁₂ step is ∼55% that of the K₂₃ step.

Determination of the Electromechanical Coupling Efficiencies at the Two Steps

Having determined the ratio of the electromechanical coupling efficiencies, we next focused on determining the coupling efficiencies themselves. It is likely that the degree of electromechanical coupling of prestin is modulated by the physiological status of OHCs (24, 25), and that our q-d analysis shown in Fig. 4E was affected by such cell-to-cell physiological variability. Because it is not readily feasible to control the physiological status of isolated OHCs, we further pursued the q-d relation by using salicylate to gradually manipulate the magnitudes of both NLC and electromotility in individual OHCs. We measured salicylate-dependent NLC with the same procedure used in Fig. 2, while OHC displacement was simultaneously recorded (Fig. 5, A and B). NLC data were analyzed by the three-state and the two-state-C_sa models, and as before, q was determined from the area between the NLC curve and C_lin or C_sa. OHC displacement, d, was measured directly. Fig. 5, C and D, shows the summary of the q-d recordings from eight different OHCs. The Deming linear regression was used to analyze the results. Strong linear q-d relationships were found in all OHCs tested (n = 8) irrespective of the models used for determining q, suggesting that the individual prestin molecule (or its dimer or tetramer as possible functional units (26, 27)) is independently functional. The most intriguing and surprising feature of the q-d relation is the positive d intercepts at q = 0, which were statistically significant (p < 0.001) for all the q-d relations irrespective of the models used for estimating basal capacitances (C_lin or C_sa) for determining q values. As shown below, the non-zero d intercepts provide an alternative proof for the two-step electromechanical coupling mechanism with distinct coupling efficiencies (m₁ < m₂). For determining the q-d relations shown in Fig. 5, we simultaneously measured NLC and motility during the application of salicylate with ±100-mV stimulus. In other words, we observed only portions of the entire NLC and motility responses through the ±100-mV window. Computer simulations shown in Fig. 5E, which slightly exaggerate the qualitative characteristics of the salicylate-dependent NLC motility response for clarity, explain how positive d intercepts can be had. During the gradual inhibition of prestin by salicylate, the K₁₂ (V_pk1) component moved outside the ±100-mV observation window (hyperpolarizing shift), whereas the K₂₃ (V_pk2) component moved into the observation window (depolarizing shift). Because of the negatively set initial V_pk1 and V_pk2 values, if m₂ were higher than m₁, the apparent overall d/q would increase as V_pk separation proceeds, which would eventually cause a positive d intercept. On the other hand, if m₁ were higher than m₂, apparent overall d/q would decrease as V_pk separation proceeds, which would eventually cause a negative d intercept. If m₁ and m₂ were the same, apparent overall d/q would not change irrespective of V_pk separation, In this case, the d intercept should become zero. Therefore, the observed positive d intercepts strongly reaffirm our conclusion that prestin has at least two voltage-dependent conformational transition steps with distinct electromechanical coupling efficiencies (m₁ < m₂).

FIGURE 5.

Relation of charge movement and OHC displacement. A and B, simultaneous measurement of NLC and motility in the presence of salicylate is shown. In the same experimental configuration as in Fig. 2, NLC and OHC motility were simultaneously measured in the presence of salicylate. NLC and motility were simultaneously recorded with one cycle of 2-Hz, 100-mV amplitude sinusoidal voltage stimulus superimposed with two higher frequency stimuli (390.6 and 781.2 Hz, 10-mV amplitude) at time points indicated by the solid triangles, while the membrane capacitance at 0 mV was constantly monitored during the measurements (A, inset). pF, picofarads. Accompanied by the reduction of the prestin-dependent charge movement, OHC displacement decreased. The same colors were used to show matching simultaneous NLC motility recordings. For determining prestin-dependent charge movement (q), C_lin and C_sa were first determined by the three-state and two-state-Csa Boltzmann models. Subsequently the area between NLC curves and the C_lin (or C_sa) was calculated. OHC displacement (d) was determined by the maximum displacement observed. C and D, shown is a summary of the q-d relation. The measurements shown in A and B were performed on different OHCs (n = 8). The d values were plotted against the q values determined by three-state model (C) or the two-state-Csa model (D) for each OHC. Different colors represent different OHCs. The solid lines are Deming's regression lines. Average r² values from eight OHCs with S.D. are shown in each figure. E, computer simulations of NLC motility responses in the presence and absence of salicylate explain how positive d intercepts can be seen at q = 0 if m₁/m₂ < 1. The following values were used: α₁ = α₂ = 0.04 mV⁻¹ (with and without salicylate), V_pk1 = −75 mV, V_pk2 = −70 mV (without salicylate), V_pk1 = −150 mV, V_pk2 = 0 mV (with salicylate), m₁/m₂ = 0.55. F, using the d-q data shown in C and Equations 8, 9, and 10, m₂ values were determined for each OHC (n = 8). The same colors are used for matching. G, the two-step electromechanical coupling mechanism of prestin is shown. z₁ and z₂ are apparent valences calculated from α₁ and α₂, determined by the three-state model (Fig. 4F). The positive signs are assigned for the rightward transitions. K₁₂ and K₂₃ are voltage-dependent equilibrium constants defined in the text, which increase with depolarizing voltage stimuli, and vice versa.

Based on Equations 2 and 7, the observed prestin-dependent charge movement, q, and the OHC displacement, d, are described as

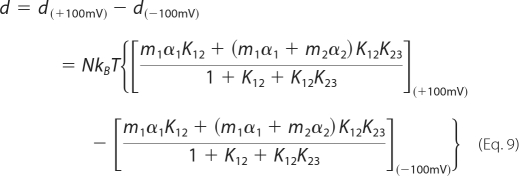The NLC parameters included in Equation 8 were determined by the three-state Boltzmann fitting of NLC data. Because our results suggest that α₁, α₂, V_pk1, and V_pk2 are the same for NLC and motility (Fig. 4, K and L) and because the ratio of m₁ to m₂ was already derived (m₁/m₂ = 0.55), the actual m values can be determined by Equation 9 using the fitting parameters obtained from the corresponding NLC data. The voltage values within the observation window (±100 mV) were corrected by the series resistance for actual calculations. Because prestin molecules are two-dimensionally distributed in the lateral membrane, the m values directly calculated by Equation 9 (m_calc) were corrected by

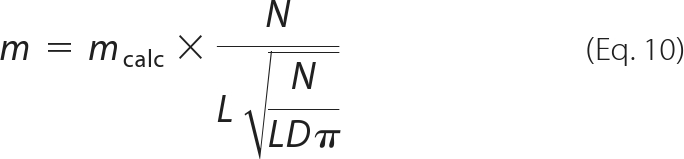where L and D are the length and the diameter of an OHC (see supplemental text for the derivation). The m₂ values determined in this way using the q-d data (three-state, Fig. 5C) are summarized in Fig. 5F. Statistical t tests did not find significant differences from zero for the slopes (p > 0.05), suggesting that m₂ values are constant irrespective of the degree of inhibition by salicylate. This supports the validity of using salicylate for determining the m₁/m₂ ratio in this study. The m₂ values were determined for each OHC by averaging each data set (2.4∼6.0 nm/atto coulomb). The variation of m₂ values found in individual OHCs is likely due to the modulation of the electromechanical coupling of prestin under different physiological status of the OHCs as mentioned above. We determined the m₂ value as 3.5 ± 1.3 nm/atto coulomb (average ± S.D., n = 8). The m₁ value was then calculated as 1.9 nm/atto coulomb simply by multiplying with the coupling ratio of 0.55. Using these numbers together with the α₁/α₂ values determined in Fig. 4F, unitary displacements of prestin at the K₁₂ and the K₂₃ steps along the axial direction of an OHC are estimated to be 0.20 and 0.34 nm, respectively, as summarized in Fig. 5G. If the diameter of monomeric prestin in the membrane were estimated to be 5∼7 nm as expected from the diameter of a potentially tetrameric prestin complex observed in the lateral membrane of OHCs (10∼14 nm (28)), the total unitary displacement of a single prestin molecule (0.20 + 0.34) nm is expected to change the membrane area 3∼4 nm², which agrees with the estimates by others (2∼4 nm² (29, 30)).

DISCUSSION

We found that two distinct voltage-dependent steps in prestin transition between its contracted and expanded states became discernable upon blocking with salicylate and that prestin function is well explained by the three-state Boltzmann model under such conditions. Two distinct peak voltages characterized the process, and the separation of V_pk1 and V_pk2 seen with salicylate could also be seen without salicylate under certain experimental conditions. Previously, three-state Boltzmann fits were found necessary in an investigation of dynamic stiffness of OHCs (10). The three-state model was also used in a recent study to better explain NLC data.³ It was also demonstrated that with reduced chloride concentration, NLC and motility no longer fully covaried.⁴ Aside from the present work, these results also imply that there are at least two voltage-dependent transition steps in the electromechanical coupling process of prestin. Theoretical work is in harmony with the recent experimental results (8, 9).

The fact that prestin function is described by the three-state Boltzmann model is not surprising if one considers that prestin is a member of solute carrier 26 anion transporter family and because non-mammalian orthologs of prestin are demonstrated to be electrogenic divalent/chloride anion exchangers (33). Kinetic models of prestin with two voltage-dependent steps have been proposed based on the transporter assumption (34). What has been unknown is how the voltage-dependent charge movement is coupled to the motor activity of prestin. It is known that non-mammalian orthologs of prestin are not electromotile while retaining transporter activity (33, 35, 36). Thus, it is very likely that mammalian prestin has acquired a unique structural element(s) that couples the voltage-dependent charge movement to mechanical displacement. Because it appears that there are at least two voltage-dependent steps, one fundamental question is which of these is responsible for generating mechanical displacement. Alternatively, if both steps generated mechanical displacement, what is the ratio of the contributions? Such information is important for understanding the molecular mechanism of prestin. Our study provides experimental evidence that prestin indeed has two voltage-dependent conformational transition steps, both of which generate mechanical displacement. The two steps have distinct electromechanical coupling efficiencies (Fig. 5G).

Implication of the Three-state Model for Understanding the Molecular Mechanism of Prestin

Recently, there has been growing evidence that supports a prestin model that postulates an intrinsic voltage sensor(s) with chloride providing allosteric modulation (37–39). Systematic mutation screens have been conducted for identifying the voltage-sensing charged amino acid(s) in prestin using the two-state model for evaluating the effects of mutations (19, 40, 41). Although some mutations were found to significantly reduce the voltage-dependent charge movement of prestin, none was found to completely abolish NLC (41). If prestin had at least two voltage-dependent steps, as strongly suggested in the present study, a mutation(s) of the critical charged amino acid(s) could abolish charge displacement only at one of the two steps.

Salicylate Action on Prestin

Salicylate is very useful for separating the two voltage-dependent electromechanical steps (characterized by V_pk1 and V_pk2), which are not readily distinguishable in a non-modified preparation. The salicylate-dependent V_pk change could be induced by intermolecular interaction of prestin molecules in the oligomer complex. Several factors are known to modulate V_pk. Turgor pressure (17, 29, 32), resting potential (14), and membrane-cholesterol content (31) are all known to affect V_pk. Therefore, it is very likely that freezing the structure of one prestin molecule in an oligomer complex at a certain conformational state by salicylate affects the V_pk1 − V_pk2 relation of other prestin molecules in the same complex. The total number of prestin molecules in individual OHCs, estimated by the three-state Boltzmann fitting as ∼5 million, is consistent with the prestin oligomer model. We collected OHCs from the apical region of the murine cochlea, having typical dimensions of ∼5 μm in diameter and ∼20 μm in length. Thus, the density of prestin molecules in the lateral membrane of OHCs is roughly estimated as ∼16,000/μm². Because prestin is not present in the apical and the basal regions of the lateral membrane, the density would be higher than this estimate. On the other hand, the density of the intramembrane particles found in the lateral membrane of OHCs is reported to be ∼5600/μm² (28). Thus, a prestin oligomer is expected to be composed of at least three prestin molecules and in conformity with the recent estimates, likely four (27, 28).

The Three-state Model Versus the Two-state-C_sa Model

A model cannot be validated simply by curve-fit analyses and associated F-tests or Akaike's information criterion tests. Presenting novel experimental evidence predicted by the model is essential for its acceptance. The two-state-C_sa model (Equation 5) (11) fit the voltage-dependent charge movement of prestin in the presence of salicylate ∼4 times better than the three-state Boltzmann model because of similar quality curve-fit with fewer numbers of free-fitting parameters. Even so, we champion the three-state model over the two-state-C_sa model for the former provides more parsimonious explanations of experimental observations. The non-zero d intercepts of the q-d relations (Fig. 5C) can be understood by two voltage-dependent steps with distinct electromechanical coupling efficiencies (m₁ < m₂) in the three-state model as discussed above. We also observed non-zero d intercepts with the two-state-C_sa model (Fig. 5D). The non-zero intercepts are hard to conceptualize with this model, which is based on only one voltage-dependent step. The salicylate-dependent ΔC change in the two-state-C_sa model is also difficult to understand (Fig. 2H and supplemental Fig. S3A). The term, ΔC, in the two-state-C_sa model is considered to represent the combination of changes in membrane surface area and in either the membrane dielectric constant or its thickness, which are all prestin-dependent (11). Observed positive correlations between the number of prestin motors and the magnitude of ΔC supported this idea (11). Based on the model, a gradual monotonic reduction of ΔC would be expected during the gradual monotonic inhibition of prestin by salicylate. However, salicylate increased ΔC after an initial rapid increment followed by small reduction (Fig. 2H and supplemental Fig. S3A). If ΔC were indeed associated with the prestin physical state, it is difficult to envision how this general parameter could increase in a non-monotonic manner during the monotonic progress of inhibition of prestin by salicylate. With the three-state model, however, the non-monotonic change in ΔC is simply understood by the V_pk1 component shifting toward the hyperpolarizing direction in a limited V_m observation window. These more parsimonious explanations of the results by the three-state model seem to provide a plausible physiological explanation of observations. However, this, of course, does not rule out the possibility that higher-order Boltzmann models with more steps might also describe the prestin operation (8).

NLC Derived from Salicylate-bound Prestin

Anions that completely abolish prestin voltage-dependent charge movement have not been found. In other words, all anions tested so far support the prestin NLC to some extent. Salicylate is not an exception (19). The fact that salicylate does not completely eliminate the prestin NLC would affect our three-state model analyses if salicylate-supported NLC were not negligible. Thus, it is quite reasonable to ask if the multistep charge movement we claim is a consequence of the presence of an additional NLC component derived from salicylate-bound prestin. Information regarding the relative magnitude of salicylate-supported NLC to that of chloride-supported NLC is difficult to be extracted from the previous study (19) because sulfate was used for replacing chloride for comparison. Sulfate is reported to support NLC with positively shifted V_pk (37, 39). Thus, a slight shift in V_pk that could be induced by salicylate would affect the magnitude of C_m observed at certain V_m. Even if the relative magnitude of salicylate-supported NLC was determined to be very small, it is still important to check if our NLC analyses might have been affected by the contribution of salicylate-supported NLC because the population of salicylate-bound prestin increases, whereas that of chloride-bound prestin decreases during the application of salicylate. If the observed salicylate-dependent NLC data are solely explained by the sum of two independent two-state NLCs (2× two-state) that is composed of chloride-supported NLC and salicylate-supported NLC, the NLC component derived from salicylate-bound prestin should continuously increase, whereas that derived from chloride-bound prestin would continuously decrease during the application of salicylate. The population of each component should be reflected in the Q_max value. We performed the 2× two-state analysis on our salicylate-dependent NLC data used for the three-state and the two-state-C_sa analyses summarized in Fig. 3. Supplemental Fig. S5 shows an example of the 2× two-state analysis. Continuous decrements of both NLC components (reflected in Q_max values), but not a continuous increment of one of the two NLC components, were observed, suggesting that NLC derived from salicylate-bound prestin is too small to explain our salicylate-dependent NLC data.

The contribution of salicylate-bound prestin to the observed NLCs can also be estimated to be very small in an alternative way. Although NLC is not completely abolished even with complete intracellular anion exchange with salicylate (19), salicylate is capable of completely abolishing OHC displacement (18), suggesting that the electromechanical coupling of prestin can be disconnected with salicylate. Incidentally, pentane sulfonate is also known to completely abolish OHC displacement (19), although it retains significant NLC (39). Very small (or zero) d/q is expected for salicylate-bound prestin. Therefore, if salicylate-supported NLC was a significant factor in explaining our salicylate-dependent NLC data (Figs. 2 and 3), negative d intercepts should be observed, which is opposite to what we have seen (Fig. 5).