Abstract
Recent neuroimaging studies have demonstrated that human brain networks have economic small-world topology and modular organization, enabling efficient information transfer among brain regions. However, it remains largely unknown how the small-world topology and modular organization of human brain networks emerge and develop. Using longitudinal MRI data of 28 healthy pediatric subjects, collected at their ages of 1 month, 1 year, and 2 years, we analyzed development patterns of brain anatomical networks derived from morphological correlations of brain regional volumes. The results show that the brain network of 1-month-olds has the characteristically economic small-world topology and nonrandom modular organization. The network’s cost efficiency increases with the brain development to 1 year and 2 years, so does the modularity, providing supportive evidence for the hypothesis that the small-world topology and the modular organization of brain networks are established during early brain development to support rapid synchronization and information transfer with minimal rewiring cost, as well as to balance between local processing and global integration of information.
Introduction
Since the Caenorhabditis elegans’ nervous system was first described as a small-world brain network (Watts and Strogatz, 1998), there has been a keen interest in the small-worldness of human brain networks in the neuroimaging research community since neuroimaging techniques facilitate in-vivo studies of the human brain anatomy and function (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009). Using graph theoretic analysis approaches, the human brain has been described and analyzed as a graph (network) with brain regions as graph nodes and regional connections as graph edges, derived from correlations of morphological or functional measures, or white matter fiber tracts (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009; Sporns et al., 2005). Functional human brain networks have been studied using electroencephalography (EEG), magnetoencephalography (MEG), and functional MRI (fMRI). Regional functional connectivity is typically estimated using cross-correlations, partial correlations, or mutual information in time series of regional signal at one or several specific frequency (Achard and Bullmore, 2007; Achard et al., 2006; Bartolomei et al., 2006; Breakspear et al., 2006; Ferri et al., 2007; Salvador et al., 2005a; Salvador et al., 2005b; Stam, 2004). The anatomical network of the human brain has been studied using diffusion MRI techniques which offer a relatively direct estimation of brain anatomical regional connection (Gong et al., 2009; Hagmann et al., 2007; Iturria-Medina et al., 2007; Iturria-Medina et al., 2008; Lewis et al., 2009). Comparable human anatomical networks can also be inferred from structural MRI data with brain regional connectivity estimated as correlations in cortical thickness or volume (Bassett et al., 2008; He et al., 2007). Despite the difference in experimental methodologies, the studies of human brain networks reveal a convergent fact that the human brain networks, anatomical and functional, have the small-world topology that can be equivalently characterized by efficiency measures of networks (Latora and Marchiori, 2001; Latora and Marchiori, 2003).
Recent neuroimaging studies of the human brain have also demonstrated that, parallel to the small-worldness, human brain networks have a modular organization (Chen et al., 2008; Fair et al., 2009; Meunier et al., 2009), which partitions a network into a set of modules, each module comprising nodes densely connected within the module and loosely connected to other modules (Girvan and Newman, 2002). Interestingly, it has been demonstrated that the modularity of functional brain networks changes little over the age ranging from 8 to 25 years (Fair et al., 2009), while the functional brain network of old individuals displayed a relatively lower modularity than the brain network of young adults (Meunier et al., 2009). It is unclear whether structural networks display age related changes.
Despite the rapidly increasing evidence of the small-worldness and the modular organization of human brain networks, it remains largely unknown when these properties of human brain network emerge and how they change in the course of brain development. It has been hypothesized that the small-world architecture and the modular organization of brain networks has been a result of the brain development and competitively selected to support rapid synchronization and efficient information transfer with minimal rewiring cost, as well as to balance between local processing and global integration of information (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009; Tononi et al., 1994). The hypothesis is supported by studies that demonstrated the efficiency of brain functional networks of normal people (Achard and Bullmore, 2007), impaired efficiency of networks in diseased brains (Liu et al., 2008), as well as decreased efficiency and modularity of brain networks of old individuals (Achard and Bullmore, 2007; Meunier et al., 2009). It has been suggested in (Bullmore and Sporns, 2009) to explore and test this hypothesis more directly using evolutionary algorithms in computation models of brain network selection (Sporns and Kötter, 2004).
In this study, we investigated efficiency and modularity of the human brain anatomical networks in the early childhood, focusing on the following questions: 1) Do the brain networks have economic small-world topology in early development? 2) Do the brain networks have modular organization in early development? And 3) how does the efficiency and modularity of the brain networks change in the course of early development?
Materials and Methods
Subjects and MRI data acquisition
The study subjects were part of a large study of brain development in normal children (Gilmore et al., 2007b). Informed consent was obtained from the parents and the experimental protocols were approved by the institutional review board. None of the subjects was sedated for MR imaging. Before the subjects were imaged, they were fed, swaddled, and fitted with ear protection. All subjects slept during the imaging examination. A 3D MP-RAGE sequence was used to obtain T1 and T2 scans. The imaging parameters were as follows: repetition time (TR) = 1820ms; echo time (TE) = 4.38 ms; inversion time = 1100ms; 144 slices; and voxel size = 1×1×1mm3. We identified 28 normal subjects (10 males/18 females), having longitudinal structural MRI brain images at the gestational ages of 41.2±1.7 (std), 94.4±2.8, and 145.9±5.9 weeks, corresponding to postnatal ages of 6.1±2.8, 59.3±3.0, and 110.7±6.8 weeks, respectively. For comparison purpose, structural MRI brain images of 27 healthy adult subjects (13 males/ 14 females, 24±3 years) were obtained.
Post-processing
The images of each subject were first skull stripped, brain tissue segmented (Shi et al., 2009), and spatially normalized to a standard template atlas with 90 anatomically labeled cortical and subcortical regions (Tzourio-Mazoyer et al., 2002) using an image registration algorithm (Shen and Davatzikos, 2002). From the resulting deformation fields, voxel-wise tissue density maps were computed to represent the local brain volume changes relative to the selected template (Shen and Davatzikos, 2003). Based on the tissue density maps, gray matter volume measures of 90 cortical and subcortical regions were computed for all subjects at different time points (see also table S1 and ref. (Tzourio-Mazoyer et al., 2002) for details of these regions). For each age group, we used linear regression to model effects of total brain volume, gender, and age on gray matter volume measures for each region separately. The effects of total brain volume size, gender, and age were removed by using the residuals of the regression as corrected gray matter volume estimates.
Anatomical brain network construction
The cortical and subcortical regions were used as nodes to construct brain networks of the early development brain using graph theoretic approaches (Bassett et al., 2008; Bullmore and Sporns, 2009), with connections between nodes defined as correlations in regional gray matter volume measures (Bassett et al., 2008; He et al., 2007). The connection between each possible pair of nodes was estimated as Pearson correlation coefficient between their corrected regional gray matter volume measures of 28 subjects for each age group separately. These pair-wise correlation measures were assembled to form a symmetric connection matrix M with zero diagonal elements, the Mi,j, i ≠ j element of which is the correlation coefficient between nodes i and j. Positive entries in the connection matrix indicate connected nodes. Similarly, a correlation matrix was obtained for the adults. The correlation matrices of these 4 age groups are shown in Fig. S1.
An unweighted brain network can be derived from each connection matrix and represented by a binary adjacent matrix by applying a threshold to the correlation matrix. The elements of the binary adjacent matrix are zero if their corresponding correlation coefficients are less than a given threshold, otherwise are unity. The nonzero elements of the binary adjacent matrix indicate that a node (row index) is connected to another node (column index) via an edge. For unweighted networks, the number of edges in a network is related to how expensive it is to build a network (Latora and Marchiori, 2001; Latora and Marchiori, 2003). The cost of a network can be quantified by the ratio of number of edges in a network to the maximum possible number of edges (Latora and Marchiori, 2001; Latora and Marchiori, 2003). Shown in the left column of Fig. S1 are adjacent matrices corresponding to a network cost of 0.16 that is the minimum network cost at which brain regions become fully connected in the brain networks of all age groups (Fig. 2).
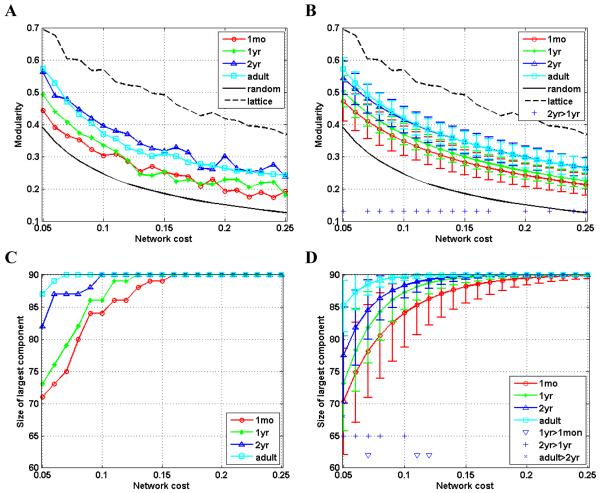
Fig. 2.
Modularity (A, B) and size of the largest connected component (C, D) as a function of cost (x-axis) for brain networks. Modularity of the comparable random graphs and regular lattices is also shown in the modularity plots for testing nonrandomness of the modular organization of brain networks. The plots of A and C show the results derived directly from the image data, while the plots of B and D show the distribution (mean ± standard deviation) of network parameters derived from bootstrap sampling. In the plots of right column, significant difference (p<0.05) is indicated for comparisons: 1yr>1mon, 2yr>1yr, and adult>2yr, respectively.
Network analysis
We investigated properties of the early development brain networks and compared with those of the adult brain network, focusing on their efficiency and modularity. We first studied global properties of the networks obtained by thresholding the connection matrices over a range of thresholds. To facilitate comparison among brain networks of different age groups at same network costs, we used the network cost to control the threshold to be used for deriving an unweighted brain network (Achard and Bullmore, 2007; Bullmore and Sporns, 2009; Meunier et al., 2009). Thus, a metric of network property can be evaluated as a function of network cost. With this functional representation of network property measures, we investigated the brain networks of different age groups with respect to their global efficiency, local efficiency, cost efficiency, and modularity. For examining the small-worldness and nonrandom modular organization of the brain anatomical networks, comparable regular lattices and random graphs with the same degree distributions to brain networks (1000 at each cost) were generated over the same range of network costs (Maslov and Sneppen, 2002; Stam and Reijneveld, 2007). The mean metrics of random graph were computed for comparison. In the case of a small-world network, the global efficiency is greater than a comparable lattice but less than a random graph, and the local efficiency is greater than a random graph but less than a lattice (Latora and Marchiori, 2001). Similarly, a network with nonrandom modular organization shall have modularity larger than that of a random network.
The modular organization of a network was detected using a fast algorithm by partitioning the network into subsets to achieve the maximum network modularity (Clauset et al., 2004). The modularity metric quantifies how different intra-modular links in a network are from a random network with the same modular organization (Newman and Girvan, 2004).
A bootstrap resampling strategy was used to assess how the network efficiency and modularity vary with the change of data (Efron and Tibshirani, 1993). In particular, 1000 bootstrap sampling of the study subjects with replacement were performed. For a study with n subjects, each bootstrap sampling consists of n pseudo-random values drawn from a uniform distribution of subject IDs. For each bootstrap sample of the pediatric subjects, 3 brain networks corresponding to the brain scans of different ages were constructed and their network efficiency and modularity were obtained as described above. The network efficacy and modularity of adult networks were obtained in the same way.
To investigate the difference between brains at two different ages with respect to a brain network metric, a permutation test was used to assess the statistical significance. A permutation samples was obtained by randomly assigning the corrected regional gray matter volume measures of two age groups to one or another while keeping the same sample sizes as the original groups. Particularly, for comparisons within the pediatric age groups, the longitudinal nature of the data was taken into account so that the regional volume measures of the same subject at two different time points were always assigned to different age groups. Based on the randomly resampled regional measures, regional correlation matrix was then computed for each age group. For each permutation, the network metric measures at different network costs were then computed and their differences between younger and older groups were calculated. Finally, the one-sided p-value of the difference was calculated as the proportion of 1000 sampled permutations where the difference was greater than or equal to the observed difference.
We also investigated the characteristics of individual nodes in brain networks of different age groups, including their nodal global and local efficiency, intra-modular degree, participation coefficient, as well as betweenness centrality.
Network metrics used in this study for characterizing brain networks
Given an unweighted network (graph) G with N nodes, its metrics for global and local efficiency can be computed as (Latora and Marchiori, 2001; Latora and Marchiori, 2003)
| (1) |
| (2) |
where di,j is the distance between nodes i and j, Gi is a subgraph comprising nodes directly connected to node i, and NGi is the number of nodes of Gi. Eglob(i) and Eloc(i) are nodal efficiency metrics. Specifically, Eglob measures the efficiency of parallel information transfer in the network, whereas Eloc measures the local efficiency of information transfer in the immediate neighborhood of each node.
A module of G is a subset of nodes which are more densely connected to each other in the same module than to nodes outsides the module. For a configuration of modular organization m with nm modules, its modularity Q(m) is defined as (Newman and Girvan, 2004)
| (3) |
where L is the total number of edges of G, ls is the total number of edges in module s, and ds is the sum of the degrees of the nodes in module s. The modularity of a graph is defined as the largest value of modularity measures associated with all possible configurations of modules, which can be found by optimization algorithms (Newman and Girvan, 2004). We adopted a fast modularity finding algorithm (Clauset et al., 2004), which has been demonstrated capable of achieving a fast solution with comparable quality to other modularity optimization algorithms, including simulated annealing (Guimera and Amaral, 2005; Meunier et al., 2009).
Once an optimal configuration of modules is found, topological roles of nodes in terms of their intra-modular and inter-modular connectivity patterns can be quantified by normalized intra-modular degree and participation coefficient. The normalized intra-modular degree z(i) measures how dense a node i connects to other nodes in the same module, and the participation coefficient p(i) measures how a node i connects to nodes in other modules. They are defined as, respectively (Guimera and Amaral, 2005),
| (4) |
| (5) |
where kni is the number of edges connecting the ith node to other nodes in its module nth, referred to as intra-modular node degree; and σkn are the mean and standard variance of intra-modular node degrees of all nodes in the nth module, ksi is the number of edges of the ith node to module Si, and K(i) is the number of edges that connect node i to all other nodes. Nodes with z(i) greater than (mean+standard deviation) of all nodes’ normalized intra-modular degree are classified as modular hubs, otherwise classified as non-hubs. Nodes with p(i) greater than 0.3 are classified as connectors, otherwise classified as non-connectors (Guimera and Amaral, 2005).
Betweenness centrality: the betweenness centrality of a node i is defined as
| (6) |
where σj,k is the number of the shortest paths from node j to k, and σj,k(i) is the number of shortest paths that traverse node i.
Results
Using graph theory analysis approaches (Bullmore and Sporns, 2009), we studied brain anatomical networks during early development brain at ages of 1 month, 1 year, and 2 years. The brain anatomical networks were derived from longitudinal structural MRI data of 28 healthy pediatric subjects, and compared with those derived from MRI scans of 27 adults.
The brain networks in early development have the economic small-world topology
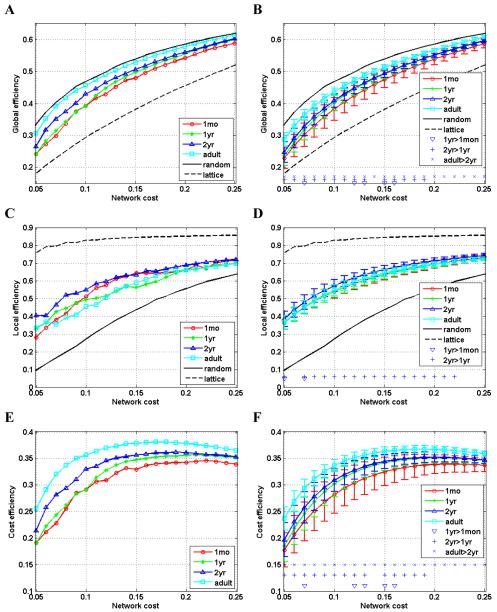
Brain networks were studied and compared with comparable random networks and lattices over a range of network costs in terms of their global efficiency, local efficiency, and cost efficiency (Achard and Bullmore, 2007; Latora and Marchiori, 2001; Latora and Marchiori, 2003). The cost of a network is measured by the number of edges or connections in the network, while the efficiency measures of networks are functions of the minimum path length between network nodes, reflecting communication efficiency of networks. As shown in panels A, B, C and D of Fig.1, the curves of global efficiency and local efficiency of anatomical networks of the early development brain locate in-between of curves of random networks and lattices, indicating that both the early childhood and the adult brain networks have characteristically economic small-world topology (Latora and Marchiori, 2001; Latora and Marchiori, 2003; Watts and Strogatz, 1998). The curves of global efficiency display a pattern of consistent and statistically significant increasing with the brain development from 1 month to 2 years, and to adulthood, over a wide range of network costs. The pattern of increasing efficiency of the developing brain is expected since functional development needs support from structural substrate of improved efficiency (Sporns et al., 2004). However, the curves of local efficiency of brain networks display a complicated pattern, and the networks of 2-year-olds have higher efficiency at some network costs than networks of younger children’s and adult brains. As shown in panels E and F of Fig. 1, the early childhood and adult brain networks all exhibit behavior of cost efficiency, i.e., positive difference between global efficiency and network cost (Achard and Bullmore, 2007). Similar to the measures of global efficiency, the cost efficiency increases with the brain development.
Fig. 1.
Global efficiency (A, B), local efficiency (C, D), and cost efficiency (E, F), as functions of network cost (x-axis) for brain networks. Global and local efficiency of random graphs and regular lattices are also shown in the plots of global efficiency and local efficiency for testing the small-worldness of brain networks. The plots in panels of A, C, and E show the results derived directly from the imaging data, while the plots in panels of B, D, and F show the distribution (mean ± standard deviation) of network parameters derived from bootstrap sampling. In these plots, significant difference (p<0.05) is indicated for comparisons: 1yr>1mon, 2yr>1yr, and adult>2yr, respectively.
The brain networks in early development have nonrandom modular organization
The early development brain networks were analyzed with respect to network modularity (Clauset et al., 2004; Newman and Girvan, 2004) over a range of network costs and compared with random networks and adult brain networks. As shown in panels A and B of Fig. 2, the brain networks have higher modularity than the comparable random networks, indicating that both in early development and the adult brain, networks have non-random modular organization (Newman and Girvan, 2004). The modularity of the brain networks of two-year-olds is higher than the modularity of the brain networks in younger and adult brains, a similar trend to the local efficiency.
In panels C and D of Fig. 2, sizes of the largest connected components corresponding to different network costs are shown for the brain networks of 4 age groups. With the relatively lower network costs, the size of the largest connected component of the early development brain networks is positively correlated with the stage of the brain development. For the brain networks of adults and 2-year-olds, the brain regions became fully connected at the network cost of 0.1, while the same parameters are 0.13 and 0.16 for the brain network of 1-year-olds and 1-month-olds, respectively, indicating that it requires a larger network cost for younger brain to make the brain network fully connected.
The developmental change pattern of brain networks in early development is complex
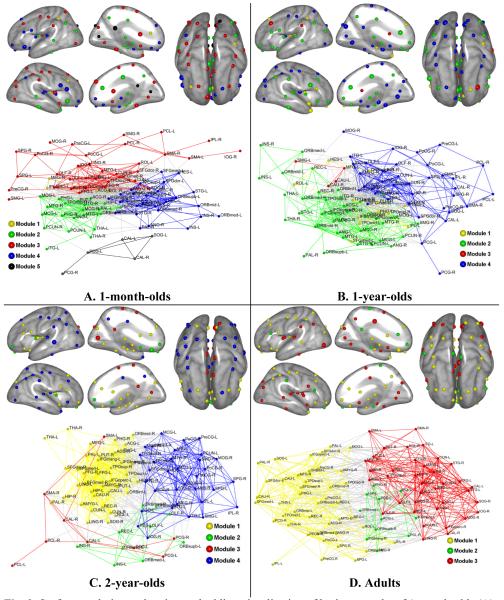
We investigated modular organization of brain networks in early development with a network cost of 0.16 that is the minimum network cost to make all brain regions fully connected for all age groups (see Fig. 2). The modular organization of the brain networks was anatomically visualized using brain surface rendering and topologically visualized using a spring-embedding algorithm (Kamada and Kawai, 1989), as shown in panels of Fig. 3 (see Table S1 for modular assignment and abbreviation for each region).
Fig. 3.
Surface rendering and spring-embedding visualization of brain networks of 1-month-olds (A), 1-year-olds (B), 2-year-olds (C), and adults (D). For the surface rendering visualization, each network node (brain region) is projected onto the brain surface of its corresponding hemisphere by minimizing its distance to the brain surface. The brain surfaces were generated with the Freesurfer image analysis suite, which is documented and freely available for download online (surfer.nmr.mgh.harvard.edu). Nodes are color-coded by modules and larger nodes are connector hubs or provincial hubs. Lateral, medial, and top views of both hemi-spheres are shown. The spring-embedding visualization of networks is implemented with Kamada-Kawai layout algorithm using Pajek software package (pajek.imfm.si/doku.php). The nodes and intra-modular connections are colored-coded by modules, while inter-modular connections are colored-coded with light-gray. The abbreviation of region labels can be found in Table S1.
The brain network of 1-month-olds comprises 5 modules. Module 1 consists of 4 regions, including right middle frontal gyrus, right rolandic operculum, left anterior cingulate gyrus, and left inferior parietal lobule. Module 2 consists of 21 regions, most of them from subcortex region, including bilateral hippocampus, bilateral parahippocampal, and bilateral thalamus. Module 3 includes 34 regions, distributed mainly in parietal and occipital lobes, as well as subcortical area, such as bilateral caudate. Module 4 consists of 26 regions, most of them from orbitofrontal cortex, inferior frontal gyrus, and temporal lobe. Module 5 had 5 regions, namely, bilateral posterior cingulate gyrus, bilateral calcarine cortex, and left superior occipital gyrus. The modular organization of brain network of 1-month-olds is shown in panel A of Fig. 3.
The brain network of 1-year-olds has 4 modules, two of them (module 2 and module 4) having 37 regions and other two (module 1 and module 3) having 12 and 4 regions, respectively. In particular, module 2 consists of 37 regions, including most regions of 1-month-old network’s modules of 2 and 4, distributed mainly in frontal and temporal lobes. Module 4 also consists of 37 regions, most of them being in 1-month-old network’s module 3. Module 4 of 1-year-old network also integrated the 1-month-old network’s module 5. Module 1 of 1-year-old network has 12 regions, including temporal pole area, regions of superior frontal gyrus, and subcortex regions, like right putamen and left parahippocampal gyrus. Module 3 of 1-year-old network only has 4 regions, including bilateral caudate, left middle frontal gyrus and left supramarginal gyrus. The modular organization of brain network of 1-year-olds is shown in panel B of Fig. 3.
The brain network of 2-year-olds also comprises 4 modules. However, its organization is dramatically different from those of younger brain networks. In particular, module 1 consists of 38 regions, most of them from subcortex, and some from temporal and frontal lobes. Module 2 has 10 regions, including bilateral insular, bilateral olfactory, bilateral medial and superior orbitofronatal cortex, left orbitofrontal cortex (middle), and left rectus gyrus. Module 3 has 9 regions, including bilateral supplementary motor area, bilateral posterior cingulate gyrus, bilateral calcarine cortex, bilateral paracentral lobule, and left superior occipital gyrus. Module 4 has 33 regions, distributed mainly in temporal, occipital, and parietal lobes. The modular organization of brain network of 2-year-olds is shown in panel C of Fig. 3.
The brain network of adults has only 3 modules and their sizes are relatively close to each other. It is a result of reorganization of 2-year-old network. In particular, module 1 has 42 regions, including majority of the 2-year-old network’s module 1 and module 4. The module 2 of the adult network consists of 11regions, mainly distributed in temporal lobe and frontal lobe. Module 3 consists of 37 regions, including regions mainly from modules 1 and 4 of the 2-year-old network. The modular organization of adult brain network is shown in panel D of Fig. 3.
The visualization results of the modular organization of the early development brain networks, as shown in Fig. 3, indicate that the temporal developmental change pattern of the brain networks through early childhood is complex with respect to their modular organization. Over ages from 1 month to 2 years, as the brain develops, the modular assignment for brain regions changes dramatically, reflecting dynamic anatomical segregation and integration of brain regions. The spring-embedding based visualization of brain networks also reflects the complex developing pattern. Anatomical spatial location based visualization of these brain networks and their modular organizations are shown in Fig. S2, for easy inspection of their development pattern.
We also investigated each node’s topological role based on its intra- and inter-modular connections (Guimera and Amaral, 2005; Meunier et al., 2009). Intra-modular connectivity was quantified by the normalized intra-modular degree that measures the number of links of a node to other nodes in the same module. A higher value of the intra-modular degree of a node indicates that it has a larger number of intra-modular connections compared with other nodes in the same module. The intra-modular degree can be used to determine if a node is a hub. Inter-modular connectivity was measured by the participation coefficient that measures how a node connects to different modules. A node with a higher participation coefficient extensively connects to different modules, referred to as a connector. Using these two measures, a node can be assigned a topological role from the following 4 categories: connector hub (H), non-connector (provincial) hub (P), connector non-hub (C), and non-connector and non-hub (N) (Guimera and Amaral, 2005).
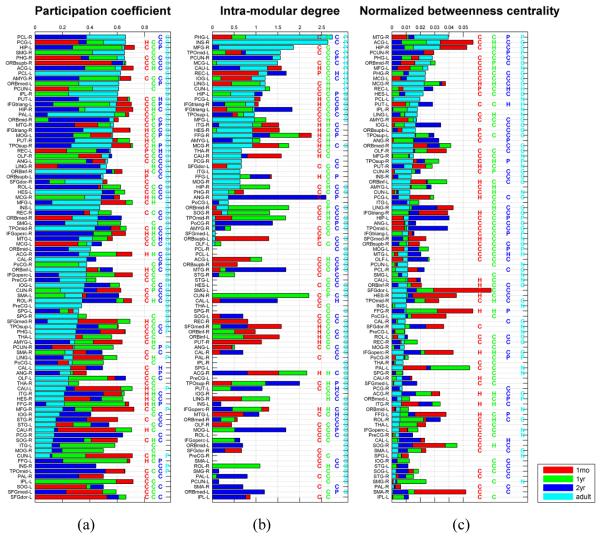
The measures of participation coefficient and intra-modular degree of all the nodes and their topological roles in the early development and the adult brain networks are shown in Fig. 4 (a) and (b). These results demonstrate interesting patterns of brain networks in early development with respect to participation coefficient and intra-modular degree. Over the early brain development stages of 1 month, 1 year, and 2 years, over 1/3 nodes consistently served as brain network connectors and over 2/3 of them served as connectors in the adult network as well, indicating that the early brain development did not dramatically change the connection patterns of brain regions with dense connections to different modules, even for the brain development from 1 month to 1 year during which the brain development is extremely dynamic (Knickmeyer et al., 2008). However, the change of the nodes’ role as network hubs is relatively large. Each node’s global topological role was also measured using the normalized betweenness centrality, which quantifies the number of the shortest paths between all other node pairs in the network passing through a given node (Bullmore and Sporns, 2009). Nodes with high betweenness centrality are global hubs, crucial to efficient communication (Freeman, 1977). As shown in Fig. 4 (c), the nodes with high betweenness centrality are modular connectors, but not necessarily modular hubs, indicating that the global topological roles are not equivalent to modular topological properties. The relatively large changes in measures of nodal topology roles over age reflect the dynamic development pattern of the early development brain networks.
Fig. 4.
Bar-plots of regional measures related to the regional role: participation coefficient (a), intra-modular degree (b), and normalized betweenness centrality (c). In each bar-plot, the brain regions are ranked by the measures obtained for the adult network. The bars in color of red, green, blue, and cyan are corresponding to measures of one-month-olds, one-year-olds, two-year-olds, and adults, respectively. The same color-coding is used for the indicators of connector hub (H), provincial hub (P), and connector non-hub (C). The abbreviation of region labels can be found in Table S1.
Discussion
This study demonstrates that brain networks in early development have economic small-world topology and nonrandom modular organization which have been discovered in the adult brain networks (Achard and Bullmore, 2007; Bullmore and Sporns, 2009; Chen et al., 2008; He et al., 2007; Meunier et al., 2009). Also, brain networks in early development display a pattern of increasing efficiency and modularity with the brain development, albeit complex is their developmental change pattern. These findings, along with results of adult brain networks (Achard and Bullmore, 2007; Bullmore and Sporns, 2009; Chen et al., 2008; He et al., 2007; Meunier et al., 2009), support the hypothesis that the characteristics of brain networks have been competitively selected to solve the economic problem of optimizing the brain information processing (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009).
The first two years of life are the most dynamic of human postnatal brain development. Total brain volume increases 130% from birth to age 2, 80-90% of adult volumes, while cortical gray matter volumes increases by 185% (Knickmeyer et al., 2008). White matter is also maturing rapidly in this time period, with the overall pattern of adult myelination present by age 2 year (Sampaio and Truwit, 2001); diffusion tensor properties of white matter also demonstrate a similar rapid maturation during this period (Gao et al., 2009a; Gilmore et al., 2007a). Resting state fMRI studies in this age group also indicate significant development of functional networks, including visual, sensorimotor and “default” networks (Gao et al., 2009b; Lin et al., 2008). This study reveals the development pattern of anatomical brain networks in this important period of early brain development.
This is the first longitudinal study of brain networks with respect to their efficiency and modular organization in early brain development, providing a picture of the emergence and developmental change of brain networks at its early development stages, complementing the existing studies of brain development and brain network research (Fair et al., 2008; Fair et al., 2009; Fransson et al., 2007; Gao et al., 2009b; Huang et al., 2006; Kelly et al., 2009; Knickmeyer et al., 2008; Lin et al., 2008; Matsuzawa et al., 2001; Sowell et al., 1999). The development pattern of brain networks has been investigated with a focus on functional default mode network or connection among specific brain regions (Fair et al., 2008; Fransson et al., 2007; Gao et al., 2009b; Kelly et al., 2009; Lin et al., 2008). In particular, recent studies of default mode network’s emergence and developmental change have documented the trajectory of default mode network from infancy, adolescence, to adulthood, primitive default mode network emerging in the brain of neonates and gradually maturing with the brain development (Fair et al., 2008; Gao et al., 2009b). However, the efficiency and modular organization of the development brain networks has not been explored so far. The emergence and developmental change pattern of the early development brain revealed in this study sheds light on the development pattern of brain network’s efficiency and modular organization. The dynamic developmental change pattern of modular organization of the early development brain networks is consistent with the observations in default mode networks which reorganize their topological architecture and composition of brain regions over the brain development from infancy, adolescence, to adulthood (Fair et al., 2008; Gao et al., 2009b). However, the pattern of brain development might be different from changes rendered by aging or diseases (Meunier et al., 2009; Paterson et al., 1999), which merits further investigation.
The early development brain networks were derived from longitudinal structural MRI brain images scanned at ages of 1 month, 1 year, and 2 years. The brain network consists of 90 nodes which are cortical and subcortical regions defined by automated anatomical labeling (AAL) (Tzourio-Mazoyer et al., 2002). The connectivity between any possible pair of nodes is defined as correlation between their regional volume measures that were computed through nonrigidly warping the AAL atlas onto each individual brain image. Therefore, the image registration between the AAL atlas and individual images plays an important role in the construction of the brain networks and its performance is directly related to the robustness of the brain networks. We adopted an image registration algorithm which has potential to achieve good registration accuracy (Shen and Davatzikos, 2002). Prior to the image registration, the brain images were segmented into white matter, gray matter, and cerebrospinal fluid using a subject-specific atlas based image segmentation, specially designed for achieving accurate segmentation of neonate images (Shen and Davatzikos, 2002; Shi et al., 2009). In particular, segmentation results of two-year-old images were used to guide the segmentation of one-year-old and one-month-old images of the same subject. These two techniques were utilized together to achieve accurate computation of regional volume measures, thus facilitating the robust construction of the early development brain networks. One limitation of this study is that the sample size is relatively small. However, the longitudinal designed may increase its statistical power since the temporal individual variance is much smaller than that in cross-sectional studies (Giedd et al., 1999; Ment et al., 2009). Another caveat in interpretation of the results of this study is that anatomical brain regions defined in the AAL atlas might not match very well with function and anatomy of the early development brains. However, the effect of utilization of this adult brain template in this study shall be similar to that in adult brain network analysis, taking into consideration the following fact that the adult brain templates have been successfully used to label brain images of two-year-olds (Gousias et al., 2008). For the general issue in terms of definition of network nodes in graph theory analysis of brain networks (Sporns et al., 2005), a better solution is needed.
The main limitation of this study is that cross-correlations in gray matter volumes are not directly related to fiber connections which could be derived from diffusion tensor MRI data. However, gray matter changes during development likely reflect myelination which continues into young adulthood (Giedd et al., 1999; Sowell et al., 2002; Thompson et al., 2005). Studies of the brain development using resting fMRI and EEG also demonstrate that functional connectivity increases with age (Bunge and Wright, 2007; Fair et al., 2008; Fair et al., 2009; Fair et al., 2007; Luna and Sweeney, 2004; Srinivasan, 1999). Although the brain networks derived from structural MRI are approximate to those derived from diffusion tensor MRI, any interpretation of the brain networks should come with a caveat that their validity depends on the accuracy of image segmentation and registration algorithms.
In conclusion, we present a study of the early development brain network and reveal a complex temporal developmental change pattern of increased efficiency and modularity with the brain development. The developmental pattern of the brain network displays a picture of the human brain network’s emergence and developmental change, which merits further investigation with respect to its difference from aging and diseased brain networks.
Supplementary Material
Acknowledgments
This work was supported in part by NSFC 30970770, the Hundred Talents Program of Chinese Academy of Sciences, the National High Technology Research and Development Program (863 Program) of China, Grant No. 2009AA02Z302, as well as NIH grants EB009724, EB006733, EB008374, EB009634, MH088520, MH070890, MH064065, NS055754, and HD053000.
References
- Achard S, Bullmore ET. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 2007;3:e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolomei F, Bosma I, Klein M, Baayen JC, Reijneveld JC, Postma TJ, Heimans JJ, van Dijk BW, de Munck JC, de Jongh A, Cover KS, Stam CJ. Disturbed functional connectivity in brain tumour patients: evaluation by graph analysis of synchronization matrices. Clinical Neurophysiology. 2006;117:2039–2049. doi: 10.1016/j.clinph.2006.05.018. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, Meyer-Lindenberg A. Hierarchical Organization of Human Cortical Networks in Health and Schizophrenia. The Journal of Neuroscience. 2008;28:9239–9248. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Bullmore ET. Small-world brain networks. Neuroscientist. 2006;12:512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- Breakspear M, Rubinov M, Knock S, Williams LM, Harris AWF, Micheloyannis S, Terry JR, Stam CJ. Graph analysis of scalp EEG data in schizophrenia reveals a random shift of nonlinear nentwork dynamics. Neuroimage. 2006;31 [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Bunge SA, Wright SB. Neurodevelopmental changes in working memory and cognitive control. Current Opinion in Neurobiology. 2007;17:243–250. doi: 10.1016/j.conb.2007.02.005. [DOI] [PubMed] [Google Scholar]
- Chen ZJ, He Y, Rosa-Neto P, Germann J, Evans AC. Revealing Modular Architecture of Human Brain Structural Networks by Using Cortical Thickness from MRI. Cerebral Cortex. 2008;18:2374–2381. doi: 10.1093/cercor/bhn003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clauset A, Newman MEJ, Moore C. Finding community structure in very large networks. Physical Review E. 2004;70:066111. doi: 10.1103/PhysRevE.70.066111. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- Fair DA, Cohen AL, Dosenbach NUF, Church JA, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. The maturing architecture of the brain’s default network. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:4028–4032. doi: 10.1073/pnas.0800376105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Cohen AL, Power JD, Dosenbach NUF, Church JA, Miezin FM, Schlaggar BL, Petersen SE. Functional Brain Networks Develop from a “Local to Distributed” Organization. PLOS Computational Biology. 2009;5:e1000381. doi: 10.1371/journal.pcbi.1000381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Dosenbach NUF, Church JA, Cohen AL, Brahmbhatt S, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. Development of distinct control networks through segregation and integration. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:13507–13512. doi: 10.1073/pnas.0705843104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferri R, Rundo F, Brunt O, Terzano MG, Stam CJ. Small-world network organization of functional connectivity of EEG slow-wave activity during sleep. Clinical Neurophysiology. 2007;118:449–456. doi: 10.1016/j.clinph.2006.10.021. [DOI] [PubMed] [Google Scholar]
- Fransson P, Skiöld B, Horsch S, Nordell A, Blennow M, Lagercrantz H, Ã…den U. Resting-state networks in the infant brain. Proceedings of the National Academy of Sciences. 2007;104:15531–15536. doi: 10.1073/pnas.0704380104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman LC. A set of measures of centrality based on betweenness. Sociometry. 1977;40:35–41. [Google Scholar]
- Gao W, Lin W, Chen Y, Gerig G, Smith J, Jewels V, Gilmore J. Temporal and spatial development of axonal maturation and myelination of white matter in the developing brain. American Journal of Neuroradiology. 2009a;30:290–296. doi: 10.3174/ajnr.A1363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao W, Zhu H, Giovanello KS, Smith JK, Shen D, Gilmore JH, Lin W. Evidence on the emergence of the brain’s default network from 2-week-old to 2-year-old healthy pediatric subjects. Proceedings of the National Academy of Sciences. 2009b;106:6790–6795. doi: 10.1073/pnas.0811221106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giedd JN, Blumenthal J, Jeffries NO, Castellanos FX, Liu H, Zijdenbos A, Paus T, Evans AC, Rapoport JL. Brain development during childhood and adolescence: a longitudinal MRI study. Nature Neuroscience. 1999;2:861–863. doi: 10.1038/13158. [DOI] [PubMed] [Google Scholar]
- Gilmore JH, Lin W, Corouge I, Vetsa YSK, Smith JK, Kang C, Gu H, Hamer RM, Lieberman JA, Gerig G. Early postnatal development of corpus callosum and corticospinal white matter assessed with quantitative tractography. American Journal of Neuroradiology. 2007a;28:1789–1795. doi: 10.3174/ajnr.A0751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore JH, Lin W, Prastawa MW, Looney CB, Vetsa YS, Knickmeyer RC, Evans DD, Smith JK, Hamer RM, Lieberman JA, Gerig G. Regional gray matter growth, sexual dimorphism, and cerebral asymmetry in the neonatal brain. J Neurosci. 2007b;27:1255–1260. doi: 10.1523/JNEUROSCI.3339-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girvan M, Newman MEJ. Community structure in social and biological networks. PNAS. 2002;99:7821–7826. doi: 10.1073/pnas.122653799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C. Mapping Anatomical Connectivity Patterns of Human Cerebral Cortex Using In Vivo Diffusion Tensor Imaging Tractography. Cerebral Cortex. 2009;19:524–526. doi: 10.1093/cercor/bhn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gousias IS, Rueckert D, Heckemann RA, Dyet LE, Boardman JP, Edwards AD, Hammers A. Automatic segmentation of brain MRIs of 2-year-olds into 83 regions of interest. NeuroImage. 2008;40:672–684. doi: 10.1016/j.neuroimage.2007.11.034. [DOI] [PubMed] [Google Scholar]
- Guimera R, Amaral LAN. Functional cartography of complex metabolic networks. Nature. 2005;433:895–900. doi: 10.1038/nature03288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Kurant M, Gigandet X, Thiran P, Wedeen VJ, Meuli R, Thiran J-P. Mapping Human Whole-Brain Structural Networks with Diffusion MRI. PLoS ONE. 2007;2:e579. doi: 10.1371/journal.pone.0000597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. Small-World Anatomical Networks in the Human Brain Revealed by Cortical Thickness from MRI. Cerebral Cortex. 2007;17:2407–2419. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang J, Wakana S, Zhang W, Ren T, Richards LJ, Yarowsky P, Donohue P, Graham E, van Zijl PCM, Mori S. White and gray matter development in human fetal, newborn and pediatric brains. NeuroImage. 2006;33:27–38. doi: 10.1016/j.neuroimage.2006.06.009. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y, Canales-Rodríguez EJ, Melie-García L, Valdés-Hernández PA, Martínez-Montes E, Alemán-Gómez Y, Sánchez-Bornot JM. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. Neuroimage. 2007;36:645–660. doi: 10.1016/j.neuroimage.2007.02.012. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y, Sotero RC, Canales-Rodríguez EJ, Alemán-Gómez Y, Melie-García L. Studying the human brain anatomical network via diffusion-weighted MRI and Graph Theory. Neuroimage. 2008;40:1064–1076. doi: 10.1016/j.neuroimage.2007.10.060. [DOI] [PubMed] [Google Scholar]
- Kamada T, Kawai S. An algorithm for drawing general undirected graphs. Information Processing Letters. 1989;31:7–15. [Google Scholar]
- Kelly AMC, Di Martino A, Uddin LQ, Shehzad Z, Gee DG, Reiss PT, Margulies DS, Castellanos FX, Milham MP. Development of Anterior Cingulate Functional Connectivity from Late Childhood to Early Adulthood. Cereb. Cortex. 2009;19:640–657. doi: 10.1093/cercor/bhn117. [DOI] [PubMed] [Google Scholar]
- Knickmeyer RC, Gouttard S, Kang C, Evans D, Wilber K, Smith JK, Hamer RM, Lin W, Gerig G, Gilmore JH. A Structural MRI Study of Human Brain Development from Birth to 2 Years. Journal of Neuroscience. 2008;28:12176–12182. doi: 10.1523/JNEUROSCI.3479-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latora V, Marchiori M. Efficient Behavior of Small-World Networks. Physical Review Letters. 2001;87:198701. doi: 10.1103/PhysRevLett.87.198701. [DOI] [PubMed] [Google Scholar]
- Latora V, Marchiori M. Economic small-world behavior in weighted networks. Eur. Phys. J. B. 2003;32:249–263. [Google Scholar]
- Lewis JD, Theilmann RJ, Sereno MI, Townsend J. The Relation between Connection Length and Degree of Connectivity in Young Adults: A DTI Analysis. Cerebral Cortex. 2009;19:554–562. doi: 10.1093/cercor/bhn105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin W, Zhu Q, Gao W, Chen Y, Toh CH, Styner M, Gerig G, Smith JK, Biswal B, Gilmore JH. Functional Connectivity MR Imaging Reveals Cortical Functional Connectivity in the Developing Brain. AJNR Am J Neuroradiol. 2008;29:1883–1889. doi: 10.3174/ajnr.A1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T. Disrupted small-world networks in schizophrenia. Brain. 2008;131:945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
- Luna B, Sweeney JA. The emergence of collaborative brain function - fMRI studies of the development of response inhibition. Adolescent Brain Development: Vulnerabilities and Opportunities. 2004;1021:296–309. doi: 10.1196/annals.1308.035. [DOI] [PubMed] [Google Scholar]
- Maslov S, Sneppen K. Specificity and Stability in Topology of Protein Networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103. [DOI] [PubMed] [Google Scholar]
- Matsuzawa J, Matsui M, Konishi T, Noguchi K, Gur RC, Bilker W, Miyawaki T. Age-related volumetric changes of brain gray and white matter in healthy infants and children. Cerebral Cortex. 2001;11:335–342. doi: 10.1093/cercor/11.4.335. [DOI] [PubMed] [Google Scholar]
- Ment LR, Kesler S, Vohr B, Katz KH, Baumgartner H, Schneider KC, Delancy S, Silbereis J, Duncan CC, Constable RT, Makuch RW, Reiss AL. Longitudinal Brain Volume Changes in Preterm and Term Control Subjects During Late Childhood and Adolescence. Pediatrics. 2009;123:503–511. doi: 10.1542/peds.2008-0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D, Achard S, Morcom A, Bullmore E. Age-related changes in modular organization of human brain functional networks. NeuroImage. 2009;44:715–723. doi: 10.1016/j.neuroimage.2008.09.062. [DOI] [PubMed] [Google Scholar]
- Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Phys Rev E. 2004;69:026113. doi: 10.1103/PhysRevE.69.026113. [DOI] [PubMed] [Google Scholar]
- Paterson SJ, Brown JH, Gsödl MK, Johnson MH, Karmiloff-Smith A. Cognitive Modularity and Genetic Disorders. Science. 1999;286:2355–2358. doi: 10.1126/science.286.5448.2355. [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Coleman MR, Pickard JD, Menon D, Bullmore E. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb Cortex. 2005a;15:1332–1342. doi: 10.1093/cercor/bhi016. [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Phil Trans R Soc Lond B. 2005b;360:937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampaio R, Truwit C. Myelination in the developing brain. In: Nelson C,A, L M, editors. Handbook of Developmental Cognitive Neuroscience. MIT Press; Cambridge, MA: 2001. pp. 35–44. [Google Scholar]
- Shen D, Davatzikos C. HAMMER: Hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Shen DG, Davatzikos C. Very high resolution morphometry using mass-preserving deformations and HAMMER elastic registration. NeuroImage. 2003;18:28–41. doi: 10.1006/nimg.2002.1301. [DOI] [PubMed] [Google Scholar]
- Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. SPIE medical Imaging. Lake Buena Vista, FL: 2009. Neonate brain MRI segmentation using subject-specific probabilistic atlas. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Holmes CJ, Jernigan TL, Toga AW. In vivo evidence for post-adolescent brain maturation in frontal and striatal regions. Nature Neuroscience. 1999;2:859–861. doi: 10.1038/13154. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Trauner DA, Gamst A, Jernigan TL. Development of cortical and subcortical brain structures in childhood and adolescence: a structural MRI study. Developmental Medicine and Child Neurology. 2002;44:4–16. doi: 10.1017/s0012162201001591. [DOI] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. Organization, development and function of complex brain networks. Trends in Cognitive Sciences. 2004;8:418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Sporns O, Kötter R. Motifs in Brain Networks. PLoS Biology. 2004;2:e369. doi: 10.1371/journal.pbio.0020369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kotter R. The human connectome: a structural description of the human brain. PLoS Comp. Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srinivasan R. Spatial structure of the human alpha rhythm: global correlation in adults and local correlation in children. Clinical Neurophysiology. 1999;110:1351–1362. doi: 10.1016/s1388-2457(99)00080-2. [DOI] [PubMed] [Google Scholar]
- Stam C, Reijneveld J. Graph theoretical analysis of complex networks in the brain. Nonlinear Biomedical Physics. 2007;1:3. doi: 10.1186/1753-4631-1-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ. Functional connectivity patterns of human magnetoencephalographic recordings: a “small-world” network? Neurosci Lett. 2004;355:25–28. doi: 10.1016/j.neulet.2003.10.063. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Sowell ER, Gogtay N, Giedd JN, Vidal CN, Hayashi KM, Leow A, Nicolson R, Rapoport JL, Toga AW. Structural MRI and Brain Development. International Review of Neurobiology. 2005;67:285–323. doi: 10.1016/S0074-7742(05)67009-2. [DOI] [PubMed] [Google Scholar]
- Tononi G, Sporns O, Edelman GM. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences of the United States of America. 1994;91:5033–5037. doi: 10.1073/pnas.91.11.5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated Anatomical Labeling of Activations in SPM Using a Macroscopic Anatomical Parcellation of the MNI MRI Single-Subject Brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.