The prediction of ⁵⁷Fe Mössbauer parameters by the density functional theory: a benchmark study

Abstract

We report the performance of eight density functionals (B3LYP, BPW91, OLYP, O3LYP, M06, M06-2X, PBE, and SVWN5) in two Gaussian basis sets (Wachters and Partridge-1 on iron atoms; cc-pVDZ on the rest of atoms) for the prediction of the isomer shift (IS) and the quadrupole splitting (QS) parameters of Mössbauer spectroscopy. Two sources of geometry (density functional theory-optimized and X-ray) are used. Our data set consists of 31 iron-containing compounds (35 signals), the Mössbauer spectra of which were determined at liquid helium temperature and where the X-ray geometries are known. Our results indicate that the larger and uncontracted Partridge-1 basis set produces slightly more accurate linear correlations of electronic density used for the prediction of IS and noticeably more accurate results for the QS parameter. We confirm and discuss the earlier observation of Noodleman and co-workers that different oxidation states of iron produce different IS calibration lines. The B3LYP and O3LYP functionals have the lowest errors for either IS or QS. BPW91, OLYP, PBE, and M06 have a mixed success whereas SVWN5 and M06-2X demonstrate the worst performance. Finally, our calibrations and conclusions regarding the best functional to compute the Mössbauer characteristics are applied to candidate structures for the peroxo and Q intermediates of the enzyme methane monooxygenase hydroxylase (MMOH), and compared to experimental data in the literature.

Introduction

Mössbauer spectroscopy^1,2 is a valuable experimental technique, especially suitable for the study of iron-containing substances. It is sensitive to the distribution of charge density around the ⁵⁷Fe nuclei and is used to probe the geometric and electronic structures of molecular systems of all types – from simple inorganic salts to metalloproteins. The investigation of complex catalytic cycles of iron-containing proteins has particularly benefited from Mössbauer spectroscopy. ^3–8

Recently there has been a surge of applications of density functional theory (DFT) to predict Mössbauer spectra.^{9–14,16–20} DFT, combining rigorous physics and numerical parameterization, serves as a de facto standard in theoretical investigations of biological processes that are dependent on quantum effects. The following parameters are most often computed and compared to experiment: the isomer shift (IS) δ, quadrupole splitting (QS) ΔE, and the asymmetry parameter η. Several papers report an acceptable agreement between theory and experiment ^14,17,20,21 for medium-sized complexes, suggesting that DFT can be regarded as a well-behaved method for predicting Mössbauer characteristics. This situation appears to be in contrast to many other applications where pure DFT suffers from drawbacks such as defective description of dispersion interaction and systematic errors in predicting thermochemistry^22,23 that need to be remedied by separate treatments. ^24,25 However, several cases have been described in which DFT completely failed to agree with experiment in accounting for the quadrupole splitting parameter, ^26,27 arguably owing to DFT’s single-reference character.

Despite extensive applications of DFT to computing Mössbauer parameters there have been very few studies with the goal of assessing the accuracy of various functionals and basis sets on a broad set of iron-containing compounds. The complexity of novel DFT functionals and the quantity of empirical parameters on which they are based have reached a point at which it is difficult to reliably predict their accuracy, judging only from the physical approximations that went into constructing the functional. In this situation benchmarking using a diverse data set becomes a necessary step. A different view of the problem is provided by the practical difficulty encountered when predicting the geometries of intermediates in catalytic cycles of iron-containing proteins. These intermediates are of often unknown structure, are typically unstable, and cannot be crystallized. When the experimental Mössbauer spectra are available, the computation of IS and QS allows one to choose the most probable candidates from the variety of considered model structures. However, the tendency of different functionals to produce somewhat different IS and especially QS parameters may not only lead to confusion (provided a few functionals have been used in the study)³ but also create the possibility of reconciling the experimental values with the theoretical ones in-PCCP-2758-10 or several candidate structures. Determining the ‘error bars’ and placing the functionals into ‘accuracy classes’ with respect to their ability to predict Mössbauer characteristics would alleviate the uncertainty of such situations. At the end of this paper we demonstrate the application of this strategy to the enzyme methane monooxygenase hydroxylase.

Several authors have made progress in assessing the quality of the functionals with respect to the accuracy of their Mössbauer parameter predictions. Nemykin and Hadt compared the performance of BPW91 and B3LYP on a broad range of ferrocene derivatives and other compounds.¹⁷ The group of Oldfield tested these two functionals on porphyrin derivatives¹² and some unusual 2- and 3-coordinate Fe(II) complexes.²¹ The first of these works concludes that B3LYP performs slightly better than BPW91 (except for ferrocene derivatives, where it seriously overestimates quadrupole splittings), whereas the second found no significant difference between the accuracy of these two functionals. At the same time, the group of Noodleman uses another set of functionals - OLYP, OPBE, and PW91,^{4,15,16,28,29} with variable success in case of PW91. Römelt et al.¹⁹ evaluated five diverse functionals (BP86, TPSS, TPSSh, B3LYP, and B2PLYP) on their accuracy in predicting isomer shift on a set of twenty compounds.

Even though these efforts set useful guidelines, a more thorough benchmarking is desired in order to improve some of the aspects of these studies. Below we review some of their deficiencies and describe the improvements that we have made to achieve our goal in the present study.

All the previous investigations considered the Mössbauer data points collected at different temperatures – from room temperature to 4.2 K. Although this choice may have been driven by the relative paucity of Mössbauer data, such data sets nevertheless seem highly questionable because Mössbauer spectra typically have a strong temperature dependence. The dependence arises from different populations of low lying excited states as well as the corresponding geometry changes. Theoretical calculations of ground states that do not take thermal smearing into account should be compared to the Mössbauer spectra measured at the lowest practical temperature −4.2 K. The linear extrapolations of both IS and QS to 4.2 K performed by Noodleman and co-workers ^16,28 may improve the quality of the data set, but this operation should be avoided in a benchmark study because nontrivial temperature dependence of Mössbauer parameters or absence thereof is very common (see, for example, Refs.^30,79). The data set employed in the present work is restricted solely to spectra taken at liquid helium temperature. Another important restriction on a data set is constructing it exclusively from the molecular systems for which X-ray and Mössbauer spectra are known and belong to the same compound. Very often simple ions (such as ${\text{FeCl}}_4^{2-}$) included in the data set have multiple Mössbauer spectra available, corresponding to different counterions and/or crystallization conditions.³⁰ Notable changes in geometry of these ions, apparent in X-ray results, naturally give rise to slightly different Mössbauer parameters and sometimes lead to the citation of different experimental values for the same ion, comparing them to Mössbauer data obtained from DFT-optimized geometries, as in the case of ${\text{FeCl}}_4^{2-}$ in Refs.¹³ and.²⁹ Whether or not the DFT can accurately predict Mössbauer parameters corresponding to different crystallographic variants of the same ion is a separate question which we leave for another study. The experimentally determined geometries selected for our test set were unimpaired: they did not have any parts of the structure missing and did not require additional reconstruction. One more restriction on the test set entries is that their multiplicity and the spin state of the iron atoms is known for certain, and those displaying spin crossover were excluded.

The issues discussed in the previous paragraph pertain to the stricter selection of the molecular systems for the test set. However, it is possible to also introduce improvements of an ‘extensive’ nature – a larger set of parameters and conditions under which benchmarking is performed. Here we study the performance of eight functionals - B3LYP,^31,35,36 BPW91,^32–34 M06,⁴⁰ M06-2X,⁴⁰ O3LYP,^31,37 OLYP,^31,38 PBE,³⁹ and SVWN5.^41–43 The first two of these have been widely used for predicting Mössbauer parameters. M06 and M06-2X are two interesting new functionals worth investigating in the light of their superior accuracy in various calculations.⁴⁰ M06 is parametrized for organometallic and inorganometallic chemistry, whereas M06-2X should have a well-balanced, universal applicability. However, there is no guarantee that the optimization protocols used to populate over 30 adjustable parameters for these functionals leads to improved performance in predicting Mössbauer spectra that were not included in the training set.

Here, M06 and M06-2X are applied for prediction of the Mössbauer parameters for the first time. O3LYP and OLYP are built upon Handy’s OPTX exchange functional and showed superior accuracy in predicting electronic densities among several functionals⁴⁴ as well as in other benchmarks.⁴⁵ The last two functionals, PBE and the local density approximiation (LDA) SVWN5, are considered more ‘physical’ rather than ‘empirical’ and, even though they are not functionals of choice in numerous modern applications, at times they display unexpected prominence. For LDA’s impressive result for the dispersion interaction energetics, see Ref.46 This set is the largest selection of functionals to be studied systematically in the context of the Mössbauer spectra. Unfortunately, we were unable to evaluate such promising modern functionals as TPSSh ⁴⁷ and B2PLYP⁴⁸ because they were not available in our computational package, Jaguar. B2PLYP was recently shown to yield the best linear fits of the isomer shift.¹⁹ However, the performance of B2LYP was only slightly superior to that of B3LYP, which is included in this study.

All the calculations in this work were performed with Gaussian-type (GT) basis sets. The alternative is Slater-type (ST) basis sets, which better approximate orbitals in the proximity of the nuclei. However, GT bases are much more computationally tractable, which makes software capable of handling ST raren excellentZhang and Oldfield compared the effect of these two types of basis sets on the predicted Mössbauer parameters and found no apparent advantage of ST versus GT bases.²¹ In this work we use two Gaussian bases on iron nuclei – Partridge⁴⁹ and Wachters. ⁵⁰ They both contain very large exponential coefficients on s-primitives to facilitate the reproduction of nuclear cusp but the Partridge basis set is completely uncontracted which makes it significantly larger than Wachters. The groups of Neese ¹³ and Filatov^20,51 prefer uncontracted bases but other authors ^12,17 suggest that the quality of the Wachters basis set (with contraction and smaller exponential coefficients) is sufficient. Kurian and Filatov,¹⁸ who computed the isomer shift from Filatov’s non-empirical approach, ⁵¹ also conclude that completely uncontracted bases are not necessary to achieve good accuracy. The comparison of the accuracy of the contracted and uncontracted basis sets on a large data set seems logical.

Another logical comparison for a comprehensive benchmarking study is that between Mössbauer parameters obtained from the X-ray geometries and DFT-optimized geometries. Both sources introduce different types of errors. The coordinates of heavy atoms in X-ray geometries, dependent on resolution and thermal atomic motion, are generally considered highly accurate for most measurements. However, such measurements are not always available. Additionally, the positions of the hydrogen atoms cannot usually be extracted from the X-ray data, and such atoms have to be added by means of computational algorithms. DFT-optimized geometries, although readily procurable, are subject to errors inherent in functionals and finite basis sets. Functionals such as B3LYP and O3LYP have established an excellent reputation in optimizing the geometries of organic molecules. Their performance on metal-containing systems is not so well tested and is therefore less reliable. Despite this deficiency, Han and Noodleman argue that it is more fair to use DFT-optimized geometries in DFT Mössbauer calculations because these geometries correspond to energetic minima within the DFT model. It perhaps assumed that the reported X-ray geometries differ, through either crystallization, distortion or bad resolution, from the ‘relaxed’ configurations for which the Mössbauer parameters are measured, and DFT optimization in principle alleviates this proposed effect. It must be noted that DFT optimizations are typically performed at a lower level of theory than that used for subsequent Mössbauer calculations, so that in such cases the single-point electronic density still does not correspond to the optimal geometry. Still, it is not clear which of these errors dominates. Nemykin and Hadt, ¹⁷ who studied the question, observed little variation of results, but their data set was not very diverse and predominantly consisted of high- and medium-temperature experimental data points.

In this work we compute the Mössbauer parameters from both X-ray and DFT-optimized geometries using a typical protocol for the optimization (see the computational details section for the details). When we pick a particular optimization protocol out of many possible protocols we do not attempt to conclude after the analysis of the results which source of the geometries (theoretical or experimental) produces better accuracy, except in a few cases where there are large differences in the results as compared to experiment. In comparing results obtained from both types of geometries we are only trying to assess the particular optimization method we have chosen and also understand to what degree the small changes of the positions of atoms influence the Mössbauer results.

To summarize, we investigate the prediction of IS and QS by 8 functionals combined with 2 Gaussian basis sets of different composition, and 2 sources of geometries (X-ray and optimized). The experimental data for our test set consisting of 31 compounds and 35 individual Mössbauer signals was obtained at liquid helium temperature. We believe ours to be the most comprehensive such study to date.

Finally, we apply our optimized DFT Mossbauer protocol to computation of Mossbauer spectra for various intermediates in the catalytic cycle of methane monooxygenase hydroxylase (MMOH), a nonheme diiron protein that converts methane to methanol under room temperature conditions. ^53,54 Using criteria developed in our benchmark study, we achieve good agreement between calculated and experimental Mossbauer data for a number of MMOH structures. The benchmarking data are essential in assessing the degree to which Mossbauer comparisons can be used to confirm, or rule out, assignment of three dimensional structures to experimentally observed intermediates.

Computational details

All the DFT calculations were performed using the locally modified Jaguar 7.5 program. ⁵² Although Jaguar commonly employs the pseudospectral approach,^55–59 speeding up the solution of the Kohn-Sham equations significantly, we computed all the integrals analytically so as not to introduce a potential source of error in the benchmarking study. The unrestricted Kohn-Sham equations converged to 10⁻⁸ Hartree in energy, and fine grids were employed for the computation of densities on iron atoms. The medium quality of wave function (converged to 10⁻⁶ Hartree) and coarse grids were generally sufficient in case of the Wachters basis but not in the case of the Partridge basis set (see Ref.13 for a detailed discussion of this effect).

The uncontracted Partridge basis set had the structure (20s,12p,9d) and the contraction scheme of the Wachters was 62111111/331211/3111. The basis set on all the non-iron atoms in single-point calculations was cc-pVDZ. These basis sets can be obtained from the EMSL Basis Set Exchange database.⁶⁰ The d-orbitals carried pure orbital momentum. For geometry optimizations, the pseudospectral approach was used, with a B3LYP functional, the LACVP* basis set⁶¹ on iron atoms and 6-31G* on all other atoms. Many complexes in our data set contained over 100 atoms (the largest being 134 atoms) so this approximation level was necessary. We realize that the offered optimization model does not serve as the single ‘ultimate’ representation of all the optimization models, to be evaluated against the X-ray crystallography in its function to furnish accurate geometries; rather, it is a functional method comparable to that which served us reliably in the past. ⁶²

The models representing the compounds from Table I were initially constructed from the experimental crystal structures. Counter-ions and solvent molecules were not included. In constructing the models, we took care to preserve as much of the original structure as possible. In some rare cases, however, we had to replace extremely large (and seemingly not important for the electric field gradient on the iron atoms) groups in the ligands by smaller ones, to reduce the size of the system. These structures were used as the starting point in the geometry optimizations. All the X-ray-based geometries used in our calculations are available in the Supplementary material.

Table 1.

The test set of compounds used for benchmarking in this work. The six-letter codes refer to the Cambridge Structural Database identifiers. The coupling constant J is given when known. The ligands are encoded as follows: BIPhMe = bis(1-methylamidazol-2-yl)phenylmethoxymethane, DTSQ = bis(dithiodithiosquarato-S,S′) dianion, Et-HPTB = N,N,N′,N′-tetrakis(N-ethyl-2-benzimidazolylmethyl)- 1,3-diaminopropane), ImH = imidazole, HB(mtda^R)₃ = tris(mercaptothiadiazolyl)borate, HBpz₃ = hydrotris-1-(pyrazolyl)borate, HO₂CAr^Mes = 2,6-bis(mesityl)benzoic acid, MBTHx = bis(N-methylbenzothiohydroxamato) anion, Me₃TACN = 1,4,7-trimethyl-1,4,7-triazacyclonane, OEP = dianion of octaethylporphyrin, OEP = dianion of trans-7,8-dihydro-octaethylporphyrin, Piv = pivalate, “S2” = 1,2-Benzenedithiolato-S,S′ dianion, TAML = tetra-amido macrocyclic ligand,¹⁰¹ TMEN = N,N,N′,N′-tetramethylethylenediamine, TMIP = tris(methylimidazol-2-yl)phosphine, TPA = tris(2-pyridylmethyl)amine, TTC = tetrachlorocatecholato-O,O′ dianion, XDK = acid anion of m-xylenediamine bis(Kemp’s triacid)-imide

No.	System	Code	Fe oxidation	Spin	δ, mm/s	|Δ E |, mm/s	J, cm−1	R-factor, %	Reference
1.	Fe2 (O2CH)2(BIPhMe)2	SISKOU	+2	0	1.26	2.56	~ 0	4.1	78
			+2		1.25	3.30
2.	Fe(HB(mtdaR)3)2	JOHCEP	+2	0	0.49	0.26	–	4.83	79
3.	Fe2 (OAc)2(TPA)22+	VUNMIA	+2	0	1.12	3.33	~ 1	4.7	80
4.	Fe2 (ImH)2(XDK)(O2CPh)2 (MeOH)	YUZKAF10	+2	0	1.35	3.04	−0.51	8	81
			+2		1.12	2.83
5.	Fe2 (py)2 (O2CArMes)4	XIGDIA	+2	0	1.14	3.23	30	5.44	82
6.	Fe(OEP)CO	YEQPOA	+2	0	0.27	1.84	–	2.85	83
7.	Fe(OEP)	DEDWUE	+2	1	0.63	2.55	–	7.2	84
8.	Fe(OEC)	BUYKUB10	+2	1	0.62	1.71	–	6	84
9.	Fe3 (SPh)6(CO)6	FATBOR	+2	2	1.00	2.00		3.9	85
			+2		0.10	0.22
10.	Fe2 (H2O)(O2CPh)4 (TMEN)2	VUPJUL	+2	2	1.25	3.11	small	4.4	86
			+2		1.26	2.70
11.	Fe2 (H2O)(OAc)4(TMEN)2	VUPJOF	+2	2	1.27	2.75	small	5.5	86
12.	$\text{Fe}{(\text{DTSQ})}_2^{2-}$	PTSQFE10	+2	2	0.67	4.01	5.5		87
13.	$\text{Fe}{(\text{SPh})}_4^{2-}$	PTHPFE10	+2	2	0.66	3.24	4.7		87
14.	Fe2 O(HBpz3)2(OAc)2	CACZIP10	+3	0	0.52	1.60	−121	4	88
15.	Fe2 (OH)(HBpz3)2(OAc)2	COCJIN10	+3	0	0.47	0.37	~ −17	4.8	93
16.	${\text{Fe}}_2(\text{OH}){({\text{O}}_2\text{P}{(\text{OPh})}_2)}_3{({\text{HBpz}}_3)}_2^{2+}$	PIMTAG	+3	0	0.44	0.44	~ minus;15	6.9	93
17.	${\text{Fe}}_2\text{O}{(\text{PiV})}_2{({\text{Me}}_3\text{TACN})}_2^{2+}$	ZOCPEM	+3	0	0.48	1.54	−111	6.6	89
18.	${\text{Fe}}_2{(\text{O})}_2{(6-{\text{Me}}_3-\text{TPA})}_2^{2+}$	YOCKAC	+3	0	0.50	1.93	54	6.5	90
19.	Fe2 (NO)2(Et-HPTB)(O2CPh)	RABHAD	+31	0	0.67	1.44	−23	8.5	91
20.	Fe2 (S-t-Bu)2 (NO)2	GIDKIN02	+3	0	0.15	0.90		2.11	92
21.	(Fe(Me3 TACN)(TTC))2O	YOHMOX	+3	0	0.46	1.41	−90	6.5	94
22.	${\text{Fe}}_2\text{O}{(\text{TMIP})}_2{(\text{OAc})}_2^{2+}$	JIGNUI	+3	0	0.52	1.61	−120	5.7	95
23.	$\text{Fe}(\text{OEP}){(4-{\text{NMe}}_2\text{Py})}_2^{2+}$	VOFLOR	+3	1/2	0.26	2.15	–	6.7	96
24.	Fe(S-t-Bu)3 NO	WEDXAF	+3	3/2	0.26	0.46	–	2.93	92
25.	FeCl5 (H2O)2−	VOCBAQ	+3	5/2	0.49	0.56	–	3.2	97
26.	$\text{Fe}{(\text{SEt})}_4^{-}$	CANDAW10	+3	5/2	0.25	0.62	–	5	98
27.	$\text{Fe}{(\text{NO})}_2{(\text{S}(p-\text{Me})\text{Ph})}_2^{-}$	SONMUE	+3	5/2	0.18	0.69	–	3.55	99
28.	FeCl(MBTHx)2	CELVEU	+3	5/2	0.43	0.98	–	3.8	100
29.	(Fe(TAML)2)2O−	KAJBIH	+4	0	−0.07	3.3	> 100	5.32	101
30.	Fe(PPh3)2(“S”)2	SOCVUB	+4	1	0.16	1.52	–	5.9	102
31.	Fe(PPh3)(“S2”)2	SOCWAI	+4	1	0.12	3.03	–	4.6	102

Data set

In constructing the data set, apart from the criteria for the soundness of the X-ray and Mössbauer experimental data, we included diverse chemical structures. The data set used in this work is presented in Table I. It comprises compounds with the iron atoms in oxidations states +2, +3, +4, and in low as well as high spin states. The total spin is n/2 where n varies from 0 to 5.

The main chemical classes from Table I are as follows where the numbers in the parentheses refer to the identity numbers in the table: (i) diiron(II) (1,3–5,10–11) and diiron(III) (14–18,22) ligand complexes with bridging carboxylates, which may be regarded as structural models for the active sites of bacterial multicomponent monooxygenases,⁶³ (ii) nitrosyl complexes (19–20,24,27), (iii) porphyrin derivatives (6–8), and (iv) compounds with multiple sulfur-atoms in the coordination sphere (9, 12–13, 26, 30–31). Complexes 6 and 9 contain CO. With the exception of [Fe(H₂O)Cl₅]²⁻ (entry 25), we did not include simple complexes containing 7–15 atoms due to the absence of a complete package of experimental data. Many Mössbauer studies of such complexes were conducted over four decades ago and are not accompanied by X-ray crystal structures, whereas the recently deciphered crystal structures and with counter-ions such as $\text{Fe}{({\text{H}}_2\text{O})}_6^{3+}$ and ${\text{FeCN}}_6^{3-}$ offer little interesting in the configuration of these counter-ions to warrant investigation by the Mössbauer spectroscopy.

Some of these complexes have been included in the test sets of others^15,16,28 but several were investigated theoretically in this work for the first time. No systematic examination of electronic structure of these compounds was attempted, for to do so would reach beyond the benchmarking objectives of this work. Although we discuss some of the numbers produced for the individual compounds, our focus is on statistics and the comparison of the general performance of theoretical methods with respect to the IS and QS properties.

Counterions or crystal inclusions were not included in the systems in our test set for the following reasons. First, the location of counterions was not always available in the crystallographic data. Including counterions in some systems and omitting them in others might introduce a bias that would be undesirable in a benchmark study. Second, some counterions were fairly large organic systems, containing a few dozen atoms each, such as ${\text{BPh}}_4^{-}$, co-crystallized with our VUNMIA system.⁸⁰ Their inclusion and treatment within a DFT scheme would make some of our calculations prohibitively expensive. Third, our experimentation with environment showed a marginal influence of counterions and co-crystallized neutral molecules on the Mössbauer parameters of the iron complex unders study. This observation is in accord with an earlier study ²¹ that reports no change in predicted isomer shift and quadrupole splitting upon inclusion of a counterion in their DFT calculations. Although some theoretical studies provide special treatment of environment, ²⁰ many other do not and still report accurate Mössbauer parameter predictions. ^12,18,19

The experimental isomer shifts varied between 1.35 and −0.07 mm/s, a typical experimental range for most iron-containing complexes. ${\text{FeO}}_4^{2-}$, often placed at the bottom of test sets for its extraordinarily low isomer shift value, ⁶⁴ did not satisfy a number of the filtering criteria mentioned in the Introduction (for instance, no data at liquid helium temperature). There is a noticeable gap in experimental isomer shifts between 0.67 and 1.00 mm/s in our data set. This region, marking a transition between diiron(III) and diiron(II) formal redox states, is also either very sparsely populated or empty in other researchers’ data sets. ^15–17,29 The absolute value of the experimental quadrupole splittings ranged from 0.22 to 4.01 mm/s. The slightly unusual maximal value corresponds to distorted complex 12, the DFT-predicted quadropole splitting of which is an outlier in Ref.28 Apart from the gap between 1.0 and 1.4 mm/s (which does not seem to be a rare interval), the rest of the quadrupole splittings in Table I set are distributed more or less uniformly.

Isomer shift

Multiple studies outline the quantum theory of the Mössbauer isomer shift (see Refs.^65,66 and references therein). The parametrization method, which represents the isomer shift as depending linearly on the electronic density on iron nuclei, ρ(0)

$$\delta =\alpha \rho (0)+C,$$ (1)

where α and C are empirically determined coefficients, has been found to be accurate and robust in a great number of DFT publications.^13,15,17,29 This linear relationship has also been observed in the complete active space self-consistent field (CASSCF) calculations on a small test set.⁶⁷ For an alternative, non-empirical computation of the isomer shift, which employs derivatives of the electronic energy with respect to the size of the non-point-like nucleus and which is more laborious, see Refs.^18,51,68,69 The slope α and intercept C are typically obtained with the least-squares method using a parametrization set of experimental isomer shifts and theoretically-computed densities ρ(0). Several high-quality studies that attempt to match experimental and theoretical values of the slope α are available.^19,20,70 Because the densities on the nuclei vary with the basis set and the functional used,⁴⁴ each such combination necessitates a separate parametrization (Eq. (1)). Since many researchers are likely to prefer different bases and ways of computing the wave function they will have to perform a parametrization of their own, but one way to simplify their task is to make available the atomic coordinates of the entries of a large and reliable test set as we do in the present work.

The mean unsigned errors (MUEs) obtained from the X-ray geometries for 8 functionals and both basis sets are given in Table II. The results can be broadly classified into two categories. For hybrid functionals such as B3LYP or O3LYP, the data lie on a single straight line, providing a parametrization (converting the calculated IS into the experimental IS) that can be applied to an arbitrary complex. For many of the other functionals, including the LDA, gradient corrected functionals, and the M06 and M06-2X functionals, the data can be better characterized as lying on two parallel straight lines, with the location of each point depending upon whether the Fe atoms have a formal oxidation state of +2 or +3/+4. Using a dual parametrization for these functionals substantially improves their results, although it can create problems for molecules where the assignment of formal oxidation state is problematic or ambiguous, e.g. Fe-nitrosyl complexes, which are well known to have a complex electronic structure in many cases.^72,73 We report results using both types of parametrizations for all functionals for completeness, although the difference for the hybrid functionals is quite small. The ability to use a single parametrization is an advantage for the hybrid functionals, making them (in our view) the approach of choice for computation of IS values.

Table 2.

The isomer shift MUE’s for the data set presented in Table I computed with the Wachters and Partridge-1 basis sets and tight convergence criteria. The MUE’s are given in mm/s. The +2 column includes the signals iron atoms with the oxidation state +2. Similarly, the +3,+4 column includes the signals iron atoms with the oxidation state +3 and +4. The ‘all’ column includes all signals. There are 17 signals from the +2 irons and 18 signals from +3,+4.

	Wachters			Partridge-1
Functional	MUE (+2)	MUE (+3, +4)	all	MUE (+2)	MUE (+3, +4)	all
B3LYP	0.0283	0.0285	0.0324	0.0272	0.0238	0.0296
BPW91	0.0358	0.0289	0.0772	0.0349	0.0253	0.0733
M06	0.0334	0.0352	0.0370	0.0524	0.0344	0.0450
M06-2X	0.0380	0.0342	0.0426	0.0581	0.0345	0.0564
OLYP	0.0352	0.0321	0.0756	0.0372	0.0269	0.0703
O3LYP	0.0320	0.0291	0.0461	0.0285	0.0277	0.0420
PBE	0.0355	0.0291	0.0793	0.0350	0.0253	0.0746
SVWN5	0.0355	0.0318	0.0845	0.0383	0.0274	0.0822

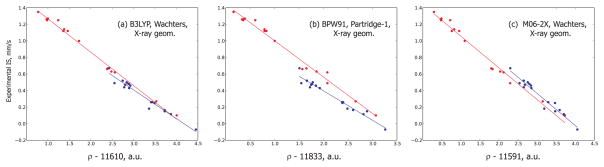
The basis set effects are relatively minor, although the larger and more flexible Partridge basis unsurprisingly set yields slightly better linear correlations overall. Either basis set can be judged suitable for practical applications. The average errors reported in Table 2 represent a best case scenario; in reality, there will be additional noise due to the use of DFT (as opposed to X-ray) geometries (discussed further below) and also the introduction of novel chemistries not covered in this data set. Nevertheless, our results provide a reasonable starting point for estimating an acceptable deviation of theory from experiment, which we develop further in the Discussion section.

We report the slope and intercept constants for all combinations of the functionals and the basis sets in the supplementary material. Direct comparison of our slope constants with the most accurate theoretical value available to date, $-0.31\pm 0.04a_0^{3}mm/s$,²⁰ is not possible because our study did not include relativistic treatment. However, our slope and intersect are in excellent agreement with those obtained by others⁷⁴ and co-workers in a non-relativistic calibration for the B3LYP/Wachters combination. Additionally, if we use a correction factor of 1.30 employed to scale non-relativistic densities to relativistic ones,^74,75 our best performing functional/basis combinations produce the α constant in the range of $-0.31÷-0.32a_0^{3}mm/s$, in excellent agreement with the best available theoretical value.

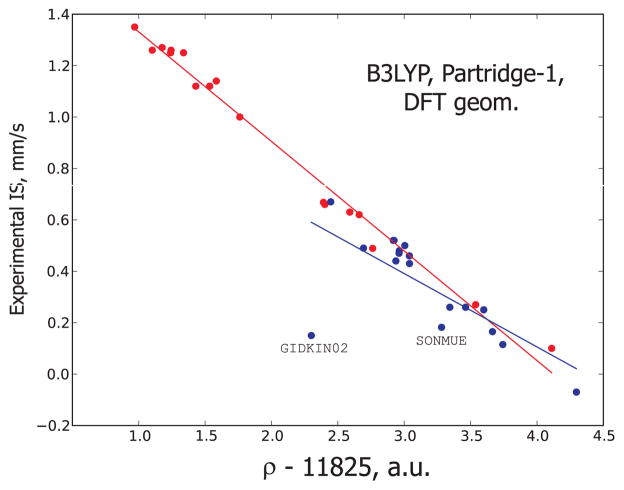
The optimized geometries produced mixed-quality isomer shift results (see Fig. 3 and compare it to Fig. 1(a)). Most of the +2 oxidation-type densities show a very good linear correlation versus the experimental isomer shifts. However, the +3, +4-type points are visibly quite scattered showing a poorer linear correlation. The two greatest outliers are the structurally similar nitrosyl complexes - Fe₂(S-t-Bu)₂(NO)₂ (GIDKIN02) and ${\text{Fe(NO)}}_{\text{2}}{(\text{S}(p-\text{Me)Ph})}_2^{-}$ (SONMUE), the former being particularly prominent. This discrepancy is all the more remarkable for the fact that the outliers of this magnitude have not been observed for any of the isomer shifts computed from the experimental geometries. Because the isomer shift of GIDKIN02 lies greatly beyond the rest of the data points regardless of the functional used, we need to seek the answer to this behavior in the optimized geometry of the complex. Table III compares the experimental and DFT-optimized geometries of the two above-mentioned outliers. Clearly, our DFT optimization protocol does not reproduce some of the geometrical elements of GIDKIN02 correctly. The Fe-N and Fe-S distances are greatly overestimated and the N-Fe-N angle is much smaller than that reported by the X-ray crystallography. The rest of the optimized geometry matches the experimental geometry quite accurately (compare, for example, the N-O and S-C distances which almost coincide). Some structural variations are also observed for the optimized structure of the SONMUE complex but they are not as serious as in the case of GIDKIN02. The DFT optimization of the other complexes did not result in obvious structural incongruities.

Figure 3.

The linear correlations observed between electronic density on iron and experimental isomer shift computed with the B3LYP functional and Partridge-1 basis set for the DFT-based geometries. The data in red correspond to the oxidation state +2, and the data in blue correspond to the oxidation states +3 and +4.

Figure 1.

Some linear correlations observed between electronic density on iron and experimental isomer shift for the X-ray-based geometries. The data in red correspond to the oxidation state +2, and the data in blue correspond to the oxidation states +3 and +4.

Table 3.

The geometrical parameters of the complexes Fe₂(S-t-Bu)₂(NO)₂ (GIDKIN02) and $\text{Fe}{(\text{NO})}_2{(\text{S}(p-\text{Me})\text{Ph})}_2^{-}$ (SONMUE) (which are the greatest outliers in Fig. 3) obtained from two sources – DFT optimization and X-ray crystallography. The distances are given in Angstrom and the angles are in degrees.

	GIDKIN02		SONMUE
Parameter	DFT opt.	X-ray	DFT opt.	X-ray
d(Fe – N)	1.85	1.67	1.76	1.71
d(Fe – S)	2.38	2.25	2.38	2.33
d(N – O)	1.17	1.17	1.18	1.18
d(S – C)	1.90	1.87	1.78	1.80
∠(NFeN)	74.8	116.6	120.3	115.7
∠(SFeS)	100.1	106.2	115.0	111.9

Inspection of the isomer shift correlations for the other combinations of the functional and the basis set (not shown) obtained with the DFT-optimized geometries reveals a bigger scatter of points in comparison with the correlations obtained from the X-ray geometries, even when the obvious outliers (for instance, GIDKIN02) are excluded. Apparently, the structural inaccuracies introduced by the optimization method outweigh the inaccuracies of the experimental determination of atomic positions.

Quadrupole splitting

The quadrupole splitting ΔE_Q in ⁵⁷Fe is the transition energy between the I_z = ±1/2 and I_z = ±3/2 substates of the nuclear excited state with I = 3/2. These substates E_I,Iz originate from the interaction between the nuclear quadrupole moment and the electric field gradient created at the excited ⁵⁷Fe nucleus by the surrounding nuclei and electrons:

$$E_{I,Iz}=\frac{1}{6}\sum _{\alpha \beta }{Q}_{\alpha \beta }(I,I_z)V_{\alpha \beta },$$ (2)

where α, β are the cartesian coordinates, Q_αβ (I,I_z) are the components of the nuclear quadrupole tensor, and V_αβ are the derivatives of the environmental electric field potential V with respect to the cartesian coordinates:

$$V_{\alpha \beta }=\frac{{\partial }^{2}V}{\partial \alpha \partial \beta }.$$ (3)

Substituting the expression for the quadrupole moment components² in the nuclear shell approximation⁷⁶ into (Eq. (2)) and taking the difference of the states with the appropriate quantum numbers we arrive at the well-known formula used to compute quadrupole splitting in zero magnetic field:

$$\mathrm{\Delta }{E}_Q=\frac{1}{2}{\mathit{eQV}}_3{\left[1+\frac{{(V_1-V_2)}^2}{3V_3^2}\right]}^{1/2},$$ (4)

where e is the absolute value of the electron charge, Q is the nuclear electric quadrupole moment for the I = 3/2 state (taken to be 0.16 barn⁷⁷), and V_k are the eigenvalues of the tensor V_αβ with the convention that V₃ has the maximal absolute value.

The sign of ΔE_Q defines the relative position of the I_z = ±1/2 and I_z = ±3/2 states but it is usually not reported in experimental studies. It is also not always reliably predicted by theoretical calculations. Because the electric field satisfies the Laplace’s equation, the eigenvalues of (Eq. (3)) sum up to zero: V₁ +V₂ +V₃ = 0. When one of the eigenvalues, for example V₁, is much smaller in absolute value than the other two, V₃ is approximately the negative of V₂. In such a situation a small error in predicting the field V (due to the basis set or the functional) might result in V₃ changing sign, because it is always defined as the largest by absolute value, and flipping the sign of ΔE_Q. For these reasons, we compare only the absolute values of the quadrupole splittings, adopting the approach of Noodleman and co-workers. ²⁸

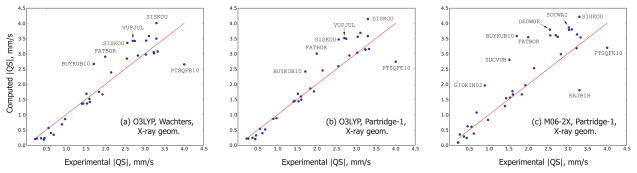
Let us first discuss the data obtained from the X-ray geometries. The MUE’s of the quadrupole splittings are presented in Table IV while the actual data points for a few representative combinations of the functional and the basis set are shown in Fig. 2. Figures 2(a) and 2(b) demonstrate some of the best performers (O3LYP, Wachters and O3LYP, Partridge-1, respectively), but 2(c) illustrates the worst combination M06-2X, Partridge-1. Note that the red line in these plots is simply the y = x function and not the best fit. Looking at the first two of these figures we immediately notice that the prediction of small (less than about 2.0 mm/s) quadrupole splittings is significantly more accurate than that of the larger ones. This conclusion is corroborated by the actual numbers in Table III: the MUE’s for the region < 2.0 mm/s in experimental values [excluding Fe(OEC), or BUYKUB10, an outlier in almost all cases] are two to three times smaller than the overall MUE’s (including all points). Except for the M06-2X functional, the Partridge-1 basis is noticeably more accurate than Wachters. The two best performers for the smaller QS are, just as in the case of the IS, B3LYP and O3LYP. They produce a remarkable accuracy of less than 0.1 mm/s on this region. Because some applications are concerned solely with the absolute QS values < 2.0 mm/s, ^3,29 using either B3LYP or O3LYP in these studies is highly recommended. The overall best performance for the QS is shared by BPW91, OLYP and PBE, with O3LYP following closely behind. M06, parametrized on the metal-containing compounds, brings a significant improvement over the related M06-2X functional even though it performs only slightly better than M06-2X for the IS. M06-2X gives some of the worst agreements with the experimental QS [see also Fig. 2(c)], The second worst performer, after M06-2X is, unsurprisingly, the LDA functional SVWN5.

Table 4.

The quadrupole splitting MUE’s for the data set presented in Table I computed with the Wachters and Partridge-1 basis sets and tight convergence criteria. The MUE’s are given in mm/s. The < 2.0 column includes the signals whose experimental quadrupole splittings are less than 2.0 mm/s except the obvious outlier Fe(OEC), or BUYKUB10, which is excluded. The ‘all’ column includes all the signals.

	Wachters		Partridge-1
Functional	< 2.0 mm/s	all	< 2.0 mm/s	all
B3LYP	0.144	0.352	0.0952	0.337
BPW91	0.172	0.314	0.133	0.284
M06	0.140	0.332	0.114	0.304
M06-2X	0.208	0.496	0.250	0.532
OLYP	0.180	0.319	0.147	0.284
O3LYP	0.147	0.320	0.0937	0.291
PBE	0.175	0.329	0.136	0.283
SVWN5	0.175	0.410	0.149	0.384

Figure 2.

Some comparisons between the experimental and computed absolute values on the quadrupole splittings. The red line is y = x: the points lying it represent the perfect agreement between the experiment and the theory. The obvious outliers are indicated by their Cambridge Structural Database code which can also be found in Table I.

The observation that the QS is predicted more accurately for smaller values has not been reported before, to our knowledge. The QS data published by some other researchers ^17,29 does not indicate a much greater prevalence of errors in the region above 2.0 mm/s although the quadrupole splittings computed by Oldfield and co-workers ¹² with the B3LYP functional do appear to have greater errors for large QS values. Currently it is not clear if our observation is simply a specious effect related to the accidental presence of several outliers with |QS| > 2.0 mm/s in our data set. For example, the removal of the five outliers from Figs. 2(a) and 2(b) would not result in much better accuracy of QS prediction in the region below 2.0 mm/s. Although we do not read much importance into this curious imbalance between the regions smaller and greater 2.0 mm/s we think that more accurate experimental data (conforming to our selection criteria from the Introduction) are needed to make a conclusion.

Let us now discuss the QS outliers, paying greater attention to the functionals that perform well (O3LYP, B3LYP). The IS data did not reveal any obvious outliers as prominent as those in Fig. 2. There may be several reasons for this observation. First, the determination of the QS from the experiment has inherently a greater incidence of error than the same procedure for the IS. The determination of IS involves finding the middle-point between two idealized peaks of finite width. Each of these peaks is recorded with a certain error of position ±Δ, so that the middle point is determined with a maximal error of Δ (when both peaks have the positioning error of the same sign). The QS is determined as the difference between the positions of these peaks, so that the maximal error becomes 2Δ (when the peak centering errors are of different signs). If peak positioning errors dominate the rest of the errors, this analysis has a consequence that particularly large QS errors would be accompanied by particularly small IS errors, and vice versa. Second, the theoretical computation of the IS is more local in nature, depending on the density of s-electrons on the iron nuclei, which is mostly determined by the immediate surroundings of the iron atom. The QS, in contrast, is potentially influenced by long-distance effects, namely, the overall symmetry of the electronic density, which is determined by all atoms of the system. In other words, the IS is computed from the values of the s-orbitals at a certain point, whereas QS requires integration over global density. Thus, QS is more sensitive to small changes in geometry. Moreover, DFT functionals have the potential to mishandle the global density because they typically incorporate either local or not entirely satisfactory gradient-corrected density formulas. Global errors in density would be less important in the typical optimization of DFT functionals than the local errors. Finally, solvation effects, counter-ion effects, possible protonation of ligands away from the iron atoms, and the error of placement of hydrogen atoms in X-ray structures all would produce a greater influence on the QS than on the IS.

The greatest QS outlier is a small distorted complex $\text{Fe}{(\text{DTSQ})}_2^{2-}$ (PTSQFE10) with the unusually large experimental QS value (over 4.0 mm/s). This QS is greatly underestimated by almost all DFT functionals studied in this work (except M06-2X) by 1.0 mm/s or more. Interestingly, the same complex also turned out to be the largest outlier among 21 complexes in the recent work by Noodleman and co-workers. ²⁸ The B3LYP geometry optimization starting from the X-ray geometry converged to a symmetric structure, which, however, only increased the discrepancy between experiment and theory. The inclusion of the two bulky ${\text{PPh}}_4^{4+}$ counter-ions PTSQFE10 co-crystallized with $\text{Fe}{(\text{DTSQ})}_2^{2-}$ typically did not alleviate the problem (only M06-2X produced a slight improvement). There is another compound in our data set taken from the same paper where $\text{Fe}{(\text{DTSQ})}_2^{2-}$ was originally described along with its Mössbauer and X-ray data⁸⁷ $-\text{Fe}{(\text{SPh})}_4^{2-}$ (PTHPFE10). Its computed QS is in an excellent agreement with the experimental value. The issue about the greatest QS outlier will perhaps be clarified when the Mössbauer characteristics of $\text{Fe}{(\text{DTSQ})}_2^{2-}$ are computed by some other ab initio approach, preferably including multiple determinants, which would be feasible in view of the small size of the complex.

Among some noticeable outliers in Figs. 2(a), 2(b) are a group of diiron, dicarboxylate complexes with small coupling constants J (SISKOU, VUPJUL, VUPJOF). The QS of the first one (SISKOU) is regularly overestimated by all the functionals, by as much as 1.0 mm/s in the worst cases, whereas the QS of the latter two vary substantially from functional to functional: either seriously overestimated (B3LYP, O3LYP, M06-2X), somewhat underestimated (PBE, OLYP), or seriously underestimated (SVWN5). VUPJUL and VUPJOF contain a protonated oxo-moiety in a critical bridging position: an error in the location of the protons might have a large effect on the computed QS.

FATBOR, another (partial) outlier in QS (as predicted by B3LYP, O3LYP, and M06-2X), is a tri-iron carbonyl complex with two equivalent terminal low-spin Fe(II) atoms (having low IS and QS), and one central high-spin Fe(II) atom (having large IS and QS). The calculations show a much better agreement with the low-spin signals and a significant overestimation of the high-spin quadrupole splittings. In any case, all eight functionals show good qualitative agreement with experiment, predicting high and low IS and QS values for two different types of Fe atoms, as described, whereas BPW91, OLYP, PBE, and SVWN5 are close to the quantitative agreement.

The last mini-group of QS outliers consists of porphyrin complexes Fe(OEC) (BUYKUB10) and Fe(OEP) (DEDWUE). The QS of Fe(OEC) in both bases ranges from 1.0 mm/s and smaller (BPW91) up to almost 4.0 mm/s (M06-2X). It is puzzling that none of the combinations of the functional and the basis comes close to the experimental quadrupole splitting (1.71 mm/s). The closest agreement is registered for O3LYP/Partridge-1 (2.42 mm/s). A related compound Fe(OEP) shows a smaller scattering range of quadrupole splittings than Fe(OEC), but the predicted QS is highly functional-dependent. However, here O3LYP yields a very good agreement with its experimental value (2.55 mm/s) in both basis sets although the other functionals are off by 1.0 mm/s or more, both under- and overestimating. Somewhat surprisingly then, the computed QS of a related porphyrin complex Fe(OEP)CO (YEQPOA) has a quantitative agreement with the experiment in almost all the functionals (except M06 and M06-2X) and bases, with little variation from approach to approach. The work of Oldfield and co-workers ¹² reports similar large overestimations of the QS by the B3LYP functional and the Wachters basis set for some porphyrin-based compounds and a more balanced performance of BPW91 on the same compounds. Although we and the cited work studied different porphyrin derivatives and the absolute values of overestimations by B3LYP and underestimations by BPW91 differ, there is an agreement in the trend.

Overall, we find some of the QS outliers (FATBOR, DEDWUE) in qualitative agreement with the experiment while some others (PTSQFE10, BUYKUB10, SISKOU, VUPJUL, VUPJOF) are probably difficult cases which require further investigation by more reliable theoretical methods than DFT.

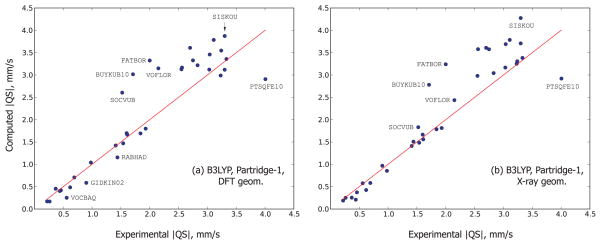
Now, let us turn to the quadrupole splitting computed for the DFT-optimized geometries. Fig. 4 juxtaposes the quadrupole splittings computed with the B3LYP/Partridge-1 method for the theoretical and experimental geometries. This particular method serves as a typical case and we believe its results are good for illustrative purposes. The overall pattern of data points in both sides of Fig. 4, each side representing one type of geometry, is quite similar: substantially better agreement with the experiment < 2.0 mm/s, and a bigger scatter and more outliers in the region > 2.0 mm/s. But both visually and quantitatively, the accuracy of prediction in case of the DFT-optimized geometries is worse. The MUE’s in the region < 2.0 mm/s are 0.168 and 0.0952 mm/s for the theoretical and experimental geometries, respectively. The MUE’s for all 35 points are 0.381 and 0.337 mm/s, respectively. The similar situation is seen for all the other combinations of the functional and the basis, again demonstrating, in parallel with the isomer shift data, that the optimization of the geometries has been somewhat detrimental for the Mössbauer calculations.

Figure 4.

The comparison of the quadrupole splittings computed with the B3LYP functional and Partridge-1 basis set using the DFT (a) and X-ray (b) geometries. The red line is y = x: the points lying it represent the perfect agreement between the experiment and the theory. The obvious outliers are indicated by their Cambridge Structural Database code which can also be found in Table I.

After the optimization, at least three minor outliers (VOCBAQ, GIDKIN02, RABHAD) and one major one (SOCVUB), appeared [compare Figs 4(a) and 4(b)] in the region < 2.0 mm/s. It is interesting that all these structures are of non-chelate type, being non-rigid and with a geometry that is therefore more likely to be distorted by the optimization method. The experimental SOCVUB structure was already a slight outlier in Fig. 4(b), and its optimization strongly deteriorated agreement with the experiment. The large outlier BUYKUB10 becomes an even larger one after the optimization. The DFT-optimized GIDKIN02 structure also produced an outlier in the isomer shift calibrations (Fig. 3). In the region > 2.0 mm/s, regardless of the geometry type, essentially the same outliers are observed (with some alterations of their positions, especially notable for VOFLOR and SISKOU).

Application to methane monooxygenase intermediates

The soluble methane monooxygenase hydroxylase (MMOH) is a well-studied enzyme hosting a di-iron active site that catalyzes the oxidation of methane into methanol.⁵³ Its catalytic cycle involves several intermediates with different oxidation states of iron atoms, and we have been studying these intermediates quite extensively in the last several years, both with DFT^103,104 and QM/MM ⁶² methods. These intermediates are rather short-lived so that their structures cannot be derived from X-ray crystallography. However, their Mössbauer spectra are available and therefore the computational Mössbauer approach becomes an important tool for investigating their structures. Han and Noodleman have recently computed the Mössbauer parameters of several candidate structures for the key intermediates P and Q.^3,16,29,105 Comparison with the experimental data allowed these authors to select the most probable structures.

Here, as an application to our benchmarking results, we are computing the Mössbauer characteristics of the same intermediates but using presumably more accurate geometries – those optimized through the QM/MM approach in our recent work. ⁶² In contrast, the models of Han and Noodleman were obtained from the conductor-like screening solvation model (COSMO)^107,108 which essentially utilizes a DFT method treating molecular systems embedded in a molecular-shaped cavity and surrounded by a dielectric medium.

As an initial calibration, we compute the Mössbauer parameters for a model of the reduced MMOH enzyme, for which there is a crystal structure. ¹⁰⁹ Hence, for this case, uncertainty about the geometry should be relatively unimportant (although errors from the QM/MM geometry optimization will still be present). The results shown in Table V indicate good agreement for the IS. For the QS, there are two sets of experiments; our results are more consistent with the second set than with the first, and reasonable in either case. These calculations give some indication of what to expect in a realistic, complex application, where there can be noise and uncertainty in both theory and experiment.

Table 5.

The comparison of the isomer shifts and the quadrupole splittings of MMOH reduced (Re) structure as well as the peroxo and Q intermediates computed in this work and in the works of Han and Noodleman.³,²⁹ Our geometries were optimized by QM/MM⁶² whereas those in Refs.³,²⁹ were produced by the DFT in continuous dielectric medium (the so-called COSMO model). The juxtaposition of the coordinations is approximate since the geometries in the same row do not exactly coincide. For the schematic geometries of the QM/MM optimized intermediates see Fig. 4. The IS and QS values of this work are computed with the methods that give the most accurate statistics – B3LYP/Partridge-1 and O3LYP/Partridge-1, respectively. The Mossbauer characteristics corresponding to the geometries of Han and Noodleman were taken from their works.³,²⁹

	This work		Refs.3,29		Experiment
Form	δ	|QS|	δ	|QS|	δ	|QS|
Re	1.27 1.16	3.00 2.46	1.26 1.34	2.87 3.00	1.3 1.3	2.87; 3.1 2.87; 2.4–3.0
P-1 (μ-η2,η1)	0.62 0.78	1.03 0.44	– –	– –	0.66 0.66	1.51 1.51
P-2 (μ-η2,η2)	0.57 0.63	0.77 1.15	0.60 0.57	0.57 0.97	0.66 0.66	1.51 1.51
P-3 (A-μ-1,2)	0.73 0.70	1.60 1.25	0.72 0.63	1.69 1.12	0.66 0.66	1.51 1.51
P-4 (S-μ-1,2)	0.57 0.58	1.86 1.31	0.64 0.61	1.81 1.21	0.66 0.66	1.51 .1.51
Q	0.11 0.38	0.78 0.69	0.18 0.22	0.33 0.33	0.17, 0.21 0.17, 0.14	0.53, 0.68 0.53, 0.55

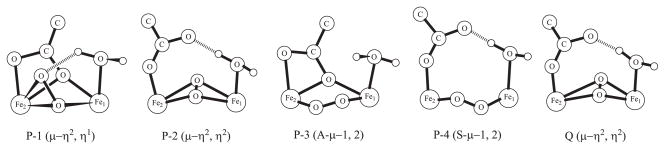
In Ref.62 we identified four P candidate structures and one Q structure. The schematic diagrams of their active sites are given in Fig. 5. In Table V we bring together the Mössbauer parameters of these models and the models from the works of Han and Noodleman.^3,29 Since these authors used somewhat different geometries the juxtaposition of our models with theirs is approximate. In placing the two models in the same row for comparison we tried to preserve the type of coordination of the oxygen and the ligands to the iron atoms. Then, because Han and Noodleman used different functionals to compute Mossbauer characteristics and they sometimes produced slightly contradictory results we select those IS and QS values computed by these authors which seem to have the best agreement with the experiment and those structures that are selected by the authors as the most likely.

Figure 5.

The schematic diagrams of the MMOH intermediates active sites. P stands for Fe⁺³, Fe⁺³ peroxo models and Q represents the Fe⁺⁴, Fe⁺⁴ species.

As our computation methodology in the present study, we take the best combination of the functional and basis to compute the IS (B3LYP/Partridge-1), and equivalently with QS (O3LYP/Partridge-1). The corresponding values are given in Table V. Analyzing the results of our calculations for the four peroxo models, we conclude that the P-3 model (A-μ-1,2) unequivocally has the closest agreement with the experiment. This type of coordination was in fact chosen as most likely by Han and Noodleman,³ despite some confusion created by multiple energetic and Mössbauer data available from two functionals (OPBE and PW91). This type of structure is also in agreement with the vibrational analysis performed by the groups of Solomon and Yoshizawa.^110,111 All other peroxo structures listed in Table V have the Mössbauer characteristics that are substantially farther from experiment than those of P-3. The computed IS of the P-3 model produced by us and the group of Noodleman have about the same proximity to the experimental values. Our QS range is ‘narrower’ however (1.60 and 1.25 mm/s), bringing the signals from both iron centers within the error bars of the single experimental value (1.51 mm/s). Encouragingly, the other two types of structures in which we and the group of Noodleman overlap (μ-η²,η², S-μ-1,2) are in good qualitative and perhaps even quantitative agreement with one another. Thus, we have to conclude that, despite the fact that our previous QM/MM calculations predicted the lowest energy for the P-2 (μ-η²,η²) structure, the analysis of the computationally obtained vibrational and Mössbauer spectra converges unambiguously on the single type of structure, P-3 (A-μ-1,2). At the same time this apparent consensus should not categorically rule out the P-2 (μ-η²,η²) structure as a participant in the MMOH catalytic cycle. It may be still energetically most stable but for some (for example, kinetic) reason undetectable in the Mössbauer experiment. Additionally, recent careful experimental analysis of the MMOH peroxo intermediates revealed the presence of the second peroxo structure the Mössbauer spectra of which are currently unknown. ¹¹²

Finally, let us discuss the Mössbauer data for the Q intermediate (which is a Fe⁺⁴, Fe⁺⁴ species) given in Table V. The table indicates that there were two corresponding experimental Mössbauer measurements, which produced somewhat different qualitative and quantitative results. The first experiment showed only one signal, but the second one gave two similar signals in both IS and QS. The central geometry of our Q structure is slightly distorted, with two oxygens that form the ‘diamond’ core being closer to Fe₂ than Fe₁. ⁶² Therefore, two types of signals in the Mössbauer experiment would be more expected than one. In this regard, our calculations qualitatively agree with the second experiment. The calculation of Han and Noodleman, however, produced two different IS signals but only one QS aggregate signal. Our isomer shift has worse agreement with the experiment than Han and Noodleman’s but our quadrupole splitting is closer to the experiment than theirs. The Q structure initially proposed by these authors as the most likely model had a somewhat better agreement with the experimental QS (two signals: 0.70 and 0.37 mm/s).²⁹ Unfortunately, this structure involved a suspicious proton transfer from the coordinated water to one of the histidine rings, and was later dismissed on energetic and spectroscopic grounds. ³ It looks like our computed IS and QS values lie within the error bars and are in good semi-quantitative agreement with the experiment.

The application to the MMOH intermediates serves as a good example of the power and utility of combining energetics calculations with Mössbauer spectral calculations in cases where the structures are not experimentally determined, agreeing with conclusions drawn by the group of Noodleman. By applying the statistically most accurate method(s) to compute the IS and QS, we arrived immediately at very good qualitative (and perhaps even quantitative) agreement with the experiment helping resolve some of the questions that are still disputed in the MMOH intermediates research.

Discussion

We summarize the conclusions that can be drawn with regard to the accuracy of DFT calculations of Mössbauer parameters, including the dependence upon the geometry and the functional employed. We first discuss the results obtained when the X-ray structures are used for the geometry, and then examine the effect of performing geometry optimization. An important goal is to understand to what degree one can rely upon Mössbauer calculations in a system like an iron-containing protein to provide accurate discrimination among alternative structures. If the noise in the calculation is larger than the difference predicted in the parameters for the alternative structures, it would be inappropriate to draw any conclusions one way or another. Hence, understanding the level of noise expected in a realistic application is essential if the method is to be profitably used to help in assigning structures in cases where crystallography cannot be carried out. The discussion below focuses on the optimal functionals and basis sets determined in our benchmarking studies.

As indicated above, we first discuss the errors observed for calculations of the IS and QS using X-ray geometries. For the IS, errors in the range 0.02–0.04 mm/s are observed. However, since this range is observed after the parametrization on the training set, the error is likely to grow somewhat if the methodology is applied to an independent test set. Nevertheless, because the isomer shift data points form a good linear correlation, the MUE that would be observed on a test set is not expected to be much larger than 0.02–0.04 mm/s. For QS, training set errors in the range of 0.15 for the QS less than 2.0 mm/s, and 0.4 for QS greater than 2.0 mm/s, are observed.

The effects of geometry optimization are more specific and system-dependent. As noted in above, there are specific complexes and chemistries where DFT geometry optimization has significant problems reproducing the experimentally observed geometry. In these cases, substantial errors can, be introduced from the geometry optimization. However, for typical cases, where the geometry optimization yields a result that agrees reasonably well with the experiment, the deviation between the Mössbauer parameters computed at the two geometries is small. Hence, the principal concern when geometry optimization is employed is whether one is dealing with a system with a potential energy surface that is poorly modeled by the variant of the DFT being employed. However, this is a serious concern in any case, whether one is computing Mössbauer parameters or just energetics; one has to be suspicious of the quality of all the results if the geometry is in poor agreement with experiment. Repairing the occasional, but sometimes large, errors in DFT geometries, particularly for transition metals, thus should be a high priority in the development of the next generation of functionals, but will not be discussed further here.

In considering what constitutes “acceptable” agreement in a Mössbauer calculation for a complex system such as an iron-containing protein, somewhat larger error bars have to be used than the MUE averaged over all of the data set, as the case at hand could lie on the high side of the error distribution. If calculations are being done with a crystal structure, an error on the order of 0.1 mm/s for the IS, 0.2 mm/s for the QS if less than 2.0 mm/s, and 0.4 mm/s if the QS is greater than 2.0 mm/s, would appear to be reasonable estimates based on our results. If geometry optimization has to be carried out, one might increase the expected level of error by 20–30%, assuming that the geometry is in fact not seriously deviant from the experiment. By this criterion, the use of the Mössbauer data to choose between the proposed MMOH peroxo structures is clearcut, and the results for the P-3 peroxo model are in reasonable agreement with the experimental data. Additionally, the Mössbauer data reported in Table V for the reduced MMOH structure modeled through geometry optimization from an oxidized MMOH structure, the X-ray geometry of which is available, lie, satisfactorily, within the error bars. For Q, the IS from the Noodleman group calculations are in good agreement, with experiment, but one of the Fe atoms in our calculations is a little outside the range proposed above. On the other hand, our QS results for Q are in good agreement with the experiment whereas the Noodleman group results are outside of the suggested error bounds, given that the QS is less than 2.0 mm/s. Since the Q models that we, and the Noodleman group, are employing are very similar but not identical, and we are using different functionals, what these data suggest is that we are both probably quite close to the correct structure, but that some detailed refinement of the geometry would be required to better match the IS and QS from experiment. This result is unsurprising in that the conformational potential energy surface of a protein is much more complicated than that of the small molecules examined in our training set, and so we can expect to see greater theory/experiment deviations based on errors in the geometry on the complex surface, which contains a large number of minima that are closely spaced in energy.

In summary, the overall results, both on the training set and for the MMOH calculations, are encouraging with respect to the goal of employing Mössbauer data, in combination with energetic criteria, to identify structures in iron-containing proteins. However, there are clearly some quantitative issues to address related to noise introduced by the complexity of the protein potential energy surface.

Conclusions

This work assembled a high-quality, good-size test set (31 compounds; 35 data points) for the benchmarking of isomer shifts and quadrupole splittings. We selected the entries of the test set on the basis of availability of their Mössbauer spectra at liquid helium temperature as well as X-ray crystallographic data. Eight functionals and two bases (on iron atoms) were applied to determine which combination predicted more accurate results and two sources of geometries (DFT-optimized and crystallographic) were used. The geometries obtained through the optimization (B3LYP functional, pseudospecral approach, LACVP* basis on the irons and 6-31G* on the other atoms) yielded somewhat worse Mössbauer results (greater scatter of points and more outliers). Non-chelate structures were particularly affected by the optimization, probably due to their non-rigidity. It is worth seeking a method for a more accurate optimization of non-chelate metal geometries in a future publication but for now the usage of X-ray geometries should not be shunned as they produce quite accurate results. For example, the mean unsigned error of quadrupole splitting is less than 0.1 mm/s in the region < 2.0 mm/s (if one obvious outlier is excluded) and below 0.3 mm/s in the whole region (all data points are counted in). The conclusions below are based on the X-ray geometries.

The isomer shift statistics indicate that the best functional to compute the isomer shift is B3LYP with O3LYP a close second. Partridge-1 set on iron atoms shows somewhat better performance than Wachters basis. M06 and especially M06-2X show some of the worst IS performance. The best functional to compute quadrupole splitting is O3LYP in Partridge-1 basis set with B3LYP being the second-best. M06-2X produces a large number of outliers and the worst overall QS performance. The Wachters basis is appreciably smaller, and the quality of the density computed with it using the loose convergence criteria is sufficient to compute good-quality isomer shifts and quadrupole splittings. So, the combination of the Wachters basis set and lower-quality wave function may be used for the rough estimate of the Mössbauer characteristics in situations where many different models have to be filtered against the experimental data. For higher quality computations of the Mössbauer spectra, the well-converged wave function computed with the Partridge-1 basis set should be used. To summarize, O3LYP and B3LYP in combination with the Partridge-1 basis on iron atoms show the best performance and SVWN5 and M06-2X are not recommended for Mössbauer calculations.

The results of our statistical analysis were used to select the best computational methods for predicting the Möbssauer spectra of the P and Q intermediates of the enzyme methane monooxygenase hydroxylase (MMOH). We compare our results to those of Han and Noodleman, who recently applied some of their Möbssauer DFT methods to determine which of the P and Q structural candidates was most likely to represent the experimental structure. For P structures, our results agree comfortably with Han and Noodleman’s whereas for the Q structure we find a significantly better agreement in the quadrupole splitting albeit a slightly worse one in the isomer shift. It is also important to emphasize what we see as a methodological improvement on the work of Han and Noodleman. Whereas their results were obtained with the functional and basis that best match the experimental Mössbauer parameters of the systems of interest, we treated our target systems with the functional/basis set combination that was first found the most accurate on an extensive and independent test set, which is a less biased approach.