Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2010 Jul 21;30(11):1860–1873. doi: 10.1038/jcbfm.2010.105

Cerebral blood flow modeling in primate cortex

Romain Guibert 1,2,3,4, Caroline Fonta 3,4, Franck Plouraboué 1,2,*
PMCID: PMC3023927  PMID: 20648040

Abstract

We report new results on blood flow modeling over large volumes of cortical gray matter of primate brain. We propose a network method for computing the blood flow, which handles realistic boundary conditions, complex vessel shapes, and complex nonlinear blood rheology. From a detailed comparison of the available models for the blood flow rheology and the phase separation effect, we are able to derive important new results on the impact of network structure on blood pressure, hematocrit, and flow distributions. Our findings show that the network geometry (vessel shapes and diameters), the boundary conditions associated with the arterial inputs and venous outputs, and the effective viscosity of the blood are essential components in the flow distribution. In contrast, we show that the phase separation effect has a minor function in the global microvascular hemodynamic behavior. The behavior of the pressure, hematocrit, and blood flow distributions within the network are described through the depth of the primate cerebral cortex and are discussed.

Keywords: blood effective viscosity, cerebral blood flow, hemodynamics, microcirculation, pressure distribution, vessel network topology

Introduction

A microscale understanding of cerebral blood flow (CBF) is of importance for many physiological, medical, and neuroimaging issues. The amazing topological and geometrical complexity of microvascular networks in the brain, and in other organs, has challenged many researchers for decades. Although accessible through experimental measurements at the local level, the blood flow results from nonlocal regulatory mechanisms associated with the complex microvascular architecture. Local analysis hardly provides a comprehensive understanding of the coupling at arteriolar, capillary, and veinular scales that ensures efficient and homogeneous cerebral perfusion. The aim of this contribution is to establish an extensive reconstruction of the cortical blood flow distribution using numerical modeling. This approach not only permits the extensive reconstruction of the blood flow from the arteriolar to the veinular level through the capillary network but also allows the evaluation of the relative contribution of each particular ingredient of the entangled hemodynamic mechanisms to be specified, which is very difficult to achieve when analyzing experimental observations in vivo (Secomb et al, 2008).

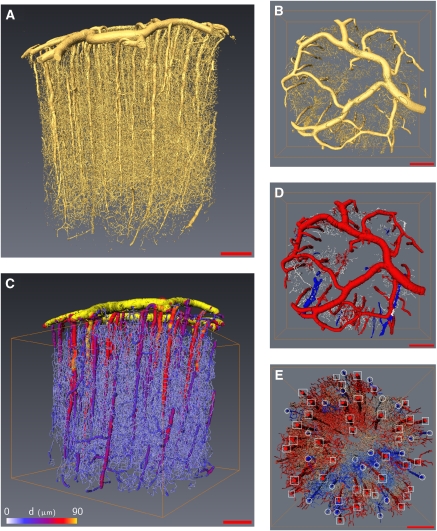
The direct computation of blood flow considering a complete mechanical description of the interactions of its components (red blood cells, plasma, vessel shape, and endothelial surface layer) over several cubic millimeters of tissue is a more than challenging task for any computer at present (McWhirter et al, 2009). It is easy to understand that such assignments require the analysis of different scales, from the interactions arising among blood cells, plasma, and endothelial surface layer to the estimation of flow within several thousand vessels such as those illustrated in Figures 1A and 1B, which represent the microvascular network inside 18 mm3 of cortical gray matter.

Figure 1.

Figure 1

Open in a new tab

Cortical sample visualization (A) volume rendering of the whole sample created from original gray-scale images, (B) volume rendering of the pial vascular structure (top view), (C) whole sample after postprocessing, color coded in accordance with vessel diameters, (D) pial structure after suitable image processing where pial arteries are easily detected (in red). (E) Differentiation of penetrating vessels from arterioles (square frame) and veinules (circle frame). (scale bar=500 μm).

In this paper, we present an improved network approach, which approximates the pressure, hematocrit, and flow fields at any point of the network inside a complete vascular bed of gray matter at moderate computational cost. It nevertheless needs some appropriate adaptations to deal with the geometrical and topological complexity of the vascular network.

The influence of red blood cells' behavior inside vessels, leading to an effective viscosity of confined blood flows, as well as their behavior at vessel branching points (the so-called phase separation effect), need to be taken into consideration (Cokelet and Goldsmith, 1991). This is an important improvement over other recent works (Reichold et al, 2009) where rectilinear, single diameter tubes with homogeneous plasma flows were used to model CBF in rat cortex. Our method is applied to primate cortical brain microvascular networks whose structure has been exhaustively analyzed (Risser et al, 2007, 2009). Moreover, the present work aims at determining how the network topology and geometry influence the pressure, hematocrit, and flow distributions in the cerebral microvascular circulation, as what has been shown in mesentery (Pries et al, 1995, 1996).

Materials and methods

We first briefly summarize the main methodological techniques that we have developed for the preparation of marmoset monkey (Callithrix jacchus) tissue, image acquisition (Plouraboué et al, 2004), image segmentation (Risser et al, 2007), vessel skeletonization and vectorization (Risser et al, 2008), and postprocessing (Risser et al, 2009). Next, we emphasize the important new steps needed for the computation of blood flow in microvascular beds associated with the topological postprocessing of the networks, implementation of boundary conditions, and blood flow modeling.

Image Acquisition and Segmentation

Intracardiac perfusion of heparinized NaCl 9% was performed first, followed by a suspension of barium sulfate (600 mg/mL, Micropaque, Villepinte, France, Guerbet) (Plouraboué et al, 2004). Brains were dissected and fixed in a 10% formol solution. Cortical samples of the cortex were removed with biopsy punches, dehydrated and cast in EPON (EPON™ epoxy resin) resin after a procedure similar to electronic microscopy preparation. The imaging of microvascular networks was performed using 3D synchrotron microtomography with a 1.43 μm3/voxel the volume rendering of which is shown in Figure 1A. These highly contrasted images were treated by a traditional image processing method without loss of information. A hysteresis thresholding method was used for the binarization step. Some morphological mathematical opening/closure procedures were then used to finalize this step, so as to remove black islands inside white vessels (Risser et al, 2007). The vessel's density, volume, and length, which is obtained after this procedure, has been recently found consistent with other reported measures in primate and rodents (Risser et al, 2009; Tsai et al, 2009).

Building Network Vessel Vectorization

To obtain a topological description of the vessel connections, together with the best representation of the vessel shapes, we use various, previously described, types of image postprocessing (Risser et al, 2009). Each vessel segment (vessel length between two successive branching points) was then discretized into a succession of points along its skeleton. Two points, with their spatial coordinates and the associated vessel diameter, separated by about a pixel size, form an element of segment. This description provided a homotopic and thin version of the shape. Thinning skeletonization produced some residual artifactual and isolated segment edges, which were then pruned using a critical value of one half for the ratio between the segment length and the diameter of the root segment. Moreover, as the injection of microcapillary vessels may not have been perfectly continuous, some small discontinuities of the vessel topology were observed. They were automatically detected and corrected by a gap closure procedure (Risser et al, 2008). Figure 1C illustrates a vectorized reconstruction of the network where the vessel diameters are color coded from yellow for the largest to blue for the smallest. The vessel number obtained after this procedure was close to 8100/mm3, which is consistent with earlier estimations in humans (Cassot et al, 2009) or in primates (Risser et al, 2009).

Topological Postprocessing of the Networks

As the topology of the vascular network is one key ingredient of the blood flow distribution, it is necessary to specify the network description best suited for the purpose of the modeling. First, we need to identify the connected components of the network. Those components are decoupled units where the flow has to be evaluated independently. Nevertheless, on the very complex network resulting from the vectorization and postprocessing of Figure 1C, it can be clearly seen that there is one major connected component. A careful numerical estimation of the network topology shows that this major component represents 99.9% of the total number of vessel segments.

Second, for flow computation, it is necessary to provide the segment connections, which can only be bifurcations. In fact, trifurcations associated with four different segments are extremely rare in the resulting network (0.5% of connections). Such events are also very seldom described in anatomical studies (Duvernoy et al, 1981). Here, they were mainly artifactual results of the vectorization procedure, which were removed by introducing a supplementary segment in the middle of each trifurcation to obtain two bifurcations. The length of this supplementary segment was <1 μm and its diameter was taken as the average of the four diameters of the connected segments.

Third, on each connected component, dead-end vessels were removed as they do not contribute to the flow. For this purpose, an automatic procedure spanning the entire vessel graph tracked and deleted dead-ends. The initial network was then decomposed into a backbone and its complementary components. The total number of backbone segments resulting from this postprocessing in an 18 mm3 volume of tissue was close to 16,000, as represented in Figure 1C. The final number of vascular segments per unit volume in the backbone was thus 882/mm3, which is almost a factor 10 smaller than the number obtained in the earlier step. This might seem to be a drastic simplification of the network, but this extracted backbone is the only relevant segments set of the network as far as its flow computation is concerned. Some important remarks need to be made here to explain the relevance of this extracted backbone. In fact, the pruning of one dead-end vessel that is useless for the flow evaluation does not simply diminish the total number of considered segments by one unit; it impacts the segment numbering by a much larger amount by merging together segments previously considered as distinct. It is then important to mention that the total number of segments gives a poor representation of the spatial extension of the network under consideration. For example, the vascular volume of the extracted backbone represents 60% of the initial volume even though its number of segments is 10 times smaller than in the initial set. Finally, it should be noted that the computation could also be performed by considering the entire network, including dead-end vessels, but it is much more computationally intensive. However, as the blood flow is zero in dead-end vessels, similar results will be obtained inside the backbone. Thus, in the following, we represent the various hydrodynamic quantities of interest inside the backbone only.

Boundary Condition Implementation

The boundary conditions are a key element for flow evaluation. The particularity of CBF is that input and output vessels are mainly located at the brain surface, in the pial matter (Figure 1B). Earlier studies in humans (Duvernoy et al, 1981) have indicated that the arteries make up approximately two thirds of the total penetrating vessels connected to the pial surface, the remaining one third being venous vessels. Hence, it is important to provide a good identification of arterial inputs and venous outputs by applying the same methodological image treatments as those previously described for intracortical vessels but using an adapted parameterization (see Figures 1D and 1E). The observation that all the arterioles were found within a single connected component testifies to the very good quality of the injection in the arterial compartment. We also observed that all penetrating arterioles fit the pial arteries perfectly, so perfect injection was achieved on this side. On the venous side, although a good venous backflow was obtained during contrast agent perfusion, imperfect vessel filling is observed, associated with a granular texture on the gray-scale images. This result in poorly contrasted and heterogeneous venous pial structures on the gray-scale images that could not easily be segmented with the tool described in the earlier section. Thus, venous structures do not clearly appear in the segmented pial network described in Figure 1D. Far from being a drawback, this incomplete injection helped with the identification of the venous network, as it was then possible to identify penetrating veinules as seen in Figure 1E. The two thirds–one third ratio of penetrating arteries—veinules is also visible on this figure in which 24 penetrating veins have been identified among a total of 62 penetrating vessels (proportion of arteries equal to 0.61). Comparing this proportion of arteries to the 0.61 found in Weber et al (2008) on 249 measurements did not show any statistically significant difference (P=0.999), so our finding in the marmoset is perfectly consistent with parallel estimates in the macaque. A similar conclusion (unless less significant (P=0.2) data are considered) is reached when our results are compared with human data (142 arteries for 200 identified penetrating vessels, i.e., a proportion 0.71 of arteries (Lauwers, 2007)). These considerations were also complemented with anatomical observations that venous vascular segments are generally situated below or parallel to the arteries in the pial matter. All these features made it possible to unambiguously distinguish between the arteriolar inputs and veinular outputs. This process could not be fully automated and necessitated some visual identifications. It is important to mention that boundary conditions are thus imposed at the level of penetrating vessels, so that the imposed pressure and the resulting blood flow are not influenced by the imperfect reconstruction of the pial venous vessels.

However, a possible difficulty arises in prescribing realistic blood pressure in these input and output vessels. This aspect is not well documented in the literature, but realistic narrow ranges of values have been proposed for the pial surface arterial (65–90 mm Hg) and venous (15–25 mm Hg) pressures (Stromberg and Fox, 1972; Tamaki and Heistad, 1986). Different measurements of arteriolar and venular pressure are available (Zweifach and Lipowsky, 1977; Pries et al, 1990; Lipowsky, 2005) but they were mainly obtained in a rat mesentery experimental model. There are very few quantitative measurements of in vivo pial pressure available in the literature, even in animals. The proposed modeling can provide results that are independent of the prescribed boundary conditions when a dimensionless formulation of the flow problem is considered. Therefore, as a first step, we prescribed 1 (arterial)/0 (venous) pressure boundary conditions to compute the blood flow. Then, the real blood pressure predicted by the simulation could be found by adapting the computed dimensionless pressure to the real pressure difference Δp. This means that, although the reported results are dimensional when associated with a definite arterial/venous pressure difference, they can be easily transposed for other pressure differences by using simple linear scaling.

We have discussed the boundary conditions associated with the upper face of the parallelepipedic surfaces that envelop the studied brain volume, but a second difficulty concerns the boundary conditions to be applied on the five other faces. To our knowledge, this issue has not been clearly discussed in earlier studies (Reichold et al, 2009). In the case of brain vessels, earlier investigations have shown that a representative elementary volume can be identified in primate cortex (Risser et al, 2007). The length scale associated with statistical decorrelation of the spatial distribution of the brain's microvascular networks has been found to be within 50 to 80 μm. The characteristic size of the volume investigated here is thus much larger than the representative elementary volume scale, as this length is of the order of 2 mm. Hence, it is valid to consider that the cortical volume analyzed in this study represents a statistically homogeneous entity. Similar volumes are then posited to surround this volume with similar vascular structures. Hence, mirror boundary conditions are taken to mimic the presence of statistically equivalent cortical vessels in the surroundings of the finite sample. Such boundary conditions, also called periodic boundary conditions, are widely used to study transport properties of heterogeneous media (Torquato, 2001).

Blood Effective Apparent Viscosity

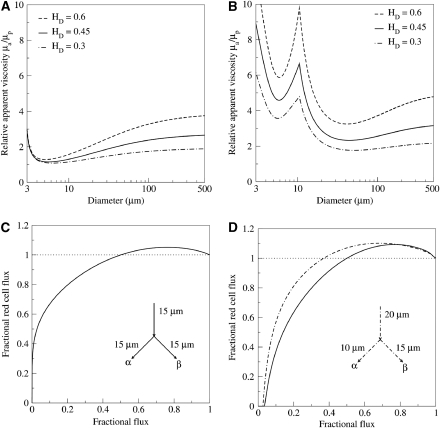
Without its cellular components, blood shows simple rheological behavior that can be described with a single constant parameter, its plasmatic viscosity μp. Under normal physiological conditions, the blood cells (the majority being red blood cells) have an essential function in the flow of blood in small vessels. This subtle rheological behavior can be lumped into an apparent viscosity μa, which is a function that depends on the tube diameter as well as on the input hematocrit (Cokelet and Goldsmith, 1991). Using this apparent viscosity leads to correct prediction of the observed relationship between the imposed flux and the observed pressure drop. When red blood cells concentrate at the vessel center, the plasma lubricates the flow and the apparent viscosity of the blood decreases. This behavior saturates when red blood cells can no longer deform, and a sudden increase in the viscosity is then observed for tube diameters smaller than 4 μm. From the different models that have been put forward in the literature, we chose two proposals for this study. The in vitro viscosity model proposed by Kiani and Hudetz (1991) is illustrated in Figure 2A. It provides an explicit nonlinear dependence for the relative apparent viscosity μa/μp. Pries and Secomb (2005) have proposed a model describing in vivo viscosity behavior (Figure 2B) obtained by minimizing the difference between experimental observations and direct simulations. The viscosity is higher than that predicted by the in vitro law because of the presence of endothelial surface layer, especially for diameters around 10 μm, where it shows a local maximum.

Figure 2.

Figure 2

Open in a new tab

Modeling of Fåhræus–Lindqvist and phase separation effects: (A) in vitro blood viscosity modeling (Kiani and Hudetz, 1991), (B) in vivo blood viscosity modeling (Pries and Secomb, 2005), (C) phase separation splitting rule (Dellimore et al, 1983), and (D) phase separation splitting rule (Pries and Secomb, 2005) for two different configurations.

Blood Phase Separation Models

Phase separation names nonuniform distribution of red blood cells in the downstream branches of a bifurcation. Different nonlinear empirical models have been proposed (Dellimore et al, 1983; Pries and Secomb, 2005) to describe experimental observations. The first of the chosen splitting rules (Dellimore et al, 1983; Figure 2C) only considers the mother branch hematocrit and the influence of blood flow on the hematocrit distribution into daughter branches of a junction. However, a more complex splitting rule (Pries and Secomb, 2005; Figure 2D) also takes into account the influence of the diameters of the three branches. It is important to note that some models can lead to a hematocrit ratio higher than one for a particular range of flow ratios between daughter and mother branches. Therefore, in certain circumstances arising in complex networks, these models can predict a problematic daughter hematocrit larger than one. The latest version of the model (Pries and Secomb, 2005) has been adjusted to prevent this effect and contains the resulting hematocrit rate. Mathematical details of the different models mentioned above can be found in the provided references.

Evaluation of the Network Transport Properties

Brain vessel segments are characterized by a diameter/length ratio of about 1/10 (Risser et al, 2009). The lubrication approximation can be profitably used to assess the induced pressure drop in a tube having a complex shape. From the asymptotic analysis of the Stokes equation, it is possible to find a Poiseuille's law that characterizes the flow in a tube. The flow rate q is proportional to the pressure gradient ∂p/∂s along the curvilinear central shape coordinate s describing each vessel skeleton, i.e.,

graphic file with name jcbfm2010105e1.jpg

The coefficient of proportionality that connects q and ∂p/∂s, known as the local hydraulic conductance, has a strong fourth power dependence on the local diameter D evaluated along the curvilinear coordinate s. It also shows a less drastic dependence on the rheological properties of the fluid, as it is only inversely proportional to the apparent viscosity μa. By integrating equation (1) between two successive bifurcations, we obtain a pressure drop relation that connects local pressures at junctions and takes the apparent viscosity of the fluid into account as well as the local vessel diameter variations:

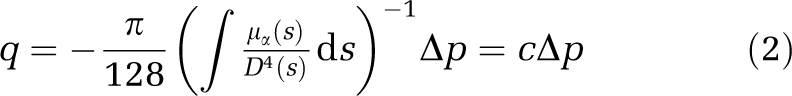graphic file with name jcbfm2010105e2.jpg

where c defines the segment's hydraulic conductance. The hydraulic conductance of a vascular segment resulting from the evaluation of the right-hand-side integral is then of great importance for a precise evaluation of the flow rate and pressure distribution inside the network. The numerical evaluation of this integral, using a composite Simpson rule, allows to take into account the vessel tortuosity as well as the local diameter variations. In the following, we evaluate the impact of such a detailed estimation of the hydraulic conductance compared with a simplified approach neglecting both vessel tortuosity and diameter variations (Reichold et al, 2009).

The apparent viscosity in the right-hand-side integral of relation (2) is evaluated from the above-mentioned viscosity models. When the hydraulic conductance has been computed, relation (2) provides the pressure drop between two successive bifurcations. It nevertheless neglects the influence of the possibly complex flow arising in the vicinity of each bifurcation. The correction to the pressure/flux relationship (2) coming from both finite ends of each vascular segment is expected to be localized within a few tube diameters D in the neighborhood of the two ends. As the segment length L is much larger than its diameter, the contribution of this supplementary hydrodynamic effect on the total flux/pressure drop relationship is expected to be of the order O(D/L). Such an effect could then safely be discarded, as it would lead to rather small corrections to the pressure drop defined in the left-hand-side of relation (2). It is then possible to use relation (2) to determine the steady-state pressure distribution using flow conservation at each bifurcation J of the network, such that

graphic file with name jcbfm2010105e3.jpg

where the index i refers to any vascular segment that crosses at bifurcation J. Equation (3) leads to a linear system applied to pressure nodes associated with each bifurcation J. We imposed the applied boundary conditions previously discussed at the border pressure nodes. The linear system obtained was then solved using a direct method (exact, robust and without parameterization) suitable for sparse matrices. We used the nonsymmetric multifrontal method with the UMFPACK set of routines (Davis, 2004a, 2004b). Solving the pressure problem is, in fact, the first step of an iterative process (Pries et al, 1990). The second step is the resolution of the hematocrit distribution within the network.

Computing the Hematocrit Distribution

In converging bifurcations, the two input hematocrits are known and a single missing hematocrit in the daughter branch has to be found. In diverging bifurcations, the mother hematocrit is known but the daughter ones are to be found from the known fluxes in each branch. Thus, two relationships are required to solve the problem, whereas a single relation is needed in converging bifurcations. Mass conservation associated with each hematocrit Hi could provide the necessary relation for the latter:

graphic file with name jcbfm2010105e4.jpg

In a diverging bifurcation, an additional plasma skimming splitting rule that implicitly respects mass conservation (4) is applied and determines the two unkown hematocrits (see, for example, Guibert et al, 2010 for more details on the model implementation). In practice, hematocrit evaluation is performed by following the flow from the arterial input and applying the appropriate form of equation (4). The hematocrit distribution obtained is then used to solve the pressure field at the next iteration. The convergence of this iterative procedure may be difficult, so overrelaxation, which consists in composing two successive evaluated fields, is used to facilitate the convergence (Pries et al, 1990).

Statistical Comparisons

To evaluate the comparison between two quantities defined throughout the vascular network, we defined a quantitative index, the average relative difference between two fields Y1 and Y2 associated with two distinct configurations such that

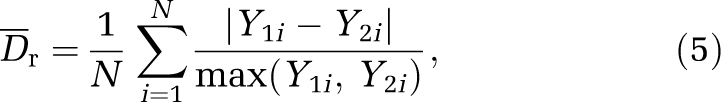graphic file with name jcbfm2010105e5.jpg

where Y1i, Y2i are the field values (pressure, hematocrit, flux) at each segment i of the network. We also defined the absolute difference as

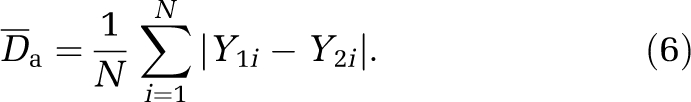graphic file with name jcbfm2010105e6.jpg

Furthermore, for the comparison of the pressures between different generations reported in Figure 5E, we used a Student's t-test as well as a Mann–Whitney nonparametric method.

Results

Extensive numerical computation of microvascular blood flow was performed in an 18 mm3 cortical reconstructed volume of primate cortex.

We first investigated the impact of the vessel geometry, the topology, and the blood rheology on pressure, hematocrit, and flow distributions to compare the various models of viscosity and phase separation used. One important side issue of these comparisons is to quantify the possible impact of the phase separation. This phenomenon complicates the blood flow computation remarkably because it requires a long iterative procedure (Pries et al, 1990) to be solved numerically. Hence, it is interesting to address its quantitative impact on the pressure distribution and the reliability of the different models previously proposed in the literature. We calculated the distributions of blood pressure and flow, and of hematocrit through the cortical depth.

Impact of Vessel Shape and Blood Rheology on the Flow

Using the apparent in vivo blood viscosity model proposed (Pries and Secomb, 2005), we first investigated the influence of diameter variations along a vessel length and compared a detailed evaluation of the conductance defined in relation (2) with a straight tube approximation associated with an arithmetically averaged diameter.

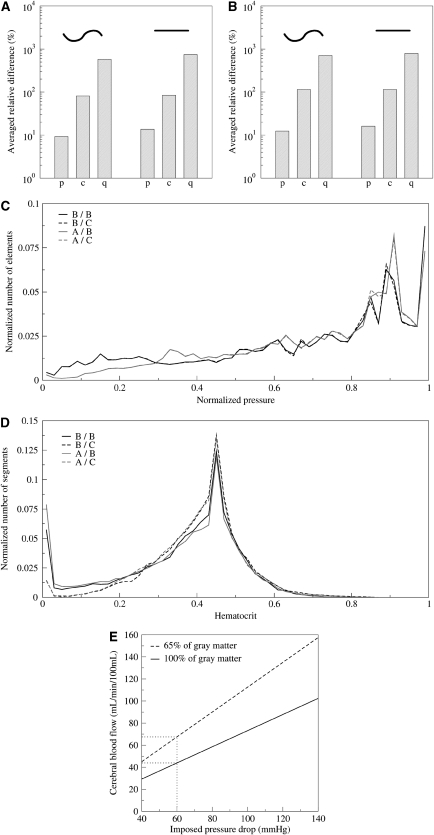
The impact of vessel shape on the hydraulic conductance, the pressure, and the blood flow are sketched in Figures 3A and 3B, which illustrates that the flow can be significantly affected if the length and diameter variations are not carefully taken into account. Figures 3A and 3B show that, even if the average pressure in each vessel is only moderately affected (close to 10%) by a refined description of the vessel shape and a good approximation of its true length, the vessel geometry can have a very significant impact on the flow conductance (close to 100%) as well as on the evaluated flux (700%). The very important relative differences shown in Figures 3A and 3B are nevertheless mainly due to extreme events where the conductance and flux are locally very different to the reference network.

Figure 3.

Figure 3

Open in a new tab

(A, B) Impact of the vessel's geometry on the flow computation. Here, we compare tortuous constant diameter tubes (left) and straight tubes (right) with real vessels. The pressure p, hydraulic conductance, c, and flux q are compared in (A) with plasma rheology and in (B) with the in vivo viscosity model of Pries and Secomb (2005) neglecting phase separation effect. (C, D) Comparison between different phase separation models Two different viscosity laws in blue (model B: Pries and Secomb, 2005) or red (model A: Kiani and Hudetz, 1991), and two phase separation splitting rules in continuous lines (model B: Pries and Secomb, 2005) or dashed lines (model C: Dellimore et al, 1983). (C) The histogram of pressure distribution and (D) the hematocrit distribution. (E) The cerebral blood flow versus the applied pressure difference using one pair of model (B/B Pries and Secomb, 2005).

Another important point addressed in this investigation is associated with the impact of the blood rheology on the flow distribution. Different effective viscosity models have been proposed for either in vitro or in vivo blood flows. In an earlier investigation, we found that different in vitro viscosity models gave very similar results for the pressure distribution (Guibert et al, 2009). Here, we complement this investigation by a systematic analysis of the relative difference between the in vivo and in vitro effective viscosity models illustrated in Figures 2A and 2B on the pressure distribution (Table 1a and c, the different blood effective viscosity and phase separation models that we have investigated are labeled by letters A, B, C, O, see Table 1 caption). It can be seen that the blood effective viscosity has a nonnegligible impact on the pressure distribution (up to 10%, Table 1a, compare A/0 and B/O versus 0/0). One can also observe that taking account of some in vivo features of the blood can have a significant impact on the pressure, up to 18% (Table 1a, A/0 versus B/0). Table 1c, e, and f provides a systematic comparison of the different pairs of effective viscosity and phase separation effects on the pressure, conductance, and flux distributions. It can be observed that the comparison between in vitro (Kiani and Hudetz, 1991) and in vivo (Pries and Secomb, 2005) effective viscosity models leads to the most striking differences. Furthermore, as noted earlier, although the impact on the pressure is relatively moderate (variations of 18%), this is not the case for either the conductances or the fluxes, for which the relative difference can reach >250 and 400%, respectively. Hence, it is an important conclusion that in vivo and in vitro blood models do not lead to similar results for the blood flow computation.

Table 1. Comparison between different couples of models used for modeling blood rheology and phase separation effects.

Viscosity models: A=Kiani and Hudetz (1991) B=Pries and Secomb (2005) O=Plasma viscosity Phase separation models: B=Pries and Secomb (2005) C=Dellimore et al (1983) O=No phase separation
Pair 1 Pair 2    
Viscosity model/phase separation model Viscosity model/phase separation model Dr (%) Da
(a) Impact of viscosity model on pressure distribution
 A/O B/O 17.63  
 O/O B/O 10.27  
 O/O A/O 5.13  
       
(b) Impact of phase separation on pressure distribution
 B/O B/C 0.46  
 B/O B/B 0.34  
 A/O A/C 0.31  
 A/O A/B 0.24  
       
(c) Pressure distributions comparison
 A/B A/C 17.97  
 A/C B/C 17.85  
 A/B B/B 17.77  
 A/C B/B 17.66  
 B/C B/B 0.25  
 A/C A/B 0.18  
       
(d) Hematocrit distributions comparison
 A/B B/C 1302.18 0.0807
 A/C B/C 7.29 0.0214
 A/B B/B 126.79 0.0388
 A/C B/B 168.23 0.0655
 B/C B/B 156.42 0.0626
 A/C A/B 1294.05 0.0720
       
(e) Conductance distributions comparison
 A/B B/C 270.34  
 A/C B/C 259.53  
 A/B B/B 246.04  
 A/C B/B/ 238.80  
 B/C B/B 13.14  
 A/C A/B 5.39  
       
(f) Flow rate distributions comparison
 A/B B/C 463.62  
 A/C B/C 410.86  
 A/B B/B/ 300.61  
 A/C B/B/ 293.93  
 B/C B/B/ 19.81  
 A/C A/B 10.54  
Open in a new tab

The different models used are represented by letters: A is used for the in vitro viscosity model (Kiani and Hudetz, 1991), B for the in vivo and phase separation one (Pries and Secomb, 2005), C for the nongeometrical phase separation model (Dellimore et al, 1983), and D for the recent one (Pries and Secomb, 2005). The letter O is used for plasma rheology and absence of phase separation effect.

We then analyzed the impact of phase separation. Table 1b shows a very convincing demonstration that, for any effective viscosity, phase separation models have little influence on the pressure distribution. Figure 3C also illustrates the very small impact of phase separation models (comparing the dotted lines with the color-corresponding continuous lines), which do not display any visible effect on the pressure distribution. This observation is also confirmed by considering the effect of the phase separation on conductance and flux distributions given in Table 1e and f. In the last two lines, it can be observed that phase separation does not affect conductances by >13% or fluxes by >20% when a given effective viscosity model is considered.

Nevertheless, it should be borne in mind that, although phase separation models may not have a strong influence on the hemodynamics, they obviously affect the hematocrit distribution inside the network as illustrated in Figures 3D and 4C and Table 1d. The last two lines of Table 1d show that relative differences of >100% are observed on the hematocrit when two different phase separation models are considered for a given effective viscosity model. This observation should nevertheless be tempered by the fact that this large relative difference mainly occurs for small hematocrit values as illustrated in Figure 3D. Such a discrepancy between different phase separation models at small hematocrit values below 0.05% explains the large relative error 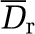Inline graphic obtained (Table 1d). Hence, only small values of the hematocrit distribution are sensitive to the phase separation splitting rule, in agreement with earlier observations (Pries et al, 1990).

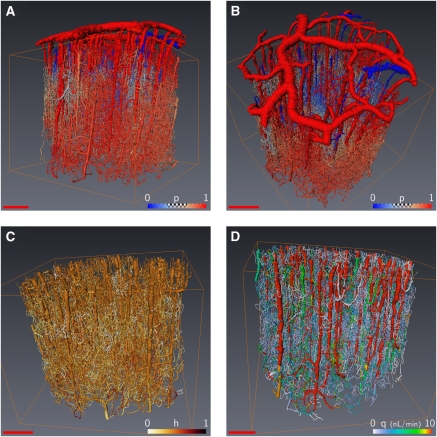
Figure 4.

Figure 4

Open in a new tab

Color-coded representations of evaluated fields within the network using (Pries and Secomb, 2005) models B on the same sample as Figure 1C with an input hematocrit of 45%. (A, B) The pressure distribution from red (arteries) to blue (veins), (C) the hematocrit distribution (from dark to light), and (D) the flux distribution from red to white (scale bar=500 μm).

The main conclusion of this section is that a detailed description of vessel shape is needed for reliable computation of its contribution to blood transportation. Furthermore, an in vivo effective viscosity model that takes the interaction between red blood cells and endothelial cells into account leads to different results compared with in vitro ones. Therefore, in the following, we use the in vivo effective viscosity model (Pries and Secomb, 2005) as a reference to analyze the pressure, hematocrit, and flow distributions.

Blood Pressure Distribution Inside the Brain

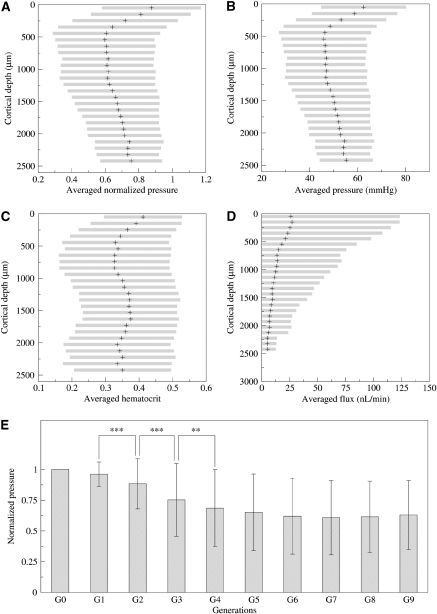
Figures 4A and 4B show the blood pressure in each vascular segment of an 18-mm3 volume of cortex for the more recent viscosity and phase separation models (Pries and Secomb, 2005). Differences between arterioles and veinules in penetrating vessels can be observed from their distinct red and blue colors. These figures show that the pressure rapidly becomes uniform inside the cortical tissue without any noticeable difference through the cortical depth. The average pressure variations with cortical depth are further investigated in Figures 5A and 5B, where it is found almost constant within the first 1.5 mm and then slightly increases when further plunging down inside the cortical depth. This observation might seem surprising at first sight, as the pressure should decay from the pial surface down to the cortex. To understand this result, it should be born in mind that the output venous pressure is also imposed at the brain surface. Furthermore, even though the penetrating arteries show some diameter reduction when plunging down inside the cortical depth, the resulting diameter is still large compared with the smallest capillaries. As most of the pressure drop results from diameter changes of the vessels (as already discussed just after relation (1), in the Materials and methods section), the pressure variations in the penetrating arterioles along their cortical pathway are quite modest. Furthermore, earlier findings (Risser et al, 2009) have shown that the relative contribution of the penetrating arterioles to the total vessel density slightly increases through the cortical depth also explains the observed slight increase of the average pressure in Figures 5A and 5B.

Figure 5.

Figure 5

Open in a new tab

In-depth variation of hemodynamic quantities. (A) Normalized pressure, (B) real pressure (mm Hg), (C) hematocrit, and (D) flux (nL/min) evolution with the cortical depth. The cortical depth is subdivided in 25 successive, 80 μm thick, slices for which the mean is represented with symbol+and s.d. with an horizontal gray bar. (E) Mean pressure and s.d. for the 10 first network generations of bifurcation starting from arterial inputs. For any couple of generations, significant differences are indicated with asterisks: ***P<10−10, **P<10−4.

Figures 4A and 4B also illustrate that there is a rapid change in pressure after a few bifurcations inside the capillary bed. We further studied the impact of the topological organization of the microvascular network by measuring the variations of the pressure versus the generation number along the vascular tree, starting from each penetrating arteriole. The variations of the pressure, which is averaged over all the vascular segments of a given generation, are presented in Figure 5E. It can be seen that the pressure difference between penetrating arterioles and their first branches is lower than 5%, confirming that the pressure drop does not arise at the level of penetrating arterioles but much further away inside the capillary bed. The average pressure decreases significantly (see the inserted statistical test in Figure 5B) in the first three generations then reaches a plateau at the fourth generation, which persists through further branches inside the capillary bed.

Hematocrit Distribution

The hematocrit variations within the cortex are illustrated in Figure 4C using a physiological input hematocrit of 45%, with the in vivo effective viscosity model (Pries and Secomb, 2005). We also investigated the impact of the rheological model on the hematocrit distributions by comparing different pairs of effective viscosity/phase separation models (Figure 3D). All the computed distributions share very similar qualitative features: they peak at the input reference hematocrit Ho=0.45 and display a nonsymmetrical distribution with preferred low values. It is interesting to note that 80% of the local hematocrit values remain between macroscopic physiological values, that is in the range 0.3 to 0.6. Thus, although different, the phase separation models proposed in the literature do not lead to drastically different hematocrit distributions when the same effective viscosity model is considered, except for small hematocrit values.

In contrast to its low impact on pressure distribution (Figure 3C; Table 1e), the phase separation model is mainly responsible for the hematocrit field variations (Table 1d). This observation is not surprising, as phase separation induces hematocrit heterogeneities in the network.

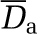The apparent relative difference Inline graphic between the two models can be large (Table 1d), but this is only a localized effect due to extreme contributions of tiny hematocrit values, so the absolute difference Inline graphic is always small. Again, this is a rather surprising observation, which consequently gives us confidence in the reliability of the hematocrit field prediction because the results are quite similar whichever model is considered. A plausible explanation for this result is related to the weak dependence of the effective viscosity on the hematocrit as compared with the local vessel diameter. The second (more methodological) consequence of the slight influence of the hematocrit field on the blood flow is the robustness of numerical prediction of the blood perfusion whichever phase separation model is considered (cf Table 1b). This is an important result as the major difficulty in these extensive computations concerns the presence of nonlinear coupling associated with the phase separation effects. We found that neglecting this effect still led to very sensible predictions for the blood pressures and fluxes, the implication of which could drastically simplify further numerical investigations. Obviously, such approximation is meaningless for addressing the issues of transport and/or exchanges between the vascular compartment and the brain tissue. It is nevertheless interesting for understanding the structure/function relationship between the very complex vascular networks and blood perfusion. Finally, it is interesting to observe in Figure 5C that the hematocrit variations inside the cortical thickness are quite modest (<15%), which confirms that, as the average pressure, the average oxygen supply is homogeneously distributed within the gray matter.

Blood Flow Distribution

The blood flux variations within the cortical depth is also represented in Figure 5D and shows a slight continuous decrease. This variation is nevertheless modest, and concomitant with a weak rarefaction of penetrating vessels, a constant capillary density, and, thus a total volume density decrease in the cortical depth (not shown here (Risser et al, 2009)). One interesting consequence of the rarefaction of penetrating vessels within the cortical depth is that high fluxes are less present so that the flux variability represented in gray bars in Figure 5D is clearly reduced within the cortical depth.

Cerebral blood flow is one important quantity of interest, as it is directly related to tissue perfusion. At the millimeter scale, our predictions can be compared with earlier experimental observations on humans or animals. As mentioned earlier, the prediction for the CBF depends linearly on the values chosen for the arteriolar/venous pressure difference. Figure 3E provides mean values of the CBF through the cortex from the pial surface, shown in Figure 5D, versus the applied pressure difference. When considering a pressure difference of 60 mm Hg and a cortical composition of 65% of gray matter (dashed line), our prediction for the CBF is 70 mL per minute per 100 mL. This prediction is in good agreement with earlier measurements in animal brain (Gobbel et al, 1999; Cenic et al, 1999). Finally, as the total flux is conserved, the total input arteriolar/output veinular fluxes are the same. This prediction is not contradictory with the observation of lower blood velocity in the veins at the cortical surface (Schaffer et al, 2006), as the diameter of pial veins is much larger than that of penetrating veins and of pial arteries.

Discussion

The present work analyzes the influence of various blood properties and the impact of the vessel shape on the pressure, hematocrit, and flow distribution inside the cortical gray matter. We have first shown that it is important to consider vessel tortuosity and real length.

Then, we have shown that reliable modeling necessitates taking the blood effective viscosity into account, which can differ drastically from that of plasma, to obtain a meaningful estimate of the blood flux. This is especially true when considering the effect of specific in vivo behavior of blood rheology. By considering the effect of endothelial surface layers on cerebral perfusion, we realize that the impact of small capillary diameter variations can be large. A first quantitative evaluation leads to the conclusion that a 10% variation homogeneously applied for all capillary diameters (smaller than 11.2 μm) could lead to 20% change in the CBF. This result challenges the concept of neurogenic/metabolic brain perfusion regulation (Rossier, 2009), as it indicates that diffuse and global diameter variations at the local scale can also regulate the blood flux. It motivates future systematic investigations of vessel regulation impacts.

Moreover, we also established that phase separation has very little influence on the pressure distribution, and a small effect on the blood flux. This conclusion could seem surprising at first sight, as it is known that the brain autoregulation mechanism is based on the influence of the local hematocrit value on the local blood flux. A plausible explanation could be the weak reliance of the effective viscosity on the hematocrit, as compared with the local vessel diameter. Although the detailed mechanism of the coupling between hematocrit and blood flux is still an open issue, there is now an established set of analyses demonstrating a local autoregulation of the brain's hemodynamics (Zonta et al, 2003; Mulligan and MacVicar, 2004; Gordon et al, 2008). In fact, our conclusion does not violate the autoregulation principle as no feedback mechanism was taken into account in our analysis. We only consider passive blood (i.e., no rheological modification of the blood occurs inside the network) flowing into passive vessels (i.e., no structural modification of the vessel diameters coming from some tissue signal). Our results strongly suggest that the blood perfusion is quite robust to any change in the hematocrit distribution. This is an important statement as the CBF value prediction is not much affected by the chosen phase separation splitting rule.

Let us now comment on the organization of the blood perfusion within the microvascular network. We investigated both the spatial and the topological distribution of the blood pressure inside the cortex, as these considerations have been previously found to be of importance in mesentery networks (Pries et al, 1995, 1996). First, we found that the blood perfusion very rapidly became uniform inside the gray matter depth, where various cellular layers are present. In this motor cortex, we found weak hematocrit variations around an average value of 0.33 within the cortical depth consistent with literature data (Oldendorf et al, 1965). It should be interesting, in future studies, to correlate possible flux in-depth variations with known anatomical layers (e.g., in sensory cortex (Gerrits et al, 2000)).

The mean blood perfusion was already homogeneous from a few hundred microns from pial arteries, and did not show much variation through the cortical depth in the cortex investigated.

Second, we also found that topological organization strongly determined the blood pressure distribution as found previously in the rat mesentery (Pries et al, 1995). The pressure drops by 40% between its pial value and the capillary one. The presence of a plateau in the pressure value distribution associated with the bifurcation generation number down each penetrating arteriole shows that homogeneous perfusion is reached inside the microvascular network within three to four bifurcations. This indicates that the capillary bed starts after three to four bifurcations from the penetrating arterioles, which is an interesting structural property. The fact that the pressure plateau persists for >10 further bifurcations also confirms that the capillary bed is associated with a homogeneous average pressure of about 50 mm Hg. This average pressure value in the capillary bed, where most of the exchanges (especially for oxygen) occur, is interesting to compare with an earlier estimate of 40 mm Hg (Zagzoule and Marc-Vergnes, 1986). Hence, the function of perforating arterioles is to provide some nominally pressurized blood through the entire cortical depth to permit homogeneous perfusion pressure inside the capillary bed. Finding a constant average pressure at the capillary level is probably related to the physiological function of capillaries in the oxygen exchange as the hemoglobin saturation depends on the oxygen partial pressure, which is directly proportional to the total pressure. Hence, providing a homogeneous capillary pressure permits the exchange to occur similarly within the whole cortex depth.

The authors declare no conflict of interest.

References

  1. Cassot F, Lauwers F, Lorthois S, Puwanarajah P, Duvernoy H. Scaling laws for branching vessels of human cerebral cortex. Microcirculation. 2009;16:331–344. doi: 10.1080/10739680802662607. [DOI] [PubMed] [Google Scholar]
  2. Cenic A, Nabavi DG, Craen RA, Gelb AW, Lee T-Y. Dynamic CT measurements of cerebral blood flow: a validation study. Am J Neuroradiol. 1999;20:63–73. [PubMed] [Google Scholar]
  3. Cokelet GR, Goldsmith HL. Decreased hydrodynamic resistance in the two-phase flow of blood through small vertical tubes at low flow rates. Circ Res. 1991;68:1–17. doi: 10.1161/01.res.68.1.1. [DOI] [PubMed] [Google Scholar]
  4. Davis TA. Algorithm 832: UMFPACK V4.3—an unsymmetric-pattern multifrontal method. ACM T Math Software. 2004a;30:196–199. [Google Scholar]
  5. Davis TA. A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM T Math Software. 2004b;30:165–195. [Google Scholar]
  6. Dellimore JW, Dunlop MJ, Canham PB. Ratio of cells and plasma in blood flowing past branches in small plastic channels. Am J Physiol-Heart C. 1983;244:635–643. doi: 10.1152/ajpheart.1983.244.5.H635. [DOI] [PubMed] [Google Scholar]
  7. Duvernoy HM, Delon S, Vannson JL. Cortical blood vessels of the human brain. Brain Res Bull. 1981;7:519–579. doi: 10.1016/0361-9230(81)90007-1. [DOI] [PubMed] [Google Scholar]
  8. Gerrits R, Raczynski C, Greene AS, Stein EA. Regional cerebral blood flow responses to variable frequency whisker stimulation: an autoradiographic analysis. Brain Res. 2000;864:205–212. doi: 10.1016/s0006-8993(00)02142-9. [DOI] [PubMed] [Google Scholar]
  9. Gobbel GT, Cann CE, Iwamoto HS, Fike JR. Measurement of regional cerebral blood flow in the dog using ultrafast computed tomography. Experimental validation. Stroke. 1999;22:772–779. doi: 10.1161/01.str.22.6.772. [DOI] [PubMed] [Google Scholar]
  10. Gordon GRJ, Choi HB, Rungta RL, Ellis-Davies CR, MacVicar BA. Brain metabolism dictates the polarity of astrocyte control over arterioles. Nature. 2008;456:745–750. doi: 10.1038/nature07525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Guibert R, Fonta C, Plouraboué F. Le réseau micro-vasculaire structure la distribution de la pression sanguine. Mec Ind. 2009;10:255–260. [Google Scholar]
  12. Guibert R, Fonta C, Plouraboué F. A new approach to model confined suspensions flows in complex networks: application to blood flow. Transp Por Med. 2010;83:171–194. [Google Scholar]
  13. Kiani MF, Hudetz AG. A semi-empirical model of apparent blood viscosity as a function of vessel diameter and discharge hematocrit. Biorheology. 1991;28:65–73. doi: 10.3233/bir-1991-281-207. [DOI] [PubMed] [Google Scholar]
  14. Lauwers F.2007. PhD Thesis: Etude quantitative tridimensionnelle du réseau micro-vasculaire du cortex cérébral humain,Toulouse, France: Université Paul Sabatier [Google Scholar]
  15. Lipowsky HH. Microvascular rheology and hemodynamics. Microcirculation. 2005;12:5–15. doi: 10.1080/10739680590894966. [DOI] [PubMed] [Google Scholar]
  16. McWhirter JL, Noguchi H, Gompper G. Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries. Proc Natl Acad Sci USA. 2009;106:6039–6043. doi: 10.1073/pnas.0811484106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mulligan SJ, MacVicar BA. Calcium transients in astrocyte endfeet cause cerebrovascular constrictions. Nature. 2004;431:195–199. doi: 10.1038/nature02827. [DOI] [PubMed] [Google Scholar]
  18. Oldendorf WH, Kitano M, Shimizu S, Oldendorf SZ. Hematocrit of the human cranial blood pool. Circ Res. 1965;17:532–539. doi: 10.1161/01.res.17.6.532. [DOI] [PubMed] [Google Scholar]
  19. Plouraboué F, Clotens P, Fonta C, Steyer A, Lauwers F, Marc-Vergnes J-P. X-ray high-resolution vascular network imaging. J Microsc-Oxford. 2004;215:139–148. doi: 10.1111/j.0022-2720.2004.01362.x. [DOI] [PubMed] [Google Scholar]
  20. Pries AR, Secomb TW. Microvascular blood viscosity in vivo and the endothelial surface layer. Am J Physiol-Heart C. 2005;289:2657–2664. doi: 10.1152/ajpheart.00297.2005. [DOI] [PubMed] [Google Scholar]
  21. Pries AR, Schonfeld D, Gaehtgens P, Kiani MF, Cokelet GR. Relationship between structural and hemodynamic heterogeneity in microvascular networks. Am J Physiol-Heart C. 1996;270:545–553. doi: 10.1152/ajpheart.1996.270.2.H545. [DOI] [PubMed] [Google Scholar]
  22. Pries AR, Secomb TW, Gaehtgens P. Structure and hemodynamics of microvascular networks: heterogeneity and correlations. Am J Physiol-Heart C. 1995;269:1713–1722. doi: 10.1152/ajpheart.1995.269.5.H1713. [DOI] [PubMed] [Google Scholar]
  23. Pries AR, Secomb TW, Gaehtgens P, Gross JF. Blood flow in microvascular networks—experiments and simulation. Circ Res. 1990;67:826–834. doi: 10.1161/01.res.67.4.826. [DOI] [PubMed] [Google Scholar]
  24. Reichold J, Stampanoni M, Keller AL, Buck A, Jenny P, Weber B. Vascular graph model to simulate the cerebral blood flow in realistic vascular networks. J Cerebr Blood F Met. 2009;29:1429–1443. doi: 10.1038/jcbfm.2009.58. [DOI] [PubMed] [Google Scholar]
  25. Risser L, Plouraboué F, Cloetens P, Fonta C. A 3D investigation shows that angiogenesis in primate cerebral cortex mainly occurs at capillary level. Int J Dev Neurosci. 2009;27:185–196. doi: 10.1016/j.ijdevneu.2008.10.006. [DOI] [PubMed] [Google Scholar]
  26. Risser L, Plouraboué F, Descombes X. Gap filling of 3-d micro-vascular networks by tensor voting. IEEE T Med Imaging. 2008;27:674–687. doi: 10.1109/TMI.2007.913248. [DOI] [PubMed] [Google Scholar]
  27. Risser L, Plouraboué F, Steyer A, Clotens P, Le Duc G, Fonta C. From homogeneous to fractal normal and tumorous microvascular networks in the brain. J Cerebr Blood F Met. 2007;27:293–303. doi: 10.1038/sj.jcbfm.9600332. [DOI] [PubMed] [Google Scholar]
  28. Rossier J. Wiring and plumbing. Front Hum Neurosci. 2009;3(2):1–2. doi: 10.3389/neuro.09.002.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schaffer CB, Friedman B, Nishimura N, Schroeder LF, Tsai PS, Ebner FF, Lyden PD, Kleinfeld D. Two-photon imaging of cortical surface microvessels reveals a robust redistribution in blood flow after vascular occlusion. Plos Biol. 2006;4(2):258–270. doi: 10.1371/journal.pbio.0040022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Secomb TW, Beard DA, Frisbee JC, Smith NP, Pries AR. The role of theoretical modeling in micro circulation research. Microcirculation. 2008;15:693–698. doi: 10.1080/10739680802349734. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Stromberg DD, Fox JR. Pressures in the pial arterial micro circulation of the cat during changes in systemic arterial blood pressure. Circ Res. 1972;31:229–239. doi: 10.1161/01.res.31.2.229. [DOI] [PubMed] [Google Scholar]
  32. Tamaki K, Heistad DD. Response of cerebral arteries to sympathetic stimulation during acute hypertension. Hypertension. 1986;8:911–917. doi: 10.1161/01.hyp.8.10.911. [DOI] [PubMed] [Google Scholar]
  33. Torquato S.2001Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Interdisciplinary Applied MathematicsIst ed.Springer-Verlag: New York [Google Scholar]
  34. Tsai PS, Kaufhold JP, Blinder P, Friedman B, Drew PJ, Karten HJ, Lyden PD, Kleinfeld D. Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels. J Neurosci. 2009;29:14553–14570. doi: 10.1523/JNEUROSCI.3287-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Weber B, Keller AL, Reichold J, Logothetis NK. The microvascular system of the striate and extrastriate visual cortex of the macaque. Cerebral Cortex. 2008;18:2318–2330. doi: 10.1093/cercor/bhm259. [DOI] [PubMed] [Google Scholar]
  36. Zagzoule M, Marc-Vergnes J-P. A global mathematical model of the cerebral circulation in man. J Biomech. 1986;19:1015–1022. doi: 10.1016/0021-9290(86)90118-1. [DOI] [PubMed] [Google Scholar]
  37. Zonta M, Angulo MC, Gobbo S, Rosengarten B, Hossmann K-A, Pozzan T, Carmignoto G. Neuron-to-astrocyte signaling is central to the dynamic control of brain micro circulation. Nat Neurosci. 2003;6:43–50. doi: 10.1038/nn980. [DOI] [PubMed] [Google Scholar]
  38. Zweifach BW, Lipowsky HH. Quantitative studies of microcirculatory and function III. Circ Res. 1977;341:380–390. doi: 10.1161/01.res.41.3.380. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Cerebral Blood Flow & Metabolism are provided here courtesy of SAGE Publications

RESOURCES