Fractional order models of viscoelasticity as an alternative in the analysis of red blood cell (RBC) membrane mechanics

Abstract

New lumped-element models of red blood cell mechanics can be constructed using fractional order generalizations of springs and dashpots. Such ‘spring-pots’ exhibit a fractional order viscoelastic behavior that captures a wide spectrum of experimental results through power-law expressions in both the time and frequency domains. The system dynamics is fully described by linear fractional order differential equations derived from first order stress–strain relationships using the tools of fractional calculus. Changes in the composition or structure of the membrane are conveniently expressed in the fractional order of the model system. This approach provides a concise way to describe and quantify the biomechanical behavior of membranes, cells and tissues.

Video microscopy reveals that a RBC must fold almost double to traverse the length of a typical capillary. Such deformation stresses the membrane nearly to its elastic limit and leads to microstructural damage that shortens the circulation lifetime of the human RBC to less than 90 days. Characterization of this damage requires an accurate viscoelastic model of membrane flexibility. In recent research, new experimental tools (e.g. magnetic twisting cytometry [1] and optical tweezers [2]) have been developed to study the membrane dynamics of single cells. These tools provide a direct means to test models of membrane viscoelasticity. Magnetic twisting cytometry, for example, can measure the complex elastic moduli, g(iω) = g′ (ω) + ig″(ω) (where g′ is the elastic modulus, g″ is the frictional loss modulus, ω = 2π f is the angular frequency in radians s⁻¹ and f is the frequency in hertz) of the RBC membrane over a wide frequency range (0.01–100 Hz). Such studies [1] found a fractional power-law dependence for g″ (g″ proportional to ω^α, with α = 0.64) in the frequency domain, and a fractional order creep response to a step input in stress in the time domain. In both cases the time and frequency data did not conform to conventional spring and dashpot viscoelastic models (e.g. Maxwell and Voigt arrangements). Subsequent studies [2] of RBC membranes using optical tweezers observed a power-law relaxation of membrane stiffness (t^−α, with α = 0.75 for fresh RBC) and of strain rate dependence that could not be explained within the framework of linear viscoelasticity. We would like to suggest, however, that linear fractional order models, as developed by Koeller [3], Bagley and Torvik [4], Suki et al [5] and Djordjević et al [6] using the so-called fractional calculus can be used to characterize many aspects of such power-law viscoelastic behavior.

It is not widely recognized that the derivative is not restricted to the integer orders (e.g. first, second, third, etc) usually encountered in college calculus. In fact, intermediate orders such as 1/2, 3/2 or even π are possible. A simple introduction to the field of fractional calculus for biomedical engineers was recently published [7], and a more advanced description emphasizing how to solve fractional order differential equations is also available [8]. Briefly, the fractional derivative of order α, 0 ≤ α < 1, for a function f (t) can be expressed most simply in the Laplace domain when the initial condition is set equal to zero as

$$L[D_t^{\alpha }(f(t))]=s^{\alpha }L[f(t)]=s^{\alpha }F(s),$$

which converges to the classical result in the limit as α goes to 1. The only restrictions on the function f (t) are those needed to ensure the existence of the Laplace transform (piecewise continuity and exponential order), and these properties are commonly satisfied by most functions of interest to bioengineers and cell biologists. Thus, manipulation of fractional order derivatives in the Laplace domain involves simply replacing sF(s), s²F(s) and s³F(s) with s^1/2F(s), s^3/2F(s) and s^πF(s). The corresponding expressions in the time domain are linear, involve the convolution integral (e.g. f (t) ∗ t^−α/Γ (1 − α), where Γ is the gamma function [8]), and are most easily obtained by using tables of Laplace transforms [9] or more rarely by evaluating the inverse Laplace transform directly [10].

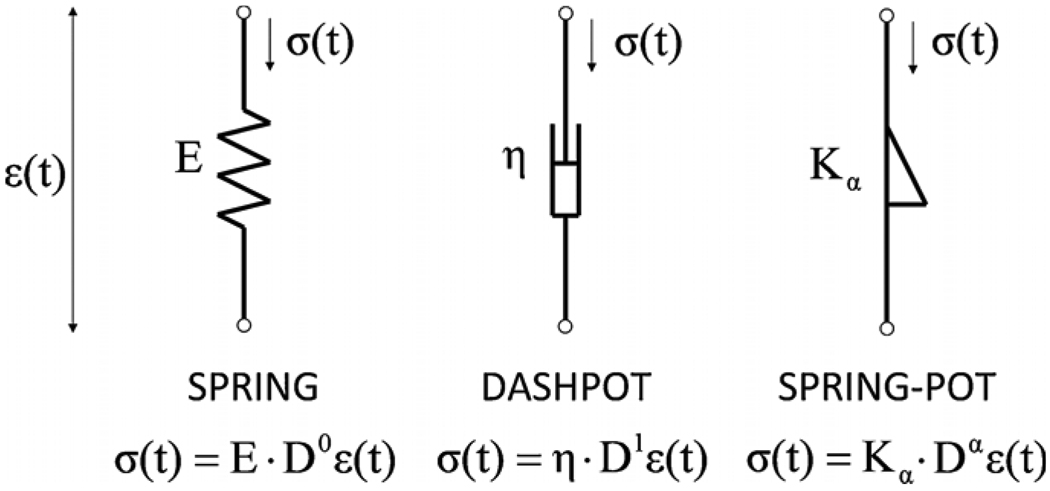
Fractional calculus is useful in the field of biorheology, in part, because many tissue-like materials (polymers, gels, emulsions, composites and suspensions) exhibit power-law responses to an applied stress or strain [11, 12]. An example of such power-law behavior in elastic tissue was observed recently for viscoelastic measurements of the aorta, both in vivo and in vitro [13, 14], and the analysis of these data was most conveniently performed using fractional order viscoelastic models. For this one-dimensional model, the stress (σ) and the strain (ε) in a material (or shear stress and strain) can be related with a fractional derivative $\sigma =K_{\alpha }{D}_t^{\alpha }(\epsilon )$ where 0 ≤ α ≤ 1 and K_α = Eτ^α. Here E is an elastic constant with the units of (N m⁻²) and τ is a time constant with units of (seconds); thus K_α had units of (Pascal) (seconds)^α. The bounding values of α represent the discrete elements employed in conventional viscoelastic models (spring, K_α = E when α = 0 and dashpot, K_α = Eτ^α = η, the coefficient of viscosity, when α = 1, see figure 1).

Figure 1.

Schematic diagram for the traditional spring and dashpot elements and the fractional order ‘spring-pot’. Also shown are the one-dimensional stress (σ) versus strain (ε) equations for the spring, the dashpot and the spring-pot. Here, $\sigma =K_{\alpha }{D}_t^{\alpha }(\epsilon )$ where 0 ≤ α ≤ 1 and K_α = Eτ^α. In this representation E is an elastic constant with the units of (N m⁻²) and τ is a time constant with units of (seconds); thus, K_α had units of (Pascal) (seconds)^α. The bounding values of α represent the discrete elements employed in conventional viscoelastic theory (spring, K_α = E when α = 0; dashpot, K_α = Eτ^α = η, the coefficient of viscosity, when α = 1).

What happens for intermediate order values of α? When the fractional derivative model above is adopted, a new element is created that exhibits linear viscoelastic behavior intermediate between pure elastic and viscous responses. This fractional order viscoelastic element is usually called a ‘spring-pot’. The spring-pot has composite elastic and viscous behavior, which carries important biophysical consequences for time and frequency responses to applied stress or strain. For example, the stress relaxation G(t) following a unit step in strain for a single spring-pot is not an exponential decay, but assuming quiescent initial conditions, it is a power law:

$$G(t)=\frac{K_{\alpha }{t}^{-\alpha }}{\Gamma (1-\alpha )}.$$

In the frequency domain where s = iω, the same power law also appears:

$$G(\mathrm{i}\omega )=K_{\alpha }{(\mathrm{i}\omega )}^{\alpha }.$$

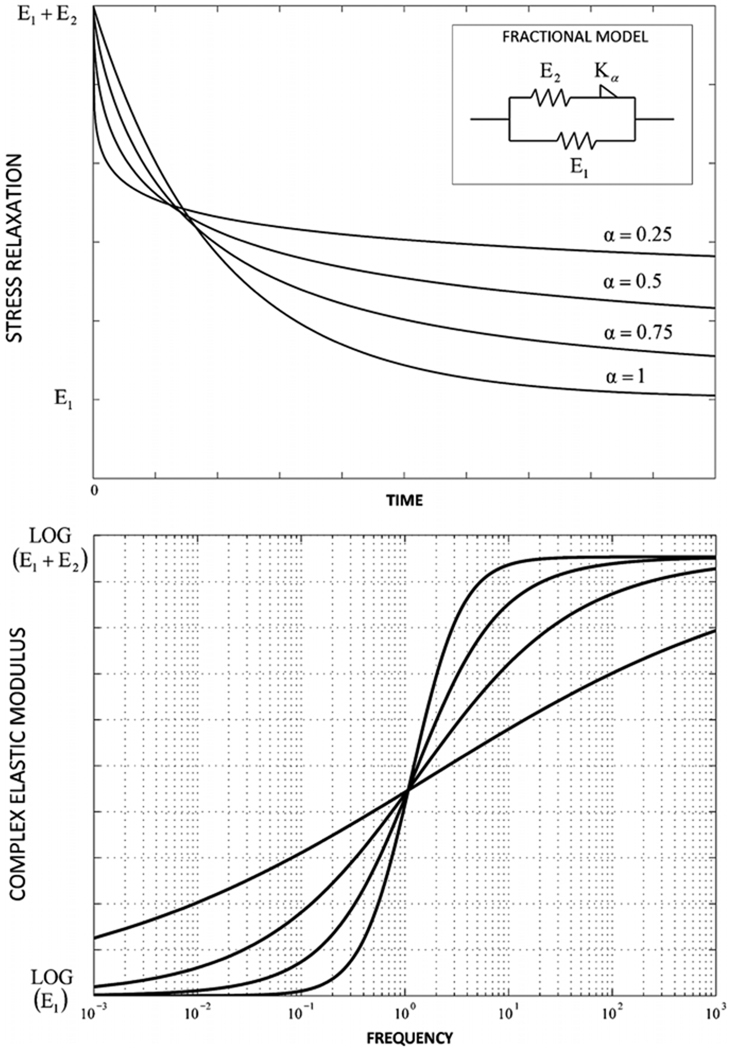
The frequency responses for a spring and a dashpot can be recovered by replacing the fractional order parameter α with its boundary values of zero or 1. A simple example of this behavior is presented in figure 2, where the traditional standard linear solid was modified by replacing the dashpot with a spring-pot [3]. In this figure the time and frequency power-law behaviors are modulated by changing the fractional order parameter α (α = 0.25, 0.50, 0.75 or 1).

Figure 2.

Modified standard linear solid model in which the dashpot is replaced with a spring-pot. Normalized stress relaxation curves (top) and frequency response curves (bottom) for different fractional orders α (α = 0.25, 0.50, 0.75 or 1).

Since the spring-pot exhibits intrinsic power-law responses in time and frequency, it can be easily combined with traditional spring and dashpots elements to model the dynamics of a particular complex viscoelastic process. As an example, Djordjević and co-workers [6] found that a parallel combination of a spring-pot and a dashpot properly predict the measured values for a rheological model of cultured smooth muscle cells. In another study by Puig-de-Morales-Marinkovic and colleagues [1], the relaxation modulus (equation (8) in [1]) is most simply described in the Laplace domain in terms of a spring in parallel with a spring-pot (a fractional order Voigt model [3]). The resulting creep compliance (equation (10) in [1]) can also be directly expressed in the time domain in terms of the single-parameter Mittag–Leffler function, E_α(z^α) [7, 8], as

$$\sigma =A^{-1}\left[1-E_{\alpha }\left(-\frac{A}{B}{t}^{\alpha }\right)\right].$$

In this equation, A corresponds to the spring constant and B to the fractional spring-pot coefficient, K_α. Furthermore, the short and long time limits derived from series expansions (equations (11) and (12) in [1]) follow directly from the asymptotic expansions of the Mittag–Leffler function [8], and finally, when α is set equal to 1, the Mittag–Leffler function becomes a single exponential and we recover the classic viscoelastsic response of the Voigt model. The inclusion of a spring-pot in this model of the RBC membrane is needed to fit the observed behavior of the dynamic modulus at high frequencies. A very similar approach could be used to model the stress relaxation data of Yoon et al [2].

These examples illustrate how adding spring-pots to traditional viscoelastic models (e.g. spring, dashpot combinations) can help resolve a number of difficulties currently present in discrete element modeling of biological tissues. Recently, for example, the stress relaxation in arteries was analyzed using fractional order dynamic models in vitro [13] and in vivo [14]. In these studies, discrete time constants were not expected due to the multiscale and multicomponent structure of the arterial wall. The fractional order model, in addition to fitting the control data, successfully described drug-induced smooth muscle activation through changes in the fractional order (α). Since, it is known that a single spring-pot can be decomposed in an infinite spring-dashpot ladder [7], such behavior might be a clue to relate fractional order dynamic models with the multi-scale, complex physical structure of biological tissues. Alternatively, the fractional order rheology observed in tissues, cells, extra-cellular matrix and membranes might reflect the dynamics of soft glassy materials, which successfully model the behavior of many complex materials (foams, emulsions and slurries) [15, 16]. In addition, a recent finding by Stamenović et al [17] suggests that the rheological behavior of living cells might be described by two power-law curves, depending on the time or frequency range.

The fractional order stress–strain element (the spring-pot) provides an alternative mathematical model that appears to describe concisely the reported viscoelastic properties of the red blood cell membrane, other cell membranes, and multilayered tissue such as cartilage or arterial wall. The connection between observed fractional order viscoelastic behavior, replicated across the cellular to bulk tissue scales and the order of the fractional element remains as a motivation for future work.