Abstract
Month of birth influences adult life expectancy at ages 50+. Why? In two countries of the Northern Hemisphere–Austria and Denmark–people born in autumn (October–December) live longer than those born in spring (April–June). Data for Australia show that, in the Southern Hemisphere, the pattern is shifted by half a year. The lifespan pattern of British immigrants to Australia is similar to that of Austrians and Danes and significantly different from that of Australians. These findings are based on population data with more than a million observations and little or no selectivity. The differences in lifespan are independent of the seasonal distribution of deaths and the social differences in the seasonal distribution of births. In the Northern Hemisphere, the excess mortality in the first year of life of infants born in spring does not support the explanation of selective infant survival. Instead, remaining life expectancy at age 50 appears to depend on factors that arise in utero or early in infancy and that increase susceptibility to diseases later in life. This result is consistent with the finding that, at the turn of the last century, infants born in autumn had higher birth weights than those born in other seasons. Furthermore, differences in adult lifespan by month of birth decrease over time and are significantly smaller in more recent cohorts, which benefited from substantial improvements in maternal and infant health.
Remarkable reductions in old-age mortality over the past half century have fueled rapid growth of the elderly population and have led to a substantial increase in life expectancy (1). Yet we still have only limited knowledge about the factors that affect mortality and survival in old age (2). Recent research highlights the role of early-life factors that affect late-life mortality (3). In particular, environmental conditions during the prenatal and early postnatal period have been found to influence adult health and mortality significantly (4, 5) although these results are still controversial (6, 7).
We conjectured that the month of birth may be an indicator for environmental factors that are linked to the seasons of the year. If this conjecture is true, then the patterns of two geographically close populations should resemble each other, and the pattern in the Northern Hemisphere should be mirrored in the Southern Hemisphere. Furthermore, lifespans of people who were born in the Northern Hemisphere but who died in the Southern Hemisphere should resemble the pattern of the Northern Hemisphere.
We obtained data on the populations of Denmark, Austria, and Australia to test our conjecture. For Denmark, the longitudinal data are based on the population register, which follows every person living in Denmark from 1968 to the present. For Austria and Australia, we used information from death certificates for all deaths that occurred in 1988–1996 and 1993–1997, respectively.
We have found that month of birth and remaining life expectancy at age 50 are related. We tested four hypotheses to explain the relationship. The first hypothesis assumes that the interaction between age and the seasons of mortality causes the differences in lifespan by month of birth. For example, people born in April are older than people born in November when the high mortality of winter strikes them. The second hypothesis tests whether the differences are due to unobserved social factors that influence or result from the seasonal timing of births. The third hypothesis explains the differences in adult lifespan by differential survival in the first year of life, whereas the fourth hypothesis assumes that debilitation in utero or in the first year of life increases the infant's susceptibility to diseases at adult ages.
Data and Methods
The Danish data consist of a mortality follow-up of all Danes who were at least 50 years old on 1 April 1968; 1,371,003 people were followed up to week 32 of 1998. The study excludes 1,994 people who were lost to the registry during the observation period. Among those who are included in the study, 86% (1,176,383 individuals) died before week 32 of 1998; 14% (192,626 individuals) were still alive at the end of the follow-up.
Exact dates of birth and death are known for a total of 681,677 Austrians who died between 1988 and 1996 and for 219,820 native-born Australians who died between 1993 and 1997 at ages 50+. Similar information was available for 43,074 people born in Britain who died in Australia.
For Denmark, remaining mean life expectancy at age 50 was calculated on the basis of life tables that were corrected for left truncation. The correction was achieved by calculating occurrence and exposure matrices that take into account an individual's age on 1 April 1968. For example, a person who was 70 at the beginning of the study and who died at age 80 enters the exposures for ages 70 to 80 but is not included in the exposures for ages 50 to 69. The central age-specific death rate is based on the occurrence-exposure matrix. The corresponding life-table death rate is derived by the Greville Method (8). For Austria and Australia, we estimated remaining lifespan at age 50 by calculating the average of the exact ages at death. We do not have populations at risk for these two countries and therefore cannot calculate mortality rates for them. We used t tests to perform pairwise comparisons between mean age at death by quarter of birth. By using the Bonferroni method, the α level of each individual test is adjusted downwards by the number of tests to ensure that the overall risk for a number of tests remains 0.05.
To test whether the seasonal difference in the risk of death accounts
for the differences in adult lifespan by month of birth, we calculated
the monthly deviations from the annual death rates. Given the data we
have, we were able to do this only for Denmark. Let x denote
age in integer years and let y denote current year. Let
i denote age in months since last birthday and let
j denote current month; let
D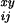 be the number of
deaths that occur for people of age x + i/12
years at time y + j/12, and let
T
be the number of
deaths that occur for people of age x + i/12
years at time y + j/12, and let
T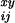 be the corresponding size
of the exposed population at risk of death. Let
nj denote the number of days in
current month j. When calculating the exposed population,
all deaths were assumed to occur in the middle of each month. The
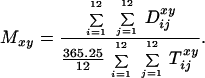
relative deviation of the monthly death rate from the annual death
rate, R
be the corresponding size
of the exposed population at risk of death. Let
nj denote the number of days in
current month j. When calculating the exposed population,
all deaths were assumed to occur in the middle of each month. The
relative deviation of the monthly death rate from the annual death
rate, R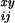 , was calculated
as
, was calculated
as
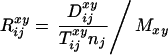 |
1 |
where
 |
2 |
The surface of the logarithm of the monthly deviations from the annual death rates is modeled by the equation
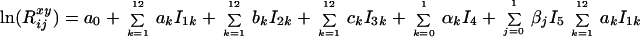 |
3 |
The variables I1 to
I5 are indicator variables. They take
the value 1 for a particular characteristic and zero otherwise.
I1k indicates month of birth
(reference month: January), I2k
current month (reference month: January),
I3k age since last birthday in months
rounded up to the nearest integer (reference age: one month),
I4 sex (reference sex: males), and
I5 cohort (reference birth cohort:
born between 1889 and 1918; other cohort born before 1889). The
parameter values a0,
ak,
bk,
ck,
αk, and
βj are estimated by applying weighted least
squares; the weights are the exposed population
Tij. The term
∑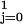 βjI5∑
βjI5∑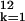 akI1k
estimates whether the differences by month of birth differ
between those born before and after 1889. The parameter values
a1,
b1,
c1,
α0, and
β0 are set equal to zero.
akI1k
estimates whether the differences by month of birth differ
between those born before and after 1889. The parameter values
a1,
b1,
c1,
α0, and
β0 are set equal to zero.
To test whether selective survival or debilitation during the first year of life explains the differences in remaining life expectancy at age 50, we used data on infant mortality for Denmark aggregated over the five-year period 1911–1915. The tabulations in the “Statistik tabelvaerk ” provide number of deaths by age of the infant in months and month of death. Thus, the actual date of birth of the deceased infants can fall within a period of 2 months and on average falls on the first day of each month. On the basis of the monthly number of births aggregated over the period 1911–1915, we then calculated death rates for each month of the first year of life. To center the number of births at the first day of each month we used the average number of births of two adjacent months in our calculations.
To estimate the impact of month of birth on the monthly death rates in the first year of life, we used a similar model as for adult ages. We modeled the logarithm of the monthly deviations from the annual death rate by applying Eq. 4:
 |
4 |
The variables I1 and
I2 are indicator variables. They take
the value one for a particular characteristic and zero otherwise.
I1k indicates month of birth
(reference month: January) and I2k
current month (reference month: January). Age x is in months
rounded up to the nearest integer. To reduce the number of parameters
in the model and because the decline in mortality during the first year
of life can be modeled by a power function, x is included as
a numerical variable. The term
∑ αkln x I2k
corrects for the interaction in the death rates between age and current
month. The infant mortality surface consists of only 144 data points
(12 birth months × 12 ages). Monthly births are available only
for both sexes combined, and infant deaths by age in months and month
of death are aggregated over the 5-year period 1911–1915. Hence, the
model does not include sex and cohort effects. The parameter values
a0,
ak,
bk, c1, and
αk were estimated by least squares regression.
αkln x I2k
corrects for the interaction in the death rates between age and current
month. The infant mortality surface consists of only 144 data points
(12 birth months × 12 ages). Monthly births are available only
for both sexes combined, and infant deaths by age in months and month
of death are aggregated over the 5-year period 1911–1915. Hence, the
model does not include sex and cohort effects. The parameter values
a0,
ak,
bk, c1, and
αk were estimated by least squares regression.
Results
Differences in Adult Lifespan by Month of Birth.
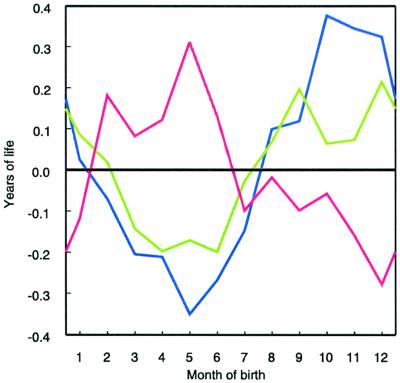
We find a similar relationship between month of birth and lifespan in both of our Northern Hemisphere countries. Adults born in autumn (October–December) live longer than those born in spring (April–June). The difference in lifespan between the spring and autumn born is twice as large in Austria (0.6 years) as in Denmark (0.3 years).
In Denmark, remaining life expectancy at age 50 is 27.52 years. For those born in the second quarter, lifespans are 0.19 ± 0.05 years shorter than average; for those born in the fourth quarter they are 0.12 ± 0.04 years longer than average (Fig. 1, green line). This difference is statistically significant (Cox-Mantel statistic: P < 0.001).
Figure 1.
Deviation in remaining lifespan of people born in specific months from the average remaining lifespan at age 50. In the Northern Hemisphere countries of Denmark (green line) and Austria (blue line), the people born in the fourth quarter of the year live longer than those born in the second quarter. For Australia (red line), the pattern is shifted by half a year.
In Austria, deaths occurred at an average age of 77.70. The deviation in mean age at death is highly significant (Bonferroni test: P < 0.001) for those born in the second and the fourth quarters. The lifespans of people born between weeks 14 and 26 are 0.28 ± 0.03 years below average; lifespans of those born between weeks 40 and 52 are 0.32 ± 0.03 years above average (Fig. 1, blue line).
We found the pattern in the Southern Hemisphere to be a mirror image reversal of that in the Northern Hemisphere. The mean age at death of people born in Australia in the second quarter of the year is 78.00; those born in the fourth quarter die at a mean age of 77.65 years. The difference of 0.35 years is statistically significant (Bonferroni test: P < 0.001; Fig. 1, red line).
For those born between November and January, the peak in mean age at death of British immigrants to Australia is 0.36 years higher than the trough of their Australian-born counterparts (one sided t test, P < 0.001). For those born between March and May, the lifespan of British immigrants is 0.26 years lower than that of native Australians (one sided t test: P < 0.007). No significant differences exist between Danes and Austrians born from November to January and from March to May and British immigrants to Australia. The pattern of Australians born in Britain is noisier, however, than the patterns in Fig. 1, probably because the population is much smaller.
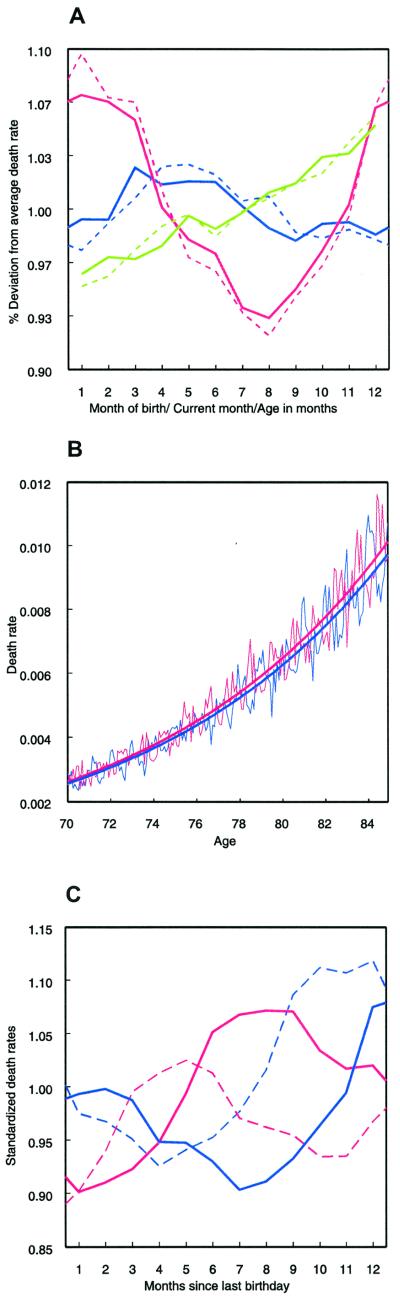
In none of the four populations was there a difference in the monthly pattern between men and women (for Denmark, see Fig. 2A). However, Fig. 2A shows that the differences between the troughs and peaks are slightly larger among males than among females. From the multivariate regression model, we find that, for Denmark, the difference between the sexes is small (females vs. males: e−0.0238 = 0.98) but significant (P < 0.001).
Figure 2.
Cohort effects (i.e., month of birth), period effects (i.e., current month), and age effects for the Danish data. (A) Deviation of the monthly from the annual death rates by age in months (green line), month of death (red line), month of birth (blue line), and sex (solid lines for females and dashed lines for males). (B) Monthly death rates and average mortality trajectories between the ages of 70 and 85 for June- and December-born. According to the different seasons of the year, the monthly death rates (solid lines) cyclically fluctuate around the exponentially increasing mortality trajectories (bold solid lines), which are fitted exponential functions. The mortality trajectory of the June-born (bold red line) is higher than that of the December-born (bold blue line). (C) Monthly deviations from the annual death rate as a result of the simultaneous effects of season of death, monthly increases in mortality, and month of birth for females (for males see supplemental Fig. 5). The monthly deviations are derived from the parameter values of two separate multivariate regression models for males and females. The mortality in the month after their last birthday of those born in January is taken as the reference mortality (relative deviation = 1). A Dane born in December (blue bold line) experiences low age-specific mortality and high seasonal mortality during the first 4 months after the last birthday. Although age-specific mortality increases continuously, the seasonal mortality risk decreases faster until it reaches its minimum in August. Thus, someone born in December experiences the lowest mortality 9 months after the last birthday. The reverse is true for a Dane born in June (red bold line). The trajectories of those born in March (blue dashed line) and September (red dashed line) are similar but shifted.
For Austria, the data permit an analysis of causes of death for the years 1990–1997. We observe a general tendency for people born in the first half of the year, especially in the second quarter, to die at younger ages than those born in the second half of the year, especially in the fourth quarter. We find a significant difference (P < 0.001) for both heart disease [international classification of diseases number (ICDN) 390–429, 440–458: spring-autumn 0.63 years] and cerebrovascular disease (ICDN 430–438: spring-autumn 0.50 years). In the group of malignant neoplasms, significant differences exist for stomach cancer (ICDN 151: spring-autumn 0.94 years) and the residual group “other malignant neoplasms” (spring-autumn 0.57 years). Differences for lung cancer (ICDN 162: spring-autumn 0.44 years) and cancer of the urinary system (ICDN 188–189: summer-autumn 0.81 years) are of borderline significance (P = 0.06). We find nonsignificant differences for cancer of the uterus and female genito organs (ICDN 179–184), cancer of the prostate and male genito organs (ICDN 185–187), cancer of the intestines (ICDN 152–154), and hemoblastoses (ICDN 201–208). Significant differences exist for chronic respiratory diseases (ICDN 460–479: 0.51 years, P = 0.05), pneumonia and influenza (ICDN 480–487: summer-autumn 0.80 years, P = 0.02), digestive diseases (ICDN 520–579: summer-autumn 0.52 years, P = 0.01), “other natural causes of death” (winter-autumn 0.84 years, P < 0.001), and violent causes of death (ICDN E800-E999: 0.90 years, P < 0.001). The difference for diabetes mellitus (ICDN 250: spring-autumn 0.53 years, P = 0.06) is of borderline significance. For differences in mean age at death for people born in a specific season from average age at death by major causes of death, see supplemental Table 2, which is published as supplemental data on the PNAS web site, www.pnas.org.
Further support that month of birth affects adult health and mortality is provided by research findings about the prevalence of various diseases among people born in specific months. A review of schizophrenia and month of birth cites 250 studies (9). All studies come to the conclusion that, in countries in the Northern Hemisphere, spring-born people experience an increased risk of developing schizophrenia. In the Southern Hemisphere, the pattern is shifted by about half a year (10). An excess number of spring births is found among patients suffering from autistic disorders (11), Down's syndrome (12), and Alzheimer's disease (13). In Sweden and Great Britain, spring-born children experience a higher risk of developing insulin-dependent diabetes (14, 15). Among 90,000 patients who died of cancer in the United States, the average lifespan of those born in winter was 1.5 years longer than that of those born in summer (16). In Sweden, women born in June have a 5% higher risk of developing breast cancer than women born in December (17). A Dutch study (18) of allergens such as birch, grass pollen, and house dust mite concludes that those born about 3 months before the main season of the allergen have an increased likelihood of developing an allergy later in life.
Seasonal Distribution of Deaths.
The first hypothesis we tested assumes that the observed relationship is caused by the interaction of the seasonal distribution of deaths and the monthly increase in adult mortality. The longitudinal nature of the Danish data permits simultaneous modeling of cohort effects (i.e., month of birth) and period effects (i.e., current month) corrected for the monthly increase in mortality over a “12 months” period. We constructed birth cohorts by year and month of birth and calculated the deviation of their monthly death rates from their annual death rates between April 1968 and August 1998. This procedure standardizes for the yearly increase with age in mortality and results in a surface of relative deviations over age and time. The deviations depend on the current month (i.e., month of death), the age in months over a “12 months” period, and sex. As expected, we find that mortality increases by about 10% for males and females within 12 months (Fig. 2A, green lines). Mortality is lowest in August and highest in January; the difference is about 17.6% for males and 13.9% for females (Fig. 2A, red lines). The maximum difference in the death rates by month of birth is approximately 5.3% for males and 4.5% for females (Fig. 2A, blue lines). The monthly pattern is similar for females (Fig. 2A, solid lines) and males (Fig. 2A, dashed lines).
Although all three factors examined influence adult mortality simultaneously (Fig. 2B), they do not influence each other. Results do not change when the impact of the three factors is estimated simultaneously by using a multivariate regression model. The model permits closer examination of the interaction between the monthly increase in adult mortality, the seasonality of death, and the differences by month of birth. It reveals that considerable differences do indeed exist in age-specific mortality trajectories over a year of life depending on the month of birth (Fig. 2C). However, over a year of life, the differences by season of death cancel each other out almost entirely whereas the differences by month of birth remain. For parameter estimates see supplemental Table 1.
Social Differences in the Seasonal Distribution of Births.
The second hypothesis we tested assumes that the causal mechanism is linked to socio-economic differences in the seasonal distribution of births: it may be that comparatively more people who belong to higher social classes are born in autumn. In Austria and Denmark, births are distributed seasonally over the year. Both social and biological factors influence this seasonality (19, 20). If the seasonality is partly driven by the preference of couples for certain seasons, then the intensity of the preference may differ between social groups.
We used education as an indicator of social group. Parental education is not contained on birth certificates in the beginning of the 20th century. We assumed that in 1991 a person's educational level was closely linked to the educational level of his or her parents. The Austrian microcensus of the year 1991 reveals that the educational status of 15- to 19-year-old Austrians depends to a large part on the social and educational status of the parents (21), despite tuition-free access to all levels of education since the 1970s. Thus, for earlier birth cohorts that did not benefit from the expansion of the Austrian educational system, the intergenerational correlation in education must have been even stronger than it is today.
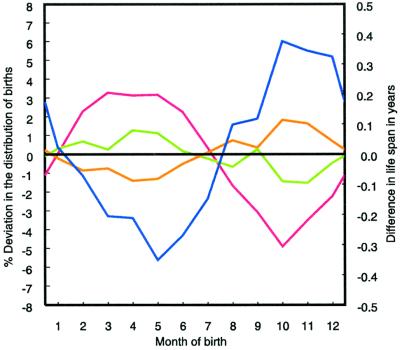
We then calculated the seasonal distribution of the birth dates of Austrians aged 50+ by educational group on the basis of the 1991 census. We found that the spring peak in births is stronger among adults with high or medium education whereas those with basic education are over-represented among the autumn born (Fig. 3). The correlation between mean age at death by month of birth and the deviations in the monthly birth distribution from the average monthly pattern is −0.93 (Pearson correlation, one-sided test; P < 0.001) for adults with high education, −0.82 (P < =0.001) for adults with medium education, and 0.91 (P < 0.001) for adults with basic education. A similar result was found on the basis of a 10% sample of the 1971 census of economically active, British-born males. Non-manual workers tended to be born in spring and manual workers in autumn and winter (22). In 1941, Goodenough showed that, in the higher occupational classes, comparatively more births occur in spring and summer (23).
Figure 3.
Percentage deviations in the seasonal distribution of births of Austrians (ages 50+ in 1991) by education from the average seasonal distribution of births. Austrians with medium (green line) or high (red line) education are predominantly born in spring, those with basic education (orange line) in autumn. Observed differences in mean age at death are shown by the blue line.
For a discussion of the effect of age at school attendance see supplemental material.
Selective Survival in the First Year of Life or Debilitation in Utero or in Infancy.
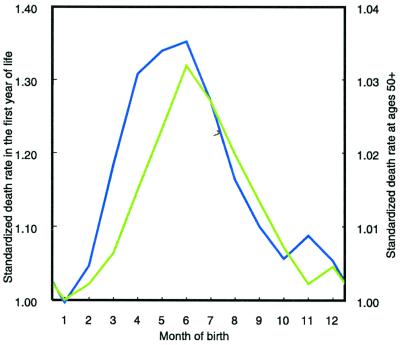
The third hypothesis assumes that selective survival during infancy is the causal mechanism that explains the relationship between month of birth and life expectancy. Specifically, the hypothesis is that autumn-born infants suffer higher mortality in their first year of life than spring-born infants. This selection would leave the relatively more robust individuals alive, who would experience lower mortality at adult ages. We used Danish data from the years 1911 to 1915 on seasonal infant mortality in the first year of life and found that, according to our model (Eq. 4), infants born in June are the most vulnerable. Compared with infants born in January, their standardized death rate during the first year of life is increased by 32% (Fig. 4). The model fits the data well with an adjusted R2 of 0.96. Studies of infant mortality by age and season of birth show a similar pattern for Switzerland (24) and Belgium (24, 25).
Figure 4.
Standardized death rates of Danish infants born in a specific month (green line) compared with standardized death rates at ages 50+ by month of birth (blue line). The standardized death rates are estimated by applying Eqs. 3 and 4. The mortality of those born in January is taken as the reference mortality (relative deviation = 1).
If selective survival during infancy explains the differences in adult lifespan, then we would expect a significant negative correlation between the probability of death in the first year of life and after age 50. If debilitation in utero or during the first year of life (our fourth hypothesis) is the causal mechanism, then we would expect a significant positive correlation because rates of debilitation are highly correlated with mortality.
For Denmark, the correlation between infant mortality in the first year of life and adult mortality after age 50 (Fig. 4) is 0.87 and statistically significant (P < 0.0001). For both infants and adults, the monthly mortality trajectory depends heavily on the age when the high mortality season of winter is experienced. Contrary to adult mortality, however, the differences between the monthly mortality trajectories do not cancel each other out over the first year of life because infant mortality declines rapidly between the first and the twelfth month. Hence, our model (Eq. 4) for infant mortality includes a term to correct for the interaction between age and current month whereas our model (Eq. 3) for adult mortality does not.
In the Danish data, differences in adult lifespan by month of birth are significantly smaller in the more recent cohorts than in the oldest cohorts. For those born before 1888, the differences are amplified by a factor of e0.72 = 1.72. That is, the difference in adult mortality by month of birth is almost twice as large for the cohorts born from 1863 to 1888 compared with those born between 1889 and 1918. This shift lends further support to the explanation that the relationship between month of birth and adult life expectancy is caused by prenatal and early postnatal conditions because considerable improvements in maternal and infant health took place between the first and second period (26).
Discussion and Conclusion
Based on population data for Austria, Denmark, and Australia, we found that month of birth and remaining life expectancy at age 50 are related. We were able to show that neither the seasonal distribution of deaths nor social factors related to the seasonal distribution of births cause the differences in remaining life expectancy at age 50. We did not find support for the hypothesis that differential infant survival is the causal factor behind the observed phenomenon. Indeed, for Denmark, we found a significant positive correlation between the differences in infant mortality and the differences in mortality after age 50 by month of birth, which is consistent with the hypothesis that debilitation early in life is the causal mechanism.
Data that contain information about both perinatal and old-age conditions for the same individuals are extremely rare. Studies that use birth weight or other direct indicators of early life circumstances are mainly based on hospital data, which are inevitably subject to selection biases, and their sample sizes tend to be modest. We draw on the widely available information about the month of birth as a proxy for the severity of prenatal and early childhood conditions, which permits the use of complete and unselected population data of over a million observations.
The environment early in life affects the susceptibility of adults to infectious (27–29) as well as chronic diseases (4). These findings are congruent with our result that significant differences in mean age at death by month of birth exist for chronic diseases related to the cardiovascular, respiratory, and digestive systems, as well as for infectious diseases such as pneumonia and influenza. Significant differences exist for violent deaths, which at old age mainly consist of traffic accidents, accidental deaths other than traffic accidents, and suicides. At old age, accidental deaths and suicides are related to the health status of the individual, mainly to cardiovascular and other chronic diseases. Thus, it seems plausible that the increased susceptibility of the spring-born to chronic diseases also affects their overall risk to die from violent deaths.
Our findings are also consistent with ecological studies that found a significant positive correlation between arteriosclerotic heart disease and lung cancer at adult ages 40 to 69, and the infant mortality in the early years of the same cohorts (30, 31). These studies, which were published a quarter century ago, stimulated extensive research on how conditions early in life might influence health later in life. As reviewed below, much of this research focuses on birth weight or adult height.
Evidence from a large number of studies (for a critical review see ref. 32) suggests that fetal growth as reflected by birth weight is related to the occurrence of chronic diseases in adult life. For example, low birth weight for gestational age is associated with increased systolic blood pressure levels (4), serum cholesterol levels (33), abdominal obesity (4), and a decrease in lung function (34) at adult ages.
A study of weight at birth in Vienna, Austria, for infants born between 1865 and 1930 (35) shows that infants born between September and November have a significantly higher weight at birth (plus 47.3 g) than those born in the other months of the year. The author explains the higher birth weight by the better nutritional status of the mothers during pregnancy. This explanation is supported by the finding that birth weight differs less over the year in social groups that were less exposed to annual cycles in food commodities.
Seasonal differences in gestational age and weight at birth have also been attributed to the seasonal incidence of infectious diseases of the uro-genital tract of the mother during the third trimester of pregnancy (36, 37).
The relationship, however, between birth weight and adult susceptibility to diseases may be complex. Recent studies find a strong inverse relation between cardiovascular mortality of the mother and birth weight of her offspring, which suggests the existence of genetic and epigenetic intergenerational factors (38, 39). Intergenerational factors affecting the seasonal distribution of births are found in a Japanese study. The findings suggest that the birth month of the mother significantly influences the seasonal distribution of births of her offspring (40). In our study, the month of birth is therefore not merely a proxy for birth weight. It is a complex indicator for the nutritional status and the disease environment during the prenatal and early postnatal period of an infant, and for the intergenerational factors that may operate through birth weight. But not all effects of month of birth must necessarily operate through birth weight as the correlation in the seasonal distribution of births of mothers and their offspring shows.
A large number of studies show that adult height and adult mortality are negatively correlated and that height is primarily determined by genetic endowment and by nutritional status and disease environment early in life (41–43). A study of differential height at age 18 by month of birth for Austrian military recruits (44) reveals a significant difference of 6 mm between the tallest, who were born in April, and the shortest, who were born in October. This sinusoidal pattern is offset by half a year from the pattern found in remaining life expectancy at age 50. The study does not correct for the social status of the recruits, which is necessary because social status and height are closely related: as noted above, more Austrians with a high level of educational attainment are born in spring than in autumn. Furthermore, it may be that height is largely determined by genetic factors and by health and nutrition in childhood rather than in utero and infancy.
Our model of infant mortality does not permit any conclusions about whether debilitation occurred in utero or during early infancy, but the research on birth weight discussed above suggests that in utero conditions as determined by the health and the nutritional status of mothers may be particularly important. Individual level data that contain birth weight and lifespan by month of birth would certainly help to further clarify this question. We have already pointed out, however, that, at present, available data are scarce and suffer from selection biases.
Seasonal differences in nutrition and disease environment early in life could explain the relationship between month of birth and adult lifespan. In past decades, the food supplies in general, and the availability of fresh fruit and vegetables in particular, differed from season to season. Mothers who gave birth in autumn and early winter had access to plentiful food and fresh fruit and vegetables throughout most of their pregnancy; those who gave birth in spring and early summer experienced longer periods of inadequate nutrition.
It is important to point out that the mothers of the birth cohorts in our study were not exposed to severe seasonally occurring malnutrition. They rather suffered from seasonally inadequate nutrition. Over time, nutrition in winter and early spring has improved considerably, which is consistent with the result in our study that the relationship between month of birth and lifespan seems to be stronger among the older birth cohorts than among the more recently born.
About a quarter of the variation in human longevity may be due to genetic factors, a quarter to early-life factors, and the remaining half to adult and current living environments (1). The variance in adult lifespan by month of birth is small compared with the total variance and to the differences among social groups or between men and women. The finding, however, that these differences by month of birth are most probably linked to prenatal or early postnatal conditions related to nutrition or disease is of broad significance, with profound implications for clinical practice and public health policy. Through the increasing availability of large population-based vital data containing information about the entire lifespan, new research opportunities are opening up to further disentangle the complex mechanisms that link early and late life.
Supplementary Material
Acknowledgments
We thank K. Andreev, K. Brehmer, K. Christensen, L. Knudsen, J. Kytir, S. Leek, S. Pletcher, R. Rau, and A. Wienke.
Abbreviation
- ICDN
international classification of diseases number
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Vaupel J W, Carey J R, Christensen K, Johnson T E, Yashin A I, Holm N V, Iachine I A, Kannisto V, Khazaeli A A, Liedo P, et al. Science. 1998;280:855–860. doi: 10.1126/science.280.5365.855. [DOI] [PubMed] [Google Scholar]
- 2.Christensen K, Vaupel J W. J Intern Med. 1996;240:333–341. doi: 10.1046/j.1365-2796.1996.d01-2853.x. [DOI] [PubMed] [Google Scholar]
- 3.Fogel R W, Costa D R. Demography. 1997;34:49–66. [PubMed] [Google Scholar]
- 4.Barker D J P. Mothers, Babies and Diseases in Later Life. London: BMJ Publishing Group; 1994. [Google Scholar]
- 5.Barker D J P. Br Med J. 1995;311:171–174. [Google Scholar]
- 6.Kannisto V, Christensen K, Vaupel J W. Am J Epidemiol. 1997;11:987–994. doi: 10.1093/oxfordjournals.aje.a009067. [DOI] [PubMed] [Google Scholar]
- 7.Christensen K, Vaupel J W, Holm N V, Yashin A I. Br Med J. 1995;310:432–436. doi: 10.1136/bmj.310.6977.432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Greville T N E. Rec Am Inst Actuar. 1943;32:29–43. [Google Scholar]
- 9.Torrey E F, Miller J, Rawlings R, Yolken R H. Schizophr Res. 1997;28:1–38. doi: 10.1016/s0920-9964(97)00092-3. [DOI] [PubMed] [Google Scholar]
- 10.McGrath J, Welham J, Pemberton M. Br J Psychiatry. 1995;167:783–785. doi: 10.1192/bjp.167.6.783. [DOI] [PubMed] [Google Scholar]
- 11.Barak Y, Ring A, Sulkes J, Gabbay U, Elizur A. Am J Psychiatry. 1995;152:798–800. doi: 10.1176/ajp.152.5.798. [DOI] [PubMed] [Google Scholar]
- 12.Viedebech P, Nielsen J. Hum Genet. 1984;65:221–231. doi: 10.1007/BF00286507. [DOI] [PubMed] [Google Scholar]
- 13.Vézina H, Houde L, Charbonneau H, Beaudry M, Cholette A, Daoud N, Mathieu J, Robitaille Y, Veilleux F, Gauvreau D. Psychol Med. 1996;26:143–149. doi: 10.1017/s003329170003378x. [DOI] [PubMed] [Google Scholar]
- 14.Rothwell P M, Gutnikov S A, McKinney P A, Schober E, Ionescu-Tigorviste C, Neu A. Brit Med J. 1999;319:887–889. doi: 10.1136/bmj.319.7214.887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Samuelsson U, Johansson C, Ludvigsson J. Arch Dis Child. 1999;81:143–146. doi: 10.1136/adc.81.2.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jansson B, Malahy M A. Cancer Detect Prev. 1981;4:291–294. [PubMed] [Google Scholar]
- 17.Yuen J, Ekbom A, Trichopoulos D, Hsieh C C, Adami H O. Brit J Cancer. 1994;70:564–568. doi: 10.1038/bjc.1994.346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aalberse R C, Nieuwenhuys E J, Hey M, Stapel S O. Exp Allergy. 1992;22:1003–1006. doi: 10.1111/j.1365-2222.1992.tb03028.x. [DOI] [PubMed] [Google Scholar]
- 19.Knodel J, Wilson C. Popul Stud. 1981;35:53–84. [PubMed] [Google Scholar]
- 20.Lam D A, Miron J A. Demography. 1996;33:291–306. [PubMed] [Google Scholar]
- 21.Anonymous. Jugend in Österreich: Fakten-Trends-Prognosen. Vienna: Forschungsbericht 13 des Instituts für Demographie; 1994. [Google Scholar]
- 22.Smithers A G, Cooper H J. J Soc Psychol. 1984;124:79–84. [Google Scholar]
- 23.Goodenough F L. J Genet Psychol. 1941;59:65–76. [Google Scholar]
- 24.Breschi M, Bacci M L. In: Infant and Child Mortality in the Past. Desjardins B, Brignoli P, editors. Oxford: Clarendon; 1996. pp. 157–173. [Google Scholar]
- 25.Huntington E. Season of Birth. New York: Wiley; 1938. [Google Scholar]
- 26.Preston S H, Haines M R. Fatal Years: Child Mortality in the Late Nineteenth-Century in America. Princeton: Princeton Univ. Press; 1991. [Google Scholar]
- 27.Moore S E, Cole T J, Poskitt E M E, Sonko B J, Whitehead R G, McGregor I A, Prentice A M. Nature (London) 1997;388:434. doi: 10.1038/41245. [DOI] [PubMed] [Google Scholar]
- 28.Chandra K R. Lancet. 1974;2:1393–1394. doi: 10.1016/s0140-6736(74)92272-7. [DOI] [PubMed] [Google Scholar]
- 29.Winick M. Pediatrics. 1971;47:969–978. [PubMed] [Google Scholar]
- 30.Fohrsdahl A. J Epidemiol Commun H. 1978;32:34–37. [Google Scholar]
- 31.Fohrsdahl A. Br J Prev Soc Med. 1977;31:91–95. doi: 10.1136/jech.31.2.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Joseph K S, Kramer M S. Epidemiol Rev. 1994;18:158–174. doi: 10.1093/oxfordjournals.epirev.a017923. [DOI] [PubMed] [Google Scholar]
- 33.Fall C H, Osmond C, Barker D J, Clark P M, Hales C N, Stirling Y, Meade T W. Br Med J. 1995;310:428–432. doi: 10.1136/bmj.310.6977.428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Barker D J, Godfrey K M, Fall C, Osmond C, Winter P D, Shaheen S O. Br Med J. 1991;303:671–675. doi: 10.1136/bmj.303.6804.671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ward W P. Ann Hum Biol. 1987;14:495–506. doi: 10.1080/03014468700009341. [DOI] [PubMed] [Google Scholar]
- 36.Rousham E K, Gracey M. Aust N Z J Public Health. 1998;22:669–672. doi: 10.1111/j.1467-842x.1998.tb01467.x. [DOI] [PubMed] [Google Scholar]
- 37.Keller C A, Nugent R P. Am J Epidemiol. 1983;118:689–698. doi: 10.1093/oxfordjournals.aje.a113679. [DOI] [PubMed] [Google Scholar]
- 38.Davey Smith G, Harding S, Rosato M. Br Med J. 2000;320:839–840. doi: 10.1136/bmj.320.7238.839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Davey Smith G, Hart C, Ferrell C, Upton M, Hole D, Hawthorne V, Watt G. Br Med J. 1997;315:1189–1193. doi: 10.1136/bmj.315.7117.1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Miura T, Shimura M, Nakamura I, Nonaka K. In: Seasonality of Birth. Miura T, editor. The Hague, The Netherlands: SPB Academic Publishing; 1987. pp. 45–55. [Google Scholar]
- 41.Waaler H F. Acta Med Scand Suppl. 1984;679:1–56. doi: 10.1111/j.0954-6820.1984.tb12901.x. [DOI] [PubMed] [Google Scholar]
- 42.Floud R, Wachter K, Gregory A. Height, Health and History. Cambridge, U.K.: Cambridge Univ. Press; 1990. [Google Scholar]
- 43.Fogel R W. Am Econ Rev. 1994;84:369–395. [Google Scholar]
- 44.Weber G, Prossinger H, Seidler H. Nature (London) 1998;391:754–755. doi: 10.1038/35781. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.