Joint Genetic Analysis of Gene Expression Data with Inferred Cellular Phenotypes

Abstract

Even within a defined cell type, the expression level of a gene differs in individual samples. The effects of genotype, measured factors such as environmental conditions, and their interactions have been explored in recent studies. Methods have also been developed to identify unmeasured intermediate factors that coherently influence transcript levels of multiple genes. Here, we show how to bring these two approaches together and analyse genetic effects in the context of inferred determinants of gene expression. We use a sparse factor analysis model to infer hidden factors, which we treat as intermediate cellular phenotypes that in turn affect gene expression in a yeast dataset. We find that the inferred phenotypes are associated with locus genotypes and environmental conditions and can explain genetic associations to genes in trans. For the first time, we consider and find interactions between genotype and intermediate phenotypes inferred from gene expression levels, complementing and extending established results.

Author Summary

The first step in transmitting heritable information, expressing RNA molecules, is highly regulated and depends on activations of specific pathways and regulatory factors. The state of the cell is hard to measure, making it difficult to understand what drives the changes in the gene expression. To close this gap, we apply a statistical model to infer the state of the cell, such as activations of transcription factors and molecular pathways, from gene expression data. We demonstrate how the inferred state helps to explain the effects of variation in the DNA and environment on the expression trait via both direct regulatory effects and interactions with the genetic state. Such analysis, exploiting inferred intermediate phenotypes, will aid understanding effects of genetic variability on global traits and will help to interpret the data from existing and forthcoming large scale studies.

Introduction

Many interesting traits are heritable, and have a strong genetic component. In simple cases, such as Mendelian diseases, the genetic cause can be found with linkage methods, and many trait genes have been mapped to date [1]. More recently, association mapping studies have focused on complex traits that include prevalent human diseases, such as type 2 diabetes, hypertension, and others. Numerous genome-wide association studies have corroborated that no single gene explains all or even a large part of the heritable variability in such traits, and that individual effect sizes due to common variants are small [2]. Mapping and understanding the genetic component in complex traits remains one of the most important challenges in modern genetics.

The effect of a single locus genotype on a global trait has to be mediated by cellular, tissue, and organ phenotypes. Many of the variants that have been identified in genome-wide association studies do not change coding sequences [2], suggesting that the genetics of gene expression is central to understanding of the genetic basis of complex traits. Technological advances in recent years have made it possible to assay transcript levels on a large scale and treat them as quantitative traits, enabling research into the genetic makeup of these basic cellular phenotypes [3]. Linkage studies in segregating yeast strains [4] followed by single [5], [6] and multipopulation experiments [7] in humans have revealed much about the genetic landscape of gene expression. Transcript levels have been found to be heritable [4], and individual regions associated with the expression values have been identified for most yeast genes in linkage studies [8], [9], and up to a third of human genes in association studies [7],[10].

Locus effects in isolation are not sufficient to account for gene expression variability. Environment and intermediate cellular phenotypes (e.g. transcription factor or pathway activation) can and do have large effects on the measured transcript levels [8], [11]. To understand the genetics of gene expression, we must therefore analyse the consequences of genetic variants in the context of these other factors. Studies in segregating yeast strains have investigated epistatic interactions [8], [12], [13], recovering interactions with genotypes of a few major transcriptional regulators. Large scale efforts to map functional epistasis between genes are currently underway with promising initial results [14]. A recent study also searched for genotype-environment effects, and found many gene expression levels affected by an interaction between the environment and the genotype of a major transcriptional regulator [15]. However, much remains to be done in this area. While gene expression has been used as an intermediate phenotype to study the genetics of global traits [16], [17], [18], genetics of gene expression itself has not been considered jointly with relevant cellular phenotypes such as pathway or transcription factor activations. This is an important gap. It is the state of the cell that determines how genetic variation can effect the gene expression levels, thus a joint analysis with the intermediate phenotypes is needed to inform us about the mechanisms involved – a crucial step for understanding the causes of phenotypic variability.

Despite their importance, the intermediate phenotypes are usually not measured, thus genetic effects cannot be analysed in their cellular context. Fortunately, statistical approaches have been developed that allow inferring unmeasured factors which influence expression levels from expression data alone. Methods such as principal components analysis [19], network components analysis [20], surrogate variable analysis [21], independent components analysis [22], and the PEER framework [10] can be used to determine a set of variables that explain a part of gene expression variability with (usually) a linear model. Their application has been shown to increase power to find expression quantitative trait loci (eQTLs) by explaining away confounding variation [10], [23], [21], and to yield variance components of the expression data that may be interpretable [10].

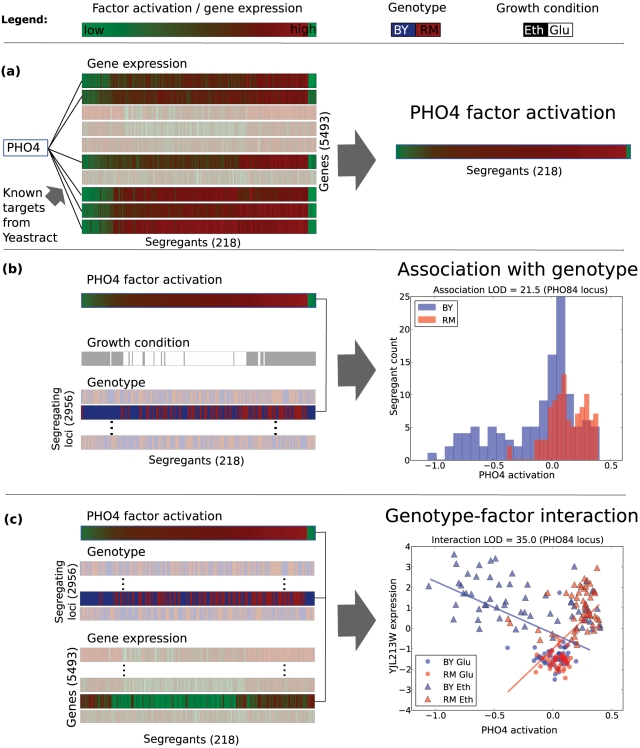
Here, we perform a thorough joint genetic analysis of a gene expression dataset with intermediate phenotypes inferred from gene expression levels. We revisit the data of Smith and Kruglyak [15], where the authors looked for gene-environment interactions affecting gene expression levels in a population of segregating yeast strains grown in two different carbon sources. First, we use a variant of a sparse factor analysis model [24], [25] to infer intermediate phenotypes from the gene expression levels (Figure 1a). Importantly, our method uses prior information to guide the inference of which factors are affecting which target genes, as opposed to unsupervised methods (e.g. PEER, SVA, ICA) that tend to learn broad effects. We use Yeastract [26] transcription factor binding and KEGG [27] pathway data as prior information in the model, which allows the inferred phenotypes to be interpreted as transcription factor and pathway activations. We then analyse the variation in the learnt activations, and find that growth condition and segregating locus genotypes have a strong influence (Figure 1b). Finally, for the first time, we consider genotype-dependent effects of the inferred intermediate phenotypes. We find genetic interactions with the inferred phenotypes that affect gene expression levels (Figure 1c), and identify regions in the genome that show an excess of these interactions. We show that many genotype-environment interactions are captured with the estimated intermediate phenotype, helping to interpret the environmental effect, and generate plausible, testable hypotheses for the mechanisms of several determined interactions. We propose that as pathway and transcription factor target annotations improve, our approach will produce even more useful intermediate traits that should be included in analysis and interpretation of high-throughput gene expression data.

Figure 1. Analysing genetic effects in the context of intermediate phenotypes using PHO4 as an example.

(a) Intermediate phenotypes are learnt from expression levels using prior information from Yeastract database on the targets of the factor. The highlighted genes are known targets of PHO4. These activations are learned jointly for all factors. (b) The variation in intermediate phenotypes can be explained by locus genotypes or the growth condition of the segregants. For most loci (greyed out), the genotype is uncorrelated with the factor activation level. For the PHO84 locus at chrIII-46084, not greyed out and indicated by arrow, it is correlated. The plot at right shows the distribution of factor activations stratified by genotype at this locus. (c) Some genotypes show a statistical interaction with the inferred intermediate phenotype affecting gene expression levels, in this case YJL213W. See also Figure 2.

Results

We carried out genetic analysis with inferred intermediate phenotypes on expression levels of 5,493 genes from 109 yeast segregants grown in two environmental conditions (Methods, [15]). We employ a model that combines unobserved intermediate factors, genotype and expression levels. At the core, this approach is based on a sparse factor analysis model (Methods) to learn intermediate phenotypes from expression data (Figure 1a). Briefly, this bilinear model expresses the gene expression 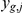of gene 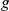for segregant 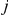as as a sum of weighted contributions from factor activations of 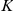factors and a noise term :

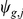(1)

The factor activations 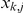inferred from (1) are then treated as the intermediate phenotypes. Prior information about which factors influence which genes is introduced as a prior on the weights 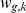, thereby guiding the learning. For example, if gene 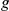is a known target of transcription factor 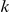, it is more likely that 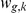is large, while for genes that are not targets, the weight is more likely to be near-zero.

We considered three alternative types of prior information. First, we hypothesised the factors to be transcription factor activation levels, and used data for 167 transcription factors from Yeastract [26] to assign a prior probability of a factor affecting a gene expression level (Methods). Second, we hypothesised the factors to be pathway activations, and used KEGG database information [27] for 63 pathways for the prior probability of a link between a pathway activation and a gene. Third, for comparison, we employed an uninformative prior, where 30 factors were a priori equally likely to affect all genes. We call the inferred factor activations Yeastract factors, KEGG factors, and freeform factors, respectively.

To ensure our findings are not affected by local optima of the factor inference, we carried out the full analysis on 20 randomly initialised runs of the factor analysis model for each prior setting. The prior information on the regulatory influence of factors (e.g. number of known targets for a transcription factor) influenced the statistical identifiability of factors and their associations; see Text S1 for a detailed discussion and validation on simulated data. Statistical significance of genetic associations and interactions was determined using a permutation procedure outlined in Methods.

Inferred intermediate phenotypes are genetically or environmentally driven

Although the factors were inferred jointly from the expression data alone, many factor activations were significantly associated with a locus (SNP) genotype or indicator variable encoding growth in ethanol or glucose as a carbon source (“environment”, Tables S1, S2, S3). Thirty Yeastract factors were associated with a SNP genotype at false discovery rate (FDR) less than 5% (Methods) and 32 with the environment. Similarly, 9 KEGG factors were associated with a SNP genotype, and three with the environment while 27 freeform factors were significantly associated with a SNP genotype and one with the environment. Some of the genotype associations were due to pleiotropic effects of single loci, while others were private to a locus-factor combination (Tables S4, S5, S6).

Many of these individual associations to Yeastract and KEGG factors can be interpreted by considering the role of the inferred factors and functional annotations of genes at associated loci. We now give some examples to further corroborate the use of factor activations as intermediate phenotypes. All associations are significant at 5% FDR, with corresponding Q-values 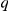(minimal FDR for which the association is significant [28]) and average log-odds scores 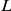over the 20 randomly initialised runs given (Methods).

Yeastract factors

Loci associated with Yeastract factor activations encode genes functionally related to the corresponding transcription factor (Table S1). The PHO84 (an inorganic phosphate transporter) locus was associated with the PHO4 (a major regulator of phosphate-responsive genes) transcription factor activation (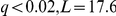). The association implicates the variation in the transporter and potentially its efficiency as a determinant for the transciptional activation of the phosphate-responsive genes through the PHO4 activation. The mechanism of action is likely a switch in transcriptional response when PHO84, a high affinity phosphate transporter, is rendered ineffective by a mutation [29].

The SUM1 (transcriptional repressor of middle sporulation-specific genes) factor activation was associated with the genotype of the RFM1 (repression factor of middle sporulation) locus (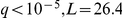). This is intriguing since RFM1 recruits the HST1 histone deacetylase to some of the promoters regulated by SUM1 [30], [31], suggesting that genetic variation in the RFM1 gene indirectly alters the effect of SUM1 on individual genes.

There is also a straightforward eQTL that regulates the HAP1 (heme activation protein) gene expression (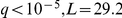), as well as factor activation (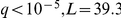). This is a cis effect, since the locus is proximal to the gene, and manifests itself as a trans eQTL hotspot by affecting expression levels of some of the 170 known HAP1 targets. Twenty eight of the 93 (30%) significant trans eQTLs are also known targets of HAP1. Our data suggest that the other 65 may either be previously undiscovered targets of HAP1, or secondary downstream effects of some of its direct targets.

The THI2 thiamine metabolism transcription factor activation was associated with the genotype of the THI5 locus (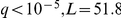). This suggests a regulatory role of THI5 upstream of THI2 in thiamine biosynthesis, and shows how our inference allows generating hypotheses for the function for genes that are implicated in a cellular pathway, but not annotated with a specific role.

KEGG factors

Associations to KEGG pathways tend to capture the effect of a pathway component genotype (Table S2). For example, the inferred activation of lysine biosynthesis pathway was associated with the LYS2 locus (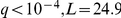), and the activation of galactose metabolism pathway with the locus containing the FSP2 and YJL216C genes (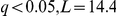), all members of the respective pathways. The latter genes are situated in the subtelomeric regions, known to be a major source of adaptive variation. Thus, it is plausible that the genotype of the locus tags the existence or copy number of these genes in the segregants. We thus hypothesise that genetic background of these genes directly affects the activation of the corresponding pathways. Also, the nitrogen metabolism pathway was associated with the ASP3 (cell-wall L-asparaginase) gene cluster locus genotype. (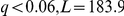). The ASP3 genes are part of the pathway, and are present in four copies in the reference strain S288c, conferring increased resistance to nitrogen starvation stress. The inferred state of the pathway thus corresponds to the ASP3 copy number via the locus genotype proxy.

Furthermore, the fatty acid metabolism pathway activation was associated with the OAF1 (oleate-activated transcription factor) locus genotype (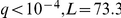), which is a known regulator of the pathway [32]. We thus hypothesise that genetic variants in OAF1 between the two strains are responsible for differences in fatty acid metabolism in the segregants, as has also been proposed in earlier work [33].

Finally, the environment was strongly associated to the very wide metabolic pathways category (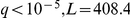). This KEGG entry comprises 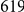genes, and captures the effect of the growth condition of the segregants on their metabolic state.

Freeform factors

The freeform factors capture broad variance components in the data, with each factor's activation contributing to every probe expression level. Regardless of the unsupervised inference of the activations, they still show strong associations to environment and locus genotypes. However, due to this global nature of the factors, the associations are less straightforwardly amenable to interpretation. The first factor was associated with the environment (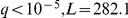), and accounts for mean shifts in gene expression levels between segregants grown in glucose and ethanol (Table S3). Several of the other factors were associated with genotypes of “pivotal loci” described before [8], [9], [15]. It may be possible to make suggestions about the functionality via methods such as overrepresentation of GO categories within sets of genes with large weights for a factor, such as a recent study that performed a similar association analysis with unsupervised factors [22]. Our approach of using existing data for guidance is stronger compared to unsupervised methods as we use evidence of which gene is affected by the factor, thus improving statistical identifiability, and do not rely on an ad hoc choice of number of factors. This yields interpretable results that are more useful for generating hypotheses for the consequence of genetic or environmental variation.

Response to small molecule stress has been measured in the same segregants to map drug response loci [34]. This study found eight QTL hotspots, six of which are within 20kb of loci that also show several associations to our inferred intermediate phenotypes (Tables S4, S5, S6), corroborating their pleiotropic effect.

Some of inferred transcription factor activations are correlated with their corresponding mRNA and protein expression

Twenty seven of 167 Yeastract factors were associated with the probe expression level measuring the transcription factor gene at the 5% FDR (Table S1, Figure S1). Eighteen of them (67%) were also significantly associated with a SNP genotype or environment. While statistically significant, these associations do not explain majority of the factor variability, as only two Yeastract factors were correlated with their probe expression level with Pearson .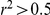

The general lack of correlation between factor activation and the corresponding measured expression level for the remaining transcription factors is perhaps not surprising. Previous studies have found poor correlation between mRNA and protein expression levels [35], [36]. Also, alternative mechanisms for activation exist. Many Yeastract factors without significant correlation to transcript levels have been shown to be activated not via increase in expression, but other means. For example, PHO4 is activated by multiple phosphorylation events [37]. Simlarly, nuclear localisation and therefore activation of ACE2 and MSN2 are controlled by phosphorylation state [38], [39]. We predict most of the other transcription factors to also be activated by non-transcriptional means.

The protein level of one of the Yeastract factors, GIS2, has been assayed quantitatively in a previous study [36] for 87 of the 109 segregants we considered in a similar growth condition. For this transcription factor, the inferred activation was better correlated to the protein level than the corresponding probe expression level for 16 of the 20 random initialisations. This example gives further support to treating the inferred factors as meaningful quantitative traits.

Genetically driven transcription factor activations explain trans eQTL hotpots

As observed before [15], [4], [9] some segregating loci showed significant associations with up to 743 (IRA2, regulator of the RAS-cAMP pathway locus) probe expression levels (Figure S2). There are nine such loci with at least 50 associations (“hotspots”). On average, 15% of the genes associated with a trans eQTL hotspot (FDR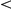5%, Methods) could be explained by a transcription factor associated with the hotspot locus genotype, and targeting the gene (Table S7). In 85% of these cases, the association with the inferred factor activation was stronger than with the locus genotype, and many additional associations with factor targets are recovered. For example, the PHO84 locus was associated with the PHO4 Yeastract factor activation (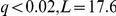), as well as 72 probe expression levels in trans. Fourteen of these were also significantly associated with the PHO4 factor activation, all showing a stronger association. PHO4 itself was significantly associated with 60 more probes, expanding the range of plausible effects of the PHO84 locus. This shows that using inferred intermediate phenotypes can reveal additional associations that otherwise would not be statistically significant.

Genetic interactions with inferred cellular phenotypes affect gene expression levels

We scanned the genome for genotype-factor interactions that effect gene expression levels (Figure 1c) using a standard linear interaction model (Methods), and recovered three broad classes of interactions (Figure 2). We tested each locus-gene pair independently for interaction with any inferred factor using 20 permutations, and information from all the random restarts of the model to assess significance (Methods). If a single factor was observed with the strongest interaction score for a locus-gene pair in at least half the multiple restarts, we interpreted it as the true interacting factor; in other cases, we did not designate a factor to an interaction effect. We give examples of interactions we find below, highlighting how they add to the understanding of the propagation of the genotype effect.

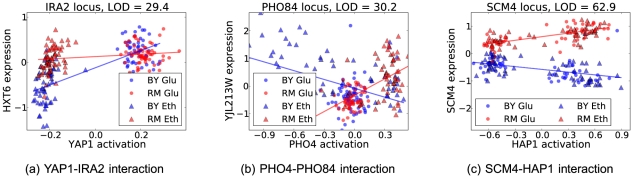
Figure 2. Three broad classes of interaction effects between locus genotype and transcription factor activation affecting gene expression (for details see text).

Each marker shows the gene expression and factor activation for one individual segregant of either BY (blue) and RM (red) background at the locus, and grown in ethanol (triangles) or glucose (circles) as a carbon source. Maximum likelihood fits for expression data for the BY and RM segregants are plotted as solid lines; an interaction effect corresponds to a difference in slope in the two genetic backgrounds. (a) Genotype-environment interaction mediated by the inferred YAP1 transcription factor activation. (b) Interaction between the PHO84 locus and PHO4 transcription factor activation, which is associated both with the PHO84 locus genotype and the PHO4 probe expression level. (c) Epistatic interaction between HAP1 and its target, SCM4, mediated by the HAP1 activation.

The largest set of interactions was found at the IRA2 locus. Many Yeastract factors, such as MIG1, HAP4, YAP1 and MSN2 showed high interaction LOD scores with this locus (Figure 2a). All these corresponding transcription factors act in glucose response, nutrient limitation or stress conditions, which is consistent with the role of IRA2 in environmental stress response by mediating cAMP levels in the cell. Their factor activations were associated with the environment (Table S1), and the interactions thus recapitulate gene-environment interactions. While all these factor activations were correlated due to the strong association with the environment, making it hard to identify the true interacting factor, we can still narrow the factor down to a few that exhibit high LOD scores. Identifiability of the interacting factor is hard in general for factors that capture large effects, or have target sets that largely overlap with other factors (Text S1). However, the inferred factors do capture the true underlying sources of variability, in this case, the environment, which is even more useful in settings where not all sources of variability are measured. Also, even having measured the relevant growth condition, we can further interpret the interactions as transcription factor activation having an effect in a specific genetic background in some cases, a more specific claim.

We recovered epistatic interactions that failed the stringent multiple testing criteria on their own, but showed a stronger signal via the intermediate factor. For example, HAP1 factor activation interacts with (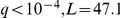) the SCM4 (suppressor of CDC4 mutation) locus genotype to influence SCM4 expression level (Figure 2c), while the epistatic interaction LOD score was only 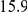. As SCM4 has a HAP1 binding site in its promoter region, it is plausible that genetic variants could disrupt the site and thereby inhibit HAP1 binding. This effect would only be observable in case HAP1 is active, which in turn is controlled by the HAP1 locus genotype (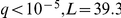). This is an example of an epistatic interaction that is mediated by an intermediate phenotype of transcription factor activity.

The PHO4 factor activation was associated with (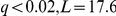) and interacted with the PHO84 locus on chromosome XIII to influence 2206 genes (Figure 2b). Its activation was also correlated with the PHO84 expression level (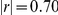), and interacted with the environment variable to influence gene expression levels. These interactions recapture genes differentially expressed in the two growth conditions, as the PHO4 activation separates segregants based on both environment as well as the PHO84 locus genotype.

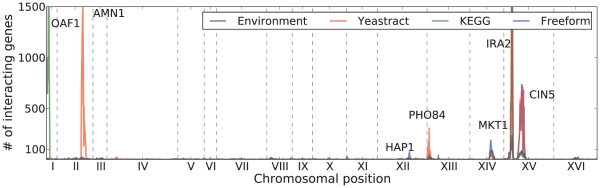
In total, we found 2,931 genes with a gene-Yeastract factor interaction effect (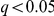). We also found 2,732 genes that show genetic interactions with KEGG factors and 2,250 with freeform factors. We noted several interaction “peaks” in the genome, such as the IRA2 locus, where the locus genotype interacts with several genes via one or multiple factors (Figure 3). These coincide with trans eQTL peaks and gene-environment interaction peaks observed before [9], [15], and have been annotated for potential causal genes. The full list of recovered interactions is given in Dataset S1.

Figure 3. Number of genes affected by a genotype-factor interaction for each locus for Yeastract factors (blue), KEGG factors (red), freeform factors (green), and environment (gray).

Interactions with inferred transcription factor activations recapitulate known gene–environment and gene–gene interactions

We found 12,161 locus-environment interactions affecting 813 gene expression levels (Figure 3) using the same model and testing approach as for inferred factor interactions (FDR 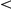5%, Methods). Of these, we recovered 6,328 interactions (62%) affecting 643 genes (79%) with the Yeastract factors, 8,406 interactions (69%) affecting 716 genes (88%) with the KEGG factors, and 1,214 interactions (10%) affecting 410 genes (50%) with the freeform factors. All environment-associated Yeastract factors had a strong interaction LOD scores with the IRA2 locus, affecting hundreds of genes. These interactions recapitulate the gene-environment interactions reported and validated in the original analysis of the data [15]. It is reassuring that we are able to recover these interactions with the inferred intermediate phenotypes, and to expand their repertoire as well as provide hypotheses for their mechanism.

Preliminary results from an ongoing screen for gene-gene interactions have shown epistatic interactions for 95,445 gene pairs [14]. Three hundred and sixty eight knockouts of a Yeastract factor gene and an interaction peak gene were tested in this large-scale assay, with 40 epistatic interactions found. We found interactions for 28 of the 368 pairs, but recovered none of the 40 interactions of [14]. Our screen is for a genetic interactions that are different from the synthetic lethal screen of Costanzo et al. Consistent with this, we find neither more nor less overlap than expected by chance.

Discussion

Our genetic analysis of the gene expression data from [15] has shown that inferred intermediate phenotypes are valuable for generating hypotheses about plausible connections between genetic and gene expression variation. Using these inferred cellular phenotypes, we identified loci associated with transcription factor and pathway activations, thus giving the genetic effect a straightforward mechanistic interpretation, and often suggesting a candidate gene responsible for the change. Perhaps most importantly, for the first time, we considered and found statistical interaction effects with inferred intermediate phenotypes.

Our work is a step towards interpreting and understanding effects of genetic variants by putting them into cellular context. Conventional analysis, relating genotype and expression levels, is restricted to observed measurements, often producing only statistical associations instead of a plausible mechanistic view. In contrast, our approach yields phenotypic variables at an intermediate level which can be used in the analysis. We showed that these provide additional interpretability and in some settings increase statistical power by reducing the number of tests. Besides standard association and interaction effects between genotype and gene expression, our approach allows more rich hypothesis spaces to be explored, where the dependent variable we model is not a global organism phenotype such as disease label, or a very specific measurement like a single gene expression level. We have shown that this analysis is both feasible, and gives interesting results.

The idea of looking for associations and interactions with inferred intermediate phenotypes will be even more useful in forthcoming studies that include other cellular measurements. The inferred transcription factor or pathway activations allow interpreting the variability in these measured phenotypes as a result of changes in regulator activity or pathway state, bridging the gap between individual molecule measurements, and states of protein complexes, cellular machines, and pathways. We believe that the inferred intermediate phenotypes can be much more informative about the state of the cell and organism than individual locus genotypes and gene expression levels, and will also show stronger associations to downstream cellular and tissue phenotypes.

The intermediate activation phenotype has lower dimensionality compared to the space of genotypes and gene expression levels, which helps against the burden of multiple testing present in genome-wide scans for epistatic interactions. We were able to infer association and interaction effects, including proxies for epistasis, while finding epistatic interactions by testing all locus pairs is usually hindered by the billions of tests performed [40], [8], [12], [13]. The incorporation of prior information to infer interpretable factors is a flexible way to reduce the number of tests by capturing relevant parts of the data variation in a few factors, and can also add power if the factor is a better proxy for the true interacting variable.

The inferred transcription factor activations did not mostly correlate with their expression level. This is expected, as the activity of a protein depends on the protein level, localisation, posttranslational modification state, and existence of binding partners to carry out its function. Expression level alone is often a poor proxy for a measure of protein activation.

A range of prior work has applied linear or generalised linear models to infer unobserved determinants of gene expression levels. For example, broad hidden factors have been inferred from gene expression that are likely to be due to confounding sources and hence can safely be explained away, thereby increasing the power of eQTL studies [10], [23], [21]. Although methodologically related, this work has a completely different aim. Also, unsupervised sparse linear models have been applied to infer hidden determinants in gene expression which are subsequently analysed for association to the genetic state [22]. This approach is closely related to the “freeform factors” included in this analysis for comparison. Overall, we show that factor learning taking prior knowledge into account adds statistical identifiability of the actual factors thereby providing interpretability. Other interesting approaches perform feature selection to capture relevant properties of the segregating sites in order to pinpoint the causative allele [33], or build a predictive (network) model of gene expression, followed by analysing its cliques and subnetworks [41]. The integration of QTL models and causal inference in trait networks has also been explored in [42], and a general statistical framework for this task has been recently proposed by [43]. While conceptually related, these approaches build on the assumption that all trait variables are fully observed and hence do not model unobserved intermediate phenotypes explicitly.

A very recent work proposed an integrated Bayesian ANOVA model that explains the gene expression profile by modules [44]. These modules in turn are modelled as a function of the genotype, taking direct and epistatic regulation into account. Importantly, this approach infers gene expression determinants in an unsupervised fashion, and hence the interpretation of these association signals can be difficult and remains as retrospective analysis step. Finally, a methodologically related sparse factor analysis model employing prior information has been applied to a narrower dataset with an aim to explain trans eQTL hotspots [45]. However, the study does not consider the idea of genetic effects in the phenotypic context, or look for interaction effects, which is a primary focus of this work.

There has been speculation that a significant proportion of heritable variability that cannot be attributed to associations with single loci is due to interaction effects. This hypothesis is intuitively appealing, since we expect some genetic variants only to have an effect in a specific context. We have found an abundance of such statistical interactions, and shown how many of them help to understand and interpret yeast gene expression regulation. Often, they recapitulated epistatic or gene-environment interactions, but nevertheless added a plausible mechanism of action. It will be especially interesting and important to see how these methods work on large, extensively genotyped and phenotyped human cohorts that are becoming available in the near future.

Methods

Datasets

Gene expression data from [15] (GEO accession number GSE9376) were downloaded using PUMAdb (http://puma.princeton.edu). In line with [15], we considered spots good data if the intensity was well above background and the feature was not a nonuniformity outlier. Transcripts with more than 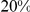of missing values were discarded. All other missing expression values were replaced with the averages across the corresponding growth condition.

The remaining expression data consisted of 5493 probe measurements for 109 crosses of BY (laboratory) and RM (wild) strains grown in both glucose and ethanol. For each strain, the mRNA from the two growth conditions was assayed on one Agilent slide composed of two arrays, resulting in a total of 218 expression profiles. We normalised the average gene expression for each slide, and thus each of the 109 segregants to be 0 to account for the potential experiment bias. Further, as the segregants were randomised with respect to which of the two dyes was used in the assay, we subtracted off a linear fit of the dye effect for each gene separately, as its influence is known to be gene-dependent (e.g. [46]). Strain genotypes were kindly provided by R. Brem. Each of the 109 segregant strains was genotyped at 2,956 loci to give a crude map of genetic background.

Transcription factor binding data were downloaded from Yeastract [26] (Version 1.1438) and contained binary indicators of binding between 174 transcription factors and 5,914 genes. We considered 3,000 most variable probes whose corresponding genes were included in the binding matrix, and transcription factors that influenced at least 5 genes. After further discarding probes for which there were no data available, the remaining Yeastract prior dataset consisted of binding data for 167 transcription factors affecting 2,941 genes.

Similarly, pathway information were downloaded from the KEGG database [27]. Only pathways with at least 5 genes were included in the network prior. This filtering procedure retained 63 pathways controlling 1,263 genes. The results of [15] were not used as a source of information for either of the prior datasets.

Statistical model

The statistical model underlying our analysis assumes that the gene expression levels are influenced by effects of locus genotypes, intermediate factors, and interaction effects between them. These effects jointly influence expression variability in an additive manner, resulting in a generative model for expression 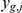of gene 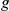in individual 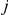of the form:

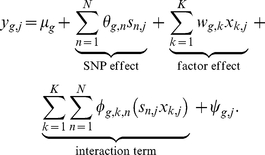(2)

Here, 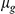is the mean expression level, 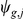the residual expression (noise), and 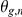denote the weights of genotypes of SNPs 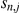. The activations 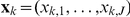of 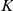intermediate factors are modelled as unobserved latent variables that linearly influence gene 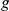with weights 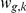. Finally, the strength of interaction effects between factor 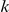and SNP is regulated by the interaction weights .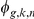

On a second level of the model, the latent factor activations 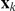may themselves be associated to the genetic state. Again assuming a linear model, these relations are cast as

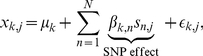(3)

where 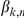is the association weight and 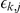denotes the observation noise.

While appealing because of its generality, it is hard to perform joint parameter inference in the model implied by Equations (2) and (3). Here, we follow a two-step approach to approximate the joint inference:

1. Factor inference. The latent factors 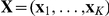and weights 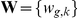are inferred from the expression levels alone, not taking the effects of SNPs 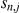via association or interaction into account.

2. Association and interaction testing. Significance of associations of factors to SNPs (Equation (3)) and SNP-gene-factor interaction terms (Equation (2)) are tested conditioned on the state of the inferred factors.

This approach renders the inferences tractable and allows for statistical significance testing of the potential influencing effects that make up the total gene expression variability (Equation (2)). In this scheme, the factor inference is approximated, as the contribution of direct SNP effects and interactions is not taken into account while learning. In the context of the dataset investigated here, this approximation is well justified because of the relative effect sizes. The total variance explained by the interactions is small compared to the direct factor effects. If necessary on other datasets, this step-wise procedure could also be iterated, refining the state of the inferred factors given the state of associations and interactions.

The implementation of the statistical models for the inference step and the statistical tests are described in the following.

Factor inference

Factors are inferred using a sparse Bayesian factor analysis model (Figure S3) [24], [25]. Starting from the full model in Equation (2), the terms for direct genetic associations and interactions are dropped. The remaining factor model explains the expression profile 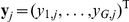of the 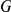genes for segregant 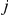by a product of activations 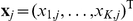of the 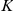factors, and the 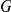times 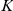weight matrix 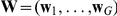and per-gene Gaussian noise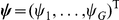

(4)

The expression data 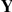is observed, and all other variables are treated as random variables with corresponding prior probabilities. The indicator variable 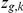encodes whether factor 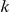regulates gene 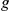(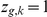) or not ().

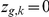(5)

The width 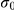of the first Gaussian is small, driving the weight to zero. In experiments, we used 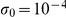. The existing knowledge about whether a factor affects a gene, extracted from KEGG or Yeastract, is then encoded as a Bernoulli prior on the indicator variables .

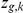(6)

The variable 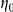can be thought of as the false negative rate (FNR) and 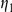as the false positive rate (FPR) of the observed prior information. We use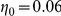d and 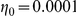for Yeastract and KEGG factors, respectively, and 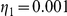for both. The ratio of the false positive and false negative rate is motivated by relatively high false positive rates in chromatin immunoprecipitation experiments, and confidence in the KEGG annotations. Altogether, this part of the model corresponds to a Gaussian mixture of the form

(7)

Prior probabilities over factors 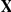are standard Gaussian distributed, 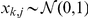. The per-gene noise is Gaussian distributed with precisions 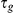, 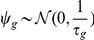. The precisions 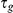are in turn a priori Gamma distributed, 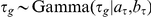. For the experiments this prior was set to be uninformative with .

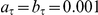Inference in the sparse factor analysis model is achieved using a hybrid of two deterministic approximations, variational learning (VB) [47] and Expectation Propagation [48], with exact details presented in [24], [25].

Orthogonality of factors to experimental covariates

We verified that the normalisation procedure applied to the gene expression profiles (Dataset S1) ruled out any artifactual dependency of the factor activations on experimental covariates. First, we checked whether the 109 strain indicator variables corresponding to the 109 Agilent slides used were correlated with the factor activations. Factor activations and the indicator variables were uncorrelated (Pearson's 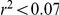) for all factor activations across restarts and choices of prior knowledge. We then permuted the indicators, and repeated the experiment, observing correlations stronger than 0.07 for each of the prior settings. Second, the correlation between the inferred factors and the dye indicator variable did not exceed 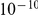for any prior setting and random restart. This is expected as all gene expression profiles were normalised to be orthogonal to the dye indicator.

Statistical identifiability of factors and model restarts

In general, factor analysis models are prone to suffering from intrinsic symmetries such as sign flips or factor permutations with impacts on the interpretability of obtained solutions. The informative sparsity prior of our factor analysis model (Equation (6)) substantially reduces these ambiguities, as it introduces constraints on possible factor configurations. A detailed discussion, including a quantitative evaluation of these symmetries can be found in Text S1.

As an additional measure, our analysis explicitly takes the variability of factor solutions into account by analysing a set of inference solutions rather than a single point estimate. In the experiments, we performed 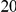independent runs of the factor analysis model with parameters randomly initialised from their respective prior distributions, and used this whole ensemble to test for significant association and interaction effects.

Association and interaction testing

We used standard marker regression to calculate test statistics for both association and interaction effects involving the inferred factor activations, using suitable approximations of the full model implied by Equations (2) and (3) (Text S1). In short, we calculated standard log-odds (LOD) scores for significance of association and interaction weights. We then repeated this procedure on permuted data to establish an empirical null distribution of LOD scores, and calculated local false discovery rates (Q-values) for the association and interaction statistics. To incorporate the uncertainty in factor inference in the significance testing, we recalculated the Q-values for every random restart of the model. Finally, we combined the Q-values across runs and used this combined statistic to assess the overall significance of any one effect. The consistency across restarts may also serve as criterion for the identifiability of a particular factor association/interaction. Full methods are given in Text S1.

Software

An open source Python implementation of the sparse factor analysis model is available from http://www.stegle.info/software/FAQTL and ftp://ftp.sanger.ac.uk/pub/rd/PEER.

Supporting Information

Dataset S1

List of interactions for each prior setting (combined q<0.05).

(1.09 MB ZIP)

Figure S1

Histogram of average Pearson R∧2 correlation values between Yeastract factor activations and their corresponding probe expression measurements.

(0.01 MB PDF)

Figure S2

Top panel: number of inferred factor activations associated (q<0.05) with the genotype of each locus in the genome. Lower panel: number of trans eQTLs (q<0.05) found for each locus in the genome.

(0.03 MB PDF)

Figure S3

The Bayesian network of the sparse factor analysis model. Observed data {y_g,j} for genes g ∈ {1,… G} in individuals j ∈ {1, … J} are modelled by the product between unobserved factor activations {x_j} and weights {w_g}, and Gaussian observation noise. The indicator variables {z_g,k} determine the state of the gate, either switching the corresponding mixing weight off or on A priori knowledge about the connectivity structure is introduced as a prior on the Bernoulli distribution parameter π_g,k. For the hybrid algorithm VB/EP, Expectation Propagation is used for inference in the submodel enclosed in the grey shaded area “EP.”

(0.05 MB PDF)

Table S1

Properties of inferred Yeastract factor activations. Q-value and average LOD score of association with SNPs (with best locus) or environment indicator is given for associations with combined Q-value<0.05.

(0.05 MB PDF)

Table S2

Properties of inferred KEGG factor activations. Q-value and average LOD score of association with SNPs (with best locus) or environment indicator is given for associations with combined Q-value<0.05.

(0.03 MB PDF)

Table S3

Properties of inferred freeform factor activations. Q-value and average LOD score of association with SNPs (with best locus) or environment indicator is given for associations with combined Q-value<0.05.

(0.03 MB PDF)

Table S4

Associations to loci with more than one Yeastract factor association. Q-value and average LOD score are given for all factors associated to each locus at combined Q-value<0.050.

(0.03 MB PDF)

Table S5

Associations to loci with more than one KEGG factor association. Q-value and average LOD score are given for all factors associated to each locus at combined Q-value<0.050.

(0.03 MB PDF)

Table S6

Associations to loci with more than one freeform factor association. Q-value and average LOD score are given for all factors associated to each locus at combined Q-value<0.050.

(0.03 MB PDF)

Table S7

Trans eQTL peaks with at least 50 associations. For each peak, the number of significant associations to probe expression levels (1.), number of associations for Yeastract factor activations significantly associated with the peak (2.), number of genes more strongly associated with the factor than the peak locus genotype (3.) are given, together with the number and fraction of trans eQTLs explained by the factors, fraction of trans eQTLs more strongly associated with the factor, and fraction of trans eQTLs associated with a factor that are more strongly associated with the factor.

(0.05 MB PDF)

Text S1

Supplementary methods and simulation study.

(0.29 MB PDF)