Simulation of surface processes

Abstract

Computer simulations of surface processes can reveal unexpected insight regarding atomic-scale structure and transitions. Here, the strengths and weaknesses of some commonly used approaches are reviewed as well as promising avenues for improvements. The electronic degrees of freedom are usually described by gradient-dependent functionals within Kohn–Sham density functional theory. Although this level of theory has been remarkably successful in numerous studies, several important problems require a more accurate theoretical description. It is important to develop new tools to make it possible to study, for example, localized defect states and band gaps in large and complex systems. Preliminary results presented here show that orbital density-dependent functionals provide a promising avenue, but they require the development of new numerical methods and substantial changes to codes designed for Kohn–Sham density functional theory. The nuclear degrees of freedom can, in most cases, be described by the classical equations of motion; however, they still pose a significant challenge, because the time scale of interesting transitions, which typically involve substantial free energy barriers, is much longer than the time scale of vibrations—often 10 orders of magnitude. Therefore, simulation of diffusion, structural annealing, and chemical reactions cannot be achieved with direct simulation of the classical dynamics. Alternative approaches are needed. One such approach is transition state theory as implemented in the adaptive kinetic Monte Carlo algorithm, which, thus far, has relied on the harmonic approximation but could be extended and made applicable to systems with rougher energy landscape and transitions through quantum mechanical tunneling.

Theoretical calculations of various sorts have been an important part of surface science for a long time. The focus here, however, is on simulation, which is taken to mean a calculation including many degrees of freedom and involving few assumptions and only well-tested approximations to the basic laws of physics. Simulations have become possible with the large increase in computational power in recent years and equally importantly, rapid improvement in algorithms and software implementations. The goal of an atomic-scale simulation is to reveal, for example, atomic-scale transition mechanism without a preconceived notion about final states of the transitions, reaction coordinates, or other special treatment of selected degrees of freedom. The information about what can happen in the simulated system should be an output of the simulation, not an input. From this point of view, I will briefly review the current status of surface science simulations and give a personal account of what I believe are some of the promising avenues for further development in the field. In this context, it is fitting to mention a few surprising results that have been obtained from some previous calculations to support the insistence on minimal preconceived input in the simulations: (i) the two-atom concerted mechanism for adatom diffusion on Al(100) and Pt(100) surfaces (1, 2), (ii) the facile descent of adatoms near but not at kink sites on Pt(111) (3, 4), which turned out to be essential for reproducing the reentrant layer by layer growth (5), and (iii) the large surface relaxation of 0.3–0.4 Å when CH₄ dissociatively adsorbs on Ni(111) and Ir(111) surfaces (6–8).

The discussion here will be based on the adiabatic or Born–Oppenheimer approximation, which enables the separation of electronic and nuclear degrees of freedom. There are important cases where this approximation is not valid, and full nonadiabatic simulations remain an important challenge. However, prevailing evidence today indicates that, for many of the critical processes in surface science such as diffusion, chemical reactions, and even dissociative adsorption (9, 10), the adiabatic approximation is accurate enough.

Electronic Degrees of Freedom

A typical system to be simulated consists of electrons and nuclei, and the task is, in general, to simulate the time evolution of the system or carry out some optimization of the atomic structure (typically by simulated annealing) (11). The first step in the Born–Oppenheimer procedure is to solve for the electronic degrees of freedom given fixed positions of the nuclei. This gives an electronic energy surface E(R), where R denotes the coordinates of the nuclei. The second step is to solve for the motion of the nuclei. In this section, the first step is discussed. The second step in the Born–Oppenheimer procedure is discussed in the following section.

Most calculations today make use of Kohn–Sham density functional theory (KS-DFT) for solving the electronic problem (12). Quantum chemistry approaches involving Hartree–Fock and post-Hartree–Fock estimates of correlation energy are generally too computationally demanding for the size of systems needed in surface science simulations. They are, however, important for rigorous calculations of small clusters that can be used to assess the accuracy of more approximate methods. The true DFT functional is not known, and current implementations rely on various approximations. The most commonly used functionals today belong to the category of generalized gradient approximation (GGA), and the PBE and RPBE functionals are most frequently used in surface science (13, 14). Simulations including more than 100 atoms can be accomplished with this approach on present day computers (15, 16). Although many remarkably successful calculations have been carried out using gradient-dependent functionals, their accuracy is, however, not always high enough. Bounds on the errors in results obtained using GGA functionals have not been established, and their accuracy has to be assessed on a case by case basis by comparison with experiments or higher-level calculations. Generally, the binding energy of molecules is too large. A particularly severe case is the PBE value for the bond energy of an O₂ molecule, which is too large by an eV (17). This overbinding has been remedied to some extent by reparametrization in the RPBE functional but then, bond lengths are slightly less accurate (14). Also, activation energy barriers tend to be underestimated by GGA functionals. This is illustrated in Table 1 by several reactions involving silanes (simple models for hydrogen desorption from a Si surface; see refs. 18 and 19 for more detailed description). The underestimate is as large as 0.5 eV. Although trends can be analyzed and understood from calculations at this level, it is clearly important to develop a more accurate approximation to the energy functional.

Table 1.

Reaction and activation energy (eV) for some silanes

	SiH4 → SiH2+H2		Si2H4 → 2SiH2	Si2H6 → SiH4 + SiH2	Si2H6 → Si2H4 + H2
Method	Erxn	Esp	Erxn	Erxn	Erxn	Esp1	Esp2	ΔΔE
PBE	−2.56	2.21	−3.06	−2.58	−2.09	3.29	2.07	0.21
PBE-SIC	−2.87	3.35	−2.68	−2.73	−2.92	4.32	3.20	0.56
Hartree–Fock	−2.63	3.22	−2.17	−2.24	−2.70	4.56	3.04	0.36
PBE-SIC/2	−2.70	2.69	−2.90	−2.64	−2.43	3.72	2.54	0.11
B3LYP	−2.51	2.44	−2.65	−2.38	−2.24	3.67	2.34	0.08
QCISD(T)	−2.60	2.60	−2.70	−2.40	−2.30	3.80	2.40

The QCISD(T) calculations are taken to give the best estimate. The orbital density-dependent PBE-SIC/2 functional gives nearly as good of results as B3LYP (see ref. 17 for more details on the previous calculations). SIC, self-interaction correction.

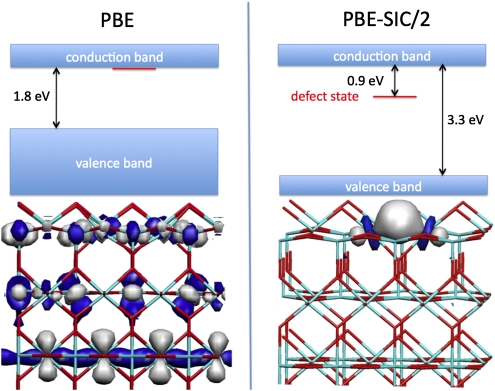
The deficiency of GGA is even more apparent in simulations related to solar cells, a research problem of great interest currently. One of the important tasks is to estimate the band gap of various materials. The KS-DFT methodology is only designed to give an estimate of the ground state energy and total electron density. Often, however, the orbital energies that are a biproduct of the minimization procedure are also used to infer other properties of the system, but this is not justified theoretically, and the estimates can be poor, as illustrated by estimated band gaps of a few oxides in Table 2. The PBE functional would, with this procedure, predict a band gap that is, in many cases, only two-thirds of the experimental value and even as low as one-half. Ge would be predicted to be a metal. However, ground state properties predicted by GGA calculations can also be qualitatively incorrect (for example, in the simulation of electronic defects such as vacancies and self-trapped holes). There is a strong tendency for delocalization in the GGA functional, and as a result, the localized electronic defect states tend to be unstable at this level of theory. This is illustrated by the oxygen vacancy at a TiO₂ surface shown in Fig. 1. When an O atom is removed, electrons localize in the vacancy, but PBE calculations give a delocalized state. Similar lack of localization has been reported in many cases (for example, an electron hole at an Al substitutional defect in SiO₂) (20, 21).

Table 2.

Band gaps (eV) of a few oxides

Crystal	Exp.	PBE	PBE-SIC/2
Al2O3	9.0	5.9	9.0
TiO2	3.0	1.8	3.3
SiO2	8.9	6.1	9.2
MnO	3.4	1.1	3.9
Fe2O3	2.3	0.8	2.6

PBE-SIC/2 gives quite good results, whereas full Perdew–Zunger SIC applied to PBE gives too large of gaps. If an estimate is made based on orbital energies obtained from PBE calculations, then too small of gaps are obtained.

Fig. 1.

Oxygen-atom vacancy on rutile TiO₂(110) surface. The PBE approximation to the energy functional predicts a delocalized electronic state with energy at the bottom of the conduction band, whereas the self-interaction–corrected PBE-SIC/2 functional predicts a localized state with energy in the gap, 0.9 eV below the conduction band edge, in good agreement with experiment (28). The self-interaction correction lowers the energy of the valence states and brings the estimated band gap into agreement with experiments (Table 2).

It seems clear that the semilocal mathematical form of the GGA functionals is too restrictive. Becke (22–24) introduced hybrid functionals that include linear combination of GGA, LDA, and Hartree–Fock exchange. This was justified theoretically from the adiabatic connection formula, but good accuracy was only obtained by adjusting the linear combination to fit a range of molecular data. This functional, B3LYP, has turned out to be remarkably successful in calculations of molecules but should be considered to be semiempirical in nature, and applications to problems outside the fitted range are questionable. An analogous functional has been developed for solid state calculations, the PBE0 functional (13). However, the evaluation of Hartree–Fock exchange for infinite solids (or slabs for surface simulations) is problematic and computationally demanding. Only a few calculations of surface properties using these hybrid functionals have been reported thus far. They should not be applied to metallic systems and tend to give worse results than GGA for the binding of molecules at metal surfaces (25). A review of several suggested improvements to energy functionals has recently been published (26).

A possible avenue for the development of more accurate functionals is to extend the functional form to include dependence on the electron density associated with each orbital rather than just the total electron density and the function space of orbitals consistent with the total electron density. When such orbital density-dependent (ODD) functionals are used, the orbitals become uniquely defined in contrast to Hartree–Fock or Kohn–Sham orbitals, where any linear combination of the occupied orbitals gives the same energy (this invariance is often used to construct more meaningful orbitals; for example, sp^N hybrid orbitals instead of s and p orbitals). The ODD form is needed, for example, to improve the predicted energy of orbitals and band gaps. An example of a functional of the ODD form is obtained when orbital-based self-interaction correction (SIC) is applied to KS-DFT as proposed by Perdew and Zunger (27). This is an appealing approach to improve on the GGA functionals, but few self-consistent calculations using this approach have been reported. The extension of the functional form to include ODD complicates the minimization of the energy and the self-consistency procedure. One can no longer simply choose the linear combination of orbitals that divides the problem into an eigenvalue problem for each electron, as in Hartree–Fock and KS-DFT. Therefore, new optimization methods are needed to deal with this more general functional form. A minimization procedure involving explicit optimization among unitary transformations of the orbitals has recently been developed (28). With this approach, the computational effort of ODD functionals is close to that of GGA functionals. The scaling is N³ for large systems as for GGA, whereas the computational effort for Hartree–Fock and hybrid functionals scales as N⁴.

Although it is clear that self-interaction is an important problem in GGA functionals, the orbital-based SIC is not exact, and when applied self-consistently to the PBE functional, for example, an overcorrection is obtained. As shown in Tables 1 and 2, the results in some cases are similar to what is obtained from Hartree–Fock. Theoretical arguments analogous to those presented by Becke (22–24) can be used to argue that the self-interaction correction should be scaled by one-half when applied to GGA functionals (28, 29). Results of calculations with PBE and such scaled self-interaction correction are also given in Tables 1 and 2 and shown in Fig. 1. In many cases, the results are quite good, and this illustrates how the accuracy can be improved significantly by including ODD while avoiding the computationally expensive Hartree–Fock exchange, which is particularly problematic when periodic boundary conditions are used to represent extended systems, such as slabs in surface science simulations. For the delocalized states in metals, the self-interaction correction is zero and leaves the successful LDA and GGA estimates unchanged. Interestingly, the orbitals that result from ODD calculations based on the self-interaction correction tend to be localized if the system is not metallic, and they correspond well to chemical intuition (for example, sp^N-hybrid orbitals for atoms that are covalently bonded).

The development of an energy functional of the ODD form where properties of both localized states and electron gas are reproduced accurately is clearly an interesting avenue to pursue. Such a functional could simultaneously give a good description of both molecular properties and condensed matter properties and thereby, make it possible to more accurately describe surface processes such as formation and breakup of molecules at metal and metal oxide surfaces.

Nuclear Degrees of Freedom

After a solution has been obtained for the electronic degrees of freedom, the task is to move the nuclei on the energy surface, E(R). In many cases, classical equations of motion are accurate enough for simulating systems at room temperature or higher. However, the challenge comes from the large time-scale difference between the fast vibrational motion of the atoms and the events of interest, such as structural rearrangements, chemical reactions, diffusion, etc. An activation barrier of, say, one-half an eV and a prefactor of 10¹³ s⁻¹ is common, and such events occur frequently at room temperature, about 1,000 times/s. However, a simulation of classical dynamics would need to follow more than 10¹⁰ vibrational periods, requiring about 10¹¹ numerical iterations (each one involving an evaluation of the energy of the system and force acting on the atoms) before a single transition can be expected to occur, on average, in the system. Such a simulation is not possible even for a small system and simple description of the interatomic interactions. A different algorithm for the simulation of time evolution is in general necessary for surface science.

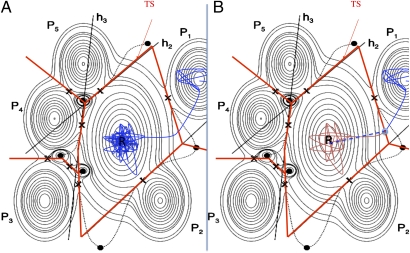
This rare event problem calls for a statistical approach as in transition state theory (TST) (30–32). Although TST is most often used to evaluate a rate constant for a given transition and a given mechanism, it can be used as the basis of a simulation method for long time-scale evolution of, for example, solid surfaces. This will be referred to as the Wigner, Keck, Eyring (WKE) two-step procedure, where the impossibly long classical trajectories are replaced by WKE trajectories (Fig. 2). For a given initial state, a dividing surface separating it from the rest of configuration space needs to be constructed, and it should correspond to a region of low probability so that, to a good approximation, the system will escape if it is found at the dividing surface and is heading away from the reactant state. In this first step, an estimate of the lifetime of the initial state is obtained. In the second step, a short time trajectory is started from the dividing surface by sampling the probability distributions for velocity and location within the dividing surface. Forward integration of the equation of motion is used to check which final state is reached (if any), and integration backward in time is used to check whether the trajectory indeed originated from the initial state (Fig. 2). If a product state is not reached and the trajectory did not originate from the initial state, then a new trajectory is generated, and the clock is advanced. When a successful trajectory has been found, the system is advanced to the product state. If a good transition state dividing surface has been identified in the first step, the success rate in the second step can be high. These much shorter WKE trajectories contain all of the relevant information needed for the long time-scale simulation, only the tedious and uninformative vibrational part of the trajectory within the initial state is replaced by a statistical estimate (33).

Fig. 2.

Schematic contour plot of an energy surface showing an initial state minimum, R, and five possible final state minima, P₁–P₅. Maxima are denoted with filled circles, and saddle points are denoted by ×. In the harmonic approximation (the case illustrated here), the dividing surfaces are hyperplanar segments containing a first-order saddle point and oriented with the normal pointing along the unstable mode. (A) A reactive classical trajectory requires impossibly long simulations of vibrations in the initial state until a transition is observed (blue line). (B) In the WKE procedure, a short trajectory containing the essential information is generated in the following way. A statistical estimate is made of the time needed to reach a point (denoted by an open blue circle) in the transition state, a short trajectory from that point forward in time is generated to determine the final state (blue line), and a short trajectory backward in time is generated to verify that it originated in the initial state (red line); otherwise, a new trajectory is generated. The configuration space is partitioned into subspaces by dividing surfaces (straight red lines), and long time-scale simulation using the adaptive kinetic Monte Carlo (AKMC) method tracks the advance of the system from one subspace to another.

The major challenge here is to define and construct the D-1 dimensional dividing surface in such a way that the second step can give reactive WKE trajectories with enough frequency. Fortunately, a variational principle can be used to optimize the location and shape of the dividing surface. Keck (32) showed that any recrossing leads to an overestimate of the rate constant, and therefore, the dividing surface that gives the smallest value of the rate constant is the best choice. Thus far, this variational principle has mainly been used to obtain better numerical estimates for rate constants of a given presumed reaction mechanism (34). However, applied more generally, it can extend TST from being a method for estimating a rate constant to a simulation method that can reveal an unexpected transition mechanism. This has been illustrated in the case of the diffusion of an Al adatom on an Al(100) surface, where a simple hyperplanar dividing surface was used but both the location and the orientation of the hyperplane was optimized (35). When the initial orientation of the hyperplane corresponded to a hop mechanism for diffusion of the Al adatom, the variational optimization of the location and orientation of the hyperplane in maximizing the free energy (which corresponds to minimizing the rate constant) could reveal the preferred two-atom concerted mechanism. The normal of the hyperplane after maximizing the free energy gives the reaction coordinate of the transition in the bottleneck region. More generally, a dividing surface could consist of a mosaic of hyperplanar segments to enclose the initial state, and it is possible to formulate a reversible work optimization, where the location and orientation of each segment are optimized to maximize the free energy of the dividing surface (33). It may be more efficient in the end to use another shape of the dividing surface, for example, based on internal coordinates. The implementation of a general variational optimization of dividing surfaces for complex systems remains an important challenge, particularly for the simulation of surface processes.

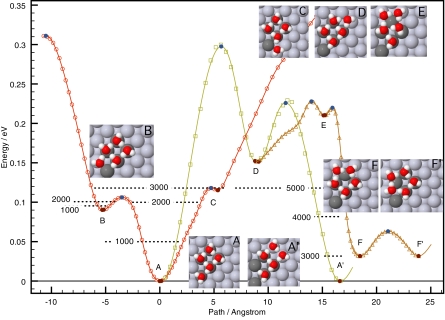
The scheme above has thus far been implemented within the harmonic approximation to TST (HTST) in the adaptive kinetic Monte Carlo (AKMC) scheme (or on the fly KMC) (36), where configuration space is partitioned by hyperplanar segments containing a first-order saddle point and oriented with the normal along the unstable vibrational mode (Fig. 2). The challenge is to find all of the relevant low-energy first-order saddle points on the potential energy rim surrounding a given initial state. This is done without preconceived notion of likely transition mechanisms using the minimum mode-following method (37, 38). Several tricks have been used to increase the efficiency of the simulation [for example, coarse graining of the energy landscape (39, 40), recycling of previously found saddle points (41), distributing of computations on a collection of computers connected by the internet (42), and using records of intermediate steps in saddle point searches to abort later searches (skipping path method)] (43). An important quality of the method is that atoms do not need to be assigned to lattice sites as in regular KMC simulations. The method can be applied to disordered systems (such as diffusion on the surface of ice) (44). A sample simulation, using coarse graining, is illustrated in Fig. 3. Although this kind of simulation is computationally demanding, it can be used to identify the important atomic-scale transitions in the system, and this information can then be used as input in a simpler simulation that can deal with larger samples and longer time scale. The extension of the AKMC method to include anharmonic corrections or even full free energy optimization of the dividing surface remains a challenge for the future (33).

Fig. 3.

An AKMC simulation of the diffusion of a pentamer water cluster on a Pt(111) surface using a model potential (39). Without coarse graining, the simulation would simply show repeated transitions between the initial state (A) and the two shoulder states (B and C). With coarse graining, states A and B are merged after a little over 2,000 iterations, and states A–C have been merged after about 3,000 iterations. After that, states D and E are revealed and then, A′ and F. Although one possible diffusion mechanism involves going from one ground state configuration to another (A–A′, etc.), a faster mechanism involves the rapid diffusion between metastable pentamer ring states (F–F′, etc), in between occasional visits to a ground state configuration.

Only one possible approach to long time-scale simulations has been sketched here. Other approaches have been proposed and used in impressive simulations, particularly of surface processes (45–47).

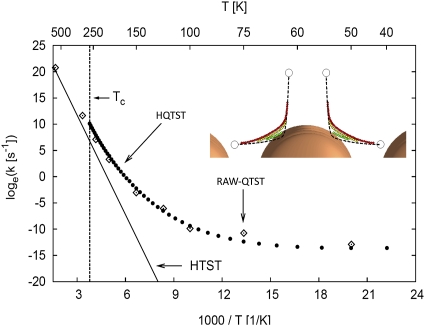
When light atoms are involved and/or temperature is low, quantum effects can be important. At low enough temperature, a cross-over from an over the barrier classical transition mechanism to tunneling will occur. This cross-over temperature can be estimated from the classical minimum energy path (48, 49). The long time-scale simulation scheme described above can be extended to include tunneling in a harmonic quantum transition state theory approximation, where instead of the first-order saddle point on the energy surface E(R), a first-order saddle point on an effective quantum mechanical energy surface, the so-called instanton, is of central importance (48, 50, 51). A more general quantum transition state theory based on free energy optimization of a dividing surface has been formulated (50, 51). The harmonic approximation has, however, been found to work remarkably well, even in simulations of, for example, H₂ desorption (Fig. 4) and molecular reactions (52). An algorithm for evaluating tunneling rates in large complex systems using atomic forces directly from DFT or ab initio calculations (without the need to parameterize a potential energy surface) has been developed (53). It is an extension of the nudged elastic band (NEB) method (54, 55), where an elastic band discretized by a predefined number of replicas of the system is used to find the classical periodic orbit on the inverted potential surface. Unlike the NEB, where the end points are fixed, this elastic band has end points that slide to and then along the given energy contour to find the optimal classical turning points (Fig. 4). For each energy, an optimal WKB tunneling path is found. Then, by calculating the classical dynamics of the system on the inverted potential along that path, the appropriate distribution of system replicas in the Feynman path integral is determined, and the time period is used to determine the corresponding temperature (48, 53). Finally, the rate constant is evaluated from a harmonic sampling of nearby Feynman paths.

Fig. 4.

Desorption of H₂ from Cu(110) simulated using quantum mechanical description of the atoms, both H atoms and Cu atoms. The temperature dependence of the rate constant shows the onset of tunneling at around 250 K. Inset shows how the tunneling paths (green = 0.4 eV, yellow = 0.2 eV, red = 0.02 eV) cut corners compared with the classical minimum energy path (black dashed line). HTST labels the results from classical harmonic TST calculations (black solid line), RAW-QTST labels the results from full quantum TST calculation (50, 51), and HQTST labels the results obtained from harmonic quantum TST (instanton approximation) (48). The HQTST approximation performs remarkably well. It involves much less computation than RAW-QTST and has been implemented in such a way that atomic forces from DFT calculations can be used directly (53).

Although the cross-over temperature for tunneling is usually well below room temperature, as in Fig. 4, there are cases where tunneling dominates even at elevated temperature. In hydrogen desorption from an ammonia borane molecule, for example, the calculated rate of tunneling is significantly larger than the rate of classical desorption, even at a temperature as high as 100 °C (53).