Density functional theory in surface chemistry and catalysis

Abstract

Recent advances in the understanding of reactivity trends for chemistry at transition-metal surfaces have enabled in silico design of heterogeneous catalysts in a few cases. The current status of the field is discussed with an emphasis on the role of coupling theory and experiment and future challenges.

Surface chemistry is interesting and challenging for several reasons. It takes place at the border between the solid state and the liquid or gas phase and can be viewed as a meeting place between condensed-matter physics and chemistry. The phenomena at the solid–gas or solid–liquid interface are complicated for this reason. A chemical reaction at a metal surface, for instance, has all of the complexity of ordinary gas-phase reactions, but in addition the usual electron conservation rules do not apply because the metal provides a semi-infinite source of electrons at the Fermi level. A new set of concepts therefore needs to be developed to describe surface chemistry.

An understanding of surface chemical reactions is necessary to describe a large number of surface phenomena including semiconductor processing, corrosion, electrochemistry, and heterogeneous catalysis. Heterogeneous catalysis alone has been estimated to be a prerequisite for more than 20% of all production in the industrial world (1), and it will most likely gain further importance in the years to come. The development of sustainable energy solutions represents one of the most important scientific and technical challenges of our time, and heterogeneous catalysis is at the heart of the problem. Most sustainable energy systems rely on the energy influx from the sun. Sunlight is diffuse and intermittent, and it is therefore essential to be able to store the energy, for example chemically as a fuel or in a battery. Such storage can then provide energy for the transportation sector and in decentralized applications, as it evens out temporal variations (2, 3). The key to providing an efficient transformation of energy to a chemical form or from one chemical form into another is the availability of suitable catalysts. In essentially all possible sustainable energy technologies, the lack of efficient and economically viable catalysts is a primary factor limiting their use (3, 4).

In the present paper, we will discuss the status of the development of an understanding of surface chemistry. We will do this from a theoretical perspective, but it is important to stress that it is a close coupling between theory and experiment which has enabled the developments thus far. Surface science experiments have been invaluable in providing a quantitative description of a range of surface phenomena (5–14). This has been essential in benchmarking computational surface science based on density functional theory (DFT) calculations and in providing experimental guidance and verification of the concepts developed. This forms a good background for the development of an understanding of heterogeneous catalysis, which is the other part of this paper. We will show how the concepts developed allow the understanding of trends for certain classes of catalysts and reactions.

The ambition is to develop concepts that are useful in understanding which properties determine the activity and selectivity of a catalyst and to be able to use calculations to search for new catalyst leads. We will discuss how far we are in this respect and point out some of the many challenges ahead before this becomes a regular way of designing new catalysts.

Density Functional Theory Calculations of Surface Chemistry

The description of the chemical bond between a surface and a molecule is the fundamental basis for understanding surface chemical reactivity and catalysis. A considerable amount of understanding has been developed for the adsorption of simple atoms and molecules onto transition-metal surfaces (15–19).

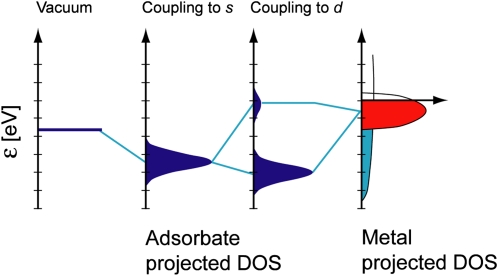
The d-band model (20, 21) has proven particularly useful in understanding bond formation and trends in reactivity among the transition metals. The d-band model is an approximate description of the bond formation at a transition-metal surface, as illustrated in Fig. 1. It describes the interaction between adsorbate valence states and the s and d states of a transition-metal surface. Coupling to the itinerant s states gives rise to a shift and broadening of the adsorbate states, but this contributes to a first approximation equal to the bond energy for all transition metals (they all have half-filled, very broad s bands). The differences between transition metals are due to the formation of bonding and antibonding states between the (renormalized) valence states and the metal d states. The strength of the bond is given by the filling of the antibonding states but, unlike gas-phase chemistry, where this is determined by the number of electrons in the system, at a metal surface the filling is given by the energy of the antibonding states relative to the Fermi level. Because the antibonding states are always above the d states, the energy of the d states (the center of the d states) relative to the Fermi level is a good first indicator of the bond strength. The higher the d states are in energy relative to the Fermi level, the higher in energy the antibonding states are and the stronger the bond.

Fig. 1.

Bond formation at a transition-metal surface. Schematic illustration of the formation of a chemical bond between an adsorbate valence level and the s and d states of a transition-metal surface. The bond is characterized by the degree to which the antibonding state between the adsorbate state and the metal d states is occupied. The higher the d states are in energy relative to the Fermi level, the more empty the antibonding states and the stronger the adsorption bond. Adapted from ref. 19. DOS, density of states.

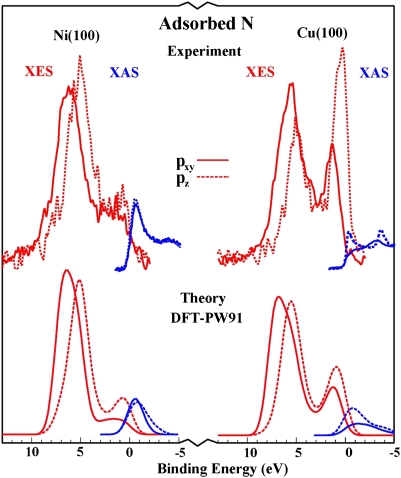
The details of the bonding picture have been confirmed in a series of X-ray spectroscopy experiments (Fig. 2). It explains trends in reactivity from one transition metal to the next, and the effects of alloying, structure, strain, defects, and so forth. A large number of calculated and experimental results have been accounted for in this way (22–36). An example of experimental results explained by the d-band model is included in Fig. 3.

Fig. 2.

Experimental verification of the d-band model. (Upper) Experimental X-ray emission (XES) and X-ray adsorption (XAS) spectra for N adsorbed onto Ni and Cu surfaces. The bonding and antibonding states originating from the adsorbate p_xy and p_z states and the metal d states are clearly seen. For Cu with the lowest-lying d states, the antibonding states are filled and the adsorption bond is weak. Adapted from ref. 19.

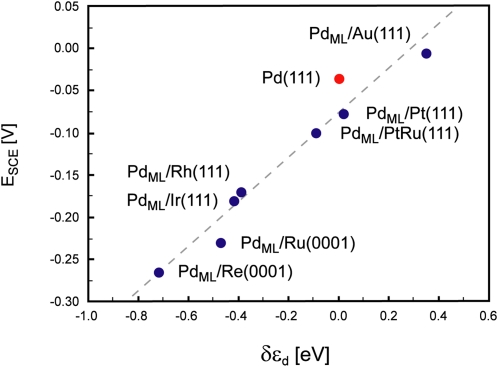
Fig. 3.

Illustration of the use of the d-band model. Electrochemically measured changes in the hydrogen adsorption energy (E_SCE) for Pd overlayers on a number of metals are shown to scale well with the calculated shift of the d-band center (δε_d). Adapted from ref. 32.

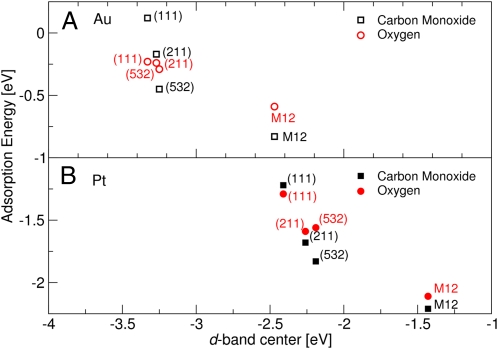
It is important to stress that variations in the width of the d band will lead to variations in the position of the d-band center. The reason is that d filling does not change for any transition metal, and this will fix the d band to the Fermi level. Hence, each metal system will have to compensate for variations in the width by shifting the d states up or down in energy depending on the nature of the change. The width of the d band varies significantly with metal coordination number and the d band will shift accordingly; however, the binding energies shift with an equal amount, as seen in Fig. 4 (37).

Fig. 4.

Illustration of the extent of the d-band model. Calculated CO and O adsorption energies for a range of different Au (A) and Pt (B) surfaces including 12 atom clusters are seen to correlate with the calculated d-band center (ε_d). Adapted from ref. 37.

As one sweeps through the transition metals from right to left, the metals become more and more reactive and binding geometries of adsorbates might change. Geometrical changes in the adsorbate will affect the position and number of adsorbate levels that couple to the metal states, and one must address such cases more cautiously.

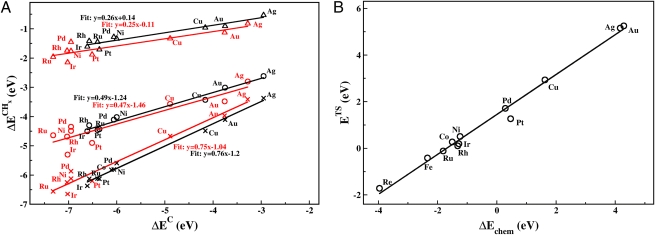
The correlation between interaction energy and d-band center has been found both for adsorption energies and transition-state energies. Because different adsorption energies and transition-state energies are correlated with the same underlying electronic structure properties of a surface, it is not surprising that correlations between different adsorption energies [so-called scaling relations (38)] and between adsorption energies and transition-state energies (so-called Brønsted–Evans–Polanyi relations) are found throughout transition-metal surface chemistry (e.g., Fig. 5).

Fig. 5.

Illustration of scaling relations. The plot on the left shows how all calculated CH_x adsorption energies scale with the adsorption energy of C for a number of metal surfaces (close-packed, black; stepped, red). The slope is given entirely by bond counting. Adapted from ref. 38. The plot on the right shows how the activation energy for CO dissociation over stepped surfaces scales with the dissociative chemisorption energy of the reaction.

From Surface Science to Heterogeneous Catalysis: Catalyst Design Principles

The kinetics of a catalytic reaction is the central property of a catalyst. The kinetics—rate and selectivity for different products—is the starting point (together with mass and heat transport) for the design of chemical reactors. The kinetics also provides the link between the microscopic properties of the catalyst, adsorption energies, and activation barriers of elementary steps, and experiments (39–48). We will focus in the following on the trends in reactivity, that is, the variations in kinetics from one surface to the next. An understanding of these trends is the basis for the design of new catalysts.

In principle, kinetics can be obtained for a given catalytic reaction if one calculates all reaction (free) energies and activation (free) energy barriers (as a function of coverage and surface structure). There are now several examples where the macroscopic kinetics of a catalytic reaction has been modeled successfully on the basis of electronic structure calculations (38, 43–46). These are important benchmarks showing that the theoretical methods work, but the procedure for calculating all energy parameters for all possible elementary steps under all possible conditions is extremely demanding.

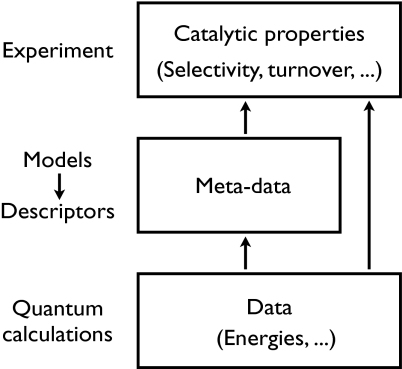
The same procedure can, in principle, be used to search for new catalysts: For each new catalyst structure and composition, a new microkinetic model is developed and the catalytic properties are evaluated. The effort to repeat this procedure thousands of times in search for new catalysts is, however, prohibitive with present-day computers. An alternative procedure is to develop models of surface reactivity and use these to pinpoint the most important microscopic materials properties of the catalyst which determine the macroscopic catalytic performance. These “descriptors” can then be scanned much more readily for a given class of materials. An additional—and perhaps even more important—result of such an approach is that it typically establishes some design concepts that experimentalists and catalyst developers subsequently can use in their daily laboratory work.

Deriving Descriptors of Catalytic Activity

Models of reactivity trends that single out the important parameters describing catalytic activity or selectivity are the essential prerequisites for the tailoring of surfaces with specified catalytic properties. In principle, there are many parameters that enter into the kinetics of a given reaction: The energy of all intermediates and of the transition states separating them is needed to specify the full reaction energetics. Even for simple reactions, this easily gives 10–20 energy variables for a specific catalytic reaction. The complexity of the problem is greatly reduced by the energy correlations discussed above. Because of the high level of correlation between various adsorbate and transition-state energies, the number of independent descriptors can often be reduced to only a few, for example one or two, without introducing errors larger than the average simulation errors that would be expected based on the quality of the modern gradient-corrected exchange-correlation functionals used in electronic structure calculations. This limited number of descriptors can then be screened much more readily. Fig. 6 illustrates this working principle. In the following, we will show how this principle can be applied.

Fig. 6.

Illustration of the link between the microscopic surface properties and the macroscopic catalytic properties as measured in a catalytic converter. They are directly linked through the kinetics, but it is far more instructive to develop models that map the large number of microscopic properties characterizing the catalyst onto a few descriptors.

Take the methanation reaction (CO + 3H₂ → CH₄ + H₂O) as an example. As seen in Fig. 5, the scaling relations of the CH_x species mean that if the C adsorption energy is known, the CH, CH₂, and CH₃ adsorption energies are also known for a given surface. Likewise, the OH adsorption energy is given by the O adsorption energy and, as shown in Fig. 5, the transition-state energy for CO dissociation scales with the dissociative adsorption energy of CO (hence the C and O adsorption energies). Finally, it turns out that the CH_x and OH formation transition-state energies are also functions of the C and O adsorption energies. The CO adsorption energy also scales with the C adsorption energy, and the same is roughly true of the H adsorption energy (although here the variation from one metal to the next is very slight). The result is that in a first approximation the activity of a given metal is given by only two descriptors: the C and the O adsorption energies.

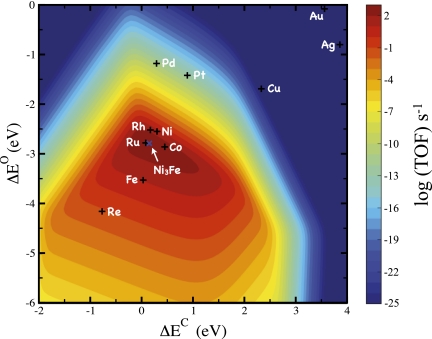
Fig. 7 shows the calculated rate of methanation under industrial conditions as a function of these two parameters. The input into the model is the set of scaling relationships for reaction energies and transition energies. The result is a volcano-shaped relationship between the catalytic rate and the adsorption energies. The mean absolute errors introduced by the scaling relations are on the order of 0.2–0.3 eV, errors that are within the limit of DFT. These errors are very small compared with the energy scale on which the volcano is defined. Hence, trends will be well-described even based on approximate scaling relations. The volcano relationship is a very fundamental concept in heterogeneous catalysis (49, 50) because it allows the identification of the best catalytic materials for a given reaction as a function of the chosen descriptors (51). A search for good catalysts therefore amounts to finding materials with descriptors that are close to the maximum of the volcano.

Fig. 7.

Theoretical volcano for the production of methane from syngas, CO, and H₂. The turnover frequency (TOF) is plotted as a function of carbon and oxygen binding energies. The carbon and oxygen binding energies for the stepped 211 surfaces of selected transition metals are depicted. Reaction conditions are 573 K, 40 bar H₂, 40 bar CO.

The most critical issue is to determine the active site for a specific reaction. For the methanation reaction, it is the step or kink sites on the metal particles that provide the proper structure for the breaking of the strong CO bond. Each structure defines a new set of scaling and Brønsted–Evans–Polanyi relations. Hence, identifying which sites are present during the reaction and identifying which of the resulting relations lead to the highest rate are the essence of determining the proper catalytic material for the process.

For the methanation reactions, the origin of the volcano is simple. We find that the breaking of the CO bond is the rate-determining step for relatively unreactive catalysts such as Ni and that this reaction step proceeds via bond breaking of the C-OH intermediate yielding adsorbed C and OH on the surface (52–55). On the more reactive metals, such as Fe, this reaction step becomes fast, and the surface becomes poisoned by adsorbed carbon and oxygen. A good methanation catalyst therefore represents a reasonable compromise between a low CO dissociation barrier and a high carbon and oxygen desorption rate (in terms of the CH₄ and H₂O desorption, respectively) (56). As can be seen in the volcano relation in Fig. 7, the theoretical results describe experimental findings (49) very well: Ru and Co lie at the top of the volcano, whereas Rh and Ni on the right and Fe on the left are calculated to have somewhat lower activities.

Industrially, the catalyst that is commonly used is based on Ni. Even though Ru and Co have been found to be the most effective (39), Ni is still preferred due to its lower price. Recently, DFT calculations identified Ni-Fe catalysts as a cheaper alternative with a higher activity than Ni (see also Fig. 7). These findings have been verified experimentally (56).

Descriptor-Based Search for New Catalysts

The identification of Ni-Fe as a possible catalyst for methanation is a very simple, early example of descriptor-based searches for new heterogeneous catalysts. There are several others in the recent literature (7, 25, 57–62). In the following, we will illustrate the approach with another example, which is a little more complex because it involves not only the rate but also the selectivity of the process.

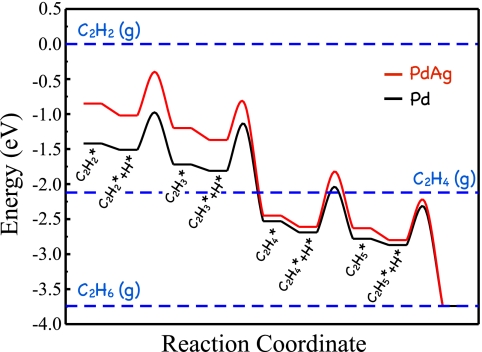
We will take the selective hydrogenation of acetylene in the presence of an excess of ethylene as an example. The reaction is important industrially, because it is used to remove trace amounts of acetylene from the ethylene used to make polymers. Fig. 8 shows the calculated pathway for the hydrogenation of acetylene to ethylene and the further hydrogenation of ethylene to ethane on the Pd(111) surface. The process starts with the adsorption and successive hydrogenation of acetylene to ethylene. Once ethylene is formed, it can desorb or react further to produce ethane, which is unwanted in this process (if this were fast, the ethylene would all disappear). A selective catalyst should have an activation barrier for the hydrogenation of ethylene that is higher than its desorption energy to favor desorption of the product rather than its further hydrogenation. Whereas these two energies are comparable for Pd(111), the desorption barrier is smaller than the activation barrier for the PdAg(111) surface (Fig. 8), making this surface more selective and explaining the addition of Ag to industrial Pd catalysts (63–66). Importantly, the addition of Ag to the Pd catalyst not only enhances its selectivity, it also decreases the activity by lowering the adsorption energy for acetylene.

Fig. 8.

Potential energy diagram obtained from DFT calculations for the hydrogenation of acetylene to ethane on close-packed surfaces of Pd (black) and PdAg (red) surfaces. Adapted from ref. 59.

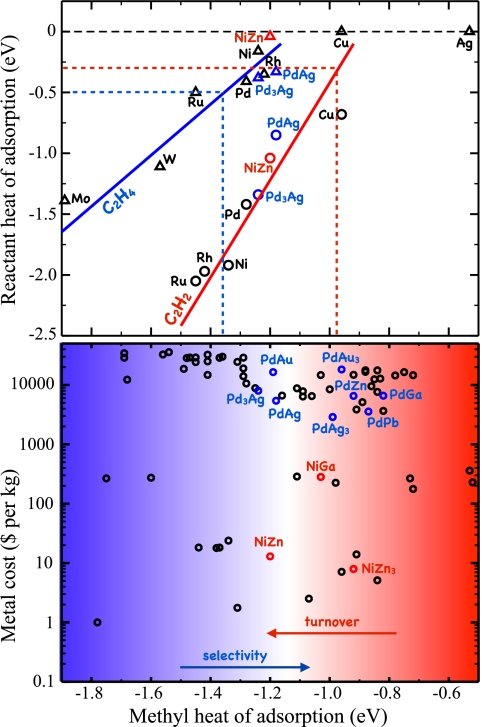
One can now use the acetylene and ethylene adsorption energies, 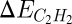and 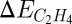, as the descriptors determining turnover and selectivity. These two descriptors are interrelated by a scaling relation as shown in the top of Fig. 9 (59). It was found that both acetylene and ethylene adsorption are well-described by the methyl adsorption energy. The slope of the scaling relations is 4 for acetylene and 2 for ethylene, a result that can be viewed as a manifestation of bond-order conservation (67, 68). Importantly, the results show that 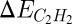and 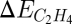are correlated. The optimal catalyst is hence a compromise between selectivity and activity. This observation allows for the determination of a window where good hydrogenation catalysts can be found. The window is limited by selectivity on the left side and activity on the right side as schematically shown in the bottom of Fig. 9. Screening of a number of different bimetallic catalysts with respect to the descriptor, the methyl adsorption energy, and the metal price per kilogram alloy led to the discovery of the NiZn and NiGa catalysts. These alloys were predicted to have an inherent selectivity that is comparable to the industrially used PdAg catalysts, while at the same time being considerably cheaper in price. Experimental testing of both NiZn and NiGa (59) has indeed shown that both catalysts have a high selectivity comparable to that observed for PdAg.

Fig. 9.

(Upper) Adsorption energy for acetylene and ethylene plotted against the adsorption energy of a methyl group. The solid lines show the predicted acetylene (red) and ethylene (blue) adsorption energies from scaling. The dotted lines define the region of interest, where the ethylene adsorption energy is less than the barrier for further hydrogenation (blue) and where the reactivity of the acetylene hydrogenation step is estimated to be 1 s⁻¹ per site (red). (Lower) Cost (in 2006 metal prices) of 70 binary intermetallic compounds plotted against the calculated methyl adsorption energies. The smooth transition between regions of low and high selectivity (blue) and high and low reactivity (red) is indicated. Adapted from ref. 59.

Challenges in Theoretical Surface Reactivity and Heterogeneous Catalysis

Finding a new catalyst lead for a given reaction is only the first of a number of necessary steps toward making a new technical catalyst. Whereas a high activity or a good selectivity are necessary requirements, and a high cost of the constituents can become prohibitive for industrial-scale use of the catalyst, there are commonly a multitude of other important requirements for a new technical catalyst. The ability of the catalyst to work in the presence of potential poisons, its ability to avoid Ostwald ripening and other sintering mechanisms, and its stability in terms of, for example, avoiding slow evaporation are typically crucial catalyst properties for achieving an economically acceptable lifetime. The production costs, the ease with which the catalyst is reduced, its capacity to be improved by secondary promoters, the role of defects, and how the catalyst interacts with different support materials can also be factors that need to be taken into account. The above-mentioned factors can all be simulated to some extent, but it would be reasonable to say that substantial improvements are needed with respect to the simulation of all these materials properties before they will provide an alternative to carrying out the corresponding experiments. Naturally, however, the push in the theoretical community is toward carrying out as much as possible of the design process in silico rather than by experiment. In the end it is only an experiment that can confirm the discovery of a good catalyst.

The couple of examples mentioned so far refer to relatively simple reactions, and the catalysts had rather well defined active sites on simple vicinal surface structures of pure and alloyed transition metals. Inorganic compounds such as zeolites, oxides in general, carbides, sulfides, and so forth are playing an increasingly important role in industrial catalytic conversion. Extending systematic computer-based design beyond transition-metal catalysts provides a considerable challenge from a theoretical point of view. We know from detailed comparisons between theory and experiment that density functional theory works quite well for the transition metals, but we also know that it often works somewhat worse for other classes of potential catalysts, such as, for example, strongly correlated oxides (69–73).

As ambition grows toward treating the catalysis of larger organic molecules, for example, the inclusion of van der Waals interactions becomes important (74, 75). Although steps have already been taken in that direction (76–78), it appears that further improvements are needed. Methodological improvements are also necessary to address the fundamental challenge related to finding the ground-state structures of unknown materials (79–81) and to do this systematically and self-consistent with in situ reaction kinetics. When a catalyst operates under conditions where the reaction is occurring without one single elementary step being the rate-determining step but with the reaction rate being the result of several competing rates, one cannot define a unique chemical potential of all of the reactive and product species. The oxidative or reducing power of the different species may be said to be determined by kinetics and not thermodynamics alone. Establishing this kind of self-consistent phase-diagram analysis under kinetic conditions poses a major challenge.

Even though some progress has been made toward understanding electrocatalytic processes and photocatalytic processes from DFT, methodological improvements are needed to systematically investigate the adiabatic assumption under electron transfer processes at interfaces and better deal with the limitations of DFT in treating the electronic bandgap and excited electronic states. Current state of the art is to use oversimplified treatments of entropic contributions such as, for example, harmonic transition-state theory for the different free-energy states of the reactants. The harmonic transition-state theory approach works reasonably for smaller well-defined systems, but as the level of ambition grows toward including more of the environment and looking at larger reactant molecules, an improved sampling of the entropic part of free-energy contributions will become increasingly relevant. This in itself will require more computational power, more efficient computer codes, and codes that scale well on massively parallel computer systems.

It is therefore clear that, in a number of cases, we need higher accuracy than current density functional theory methods can provide to have predictive power. In addition, we need methods and associated computer codes that are more efficient computationally to be able to treat the complexity that characterizes most technically interesting systems and their environments—real materials including defects and two- or three-phase systems.

On the conceptual level, a number of improvements are equally desirable. For transition-metal alloys there are known exceptions to the d-band model, and this can result in outliers on the linear energy relations and suggests that improved descriptors may exist. Development of systematic approaches for determining the underlying electronic structure-materials functionality descriptors without as much input of external knowledge could be desirable. Scaling relations carrying over to inorganic compounds suggests that the ideas of the d-band model have wider applicability than to only metallic surfaces, but a counterpart to the d-band model working for oxides so far remains elusive.

As there is a push toward single-active-site control and high selectivity, we can perhaps find inspiration from the fact that enzymes developed in nature tend to have exactly these attributes. Although many enzyme processes are not able to compete with modern industrial processes in terms of energy management, much can still be learned about low-temperature/highly selective catalysis by studying the active sites in enzymes, and a further integration of the concepts in homogeneous, biological, and heterogeneous catalysis is highly desirable.

To address some of the challenges outlined above, it seems that the catalysis science community as a whole could help itself by establishing a generally accessible structured database of simulated materials properties. If most groups systematically used this database it would make it much easier to look up what systems have already been looked at by other groups. It would also improve reproducibility of results, and systems that were originally calculated for one purpose by one group could readily be reused for different purposes by another group. Establishing such a database could potentially have the same enormous impact on the computational materials design community as the Brookhaven database of biological structures has had on the bioinformatics community.

There are, as outlined above, a number of challenges on the road ahead. The challenges above are stated primarily as challenges for theory. They should, however, also to a large extent be viewed as challenges to experimentation. In the same way that well-defined experiments in ultra-high vacuum on single-crystal surfaces were of central importance in establishing the current reliable level of theoretical treatment of adsorption of small molecules onto transition-metal surfaces, so will new detailed experiments be of central importance in extending the reliability of electronic structure calculations to new areas. The fact that it has been possible in a few simple cases to tailor surfaces with improved catalytic properties on the basis of insight and DFT calculations provides some hope that this may with time develop into a general and versatile design strategy. The rapid developments that we are seeing now are, we hope, only the beginning.