Artificial atoms on semiconductor surfaces

Abstract

Semiconductor nanocrystals are called artificial atoms because of their atom-like discrete electronic structure resulting from quantum confinement. Artificial atoms can also be assembled into artificial molecules or solids, thus, extending the toolbox for material design. We address the interaction of artificial atoms with bulk semiconductor surfaces. These interfaces are model systems for understanding the coupling between localized and delocalized electronic structures. In many perceived applications, such as nanoelectronics, optoelectronics, and solar energy conversion, interfacing semiconductor nanocrystals to bulk materials is a key ingredient. Here, we apply the well established theories of chemisorption and interfacial electron transfer as conceptual frameworks for understanding the adsorption of semiconductor nanocrystals on surfaces, paying particular attention to instances when the nonadiabatic Marcus picture breaks down. We illustrate these issues using recent examples from our laboratory.

When the size of a semiconductor crystal is smaller than the natural length scale of an electron-hole pair in the bulk, charge carriers are confined by the physical boundary. This natural length, i.e., the Bohr radius of an exciton, is on the order of a few to a few tens of nanometers, depending on the dielectric constant and the effective electron/hole mass. Confinement of the charge carrier discretizes the electronic energy band. As a result, the electronic/optical behavior of a semiconductor nanocrystal is atom-like and is often called an “artificial atom” or “quantum dot” (QD) (1, 2). The most attractive property of a QD is the tunability of electronic energy levels. Since the discovery of solution based synthesis with excellent size control, colloidal QDs have become some of the most actively studied materials in chemistry and associated fields (3). Exciting applications of these artificial atoms include, among others, nanoscale electronic (4) and optoelectronic (5) systems, chromorphores in solar energy conversion (6, 7), and building blocks for assembly into designer solids for charge (8, 9) and energy transport (10).

In many of these applications, the artificial atoms or molecules must interact with macroscopic solids, e.g., electrodes or electron/hole conductors. How semiconductor nanocrystals interact with the macroscopic solid is a key question in determining the physical properties. Answers to this question should come from the realms of surface science: the artificial atoms or molecules are now the adsorbates, as illustrated in Fig. 1 for a submonolayer of PbSe QDs adsorbed on a silicon surface.

Fig. 1.

Scanning electron microscope images of submonolayers of PbSe QDs (diameter = 5.5 ± 0.4 nm) adsorbates on a Si surface. The QDs are capped with (A) oleic acid, or (B) ethanedithiol. Image courtesy of A. Wolcott.

From a fundamental perspective, a semiconductor surface with QD adsorbates represents an ideal model system for studying the coupling between localized and delocalized electronic systems. This kind of coupling is a pervasive scheme in condensed matter research. In fact, the simplest chemisorption theory, as put forward by Newns more than 40 years ago, was adapted from the Anderson model for localization/delocalization interaction (11). We may treat the adsorption of a QD on a semiconductor surface within the Newns-Anderson chemisorption theory. Here, discretized QD electronic states that are resonant with the bulk semiconductor band broaden as the QD approaches the surface, while those in the bulk band gap do not. However, such a simple model is less applicable when electronic coupling is weak and electron-nuclear coupling becomes important; instead, Marcus theory is a better starting point.

In the following, we first briefly review the electronic structure of semiconductor QDs and discuss how these artificial atoms may couple to form artificial molecules. This review is followed by the application of Newns-Anderson theory and electron transfer theories, depending on the strength of electronic coupling and electron-nuclear interaction. Finally, we use recent experimental results from our laboratory on the PbSe QDs/TiO₂(110) model system to demonstrate the feasibility of this conceptual framework.

Electronic Structure of Nanocrystals

Artificial Atoms.

The electronic structure of a QD is determined by both the constituent atoms and by the size and shape of the crystallite. If the crystallite is much larger than the lattice constant, then single-electron wave functions can be expressed as,

[1]

where 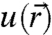is a function with the periodicity of the crystal lattice and 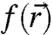is the envelope function that contains the dependence of the eigenstates on nanocrystal size and shape (12). Conveniently, 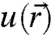is the same periodic function used to describe Bloch waves in the extended crystal. All information relevant for interfacial electronic coupling and charge transfer, such as eigen energy and probability density distribution, is contained within the envelope function 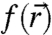. Under the simplest approximation, the envelope functions are solutions to the quantum mechanical particle-in-a-sphere problem and the effective mass approximation is invoked within the parabolic and isotropic band limit. The resulting atom-like single-electron (hole) eigenstates have well defined angular momentum and are labeled by the usual quantum numbers n = 1,2,3,… and ℓ = s,p,d,… with a subscript “e” (“h”) denoting an electron (hole) wave function.

The real electronic structure of a semiconductor nanocrystal is, of course, exceedingly more complex than the picture presented here. Accurate treatment must include a realistic description of the bulk band structure and nanocrystal boundary conditions (13–15). Real semiconductor nanocrystals are far from idealized spheres and have different shapes with various terminations of crystalline planes. Such heterogeneity is a salient feature distinguishing “artificial atoms” from real atoms. Despite the assortment of nonidealities, real nanocrystal eigenstates still possess principal and angular momentum quantum numbers of the envelope functions (16).

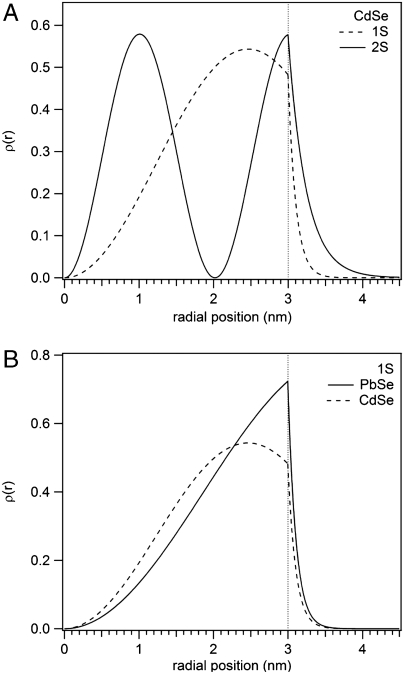
For the problem of interfacial electronic coupling and charge transfer, we care not only about the eigen energies but also about the wave functions. Fig. 2A shows the radial probability density distribution ρ(r) = 4πr²|ψ|² for the two lowest-energy S states of an idealized 3 nm radius CdSe QD (in an organic shell of ε = 2), calculated according to the method of Brus (17). There is substantially greater probability density outside of the QD for the higher energy 2S state than for the 1S state. This difference has the important consequence that (all other things being equal) electron transfer from “hot” electronic states is faster than that from the 1S state.

Fig. 2.

Radial probability density distributions ρ(r) = 4πr²|ψ|² for (A) the two lowest-energy S (ℓ = 0) eigenstates in an idealized 3 nm radius spherical CdSe nanocrystal and (B) the lowest-energy eigenstates in 3 nm radius CdSe and PbSe nanocrystals, calculated according to the method described by Brus (17). The discontinuity in the first derivative of the probability density at the nanocrystal surface arises from different effective masses of the electron inside and outside the nanocrystal core. The wave functions of higher-energy eigenstates extend farther beyond the nanocrystal surface, facilitating strong electronic coupling to neighboring nanocrystals or bulk semiconductor substrates.

Charge-carrier effective mass (m^∗) and dielectric constants (ϵ) are also important. For instance, CdSe has m^∗ = 0.11m_e and ε = 6.2 at optical frequencies, resulting in a bulk exciton Bohr radius of r_B ∼ 6 nm; the corresponding properties in PbSe are m^∗ = 0.04m_e and ε = 23.9, leading to r_B ∼ 46 nm. In Fig. 2B we see that the lighter electron in an idealized PbSe nanocrystal spends more time near the QD surface than in CdSe, resulting in larger wave function overlap with neighboring QDs or bulk semiconductor substrates. For charge carriers residing in the 1S states, the Coulomb attraction is E_C = 1.8q²/4πεε₀D, where D is the QD radius and the numerical constant 1.8 arises from integration of the 1S eigenfunctions. Continuing our comparison of CdSe and PbSe, we note that the Coulomb binding energies in PbSe nanocrystals (∼25–100 meV for 4–1 nm radius) are 1/4 of those in CdSe nanocrystals (∼100–400 meV for similar sizes). Consequently, it is not surprising that resonant energy transfer is common for excitons in cadmium salt QDs whereas exciton dissociation dominates in strongly coupled lead salt QDs (18, 19). Note that the motion of charge carriers in a QD is not strongly correlated because the kinetic energy imparted by quantum confinement is larger than the Coulomb binding energy (20).

Artificial Molecules and Solids.

For an assembly of QDs to be different than a simple collection of isolated QDs, there must be electronic interaction. The result is an artificial molecule. Consider two QDs with diameter D and at a small separation (d); the leaked out portions of the electron wave function is largely responsible for interQD electronic interaction. The most important parameter is the electronic exchange coupling energy (t) between neighboring QDs,

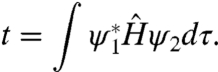[2]

In the tight binding approximation, artificial atom states split into a bonding and an antibonding molecular orbital, with energies approximately ± t with respect to the noninteracting atomic orbitals. This picture can be extended to larger artificial molecules and QD solids. However, one must be very cautious in overrelying on such a simple-minded picture, as two complications can greatly alter our view of artificial molecules.

The first complication is the presence of capping molecules on the QD surface. When the electronic states of the molecules are far from those of the QD, we can simply treat the intervening molecules as a dielectric. When the electronic states of the molecules are close in energy to those of the QDs, they can be viewed as electronic bridges. Electronic coupling between the QDs involves the mixing of the highest occupied molecular orbital and/or the lowest unoccupied molecular orbital of the bridges. As synthesized, QDs are usually capped with insulating molecules that lead to poor interQD electronic coupling. Replacing these insulating molecules with short and/or conjugated ones can significantly increase interQD electronic coupling, as revealed by both optical spectroscopy (21, 22) and electrical conductivity in the case of QD thin films (8, 9).

The second complication comes from the intrinsic heterogeneity. Real semiconductor nanocrystals are heterogeneous in size, shape, and crystalline planes exposed. This heterogeneity translates to local variations in electronic coupling and thus variations in the electronic structure of artificial molecules as observed in scanning tunneling microscopy/spectroscopy (23). The presence of intrinsic heterogeneity calls into questions how we should view the electronic structure of a QD solid. The conventional picture of band structures from crystalline solids is of limited use. Rather, we should learn from theories developed for disordered semiconductors (24), particularly the central concept of Anderson localization (25).

Electronic Coupling and Charge Transfer

Theoretical Framework.

Charge transport within colloidal QD films (8, 9) has typically been treated within the framework of disordered semiconductor theory (24), While the concepts of charge localization and site-to-site hopping play a central role in understanding electronic conduction in QD films, they are insufficient for describing charge transfer between a QD and a bulk semiconductor. The concepts for electronic coupling borrowed from chemisorption are directly applicable to QDs on semiconductor surfaces.

Despite the similarities between true atoms or molecules and QDs, there are a few differences that add richness to the problem. Most notable is the extent to which an electronic excitation in a QD is (or isn’t) solvated by the surrounding dielectric. Because of dielectric screening by the QD lattice and the ligand shell, reorganization energies for QD electron transfer reactions are likely an order of magnitude less than that in the corresponding molecular system. The smaller reorganization energy has the important consequence that the underlying assumptions of Marcus theory are more easily violated.

Electron transfer between a QD and a bulk semiconductor is in the nonadiabatic limit when a localized state on the QD is located in the band gap of the bulk semiconductor, or when the QD is physically separated from the bulk semiconductor surface by an insulating molecular linker. Nonadiabatic electron transfer within the weak electronic coupling limit is well described by theories attributed mainly to Marcus (26). When applied to electron transfer between a localized state and a delocalized continuum, the rate is given by the well-known formula (27):

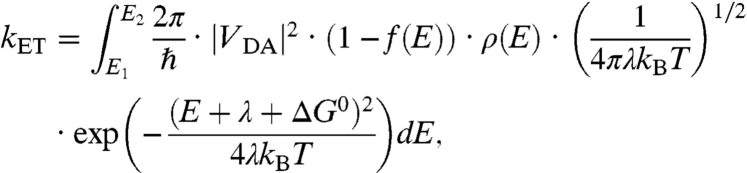[3]

where ΔG_o is the free energy change for the electron transfer process; λ is the reorganization energy (∼0.1–1 eV for ions and molecules in aqueous solutions) (28), which is the free energy cost if the system hypothetically changes from the equilibrium configuration for the donor to that of the acceptor without actual electron transfer; k_B is the Boltzmann constant, and T is temperature; ρ(E) is the density-of-states (DOS) of the acceptor; f(E) is the Fermi-Dirac distribution; and V_DA is the k-space integrated and energy-dependent electronic coupling strength. The integration is from the conduction band minimum to maximum.

When a QD interacts with bulk semiconductor surface directly (no capping molecules) or through very short or highly conducting linker, electronic coupling is strong and we reach the adiabatic region. Under this condition, the central hypothesis underlying Eq. 3 that thermally activated nuclear rearrangement is the rate-limiting step becomes invalid. Adiabatic electron transfer is best described as a time-dependent redistribution of charge on one continuous potential energy surface. The treatment of strong adsorbate-surface electronic interaction is best handled within the framework of chemisorption theory, which deals with the coupling of discrete atomic or molecular orbitals to electronic bands in solids. While density functional theory is most commonly used (29), we illustrate the problem using the simplest and physically transparent Newns-Anderson model (11). When a single adsorbate state |a〉 interacts with a substrate band |k〉, the discrete adsorbate DOS broadens into a Lorentzian line shape with width 2Δ,

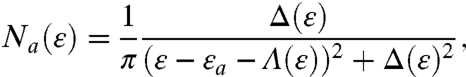[4]

where ε_a is the original energy of the adsorbate orbital; the width Δ(ε) is equivalent to a local projection of the bulk DOS onto the adsorbate and is determined by the strength of electronic coupling. The term Δ is related to the electronic exchange coupling energy (t) between two localized states, as defined in Eq. 2, through the summation for all k states. Interfacial electron transfer processes are discussed within three coupling regimes, depending on the relative magnitudes of Δ and λ (27, 30).

In the first regime Δ ≪ 2λ/π, Δ has little effect on the activation energy for charge transfer, which is determined almost entirely by λ and ΔG^o. This regime is the nonadiabatic limit. In the second (intermediate coupling) regime, k_BT < Δ < 2λ/π, and electron transfer occurs adiabatically with the activation energy lowered by Δ. Electron transfer is still a thermally activated process and depends on nuclear rearrangement, but the constraints on the charge transfer configuration are lifted to some extent. Finally, when Δ > 2λ/π, we have reached the strong-coupling regime and nuclear rearrangement plays little role in the charge transfer process. In this limit, the donor and acceptor states are no longer distinguishable. Charge transfer amounts to electronic dephasing between the adsorbate resonance and continuum states within the solid. This ultrafast process occurs on femtosecond time scales, with the electron lifetime in the adsorbate resonance governed by the Uncertainty Principle, τ ≈ ℏ/Δ.

Electronic Coupling and Reorganization Energy at QD/Semiconductor Interfaces.

As is clear from the above arguments, the relative magnitudes of λ vs. Δ determine the mechanism of interfacial electron transfer between QDs and the bulk semiconductor surface. Varying the length or structure of molecular spacers has been the most direct approach for controlling these relative magnitudes. Additionally, changing the solvent or matrix surrounding the QD could affect the magnitude of λ, though such solvatochromic effects in QDs are less dramatic than in molecular systems (31).

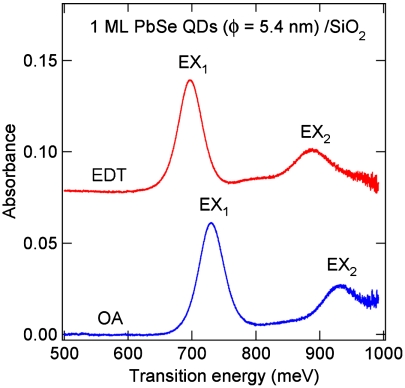
The interfacial electronic coupling energy Δ can be obtained from measurements in the energy or time domains. In principle, Δ can be directly determined from the broadening of valence electronic structure from ultraviolet photoemission spectroscopy (UPS) (32), but this is often not feasible because of the dominance of spectral width due to heterogeneity. Increased interQD electronic coupling strength has been inferred from a variety of other experimental observations, including the much increased electrical conductivity of QD films (8, 9, 18, 33–35), the broadening of the discrete QD levels in scanning tunneling spectroscopy (23, 36), and the red-shift in excitonic transition in optical absorption (18, 21, 22, 34). The latter is shown in Fig. 3 for one monolayer PbSe QDs adsorbed on native oxide terminated silicon. Replacing oleic acids with the shorter 1,2-ethanedithiols red-shifts the first and the second exciton transitions by 33 and 45 meV, respectively. The increased interQD electronic coupling leads to electronic band formation; as a result, the excitonic transitions in the band gap are red-shifted. Additional contributions to the red-shift are the increased local dielectric constant as the QDs are packed closer (31), and dipole-dipole coupling between neighboring nanocrystals (37).

Fig. 3.

Optical absorption spectra for one monolayer of 5.4 nm diameter PbSe QDs adsorbed on the native oxide terminated silicon surface. The QDs are capped with the long oleic acid molecules (blue) or shorter EDT.

Initial estimates of the QD/substrate interfacial coupling energy Δ can be obtained from measurements of nearest-neighbor coupling. Earlier work from our lab probed two-dimensional assemblies of PbSe nanocrystals (21). By observing the magnitude of the red-shift in the first optical transition frequency, we estimated nearest-neighbor coupling energies of |t|≈7–13 meV for PbSe QDs in the absence of capping molecules, but more recent experiments in our laboratory showed this number to be an overestimation as it neglected contributions from polarization effects and dipole-dipole coupling (38). Liljeroth et al. used scanning tunneling spectroscopy to study electronic coupling in hexagonally close-packed two-dimensional arrays of PbSe nanocrystals (23). The observed bandwidths of 50–150 meV correspond to nearest-neighbor coupling energy of |t|≈4–13 meV. For coupling between a nanocrystal and a bulk semiconductor surface, one might expect a similar exchange coupling energy between the adsorbate state (e.g., 1s_e state of a QD) and each k state in or near resonance. The summation over the substrate band structure necessarily makes Δ larger than |t|, by approximately one order of magnitude.

Reorganization energies, λ, in electron transfer involving QDs have been analyzed theoretically (31, 39–42) but experiments are scarce (43). The bulk semiconductor acceptor is expected to contribute little to the reorganization energy. The QD donor contribution can be separated into an inner-sphere component λ_i and outer-sphere components λ_o (44), λ = λ_i + λ_o. λ_i comes from electron-phonon coupling within the nanocrystal. In nonpolar semiconductors, such as Si, λi is mainly due to interaction with acoustic phonons through the deformation potential with a 1/D³ dependence on nanocrystal size (39). For polar semiconductors, coupling to optical phonons dominates through the more efficient Fröhlich interaction and λ_i also increases rapidly with decreasing QD size (40). For the addition of an extra charge to a QD at the lower size limit of D = 2 nm, λ_i has been estimated to be ∼12 meV for Si and ∼30 meV for CdSe (39, 40); these values are close to the phonon energies. The situation is completely different for an optically excited e-h pair. In this case, the partial compensation of the e-h pair substantially reduces reorganization energies, e.g., to < 1 meV for CdSe QDs (41).

The outer-sphere component λ_o comes from nuclear contributions to the dielectric response of the ligand shell and the solvent. A useful measure of nuclear vs. electronic contributions is the difference between the static and optical (high frequency) dielectric constants, ε_s and ε_op. One must be careful, though, when considering the dielectric response of the ligand shell. For highly polar capping molecules, ε_op and ε_s in the liquid state can be very different due to the freedom of movement of the dipoles in the fluid phase. This freedom is absent in the anchored state on the QD surface. Thus, instead of using ε_op and ε_s of pure molecules in the liquid state, we should use values for the backbone of the capping molecules in the solid state or in self-assembled monolayers. Because of the closeness of these values, we can conclude that the ligand shell contributes very little to the reorganization energy. In the simplest picture of adding (or removing) an electron to a QD embedded in a dielectric continuum, the outer-sphere reorganization energy is approximated by,

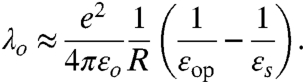[5]

More rigorous treatments have been carried out by Iwamatsu et al. (42) and Leatherdale and Bawendi (31). λ_o varies weakly with ligand shell thickness and core material, but is strongly dependent on size. For a CdSe core covered by a 1.0 nm thick alkanethiol shell (ε = 2.4) embedded in an organic matrix such as poly(3-hexylthiophene) (P3HT; ε_s = 6.5, ε_op = n² = 4.0), λ increases from 12 meV to 33 meV as D is decreased from 8 nm to 2 nm in diameter. For PbSe, λ varies between 14 meV and 35 meV over the same size range. The difference between core materials becomes more significant for larger QDs embedded in a strongly polar solvent such as water (ε_s = 80, ε_op = 1.7). For CdSe with a 1.0 nm thick shell in water, λ increases from ∼50 meV to 200 meV as D is decreased from 8 nm to 2 nm; with a PbSe core, λ varies between ∼80 meV and 20 meV over the same size range. If the surrounding medium is vacuum, λ_o vanishes.

The estimation of Δ and λ sheds light on the nature of electron transfer processes at QD/bulk semiconductor interfaces. Earlier in this section we estimated the interfacial coupling energy, in the absence of organic ligands or the presence of very short ligands, to be Δ≈10^1-2 meV, which is of the same order of magnitude as λ; thus all three coupling regimes are possible. In polar solvents with longer ligands, we expect to be in the weak-coupling limit where electron transfer is described well by Marcus theory; experiments have shown this to be indeed the case (43, 45). In contrast, when the QDs are in direct contact with the bulk semiconductor in inert gas or vacuum, the strong-coupling regime may be reached. In this limit, the electron transfer time constant or, more accurately speaking the charge redistribution time, is given by the Uncertainty Principle. More studies are needed to distinguish these different coupling regimes.

The PbSe QDs/TiO₂(110) Model System

To explore the nature of interfacial electron transfer at QD/bulk semiconductor interfaces in the strong-coupling limit, we investigated monolayer films of PbSe nanocrystals deposited on the single crystal rutile(110) surface of TiO₂. To enhance electronic coupling between neighboring nanocrystals and between the QDs and the substrate (i.e., maximize Δ), the PbSe films are chemically treated with either hydrazine (HYD) or 1,2-ethanedithiol (EDT). HYD strips away the ligands leaving a nominally bare QD, while EDT quantitatively substitutes for the insulating oleic acid ligands native to the PbSe QD surface (21, 46). The morphology of the QD film before and after ligand replacement is shown in Fig. 1.

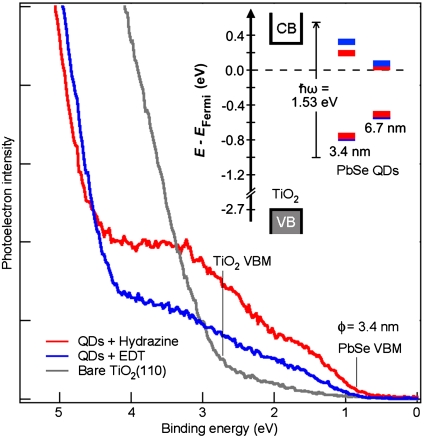
Fig. 4 shows UPS data for one monolayer of PbSe QDs (diameter = 3.4 nm) assembled on the TiO₂(110) surface. The bare TiO₂ spectrum (gray) shows the valence band maximum (VBM) at a binding energy (BE) of 2.7 ± 0.1 eV; the conduction band minimum (CBM) is at 0.3 ± 0.1 eV above the Fermi level. When the TiO₂ surface is covered with PbSe QDs (red or blue traces), the TiO₂ features are attenuated and photoemission from occupied electronic states of the QDs is detected. The spectra show clear distinctions of the valence DOS of PbSe from that of TiO₂, but the quantized electron states in the QDs are not resolved. Nevertheless, we obtain a critical piece of information: the alignment of the VBMs of QDs to that of the bulk semiconductor, as shown schematically in the inset for two QD sizes (diameter = 3.4 and 6.7 nm). With the relative alignment of valence levels, the alignment of unoccupied energy levels can be inferred from optical absorption (32, 46), because the exciton binding energy is negligible in PbSe. For the larger QDs (6.7 nm), the CBM of PbSe is below that of TiO₂ for both chemical treatments; for the smaller QDs (3.4 nm), the CBM is at or below that of TiO₂. Thus, electron transfer from photo-excited PbSe QDs to TiO₂ requires hot electrons.

Fig. 4.

UPS of one monolayer PbSe QDs (3.4 nm diameter) assembled on the TiO₂(110) surface. The oleic acid capping molecules have been removed by reaction with hydrazine (red) or replaced with EDT (blue). Also shown is a spectrum for clean TiO₂(110). Energy scale is referenced to the substrate Fermi level. Experimental details can be found in refs. 32 and 46.

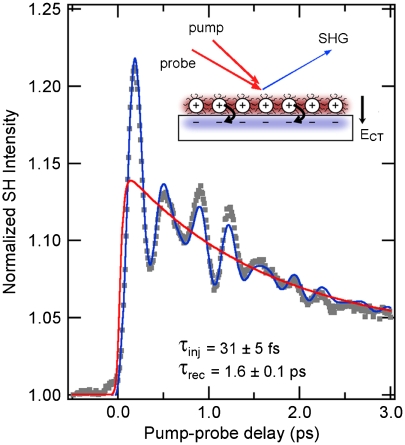
Unlike the energy-domain results above, time-domain experiments on interfacial electron transfer can provide a more reliable measure of interfacial electronic coupling (Δ), particularly in the strong-coupling limit when the Uncertainty Principle applies. We applied time-resolved surface second harmonic generation (TR-SHG) to follow the dynamics of interfacial electron transfer at the PbSe QDs/TiO₂(110) interface (Fig. 5) (46). The 1–2 monolayer QD films are photoexcited by a 50 fs laser pulse at 810 nm, then the SHG response of the system is probed at a variable time delay later. When electrons transfer across the PbSe/TiO₂ interface, an interfacial electric field is established in the surface-normal direction (E_CT, see inset to Fig. 5). Through a four-wave mixing process, the quasi-static field enhances the efficiency of nonlinear optical conversion—a process known as electric field-induced second harmonic (EFISH) generation (46). By monitoring the intensity of reflected second harmonic (405 nm) light, we are able to follow the buildup (electron transfer) and decay (diffusion into the TiO₂ bulk or recombination across the interface) of the electric field, E^CT. Conveniently, the EFISH signal ΔI^(2ω) is proportional to the number of charge separation events (Q^CT): ΔI^(2ω) ∝ E^CT ∝ Q^CT, so that dynamics of interfacial charge separation may be extracted directly from the time-domain signal. Interestingly, the TR-SHG response also contains oscillatory components, which are due to coherent excitation of phonon modes. The dominant coherent phonon mode here is the excitation of a surface-specific optical phonon mode (2.9 THz) on TiO₂(110) due to the injection of hot electrons from PbSe QDs. In addition, ultrafast hot carrier relaxation within photo-excited PbSe QDs also induces the excitation of a coherent phonon mode (2.1 THz) of the two-dimensional coupled QDs and bulk-like PbSe optical phonon mode (4.0 THz).

Fig. 5.

Time-resolved SHG (dots) of the TiO₂ surface coated with 1.5 monolayers of EDT-treated 6.7 nm PbSe nanocrystals probed with p-polarized light with the electric field of the optical wave in the plane of incidence. The sample temperature was 12 K. Both pump and probe were 50 fs pulses of 810 nm light. The intensity of reflected second harmonic light at 405 nm was recorded as a function of time delay between the pump and probe pulses. The blue curve shows a least-squares fit incorporating electron injection and recombination (red) and three coherent phonon modes. Adapted from Tisdale et al., ref. 46.

By fitting the TR-SHG results to a model function that incorporates electron injection, charge recombination, and three coherent phonon modes, we are able to separate the oscillatory part of the signal from the underlying charge separation dynamics (red trace in Fig. 5). Our fitting procedure reveals an electron injection time constant of τ_inj = 31 ± 5 fs and a charge migration/recombination time constant of τ_rec = 1.6 ± 0.1 ps (46). Note that the measurement presented here does not provide quantitative information on the percentage of hot electron injection vs. relaxation. We are currently investigating this issue in our laboratory using time-resolved photoemission techniques.

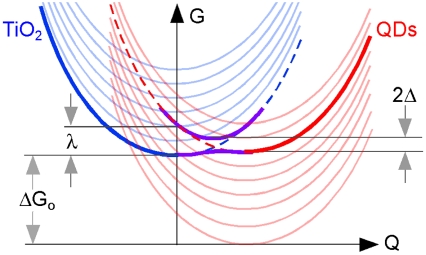
In the strong-coupling limit, the ultrafast electron injection time observed here corresponds to an electronic coupling energy of Δ≈20 meV, which is in good agreement with our earlier estimations. Similar (or faster) electron injection time was observed for samples with HYD treatment. Importantly, we observe that electron injection is ultrafast at all temperatures from 300 K down to 12 K; this is further evidence that we are indeed in the strong-coupling regime. Based on the estimated reorganization energy (λ ≤ 100 meV) and electronic coupling energy (Δ≈20 meV), we can construct a qualitative free energy diagram, Fig. 6. The free energy change (ΔG_o) is not relevant as transfer of a photo-excited hot electron (one of the red curves) is always in resonance with one of the continuum states (blue curves) within the TiO₂ conduction band. The purple curves are adiabatic surfaces resulting from avoided crossing, shown here for one of the excited PbSe QD states and that corresponding to the bottom of the TiO₂ conduction band. The closeness of Δ and λ gives rise to adiabatic curves with negligible barrier, supporting the argument for the strong-coupling limit.

Fig. 6.

Free energy as a function of configuration coordinate (Q) for electron transfer from one of the QD exited states (red) to a delocalized conduction band (blue). The dotted (crossing) curves are parabolic diabatic free energy surfaces in the weak-coupling limit. The solid anticrossing curves (purple) are adiabatic free energy surfaces of the coupled donor-acceptor system. Δ is electronic coupling strength and λ the reorganization energy.

Remarks

We attempt to summarize our initial understanding on the adsorption and electron transfer at QDs and bulk semiconductor interfaces. Semiconductor nano-materials in general and QDs in particular are being explored for a wide range of electronic and optoelectronic applications; these applications often require interfacing semiconductor nanocrystals to bulk materials. From a fundamental perspective, the adsorption of QDs on a bulk semiconductor surface represents an ideal model for addressing the electronic coupling between zero dimensions and three dimensions. While we attempt to establish a conceptual framework by borrowing well established theories of chemisorption and interfacial electron transfer, these efforts are clearly not sufficient. A recent experiment revealed the rich many body physics due to coherent electronic interactions between a QD and a bulk continuum (47). On the experimental side, the complexity of the problem necessitates quantitative tools and rigorous methodologies from the field of surface science. We must probe, understand, and control not only the surfaces of semiconductor nanocrystals, but also their interfaces to bulk solid materials. It is our belief that both the importance and the richness of the problem will inspire much increased experimental and theoretical efforts in this new research direction in surface science.