Abstract
After injections of indocyanine green into the pulmonary artery or left ventricle of anesthetized dogs, indicator-dilution curves were recorded, via identical short sampling systems, from the root of the aorta, the lower thoracic aorta, and the bifurcation of the aorta. The distributions of transit times (transport functions) between each of the three pairs of sampling sites were determined in terms of a mathematical model using the whole of each recorded curve. The accuracy of each transport function was demonstrated by convoluting it with the upstream dilution curve to produce a theoretical downstream dilution curve closely matching the recorded downstream dilution curve. Linearity and stationarity of the aortic system were then tested by comparing the convolution of the transport functions of the upper and lower segments of the aorta with the transport function from aortic root to bifurcation. The results indicate that it is reasonable to apply the superposition principle, as is assumed when calculating flows or mean transit times by indicator-dilution methods, and that cardiac fluctuations in flow produce relatively little error.
Keywords: blood flow, indicator dilution, peripheral blood vessels, cardiac output, dye curve theory, circulation model, circulatory transport, circulatory-transport functions
THE CLASSICAL indicator-dilution methods for the measurement of blood flow and mean transit times in the circulatory system depend on the applicability of Duhamel's principle of superposition (15, 20). For this, the system must be stationary (constant flow rate) and linear (as defined by González-Fernández) (12). Since circulatory flow is continuously varying, and therefore not stationary, it has been difficult to show that the system is linear.
In order to test for linearity, steady flow is needed. Unfortunately, large spontaneous variations in cardiac output and in regional flow occur from minute to minute, and slow cyclic changes in flow are often superimposed on the rhythmic changes due to respiration and cardiac contraction. It is obvious that cardiac cyclic variations are unavoidable but, since these are of relatively high frequency, they might have only the effect of a little noise in the system. In order to avoid the slow changes in flow, experiments were designed so that linearity could be tested on data acquired over periods of 20–40 sec.
In the work reported in this paper, dye-dilution curves were recorded simultaneously from three sampling sites: the aorta just above the valve (A), the middle of the thoracic aorta (B), and the bifurcation of the aorta (C). The transport function (19), hAB(t), which is the distribution of transit times, the frequency function of transit times (25), or the impulse response of the vascular segment between sampling sites A and B, was computed from the curves recorded from A and B by previously established methods (1). Similarly, the transport functions hBC(t) and hAC(t) were also calculated. Because these three transport functions existed simultaneously and because the two short circulatory segments AB and BC make up the larger segment AC, if the aortic system is linear and stationary then the convolution of process hBC(t) with process hAB(t) should be exactly the same as hAC(t). That is,
| (1a) |
or
| (1b) |
Equation 1, the convolution integral, states that the convolution of hAB(t) on hBC(t) results in hAC(t). λ is a variable used only in the performance of the integration. Therefore, close similarity of the experimentally calculated hAC(t) with the distribution function obtained by the convolution of its parts would permit the conclusions that 1) the aortic system is linear and functionally stationary for short periods, and 2) the experimental methods for obtaining the transport functions were adequate.
Definitions
The general terminology is used in accordance with the definitions of Wood (23). Certain other terms must also be defined.
A = site of catheter tip in aortic arch just above the aortic valve
B = site of catheter tip in aorta near the body of the 12th thoracic vertebra
C = site of catheter tip in aorta near the bifurcation
A(t), B(t), and C(t) = indicator concentration-time curves in arterial bloodstream at A, B, and C
h(t) = transport function (frequency distribution of transit times) between any two points; hAB(t) is the transport function between A and B
h′(t) = an approximation to h(t) defined in terms of a particular mathematical model, the lagged normal density curve
hs(t) = transport function of sampling systems, which were identical
* = denotes the process of convolution integration as in equation 1
As(t), Bs(t), and Cs(t) = indicator concentration-time curves recorded from A, B, and C after distortion by sampling systems; no extrapolation or adjustment of these curves was made
= computed approximation to Bs(t) by
= computed approximation to Cs(t) by
= computed approximation to Cs(t) by
= computed approximation to hAC(t) by
Mathematical approach to the experiment
The basic problems of such an experiment involve not only the linearity and stationarity of the system but also, because flow is unsteady, errors due to the use of time-averaged sampling of the flowing bloodstream instead of the desired flow-proportional sampling (12). Crude tests of linearity have been made by injecting, in sequence, boluses of different amounts of dye and comparing the relative amplitudes of the resultant curves (7, 16). Precision could not be obtained because mean flow changed in the period between injections.
The summation of two input functions, whose individual output responses are known, should produce an output function of predictable form. This similarly crude test was made by injecting two boluses within a few seconds and fitting the downstream curve with the sum of two curves, each of which was given by a mathematical model of the expected response to a single injection (2). The results were encouraging but not decisive.
Nonstationarity obviated effective testing for linearity in the above experiments and in previous studies on anesthetized dogs (4) but not in a set of experiments on humans in which the spontaneous fluctuations in flow in the femoral artery were suppressed by intra-arterial infusion of a vasodilator (adenosine triphosphate) (1, 6). The present experiment was designed to acquire test data over periods long enough to define the transport function, and long relative to the cardiac cycle, but short relative to the slow, spontaneous variations in flow. The length of the respiratory cycle was shortened but unfortunately could not be made very short relative to the passage time of aortic transport functions, and thus it remains as a significant source of variation.
It has been suggested that the inability to use flow-proportional sampling is not too serious because areas of dye curves obtained by time-averaged (continuous) sampling at the pulmonary artery and the aortic root were not significantly different from each other or from areas of curves obtained simultaneously by sampling from the relatively steadily flowing femoral artery (4). This conclusion is reasonable when the dye curves are broad and the concentration at the sampling points does not change too rapidly during each cardiac cycle (3), but it remains as a source of error in the present experiment.
The requirement that indicator be dispersed in the bloodstream in proportion to the flow in each portion of the stream is certainly not met at the site of a forceful injection which tends to produce approximately cross-sectional labeling. An assumption that any injection can be an impulse function (with either flow labeling or cross-sectional labeling) is quite wrong. Probably, the redistribution of the indicator, which occurs during passage downstream, produces a more appropriate plasma label. On this basis, sampling at the input to the circulatory segment of interest was deemed appropriate and obviates the need to make an assumption as to the form of the injection.
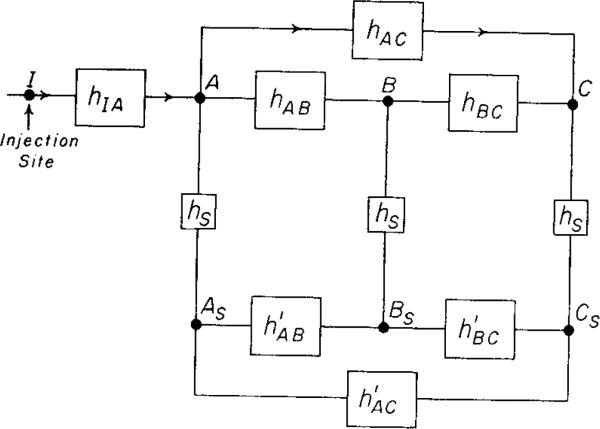
In the present experiment, diagrammed in Fig. 1, the three transport functions, hAB(t), hBC(t), and hAC(t), must be estimated before linearity and stationarity can be tested by means of equation 1. The recorded dye-dilution curves do not represent the actual concentration-time curves at the catheter tips at points A, B, and C in the vascular system because of distortion by the sampling systems. By using identical sampling systems and sampling flow rates, the responses to a step input (and presumably the transport functions, hs(t)) of the three sampling-recording systems were made identical. On the assumptions that the sampling was volume averaged and that the system ABC was linear and stationary, the transport functions , , and should be identical to hAB(t), hBC(t), and hAC(t), respectively. The mathematical basis for this statement was given previously (1). The problem is then to determine the h′(t)'s correctly. The method used here (1) is empirical and is only useful when the transport function is a simple distribution function.
FIG. 1.
Block diagram of the experiment. The bolus of injectate introduced at I (pulmonary artery or left ventricle) is somewhat dispersed in the vascular system by the process hIA(t) before it reaches the three aortic sampling sites A, B, and C. The sampling system transport functions, hs(t), were identical, so that the transport functions , , or between pairs of the simultaneously recorded curves As, B , and Cs, would be the same as the transport functions hAB, hBC, or hAC between the corresponding pairs of the actual arterial curves.
When the transport functions and have been obtained, then a transport function for the whole system AC may be computed by convolution of the two segmental transport functions:
| (2) |
If is the same as , then it is reasonable to suggest that all of the above assumptions were not seriously invalidated and that, for practical purposes, flow through the segment AC of the vascular system may be considered as linear and stationary in spite of the presence of pulsatile flow, elastic vessels, and a nonhomogeneous fluid.
METHODS
The experiments were performed on four dogs, weighing 16.8, 18.0, 22.5, and 25.5 kg, anesthetized with pentobarbital (25 mg/kg initially, plus supplemental doses), and lying in the lateral position (left or right) on a padded fluoroscopic table. They were ventilated with a Bird respirator (Bird Oxygen Breathing Equipment, Inc., Palm Springs, Calif.) at rates of 35–40 breaths/min. The cardiac output of each dog was changed for parts of each experiment by constant-rate infusions of solutions of either angiotensin (2.5–6.1 μg/min) or adenosine tri-phosphate (0.5–1.24 mg/min) for 20–40 min into the superior vena cava or by repeated intravenous injections of atropine sulfate (1.3 mg).
For the injection of dye, 100-cm, 5 F, regular catheters (internal diameter, 1.0 mm; volume, 0.7 ml) were introduced into the pulmonary artery and left ventricle via percutaneous needle punctures of the right jugular vein and right femoral artery, respectively. In two animals, similar catheters were also introduced into the left atrium via transseptal puncture. Indocyanine green (11) (1.25 mg/ml solution) (Hynson, Westcott & Dunning, Baltimore) was injected from any of these catheters, previously filled with dye solution, by means of a pneumatically driven syringe (13) whose travel was recorded via a linear slide-wire potentiometer mechanically linked to it. Single-slug dye injections (duration, 0.46 sec) or double injections consisting of two-slug injections 1–4 set apart were made. The wide range of cardiac outputs and the variety of forms of injection and of injection sites provided a wide range of shapes of recorded dye-dilution curves, which were essential to this study.
Dye-dilution curves were recorded simultaneously from the three sites in the aorta via three identical sampling-recording systems. Each consisted of 19 cm of polyethylene tubing (Intramedic, PE-160) connected directly with the steel tubing of a densitometer (10) (XC100A, Waters Corp., Rochester, Minn.) so that there was a total volume of 0.24 ml from the tip of the sampling tubing to and including the densitometer lumen. Harvard constant-rate sampling devices (Harvard Apparatus Co., Dover, Mass.) were used to obtain steady flow rates of 25 ml/min, resulting in sampling-system mean transit times of 0.58 sec. One of these sampling catheters was placed in the ascending aorta via a cutdown on the right carotid artery, the second was introduced into the aorta at about the level of the diaphragm by percutaneous aortic puncture at the level of the body of the 12th thoracic vertebra, and the third was placed at the aortic bifurcation via percutaneous introduction into the left femoral artery. The response of each of the sampling-recording systems to a step input was recorded four to six times, and the appearance times and mean transit times were found to differ in a random fashion but not by more than 0.04 and 0.02 sec, respectively.
The three densitometers were calibrated twice for each experiment by means of dye solutions, 0, 5.0, 9.9, 14.8, and 19.7 mg/liter, in blood taken at the beginning of the experiment before dye was injected and in blood drawn at the end of the experiment and therefore containing some background dye. The densitometers’ output signals, recorded on analog magnetic tape, were converted to digital tape (24) and then converted to calibrated dye-dilution curves by a digital computer adaptation of the methods previously described (4, 5, 10). Zero time for dye curves was obtained by computer recognition of the early portion of the injection-syringe travel and was identical for all three curves. The dye-curve data, sampled 139 times/set, were smoothed by a 15-point moving average and every 28th point was selected (sampling period, 0.201 sec) for preserving the data on IBM punched cards.
Analysis
The transport functions between each of the sampling sites were estimated empirically in terms of a four-parameter equation, the lagged normal density curve (2, 6), which was modified slightly for this study:
| (3) |
in which σ and tc are the standard deviation and median of a random dispersion process, τ is the time constant of a superimposed washout or lag process, λ is a dummy variable of integration, and K is a gain factor which is ordinarily 1.0 when no indicator is lost in the circulatory segment under study The distribution of transit times was modified from that given by this equation by approximating the middle portion of the rising slope of the distribution function with a straight line which was then extrapolated to the base line. These new distribution functions were found to describe the experimental data better, and their representation in terms of a velocity profile is more realistic because the shortest transit times given by the lagged normal density curve would be found only with unrealistically high velocities relative to the mean velocity.
Details of the method used to estimate the transport functions have been previously presented (1) and may be summarized by saying that the parameters of h′(t) were adjusted until an accurately descriptive h′(t) was found. For example, when Bs′(t), obtained by the convolution of and As(t), was very closely matched to Bs(t), then was accepted as a best estimate of hAB(t). For each such transport function, trials were repeated up to 75 times or until the coefficient of variation between the observed and computed downstream curves was less than 0.01.
When estimates of the three simultaneous transport functions had been obtained, a test for mathematical linearity was applied by comparing (from the convolution of and as in equation 2) with . This was done graphically (Fig. 2, right panel) and by finding the coefficient of variation between the curves. Comparisons were also made between the parameters of and hAC(t). The parameters (σ, τ, and tc) of can be computed from the parameters of and by using the known relationships between the moments of two functions convoluted together (9) and the facts that, in terms of the parameters of the model, the first moment (mean transit time), t̄ = τ + tc, the second moment about t̄ is variance and equals σ2 + τ2, and the third moment is given by 2τ3. Thus:
| (4a) |
| (4b) |
| (4c) |
FIG. 2.
Aortic transport functions. Left panels: recorded curves As, Bs, and Cs are shown by the continuous lines. (triangles) (the asterisk denotes the process of convolution); (circles); and (plus signs). Right panels: convolution of the transport functions hAB and hBC should be the same as hAC if the whole system is linear. The test is only as good as the weakest of the representations of hAB by , of hBC by , and of hAC by . However, the result that (plus signs) is similar to is strong evidence that the system is linear and stationary.
The fourth moment, 3σ4 + 6σ2τ2 + 9τ4, and the higher moments are not needed for the calculation. The parameters may be calculated directly from the moments:
| (4d) |
| (4e) |
| (4f) |
These equations are not quite exact because of the modification of the model described above, which caused slight (less than 1%) increases in the skewness and in the mean transit time. If the three parameters of were the same as those of there would be little doubt that the requirements for superposition were fulfilled but, in view of the several sources of deviations from stationarity alone—for example, pulsatile flow and volume—such an excellent result is unlikely.
RESULTS
A total of 70 sets of three simultaneously recorded curves were obtained in the four dogs at a variety of heart rates and flows. Two-thirds of the injections were single and one-third were double. In 54 sets (162 dye curves), all three of the coefficients of variation between the recorded downstream curve and the convoluted curve fitted to it were less than 0.09. The other 16 sets were not tested further because linearity could not be tested unless all three of each set of transport functions were determined accurately. Among the 16 rejected sets, actually only 17 of the 48 individual transport functions gave poor fits. There was no apparent influence of the type of injection on the accuracy with which the transport functions could be determined, and therefore all the results have been lumped together. For the same reason, the results from all four dogs were combined.
Figures 2 and 3 illustrate virtually the whole experiment. The whole of each recorded curve, including the recirculation portion, was used in the computation. Bs′(t), Cs′(t), and Cs″(t) were calculated at 0.2-sec intervals by means of the convolution integral, and they conform to the recorded curves very closely, indicating that , , and provide good descriptions of the transport functions. The convolution of and is and is very similar to .
FIG. 3.
Aortic transport functions (double injection into pulmonary artery). The convolution of the estimated transport functions, , results in a theoretical curve, (plus signs, right panel) which is similar to the experimental estimate of the transport function between the aortic arch and the bifurcation of the aorta.
The curves in the upper left panel of Fig. 2 were recorded after injection of dye into the pulmonary artery at a time when no drugs were being infused. The coefficients of variation between Bs′(t) and Bs(t), between Cs′(t) and Cs(t), and between Cs″(t) and Cs(t) were 0.036, 0.021, and 0.034, respectively. The transport function parameters (equation 3) σ, τ, and tc, were, respectively, 0.19, 0.35, and 0.99 for ; 0.61, 0.35, and 1.81 for ; and 0.50, 0.96, and 2.79 for . The coefficient of variation between and was 0.26. The curves in the lower left panel of Fig. 2 were recorded from another dog after injection into the left ventricle during a period of constant-rate infusion of adenosine triphosphate (1.24 mg/min) into the superior vena cava. The transport function parameters σ, τ, and tc were 0.04, 0.51, and 1.57 for ; 0.33, 0.89, and 2.10 for ; and 0.32, 0.89, and 3.97 for . The coefficients of variation were 0.050 between Bs′(t) and Bs(t), 0.038 between Cs′(t) and Cs(t), and 0.060 between Cs″(t) and Cs(t). The coefficient of variation between and was 0.14.
Figure 3 shows that the same analysis can be applied to dye-dilution curves of abnormal form. These three curves were recorded simultaneously after a double injection of dye (1.22 mg at t = 5.2 sec, 1.31 mg at t = 8.5 sec) into the pulmonary artery during the control state. The parameters σ, τ, and tc of the transport functions were 0.23, 0.35, and 1.17 for , 0.49, 0.65, and 2.07 for , and 0.35, 1.03, and 3.28 for . The coefficients of variation were 0.024, 0.038, and 0.027 for Bs(t) and Bs′(t), Cs′(t) and Cs(t), and Cs″(t) and Cs(t), respectively. The coefficient of variation for and was 0.42, which is worse than the average goodness of fit.
For the 54 sets of curves the mean coeficient of variation between the approximating curve and the recorded curve (Bs′(t) and Bs(t)) was 0.0380 (N = 162, sem = 0.0014). The mean coefficient of variation between and was 0.366 (N = 54, sem = 0.037).
Comparison of with hAC may be made in terms of the various parameters of their shapes, including the moments, and also by examining the adequacy of to describe the transport function of the aorta from root to bifurcation.
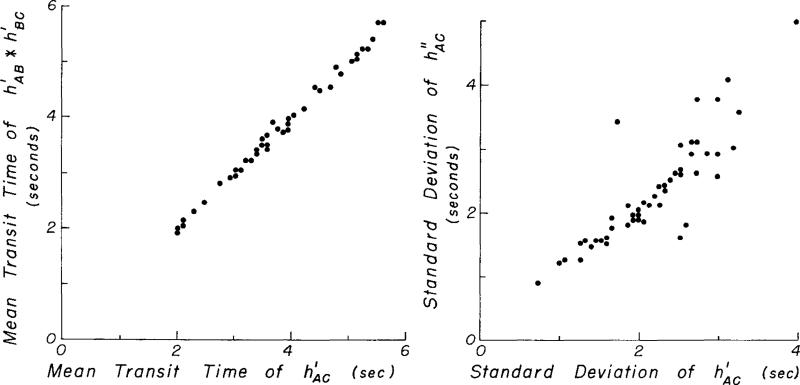
A comparison of the first two moments of and is shown in Fig. 4. The ratios of mean transit times, t̄, and of the standard deviations, , of and are given in Table 1.
FIG. 4.
Comparison of mean transit time and standard deviation of theoretical and observed aortic transport functions. The equation for the data in the left panel is (N = 54, r = 0.997) and for the right panel is (N = 54, r = 0.87), in which π2 is the variance and π21/2 is the standard deviation. (One dot represents more than one data point on these plots when the points coincide.)
TABLE 1.
Comparison of parameters of and
| Parameter* | Ratio† ± sd |
|
|---|---|---|
| Coef <0.09 (N = 54) | Coef <0.06 (N = 40) | |
| t̄ | 1.006 ± .019 | 1.005 ± .016 |
| π 2 1/2 | 1.030 ± .174 | 1.015 ± .119 |
| σ | 1.99 ± 1.43 | 1.69 ± 1.23 |
| τ | .988 ± .270 | .988 ± .241 |
| tc | 1.001 ± .079 | 1.004 ± .062 |
t̄ and π21/2 were calculated from the moments of h(t); σ, τ, and tc were calculated by equations 4a, b, and c.
Ratio = (parameter of )/(same parameter of ).
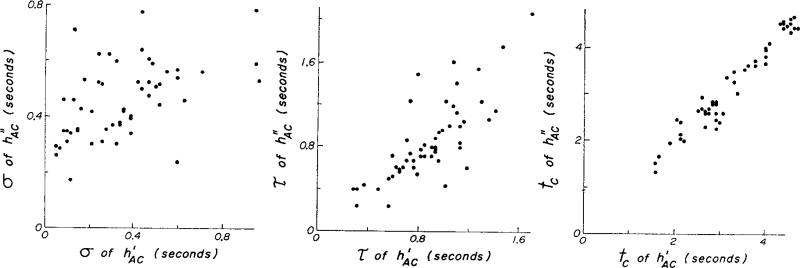
Comparison was made of the parameters of and which define their shape in terms of a lagged normal density curve. For these are calculated by equations 4a, b, and c. Figure 5 and Table 1 show that there is scatter around the line of identity but not a significant difference from it. When calculated by means of equations 4d, e, and f, τ and tc were slightly smaller and σ was larger, principally because of slight underestimation of the higher moments. The calculation of σ is particularly subject to overestimation because of these errors. This problem is reduced by prolonging the exponential tail of the transport functions instead of truncating the curve when an ordinate value of 1% of the peak is reached. It was also apparent, as in Figs. 2 and 3, that was slightly but consistently a little broader than , as suggested by (Fig. 4 and Table 1).
FIG. 5.
Comparison of the parameters of with those of . Regression equations for 54 sets are σh″ = 0.25 + 0.58 σh′ (sd = 0.16); τh″ = –0.24 + 1.26 τh′ (sd = 0.21); and tch″ = –0.07 + 1.02 tch″ (sd = 0.21).
Because the comparison of with is only pertinent when , , and are good representations of hAB, hBC, and hAC, it is inappropriate to make the comparison unless h′ has been determined accurately. For this reason, and were compared only when Bs′, Cs′, and Cs″ had coefficients of variation with Bs, and Cs, respectively, that were less than 0.09. If only those transport functions whose convolution with an upstream curve resulted in computed downstream curve having a coefficient of variation less than 0.06 when compared with the recorded downstream curve are considered, then and are more similar. For the 40 sets of curves in which all three transport functions fulfilled this criterion, the coefficients of variation between and averaged 0.30 ± 0.030. The relationships between the moment and the parameters of and were also closer (Table 1). These selected data are more useful in testing for linearity and give better evidence of it.
From the practical point of view, a good test of is whether or not it describes the circulatory transport function—that is, if , how close is Cs‴ to Cs. This is shown in Fig. 6 for two of the same curves shown in Figs. 2 and 3. The coeficients of variation for Cs‴ and Cs were 0.0390 and 0.0385 in the upper and lower panels, respectively, and were similar to those found for the 54 sets of curves (mean = 0.0438, se = 0.0030). The slight effect of too much dispersion in is barely perceptible, illustrating that this test is not quite so sensitive as the direct comparison of and (right panels of Figs. 2 and 3).
FIG. 6.
Comparison of convolution of upstream curve with theoretical and observed transport functions. The curves are those shown in Figs. 2 (lower) and 3. The upstream curve As was convoluted with both the theoretical () and observed () transport functions, resulting in two theoretical downstream curves (the X's and O's, respectively) which can be compared with the recorded downstream curve, Cs.
These comparisons indicate that , produced by the convolution of the two segmental transport functions and is similar to and, therefore, that the system is approximately linear and stationary during the recording of each set of curves.
Transport in the aorta
The transport functions for these segments of the aorta provide specific information concerning the distributions of transit times through the aorta while the cardiac outputs ranged from 1 to 4 liters/min.
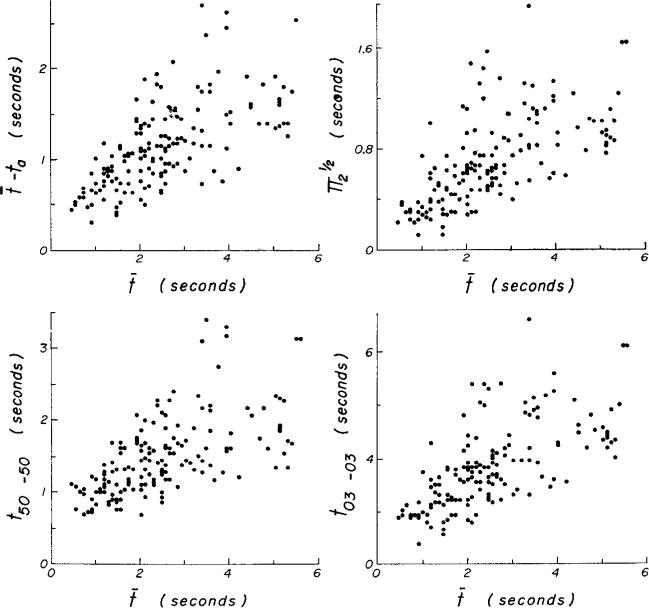
The dispersion and skewness of these transport functions can provide approximate descriptions of the velocity profile in the aorta over this range of flows. Of course, the description is an average for each observation (the period of recording) and tells nothing of the changes in profile within each cardiac cycle. The data indicate that the profile is fairly constant and is not influenced by the flow rate. Figure 7 illustrates certain time intervals which can be used as estimates of spread of indicator transit times. t50–50 and t03–03 are the times between points on the rising and descending portions of the curve of h(t) at values of 50 and 3%, respectively, of the peak values. ta, is the shortest transit time, actually defined as the first time the ordinate value reached 3% of the peak; is the standard deviation. These parameters are all related linearly to each other and with less variation than they are to the mean transit time, t̄.
FIG. 7.
Parameters of spread of transport function. Various parameters of an average aortic transport function are shown. t03–03 may be considered the passage time of the curve although it is slightly shorter than the maximal measurable passage time.
Approximately linear relationships of t̄ – ta, , t50–50, and t03–03 to t̄ are shown in Fig. 8. The equations for 162 curves are: t̄ – ta = 0.21 + 0.38 t̄ (sd = 0.71, r = 0.66); t̄ (sd = 0.71, r = 0.64); t50–50 = 0.45 + 0.42 t̄ (sd = 0.77, r = 0.60); t03–03 = 0.60 + 1.20 t̄ (sd = 1.05, r = 0.66). The ratios ± sd are: (t̄ – ta)/t̄ = 0.49 ± 0.17; ; t50–50/t̄ = 0.70 ± 0.31; t03–03/t̄ = 1.63 ± 0.64. These are all essentially estimates of spread and therefore are closely related to each other. They do not express skewness or kurtosis. The ratio of the interval from the mean transit time to the tail of the curve to the interval from the beginning of the curve to t̄ does express skewness well. The ratio is (t03–03 + ta – t̄)/(t̄ – ta) = 1.01 + 0.98β1 (sd = 0.19, r = 0.82); β1 is the skewness and equals . As expected theoretically, the ratio approaches unity as the transport function becomes symmetric (as β1 → 0). Because the shapes of the transport functions are defined by the three parameters of the model, the third and fourth moments are closely related; the kurtosis β2 = π4/π22 = 2.17 + 2.16 β1 (sd = 0.13, r = 0.98). All moments higher than the third can be expressed in terms of the lower moments.
FIG. 8.
Effect of mean transit time on temporal dispersion of indicator in canine aorta.
DISCUSSION
It is not surprising that linearity might be demonstrated in a stationary fluid system from which there is neither loss nor gain of fluid or indicator. This is most obvious when indicator is mixed into a specific volume of medium. It is still obvious when indicator is introduced into a constant-flow system. However, if the system is not stationary, then linearity ceases to be obvious and tests for it become experimentally and analytically difficult. The present experiment does not entirely eliminate the difficulty. The effect of spontaneous variations in flow, which are usually slow, is reduced by obtaining the data over short periods. The respiratory effects, which may cause 30–50% variation (17), are minimized by the rapid ventilation rates. The pulsations in flow with cardiac contraction are unavoidable. The pulsations in pressure result in variations in aortic diameter, which are certainly somewhat nonlinear (21) and produce a very complex flow profile. However, as Zierler (25) has said, the violation of stationarity may be negligible if the phasic variation in flow (and in the distribution of transit times) fluctuates about some constant value with a period that is brief compared to the period between the shortest and longest transit times. Zierler's prediction is more or less borne out even by this study, in which the periods of flow fluctuation were not brief—cardiac cycles lasted up to 25% of the passage time of the transport function and respiratory cycles, up to 80%.
Because of the pentobarbital anesthesia and the periodic administration of atropine intravenously, the dogs’ heart rates were high (130–210 beats/min). Mean transit times as short as 0.72 sec were observed for the segment between the aortic arch (A) and the aorta at the diaphragm (B) (Fig. 8) but for those transport functions having t̄ < 1.0 sec, the passage times (from appearance time to slowest transit time, approximately the same as t03–03) were 1.8–2.4 sec. For example, the passage time of in the upper right panel of Fig. 2 was 2.5 sec, and for it was 4.8 sec while the heart rate was 160/min. Because the shortest passage times encompass only 4–8 cardiac cycles, some doubt must be retained as to the validity of experimental results obtained during the highest flow rates in the smaller dogs. With slower flows, in larger dogs, and between sampling sites B and C, the mean transit times t̄ were 1.5–3.3 sec while the passage times t03–03 were 1.7–5.7 sec, encompassing 4–20 cardiac cycles; here cardiac cyclic variation in flow is more justifiably regarded as noise. The greatest source of error is undoubtedly the flow variation with respiration, which can produce up to 40% error in t̄, in curve area, and in shape (3).
The comparison of the cardiac frequency with passage time is the most critical approach and is an overly severe one. It is more appropriate to consider the number of cardiac cycles occurring during the passage time in the primary portion of the recorded dye-dilution curve—that is, the interval from appearance time to a time when a line extrapolated exponentially from the downslope of the recorded curve approaches the base line. During the passage time for the aortic root curves there were 22–85 pulse beats, while during the passage time for curves recorded at the bifurcation of the aorta there were 30–100 beats. Because the transport functions are obtained from pairs of these relatively smooth recorded curves, the noise due to lack of stationarity has less effect on the transport function.
In this study, the transport functions h(t) have been defined in terms of a specific four-parameter model, the lagged normal density curve. In general, it may be stated that arterial transport functions can be defined in terms of the zeroth to third moment—the gain, the mean transit time, the variance, and the skewness—and it is not likely that the higher moments contribute much useful information. With the lagged normal density curve (equation 3) as the transport function, the gain K, which is the area of the curve, should be close to 1.0, and the higher moments can be defined in terms of σ, τ, and tc (see Analysis under METHODS). There is nothing unique about the lagged normal density curve, and many four-parameter models should serve equally well as the transport function. Some of these have been reviewed recently (2). Since any transport function model that produces a correct result (produces a Bs′ or a Cs′ that closely matches Bs or Cs) is a suitable model, it becomes appropriate to use one that is easily handled. The gamma variate (22) or the random walk (18) equations should be equally useful but, because of our familiarity with the effects of varying each of the parameters, we used the lagged normal density curve in this study. It is most desirable to have a method of obtaining the transport functions in a manner independent of any model. Such a generalized approach using Fourier transforms is now being employed (8).
The question of linearity and the applicability of superposition cannot be completely settled because and were not identical. However, the data certainly indicate that and are similar to each other and suggest that both should be similar to hAC, the actual arterial transport function. Since there is no way of knowing exactly what the real arterial transport functions hAB, hBC, and hAC are, one can only guess at the magnitude of the error in , , and . The convolution of and produces whose error is larger than that for either of the components. For this reason, the great amount of scatter seen in Figs. 4 and 5 is not at all unexpected.
The same test has been used in experiments on the influence of flow on transpulmonary transport functions (14), in which the injection of indicator was made into the right atrium and the dye-dilution curves were sampled simultaneously from the pulmonary artery, left atrium, and aorta. The transport functions were all slower and broader, therefore encompassing more cardiac cycles and, as a result, the transport functions () computed by convolution of the segmental transport functions were almost exactly superimposable on the pulmonary artery-to-aorta transport function, . This leads one to suspect that most of the variation in the present experiment was due to the fact that the transport functions were short compared to the major sources of noise: the cardiac pulsation and the respiratory variation in flow.
The practical point that may be made from these experiments is that, if one wishes to use the areas and mean transit times of dye curves to measure flow and volume in the circulatory system, not only must the injection and sampling sites be fairly well separated but also the pair of sampling sites delineating the segment whose volume is desired must be separated by a distance fairly long compared to the mean distance traveled by the blood in one cardiac cycle. The mean transit time between sites should probably always be greater than three cardiac cycles. In situations in which close sites must be used, the heart rate should be increased artificially in order to obtain t̄ accurately.
One other point is worth reiterating. The mean transit time of indicator between an injection site and a sampling site tends to be greater than the mean transit time of the blood. The main reasons for this are: 1) the force of injection usually produces a broad bolus extending upstream and downstream from the injection site (the extent of this depends on how and where the injection is made), and 2) the injection tends to produce cross-sectional labeling and therefore puts a disproportionately large amount of indicator into the parts of the stream with slow flow, instead of labeling in proportion to the flow in each part of the stream. As a result, some of the injectate travels very slowly along the vessel wall, mixing poorly with the stream. These labeling errors may result in a 30–40% overestimation of mean transit time. In the present experiments it is hoped that, by the time the indicator reaches the upstream sampling point, the indicator is mixed freely with the blood and travels with it as an appropriate label. This is probably true and, therefore, the use of the transport functions should eliminate these sources of error.
When one does not need to know the distribution of transit times through a segment but only its mean transit time, taking the difference between the mean transit times of the dye curves recorded at the upstream and downstream ends of the segment may be sufficiently accurate. Of course, the sampling-system mean transit times should either be identical or should be determined accurately and subtracted from the mean transit times of the curves. When very accurate mean transit times are required, the transport function mean transit time is the one to use because it is not dependent on any extrapolation of the downslope of the recorded curves.
Birkhead and co-workers (7) and Nicholes and co-workers (16) compared the areas of dye curves sampled after injections of one, two, and four times a standard amount of dye. This is a reasonable approach to testing linearity but is hampered experimentally by the fact that the flow is seldom constant for the 3- to 10-min periods between dye curves. With constant flow the test becomes as much a test of densitometer calibration as of linearity in the vascular system. The sensitivity of the test is also reduced by the constancy of shape of the dye curves: small deformities are not readily observable. The twin injections used in this study (Fig. 3) allowed examination of a wide variety of forms of curves and, since the data for each test of linearity were collected in a short period, the system was usually stationary (apart from cardiac cycle pulsations).
Transport and dispersion in the aorta
The transport functions, based on steady flow, provide no information on the instantaneous flow profile in the aorta but do allow some deductions to be made on the profile averaged over each cardiac cycle. From Figs. 7 and 8 it is apparent that the shortest transit time ta is about half the mean transit time. The transport function in Fig. 7 has a shape given by the average values in this study; it shows that the peak is significantly delayed beyond the appearance time, that the return to the base line is much faster than the 1/t2 relationship expected with parabolic flow, and that the slowest velocities are effectively much greater than zero, being about one-third to one-half the mean velocity. On the average, therefore, the flow is not parabolic but has a blunter front, a narrower range of velocities (from about 0.3 to 1.9 times the mean velocity), and a finite velocity at the wall. The ratio of fastest velocity to mean velocity, of nearly 2.0, is the same as would be observed with parabolic laminar flow, but it is more likely that this ratio and the dispersion are due to longitudinal mixing in the vessel secondary to turbulence, branching, diameter changes, and pulsatile flow, and that the mean velocity profile is much more blunt than a parabola.
These data suggest that the characteristics of flow through the aorta of the dog are somewhat different from those of flow through the arteries of the human leg (1); the dispersion relative to the mean transit time is greater but still appears to be uninfluenced by the flow rate since the relationships of Fig, 8 are probably linear.
Footnotes
This investigation was supported in part by a grant from the Minnesota Heart Association and by National Institutes of Health Research Grants H-4664, HE-9719, and FR-00007.
Presented in part at the meeting of the Federation of American Societies for Experimental Biology, Atlantic City, April 9–14, 1965.
REFERENCES
- 1.Bassingthwaighte JB. Plasma indicator dispersion in arteries of the human leg. Circulations Res. 1966;19:332–346. doi: 10.1161/01.res.19.2.332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bassingthwaighte JB, Ackerman FH, Wood EH. Applications of the lagged normal density curve as a model for arterial dilution curves. Circulation Res. 1966;18:398–415. doi: 10.1161/01.res.18.4.398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bassingthwaighte JB, Anderson D, Knopp TJ. Effects of unsteady flow on indicator dilution in the circulation. Proc. Ann. Conf. Engnr. Med. Biol., 8th. 1966:184. [Google Scholar]
- 4.Bassingthwaighte JB, Edwards AWT, Wood EH. Areas of dye-dilution curves sampled simultaneously from central and peripheral sites. J. Appl. Physiol. 1962;17:91–98. doi: 10.1152/jappl.1962.17.1.91. [DOI] [PubMed] [Google Scholar]
- 5.Bassingthwaighte JB, Edwards AWT, Wood EH. Use of an optical density ruler in measurements of dye-dilution curves. J. Appl. Physiol. 1964;19:347–353. doi: 10.1152/jappl.1964.19.2.347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bassingthwaigwte JB, Warner HR, Wood EH. Analog computer analysis of dispersion of indicator in the circulation. Med. Res. Eng. 1966;5:30–37. 47. [PMC free article] [PubMed] [Google Scholar]
- 7.Birkhead NC, Fox IJ, Wood EH. Effect of doubling and quadrupling indicator dose on indicator dilution curves. Physiologist. 1957;1:11. [Google Scholar]
- 8.Coulam CM, Warner HR, Wood EH, Bassingthwaighte JB. A transfer function analysis of coronary and renal circulation calculated from upstream and downstream indicator-dilution curves. Circulation Res. 1966;19:879–890. doi: 10.1161/01.res.19.5.879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cramer H. Mathematical Methods of Statistics. Princeton Univ. Press; Princeton: 1946. [Google Scholar]
- 10.Edwards AWT, Isaaoson J, Sutterer WF, Bassingthwaighte JB, Wood EH. Indocyanine green densitometry in flowing blood compensated for background dye. J. Appl. Physiol. 1963;18:1294–1304. doi: 10.1152/jappl.1963.18.6.1294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fox IJ, Wood EH. Indocyanine green: physical and physiologic properties. Proc. Staff Meetings Mayo Clinic. 1960;35:732–744. [PubMed] [Google Scholar]
- 12.González-Fernández JM. Theory of the measurement of the dispersion of an indicator in indicator-dilution studies. Circulation Res. 1962;10:409–428. doi: 10.1161/01.res.10.3.409. [DOI] [PubMed] [Google Scholar]
- 13.Grace JB, Fox IJ, Crowley WP, Jr., Wood EH. Thoracic-aorta flow in man. J. Appl. Physiol. 1957;11:405–418. doi: 10.1152/jappl.1957.11.3.405. [DOI] [PubMed] [Google Scholar]
- 14.Knopp TJ, Bassingthwaighte JB. Effects of varying flow on transpulmonary circulatory transfer functions. Federation Proc. 1966;25:630. [Google Scholar]
- 15.Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J. Appl. Physiol. 1954;6:731–744. doi: 10.1152/jappl.1954.6.12.731. [DOI] [PubMed] [Google Scholar]
- 16.Nicholes KK, Warner HR, Wood EH. A study of dispersion of an indicator in the circulation. Ann. N. Y. Acad. Sci. 1964;115:721–737. [PubMed] [Google Scholar]
- 17.Opdyke DF, Sniffen RE. Estimation of cardiac output by rapidly repeated dye-dilution technic. Proc. Soc. Exptl. Biol. Med. 1959;102:725–728. doi: 10.3181/00379727-102-25377. [DOI] [PubMed] [Google Scholar]
- 18.Sheppard CW. Mathematical considerations of indicator dilution techniques. Minn. Med. 1954;37:93–104. [PubMed] [Google Scholar]
- 19.Sherman H. On the theory of indicator-dilution methods under varying blood-flow conditions. Bull. Math. Biophys. 1960;22:417–424. [Google Scholar]
- 20.Stephenson JL. Theory of the measurement of blood flow by the dilution of an indicator. Bull. Math. Biophys. 1948;10:117–121. doi: 10.1007/BF02477486. [DOI] [PubMed] [Google Scholar]
- 21.Streeter VF, Keitzer WF, Bohr DF. Energy dissipation in pulsatile flow through distensible tapered vessels in pulsatile blood flow. In: Attinger EO, editor. International Symposium on Pulsatile Blood Flow. McGraw; New York: 1964. pp. 149–177. [Google Scholar]
- 22.Thompson HK, Jr., Starmer CF, Whalen RE, McIntosh HD. Indicator transit time considered as a gamma variate. Circulation Res. 1964;14:502–515. doi: 10.1161/01.res.14.6.502. [DOI] [PubMed] [Google Scholar]
- 23.Wood EH. Definitions and symbols for terms commonly used in relation to indicator-dilution curves. Circulation Res. 1962;10:379–380. [Google Scholar]
- 24.Wood EH, Sutterer WF, Marshall HW, Nolan AC. Use of the Human Centrifuge to Study Circulatory, Respiratory and Neurologic Physiology in Normal Human Beings and a Description of an Electronic Data Processing System Designed to Facilitate These Studies. Tech. Docum, Rept. AMRL-TDR-63-105. 1963 December; Aerospace Medical Division, Wright-Patterson Air Force Base. [PubMed] [Google Scholar]
- 25.Zierler KL. Theoretical basis of indicator-dilution methods for measuring flow and volume. Circulation Res. 1962;10:393–407. [Google Scholar]