Diffusion of sucrose, sodium, and water in ventricular myocardium

Abstract

The cumulative fluxes of radioactive sucrose, sodium, and water across a sheet of cat right ventricle were studied simultaneously to obtain the apparent tissue diffusion coefficients for extravascular diffusion at 37°C. The sucrose data fitted the equations for diffusion in tortuous channels in a plane sheet with a tortuosity factor, λ, of 2.11 ± 0.11 (mean ± SE, n = 10). The fit of the earliest data before attainment of steady state was improved by assuming a Gaussian distribution of diffusion path lengths through the extracellular space, but λ was only changed by a few percent. The sucrose diffusion channel contained 0.27 ± 0.03 ml of total tissue water, which is more than measured by others but still less than the expected sucrose space. The steady-state data for sodium agreed with the model for extracellular diffusion using λ and the area available for diffusion for sucrose when sodium equilibration with a dead-end pore volume (presumed to be intracellular) was taken into account. The cumulative flux data for water were monotonic and lacked secondary inflections. Thus the apparent tissue diffusion coefficients for sucrose, sodium, and water were (in 10⁻⁶ cm²/s) 1.77 ± 0.23, 5.13 ± 0.68, and 7.39 ± 0.99, respectively, representing a reduction to 23% of the free diffusion coefficient for sucrose and sodium and 22% for water.

Fundamental to the analysis of capillary-tissue exchanges is a knowledge of tissue transfer rates by diffusion outside the capillaries (2, 30). The purpose of this work was to determine the apparent tissue diffusion coefficients for sucrose, sodium, and water at body temperature in the cat myocardium. The studies were made in a diffusion cell (32) on a sheet of cat myocardium by a method modified from that described by Page and Bernstein (26). These authors found at 23°C that sodium did not enter the cells and that the steady-state diffusion of water, sodium, and sucrose could be accounted for by fluxes occurring only in the extracellular space. Since cell membrane permeability to water is so high that restriction of water diffusion to the extracellular space seemed unlikely, we felt that a study of the three tracers simultaneously at 37°C was needed.

Experimental Methods

General

From the excised hearts of cats (1.5–3.0 kg) anesthetized with sodium thiamylate (50 mg/kg) the relatively non-trabeculated upper part of the anterior wall of the right ventricle was isolated and mounted between the two chambers of the Lucite diffusion cell (Fig. 1). Three to five minutes were taken for excision and filling of the chambers with oxygenated bathing solution. The diffusion cell, surrounded by a water bath at 37°C, consisted of two cylindrical chambers of identical dimensions. Each chamber was stirred by a magnetic stirrer and by a stream of 5% CO₂ in O₂ directed toward the tissue to reduce the effect of an unstirred layer at the tissue surface. The sheet was exposed to the bathing solution through a 6-mm-wide hole in the center plates (0.5 mm thick) of the apposed chambers and was sealed at its rim by a 1.6-mm O ring machined into one of the center plates.

FIG. 1.

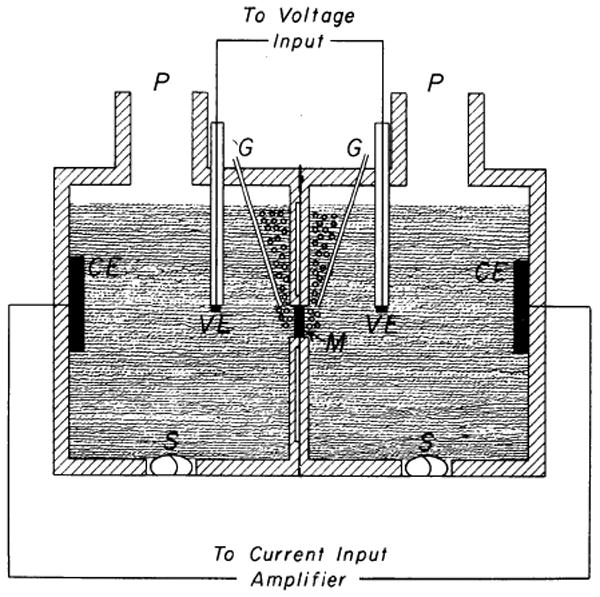
Diffusion cell. M, right ventricular sheet; P, sampling port; G, gas inlets; S, magnetic stirrer rod; CE, current electrode; VE, voltage electrode. Each half of diffusion cell is 2.9 cm long, 2.5 cm in internal diameter, and 14.5 ml in volume.

Tissue Resistance Measurements

The resistance of the sheet was obtained from the current necessary to give a voltage difference of 10 mV across the sheet and was automatically measured during 1.4 s every minute; the technique was devised for us by Dr. R. C. La Force, following his earlier design (22). Ag-AgCl electrodes were placed as shown on Fig. 1 (corrections were made for the resistance of the solution between the voltage electrodes and the sheet). In seven flux experiments the specific resistance (sheet resistance × area of sheet divided by its mean thickness) averaged 647 Ωcm at the onset of the experiment (see Table 1). The mean change after 3 h was −2%. For the following reasons it was concluded that a constant resistance throughout an experiment reflected the absence of developing tissue hypoxia: oxygen deprivation invariably increased the resistance by approximately 40%; a typical example is shown in Fig. 2, upper curve. Addition of NaF to the solution in both chambers caused a similar rise in resistance following an initial drop due to increased electrolyte concentration; the latter effect could be repeated by further addition of fluoride but not the former, indicating that the increase in resistance was linked to an irreversible block of oxidative metabolism (Fig. 2, lower). Last, omitting glucose from the solution or using sheets thicker than 2.5 mm resulted in similar increases in resistance.

TABLE 1. Data on sheets from cat right ventricular myocardium.

	Mean	±SE	n
Thickness of sheets, l, cm	0.175	0.010	10
Tissue water, Vdw, ml/ml tissue	0.84	0.004	10
Specific resistance, Ωcm
Initial	647	70	7
Final	633	63	7
Sucrose
Single-pathway model	2.08	0.11	10
λ Parallel-pathway model	2.11	0.11	10
σ/l	0.10	0.04	10
Ad/As	0.22	0.02	10
Vd, ml/ml tissue water	0.27	0.03	10
D/λ2, 10−6 cm2/s	1.77	0.23	10
Sodium
Vdep, true, ml/ml tissue water	0.69	0.12	9
Vdep, true + Vd, ml/ml tissue water	0.96	0.14	9
D/λ2, 10−6 cm2/s	5.13	0.68	9
THO
D′, 10−6 cm2/s	7.39	0.99	5

The values taken for the diffusion coefficients (10⁻⁵ cm²/s) at 37°C were: sucrose, 0.72 (24, 25); sodium, 2.0 (25, 35); water, 3.3 (39). The duration of the experiments was from 3 to 4 h.

FIG. 2.

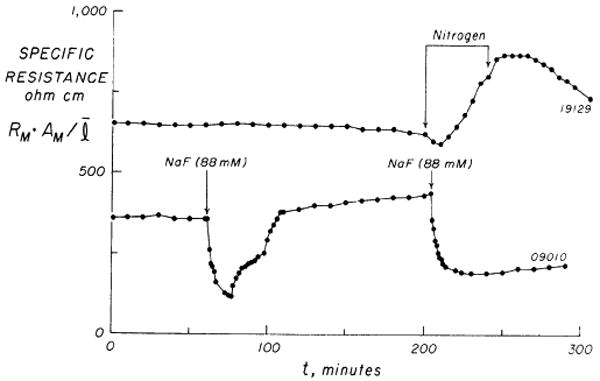
Time course of specific resistance, R_MA_M/l, in 2 experiments. Upper curve shows a 200-min control period (95% O₂, 5% CO₂) followed by oxygen deprivation (100% N₂) which was accompanied by a prompt increase in resistance. Recommencement of O₂ was followed after a time lag by a slower decline of resistance toward control levels. Lower curve demonstrates resistance changes following 2 additions of 88 mM NaF to each chamber. (For details see text.)

Solutions

Equal volumes of modified Krebs-Ringer solution (12) were added on each side of the sheet. The composition, in millimoles per liter, was: Na, 152; K, 3.6; Mg, 0.6; Ca, 2.5; Cl, 135; HCO₃−, 25; H₂PO₄, 0.66; SO₄, 0.6; and glucose 5.6; pH, 7.4. The sheet was equilibrated in this solution for 1.5–2 h. Following an initial period of 15 min with gradual decline, the tissue resistance remained constant. After equilibration the test tracers were added to the chamber facing the epicardium (donor) and an unlabeled solution of the same volume and composition was added to the other (recipient) chamber.

Sampling

Samples of 0.2 ml of the recipient solution were taken by an Eppendorf micropipette (Brinkmann Instruments, West-bury, N. Y.) at 2-min intervals for 100 min and thereafter at 5-min intervals for 3–4 h, and two samples of 0.2 ml were taken from the donor solution before and after the test period. All samples were replaced by an equal volume of unlabeled solution. The duration of the experiment assured that an apparent steady state existed for at least 100 min for the slowest moving tracer. The total quantity of tracer traversing the sheet was calculated from the measured concentrations and the chamber volume, taking into account the tracer removed with each sample.

Thickness of Sheet

After the experiment the sheet was frozen between pieces of Dry Ice and 16-μm sections were cut in a cryostat at −23°C and stained with toluidine blue. With the use of a micrometer eyepiece, 150–200 measurements of the sheet's thickness were made at approximately 100-μm intervals along three or four full-width sections. The accuracy was ±25 μm, which is less than 2.5% of the average sheet thickness. The relatively smooth and parallel nature of the surfaces of the sheets was reflected by an average coefficient of variation of 8.7%.

Water Content

In each experiment, the water content (g/g) of two pieces of right ventricular myocardium adjacent to that used in the diffusion cell was measured by drying at 110°C for 24–36 h; this gave a value within 1% of that of the sheet (four paired experiments) which was found unaltered by 4 h of incubation with or without oxygenation (two experiments), as found for the frog heart (1).

Specific Gravity

Specific gravity of right ventricular tissue from six hearts was measured by the copper sulfate method (31).

Tracers

Sucrose-¹⁴C (New England Nuclear Corp., Boston), ²⁴Na (Cambridge Nuclear Corp., Cambridge, Mass.), and tritium-labeled water (THO; Abbott Laboratories, North Chicago) were used in amounts of 200, 450, and 100 μCi, respectively, in each experiment. In seven experiments the gamma activity of ²⁴Na was counted with use of an Autowell II (Picker Corp., North Haven, Conn.); in the rest of the experiments it was counted along with the ¹⁴C and ³H labels in a liquid scintillation spectrometer (Tri-Carb series 3375, Packard Instrument Company, Inc., Downers Grove, Ill.) as previously reported from this laboratory (36).

Source of Error

Redundant tissue peripheral to and in the 1.6-mm–wide O ring which crushed the sheet to one-sixth of its initial thickness was shown in two separate experiments to accumulate up to 15% of the cumulative flux of sucrose-¹⁴C and THO after 3 h. The procedure was to cut the exposed circular part of the sheet away, then to rinse the cut edge with tracer-free solution and take the remaining tissue for measurement of its amount of retained tracer. Clearly this “radial diffusion does affect the tracer concentration profiles near the rim of the exposed disk. The nontrivial solution of the diffusion equation for this case has not been obtained, but we estimate that a correction for the radial loss of tracers would change the values of the diffusion coefficients by less than 3%.

The method of Longsworth (25) has been used for calculating the free-diffusion coefficient for sodium and sucrose at 37°C from the values at 25°C.

Methods of Analysis

Theory

Crank's solution (7) for diffusion in a plane sheet with constant surface concentrations, as modified by Page and Bernstein (26), gives the cumulative amount of tracer, Q_R(t), in the recipient chamber at time t after injecting tracer into the donor chamber, in which the concentration, C_D, is considered to be constant for the duration of the experiment

$$Q_{\text{R}}(t)=\frac{D{C}_{\text{D}}{A}_{d}t}{{\lambda }^{2}l}-\frac{l{C}_{\text{D}}{A}_d}{6}-\frac{2l{C}_{\text{D}}{A}_d}{{\pi }^2}\sum _{m=1}^{m=M}\frac{{(-1)}^m}{m^2}\text{exp}\left(\frac{-D{m}^2{\pi }^{2}t}{{\lambda }^2{l}^2}\right)$$ (1)

Here, l is the average thickness of the sheet; A_d is an area associated with the diffusion channel such that l·A_d is the volume of the diffusion channel; λ is a tortuosity factor accounting for microscopic impedances to diffusion and is the ratio of the apparent diffusion path length to l; D is the free-diffusion coefficient in water at 37°C. The M is the number of terms in the series approximation to the solution; an M of 20 was used routinely, a value of 100 changing the result by less than 0.1%.

When the transient phase of the response is over, (Dπ²t/λ²l² > 6 suffices), the third term of equation 1 vanishes and Q_R(t) is a straight line whose intercept, L, on the time axis is given by the first two terms. From this, the apparent tissue diffusion coefficient, D/λ², is calculated

$$\frac{D}{{\lambda }^2}=\frac{l^2}{6L}$$ (2)

From the slope, dQ_R(t)/dt, one can calculate the area available for diffusion, A_d

$$A_d=\frac{\text{d}{Q}_{\text{R}}(t)}{\text{d}t}\cdot \frac{{\lambda }^{2}l}{D{C}_{\text{D}}}=\frac{\text{d}{Q}_{\text{R}}(t)}{\text{d}t}\cdot \frac{6L}{l{C}_{\text{D}}}$$ (3)

However if there is a variety of independent paths of differing lengths, then the equation can be further modified to take this into account, in the fashion diagrammed in Fig. 3

FIG. 3.

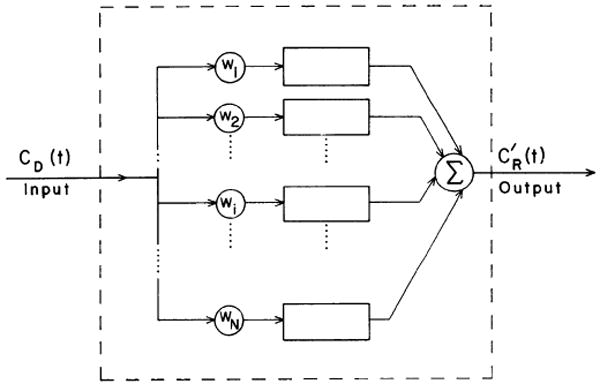
Block diagram of parallel-pathway model. C_D(t) is donor concentration of tracer and C_R(t) is recipient concentration corrected for sample replacement. w_i is weighting factor, which gives the fractional utilization of each path length, l_i.

$$Q_{\text{R}}(t)=\sum _{i=1}^{i=N}{w}_i\left(\frac{D{C}_{\text{D}}{A}_{d}t}{{\lambda }^2{l}_i}-\frac{l_i{C}_{\text{D}}{A}_d}{6}\cdot -\frac{2l_i{C}_{\text{D}}{A}_d}{{\pi }^2}\sum _{m=1}^{m=M}\frac{{(-1)}^m}{m^2}\text{exp}\left(\frac{-D{m}^2{\pi }^{2}t}{{\lambda }^2{l}_i^2}\right)\right)$$ (4)

This is the parallel-pathway model. Here N independent pathways of lengths, l_i, are assumed, and λ is defined as the ratio between the apparent diffusion path length and l_i and is taken to be constant throughout the sheet; the relative frequency of occurrence of each l_i is given by the weighting factor, w_i. For simplicity, the w_i's were assumed to be Gaussian, and an N of 13 was found to be adequate to define the distribution function. While it might be considered more reasonable to assume that the w_i formed a right-skewed distribution such as a random walk with a first traversal, a description in terms of a mean and standard deviation is about all that one can obtain from experimental data of this sort, and, since no systematic difference between the data and the Gaussian model could be observed for the transient phase, the Gaussian function was considered adequate.

To determine the standard deviation of the l_i's, a best fit between the transient portion of Q_R(t) in equation 4 and the data points was obtained by trial and error, minimizing the sum of squares of the differences between Q_R(t) and the data. Families of different solutions to equation 4 were generated, all with the same steady-state slope and intercept fitting the final portions of the data and having the same average path length, l, but with different Gaussian distributions of the path lengths, l_i. The relative dispersion, σ/l, of each Gaussian distribution is defined as the standard deviation σ of the lengths, l_i, divided by the mean length l; values of σ/l of less than 0.32 covered the range of the data. With larger σ/l, Q_R(t) is less sharply curved and the curved portion is more prolonged, beginning earlier and ending later.

If all the l_i's were equal, equation 1 would fit the data. With unequal l_i's, a value of σ/l greater than the standard deviation of the surface-to-surface path lengths measured by microscopy implies local intratissue obstructions increasing the diffusion path length by sizable fractions of λl_i and points to the likelihood of a variation in λ on top of the variation in l_i. (Values of σ/l less than the measured standard deviation could result if the local variations in sheet thickness were quite abrupt, so that tracer “streamlines” did not extend straight to the ends of protuberances but terminated in sideway directions into the bathing fluid.)

In the steady state the third term in equation 4 vanishes and the cumulative amount of tracer on the recipient side is given by the first and second terms

$$Q_{\text{R}}(t)=\sum _{i=1}^{i=n}\frac{w_{i}D{C}_{\text{D}}{A}_{d}t}{l_i{\lambda }^2}-\frac{\text{∑}_{i=1}^{i=N}{w}_i{l}_i{C}_{\text{D}}{A}_d}{6}$$ (5)

With the abscissal intercept given as L and since

$$\sum _{i=1}^{i=N}{w}_i{l}_i=l,$$

the apparent tissue diffusion coefficient is given by

$$D/{\lambda }^2=l/\left(6L\sum _{i=1}^{i=N}\frac{w_i}{l_i}\right)$$ (6)

where λ is seen to depend on the distribution of l_i's. A_d is still given by equation 3.

The parallel-pathway model was used for interpretation of the sucrose flux data in the following way. First, the experimental cumulative flux corrected for sample replacement by unlabeled solution was calculated. Next, linear regression analysis gave the slope, dQ_R(t)/dt, of the steady-state part of the flux curve and its abscissal intercept, L. No correction was made for backdiffusion. C_R(t)/C_D(t) was less than 0.2, 0.3, and 1.0% for sucrose-¹⁴C, ²⁴Na, and THO, respectively, at the end of the experiment. The donor chamber concentration, C_D, was taken as the mean of the concentrations at the start and the end of the experiment. By inserting L and the measured l into equation 6, a family of solutions for λ (or D/λ²) is obtained and A_d is found from equation 3 by use of the slope, dQ_R(t)/dt. With these values inserted into equation 4 a family of curves was generated in which each curve has been forced to fit the steady-state flux data, whereas the transient parts of the curves all differ. A family of model curves is shown in Fig. 6, superimposed on the experimental data (the x's during the transient). The best fit provided a value for the tortuosity, λ, and for the relative dispersion of path lengths, σ/l.

FIG. 6.

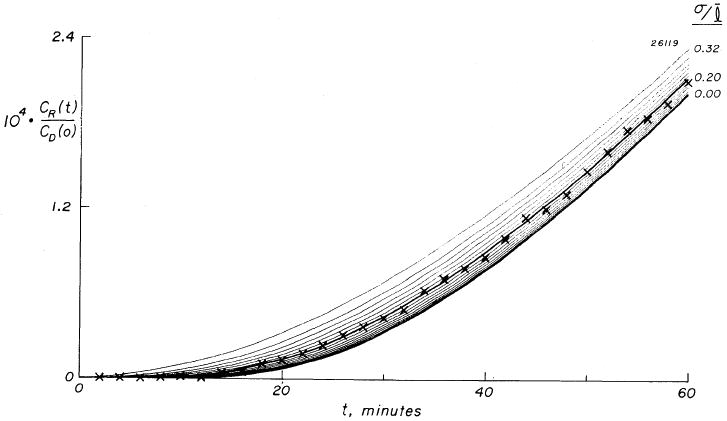
Transient phase of normalized accumulation, ×, of sucrose-¹⁴C in a sheet of mean thickness, l = 1.48 mm (SD, σ = 0.14 mm). Continuous curves are a family calculated from multiple-pathway model. Each curve represents a single Gaussian distribution of path lengths characterized by its relative dispersion (σ/l). Seventeen curves are shown with σ/l varying between 0.00 and 0.32. Curves differ only in transient portion and are superimposed at steady state, a σ/l of 0.20 providing best fit to data.

A different model, the dead-end pore model, was used for sodium because analysis of the sodium data using the parallel-pathway model gave poor fits of model to data in 8 out of 10 experiments, giving values for A_dl which were much larger than the expected extracellular volume and suggesting that sodium had entered the cells. The dead-end pore model was developed for diffusion in porous media (13, 14). As diagrammed in Fig. 4, it includes a volume which is not in the direct diffusion channel, but which becomes loaded with tracer during the transient phase and remains in equilibrium with tracer in the diffusion channel during the steady state. We ascribed a significant part of this volume to the intracellular volume of distribution for sodium. In this model the abscissal intercept, L, is related to the tissue diffusion coefficient (D/λ²) by

FIG. 4.

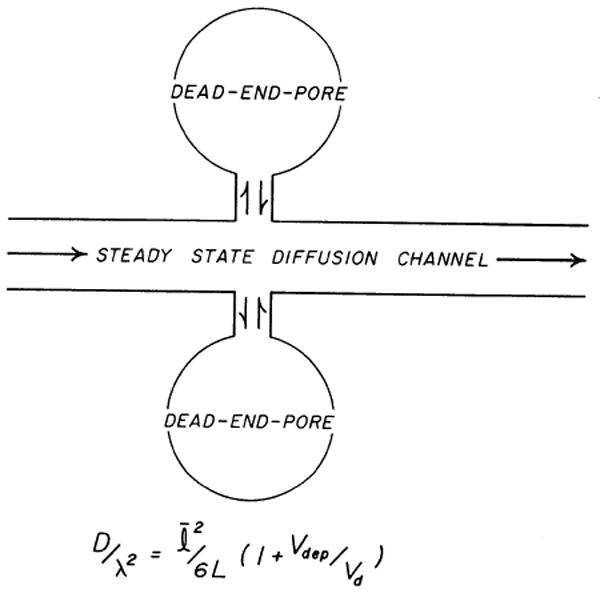
Dead-end pore model of Goodknight, Klikoff, and Fatt (14). Sequestered regions are schematized as dead-end pores which at steady state are in equilibrium across cell membrane with extracellular diffusion channel where net diffusion occurs. V_dep is dead-end pore volume and V_d is steady-state diffusion volume.

$$L=l^2(1+V_{\mathit{\text{dep}}}/V_d)/(6D/{\lambda }^2)$$ (7)

where V_dep is the total volume of the dead-end pores and V_d is the diffusion volume, A_dl. In the present situation in which the steady-state concentrations of sodium in the V_dep and the diffusion volume differ, the V_dep in equation 7 is a virtual volume, so that V_dep,true = V_dep,virtual × [Na⁺]_o/[Na⁺]_i. We used the value of approximately 4.7 for the concentration ratio, utilizing Page and Solomon's (29) finding that Na⁺ was 38 mmol/kg cell water in contracting cat papillary muscle at 37–38°C (after 2 h) with a [Na+]_o of 178.5 mM. The dead-end pores do not affect the steady-state slope, but delay the intercept and change the shape of the transient. Page and Bernstein (26) interpretated their data on the diffusion of permeant substances in the light of the dead-end pore model. However, with L given experimentally, equation 7 permits calculation of V_{dep, true} for sodium, after which the applicability of the model can be checked by seeing how well V_dep,true and V_d (taken as that for sucrose) add up to give total water space (see RESULTS).

Neither the parallel-pathway model nor the dead-end pore model fitted the THO flux data. However, the overall tissue diffusion coefficient, D′, was calculated by inserting the steady-state flux, dQ_R(t)/dt, into the first-order Fick equation

$$D^{\prime }=(d{Q}_{\text{R}}(t)/\text{d}t)l/(C_{\text{D}}{A}_{dw})$$ (8)

permitting an estimate of the intracellular diffusion coefficient for THO (see RESULTS). A_dw was estimated from the measured right ventricular water content (converting grams water/grams tissue to milliliters water/milliliters tissue): A_dw = A_sV_dw, where A_s is the exposed area of the sheet and V_dw is milliliters water per milliliter muscle (see Table 1).

Results and Discussion¹

Physical Data on Right Ventricular Muscle Sheets

The specific gravity was 1.053 ± 0.0022 g/ml, n = 6 (mean ±1 SD, n is the number of observations), which is less than 1.062 ± 0.003 g/ml found for the right ventricle in the dog heart by Yipintsoi et al. (37) but close to the 1.055 g/ml found by Creese (8) for rat diaphragm. The water content (see Table 1) was 0.796 ± 0.04 g/g wet wt, or 0.840 ± 0.012 ml/ml, or 3.90 g/g dry wt. Page and Bernstein (26) found 0.774 ± 0.046 g/g wet wt, or 3.42 g/g dry weight. The difference of 14% between the values expressed as water content relative to dry weight is explained well by a similar difference between their sodium content in the bathing solution (178.5 mM) and ours (152 mM).

The average thickness, l, of the sheets was 0.175 cm (range 0.114–0.226). With sheets of this thickness, tissue oxygenation at 37°C appears adequate. The maximum thickness of a plane sheet without an anoxic central portion can be calculated from: a) an O₂ consumption of 2.0 μl/mg dry wt per hour from Coleman et al. (5), or 1.19 × 10⁻⁴ ml O₂ per second per milliliter wet tissue in the cat heart (using our values for water content and specific gravity); b) a diffusion coefficient for O₂ in rat heart of 1.95 × 10⁻⁵ cm² s⁻¹ from Grote and Thews (16), as corrected by Grote (15); and c) the value of 0.0228 ml/ml for O₂ dissolved in water in 95% O₂ at 1 atm. Assuming uniform O₂ consumption in a plane sheet and allowing the PO₂ to approach zero in the middle of the parabolic concentration profile, the thickness in centimeters would be the square root of (8 × 1.95 × 10⁻⁵ × 0.0228/1.19 × 10⁻⁴) or 1.73 mm. This theoretical maximum thickness is really a “worse case” viewpoint, for irregularities in the surfaces, and a diminution of O₂ consumption at depths where Po₂ is lower, will significantly increase the depth for viability. Support for this view is provided by the result that values of D/λ² for the thickest sheet were no different from the others.

Further evidence for adequacy of oxygenation is that the electrical resistance of the sheets did not change in any consistent fashion during the experiments. There were small random variations with an average change of 2% from beginning to end. Since O₂ deprivation and metabolic poisons were observed to cause increased resistances, these results indicate at least that no more of the tissue became anoxic during the experiments than the amount that was initially present. (In gastric mucosa (6) and in skeletal muscle (33) hypoxia caused increased tissue resistance, which presumably is related to the cellular swelling and the reduction of extracellular space which are so apparent in the brain (34)). The absence of associations among sheet thickness, specific resistance, and D/λ², therefore, leads us to conclude that none of the muscle sheets showed evidence of developing anoxia or swelling of the cells.

Sucrose

Examples of curves of C_R(t)/C_D for all three tracers are shown in Fig. 5; only the data at early times are presented so that the form of the transients can be seen. As in Fig. 6, 5 out of 10 experiments were fitted by the parallel-pathway model with the best fits obtained using σ/l ranging from 0.10 to 0.28 (mean = 0.20); this is larger than the variation in the direct measurements of thickness. However, when averaged with the rest of the experiments which were fitted by σ/l = 0 (the single-pathway model) the mean relative dispersion was 0.10, not much different from the mean value of the relative dispersions of the direct measurements on each sheet, namely 0.087. The use of the parallel-pathway model gave an average value for λ of 2.11 ± 0.11, which is only 1.4% larger than the value found by means of the single-pathway model. Thus, a mild heterogeneity of lengths provided a more precise description of the transient without significantly influencing the value obtained for λ. Therefore, it appears that the more accurate but cumbersome parallel-pathway model can be reserved for tissues with greater heterogeneity than these sheets.

FIG. 5.

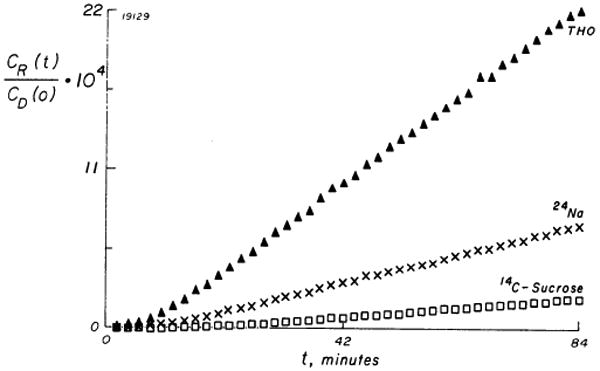
Normalized accumulation of sucrose-¹⁴C (□), ²⁴Na (×), and THO (▲) on initially tracer-free side of myocardial sheet. Data were obtained simultaneously on a sheet of mean thickness 1.14 mm (SD = 0.16 mm), which was 2nd most uneven sheet used. C_R(t) is recipient concentration corrected for sampling replacement and C_D(o) is donor concentration at onset of the sampling period.

The tissue diffusion coefficient, D/λ², was 1.77 ± 0.23 × 10⁻⁶ cm²/s, giving a value of 1/λ² of 0.23; this is identical to the reduction in the diffusion coefficient found by Johnson (18) for sucrose in frog sartorius muscle at 22°C (observed D′ of 1.2 × 10⁻⁶ cm²/s compared to 5.2 × 10⁻⁶ cm²/s in water), whereas Page and Bernstein's (26) value for 1/λ² was twice as big.

Our value of A_d/A_s, 0.22 ± 0.02 cm²/cm², and, therefore, of lA_d, 0.27 ± .03 ml/ml tissue water, was larger than that of Page and Bernstein (26) (A_d/A_s = 0.17 ± 0.02), but was still less than their measured sucrose space of 0.39 ± 0.14 ml/ml tissue water (26); or 0.50 ± 0.046 ml/ml rabbit heart water recalculated from Johnson and Simonds (19) on the assumption of a water content of 0.80 ml/g; or 0.6 ml/ml water found for the rat heart by Page and Page (28). The differences between an lA_d of 0.27 and the higher estimate for sucrose space cannot be explained by the volume of the sarcoplasmic reticulum (SR) which sucrose and other small solutes can apparently permeate (4, 10), for myocardial SR volumes occupy only 3.5% of cell volume in rats (27) or perhaps 4% in dogs and cats (3). The T-tubular (T) system would contribute another 1% (3, 27), but the total of SR plus T appears insufficient to explain the discrepancy.

Sodium

The sodium data could not be fitted by either equation 1 or equation 4 during the transient phase. Also the value for A_d from equation 3 gave a volume of the diffusion channel which was greater than reasonable estimates of the extracellular sodium space. This pointed toward the existence of a dead-end pore volume which took up ²⁴Na in the beginning of the experiment and delayed the achievement of steady-state diffusion, thus increasing L. To obtain values of λ and A_d for sodium, we compared the steady-state flux data described by the equation dQ_R/dt = (D/λ²) C_DA_d/l for sodium and sucrose. The ratios of the values for A_d/λ² for sodium and sucrose averaged 1.23 (or 1.04 if two experiments were excluded). Since it is unlikely that A_d for sodium could be smaller than that for sucrose or that λ_Na could be larger than λ_sucrose we concluded that values of λ and A_d for sodium must be approximately those for sucrose. Using these values in equation 7, V_dep,true was found to be 0.69 ± 0.12 ml/ml tissue water. Since the diffusion channel itself was 0.27 ± 0.03 ml/ml tissue water, V_dep,true + V_d accounts for 97% of tissue water. Provided that all intracellular sodium is exchangeable, this suggests that the dead-end pore model is appropriate for the sodium data. This argument and the mathematical analysis are unaffected by intracellular compartmentalization, but the transient would be prolonged by exchanges that are slow compared to diffusion across the sheet. However, both a small intravascular volume and some other extracellular volume may act as a dead-end pore volume. One must note here that the membrane area available for exchange of sodium between the extracellular diffusion channel and the intracellular space is roughly 100-fold larger than the membrane area permitting a transcellular sodium flux in the direction normal to the surfaces of the sheet. Only because the latter flux can be neglected in these experiments do the cells behave as dead-end pores. A λ of 2.11 for sodium means an apparent tissue diffusion coefficient of 23% of the free-diffusion coefficient, which is similar to the values found by Johnson (18) and Harris and Burn (17) from the fast component of the sodium washout curve from skeletal muscle.

Water

Page and Bernstein (26) found an A_d for THO approximately equal to A_d for sucrose and assumed that the steady-state water flux occurred exclusively in the sucrose diffusion channel. This was not the case in the present experiments because the assumption of an A_d equal to that for sucrose for the steady-state diffusion data results in a λ of 1.09, suggesting no tortuosity for the extracellular diffusion of THO, which is unrealistic. A temperature effect will only explain some of the discrepancy between their results and ours, considering Longsworth's (25) demonstration of the nonuniformity of Q₁₀'s of diffusion coefficients and that a difference in radial loss of water seems an unlikely explanation. All cumulative flux curves were monotonic and thus free of the humps seen during the transient phase by Page and Bernstein (26, their Fig. 2).

An estimate of the lower limit of the intracellular diffusion constant for THO was obtained in the following way. First the average diffusion coefficient was calculated from the steady-state data, on the assumption that THO diffuses freely through the water volume of the sheet, to be 7.4 ± 1.5 × 10⁻⁶ cm²/s. This is 22% of the free-diffusion coefficient interpolated for 37°C from the data of Wang et al. (39). Next, the simplifying assumptions were made that the transcellular and the extracellular fluxes occur in parallel and with A_d and λ for sucrose valid for the extracellular flux and with the permeability of the cell membranes being infinitely high. The intracellular diffusion coefficient was then given by D_avg = 0.27 × (D_free/λ²_sucrose) + (1 − 0.27) × D_{intracellular}, or D_{intracellular} = (7.4 × 10⁻⁶ − 0.27 × 33.0 × 10⁻⁶/2.11²)/0.73 = 7.4 × 10⁻⁶ cm²/s. This is the same as the value of the average diffusion coefficient within the experimental error, which again illustrates the importance of the transcellular water movement in the sheet. Also this value is in accordance with the conclusions of Krogh et al. (20) and Ling et al. (23).

The observations of Kushmerick and Podolsky (21), that the diffusion coefficients for intracellular movements of small hydrophilic solutes in skinned frog skeletal muscle fibers were about 50% of the value in aqueous solutions, indicate the role of a finite membrane permeability. Our data are not at all compatible with diffusion coefficients of about 10⁻⁹ cm²/s calculated by Fenichel and Horowitz (11) for small organic solutes in skeletal muscle, or with the value of 10⁻⁹ cm²/s or less that Dick (9) calculated for THO from curves of tracer washout from animal cells assuming purely cytoplasmic diffusional resistance and infinite membrane permeability.

We come to the conclusion that water diffuses through both cells and extracellular fluid and has the same apparent diffusion coefficient for extracellular and transcellular diffusion. The data do not permit speculation concerning the state of the intracellular water (38). Apparently, most, perhaps all, of the intracellular sodium exchanges across cell membranes during the transient phase of the experiment.