Network Bistability Mediates Spontaneous Transitions between Normal and Pathological Brain States

Abstract

Little is known about how cortical networks support the emergence of remarkably different activity patterns. Physiological activity interspersed with epochs of pathological hyperactivity in the epileptic brain represents a clinically relevant yet poorly understood case of such rich dynamic repertoire. Using a realistic computational model, we demonstrate that physiological sparse and pathological tonic-clonic activity may coexist in the same cortical network for identical afferent input level. Transient perturbations in the afferent input were sufficient to switch the network between these two stable states. The effectiveness of the potassium regulatory apparatus determined the stability of the physiological state and the threshold for seizure initiation. Our findings contrast with the common notions of (1) pathological brain activity representing dynamic instabilities and (2) necessary adjustments of experimental conditions to elicit different network states. Rather, we propose that the rich dynamic repertoire of cortical networks may be based on multistabilities intrinsic to the network.

Introduction

Cerebral cortex exhibits a broad spectrum of physiological spatiotemporal activity patterns that range from synchronized oscillations during slow-wave sleep to desynchronized firing during waking (Steriade et al., 1993). These cortical activity states are thought to be initiated and maintained by different afferent input patterns and levels of neuromodulators (McCormick et al., 1993). Accordingly, in computational models, different choices of intrinsic neuronal and synaptic parameter values reproduce different activity states (Destexhe, 1999; Bazhenov et al., 2002; Compte et al., 2003; Hill and Tononi, 2005). In this framework of “parameter-mediated dynamic repertoire”, the dynamic flexibility of cortical networks results from the number and complex action of parameters that can be tuned to achieve different network behaviors (Prinz et al., 2004).

However, the ubiquitous presence of multistabilities in neurons (Hounsgaard and Kiehn, 1989; Fraser and MacVicar, 1996; Marder and Calabrese, 1996; Hahn and Durand, 2001; Shilnikov et al., 2005; Fröhlich and Bazhenov, 2006; Kass and Mintz, 2006; Fernandez et al., 2007) suggests that changes in parameter values may not be required for generation of different network activity patterns. In such an alternative framework of “multistability-mediated dynamic repertoire”, several stable activity states coexist without any parameter change. Rather, a transient perturbation is sufficient to induce a long-lasting change in network behavior by causing a switch from one stable state to another, a form of hysteresis. Once such a transition has occurred, the network remains in the new activity state at the offset of the perturbation. Although multistability is a fundamental property of nonlinear systems (Strogatz, 2000; Shilnikov et al., 2008) little is known how such dynamics could emerge in the case of cortical circuits.

Epileptic seizures are commonly assumed to be the result of changes in network properties that eliminate the negative feedback mechanisms providing a break on excessive neuronal activation. Therefore, routinely used parameter modifications that cause seizure-like activity include removal of synaptic inhibition and reduction of intrinsic outward currents by pharmacological means or changes in extracellular ionic milieu (Traub et al., 1993; Kager et al., 2000; Bikson et al., 2003; Pinto et al., 2005; Ziburkus et al., 2006; Cressman et al., 2009; Ullah et al., 2009). However, the fundamental question of how epileptic brains can exhibit seemingly normal physiological network dynamics most of the time yet spontaneously switch to epochs of aberrant pathological activity in absence of such experimental manipulations remains unanswered.

Using computational network models that include extracellular potassium concentration dynamics (Bazhenov et al., 2004), we investigated the transition between physiological and pathological network activity at seizure onset. We tested the hypothesis that “multistability-mediated dynamic repertoire” can explain the irregular occurrence of seizures. Specifically, we asked whether (1) the physiological and pathological network state can coexist in the same network model without any parameter change, (2) seizure initiation is mediated by switching from one to the other state, (3) a sufficiently strong yet transient perturbation induces seizures, and (4) the stability of the pathological state depends on the network properties to account for the fact that not all brains exhibit overt seizures.

Materials and Methods

Neuron models.

Both pyramidal cells (PYs) and fast-spiking inhibitory interneurons (INs) were modeled as two-compartment, conductance-based neurons. Each neuron had a dendritic and an axosomatic compartment. The coupling conductance of these two compartments determined the firing pattern of the model neurons in response to superthreshold depolarizing current injection (regular spiking for pyramidal cells, PYs, and fast-spiking for inhibitory interneurons, INs). The dendritic and axosomatic membrane voltages V_D and V_S are given by:

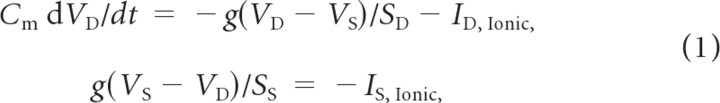where g = 0.1 mS is the coupling conductance between the dendritic and axosomatic compartments, I_D,Ionic and I_S,Ionic are the corresponding ionic currents, and C_m = 0.75 μF/cm² is the membrane capacitance. The surface areas of the two compartments are S_D = 1.65 10⁻⁴ cm² and S_S = 10⁻⁶ cm². All ionic currents follow the classical Hodgkin-Huxley form of I_j = g_j(V_D,S − E_j) with conductance g_j and reversal potential E_j. In addition to the leak ionic current, the axosomatic compartment was endowed with a voltage-gated sodium (PY: G_Na = 3000 mS/cm², IN: G_Na = 2500 mS/cm²) and a delayed-rectifier potassium (G_Kv = 200 mS/cm²), and a leak conductance (G_Kl = 0.1 mS/cm²). The dendritic compartment had high-threshold calcium, calcium-activated potassium, slowly activating potassium, persistent sodium, hyperpolarization-activated depolarizing mixed cationic, potassium leak, and mixed cationic leak conductances (PY: G_HVA = 0.016 mS/cm², IN: G_HVA = 0.01 mS/cm²; PY: G_KCa = 3.5 mS/cm², IN: G_KCa = 0.3 mS/cm²; PY: G_Km = 0.01 mS/cm², IN: G_Km = 0.0 mS/cm²; PY: G_NaP = 4.0 mS/cm², IN: G_NaP = 0.0 mS/cm²; G_h = 0.05 mS/cm²; PY: G_Kl = 0.01 mS/cm², IN: G_Kl = 0.005 mS/cm²; G_L = 0.033 mS/cm²). Equations and parameters for these ion channels and intracellular calcium dynamics were previously described in detail (Fröhlich and Bazhenov, 2006). Network heterogeneity was introduced by drawing random values for the potassium leak conductance from a normal distribution (mean 0.01 mS/cm², SD 0.001 mS/cm² for PYs; mean 0.005 mS/cm², SD 0.0005 mS/cm² for INs).

Network geometry and synapse models.

The network used in this study consisted of 200 PYs and 40 INs. The network included recurrent excitatory connection between PYs and recurrent feedback inhibition. Synaptic connectivity was random (connection probability p = 0.1) with doubled value of p within local footprint (radii: PY-PY: 5; PY-IN: 1; IN-PY: 5). All excitatory connections had a fast AMPA and a slow voltage-dependent NMDA component (total conductances: g_AMPA(PY-PY) = 9.6 nS, g_NMDA(PY-PY) = 0.96 nS, g_AMPA(PY-IN) = 3.0 nS, g_NMDA(PY-IN) = 0.30 nS). Inhibition was mediated by fast GABA_A synaptic conductances (g_GABA(IN-PY) = 9.6 nS). A detailed description of the synaptic dynamics has been previously provided (Fröhlich et al., 2008a). Afferent excitatory input (G_PY = 0.9 nS, G_IN = 0.9 nS) was modeled with a Poisson process with frequency f = 140 Hz for both PYs and INs. Perturbations to switch between network states were modeled with a transient increase of the PY afferent input to f = 150 Hz.

[K⁺]_o regulation apparatus.

Each cell was surrounded by an extracellular compartment that modeled the [K⁺]_o dynamics in the interstitial space (Bazhenov et al., 2004; Fröhlich et al., 2006). [K⁺]_o was determined by the interaction of the neuronal potassium currents I_ΣK, Na⁺/K⁺ ATPase activity

with [K⁺]_o(eq) = 3.5 mm, I_max = 5 mA/cm² in the dendritic compartment, I_max = 40 mA/cm² in the somatic compartment. K⁺ clearance by glial elements was modeled by a K⁺ buffer with first-order kinetics, as follows:

where k₁ = 0.008; k₂ = k₁/(1+exp(([K⁺]_o − [K⁺]_o(th))/−1.15)).

Half-maximum activation values of the K⁺ buffer were set to soma: [K⁺]_o(th) = 15 mm (soma) and 9 mm (dendrites). Lateral diffusion between neighboring compartments was computed by

with δ = 4 10⁻⁶ cm²/s and Δx = 100 μm. In sum, the potassium regulation apparatus was governed by the following differential equation:

where k = 10 denoted a conversion factor, F = 96,489 C/mol was the Faraday constant, and d determined the ratio of the volume of the extracellular compartment to the surface area. Equilibrium potentials were continuously updated under the assumption that diffusion-drift equilibrium was reached immediately and that all other ion concentrations remained constant ([K⁺]_i = 130 mm, [Na⁺]_o = 130 mm, [Na⁺]_i = 20 mm, [Cl⁻]_o = 130 mm, [Cl⁻]_i = 8 mm):

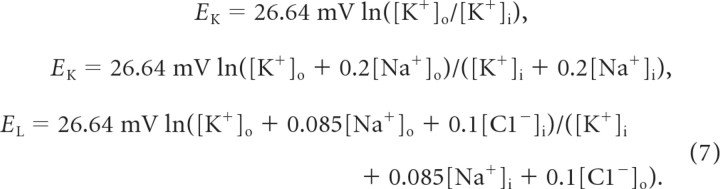The main properties of the model dynamics, such as existence and stability of the “physiological” asynchronous state and existence and stability of the epileptic state characterized by transitions between fast runs and slow bursting, were tested against synaptic and intrinsic parameter change to ensure structural stability of the model. This included varying of synaptic coupling, maximal conductances of intrinsic currents and parameters characterizing efficiency of [K⁺]_o regulatory system.

Results

The local extracellular potassium concentration [K⁺]_o reflects a spatiotemporal average of local neuronal activity since neuronal action potential firing predominantly determines [K⁺]_o. Previously, strongly elevated [K⁺]_o has been implicated in pathological activity patterns that are characterized by neuronal hyper-activation since an increase in [K⁺]_o causes a decrease in the driving force of potassium currents that play a key role in repolarizing neurons. However, very little attention has been paid to how networks are resilient to transient increases in [K⁺]_o caused by activity without triggering pathological hyperactivity. In fact, the question of understanding the transition dynamics from physiological to pathological network activity has been mostly avoided by choosing parameters or experimental conditions to reach an (artificial) set point where seizure-like activity dominates. We here revisit the role of [K⁺]_o dynamics to investigate whether they may play a role in mediating a “multistability-mediated dynamic repertoire” that includes physiological and pathological activity states coexisting in the same network.

To address this question, we used a conductance-based computational network model of a cortical circuit that was composed of pyramidal cells (PYs) and fast-spiking inhibitory interneurons (INs) for our simulations. The model neurons were endowed with a rich set of intrinsic conductances to reproduce the experimental observation that cortical neurons can exhibit both tonic firing and intrinsic bursting depending on [K⁺]_o (Jensen et al., 1994; Fröhlich and Bazhenov, 2006). Each model neuron was enclosed by an extracellular compartment that included a model of the [K⁺]_o regulatory apparatus (buffering by glia, neuronal reuptake, diffusion). All neurons in the network received random afferent synaptic input. We first tested for asynchronous, sparse activity and then investigated the effect of transient increases in afferent excitatory input without changing any model parameter to identify whether (1) such a network can exhibit a “multistability-mediated dynamic repertoire” and (2) under what conditions transitions between stable states occur.

Physiological activity in a network with [K⁺]_o dynamics

For the baseline afferent input, the model network exhibited asynchronous firing with low average firing rate accompanied by minor local [K⁺]_o fluctuations initiated by individual action potentials (Fig. 1A, Subthreshold membrane voltage map for all PYs; Fig. 1B, [K⁺]_o map). Throughout the simulations, the network activity remained stable with average firing frequencies of 1.18 Hz and 9.96 Hz for PYs and INs, respectively (Fig. 1C, Firing frequency distribution histograms). The [K⁺]_o fluctuations in the extracellular compartment surrounding a given cell (e.g., PY2, Fig. 1D) were primarily determined by the action potential firing of the corresponding cell yet action potentials in neighboring cells also contributed by K⁺ diffusion. Thus, the transient increases in [K⁺]_o during low-frequency activity did not cause an activity-outlasting increase in [K⁺]_o. With these simulations, we established that the model is capable of exhibiting physiological activity in presence of [K⁺]_o dynamics. We next studied the stability of this physiological state in response to transient increases in afferent input.

Figure 1.

Physiological activity in cortical network with [K⁺]_o dynamics. A, Color-coded activity map of 200 PYs (cool and hot colors indicate hyperpolarization and depolarization, respectively). B, Color-coded [K⁺]_o map corresponding to activity in A. C, Firing rate histograms for pyramidal cells and inhibitory interneurons. D, Top, Overlaid membrane voltage traces of three neighboring pyramidal cells (PY 1, PY2, and PY 3 in blue, black, and red, respectively). Bottom, [K⁺]_o in extracellular compartment surrounding PY 2. Minor deflections stem from action potentials in neighboring cells PY 1 and PY 3 (diffusion), major deflection from action potentials in PY 2.

Prolonged increase in global input triggers pathological activity

So far, we have established the stability of an asynchronous, low-frequency firing regime in presence of [K⁺]_o dynamics. We next investigated whether the network can respond to an increase in afferent excitatory drive without switching to pathological network dynamics. We tested for such resilience of the network to excitatory input by applying perturbations of different length to the rate of excitatory synaptic input. To preclude spatial dynamics from buffering such an increase in excitation, all perturbations were uniformly applied to all PYs.

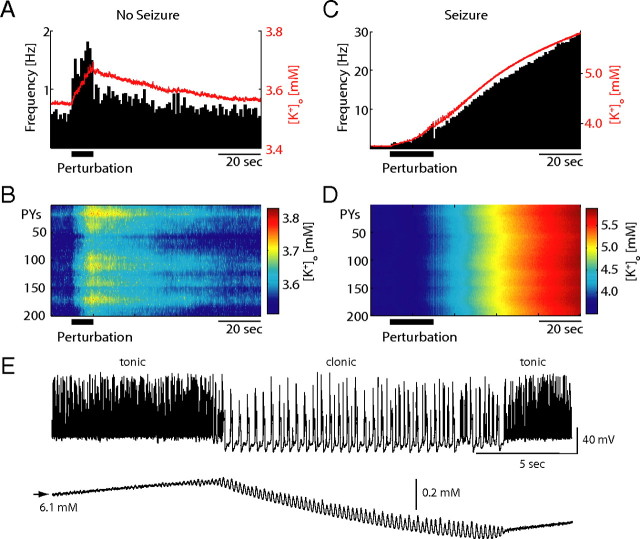
A transient increase (duration T = 10 s) in the afferent input (“perturbation”) to the PY population resulted in an almost immediate increase in the average PY firing rate (Fig. 2A, horizontal bar: perturbation duration, histogram). In contrast, [K⁺]_o (averaged across network, red line in Fig. 2A) increased only gradually by activity-dependent accumulation of K⁺ ions in the extracellular space over the entire interval of elevated afferent input. At the offset of the input perturbation, [K⁺]_o recovered back to its resting value (Fig. 2B, color-coded [K⁺]_o for entire network as a function of time). Due to the relatively slow recovery of [K⁺]_o after the offset of the perturbation, the averaged firing-rate did not instantaneously recover back to base-line but rather exhibited a similarly slow recovery. Thus, this perturbation of the PY firing did not elicit seizure-like activity and the network eventually returned to the stable physiological activity state. For such perturbations, [K⁺]_o alterations were delayed relative to changes in the activity level due to the slow rate of [K⁺]_o accumulation. In the case of more prolonged perturbations (T = 20 s), however, sufficiently elevated [K⁺]_o prevented the network from returning to the physiological state at the offset of the input perturbations (Fig. 2C, firing histogram and average [K⁺]_o; Fig. 2D, color-coded [K⁺]_o). Rather, both [K⁺]_o and activity levels further increased until the network converged to another stable yet dramatically different activity mode that was characterized by network-wide hyperactivity. In contrast to the previously shown shorter perturbation, [K⁺]_o was sufficiently elevated at the end of the longer perturbation such that positive feedback between neural firing and [K⁺]_o occurred for the same input level that previously supported stable physiological activity levels (Fig. 1). This second stable network state qualitatively resembles pathological activity patterns that are associated with neocortical epileptic seizures (Sypert and Ward, 1974; Jensen and Yaari, 1997). Specifically, this pathological network state is patterned into alternating epochs of tonic firing and clonic bursting (Fig. 2E). This seizure-like state represents a second stable network state as it (1) lasted for the duration of the simulations (up to 500 s, data not shown) and (2) was resilient to a range of perturbations in the afferent excitatory drive. In addition, [K⁺]_o fluctuates during the pathological state yet fails to exhibit unstable “runaway” dynamics. Therefore, identical cortical networks can exhibit either physiological or pathological activity patterns without any change in any parameters of the network. Rather, in agreement with our hypothesis of “multistability-mediated dynamic repertoire,” a sufficiently long yet transient global perturbation in the afferent excitatory drive can mediate a transition between these fundamentally different activity regimes.

Figure 2.

Transition from “physiological” to “pathological” activity. A, Average PY firing frequency (black histogram) and average [K⁺]_o trace (red) for 10 s perturbation (increase in afferent input). The average firing frequency increased instantaneously while [K⁺]_o increased and decreased only gradually. B, Color-coded [K⁺]_o map. C, Same representation as in A but for a 20 s perturbation that is long enough to sufficiently increase [K⁺]_o for seizure initiation. D, Color-coded [K⁺]_o map. E, The pathological seizure state is characterized by epochs of tonic and clonic activity. Top, PY membrane voltage trace. Bottom, Corresponding [K⁺]_o trace.

Mechanism of transition from physiological to pathological activity state

The above results suggest that the duration of increased neuronal activity determined whether a transition into the pathological network state occurred. Since we found [K⁺]_o to increase during the input perturbation, we tested whether there was a corresponding elevation of [K⁺]_o above which a transition to the pathological network state occurred. We systematically varied the duration T of the globally elevated afferent input to achieve different peak [K⁺]_o values at the offset of the perturbation (average [K⁺]_o traces in Fig. 3A). For T ≤ 15 s, the network only exhibited the physiological activity pattern (traces labeled “no seizure” in Fig. 3A). For input perturbations longer than that, however, increased afferent synaptic input invariably initiated a transition into pathological, seizure-like discharge patterns (traces labeled “seizure” in Fig. 3A). A closer consideration of the average increases in [K⁺]_o that were caused by perturbations of different duration suggests that [K⁺]_o values indeed had to reach a critical value for the transition into the seizure state to occur (estimated threshold indicated by dashed line in Fig. 3B). Interestingly, however, the average [K⁺]_o values at the offset of the elevated input (Fig. 3B, zoom in of region of interest from Fig. 3A) were initially very similar for values of T that failed and succeeded in causing a transition from physiological to pathological activity. Since the exact determination of a [K⁺]_o threshold was difficult when only considering the network-wide average, we then determined the [K⁺]_o values in the extracellular compartments around individual neurons. In agreement with the average traces (Fig. 3A,B), the histogram of these values (averaged over 1 s after offset of perturbation) for T = 15 (no seizure) and T = 16 (seizure) strongly overlapped (Fig. 3C). This may explain the experimental difficulty in identifying a threshold value from a single local [K⁺]_o measurement (Sypert and Ward, 1974) (see also Fig. 4C below). In fact, our model predicts that [K⁺]_o measurements in a single local area in experiments without seizure initiation could exceed similar measurements in another experiment where a seizure was initiated. In sum, our modeling results support the role of the previously proposed threshold of [K⁺]_o for the initiation of pathological network dynamics (Somjen, 2004; Fröhlich et al., 2008b) yet we predict that clean experimental establishment with single location measurements of such a threshold may be elusive.

Figure 3.

Threshold for seizure initiation. A, Average [K⁺]_o traces for perturbation durations ΔT = 5, 10, and 15 s (no pathological activity induced) and ΔT = 16, 17, 18, 19, 20 s (transition into pathological seizure state). B, Same as in A but with increased temporal resolution. C, Histograms of [K⁺]_o at perturbation offset across the PY network (averaged over 2 s) for ΔT = 15 and 16 s (“no seizure” and “seizure”). D, Network with frozen [K⁺]_o exhibited constant activity level during perturbation without transition to pathological activity state. E, Prolonged reduction of the afferent input triggered switch back to physiological state. Left, Color-coded PY activity map. Right, Sample PY membrane voltage trace (top) and corresponding [K⁺]_o trace (bottom). Plots show alternating epochs of tonic firing and slow bursting interrupted by reduction in afferent input (indicated by vertical arrow). At the onset of the input reduction, the network switched to bursting and [K⁺]_o returned back to baseline.

Figure 4.

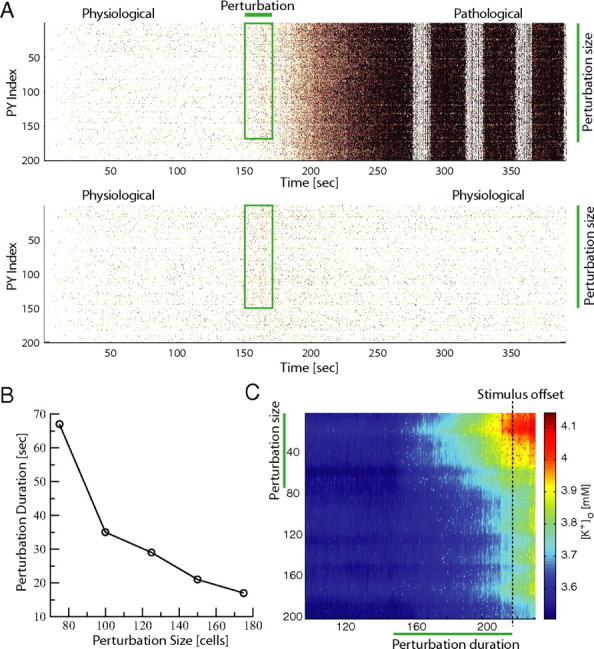
Spatial network dynamics. A, Perturbation needs to span a substantial number of PYs for a transition into the pathological network state to occur. Perturbation that targeted 175 contiguous PYs elicited a transition from physiological to pathological network activity (top) whereas the same duration perturbation applied to 150 PYs failed to cause a transition (bottom). B, Critical perturbation duration to elicit state transition to pathological activity depends on the size of stimulated cell population (perturbation size). C, Color-coded [K⁺]_o map for simulation critical stimulation (duration: 68 s; size: 75 cells). Note variability of the [K⁺]_o across the network.

To further establish the causal role of [K⁺]_o in the seizure initiation process, we ran control simulations where we froze all [K⁺]_o values in advance of the input perturbation. With [K⁺]_o dynamics absent, activity levels increased and decreased in close temporal alignment with the change in afferent input (Fig. 3D). Independent of the duration of the perturbation, the network always returned to the physiological state. Therefore, the inclusion of [K⁺]_o dynamics causes the existence of the second stable network state. Input perturbations of sufficient length to increase [K⁺]_o above a critical value caused a transition from the physiological to the pathological network state. Above this [K⁺]_o threshold value, neural activity and [K⁺]_o were transiently linked in a positive feedback loop between neural activity and intrinsic excitability determined by [K⁺]_o. The pathological networks state itself, however, represent a stable state that was robust to perturbations and prevented further increases in [K⁺]_o.

Further confirmation for the existence of network bistability between physiological and pathological activity patterns results from the existence of perturbations that are capable of switching the network back to the physiological state. Indeed, when we significantly reduced the afferent input (Fig. 3E, labeled arrow), the network switched from tonic firing to bursting mode during which [K⁺]_o monotonically decreased. At [K⁺]_o = 4.85 mm (network average), the network returned to physiological random firing and [K⁺]_o returned back to baseline with accelerated pace (PY activity map in Fig. 3E, left panel; sample membrane voltage and corresponding [K⁺]_o trace in right panels).

Global stability versus local ignition

So far, we have used different durations of global (i.e., network-wide) perturbations to probe the dynamic repertoire of the network model with [K⁺]_o dynamics. We next investigated how spatial network dynamics contribute to the transition between the physiological and pathological stable network states. The neurons in the model network are coupled through recurrent excitation, feedback inhibition (mediated by fast-spiking inhibitory interneurons), and diffusion of K⁺ in the extracellular space. Therefore, perturbations of a subset of neurons can potentially have a broad range of effects. Specifically, on the one hand, excitation within the network can spread both via excitatory synaptic connections and via K⁺ diffusion. On the other hand, additional recruitment of feedback inhibition and reduction of local peaks in [K⁺]_o by diffusion can potentially quell increases in local network excitation. To probe how this complex interplay of enhancing and dampening by spatial dynamics affects the transition from the physiological to pathological network state, we considered (1) the effect of the “perturbation size” (fractions of neuron subject o transient increase in afferent excitation) and (2) the role of local, sustained increases in [K⁺]_o.

We found that limiting the spatial extent of the perturbation (i.e., reducing the number of PYs subject to a transient increase in afferent excitatory drive) increases the resilience of the physiological state to such perturbations. A perturbation (T = 20 s) that targeted a contiguous block of 175 of the 200 PYs caused a transition to the pathological network state (Fig. 4A, top, spiking activity). However, if the same perturbation was reduced to target only 150 of 200 PYs, no such transition occurred (Fig. 4A, bottom, spiking activity). Thus, on the one hand, in addition to extending the duration of the perturbation (Fig. 3), increasing the perturbation size represents another pathway toward a switch to pathological network activity. On the other hand, the smaller the perturbation size, the longer the perturbation can last without causing a switch to pathological activity (Fig. 4B). This explains the stability of the normal physiological network against even long perturbations as long as they do not target large fractions or even the entirety of the network. Importantly, when a prolonged yet local perturbation is just sufficient to trigger a switch to the pathological state (Fig. 4C), the values of [K⁺]_o at the stimulus offset (Fig. 4C, vertical line) vary substantially across the population of neurons. These results provide further evidence for why a [K⁺]_o threshold for seizure initiation cannot be determined from any single site measurements. Blocking K⁺ diffusion caused a transition to the pathological state (data not shown) for both perturbation sizes. Therefore, K⁺ diffusion here acts as a mechanism to stabilize the physiological state in case of local perturbations. Together these simulations show that transient, spatially constrained, moderate perturbations in the afferent excitation are unlikely to trigger a transition away from physiological activity in presence of K⁺ diffusion.

This result suggests that extreme events are required to exceed level of activity required for K⁺ feedback to take over the network dynamics in the normal (nonepileptic) brain. Patients suffering from epilepsy would have a reduced basin of attraction for the stable physiological state such that random input fluctuations can more easily cause a transition into the seizure state. Specific forms of activity, such as relatively synchronized neuronal activity during sleep, could facilitate transitions to the seizure state which may explain higher likelihood of seizures during sleep (Steriade 1974; Gigli et al., 1992). Brains without detectable seizures would have cortical networks with much larger domains of attraction for the physiological activity state at the expense of very small (and thus hard to reach and persist in) domains of attraction for the pathological network state.

However, if the perturbation is of a nature such that it has a very pronounced, unphysiological effect on individual neurons, it is sufficient for the perturbation to be constrained to a small population of neurons to eventually cause a network-wide switch to pathological activity. Specifically, we modeled a local network abnormality by introducing an extra K⁺ source in the middle of network (extracellular compartment of PY 100). As a result, PY 100 rapidly switched to a pathological bursting mode (Fig. 5). As a consequence of the excess K⁺ spreading through the network by diffusion, eventually the entire network switches to the pathological activity state characterized by alternating epochs of tonic firing and slow bursting with exception of the few cells close to the network abnormality that continue to display pathological bursting (Fig. 5). Further support for the key role of K⁺ diffusion comes from the fact that abolishment of all synaptic connections between PY 100 and the remainder of the network had no qualitative effect on the network dynamics (data not shown). These results show that even spatially constrained perturbations can play the role of the epileptic focus by recruiting the entire network and inducing a transition from physiological to pathological activity by means of K⁺ diffusion if these perturbations reflect a failure of the potassium regulatory mechanisms.

Figure 5.

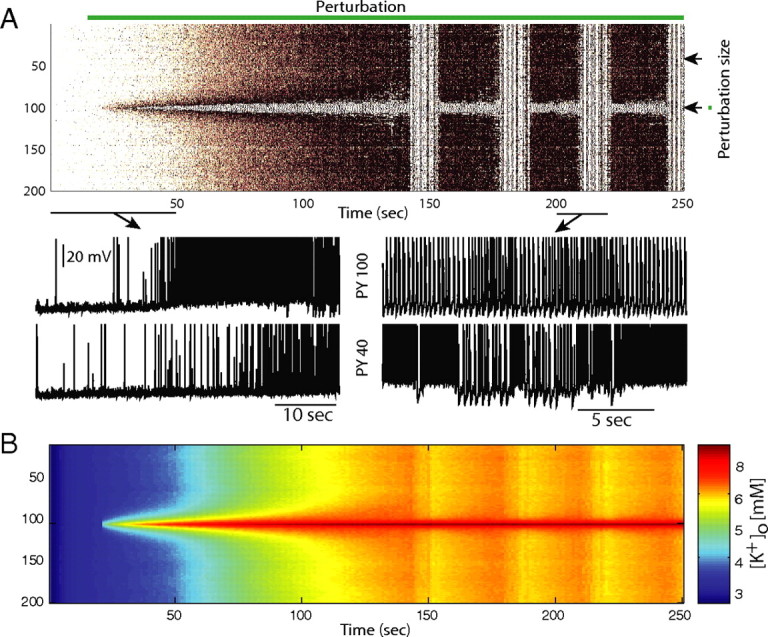
Pathological state initiation by local imbalance in [K⁺]_o. A, Extracellular potassium source in the center of the network is sufficient to recruit the entire network into a transition to the pathological state. PYs in the areas of the [K⁺]_o abnormality exhibit bursting behavior and do not show epochs of tonic firing as the remainder of the network. B, Color-coded [K⁺]_o map.

Spontaneous transitions from physiological to pathological activity

So far, we characterized the types of perturbations that can induce a transition from the physiological to the pathological activity state. To determine whether such transitions can occur spontaneously, we ran simulations where we randomly modulated the amount of afferent excitation the entire network receives. The resulting fluctuation in spiking activity in the network modeled the commonly observed changes in activity levels as a function of inputs from other cortical networks and areas. In agreement with the above results, we found that the network can support a broad range of activity levels within the stable state of physiological activity (Fig. 6, top two traces). However, in other cases with more prolonged epochs of globally elevated activity, transition into the pathological activity state occurred (Fig. 6, bottom two traces). These simulations show that the network can support both physiological and pathological activity in presence of randomly fluctuating input. Also, the transition from physiological to pathological activity occurs as a function of the afferent input and therefore in a random and spontaneous fashion.

Figure 6.

Spontaneous transitions from physiological to pathological network state. Network responds with changes in firing rate to random changes in the afferent excitatory input without transition into the seizure state (top two traces). However, if random fluctuations cause a prolonged increase in afferent input, transitions into seizure state occur (bottom two traces).

K⁺ clearance defines resilience to network transitions

Together, our modeling results predict that both physiological and pathological activity patterns represent stable network states. Importantly, no parameter change was necessary in our model to elicit either of the two activity patterns. Therefore, neural circuits in brains of patients suffering from pathologies associated with neural hyperactivity may exhibit intrinsic multistabilities that form the substrate for seemingly normal brain activity during prolonged times that yet is interspersed with bouts of pathological activity. As a consequence of this hypothesis, our model further predicts that (subtle) differences in the biophysical mechanism that mediates this bistability may explain why certain people suffer form pathological network activity whereas others do not. From a dynamic system viewpoint, the resilience to perturbations can be considered as the size of the basin of attraction of the stable physiological activity state. Specifically, the larger the size of the basin of attraction, the more severe transient perturbations the network can withstand without switching to the pathological network state. We thus hypothesized that the size of this basin of attraction of the physiological network state and therefore the likelihood of triggering a transition from physiological to pathological activity depends on the “efficiency” of the [K⁺]_o regulating systems in maintaining baseline [K⁺]_o in the presence of increase neural activity. To test this hypothesis, we altered the threshold parameter [K⁺]_o(th) in our model that defines the [K⁺]_o dependence of the rate by which the glial system clears extracellular potassium ([K⁺]_o threshold level of binding rate of free extracellular K⁺ to the glial buffer). Specifically, an increase of this threshold, [K⁺]_o(th), reduces the binding rate constant for a given level of [K⁺]_o and therefore renders the glial potassium clearance apparatus less efficient. A decrease of [K⁺]_o(th) has the opposite effect. We determined the minimal duration of elevated input to the network that caused a transition out of the basin of attraction of the physiological network state (Fig. 7A). This critical perturbation duration measures the size of the basin of attraction of the physiological state. For [K⁺]_o(th) less than ∼10 mm, no perturbation of any duration induced transition to the pathological network state. Therefore, this regime may model cortical networks with strong resilience to pathological hyperactivity. Higher values of [K⁺]_o(th) decreased the critical perturbation duration which saturated at ∼10 s for [K⁺]_o(th) >15 mm. Networks with such weakened resilience to excitatory perturbations and therefore smaller basins of attraction for the physiological activity state may correspond to networks in brains of seizure-prone patients. These data show (1) that the efficiency of the glial potassium clearance apparatus defines the duration of increased input required to cause a transition out of the stable physiological network state and (2) that the same perturbation can trigger an epileptic seizure in a network with a higher value of [K⁺]_o(th) but only cause a transient increase in activity in a network with a lower value of [K⁺]_o(th) (Fig. 7B, representative example).

Figure 7.

Effect of glial buffering of excess K⁺ on network activity. Decreased effectiveness of the glial uptake system reduced the amount of excitatory input the network was able to withstand in the physiological state without switching to the pathological state. A, Critical stimulus duration required to trigger a transition to pathological network activity as a function of the threshold [K⁺]_o(th) concentration (when [K⁺]_o = [K⁺]_o(th) the binding rate of the free extracellular K⁺ to the buffer is ½ of the unbinding rate). B, The same stimulus (20 s, shown with box) triggered a transition into the seizure state for [K⁺]_o(th) = 17 mm but failed to do so for [K⁺]_o(th) = 12 mm. Spikes are truncated at V_m = 0 mV for visualization purposes.

Discussion

Multistability-mediated dynamic repertoire

In agreement with our hypothesis of “multistability-mediated dynamic repertoire,” we found that a cortical network can exhibit two distinct activity patterns without any change to the model parameters. This network bistability between physiological and pathological activity was mediated by the inclusion of the commonly overlooked yet ubiquitous biophysical mechanism of extracellular potassium concentration regulation. Sufficiently strong yet transient perturbations in the afferent input triggered a transition from the stable sparse asynchronous activity to the stable tonic-clonic seizure state.

The emergence of the network bistability proposes a fundamentally different viewpoint on how cortex can exhibit different activity states. In contrast to the “parameter-mediated dynamic repertoire,” the dynamic richness of our network model is not mediated by external, modulating factors but rather is a direct consequence of the dynamic mechanism endogenous to the network. This novel framework may eliminate the common limitation of current conceptual and mathematical models that invoke a sustained change in parameters or input levels to explain both the transitions between different activity regimes and the persistence of such states. It remains to be seen to which other cortical activity states beyond epileptic seizures this model of network multistability will apply. Furthermore, our findings suggest that the experimental study of transient perturbations to active neuronal networks may provide novel insights into network dynamics.

Network multistability versus runaway dynamics

We found that a cortical network with K⁺ dynamics exhibits a stable network activity state that resembles both electrographic seizures in animal models (Steriade et al., 1998) and tonic-clonic seizures in humans (Niedermeyer, 2002). The consideration of K⁺ dynamics as a factor in epileptic seizures has a long history without ever having found broad acceptance as a mechanistic explanation for seizure dynamics (Somjen, 2002, 2004; Park and Durand, 2006; Fröhlich et al., 2008b). Although our model shows that the inclusion of K⁺ dynamics is essential for the occurrence of the stable seizure state, our results suggest a revision of the original hypothesis on the role of K⁺ in epileptic seizures (Green, 1964; Fertziger and Ranck, 1970). According to this so-called potassium accumulation hypothesis, an elevation in [K⁺]_o depolarizes neurons and therefore increases their activity level. As a result, further accumulation of [K⁺]_o occurs. Based on this positive-feedback model, it was hypothesized that there is a critical value of [K⁺]_o for which seizures are triggered, that [K⁺]_o monotonically increases during seizures, and that seizures terminate when [K⁺]_o is sufficiently elevated to induce depolarization block. In vivo measurements of [K⁺]_o during electrographic seizures, however, failed to provide evidence in support of this hypothesis (Somjen, 1979).

In contrast, we here show that [K⁺]_o dynamics cause the emergence of a second stable network state characterized by seizure-like activity instead of unstable runaway dynamics. Although seizure initiation (transition from normal to pathological activity) is dominated by a positive-feedback reaction in our model, the seizure itself represents a stable network state. The robustness of a stable state in presence of multistability is measured by the size of its basin of attraction which defines how strong perturbations need to be to move the network into a different state (Fig. 8A). Our results propose that duration, size (spatial extent), and amplitude of a transient excitatory perturbation contribute to the overall effect of the perturbation in the case of a cortical network with K⁺ dynamics.

Figure 8.

Conceptual model of bistability-mediated dynamic repertoire in cortical network mode with [K⁺]_o dynamics. A, Physiological state is resilient to perturbations in afferent excitatory drive as long as duration, strength, and size are within limits. B, Schematic illustration of bistability between physiological and pathological network activity states. An epileptic seizure occurs as the network switches from the physiological to the pathological state (top). In nonepileptic brains, the basin of attraction of the physiological state is comparably bigger than the basin of attraction of the pathological seizure state (bottom). Perturbations in the form of transient increase in excitability are very unlikely to switch the network to the pathological seizure state. In the case of an epileptic brain, however, the domain of attraction of the seizure state is expanded at the expense of the physiological activity state. The same perturbation that failed to trigger a seizure in the nonepileptic brain suffices to trigger a seizure.

Our results suggest that the pertaining dynamics can be conceptualized as a dynamic system with two stable states (Fig. 8B). The network can either be in the physiological or the pathological activity state. As the overall network excitability becomes elevated, the likelihood for the network to be in the pathological state (red) instead of the physiological state (blue) is increased. Both activity states are stable states and thus represented by local minima to which the system converges. The broader and deeper the trough is that corresponds to a given activity state (i.e., domain of attraction) is, the more resilient is the state to perturbations. Therefore, in this conceptual model, the relative size of the domain of attraction of the physiological state defines the resistance to seizure initiation. On the other hand, the relative size of the domain of attraction of the seizure state may define how pronounced and prolonged individual seizures are. Different relative sizes of these two domains of attractions will thus define whether and how severely a brain will develop epileptic seizures. Together with the increasing evidence for aberrations in potassium regulation apparatus in human patients with epilepsy (Hinterkeuser et al., 2000; Schroder et al., 2000; Binder and Steinhäuser, 2006) and animal models (Grisar et al., 1992; Jansen et al., 2005; Ivens et al., 2007), our simulations support the key role of [K⁺]_o in cortical seizures and yet suggest a substantial revision of the conceptual framework of seizure dynamics.

Elevated extracellular K⁺ and other epileptogenic factors

As for any model of a highly complex dynamic system, our model has limitations and does not incorporate all mechanisms that potentially contribute to shaping the seizure dynamics. Deficiencies of the K⁺ regulatory system that reduce its effectiveness in controlling [K⁺]_o and facilitate [K⁺]_o increase may synergistically interact with other epileptogenic factors (e.g., structural reorganization after loss of neurons). For example, in the temporal lobe epilepsy model, the recurrent mossy fiber pathways associated with loss of hilar interneurons mediate reverberating excitation that can reduce the threshold for paroxysmal granule cell synchronization. Even a modest elevation of extracellular K⁺ (by 1.25 mm) more than triples the probability that mossy fiber stimulation evokes an epileptiform response (Nadler, 2003). Other mechanisms may shift the balance between synaptic excitation and inhibition. For example, accumulation of intracellular Cl⁻ during seizures may shift its reversal potential and thus reduce the inhibiting effect of inhibition of GABA_A receptor-mediated synaptic currents.

The focus of this paper has been seizure initiation. Although sufficiently strong random input fluctuations can lead to spontaneous seizure termination, we have not directly investigated termination of epileptiform activity and this mechanism does not explain the characteristic time-scale of seizure duration or the post-ictal depression state commonly observed after tonic-clonic seizures. A variety of factors including synaptic depression, fast decrease of the extracellular K⁺ concentration mediated by Na⁺/K⁺ exchange, activity-dependent outward currents (e.g., K(Na)), progressive depolarization of Cl⁻ reversal potential that changes balance between excitation and inhibition (Frohlich et al., 2007a) as well as other factors may contribute to the termination of a seizure and promote post-ictal depression. These factors are less likely to be significant near seizure onset.

Multistability in the brain

We have explored cortical models to confirm our hypothesis that multistable behavior of cortical networks can explain the (spontaneous) occurrence of qualitatively different network states. Transient perturbations of sufficient strength can induce transitions between these different stable states. Bistable dynamics is a structurally stable property of our model and is likely to be qualitatively preserved in a broad class of models. As the main parameters in the model were continuously varied the model dynamics changed smoothly rather than abruptly. Achieving bistability did not require precise parameter tuning. Indeed, we analyzed the existence and stability of the “epileptic” state represented by transitions between fast runs and slow bursting previously (Fröhlich and Bazhenov, 2006; Frohlich et al., 2006, 2007b). By including afferent synaptic inputs in the model we showed here that a more “physiological” state characterized by asynchronous, low-frequency firing was also stable as long as the mechanisms responsible for control of [K⁺]_o (pumps, glial buffering, diffusion, etc) were sufficiently strong to accommodate the flow of K⁺ to the extracellular space for the range of physiological activities.

Bistable and multistable network behavior has received attention as a computational paradigm for specialized cortical circuits that perform short-term memory-related tasks, as for example, prefrontal cortical circuitry, that exhibit persistent activity that outlasts the stimulus to be remembered by the subject (Goldman-Rakic, 1995; McCormick et al., 2003; Shu et al., 2003). Computational models of this working memory have focused on the role of recurrent excitation in mediating this bistability between relative quiescence (baseline) and sustained elevated firing activity (Wang, 2001). Our work generalizes this concept of multistable network behavior to the case of coexistence of physiological and pathological (tonic-clonic) activity as an extreme case of “multistability-mediated dynamic repertoire.” Based on our findings, we hypothesize that this framework can be extended to other pathological network states that are characterized by hyperactivity.

In conclusion, our modeling suggests a shift away from parameter optimization to reproduce different network states toward the study of the role of transient perturbations to induce transitions between different stable network states (Shu et al., 2003). Combined with the discovery and further study of biophysical mechanisms that mediate multistability (e.g., ion concentration dynamics, short-term synaptic plasticity), such an approach to probe the system with perturbations instead of complex parameter modulation may lead to a more in-depth and mechanistic understanding how the rich spectrum of cortical network activity patterns arises.