Behavior of a train of droplets in a fluidic network with hydrodynamic traps

Abstract

The behavior of a droplet train in a microfluidic network with hydrodynamic traps in which the hydrodynamic resistive properties of the network are varied is investigated. The flow resistance of the network and the individual droplets guide the movement of droplets in the network. In general, the flow behavior transitions from the droplets being immobilized in the hydrodynamic traps at low flow rates to breaking up and squeezing of the droplets at higher flow rates. A state diagram characterizing these dynamics is presented. A simple hydrodynamic circuit model that treats droplets as fluidic resistors is discussed, which predicts the experimentally observed flow rates for droplet trapping in the network. This study should enable the rational design of microfuidic devices for passive storage of nanoliter-scale drops.

INTRODUCTION

Droplet-based microfluidics is emerging as a high throughput means to conduct biochemical reactions in nanoliter-scale immiscible fluid plugs.^{1, 2} In lab-on-chip applications such as protein crystallization,^{3, 4} nucleic acid amplification,^{5, 6, 7} and single-cell analysis,^{8, 9, 10} it is beneficial to store droplets on the device for monitoring the kinetics of the biochemical reactions. Both passive^{11, 12, 13, 14, 15, 16} and active^{7, 17, 18, 19} methods have been reported in the literature to array and store droplets in microfluidic devices. Passive approaches are particularly attractive because they scale favorably with an increase in system size. Recently, Shi et al.¹¹ reported a passive means to array and store microfluidic droplets. The method involves introducing a train of confined monodisperse droplets into a fluidic network containing a repeated sequence of loops as shown in Fig. 1a. Each loop consists of two branches with the lower branch containing a hydrodynamic trap. Two possibilities exist for droplets to be immobilized in the hydrodynamic trap. When the hydrodynamic resistance of lower branch (R_l) is smaller than the hydrodynamic resistance of the upper branch (R_u), the first droplet in the train enters the lower branch and has the possibility to get captured in the hydrodynamic trap as shown in Fig. 1b. If the droplet indeed gets captured, then the subsequent droplet chooses the upper branch because of the increased hydrodynamic resistance generated by the trapped droplet in the lower branch. We refer to this approach as direct trapping. Alternatively, when R_l>R_u, the first droplet will enter the upper branch, blocking the flow due to the hydrodynamic resistance of the moving droplet, and then the next droplet will enter the hydrodynamic trap in the lower branch and might get captured. We refer to this approach as indirect trapping as shown in Fig. 1c. Although it is evident that both the direct and indirect trapping approaches require precisely configuring the hydrodynamic resistance of the network to the hydrodynamic resistance of the individual droplets, the behavior of a train of droplets in which the hydrodynamic resistive properties of the network are varied has not been investigated to date. In this study, we vary the ratio of R_l to R_u in the loop and characterize the dynamics of a droplet train. We find that the droplets undergo a variety of dynamics including trapping, breakage, and squeeze-through. A state diagram is presented characterizing these behaviors. We also present a simple model that is able to predict the flow conditions under which droplet trapping is experimentally observed.

Figure 1.

(a) Schematic of the microfluidic trapping device. (b) Droplet capture in the traps using direct trapping approach, where R_l<R_u. (c) Droplet capture in the traps using indirect trapping approach, where R_l>R_u.

MATERIAL AND METHODS

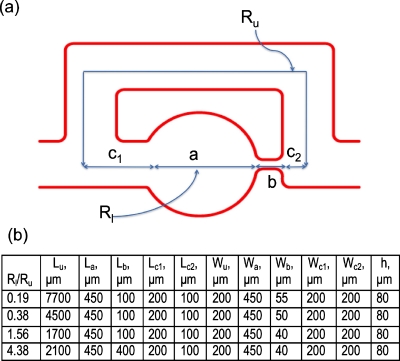
We fabricated microfluidic devices with four different ratios of lower to upper branch resistance (R_l∕R_u=0.19,0.38,1.56,4.38) using soft lithography.²⁰ The ratio was tuned by varying the width and length of the constriction in the hydrodynamic trap and, the length of the upper branch as shown in Fig. 2. The trap size (w_a=450 μm) and device height (h=80 μm) were fixed. Here, both of the channel resistances (R_l and R_u) were calculated using the exact analytical solution of Poiseuille flow in a rectangular channel along each path [Eq. 1] from measured geometry dimensions,²¹

$$\text{R}=\frac{12\mu \text{L}}{{\text{h}}^3\text{w}}{\left[1-\sum _{\text{n},\text{odd}}^{\infty }\frac{1}{{\text{n}}^5}\times \frac{192}{{\pi }^5}\times \frac{\text{h}}{\text{w}}\text{tanh}\left(\frac{\text{n}\pi \text{w}}{2\text{h}}\right)\right]}^{-1}.$$ (1)

The upper branch is a rectangular channel with uniform width (Fig. 2), so the hydrodynamic resistance is readily calculated using Eq. 1. The lower branch is divided into four sections—a, b, c1, and c2 (as shown in Fig. 2)—for calculating hydrodynamic resistance. Section a corresponds to the trap, which is circular in shape in top view and rectangular in cross-section. Although the hydrodynamic resistance of the lower branch can be experimentally measured using the comparator technique,^{22, 23} here we approximate the circular shape with the square that circumscribes it. This approximation does not introduce significant error in the calculation of the total lower arm resistance since the trap contributes less than 3% to the total hydrodynamic resistance of this arm.

Figure 2.

(a) Schematic of a single loop highlighting the various geometric dimensions. (b) The table shows four different ratios of lower to upper branch resistance that were tuned by varying the width (w) and length (l) of the constriction in the hydrodynamic trap and the length of the upper branch. The subscripts denote the various sections of the geometry.

A train of confined aqueous droplets was generated in an oil phase (mineral oil, Sigma Aldrich) containing 2 wt % Span 80 at the T-junction using syringe pumps (PHD 2000, Harvard Apparatus, Massachusetts). The interfacial tension (γ) for this system was measured in previous work as 5 mN∕m.²⁴ The behavior of the droplets was visualized using a stereo microscope (Stemi 2000C, Zeiss, New York) and camera (PCO 1200s, Cooke Corp., Michigan) at 5–10 frames∕s. The dynamics of the droplet train was investigated in each device by choosing three different oil flow rates (Q_o=10, 20 and 50 μl∕h) as the basis and adjusting the water flow rate (Q_w) to yield different ratios of Q_w∕Q_o (0.1, 0.3, 0.5, 0.8, and 1) as shown in Fig. 3. Note that the droplet size was found to be a function of flow rate ratio rather than the individual flow rates;^{25, 26} therefore, in Fig. 3, the different flow rate ratios represent droplets of different size. Upon increasing Q_w∕Q_o from 0.1 to 1, we find that drop length increases from ≈200 to 500 μm, irrespective of Q_o. We performed the experiments in the capillary number range of Ca≈10⁻⁴–10⁻³ and Reynolds number Re<0.004. In this study, Ca=μ_oU∕γ and Re=ρ_oUh∕μ_o, where μ_o, ρ_o, and U are the viscosity, density, and mean velocity of oil phase, respectively.

Figure 3.

State diagram showing the four different behaviors observed in experiments at three different oil flow rates: (a) Q_o=10 μl∕h, (b) Q_o=20 μl∕h, and (c) Q_o=50 μl∕h. Images (d)–(g) are representative snapshots of these behaviors. Scale bar in all images correspond to 500 μm.

RESULTS AND DISCUSSIONS

State diagram for droplet trapping

In Fig. 3 we show the different droplet dynamics observed in the four devices. When R_l∕R_u=4.38, for all flow conditions, we find that droplets choose the upper branch bypassing the hydrodynamic trap in the lower branch [see Fig. 3d], indicating that the hydrodynamic resistance of the lower branch is still large even when confined droplets are present in the upper branch. We refer to this behavior as bypassing. Similar behavior has been observed in an investigation of traffic of unconfined droplets at a microfluidic bifurcation.²⁷

When R_l∕R_u=1.56, for Q_w∕Q_o=0.1–0.5 and at low Q_o (10 μl∕h), droplets get captured successfully in the hydrodynamic traps following the indirect trapping approach. We characterize this behavior as uniform trapping [Fig. 3e]. Interestingly, we find that doublets are trapped at these conditions because (i) the trap size is large enough to accommodate two droplets and (ii) when a droplet enters the hydrodynamic trap, it does not completely block the flow in the lower branch and the spacing between droplets is just right enough that the subsequent drop also enters the trap. In Fig. 4a (enhanced), we show a video of droplet trapping in the fluidic device with R_l∕R_u=1.56, Q_w∕Q_o=0.5, and Q_o=10 μl∕h. Such behavior has not been previously reported. In the same device, at higher Q_w∕Q_o (=0.8 and 1), the drop sizes were larger and they break at the junction of the loop. The fragmented parts of the drop remained in the traps. We refer to this behavior as break-up induced nonuniform trapping [Fig. 3f]. When the base oil flow rate is raised to 20 μl∕h, we observe uniform trapping only for Q_w∕Q_o=0.1; at other flow rate ratios, break-up induced nonuniform trapping was observed. At even higher base oil flow rate of 50 μl∕h, we do not observe any uniform trapping. Unexpectedly, at Q_w∕Q_o=0.1, we observe bypassing because the spacing between droplets was increased to such an extent that the droplet in the upper branch exits the loop before the subsequent droplet arrives at the junction, i.e., there is no hydrodynamic resistive feedback between the two droplets. However, at Q_w∕Q_o=0.3, drop size increased and spacing decreased, causing a hydrodynamic resistive feedback that led to break-up induced nonuniform trapping. At higher flow rate ratios (0.5, 0.8, and 1), the primary droplets split at the junction and the fragmented droplets, instead of remaining in the traps, squeezed through the hydrodynamic trap because of the higher flow rate. This behavior is identified as no trapping–squeeze-through in Fig. 3g. Thus, for the device with R_l∕R_u=1.56, we observed a variety of droplet dynamics. In this study, because of the larger trap size, we obtained mostly doublet drop trapping. We also conducted experiments (at the same flow rates of oil and water as in Fig. 3) in another device with R_l∕R_u=1.56 but with the trap size modified from 450 to 320 μm. In this case, we still observed the four different behaviors reported in Fig. 3 and single droplets being captured in the hydrodynamic traps as shown in Fig. 4b.

Figure 4.

Download video file ^{(14.6MB, avi)}

(a) Still image from the movie that shows uniform doublet trapping where the conditions were R_l∕R_u=1.56, Q_w∕Q_o=0.5, and Q_o=10 μl∕h. (b) Single droplet trapping in the device with R_l∕R_u=1.56 at Q_o=10 μl∕h and Q_w∕Q_o=0.3 (enhanced online). 1

In both the devices with R_l∕R_u<1, uniform trapping according to the direct trapping approach was found for only small drop size and lower base oil flow rates. At other flow conditions, no trapping–squeeze-through was observed.

Overall, we find that the behavior of droplets in this network depends on both the droplet size and droplet spacing and R_l∕R_u. The droplet size is determined by the flow rate ratio, and the droplet spacing is a function of the flow rate of carrying liquid and the flow rate ratio.^{25, 26} Thus, in Fig. 3, for a given oil flow rate, the abscissa represents droplets of increasing size. Alternatively, at a given flow rate ratio, increasing the oil flow rate yields increased droplet spacing. In our system, for effective trapping using the indirect approach, droplets need to be of a certain size otherwise they break. Likewise, the droplet spacing need to be optimal; otherwise, there is no hydrodynamic resistive feedback between droplets. This is particularly exemplified by the data in Fig. 3 for Q_w∕Q_o=0.1, where oil flow rates of 10 and 20 μl∕h lead to uniform trapping; however, an oil flow rate of 50 μl∕h leads to bypassing behavior.

A model to predict the flow rate for droplet trapping

To predict the flow rate range where uniform trapping was observed, we consider the equivalent Ohmic circuit of our fluidic network, as shown in Fig. 5, by treating the moving (R_md) and trapped droplets (R_td) as fluidic resistors. Here, we focus on a static model of the trapping process and do not consider other complex behaviors reported in Fig. 3. Note that when R_md is set to zero, the circuit sketched in Fig. 5 represents the direct trapping scheme. The conservation of flow and the fixed fluid pressure drop (ΔP_f) across the loop yields the following two relations:

$${\text{Q}}_{\text{o}}={\text{Q}}_{\text{u}}+{\text{Q}}_{\text{l}},$$ (2)

$$\Delta {\text{P}}_{\text{f}}=\left({\text{R}}_{\text{u}}+{\text{n}}_{\text{i}}{\text{R}}_{\text{md}}\right){\text{Q}}_{\text{u}}=\left({\text{R}}_{\text{l}}+{\text{n}}_{\text{j}}{\text{R}}_{\text{td}}\right){\text{Q}}_{\text{l}}.$$ (3)

In Eq. 2, Q_u and Q_l denote the flow rates in the upper and lower branches, respectively. In Eq. 3, we assume that the excess hydrodynamic resistance due to n_i number of droplets in the upper branch is given by the additive contribution from each droplet. The n_j number of droplets that enter into the hydrodynamic trap will remain in trap if the fluid pressure drop (ΔP_f) in the lower branch is less than (or equal to) the Laplace pressure gradient (ΔP_L) across the drop, i.e.,

$$\Delta {\text{P}}_{\text{f}}\le \Delta {\text{P}}_{\text{L}}=\gamma \left(1∕{\text{R}}_{\text{r}}-1∕{\text{R}}_{\text{f}}\right)\approx 2\gamma \left[\left(1∕{\text{w}}_{\text{b}}+1∕\text{h}\right)-\left(1∕{\text{w}}_{\text{a}}+1∕\text{h}\right)\right]=2\gamma \left(1∕{\text{w}}_{\text{b}}-1∕{\text{w}}_{\text{a}}\right),$$ (4)

where R_r and R_f are the radii of curvature at the rear and front ends of the trapped droplet, respectively,^{28, 29} and w_a and w_b are the trap and constriction widths, respectively. In Eq. 3, R_r and R_f are approximated by the sum of half-width and half-height of the constriction and the trap, respectively. Combining Eqs. 2, 3, 4, we arrive at a prediction for the critical oil flow rate (Q_o^*) needed to trap droplets. Note that Eq. 5 corresponds to critical oil flow rate for the indirect trapping process when R_md≠0 and direct trapping process when R_md=0,

$$\text{Q}_{\text{o}}{}^{\ast }\le \frac{\Delta {\text{P}}_{\text{L}}\left({\text{R}}_{\text{l}}+{\text{n}}_{\text{j}}{\text{R}}_{\text{td}}+{\text{R}}_{\text{u}}+{\text{n}}_{\text{i}}{\text{R}}_{\text{md}}\right)}{\left({\text{R}}_{\text{l}}+{\text{n}}_{\text{j}}{\text{R}}_{\text{td}}\right)\left({\text{R}}_{\text{u}}+{\text{n}}_{\text{i}}{\text{R}}_{\text{md}}\right)}.$$ (5)

Figure 5.

The equivalent Ohmic circuit of the microfluidic loop with hydrodynamic trap in which the moving and trapped droplets are identified as fluidic resistors R_md and R_td, respectively.

To predict the critical flow rate Q_o^* for trapping using Eq. 5, we need estimates of the hydrodynamic resistance of moving drop (R_md) and trapped drop (R_td) since all other quantities are known experimentally. Although it is possible to directly measure the hydrodynamic resistances of drops³⁰ using a microfluidic comparator technique,²³ here we use an indirect technique to estimate the bounds for R_md and R_td by analyzing the decisions (Figs. 67) that the drops made in network.³¹ In the foregoing analysis, we assume that the hydrodynamic resistance of the moving droplet is (i) independent of droplet size, (ii) independent of flow rate, and (iii) is not affected by the bends in branch. Similar to that discussed in Eq. 3, we assume that the hydrodynamic resistance of the individual droplets can be added regardless of their spacing. Given these assumptions, we illustrate the process for estimating the bounds on R_md by considering the instantaneous snapshots of droplet dynamics as shown in Fig. 6. Figure 6a shows a snapshot of the droplet dynamics in the device with R_l∕R_u=1.56 at a certain flow condition. The droplet highlighted by the arrow is about to enter the lower branch, implying that (A) R_u+R_md≥R_l or R_md≥(R_l−R_u)=4.51 kg∕s mm⁴. Similarly, the snapshots shown in Fig. 6b and Fig. 6c imply that (B) R_u+2R_md≥R_l and (C) R_u+3R_md≥R_l, respectively. From these two relations, we derive that R_md needs to be greater than or equal to 2.25 or 1.5 kg∕s mm⁴, respectively. Among these values, R_md≥4.51 kg∕s mm⁴ satisfies all the three inequalities A, B, and C. So, we take this value as the lower bound for R_md. Likewise, the decision-making of the droplet in the device with R_l∕R_u=4.38, as shown in Figs. 6d, 6e, 6f, yields (D) R_u+R_md≤R_l, (E) R_u+2R_md≤R_l, and (F) R_u+3R_md≤R_l. These three equations imply that R_md needs to be smaller than or equal to 33.33, 16.66, or 11.11 kg∕s mm⁴, respectively. Among these, the condition R_md≤11.11 Kg∕s mm⁴, satisfies all the three inequalities (D, E and F) so this value is selected as the upper bounds for R_md. By combining both of the bounds, we arrive at the final bounds on R_md as 4.51≤R_md≤11.11 kg∕s mm⁴.

Figure 6.

[(a)–(f)] Representative images for estimating the bounds on the hydrodynamic resistance of the moving droplet (R_md). Images (a)–(c) are from device with R_l∕R_u=1.56 and were used to estimate the lower bound of R_md; Q_o and Q_w for these images are 10, 20, and 50 μl∕h and 8, 6, and 15 μl∕h, respectively. Images (d)–(f) are from the device with R_l∕R_u=4.38 and were used to estimate the upper bound of R_md; Q_o and Q_w for these images are 20, 20, and 20 μl∕h and 2, 6, and 10 μl∕h, respectively. Arrows denote the decision-making droplets at the junction.

Figure 7.

Representative images for estimating the bounds on the hydrodynamic resistance of the trapped droplet (R_td). (a)–(c) are from device with R_l∕R_u=0.38 and were used to estimate the lower bound of R_td; Q_o and Q_w for these images are 10 and 1 μl∕h, respectively. Images (d)–(g) are from the same device and were used to estimate the upper bound of R_td. Q_o and Q_w for these images are 10, 10, and 20 μl∕h and 1, 1, and 2 μl∕h, respectively. Arrows denote the decision-making droplets.

Similar to estimating the bounds on the hydrodynamic resistance of the moving drops, we also estimate the bounds on the hydrodynamic resistance of the trapped droplets. To begin with, we consider that the hydrodynamic resistance of the trapped droplet is also independent of flow rate and that the additivity assumption holds. Figure 7 corresponds to the experiments with devices in which R_l∕R_u<1. Images 7a–7c are used for calculating lower bounds for R_td. These are from the device with R_l∕R_u=0.38 under different flow rate combinations as reported in the figure caption. The decision-making events in those images can be correlated with the following equations: (A) R_l+R_td>R_u, (B) R_l+2R_td>R_u, and (C) R_l+3R_td>R_u. As we know, the hydrodynamic resistances (R_u and R_l), in each case (A, B, and C), we can compute that R_td needs to be greater than 13.06, 6.53, or 4.35 kg∕s mm⁴, respectively. Among these, R_td>13.06 kg∕s mm⁴ satisfies all the three equations A, B, and C. So, we choose this as the lower bound for R_td. In the same device, we see some flipping conditions [Figs. 7d, 7e, 7f, 7g]. For these images, the mathematical relations are (D) R_l+R_td<R_u+3R_md, (E) R_l+R_td<R_u+4R_md, (F) R_l+2R_td<R_u+4R_md, and (G) R_l+2R_td<R_u+5R_md. In these cases, we choose the bounds on R_md estimated earlier to extract R_td. These four equations imply that R_td needs to be smaller than 26.59, 31.1, 15.55, and 17.8 kg∕s mm⁴ when R_md=4.51 kg∕s mm⁴ and 46.39, 57.49, 28.75, and 34.3 kg∕s mm⁴ when R_md=11.11 kg∕s mm⁴. Among these values of R_td, the condition R_td<15.55 kg∕s mm⁴ satisfies all the four equations (D, E, F, and G). So, this value is selected as the upper bounds for R_td. By combining both of the bounds, we can get the final range for R_td as 13.06<R_td<15.55 kg∕s mm⁴. It is interesting to note that the estimates for the hydrodynamic resistance of the trapped droplet are higher than the moving droplet, as would be expected.

Based on the above analysis, we obtained four different values of the predicted flow rate for trapping using Eq. 5 because of the lower and upper bounds on the hydrodynamic resistance of the moving and trapped droplets. From these four values, we determined the flow rate range as that bounded by the lowest and highest predicted flow rate. Thus, we obtain from Eq. 5 that the flow rate needs to be less than 30–50 μl∕h for uniform trapping according to the indirect approach, In Fig. 3, we show that uniform trapping is observed at Q_o≤20 μl∕h and not at 50 μl∕h. We conducted additional experiments in the device with R_l∕R_u=1.56 to refine the boundary that delineates uniform trapping. We found that with Q_w∕Q_o=0.3, uniform trapping was also observed at Q_o=30 and 40 μl∕h. These experiments indicate that the predicted flow rate range is in good agreement with experiments. Similarly, for the devices with R_l∕R_u<1, Eq. 5 predicts that the flow rate range for trapping is 8–20 μl∕h, and the experimental data showed all uniform trapping to occur at Q_o≤20 μl∕h, which is also in good agreement with the experimental data.

Discussion of assumptions in the model

Although the simple model yields good agreement with the data, the model is based on a number of assumptions. Here, we discuss these assumptions in relevance to prior work and, where applicable, provide the necessary justification. In Eq. 3, we assume the overall hydrodynamic resistance in the branch is the sum of R_u and the resistances of the individual droplets. This assumption may not strictly hold. Although, conceptually, the total hydrodynamic resistance in the branch can be visualized as the summation of R_(single phase) and R_md, where R_(single phase) is now a Poiseuille resistance, but only of that part of the channel that remains unoccupied by the drop, the analysis is far from trivial. This is because the presence of a confined droplet in the channel disturbs the Poiseuille flow field around the caps of the droplet.^{32, 33, 34} How far this disturbance pervades exactly as a function of drop size and drop speed is currently unknown, particularly in rectilinear microchannels. The estimation of flow field disturbances in our experiments is further complicated by the fact that the droplet size, spacing, and velocity are not independently controlled in this study, implying that the flow-field modifications could be different for each of the flow conditions tested in Fig. 3. Therefore, as a first approximation, here we consider the total hydrodynamic resistance in the branch as the sum of the unmodified Poiseuille resistance of the branch and the hydrodynamic resistance of the droplets. Also, when multiple droplets are present, we determine their contribution as the summation of individual droplet hydrodynamic resistances. When the droplets are spaced far apart, this assumption might be valid. Labrot et al.³¹ showed that in case of surfactant-free drops, the critical drop spacing needs to be λ∕L>10 (where λ is the interdroplet end to end distance and L is the drop length) to avoid the hydrodynamic interaction between droplets. However, their observation is not strictly valid since in their experiments, the droplet spacing and velocity were not independently controlled. In our study, for uniform trapping conditions, we find the droplet spacing to be λ∕L≈2–4, where hydrodynamic interaction between droplets may be present.

In our model, we assume that the hydrodynamic resistance of a moving droplet to be independent of the flow rate. This assumption may not be strictly correct. The motion of confined droplets in cylindrical conduits has been extensively studied; however, similar studies in rectilinear microfluidic channels are few.^{30, 31, 35} Unlike in cylindrical conduits, the carrying liquid can also flow through the corners of the droplets in microchannels, in addition to the thin lubricating films. Bretherton³⁶ showed that for a surfactant-free long bubble in cylindrical channels, the hydrodynamic resistance varies as ∼Q^−1∕3, where Q is the carrier fluid flow rate. Recent work by Vanapalli et al.³⁰ in microfluidic channels has shown that for small (length∕width, L∕w<4) surfactant-free droplets, the Bretherton relation does not hold and that R_md is independent of droplet size and capillary number (10⁻²–10⁻³). In this study, although the droplets are small (length∕width, L∕w<4), the capillary number range is different (10⁻³–10⁻⁴) and the droplets are not surfactant-free. Fuerstman et al.³⁷ reported a complex dependence of surfactant on pressure drop due to bubbles. They find in the absence of surfactant and at high surfactant concentration that the pressure drop depends on the number of bubbles in the channel. At intermediate surfactant concentration, the bubble size influences the pressure drop. In our study, the droplets have a finite viscosity ratio (μ_i∕μ_o=0.03, where μ_i is internal phase viscosity and μ_o is external phase viscosity), and therefore it is unclear whether the results pertaining to the effect of surfactant on bubbles would also apply to droplets. Overall, we find that there have been no systematic studies of the effects of droplet size, speed, spacing, viscosity ratio, surfactant concentration and confinement on the hydrodynamic resistance of moving droplets in microfluidic channels. Similar conclusion also holds for the hydrodynamic resistance of trapped droplets in rectilinear channels. Therefore, future investigations need to be pursued in these directions to obtain a quantitatively robust model.

CONCLUSION

In conclusion, this study investigates the dynamics of a train of droplets in a fluidic network with hydrodynamic traps. By varying the hydrodynamic resistive properties of the network, we find that droplets can undergo a variety of dynamics including bypassing, breakage, trapping, and squeeze-through. For effective uniform trapping of droplets, we show that the droplet size, droplet spacing, and the magnitude of Laplace pressure (relative to fluid pressure) need to be tuned optimally. The magnitude of Laplace pressure depends linearly on the interfacial tension, which plays a crucial role in flow resistance based trapping as discussed in our work. Equation 5 indeed captures this interfacial tension effect, i.e., the flow rate window for droplet trapping increases with increase in surface tension. So changing the oil (or surfactant) system will alter the window of operation. Likewise, for a fixed loop configuration, the fluid pressure is proportional to the viscosity of the oil phase, implying that oils of lower viscosity will enable uniform trapping to occur at larger flow rates. The identification of these driving parameters together with the simple model should provide a guide to rational design of devices for large-scale passive storage of droplets on a chip for potential applications in biological analysis