Treatment Effects in the Presence of Unmeasured Confounding: Dealing With Observations in the Tails of the Propensity Score Distribution—A Simulation Study

Abstract

Frailty, a poorly measured confounder in older patients, can promote treatment in some situations and discourage it in others. This can create unmeasured confounding and lead to nonuniform treatment effects over the propensity score (PS). The authors compared bias and mean squared error for various PS implementations under PS trimming, thereby excluding persons treated contrary to prediction. Cohort studies were simulated with a binary treatment T as a function of 8 covariates X. Two of the covariates were assumed to be unmeasured strong risk factors for the outcome and present in persons treated contrary to prediction. The outcome Y was simulated as a Poisson function of T and all X’s. In analyses based on measured covariates only, the range of PS's was trimmed asymmetrically according to the percentile of PS in treated patients at the lower end and in untreated patients at the upper end. PS trimming reduced bias due to unmeasured confounders and mean squared error in most scenarios assessed. Treatment effect estimates based on PS range restrictions do not correspond to a causal parameter but may be less biased by such unmeasured confounding. Increasing validity based on PS trimming may be a unique advantage of PS's over conventional outcome models.

Restriction of treatment comparisons to subjects with a common range of covariates (e.g., age) or any summary score of covariates (1) can improve the validity of effect estimates regardless of the analytic technique used. Such restriction provides a pragmatic focus on persons for whom uncertainty regarding the value of treatment is most relevant. In practice, implementation of such restrictions can be complicated and is rarely done outside of propensity score (PS) analyses (2, 3).

PS analyses offer some advantages in the context of nonexperimental treatment comparisons. These include a focus on treatment assignment, improved control of confounding with scarce outcomes, and the ability to easily match cohorts on a large number of covariates (3). PS analyses do not offer any advantages with respect to unmeasured confounders, however (4).

Frailty is a plausible explanation for paradoxical treatment effects observed in the elderly (5). Frailty may reduce the likelihood of a particular treatment if physicians focus on a patient's main medical problem and do not initiate useful therapies for alternative conditions (6). The practitioner may determine that in the presence of competing risks, a new therapy offers little expected benefit (7). Conversely, in patients with short life expectancies, physicians may be more willing to try therapies with potentially serious side effects as a last resort. Thus, if mortality is the outcome of interest, frailty can be a powerful confounder that is difficult to measure and can either increase or decrease the likelihood of treatment. Although we describe the problem using the terminology of pharmacoepidemiology, the issues are more general and the principles should apply broadly to any type of epidemiologic study.

Recent studies have provided examples of strong heterogeneity of treatment effect estimates over the PS that may be explained by confounding due to unmeasured frailty (8, 9). In one study of the effects of thrombolysis on all-cause in-hospital mortality among patients with stroke, mortality was much higher in the 17 stroke patients (out of a total of 212) who received thrombolytic therapy despite having the lowest PS for receiving it (41% mortality), in comparison with the remaining 195 patients (14% mortality) (8). These 17 patients with a very low predicted probability of receiving treatment may have received it because they were very frail—that is, as a treatment of last resort.

In another study that addressed the effects of treatment with biologics on all-cause mortality in patients with rheumatoid arthritis, mortality was much higher in the untreated patients in the highest PS quintile (72/1,000 person-years) than in the remainder of the untreated patients (11/1,000 person-years) (9). Frailty may also explain this difference, if the high-risk untreated patients did not receive the treatment that they might have received given their clinical condition because they were deemed too frail by the treating physician (treatment withheld).

If increases in mortality in a few patients who are treated contrary to prediction are due to unmeasured frailty, then treatment effects over the PS will appear heterogeneous, and excluding some or all of the patients treated contrary to prediction could reduce unmeasured confounding by this frailty under the assumption of uniform effects (10). In theory, if we excluded all patients with unmeasured frailty, the resulting treatment effect estimate would not be biased from unmeasured confounding by frailty. In practice, excluding all such patients will be impossible. Excluding increasing proportions of those treated contrary to prediction, however, would increase internal validity at the price of not being able to describe precisely the population to which the treatment effect estimate would apply (11, 12). In other words, the treatment effect that is estimated would not be a causal parameter even when implementing the PS in a way that should produce a causal estimate (13). If, contrary to this assumption, treatment effect heterogeneity is real and not due to unmeasured confounding, then excluding some patients will affect the generalizability of the results.

Our aim in this simulation study was to compare bias and mean squared error in the treatment effect estimates for varying degrees of asymmetric restriction of the PS distribution under the assumption of the presence of unmeasured frailty that leads to “last resort” treatment, “treatment withheld,” or both. We analyzed the data using a variety of methods to control for confounding using PS's.

MATERIALS AND METHODS

Simulation

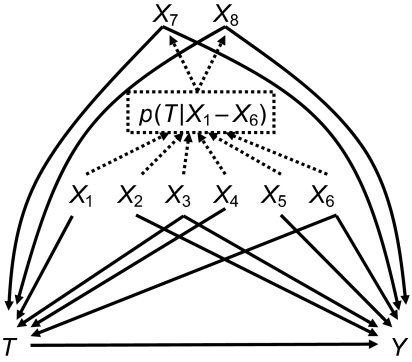
To simulate confounding by frailty in persons who are treated contrary to prediction, we used a 2-step process to define covariates (see Figure 1). We started with 3 dichotomous covariates, X₁, X₂, and X_3, each with a prevalence of 0.2, and 3 continuous covariates, X₄, X₅, and X₆, each with a mean of 0 and unit variance. All covariates were independent of one another. We then calculated the predicted probability of the dichotomous intended treatment T based on these 6 “measured” covariates and the covariate-treatment associations presented in Table 1, using a logistic model:

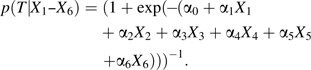(1)

Figure 1.

Conceptual diagram of a simulation study depicting treatment (T) and outcome (Y) as a function of measured covariates (X₁–X₆) and unmeasured covariates (X₇ and X₈). The solid lines represent causal associations, and the dashed lines represent noncausal associations used in the 2-step simulation process to mimic treatment contrary to prediction by measured covariates (X₁–X₆).

Table 1.

Parameters Covered in the Simulation Study and Their Values^a

Variable	Prevalence	ORTb	Parameter	Equation No(s).c	RRYd	Parameter	Equation No(s).c
X1	0.2	2.0	α1	1, 2	1.0	β1	3
X2	0.2	1.0	α2	1, 2	2.0	β2	3
X3	0.2	0.2	α3	1, 2	0.2	β3	3
X4	Continuous (0, 1)	1.5	α4	1, 2	1.0	β4	3
X5	Continuous (0, 1)	1.0	α5	1, 2	1.5	β5	3
X6	Continuous (0, 1)	0.5	α6	1, 2	0.5	β6	3
X7	0.01ef	1, 10	α7	2	1, 10	β7	3
X8	0.01fg	1, 0.1	α8	2	1, 10	β8	3
T	0.2, 0.05f		α0	2	2.0	βT	3
Y	0.1f (incidence rate in untreated)					β0	3

Abbreviations: OR, odds ratio; RR, rate ratio.

^aParameter values are chosen to represent a study with both prevalent and rare treatment and a low incidence of outcomes over a fixed follow-up time. Covariates are either instruments (X₁ and X₄), risk factors for the outcome (X₂ and X₅), or confounders (X₃, X₆, X₇, X₈). X₇ and X₈ are strongly associated with both treatment and outcome but very rare, to mimic few patients treated contrary to prediction. Some parameter values are set to 1 (no association) for the tables separating “last resort” treatment from “treatment withheld.”

^bOdds ratio for the relation between the covariate and treatment T; parameters are for log(OR_T).

^cFor equations, see text.

^dRate ratio for the relation between the covariate and the outcome Y; parameters are for log(RR_Y).

^e“Last resort” treatment if random uniform number ≤[γ – p(T|X₁–X₆)]; γ was chosen so that the prevalence of X₇ was close to 0.01.

^fApproximate numbers.

^g“Treatment withheld” if random uniform number ≤[p(T|X₁–X₆) − δ]; δ was chosen so that the prevalence of X₈ was close to 0.01.

We used this probability of intended treatment to assign 2 additional dichotomous covariates. One, X₇, was defined as most likely to be present when the intended treatment was least likely. X₇ was set to 1 (present) when a random uniform number was less than or equal to [γ − p(T|X₁–X₆)] and set to 0 otherwise. Thus, observations with a probability of intended treatment close to 0 would be most likely to have X₇ = 1. The second covariate, X₈, was likely to be present when the intended treatment was most likely. X₈ was set to 1 (present) when a random uniform number was less than or equal to [p(T|X₁–X₆) − δ], absent otherwise. Thus, observations with a probability of intended treatment close to 1 would be most likely to have X₈ = 1. The values for γ and δ were chosen to result in a low prevalence of both X₇ and X₈ (see Table 1). We assumed a low prevalence for persons treated contrary to prediction because of the empirical examples.

Based on these 8 covariates (i.e., the “measured” covariates X₁–X₆ and the “unmeasured” covariates X₇ and X₈), we then recalculated the probability of actual treatment, again using a logistic model:

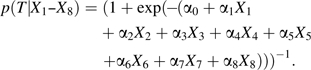(2)

The actual treatment T was then assigned on the basis of this probability using a random uniform number. Finally, the expected number of disease outcomes Y over a fixed follow-up time interval was derived from all 8 covariates and the treatment T using a log-linear model:

(3)

The number of outcomes Y was assigned using a random number from a Poisson distribution based on this expected value. The Poisson outcome and the log-linear outcome model were chosen because the incidence rate ratios obtained are collapsible under exchangeability (14) and therefore allow direct comparisons between the analytic strategies (15).

The range of values covered in the simulation study is presented in Table 1. The 6 measured covariates X₁–X₆ were associated only with treatment (X₁ and X₄), associated only with outcome (X₂ and X₅), or associated with both treatment and outcome (X₃ and X₆). X₇ was strongly positively associated with both actual treatment and outcome (or not), mimicking frailty that leads to “last resort” treatment. X₈ was strongly inversely associated with actual treatment and positively with outcome (or not), mimicking frailty that leads to “treatment withheld.” The parameter value for α₀ in equation 2 was chosen to result in a prevalence of T of approximately 0.2 or 0.05, the one for β₀ in equation 3 for an incidence of approximately 0.1 per observation over a fixed follow-up time in the untreated. For each scenario or parameter constellation, we simulated 1,000 closed cohort studies with n = 10,000.

Analysis

PS estimation and implementation.

We first estimated PS_X1–X6 based on the measured covariates X₁–X₆ using logistic regression. The treatment-outcome incidence rate ratio controlling for confounding by the measured X’s was estimated using log-linear models and 5 different methods to implement PS_X1–X6: modeling, stratification assuming uniform effects, stratification not assuming uniform effects, matching, and weighting (4).

We first estimated the rate ratio based on treatment and PS_X1–X6 as a continuous covariate, not to encourage this PS implementation but because it is widely used in medical research (16). We then stratified the study population into 5 equal-sized strata of PS_X1–X6 based on the overall (marginal) distribution of PS_X1–X6. We used 5 strata because that number of strata has been shown to be sufficient to remove most confounding (17) and thus has become a widely used approach in stratifying PS's (16). We estimated the rate ratio based on a model including treatment and 4 indicator variables for PS_X1–X6 quintiles 2–5.

In addition to these 2 PS implementations based on the assumption of uniform effects, we analyzed the data using 3 different approaches that do not rely on this assumption. First we combined the 5 PS_X1–X6 quintile-specific treatment effect estimates based on the standardized mortality ratio—that is, using weights that reflect the distribution of treated patients over the quintiles as the standard. We then tried to find untreated matches for every treated patient based on the estimated PS_X1–X6 (1:1 individual matching). We used 5-digit to 1-digit matching: starting with a very narrow caliper of the PS_X1–X6 (±0.000005) to find an untreated match for every treated observation without replacement and gradually increasing the width of the caliper up to ±0.05 if no match could be found (18). Within the matched data set, we estimated the unconfounded treatment effect without taking matching into account. This approach is commonly used and valid, though it is slightly less efficient than taking matching into account (19). Both the standardized mortality ratio method and matching as we implemented it result in an estimate of a causal treatment effect in the treated, in the presence of nonuniform treatment effects (13).

Finally, we analyzed the data using inverse probability of treatment weighting (IPTW). IPTW creates a pseudo-population in which the association between covariates and treatment is removed by weighting each observation by the inverse of the probability of receiving the actual treatment. To end up with a sum of weights close to the size of the original study population, we used stabilized weights—that is, we multiplied the IPTW weights by the marginal prevalence of the treatment actually received (20). We used a (conservative) robust variance estimation. IPTW produces an estimate of a causal treatment effect in the population in the presence of nonuniform treatment effects (13, 20).

PS trimming.

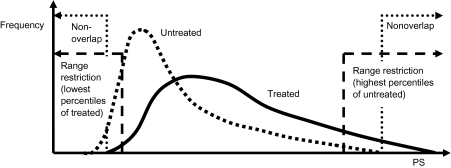
All of the above analyses were first conducted without any restriction of the PS range. We then restricted the analysis to observations within a PS range that was common to both treated and untreated persons—that is, by excluding all patients in the nonoverlapping parts of the PS distribution (see Figure 2). Individual matching on the PS also effectively resulted in a PS range that is common to treated and untreated persons.

Figure 2.

Schematic of asymmetric range restriction. PS, propensity score.

We then applied additional asymmetric PS trimming in order to exclude those patients who were treated most contrary to prediction. We assessed 3 different cutpoints corresponding to the 1st and 99th percentiles, the 2.5th and 97.5th percentiles, and the 5th and 95th percentiles of the PS distribution in the treated and untreated patients, respectively. Stratification into quintiles and matching were performed after trimming.

RESULTS

In Table 2, we present the mean number of observations and mean incidence rates in treated and untreated persons, as well as the corresponding rate ratio from the simulated data sets, according to a combination of the PS_X1–X6 percentiles in treated and untreated patients. At the lower end of the PS_X1–X6 range (up to the 5th percentile), percentiles are derived from the distribution of PS_X1–X6 in the treated. All other percentiles, including those at the high end of the distribution, are derived from the distribution of PS_X1–X6 in the untreated. This approach allows us to concentrate on the patients treated contrary to prediction (which would otherwise be swamped by patients treated according to prediction). It also leads to untreated patients below the 0th percentile and treated patients above the 100th percentile.

Table 2.

Mean Incidence Rates and Rate Ratios as a Function of Estimated Asymmetric Propensity Score Percentiles From 1,000 Simulated Data Sets in the Presence of Unmeasured Confounding Due to “Last Resort Treatment” and “Treatment Withheld”

PS “Percentile”a	Treatment Prevalence = 0.2					Treatment Prevalence = 0.05
	Treated		Untreated		RRb	Treated		Untreated		RRb
	No.	IRc	No.	IRc		No.	IRc	No.	IRc
“Last resort treatment”
<0d			63	11				261	12
0–1	19	133	561	22	6.68	4	117	635	24	5.51
1–2.5	29	188	528	34	5.85	7	181	685	38	5.07
2.5–5	49	219	659	45	5.04	12	244	771	53	4.75
5–25	18	207	201	52	4.58	3	231	117	59	4.68
25–50	242	160	2,007	67	2.40	62	287	2,283	81	3.56
50–75	451	221	2,010	108	2.06	112	259	2,376	120	2.17
75–95	719	360	1,608	172	2.10	182	399	1,901	190	2.10
95–97.5	163	514	201	256	2.06	42	579	238	282	2.09
97.5–99	129	607	121	301	2.10	34	673	143	335	2.06
99–100	137	834	80	406	2.14	36	949	95	455	2.15
>100d	5	1,679				1	1,772
“Treatment withheld”
<0d			91	6				321	10
0–1	19	33	718	15	2.48	4	39	705	19	2.08
1–2.5	29	54	601	27	2.18	7	66	712	32	2.13
2.5–5	49	79	683	40	2.06	12	96	813	47	2.12
5–25	2	99	19	44	2.54	1	97	44	48	2.30
25–50	239	136	1,914	66	2.07	57	151	2,160	74	2.06
50–75	474	222	2,014	108	2.06	117	242	2,378	119	2.04
75–95	767	367	1,611	183	2.01	188	408	1,903	233	1.76
95–97.5	160	591	201	554	1.10	41	618	238	526	1.20
97.5–99	114	830	121	1,058	0.81	31	777	143	803	1.00
99–100	92	1,623	80	2,348	0.71	29	1,296	95	1,673	0.80
>100d	2	5,662				1	4,726
“Last resort treatment” and “treatment withheld”
<0d			61	11				261	12
0–1	19	125	550	21	6.75	5	103	627	22	5.25
1–2.5	29	173	516	31	5.99	7	159	651	35	4.87
2.5–5	49	199	650	41	5.01	12	219	754	49	4.65
5–25	21	200	238	48	4.84	3	238	150	55	4.75
25–50	248	148	2,013	64	2.35	65	261	2,308	77	3.44
50–75	466	212	2,013	104	2.05	117	241	2,375	114	2.12
75–95	752	349	1,611	173	2.03	188	389	1,900	222	1.76
95–97.5	158	562	201	500	1.16	41	591	238	500	1.21
97.5–99	112	778	121	978	0.82	31	742	143	760	1.01
99–100	91	1,518	80	2,197	0.71	29	1,236	95	1,592	0.80
>100d	2	5,219				1	4,170

Abbreviations: IR, incidence rate; PS, propensity score; RR, rate ratio.

^aAsymmetric PS percentiles according to PS distribution in treated and untreated persons separately (to allow closer assessment of persons treated contrary to prediction). Percentiles between 0 and 5 are derived from the PS distribution in the treated patients; all other percentiles are derived from the PS distribution in the untreated patients.

^bControlled for measured covariates based on PS stratification; inconsistencies with the incidence rates in the treated and untreated are due to rounding.

^cPer 1,000 person-years (repeated events).

^dUntreated patients in the <0 asymmetric PS percentile stratum are those with a lower PS than the lowest one observed in the treated patients (nonoverlap). Treated patients in the >100 asymmetric PS percentile stratum are those with a higher PS than the highest one observed in the untreated patients (nonoverlap).

The first set of rows in Table 2 is based on the “last resort treatment” hypothesis, in which very sick patients receive a treatment contrary to the prediction of no treatment; it mimics the results presented in Table 2 of the Kurth et al. paper (8). Added to the monotonic decrease of incidence rates in both treated and untreated persons with decreasing PS_X1–X6, the presence of the unmeasured covariate X₇ leads to “abnormally” high incidence rates in the treated with low PS_X1–X6. Because we know that the true rate ratio is 2.0, the higher rate ratios are confounded by X₇. There is some residual confounding despite stratification on narrow PS_X1–X6 strata, even at the high end of PS_X1–X6 (e.g., for the 99th–100th percentile, rate ratio (RR) = 2.14). The maximum rate ratio in any stratum is less extreme than the most extreme stratum-specific rate ratio reported by Kurth et al. (8) (RR = 13).

The second set of rows in Table 2 is based on the “treatment withheld” hypothesis, in which a very frail patient does not receive a treatment as expected because of severe disability and/or multiple concurrent medical conditions. It mimics the results presented by Lunt et al. (9) in their Table 4. Added to the monotonic increase of incidence rates in both treated and untreated persons with increasing PS_X1–X6, the presence of the unmeasured covariate X₈ leads to “abnormally” high incidence rates in the untreated with high PS_X1–X6. This pattern is more difficult to detect because the increase of incidence rates in the untreated over PS_X1–X6 remains monotonic. High incidence rates in the untreated patients lead to enough confounding to reverse the direction of the association, resulting in apparently “protective” effect estimates confounded by X₈. The minimum rate ratio in any stratum is less extreme than the most extreme stratum-specific rate ratio reported by Lunt et al. (9) (RR = 0.24).

Table 4.

Mean Rate Ratios, Empirical Variance, and Percent Coverage of 95% Confidence Intervals From 1,000 Simulated Data Sets in the Presence of Unmeasured Confounding Due to “Treatment Withheld” Without or With Asymmetric Trimming of the Propensity Score According to Analytic Strategy (True RR = 2.0)

PS Implementation and Trimming Range	Treatment Prevalence = 0.2				Treatment Prevalence = 0.05
	RR	Variancea	MSEb	Coveragec	RR	Variancea	MSEb	Coveragec
Crude	2.85	0.007	0.130	0.1	2.93	0.016	0.157	4.4
True outcome model	2.00	0.003	0.003	94.0	2.00	0.007	0.007	94.1
Outcome model (X1–X6)d	1.30	0.006	0.193	0.0	1.34	0.013	0.182	1.1
PS analysesd
PS continuous
Unrestricted	1.31	0.007	0.191	0.0	1.38	0.023	0.171	5.9
Restricted
0–100	1.31	0.007	0.190	0.0	1.41	0.019	0.146	5.9
1–99	1.53	0.006	0.078	1.7	1.50	0.014	0.099	14.0
2.5–97.5	1.75	0.006	0.004	38.5	1.63	0.014	0.059	39.3
5–95	1.95	0.005	0.006	91.0	1.75	0.014	0.033	71.9
PS quintiles (Mantel-Haenszel)
Unrestricted	1.52	0.008	0.086	2.1	1.61	0.016	0.066	23.9
Restricted
0–100	1.50	0.007	0.092	1.5	1.58	0.015	0.073	19.6
1–99	1.65	0.006	0.045	11.7	1.63	0.012	0.056	33.8
2.5–97.5	1.82	0.005	0.015	59.7	1.71	0.013	0.040	56.6
5–95	1.98	0.005	0.005	91.8	1.80	0.014	0.027	77.5
PS quintiles (standardized mortality ratio)
Unrestricted	1.46	0.009	0.109	1.3	1.60	0.016	0.070	22.4
Restricted
0–100	1.45	0.008	0.116	1.1	1.57	0.015	0.077	19.0
1–99	1.59	0.006	0.060	6.7	1.62	0.013	0.059	30.9
2.5–97.5	1.78	0.006	0.020	49.4	1.70	0.013	0.042	53.6
5–95	1.97	0.005	0.006	91.3	1.79	0.014	0.028	76.7
PS matching
Unrestricted	1.22	0.008	0.255	0.0	1.28	0.033	0.250	9.5
Restricted
0–100	1.22	0.008	0.254	0.0	1.28	0.033	0.249	9.4
1–99	1.45	0.008	0.113	1.4	1.49	0.030	0.127	33.3
2.5–97.5	1.69	0.008	0.037	38.5	1.63	0.031	0.080	60.7
5–95	1.94	0.008	0.009	89.2	1.77	0.034	0.054	81.7
Inverse probability of treatment weighting
Unrestricted	1.31	0.007	0.192	0.0	1.57	0.014	0.076	50.2
Restricted
0–100	1.29	0.007	0.203	0.0	1.52	0.013	0.093	38.6
1–99	1.62	0.005	0.052	19.3	1.69	0.013	0.045	70.4
2.5–97.5	1.82	0.005	0.014	75.2	1.77	0.013	0.029	83.2
5–95	1.99	0.005	0.005	94.5	1.85	0.014	0.022	91.1

Abbreviations: MSE, mean squared error; PS, propensity score; RR, rate ratio.

^aVariance of treatment effect estimates [log(RR)] over 1,000 simulated data sets.

^bMean of [log(RR) – log(2.0)]² over 1,000 simulated data sets.

^cPercentage of simulated studies in which the 95% confidence interval includes the true value (RR = 2.0).

^dOutcome and PS models including all measured covariates X₁–X₆ but not including unmeasured covariate X₇.

The bottom set of rows in Table 2 combines the “last resort treatment” with the “treatment withheld” hypothesis. These simulations show both overestimated rate ratios in the lowest PS_X1–X6 strata and underestimated rate ratios in the highest PS_X1–X6 strata.

In Table 3, we present the treatment effect estimates obtained with various restrictions of the PS_X1–X6 under the “last resort treatment” hypothesis. Note that the true rate ratio equals 2.0 and that all PS analyses presented rely exclusively on control for the measured covariates X₁–X₆. The main confounding is due to measured covariates (crude RR = 3.52 vs. RR = 2.13 based on the outcome model for a treatment prevalence of 0.2). There is, however, some uncontrolled confounding due to the unmeasured X₇. The confounding by X₇ is not strong despite its strong associations with both treatment and outcome because the prevalence of X₇ = 1 is only 0.01 (Table 1).

Table 3.

Mean Rate Ratios, Empirical Variance, and Percent Coverage of 95% Confidence Intervals From 1,000 Simulated Data Sets in the Presence of Unmeasured Confounding Due to “Last Resort Treatment” Without or With Asymmetric Trimming of the Propensity Score According to Analytic Strategy (True RR = 2.0)

PS Implementation and Trimming Range	Treatment Prevalence = 0.2				Treatment Prevalence = 0.05
	RR	Variancea	MSEb	Coveragec	RR	Variancea	MSEb	Coveragec
Crude	3.52	0.003	0.320	0.0	3.69	0.009	0.378	0.0
True outcome model	2.01	0.003	0.003	95.0	2.01	0.007	0.007	94.1
Outcome model (X1–X6)d	2.13	0.003	0.007	79.6	2.20	0.008	0.016	76.3
PS analysesd
PS continuous
Unrestricted	2.15	0.004	0.009	74.0	2.25	0.009	0.022	69.2
Restricted
0–100	2.15	0.004	0.009	74.3	2.25	0.009	0.022	68.1
1–99	2.13	0.004	0.008	80.2	2.21	0.010	0.018	76.9
2.5–97.5	2.11	0.004	0.007	85.7	2.21	0.011	0.020	77.0
5–95	2.07	0.005	0.006	90.9	2.21	0.013	0.021	82.3
PS quintiles (Mantel-Haenszel)
Unrestricted	2.28	0.003	0.020	35.8	2.42	0.008	0.043	36.0
Restricted
0–100	2.27	0.003	0.019	39.2	2.40	0.008	0.040	39.0
1–99	2.19	0.004	0.011	66.5	2.30	0.009	0.027	62.0
2.5–97.5	2.14	0.004	0.009	78.0	2.27	0.010	0.025	70.7
5–95	2.09	0.005	0.007	88.1	2.24	0.012	0.024	77.8
PS quintiles (standardized mortality ratio)
Unrestricted	2.26	0.004	0.019	42.3	2.40	0.008	0.040	38.8
Restricted
0–100	2.25	0.004	0.017	47.4	2.38	0.008	0.037	41.8
1–99	2.16	0.004	0.009	75.2	2.28	0.009	0.025	65.6
2.5–97.5	2.12	0.004	0.007	84.3	2.25	0.010	0.023	73.1
5–95	2.08	0.005	0.006	90.4	2.22	0.012	0.022	79.8
PS matching
Unrestricted	2.08	0.005	0.006	91.7	2.18	0.018	0.024	90.3
Restricted
0–100	2.08	0.005	0.006	91.8	2.18	0.018	0.024	90.4
1–99	2.08	0.006	0.007	91.3	2.20	0.022	0.029	90.3
2.5–97.5	2.08	0.007	0.008	93.5	2.22	0.025	0.034	90.1
5–95	2.06	0.008	0.008	93.7	2.23	0.030	0.039	91.2
Inverse probability of treatment weighting
Unrestricted	2.26	0.005	0.019	64.3	2.50	0.019	0.065	66.7
Restricted
0–100	2.24	0.005	0.017	68.4	2.44	0.018	0.055	74.3
1–99	2.25	0.005	0.018	65.8	2.48	0.018	0.060	68.6
2.5–97.5	2.21	0.005	0.014	75.4	2.46	0.018	0.057	72.0
5–95	2.12	0.005	0.009	88.0	2.40	0.020	0.050	76.3

Abbreviations: MSE, mean squared error; PS, propensity score; RR, rate ratio.

^aVariance of treatment effect estimates [log(RR)] over 1,000 simulated data sets.

^bMean of [log(RR) – log(2.0)]² over 1,000 simulated data sets.

^cPercentage of simulated studies in which the 95% confidence interval includes the true value (RR = 2.0).

^dOutcome and PS models including all measured covariates X₁–X₆ but not including unmeasured covariate X₇.

Bias due to the unmeasured confounder X₇ is reduced by asymmetric PS trimming in most implementations of the PS (the rate ratio moves closer to the true value of 2.0 and the mean squared error gets smaller). The exception is PS matching, where bias is constant (p(T = 1) = 0.2) or increases with increasing range restrictions (p(T = 1) = 0.05). PS matching provides the least bias without restriction, however, and remains among the least biased implementations with a 5–95 range restriction. With a lower prevalence of the treatment (p(T = 1) = 0.05), IPTW becomes most biased without range restriction. A lower prevalence of treatment leads to more extreme weights in the patients who receive treatment contrary to prediction. Given the increase in variance and the bias reduction following increasing trimming, the effect on the coverage of the 95% confidence interval is very pronounced for most implementations.

In Table 4, we present the treatment effect estimates obtained with various restrictions of the PS_X1–X6 under the “treatment withheld” hypothesis. The unmeasured confounding due to X₈ is stronger than the one by X₇. It leads to a rate ratio of 1.3 based on control for measured covariates. Consequently, the effects of trimming are more pronounced in this setting, monotonic, and similar for all PS implementations. The effects of unmeasured confounding due to X₈ are most pronounced for PS matching with an unrestricted rate ratio of 1.2 (p(T = 1) = 0.2).

When combining the 2 hypotheses (Table 5), asymmetric PS trimming again leads to reduction of bias caused by the unmeasured confounders with all PS implementations. Interestingly enough, increasing restrictions lead to increasing reduction of bias with all implementations except IPTW. With IPTW, there is a reduction of bias with restriction up to the 2.5–97.5 level, but further restriction to the 5–95 level increases rather than decreases bias.

Table 5.

Mean Rate Ratios, Empirical Variance, and Percent Coverage of 95% Confidence Intervals From 1,000 Simulated Data Sets in the Presence of Unmeasured Confounding Due to “Last Resort Treatment” and “Treatment Withheld” Without or With Asymmetric Trimming of the Propensity Score According to Analytic Strategy (True RR = 2.0)

PS Implementation and Trimming Range	Treatment Prevalence = 0.2				Treatment Prevalence = 0.05
	RR	Variancea	MSEb	Coveragec	RR	Variancea	MSEb	Coveragec
Crude	2.86	0.006	0.131	0.0	2.98	0.015	0.169	3.6
True outcome model	2.00	0.003	0.003	95.5	1.99	0.007	0.007	93.7
Outcome model (X1–X6)d	1.39	0.006	0.142	0.0	1.45	0.014	0.124	5.0
PS analysesd
PS continuous
Unrestricted	1.38	0.007	0.149	0.0	1.46	0.022	0.128	10.6
Restricted
0–100	1.38	0.007	0.149	0.0	1.49	0.018	0.109	12.0
1–99	1.63	0.006	0.049	9.6	1.62	0.015	0.061	33.4
2.5–97.5	1.85	0.006	0.012	69.3	1.77	0.015	0.032	66.2
5–95	2.01	0.005	0.005	93.6	1.90	0.015	0.018	85.9
PS quintiles (Mantel-Haenszel)
Unrestricted	1.60	0.007	0.057	6.3	1.72	0.016	0.041	44.7
Restricted
0–100	1.59	0.007	0.062	4.8	1.69	0.015	0.046	40.8
1–99	1.75	0.006	0.024	35.2	1.77	0.014	0.031	61.6
2.5–97.5	1.92	0.005	0.007	83.3	1.86	0.014	0.021	78.8
5–95	2.04	0.005	0.005	92.3	1.95	0.015	0.016	88.1
PS quintiles (standardized mortality ratio)
Unrestricted	1.53	0.008	0.084	3.1	1.69	0.016	0.047	39.4
Restricted
0–100	1.51	0.008	0.089	2.1	1.67	0.015	0.052	34.5
1–99	1.67	0.006	0.039	17.3	1.74	0.014	0.035	57.2
2.5–97.5	1.87	0.006	0.011	73.2	1.83	0.014	0.023	76.0
5–95	2.02	0.005	0.005	93.4	1.93	0.015	0.016	88.0
PS matching
Unrestricted	1.28	0.009	0.215	0.0	1.35	0.036	0.202	15.0
Restricted
0–100	1.28	0.009	0.214	0.0	1.35	0.035	0.201	15.0
1–99	1.53	0.008	0.084	5.1	1.59	0.035	0.096	48.3
2.5–97.5	1.78	0.008	0.023	59.3	1.76	0.037	0.059	60.7
5–95	1.99	0.008	0.008	93.2	1.90	0.040	0.045	81.7
Inverse probability of treatment weighting
Unrestricted	1.49	0.008	0.096	8.9	1.90	0.019	0.023	92.5
Restricted
0–100	1.48	0.008	0.101	6.7	1.86	0.019	0.026	89.9
1–99	1.83	0.006	0.014	79.5	2.05	0.019	0.019	94.0
2.5–97.5	2.02	0.005	0.005	96.4	2.13	0.019	0.022	92.9
5–95	2.11	0.005	0.008	90.2	2.18	0.020	0.026	90.7

Abbreviations: MSE, mean squared error; PS, propensity score; RR, rate ratio.

^aVariance of treatment effect estimates [log(RR)] over 1,000 simulated data sets.

^bMean of [log(RR) – log(2.0)]² over 1,000 simulated data sets.

^cPercentage of simulated studies in which the 95% confidence interval includes the true value (RR = 2.0).

^dOutcome and PS models including all measured covariates X₁–X₆ but not including unmeasured covariate X₇.

DISCUSSION

We simulated data sets to mimic treatment effect heterogeneity in 2 separate published clinical studies under the assumption that such heterogeneity is due to unmeasured confounding by patient frailty. Our simulation study shows that under this assumption, increasing asymmetric PS trimming can increase the validity of the treatment effect estimates. This increase in validity was observed with most of the different PS implementations and over all of the scenarios assessed in the simulations.

How can we detect unmeasured confounding by frailty? Sensitivity of treatment effects to the approach of estimation, especially very different results from untrimmed IPTW, raised caution in the examples cited (8, 9). “Last resort treatment” and “treatment withheld” will lead to apparent heterogeneity of treatment effect estimates in the opposite ends of the overlapping PS distribution. This heterogeneity could easily be missed by stratifying the data into broad PS categories, such as quintiles. The heterogeneity becomes apparent, however, if one stratifies the data finely by PS at both ends of the PS distribution. Disadvantages of stratifying by broad percentile categories such as quintiles have been pointed out in other settings (21). Combining the lower percentiles from the treated patients and the higher percentiles from the untreated patients into a single “percentile” is an idea proposed previously by Stürmer et al. (10). Although some variability will occur by chance, trends such as those reported (8, 9) should raise caution.

We are aware of few published implementations of PS range restrictions (8, 22, 23). Here we assessed the performance of asymmetric PS trimming (10) when the treatment effect is homogeneous. We observed some differences between different methods of using the PS to control confounding. PS matching was least affected by bias due to unmeasured frailty that led to “last resort treatment.” This result can be explained by the fact that the treatment effect in the treated patients estimated by PS matching is based on few matched sets with very low PS's. Estimating the treatment effect in the treated patients thus guards against major bias due to “last resort” treatment, even without trimming. Without trimming, however, estimating the treatment effect in the treated is more susceptible to bias due to “treatment withheld.” In the scenario with both “last resort treatment” and “treatment withheld,” trimming IPTW provided the least correction of uncontrolled confounding and increasing trimming did not monotonically lead to reduced bias. This result is in contrast to all other PS methods and scenarios that we assessed.

It was difficult to mimic the results presented by Kurth et al. (8) and Lunt et al. (9) in simulations. The difficulty relates to the hypothesized phenomena being concentrated within a few people in the extremes of the PS distribution. With our 2-stage process, which first calculates the probability of intended treatment given the measured covariates to assign our frailty covariates and then assumes strong associations between the frailty covariates and both actual treatment (odds ratio = 10) and outcome (RR = 10), we came close. Nevertheless, the treatment effect heterogeneity in our simulation study is still less extreme than the heterogeneity observed in published clinical studies (8, 9). Owing to this concentration of the effect in the extremities of the PS distribution, other methods that have been proposed to deal with unmeasured confounders in pharmacoepidemiology (e.g., 24–28) are likely to not perform well in this setting, even if a measure for frailty were available.

Asymmetric trimming does not always lead to bias reduction with IPTW. With unmeasured confounding at both ends of the PS distribution (Table 5), the 5–95 trimmed estimate is slightly more biased than the 2.5–97.5 trimmed estimate. We do not have an explanation for this observation, and we encourage more research into the behavior of IPTW in the presence of unmeasured confounders such as frailty and the value of trimming the population to reduce such bias. Reestimation of PS within the trimmed population slightly alleviated but did not suppress this problem (e.g., RR = 2.06 for 5–95 trimming vs. RR = 2.11 for p(T = 1) = 0.2), while results for all other scenarios assessed were virtually identical.

Because IPTW estimates the treatment effect in the whole population, it should only be implemented if everyone in the study has the potential to be treated. Cole and Hernán (29) have proposed truncation of IPTW to improve the trade-off between variance and residual confounding by measured covariates. Thus, truncation is not intended to reduce bias due to unmeasured confounders, nor does it result in bias reduction in this setting (data not shown). Trimming by the absolute value of the PS has recently been proposed to address lack of PS overlap and to reduce the variance of an IPTW estimator of the average treatment effect (30). Crump et al. (30) proposed a selection method that maximizes precision and concluded that a simple rule of thumb excluding all observations outside a PS range of 0.1–0.9 is a good approximation to maximize precision.

Real treatment effect heterogeneity is another plausible explanation for nonuniform treatment effects. Treatment may be more beneficial and less harmful in patients most likely to be treated because they have the strongest indications and the fewest contraindications, and vice versa. If treatment effect heterogeneity is real rather than caused by unmeasured confounders, then methods of PS implementation that do not assume uniform treatment effects should be used and trimming will limit generalizability. Separate analyses after trimming may provide a more meaningful estimate in the patients where there is equipoise, however, and highlight the difficulties in reliably estimating the treatment effect in patients with reduced equipoise. In the study by Kurth et al. (8), thrombolysis may have been the cause of the increased mortality observed in a subgroup of patients defined by their low probability of receiving thrombolysis. In contrast, it is not plausible that treatment with biologics would prevent 75% of all deaths in a subgroup of patients defined by a high probability of receiving biologics in the study by Lunt et al. (9).

Because the data cannot distinguish bias caused by unmeasured confounders from real treatment effect heterogeneity, the validity benefit of any range restriction is arguable. Any data excluded from primary analyses by trimming should be presented for readers to evaluate, along the lines of our Table 2. Such a table will illuminate the nature of the population to which the treatment effect estimate based on PS range restrictions applies. After range restriction, these estimates will not be causal in the sense that they do not apply to any clearly defined population, such as all treated patients, anymore. Thus, there will be a trade-off between validity and estimating the treatment effect in a clearly defined population.

The conclusions of all simulation studies are limited to the scenarios assessed. We explicitly simulated our data sets so that the treatment effect estimate based on restricting the range to the 5th–95th percentiles was not unbiased, to avoid the false impression that this arbitrary cutpoint will eliminate bias caused by unmeasured confounders. Misspecification of the PS model in addition to the one due to the unmeasured confounders in persons treated contrary to prediction (e.g., by additional unmeasured confounders or misspecification of measured covariates) could affect the performance of trimming. The interpretation of results following asymmetric PS trimming will depend on the observed change in treatment effect estimates over increasing PS range restrictions.

We conclude that one plausible explanation for the very heterogeneous treatment effects on mortality presented by Kurth et al. (8) and Lunt et al. (9), unmeasured confounding by frailty, can be reduced by increasing asymmetric trimming of the PS. Under this assumption, trimming enhances validity. The ability to trim outliers based on a single variable that summarizes confounding from other, measured variables is an important advantage of PS's compared with conventional outcome models.

Because real treatment effect heterogeneity cannot be excluded as an alternative explanation, asymmetric PS trimming should be used judiciously, perhaps as a sensitivity analysis. To inform interpretation, investigators should present data on the outcomes in treated and untreated patients finely stratified according to the PS distribution for treated patients at the lower end and the PS distribution for untreated patients at the higher end.

Glossary

Abbreviations

IPTW

inverse probability of treatment weighting

PS

propensity score

RR

rate ratio