The temporal selfish herd: predation risk while aggregations form

Abstract

The hypothesis of the selfish herd has been highly influential to our understanding of animal aggregation. Various movement strategies have been proposed by which individuals might aggregate to form a selfish herd as a defence against predation, but although the spatial benefits of these strategies have been extensively studied, little attention has been paid to the importance of predator attacks that occur while the aggregation is forming. We investigate the success of mutant aggregation strategies invading populations of individuals using alternative strategies and find that the invasion dynamics depend critically on the time scale of movement. If predation occurs early in the movement sequence, simpler strategies are likely to prevail. If predators attack later, more complex strategies invade. If there is variation in the timing of predator attacks (through variation within or between individual predators), we hypothesize that groups will consist of a mixture of strategies, dependent upon the distribution of predator attack times. Thus, behavioural diversity can evolve and be maintained in populations of animals experiencing a diverse range of predators differing solely in their attack behaviour. This has implications for our understanding of predator–prey dynamics, as the timing of predator attacks will exert selection pressure on prey behavioural responses, to which predators must respond.

1. Introduction

Aggregation into groups of individuals is a widespread phenomenon across many animal species. There are a number of well-recognized benefits to aggregation through mechanisms that act to reduce predation risk [1], including the dilution [2], encounter–dilution [3] and confusion [4,5] effects, where the presence of other animals acts to reduce the risk to any given individual.

However, there are also potential costs to forming aggregations, of which the most commonly considered are reduction in resource uptake rate through competition; increased aggression; local resource depletion; and increased detection by predators (for a review, see [1] and references therein). Thus, many taxa use grouping facultatively in response to the strength of perceived predation risk, initiating or enhancing aggregation in response to heightened threat [2,6,7]. The process of forming an aggregation can take a non-trivial amount of time, being dependent at least on the finite rates of turning and movement of the individuals concerned [8,9]. Thus, it may commonly be that predators attack while the aggregation is forming. By contrast, existing theory, almost without exception, ignores this case and focuses on stable groups (that are either permanently maintained or are the behavioural outcome of the process of aggregation studied here).

A particularly influential body of theory for understanding the anti-predatory benefits of aggregation has been the selfish herd hypothesis stemming from the classic paper of Hamilton [10]. This hypothesis assumes that the relative risk of two individuals can be evaluated by comparison of the areas around them that include all points closer to that individual than to any other (the so-called ‘domains of danger’). There have been important recent works refining the definition of domains of danger [8,11] and evaluating the types of behavioural patterns that generate aggregations through the selfish herd effect [8,12–16]. Many of these latter works take an evolutionary approach, comparing the relative predation risk of interacting prey adopting different strategies. However, implicitly or explicitly, these previous works evaluate the relative effectiveness of different behavioural strategies only after the process of aggregation has resulted in a stable group configuration. Here, we aim to generalize this to the biologically realistic case where attacks occur while aggregations are still in the process of forming.

Facultative group formation may be triggered by cues that provide either information about general risk of attack or warning of an impending specific attack. An example of the first case may be aggregation driven by lower environmental light levels (triggered by cloud formation or impending dusk) that are correlated with enhanced attack rates by predators and/or reduced ability to detect or evade attacks that do occur [17,18]. An example of the second case might be a predator that has to break from cover and travel a distance across open ground before making contact with the prey (such as a cheetah stalking prey through long grass before attacking [19]). As soon as the predator breaks cover, it is likely to be much more easily detectable than it was previously. In response to such detection, there may be sufficient time for the prey to initiate (and perhaps even complete) the process of aggregation before the predator has closed on the prey; however, sometimes the prey may still be in the process of aggregating when the predator strikes. This last situation is an exemplar of the type of phenomenon modelled in this paper.

As discussed above, the process of aggregation can be thought of as being triggered by cues that a specific attack is imminent. However, the point at which individual prey are at risk from the attack may be later than that [20]. Implicit in the concept of the domain of danger and its modifications is the issue of target selection by the predator. A relatively large domain of danger indicates a large relative risk of being the target of a particular attack [10,12]. If we take the example of a cheetah breaking cover from some trees and closing in across grassland on a number of gazelle, it is likely that distance from cover to any prey is sufficient that there may be changes in the relative positioning and behaviour of the gazelle before the cheetah has closed sufficiently to tackle any one individual. Hence, in such cases, it is likely to be advantageous to the cheetah to delay selection of a particular gazelle to target in the attack until some time into the closing phase of its attack. It is at this moment of target selection that the relative predation risks of prey in different positions (relative to others) most directly impacts on the outcome of the attack for specific prey individuals [20]. Thus, it is at this point in the predation sequence that the relative effectiveness of different aggregation strategies is evaluated in our model. This moment may well occur while the process of aggregation is still ongoing. Neill & Cullen [21] and Lima [22] both discuss the value of clearly separating predator strategy from tactics. Our paper can be seen as a small step in correcting the current imbalance of research focus on the first of these. We deal not with the larger scale question of how animals trade-off predation risk and resource exploitation, but the finer scale issue of identification of the anti-predator tactics that would be useful in different circumstances.

Throughout this paper, the timing of attacks refers to the timing of the moment of target selection by the predator relative to the time when the predator could first be detected by the prey (causing the prey to initiate defensive aggregation [20]). We demonstrate the importance of considering the temporal aspect of movement decisions in the reduction of individual risk within groups of animals. We investigate the relative success of different movement rules, and the success of a mutant strategy invading a population of individuals using an alternative strategy. We explore a variety of rules of increasing complexity, since some complex movement rules have been criticized [12,13] on the basis that they may be cognitively too demanding for animals to follow. We find that the invasion dynamics depend critically on the time scale of movement and focus our evaluation of these results on the evolutionary consequences of variation in attack time.

2. Methods

We use the agent-based modelling framework described by James et al. [8] and Morrell & James [16] as the basis for our simulation model of aggregation behaviour. N point-like agents (prey individuals; we use N = 20 as the default here) are placed in a two-dimensional circular arena of radius R (measured in m, although the model is applicable to any unit) following a uniform random distribution. The density of individuals (per m²) within the group, d, is given by N/πR². We investigate the effect of altering N and d(R) on the results in the electronic supplementary material. Each agent is surrounded by a two-dimensional domain of danger (a limited domain of danger (LDOD)) in the shape of a circle of radius r, with a maximum area A_max =πr². We use the LDOD framework [8], rather than one where peripheral individuals have infinite domains of danger, as it is thought to more closely resemble predation risk in the wild [8,16]. Only isolated individuals (those at least 2r from any others) have an LDOD area of A_max. For other individuals, the circular LDOD is reduced by any bisector generated by an agent within a distance of 2r, giving an LDOD area A. In each simulation, each agent is allocated a movement rule from those defined below.

We consider three different movement rules (a subset of previously proposed rules and those considered in Morrell & James [16]). In line with Hamilton's [10] original ideas, and to allow for comparison with other published studies [8,12,13,16], we do not explicitly model predator behaviour: agents do not receive any directional information regarding the predator's approach direction. Such directional information has been shown to result in a movement decision that comprises both movement away from the predator and movement towards other individuals within the group [23]. Here, we focus our attention on the more controversial aspect of movement towards other individuals, rather than simply away from the predator. In addition, the habitat is assumed to be homogeneous, with no areas of cover that could potentially be used by the prey for protection.

The rules we consider are the following.

• — Nearest neighbour (NN). Each agent moves directly towards its closest neighbour [10]. NN is the simplest rule we consider.

• — Multiple nearest neighbour (nNN). Individuals move towards the average location of several (n) nearest neighbours [12]. For simplicity, we consider only n = 3 here.

• — Local crowded horizon (LCH). Each individual moves towards the area with the densest concentration of conspecifics, depending on their positions relative to the focal individual. Individuals calculate the distance to their (up to) 20 closest neighbours, and close neighbours have a strong influence on movement direction, while distant group-mates exert a much weaker influence. We use the perception function suggested by Viscido et al. [13] as being biologically plausible:

  

  where x is the distance from the focal individual and k = 0.375 [13]. The influence of each neighbour is weighted by f(x).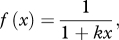

In our simulations, N_NN agents used the NN rule, N_3NN agents used the 3NN rule and N_LCH agents used the LCH rule (N_NN + N_3NN + N_LCH = N).

In each time step t, until a maximum t_max (here, t_max = 10 s), each agent identifies its target location, based on the movement rule it is following, and then moves at a speed of 0.15 m s⁻¹ towards that target location (the approximate swimming speed of a three-spined stickleback [8,16]). Each time step in our simulations lasts 0.1 s. The start of the simulation (t = 0) represents the point at which the agents begin moving. All individuals move simultaneously, as is likely to occur in nature, rather than sequentially, and thus each agent updates its target location and direction in every time step. Bode et al. [24] demonstrate that under higher predation threat, synchronous behaviour becomes increasingly probable. LDOD areas are calculated after every time step and for every individual. We ran 1000 simulations for each set of parameter values. All simulations were run in C, and resulting data were analysed using Matlab R2007b.

At each time step, we calculated the total LDOD area (the sum of A for all individuals, A_tot). We then calculated the proportion of A_tot occupied by each individual to give a measure of the way predation risk is distributed among individuals. For each time step, we then calculated the mean proportion of A_tot for all individuals using each strategy. Finally, we calculated the mean and standard error of these values across 1000 replicate simulations. This method allows us to compare the relative success of strategies in reducing individual risk: if the mean proportion of A_tot occupied by individuals using one strategy is less than the mean proportion of A_tot occupied by individuals using an alternative strategy, then the first strategy is more successful at reducing individual risk.

3. Results

(a). Proportion of risk: mixed-strategy population

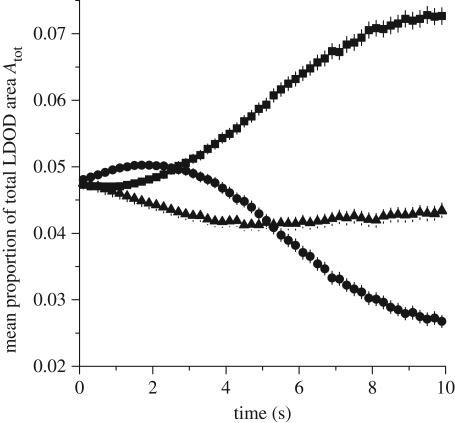
Figure 1 shows how the proportion of the total LDOD area (A_tot) occupied by individuals using each strategy changes over the course of 10 s of movement, when each strategy is equally represented in the population (N_NN = N_3NN = N_LCH = 7). Figure 1 indicates that the relative success of the different movement rules is dependent on the time elapsed since the start of prey movements towards each other. This can be thought of as the time at which the predator closes on and makes its attack on the moving prey group. Time t = 0, when the prey start moving, can be thought of the time when the prey first detect the presence of the predator and/or cues of imminent attack. At very rapid predator attack times (less than 1 s after detection), NN and 3NN individuals do equally well and are more successful than LCH individuals in the population (figure 1). If predators attack more slowly (after between 1 and 5 s of movement), 3NN individuals do considerably better than individuals using other rules. After 5 s of movement, LCH individuals are most successful. Thus, if we considered only what happened when the population reached equilibrium (i.e. when movement ceases), we could conclude that the LCH strategy was the most successful, yet the 3NN strategy performs better for a considerable proportion of the movement time. Thus, selection pressure on movement rules depends on the characteristic interval that prey have for aggregative movements between them first detecting the predator and the predator being in a position to capture an individual.

Figure 1.

Proportion of risk: mean (±2 s.e.) proportion of the total LDOD area occupied by individuals using NN (squares), 3NN (triangles) and LCH (circles), when all strategies are equally represented in the population. Parameter values: N_NN = N_3NN = N_LCH = 7, d = 4.

(b). Mutant invasions

We next consider the ability of ‘mutant’ rules to begin to invade a population using a different movement rule. In each set of simulations, 19 individuals use the ‘population strategy’, and one individual uses an alternative strategy. We investigate all six potential mutant–population combinations. Figure 2 illustrates the ability of the mutant rules to invade each population type, showing the mean proportion of the total LDOD area (A_tot) occupied by the mutant and population members.

Figure 2.

Mean (±2 s.e.) proportion of the total LDOD area occupied by the mutant (open circles) and an average population member (filled squares), for each possible combination of mutant and population strategy. (a) An NN mutant in a population of 3NN (‘NN versus 3NN’), (b) 3NN versus NN, (c) NN versus LCH, (d) LCH versus NN, (e) 3NN versus LCH, and (f) LCH versus 3NN. Other parameter values: N = 20, N_m = 1, d = 4.

The ability of a mutant using one strategy to invade a population using an alternative strategy is highly dependent on the time at which the invasion is considered. An NN population (figure 2b,d) is stable against invasion by both the 3NN (figure 2b) and LCH (figure 2d) mutant for the first approximately 1.5 s of movement. After this time, the 3NN mutant can successfully invade, but the population is stable against invasion by the LCH mutant for intervals less than approximately 4 s. A 3NN population (figure 2a,f) is always stable against invasion by NN mutants (figure 2a) and against LCH mutants for intervals less than approximately 7 s (figure 2f). If the predator attacks with a longer interval than this, the LCH mutant can invade the population. Finally, in a population of LCH individuals (figure 2c,e), both NN and 3NN mutants can invade if predators attack rapidly (less than 1 s for NN, less than 2 s for 3NN), but if the predator attacks after more than 2 s of movement has taken place, an LCH population will be stable against invasion.

(c). Invasion dynamics

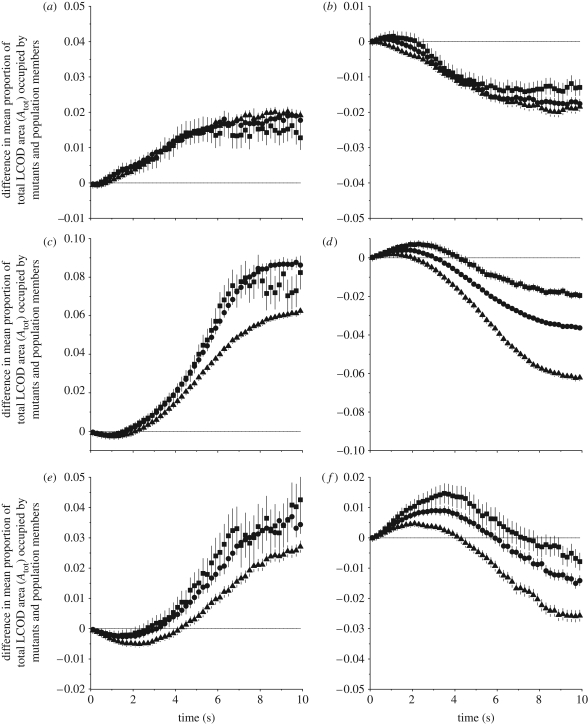
We now consider what happens as the number of mutants in a population increases (either through individuals using different strategies entering the group, individuals switching strategy or through reproduction where parental strategies are passed on to offspring). We initially consider a single mutant individual using one strategy invading a population using an alternative strategy (thus considering the strategies in a pairwise game), then increase the number of mutants (five and 10 mutant individuals in a total population of 20). As before, we calculate the mean proportion of the total LDOD area occupied by individuals using each strategy. We then calculate the difference in these values as (mutant mean − population mean), giving a positive value where the population is stable against invasion, and a negative value where the mutant is able to invade. This is shown in figure 3, where each panel represents a different mutant-versus-population comparison, with three different mutant frequencies.

Figure 3.

Invasion dynamics: invasion success as mutant numbers increase, measured as the difference in the mean proportion of the total LDOD area occupied by mutants and population members. The horizontal line at zero indicates equal success (measured as the proportion of the total LDOD area); positive values indicate that the population is stable against invasion by the mutant, and negative values that the mutant can invade the population. Squares, N_mut = 1; circles, N_mut = 5; triangles, N_mut = 10. (a) NN versus 3NN, (b) 3NN versus NN, (c) NN versus LCH, (d) LCH versus NN, (e) 3NN versus LCH, and (f) LCH versus 3NN. Error bars represent 1 s.d. Parameter values: N = 20, d = 4.

At the start of each predator attack, there are initial intervals of a few tenths of a second where invasion is possible in all populations (t < 0.3). These occur when the individuals have only just begun movement and are close to being randomly positioned in the arena. There is a possibility, then, that a mutant using any strategy could invade a population using any alternative strategy, if predators attack in the first moments after detection by the prey (e.g. an ambush predator).

We now consider whether populations are stable against invasion after potentially adaptive movement has taken place. If we consider pairs of populations in turn, we can investigate whether a population using strategy ‘A’ is stable against a mutant using strategy ‘B’ and vice versa. A single NN mutant can invade a 3NN population (figure 3a, squares) only in the first moments of movement, and thus 3NN is stable against NN. NN populations are stable against 3NN (figure 3b) only if the predator attacks within the first 2 s, otherwise the 3NN mutant can invade. When NN plays LCH (figure 3c), the LCH population is stable after 1.5 s of movement, while an NN population is stable against invasion by a single mutant for intervals of less than 4.5 s (figure 3d). In the final combination, 3NN can invade LCH for around 2.5 s after movement begins (figure 3e), while being stable against an LCH mutant unless the interval is greater than approximately 7.5 s (figure 3f).

If a mutant can invade a population, then that mutant can increase in frequency in the population, and there is the potential for the mutant strategy to become the dominant strategy in the population or for a combination of strategies to coexist. Figure 3a–f also shows the invasion success of mutants as their numbers increase to five (circles) and then 10 (triangles). Our results show that once a mutant strategy has gained a foothold in the population, the range of intervals over which that strategy is more successful than the original population strategy increases (the areas where the difference between the means is negative increase). We consider first the case where predator attack times are fixed (i.e. the predator always attacks at a certain point in time) and discuss how each pairwise combination of strategies is likely to evolve.

(i). NN and 3NN

For the majority of predator attack times, a 3NN population is stable against invasion by NN, and a 3NN mutant can invade an NN population. However, if predators attack rapidly, invasion by an NN mutant is possible, and an NN population is stable (figure 3a,b). If NN initially invades, then it can increase in numbers until the population consists of 10 NN and 10 3NN individuals (figure 3a). For slower (later) predator attack times (larger values of t), the opposite is true: 3NN mutants can increase in number and persist at increasingly rapid attack times (figure 3b).

(ii). NN and LCH

A single NN individual can invade an LCH population at rapid predator attack times and remains more successful at these times as its numbers increase (figure 3c). A single LCH individual can successfully invade an NN population after 4.5 s (figure 3d) and remains more successful at later attack times as numbers increase. When the group is equally divided between the two strategies, there is a very small period of time (at around 2 s) where success of the two strategies is similar (the point at which the triangles on figure 3c,d cross the ‘zero’ line). For intervals of this length, it is possible that a mixed group of individuals might persist, unless random drift allows the numbers of one or the other to increase to fixation. Otherwise, the population is likely to fix at NN (if attack times are rapid) or LCH (if attack times are slower).

(iii). 3NN and LCH

A similar pattern is seen for the remaining strategy combination: 3NN can increase in numbers if predators attack rapidly (figure 3e), whereas LCH can increase if predators attack later (figure 3f). When the group consists of half 3NN and half LCH, there is again a small period of time where strategies could coexist, but generally, we would expect the population to evolve to either 3NN (if attacks are rapid) or LCH (if attacks are slow).

4. Discussion

Our results suggest that the consideration of the timing of predator attacks (relative to the movement speed of the prey) is critically important in understanding the anti-predator responses of prey. The timing parameter studied in our model is the delay between prey first being aware of impending attack and an individual actually being struck by the predator. This will be influenced both by the nature of the predator and by the environment. For predators that attack from protective cover, the greater the distance between such cover and the prey group the greater the attack time. Thus, we would expect this attack time to be longer in open environments (like Steppe grasslands, tundra, savannah, lakes and seas) than more complex environments where prey can less easily avoid potential hiding places of their predators (like scrubland, forest, or narrow rivers and streams). While we found that complex strategies are generally favoured over longer attack times, no defence is effective at very short attack times (against ambush predators). This is because there is insufficient time between predator detection and attack for a significant amount of adaptive movement to take place, and individuals remain close to their random starting positions. The benefits of potentially adaptive movement are only seen later in the movement sequence. Complex strategies are not immediately favoured, particularly in low-density groups (see the electronic supplementary material), owing to the fact that individuals using these rules can be left moving ‘alone’ with no reduction in the LDOD area, for a longer time period, as their strategy does not take them directly towards another individual (thereby rapidly reducing the LDOD area). With the exception of the initial moments of the movement sequence, we found no evidence that multiple strategies might coexist in a population at any given attack time, suggesting that variation in predator attack timing would be necessary to allow for multiple strategies to coexist.

Our results also suggest that there may be positive frequency dependence to rule success. A strategy can invade across a wider range of attack times if it starts at a higher frequency. Thus, both simple and complex rules are favoured when they are already abundant in the population. A population consisting predominantly of one strategy is much more stable against invasion than one consisting of a mixture of strategies. This suggests that each strategy is most successful when in a group containing others playing the same strategy and may work against polymorphism at any fixed attack time, again suggesting that a mixture of attack times is needed to select for mixed responses in prey.

Overall, if predator attack times are fixed, then there are very few opportunities for a mixture of different strategies to persist in the population. A second, and perhaps more likely, possibility is that predator attack times are not fixed, but that predators may attack a group across a range of times. Together, our results point to the following hypothesis: if predators are fixed in their attack strategy (i.e. they always attack at the same point in time), we predict that prey populations should evolve towards a single, evolutionarily stable movement rule. However, if predator attacks are unpredictable in time, then we predict mixed responses in prey. This unpredictability may arise because different individual predators have different, fixed attack times; different species of predators differ in their hunting methods and therefore attack timing; or because other factors (such as distance from cover) cause variation in attack timing. Some prey individuals may use simple rules, and others more complex rules (a polymorphism), or individuals may respond using alternative rules (a mixed solution), perhaps dependent upon other factors, such as the immediate size and density of the group, or their own individual perceived risk. For example, individuals may use their distance to neighbours to choose which rule to use; using one rule when close to a neighbour, and a different rule if isolated. In a group consisting of individuals using NN and LCH, for example, the individuals using LCH would be safer on those occasions where predators attack slowly, whereas those using NN would be safer on those occasions where predators attack more rapidly; thus, prey could select their strategy based on the distance between the predator and the group. The overall success of the two strategies and the dynamics of the population evolution would be dependent on the distribution of predator attack times.

Many species are preyed upon by a variety of predators differing in their attack behaviour, and where multiple predators are present, prey are likely to evolve a range of risk-sensitive responses [25,26]. Vervet monkeys (Cercopithecus aethiops), under threat from leopards, martial eagles and pythons, show predator-specific alarm calls and anti-predator responses [27,28]. In fishes, guppies (Poecilia reticulata) fall prey to a variety of other organisms and respond in a risk-sensitive manner [29]. Thus, we may expect different movement rules to evolve in response to different predators. Individuals of the same predatory species may also differ consistently in their attack strategies [30]. While some variation in attack times can be attributed to predator species or strategy, variation in attack timing is also likely to result from random factors, such as the distance from the prey group at which the predator is first detected. Testing this hypothesis is a fascinating route for future study.

Previous studies have shown that individuals using simpler strategies (such as NN) can achieve protection through encounter–dilution effects [16], and here we show that these individuals can also benefit at the expense of others in the group (i.e. through the selfish herd effect), given the right ecological conditions.

Using an evolutionary genetic algorithm, Reluga & Viscido [14] demonstrated that complex averaging rules could evolve from simpler ones, but considered only equilibrium domain of danger areas once the aggregation had formed, and not attacks that occur while the aggregation is in the process of forming. Empirical evidence for the use of different movement rules is limited [16], although in three-spine sticklebacks, individuals appear to prefer neighbours that can be reached more quickly over those that are spatially closer [31].

In line with previous explorations of the selfish herd, we assume here that predators appear at random and attack the closest individual, so that risk is related entirely to the LDOD area. In reality, predators may target specific individuals within a group, or certain positions within the group may be more risky than others. Peripheral individuals should theoretically be more at risk than those in the centre of a group [10,32], something that has received support across taxa ([33,34]; but see [35]). An individual's position within a group may therefore affect the best way for it to respond to a predator attack, and thus movement rules may also be state-dependent [36], perhaps related to each individual's perception of its position within the group or level of risk (LDOD area). Vigilance and the detection of predators by prey may also affect optimum movement decisions. If predators delay target selection until after some individuals have detected and responded to the predator [20], any delay in responding may also influence optimal movement rules. Here, we have shown the importance of closing speed of the predator relative to the movement speed of prey on selection on anti-predator grouping behaviours. Interestingly, Wood [9] demonstrates a similar strong influence of predator speed on the final shape of aggregations predicted by plausible prey movement rules.

We also assume that all individuals begin moving at the same point in time, and at the same speed, when in many animal groups there is variation in both ‘starting time’ and movement speed. We suggest that the optimal movement rule for any given individual should depend on its escape speed. A fast-moving individual may benefit by using a simple rule, particularly if predators attack quickly. Presumably, a fast NN animal could easily invade a population using slow NN, leading to the evolution of faster escape responses. The speed of decision-making may also be important: complex movement rules have been criticized [12,13] on the basis that they may be cognitively too demanding for animals to follow. Incorporating a ‘thinking time’ into each movement step could account for the complexity of the calculations.

Our findings have implications for our understanding of predator–prey dynamics, as the timing of a predator attack relative to the detection of the predator by the prey, and the prey response, is critical in determining the optimal escape decision of the prey. Early and late attacking predators may exert different selection pressures on prey, resulting in a mixture of escape strategies within a single prey population. The movement rules used to escape from predators could also influence positioning outside attack periods, allowing individuals to choose a position in a group which allows for successful reduction of risk when attacks occur. Clearly, the ability of prey to respond appropriately to predators will be critical for their fitness, but equally, predators that behave unpredictably (by attacking at different times) may ensure that a single optimal prey response cannot evolve and leave a mixture of different escape strategies within a population. We have adopted a modelling framework in this study that allows effective comparison with previous relevant studies. However, it should be acknowledged that this represents a highly idealized description of any natural system. As the body of theory on the selfish herd becomes more and more substantial, the need to explore how well the predictions of idealized models transfer to system-specific, more-realistic case studies grows also. In our modelling framework, we do not consider predator success and thus cannot evaluate selection pressures on the predator, thus, the longer term evolutionary consequences of the aggregative tactics explored here are also worthy of exploration within a coevolutionary modelling framework.