Adaptive Pattern Recognition of Myoelectric Signals: Exploration of Conceptual Framework and Practical Algorithms

Abstract

Pattern Recognition is a useful tool for deciphering movement intent from myoelectric signals. Recognition paradigms must adapt with the user in order to be clinically viable over time. Most existing paradigms are static, although two forms of adaptation have received limited attention. Supervised adaptation can achieve high accuracy since the intended class is known, but at the cost of repeated cumbersome training sessions. Unsupervised adaptation attempts to achieve high accuracy without knowledge of the intended class, thus achieving adaptation that is not cumbersome to the user, but at the cost of reduced accuracy. This study reports a novel adaptive experiment on eight subjects that allowed repeated measures post-hoc comparison of four supervised and three unsupervised adaptation paradigms. All supervised adaptation paradigms reduced error over time by at least 26% compared to the nonadapting classifier. Most unsupervised adaptation paradigms provided smaller reductions in error, due to frequent uncertainty of the correct class. One method that selected high-confidence samples showed the most practical implementation, although the other methods warrant future investigation. Supervised adaptation should be considered for incorporation into any clinically viable pattern recognition controller, and unsupervised adaptation should receive renewed interest in order to provide transparent adaptation.

I. Introduction

PATTERN recognition, or pattern classification, of myoelectric signals has been widely investigated with promising results in the laboratory setting. A wide range of feature sets, including time-domain [1-7] and frequency domain [8], combined with a wide range of classifiers, including fuzzy logic [5, 9-11], neural networks [2, 3, 12-16], and Bayesian statistics [16-18], have yielded low classification error (error) on able-bodied subjects. Several studies have produced low error on subjects with an amputation [9, 13, 14, 16, 17, 19].

Although these studies report low error in a single session, robustness over time or during different activities has rarely been evaluated [20]. Pattern recognition involves learning the nature of muscle contraction patterns for the intended movements of a specific user. This tool provides the advantage of recognizing the subtleties of an individual user's muscle activity at a particular instance in time, but does not accommodate changes in the user's patterns over time. These variations may be caused by electrode conductivity changes (perspiration, humidity), electrophysiological changes (muscle fatigue, atrophy, or hypertrophy), spatial (displacement) changes (electrode movement on the skin or soft tissue fluid fluctuations), user changes (cognitive intent variations or contraction intensity changes), and potentially other factors. Although spatial changes can increase error [21-23], the influence of displacement may be minimized by collecting training data from areas covering the displacement range and using a robust feature set [23]. It is conceivable that the other categories of change might also be incorporated into a robust training protocol, but the time required to obtain exemplars¹ from each permutation of change would limit the clinical viability of such a protocol. In contrast, a pattern classifier capable of adapting to changes might provide an increased level of robustness by responding to changes as they occur. A robust training protocol, combined with an appropriate adaptation paradigm based on a proper theoretical framework of robust control, is likely required to implement a clinically viable system.

Adaptation can be introduced either in a supervised manner, in which the user's intended class is known, or in an unsupervised manner, in which the intended class is unknown. Supervised adaptation is easier to implement practically, but requires frequent retraining sessions with the user. It also requires an appropriate interface system outside of the laboratory to conduct the retraining and prompt for these intended classes. Nishikawa et al. [21] has demonstrated reduced classification error using supervised adaptation, but has not compared different strategies of data selection (i.e., which training data should be selected for recalculating the classifier).

Unsupervised adaptive pattern recognition of myoelectric signals potentially reduces the need for retraining to account for changes over time. Fukuda et al. [13] has demonstrated an adaptation paradigm that monitors the entropy associated with each classification decision and recalculates the classifier boundaries whenever the entropy is sufficiently low to ensure correct classification. Entropy is a measure of the confidence of a classification (decision) as a function of the probability that a feature set belongs in each class:

$$E\left(n\right)=-\sum _{k=1}^K{p}_k\left(n\right)\ln \left(p_k\left(n\right)\right),$$ (1)

where p_k(n) is the probability of class k in time window n and K is the number of classes to be considered. A decision has low entropy (high confidence) if only one class has a high probability. A classification has high entropy (low confidence) if all of the classes have similar probabilities. Entropy may serve as a good selector of exemplars, allowing for real-time adaptation that does not require the user's attention. Fukuda et al. [13] has achieved 99% classification accuracy over the course of 120 minutes of continuous movement for classification of eight movements. Related work by Bu and Fukuda [12] achieved similar results (94% accuracy) using a recurrent log-linearized Gaussian mixture model, while reporting lower accuracy (89%) for the non-recurrent model.

The Neural Engineering Center for Artificial Limbs performs research on subjects with targeted muscle reinnervation (TMR) - a novel surgical technique that provides the residual muscles of amputees with similar signal content to the normal muscles of able-bodied subjects [25-29]. Because we see the same subjects several times each year, our laboratory has transitioned from accepting classification paradigms that work well for a single session to systematically searching for clinically viable pattern recognition techniques that address a wide range of topics. This search has included:

• Proper training and therapy with the subject to produce consistently discernable patterns for each of their intended movements

• Consistent electrode placement using clinically viable socket design and donning techniques

• Classifiers that can robustly adapt to the changing behavior and environment of the user

These clinically oriented motivations have paradoxically caused our laboratory to reevaluate foundational presuppositions of the application of pattern recognition techniques to myoelectric prosthesis control, including a reevaluation of concepts such as robustness and proper metrics of optimal performance. The work reported in this study was specifically designed to explore and evaluate concepts for real-time adaptive pattern recognition using a novel experimental framework that allowed robust post-hoc comparison of paradigms, in an attempt to influence the direction of future research into algorithms for implementation of a more clinically viable classifier.

II. Methods

Eleven subjects were tested in total. Two able-bodied subjects and one TMR amputee subject with a unilateral shoulder disarticulation participated in a pilot study to optimize parameter settings. Five able-bodied subjects and three TMR amputee subjects (2 with shoulder disarticulations and 1 with a transhumeral amputation) participated in the resulting study. Able-bodied subjects were chosen who had little to no experience with pattern recognition and spanned a wide range of ages. All procedures were performed with informed consent and approved by the Northwestern University Institutional Review Board.

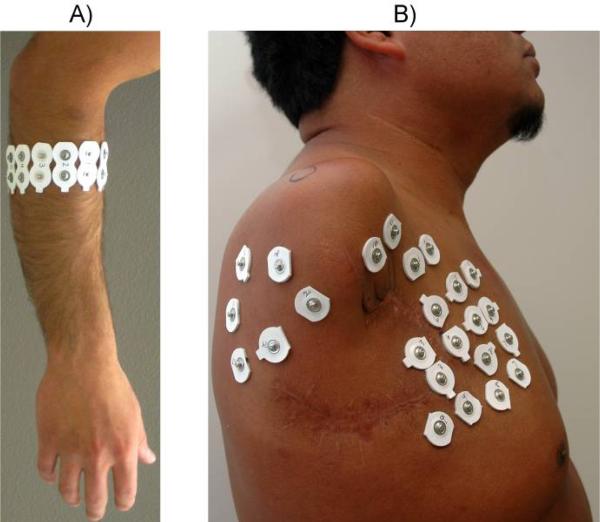
Twelve disposable self-adhesive silver/silver chloride (Ag/AgCl) snap electrode pairs with 2-cm spacing (Noraxon # 272) or stainless steel dome electrodes were used for EMG recording. For able-bodied subjects, electrodes were placed equidistantly around the circumference of the proximal third of the forearm with a longitudinal orientation (Fig. 1a). On TMR subjects, electrodes were placed at predetermined locations that had yielded the best classification accuracy using a high-density electrode array [26] (Fig. 1b). Signals were pre-amplified and filtered using commercially available myoelectric amplifiers (Liberating Technologies Inc. BE328 Remote AC electrodes, 30 Hz – 420 Hz -3dB band pass filter) and recorded with a custom-built 16-bit EMG amplification and acquisition system at a sampling rate of 1 kHz. Feedback was provided based on real-time classification using a 3-GHz Pentium 4 dual-core computer.

Fig. 1.

Electrode placement. A) 12 electrodes were placed in a circumferential array around the proximal third of the forearm for able-bodied subjects. B) Placement of the 12 electrodes was chosen for TMR subjects based on a high-density electrode array optimization.

A Linear Discriminant Analysis (LDA) classifier was used to provide real-time non-adapting classification. Four time domain features (mean absolute value, number of zero-crossings, waveform length, and number of slope sign changes) from 12 channels were input into the system. Data were segmented into 150 ms windows, and overlapped at 30 ms intervals. The classifier output one of eleven classes every 30 ms for each subject. For amputees, these classes included elbow flexion/extension, forearm pronation/supination, wrist flexion/extension, hand open, three self-selected grasp patterns, and no movement. For able-bodied subjects these classes included forearm pronation/supination, wrist flexion/extension, hand open, five grasp patterns (three-jaw chuck, lateral/key, fine pinch, trigger/tool, power), and no movement.

A custom Acquisition and Configuration Environment (ACE) myoelectric control software program developed by the University of New Brunswick was used to process non-adapting classification in real-time. This system also provided a graphical user interface for guiding data acquisition sessions and promptings for real-time testing. Using ACE, subjects alternated between classifier training and real-time testing trials. Training data were used to calculate the boundaries of a pattern recognition classifier. This classifier was then used to provide real-time feedback during the subsequent (paired) real-time testing trial. This cycle of acquiring training data, calculating a new classifier, and testing was repeated for a total of ten pairs of training and real-time testing data.

For classifier training trials, subjects were prompted with onscreen word and image cues for each class. Training trials consisted of two repetitions of each class in random order; subjects held the muscle contraction corresponding to the prompted motion for four seconds with a three-second resting delay between movements. For real-time test trials, subjects were prompted with the same visual display as the training session and instructed to attempt that class of motion. Testing trials consisted of two repetitions of each class in random order, held for three seconds with a three-second delay between classes. Subjects were given visual feedback regarding the class they were activating in test sessions.

A. Post-Hoc Adaptation Paradigms

Classification errors from the first through third testing data sets were calculated from classifiers computed on their paired training data sets. Training data from the trial that produced the least error was used as the baseline data set (B=Tr_{n = 1, 2, or 3}). The minimum-error classifier of the first three was chosen over solely using the first data set to ensure that the baseline data set did not accidentally create a poor classifier. This baseline data set was used to calculate the non-adapting classifier (NA=B) and as the data set to which tagged samples from adaptation algorithms were successively added. Examples in the remaining portion of this section will assume the second trial was chosen as the baseline (i.e., n=2) to illustrate the process.

Six to eight pairs of data sets remained after the baseline data set had been selected. The training data sets for these pairs were ignored for the rest of the post-hoc analysis, although they played a vital role in the nature of the analyzed data. The feedback given to subjects from the static classifiers calculated using each successive training data set may be thought of as originating from snapshots of an adaptive classifier, because testing trials provided real-time feedback between each of the training datasets used to calculate a classifier.

Adaptive classifiers were calculated from data sets that combined data from the baseline data set with tagged samples from the remaining testing trials. Real-time testing samples were tagged based on a given adaptation paradigm, each of which looked for different qualities in every sample and selected any samples that passed an appropriate threshold or requirement. Starting with the baseline classifier's paired testing set (i.e. Ts₂), selected points were tagged and added to the baseline data set. The adaptive classifier recalculated boundaries based on this enlarged data set (A₂=B+Tag[Ts₂]). Both the non-adapting classifier (NA) and the adaptive classifier (A₂) were then compared by calculating the error on the succeeding set of testing data (Ts₃). Successive cycles of adaptation added points from the next set of testing points to the adaptive classifier (A₃=A₂+Tag[Ts₃]) and calculated errors on the next set of testing data (Ts₄).

1) Supervised Adaptation

Four supervised adaptation paradigms were employed:

• Supervised High-confidence (SH). Real-time decisions tagged as high confidence (low-entropy) were collected, paired with their supervised (correct) class, and the reduced data set was concatenated to the existing classifier data set. Feature space boundaries of the adaptive classifier were then recalculated using this expanded data set. By definition, these high-confidence points were closest to the mean of a given class. Any resulting adaptation was accordingly small, since the added points were already close to the center of the class boundaries. Because of these attributes, SH adaptation essentially accounted for a slow drift in the boundaries, constantly updating the center based on previous high-confidence decisions to make sure the center of the classifier remained consistent with the center of the user's decisions.

• Supervised Low-confidence (SL). Real-time decisions tagged as low confidence (high-entropy) were collected, paired with their supervised (correct) class, and the reduced data set was concatenated to the existing classifier data set. Boundaries of the adaptive classifier were then recalculated using this expanded data set. This paradigm, rather than reinforcing good decisions like SH, focused on correcting bad decisions. Instead of centering the boundaries on the data, SL gave added bias to correct errors. In the process, the classifier lost some confidence about its previously high-confidence decisions, since the boundaries were no longer centered. At the same time, the resulting boundaries were better defined in those ambiguous regions where errors commonly occurred, resulting in better distinction of errors. Because the performance of the classifier was ultimately dependent not on how confident a decision was, but whether or not the correct class was made, the SL paradigm should be better at fine-tuning the classifier for a stable user than SH.

• Supervised High & Low confidence (SHL). A combination of SH and SL, where both high and low confidence decisions were collected and paired with their supervised (correct) class and the reduced data set was concatenated to the existing classifier data set. Boundaries of the adaptive classifier were then recalculated using this expanded data set. SH allowed the classifier to track drifting patterns. SL adjusted the classifier to minimize the number of errors for a given pattern. The combination of the two, although performing neither function as well as SH and SL independently (since at times they might pull in opposite directions), should provide some level of both functions.

• Supervised All (SA). All of the samples in each new set of real-time testing data were concatenated in full to the existing classifier data set. Boundaries of the adaptive classifier were then recalculated using this expanded data set. In non-adapting pattern recognition, all of the data sets are collected at once. In the SA paradigm, however, the user had feedback and time to adjust patterns between each data set to provide some measure of adaptation. Including the entire data set ensured that the whole scope of the user's patterns were considered, and provided a large enough number of data points to have a sizeable impact on the boundaries of the classifier.

2) Unsupervised Adaptation

To investigate different approaches to unsupervised adaptation, either predicted exemplars or predicted errors were added to an existing classifier to adapt the classifier to changes in the user's patterns.

Unsupervised High-confidence (UH)

Similar to Fukuda's algorithm [13], UH adaptation tagged classifications that had high confidence (low entropy) and added these samples to recalculate the classifier boundaries. UH assumed that these high-confidence samples correctly predicted the desired class. Confidence values for pattern recognition of myoelectric signals are generally high. As a result, the vast majority of trials (~90%) had high confidence and they were included in the adaptive data set. The confidence threshold for inclusion was the only parameter requiring optimization. Two UH adaptation approaches were explored, one that employed a verification step that added significant processing load, and a second which skipped the verification process:

• UH₁: Conservative Unsupervised High-confidence. A conservative verification step was imposed in which the classifier reevaluated its prior data using the adaptive classifier, and only preserved the added sample if the energy of the system decreased by its inclusion [13]. Energy is the sum of entropy across time:

  $$J=\sum _{n=1}^{N}E\left(n\right)$$ (2)

• UH₂: Fast Unsupervised High-confidence. A second version of UH adaptation was tested that did not require tagged samples to reduce the energy of the previous classifications. This faster version substantially reduced the processing time of the adaptation algorithm, since the conservative method required the classifier to be recalculated and evaluated for each potential exemplar.

• Unsupervised Low-confidence (UL). This paradigm tagged class decisions as potential errors if the decisions had low confidence (high entropy). The class in the neighboring set of class decisions with the highest confidence was used instead, if that class coincided with the second most probable class for the sample in question. Samples that passed this criterion were added to the adaptive data set. Parameters to be tuned included the confidence threshold to consider the class decision as an error, and the number of neighbors to consider in reassigning tagged errors.

Unsupervised Blip-triggered (UB)

• UB₁: As suggested by Kato et al. [30], class decisions were tagged as errors if they quickly switched from one class to another, only to be followed in the decision stream by the original class. These samples were termed “blips” and reclassified as the same class as the neighbors on either side of them. The only parameter that needed to be optimized was the longest acceptable blip as indicated by a number of neighbors to span. This paradigm was motivated by the assumption that users could not physiologically transition between classes in less than 200 ms. As such, since new class decisions arrived every 30 ms, this blip-detection technique would serve as a useful indicator of errors.

• UB₂: This paradigm only added a subset of the samples tagged in UB₁. Only proposed errors that had high confidence (low-entropy) were added. This strategy was believed to be more robust than UB₁, because it would only add samples where the classifier was confident – yet wrong. In addition to the same neighbor-span tuning parameter for UB₁, the confidence threshold also needed to be tuned.

UH was an unsupervised version of SH. UH₂ added a verification step to accommodate for the fact that its decisions were not supervised, and thus subject to error. UL and UB were both unsupervised versions of SL. Because they were unsupervised, they needed some technique to determine if a decision was an error. They also needed a way to choose the correct class. UL and UB differed in their approach to deciding if a decision was an error, as well as in their approach to picking the correct class, but their underlying paradigm of minimizing errors by modifying ambiguous error regions of the boundary remained equivalent to the UL approach. These adaptation paradigms are tabulated in Table 1.

TABLE 1.

Adaptation Paradigms

	Adaptation Paradigm		Detection	Reclassification	Verification	Tunning Parameters
Supervised	High Confidence	SII	High Confidence	Prompted Class		Confidence Threshold
	Low Confidence	SL	Low Confidence	Prompted Class		Confidence Threshold
	High / Low Confidence	SHL	High Confidence	Prompted Class		High Confidence Threshold
			Low Confidence	Prompted Class		Low Confidence Threshold
	All	SA	High Confidence	Prompted Class
Unsupervised	High Confidence	UH1	High Confidence	Predicted Class	Reduced Energy	Confidence Threshold
		UH2	High Confidence	Predicted Class		Confidence Threshold
	Low Confidence	UL	Low Confidence	Maximum Confidence	2nd Choice Class = Reclassification	Confidence Threshold
				Neighbor
		UB1	Blip	Maximum Confidence		Span of Neighbors
	Blip	UB2	Blip	Maximim Confidence	High Confidence	Confidence Threshold
						Span of Neighbors

B. Data Analysis

Subjects’ muscle contractions were sometimes delayed after being prompted to perform a particular class. This reaction delay was understandable and resulted in “No movement” class decisions during the time of a prompted class for a given movement at the beginning of many trials. Adaptation paradigms might then incorrectly tag the sample as an error or exemplar depending on the paradigm, resulting in an improper portrayal of the paradigms that only resulted from the construction of the protocol. Delays between the randomized command prompt and the start of the subject's movement were accordingly removed in order to process only data during those times when the subject was actually performing a class. An exception to this delay removal was the “No movement” class, for which all data samples were used.

Twenty different values for each tuning parameter were used to optimize each paradigm across three pilot subjects, including one TMR subject and two able-bodied subjects. Confidence thresholds were calculated using a histogram segmented into 100 bins. Bins starting at one and incrementing by two's to 39 were tested. Neighbor spans started with the inclusion of only the closest temporal neighbor, and linearly incremented by twos to include all neighbors within 39 temporal decisions (1.2s) on either side of the selected sample.

Presentation of results for this study, which involved multiple trials for multiple subjects, necessitated data averaging. It is important when averaging differences in paired data to use the best representative metric such that averaging does not remove important results. Towards this end the authors compared absolute reductions in % classification error and relative reductions in % error (i.e. a reduction in error from 50% to 25% error = 25% absolute reduction and 50% relative reduction). Relative error had a larger kurtosis than absolute error, indicating better consistency or representation between trials and paradigms. Preference should accordingly be given to relative error measurements. Errors were calculated from the concatenated testing data for each subject. Statistical significance was assessed using reductions in relative error between the adaptive classifiers and non-adapting classifier. It should be noted that the average relative error reduction cannot be calculated from the average initial error and the average absolute error reduction, due to the effect of averaging. Thus, results that report the same average initial error and absolute error reductions may report different average relative error reductions.

III. Results

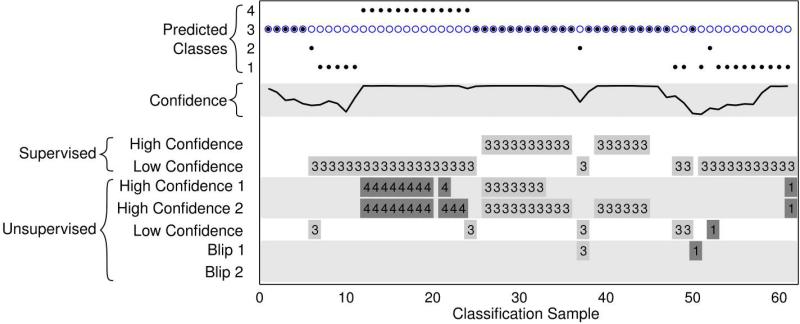
Adaptation paradigms frequently tagged samples to add to the baseline classifier (Fig. 2). The top of this figure shows the prompted class (class 3) as circles and real-time predictions as dots. The confidence of each decision is shown in the middle of the figure. Post-hoc adaptation strategies tagged some samples to add to the training set. The class number chosen by adaptive classifiers in each tagged sample is shown in the bottom of the figure. Adaptation strategies used the prompted class (supervised strategies), kept the same predicted class (UH), or suggested a new predicted class (UL, UB) if they thought the original classifier had made an error. All of the unsupervised adaptation paradigms incorrectly tagged some samples (Fig. 2).

Fig. 2.

Sample Classification decisions. From top to bottom: real-time test (circles/dots), confidence of decisions (line), and samples tagged in post-hoc analysis for inclusion in the adaptive data set (numbers). Out of 11 classes, only class 3 was prompted during this snapshot (shown as circles) and four classes were predicted during the real-time test (shown with dots). Post-hoc adaptation paradigms selected different samples to add to the adaptive data set, based on criteria specific to each adaptation paradigm. All adaptation paradigms tagged samples from this snapshot except UB₂. Sometimes unsupervised adaptation strategies suggested the inclusion of a sample but incorrectly changed the class: these incorrectly tagged samples (class ≠ 3) are highlighted in dark gray.

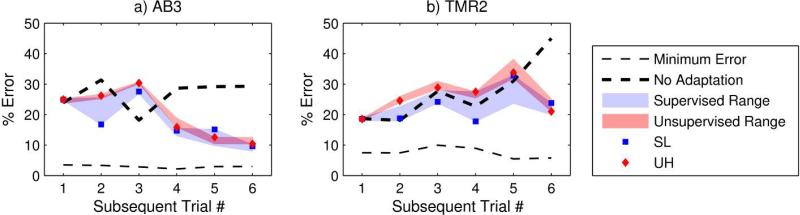
If the non-adapting classifier was stable over time (Fig. 3a), adaptive classifiers typically reduced the error over time. If the non-adapting classifier produced increased error over time (Fig. 3b), adaptive classifiers typically maintained the original level of error. As a result, all supervised adaptive classifiers and some unsupervised adaptive classifiers reduced the average error for most subjects (Table 2). Minimum error is also presented in this figure to provide a baseline of how consistently the subject performed. Minimum error was calculated by testing and training on the same real-time data.

Fig. 3.

Examples of classifier error over time. Supervised and unsupervised classifier ranges are shaded, and two illustrative adaptive classifiers are highlighted in comparison to the non-adapting classifier: Supervised Low-confidence (SL) and Unsupervised High-confidence (UH). AB3's non-adapting classifier was stable over time, and her adaptive classifiers reduced this error as time progressed. TMR2's non-adapting classifier produced more error over time, but adaptive classifiers maintained a low level of error. Supervised adaptive classifiers typically had lower error than unsupervised adaptive classifiers for both of these subjects. Minimum error is the error produced by training and testing on the same real-time data. Minimum error was low for both subjects, suggesting that their patterns were consistent (minimal overlap in feature space) and that the adaptive classifiers could have further reduced error.

TABLE 2.

Average % Error of Non-adapting and Adaptive Classifiers

Adaptation		Average ± SD	p-value	Able-bodied					TMR
				1	2	3	4	5	1	2	3
	None	30 ± 16		29	19	27	69	24	11	29	29
Supervised	SH	22 ± 8	0.018	28	8	21	25	10	11	27	29
	SL	21 ± 7	0.009	27	9	20	26	10	11	24	25
	SHL	20 ± 8	0.007	27	8	20	26	9	10	23	25
	SA	19 ± 7	0.006	26	8	19	24	9	10	22	25
Unsupervised	UH1	23 ± 9	0.051	30	8	22	32	11	11	28	29
	UH2	23 ± 9	0.049	29	8	22	28	11	11	27	30
	UL	24 + 9	0.068	31	10	22	30	12	11	29	29
	UB1	24 ± 9	0.104	32	10	22	32	14	12	30	30
	UB2	24 ± 9	0.101	32	10	22	32	13	12	30	30

Non-adapting Classifier

Subjects typically had large errors when the non-adapting classifier was used on the data throughout the last six to eight testing trials. The average nonadapting error across subjects was 30 ±16%, and ranged from 11% to 69%.

Supervised Adaptation

All supervised adaptation paradigms significantly reduced the error of the classifier relative to the non-adapting classifier (p<0.03). Supervised High-confidence adaptation (SH) had a 26 ± 28% relative reduction in error, Supervised Low-confidence adaptation (SL) had a 30 ± 24% relative reduction in error, Supervised High/Low-confidence adaptation (SHL) had a 32 ± 25% relative reduction in error, and adding all of the samples (SA) had a 34 ± 24% relative reduction in error. Despite wide fluctuations among users, paired differences in the relative error reduction of the adaptive classifiers were significant (p<0.02), except between SH and SL (p=0.1)

Unsupervised Adaptation

Unsupervised adaptation paradigms did not reduce error as much as supervised adaptation paradigms. The Unsupervised High-confidence (UH) paradigms showed the most relative reduction in error (23 ± 28%), which bordered on statistical significance across subjects (p=0.05). Unsupervised Low-confidence (UL) and Unsupervised Blips (UB) had lower relative reductions in error (UL: 21 ± 27%, UB: 17 ± 26%) that did not achieve statistical significance (p>0.07). These lower relative reductions in error are likely due to the fact that adaptation paradigms that had to recalculate the predicted class (UL & UB) were frequently unable to guess correctly the correct class: 35% of the samples added by the UL paradigm and 54% of the samples added by the UB paradigm incorrectly reassigned the class. In comparison, 9% of the samples added by UH were actually errors even though the classifier was confident they were correct.

Summary

The influence of relative improvements in error on the actual classification error for supervised and unsupervised classifiers is shown in Table 2. For each subject, average adaptive error was calculated from the average non-adapting error, scaled by the average relative improvement of the adaptive classifier.

IV. Discussion

A novel strategy and protocol are presented in this study for assessing adaptive classifiers. Feedback is presented to users using a classifier that is free to shift throughout the experiment. This boundary shifting is not biased towards any single adaptation strategy, yet it preserves the dynamic effects of feedback from an adaptive controller by providing static snapshots of the boundary movement. The resulting data may then be analyzed using numerous adaptation strategies, in which direct repeated-measures comparison between strategies may be made using the same data set. This strategy provides an efficient way to robustly examine new strategies as they become available, while allowing for direct comparison with existing strategies to examine for the presence of statistically significant improvements.

Although many adaptive classifiers reduced relative error compared with the non-adapting classifier, the number of added points varied widely among them. On average, Supervised High-confidence adaptation (HC) added 62% of available samples, Supervised Low-confidence (SL) adaptation added 16% of available samples, and Supervised High/Low-confidence (SHL) adaptation added 75% of the available samples. SL provided better reduction in error than SH, despite the fact that it only added 25% as many samples. It seems likely that, over time, repeatedly adding a large number of samples would lead to over-training, requiring a more selective inclusion criterion. SL likely preserves the responsiveness of the classifier to new adaptation by limiting the growth rate of the data set.

The Unsupervised High-confidence (UH) paradigm provided an implementable reduction in classification error. Although the Supervised Low-confidence paradigm provided a substantial increase in accuracy, the Unsupervised Low confidence (UL) paradigm was unable to consistently predict the correct class. Future algorithms that correctly identify the class in an unsupervised environment may be useful for long-term adaptation, but present implementations of UL appear unacceptable for clinical implementation.

The results from this study and others [21] suggest that some form of supervised adaptation should be incorporated into future clinically viable algorithms. Although supervised adaptation paradigms require conscious training by the user, they are useful when the performance degrades to the point where the user is willing to push a button to go through a short training session to tune the classifier. The authors suggest that SL is the best supervised adaptation method, since it provides substantial reduction in error without adding a large number of samples.

Data set size

This study did not control the number of added data points. Constraining the number of data points, while removing one confounding variable, would have introduced another. If adaptive strategies started with fewer data points than the non-adapting classifier, then the initial classifier may not have been sufficiently robust to ensure correct adaptation. Adaptation strategies that included larger number of points would have likewise started with a smaller baseline data set, in which case comparative improvements might be either due to the adaptation strategy or to the size of the baseline data set. Thus data size appears to be a confounding variable in any adaptive paradigm. It must be remembered that the subjects adapt even in the absence of feedback as they become familiar with the experiment, and thus any pool of non-adapting data is not homogeneous – later trials may have different boundaries than earlier trials. As a result, similar to Fukuda's study [13], all of the adaptive classifiers calculated boundaries from a larger sample of data than the non-adapting classifier. Similarly, some adaptive classifiers calculated boundaries from larger samples of data than others did. The topic of data quantity vs. data quality merits future investigation. Too much data results in overtraining, whereas insufficient data results in a poorly constructed classifier, but the optimal amount of data for EMG signals has yet to be determined, and depends in large part on the quality of the signals and the number of classes in the classifier. It is noteworthy that SL performed better than SH, yet with only a quarter of the data points. This observation suggests that quality of data is important, and that an increased number of data points do not inherently reduce classification errors.

Classifier

A linear discriminant analysis (LDA) classifier was chosen in this study for two reasons: the authors wished to provide real-time control in 30 ms increments, which required a computationally simple classifier. They also wanted to test a variety of adaptation paradigms over a range of tuned parameters. Even using an LDA required over a month of offline continuous data processing on a 3GHz computer to optimize tuning parameters and process results. Using a more computationally intensive classifier would have limited the scope of the present study. Although previous studies have shown that LDA's perform just as well as neural networks for static systems [19], it must be acknowledged that adaptation may allow neural networks to be tweaked in ways that LDA classifier cannot, resulting in advances that may only be realized using a neural network. Despite that potential limitation, the low obtainable minimum error demonstrates that the LDA classifier did not unduly inhibit the range of available adaptation.

Minimum error

Minimum error is a useful metric in adaptive pattern recognition work, because it separates the limitations of the feature set, classifier, and subject from the limitations of the adaptive algorithm. If the user performs the same pattern for two different classes, these patterns will overlap and the reported minimum error will be high. Likewise, if a poor set of features are used, the two patterns will still overlap in feature space, resulting in high minimum error. Finally, if boundaries are clearly defined in feature space but the classifier is unable to construct a border that maintains these boundaries, then the minimum error will be high. Reporting minimum error in the field of adaptive pattern recognition enables future researchers to determine whether the feature set/classifier/user-training needs revision, or whether the adaptive paradigm needs revision.

The results reported here defined minimum error as the error produced by training and testing on the same real-time data set. This is a useful definition, provided it is correctly understood and not used as the actual performance of the system – it is only the best conceivable performance of the system. An important distinction must be made, however. Training and testing on the same data using an LDA does not achieve the optimal system – it only achieves a centered system. It is conceivable, using the arguments underlying the Low-confidence paradigm, that biasing the boundaries might provide better clarity in regions where errors frequently occurred, resulting in a better classifier and a smaller minimum error. Although in the field of prosthetics LDA classifiers are preferable compared with more complex algorithms due to their lower computational cost, future studies should attempt to optimize boundaries rather than center them. This approach will require more computational training time, but the resulting classifier will be just as fast in real-time and will produce fewer errors.

High-confidence errors

Using high-confidence errors to tune a classifier is a theoretically appealing paradigm, in that the classifier only tunes decisions that were confident – yet wrong. The authors have observed that such concept makes a useful quantifiable metric of classifier or data robustness. Towards this end, the authors implemented the UB₂ paradigm, which only tagged errors with high confidence. Unfortunately, practical implementation of such an approach is difficult, in part due to unintentional or confused movements by users, and in part due to the fact that if the classifier is confident about a particular sample, suggesting an alternative class is problematic. The UB₂ paradigm illustrates this difficulty – by only including perceived errors with high confidence, the percentage of errors introduced into the classifier rose from 54% to 64%.

Session limitation

This study only involved a single two-hour session per subject. Studies that investigate adaptation over days or months require prostheses capable of myoelectric pattern recognition that can be tested in the field, not just in the laboratory. Once these prostheses are available, results that are more practical will be obtainable. The authors designed this experiment to commence capturing patterns without any subject training in order to capture the greatest extent of adaptation on the part of the user. In retrospect, this methodology, although capturing a greater range of adaptation, also allowed greater variability within the classes of the user and potentially greater overlap in feature space between the classes. As a result, future studies should investigate more time spent coaching the subject to provide consistent, stable patterns.

The ability to design and evaluate adaptation algorithms is limited in part by our field's conceptual weakness regarding what constitutes robustness or optimal performance. Adaptation work would greatly benefit from future research that provides a better mathematical and therapeutic framework through which to understand these critical concepts.

V. Conclusion

A novel data collection methodology has been presented that allows repeated-measures post-hoc analysis of numerous adaptation strategies. Variants of three supervised and three unsupervised adaptation strategies were analyzed using this method. All supervised adaptation paradigms reduced classification error of myoelectric control of an 11-class system. Incorrect classification prevented unsupervised paradigms from achieving as substantial results, and only high-confidence adaptation introduced a sufficiently high percentage of correct samples to significantly reduce classification errors.

Biography

Jonathon W. Sensinger (M’09) received the B.S. degree in bioengineering from the University of Illinois at Chicago in 2002, and the Ph.D. degree in biomedical engineering from Northwestern University, Chicago, IL in 2007.

He is a Research Assistant Professor within the Neural Engineering Center for Artificial Limbs at the Rehabilitation Institute of Chicago, IL. His research interests include myoelectric and body-powered prosthesis theory and design.

Blair A. Lock received the B.S. and M.S. degrees in electrical engineering, in 2003 and 2005, respectively, from the University of New Brunswick, Fredericton, NB, Canada, where he also received a diploma in technology management and entrepreneurship, in 2003.

He works as a Research Engineer and the Laboratory Manager for the Neural Engineering Center for Artificial Limbs at the Rehabilitation Institute of Chicago, Chicago, IL. His research interests include pattern recognition for improved control of powered prostheses and virtual reality in rehabilitation.

Todd A. Kuiken, (M’99-SM 07) completed his BS in BME at Duke University, Durham, North Carolina in 1983. He received his PhD in BME (1989) and MD (1990) from Northwestern University, Chicago, IL. He completed his residency in Physical Medicine and Rehabilitation at the Rehabilitation Institute of Chicago and Northwestern University Medical School, Chicago, Illinois in 1995.

He is currently the Director of the Neural Engineering Center for Artificial Limbs and Director of Amputee Services at the Rehabilitation Institute of Chicago. He is an Associate Professor in the Depts. of PM&R and Biomedical Engineering of Northwestern University. He is also the Associate Dean, Feinberg School of Medicine, for Academic Affairs at the Rehabilitation Institute of Chicago.