State reduction for network intervention in probabilistic Boolean networks

Abstract

Motivation: A key goal of studying biological systems is to design therapeutic intervention strategies. Probabilistic Boolean networks (PBNs) constitute a mathematical model which enables modeling, predicting and intervening in their long-run behavior using Markov chain theory. The long-run dynamics of a PBN, as represented by its steady-state distribution (SSD), can guide the design of effective intervention strategies for the modeled systems. A major obstacle for its application is the large state space of the underlying Markov chain, which poses a serious computational challenge. Hence, it is critical to reduce the model complexity of PBNs for practical applications.

Results: We propose a strategy to reduce the state space of the underlying Markov chain of a PBN based on a criterion that the reduction least distorts the proportional change of stationary masses for critical states, for instance, the network attractors. In comparison to previous reduction methods, we reduce the state space directly, without deleting genes. We then derive stationary control policies on the reduced network that can be naturally induced back to the original network. Computational experiments study the effects of the reduction on model complexity and the performance of designed control policies which is measured by the shift of stationary mass away from undesirable states, those associated with undesirable phenotypes. We consider randomly generated networks as well as a 17-gene gastrointestinal cancer network, which, if not reduced, has a 2¹⁷ × 2¹⁷ transition probability matrix. Such a dimension is too large for direct application of many previously proposed PBN intervention strategies.

Contact: xqian@cse.usf.edu

Supplementary information: Supplementary information are available at Bioinformatics online.

1 INTRODUCTION

To date, probabilistic Boolean networks (PBNs; Shmulevich et al. 2002) form one of the widely accepted mathematical models for cellular systems. One of their important applications is to design intervention strategies that beneficially alter cell dynamics through studying the long-run network behavior. Since the probabilistic description of a PBN is an ergodic and irreducible finite Markov chain (MC; Qian and Dougherty 2008; Shmulevich et al. 2002), it possesses a steady-state distribution (SSD) reflecting its long-run dynamics. Different stochastic control policies have been employed to change the long-run dynamics so as to reduce the risk of entering aberrant states and thereby alter the extant cell behavior (Datta et al. 2006; Pal et al. 2006); however, owing to the inherent computational complexity of optimal control methods using Markov chain theory, it is often computationally prohibitive to achieve optimal control policies for large networks (Akutsu et al. 2007; Bertsekas, 2005). Several approximate and greedy algorithms (Ng et al., 2006; Qian et al. 2009; Vahedi et al. 2008)) have been proposed to find suboptimal solutions but many of them still have complexity that increases exponentially with the number of genes in the network. Hence, there is a need for size reducing mappings that produce more tractable models whose stationary control policies induce suboptimal stationary control policies on the original network. This article proposes a greedy procedure to reduce the network state space. We study the effects of the proposed reduction with respect to the changes of the long-run network dynamics and intervention performance of stationary control policies derived using long-run network dynamics.

Whereas the available reduction mappings (Dougherty and Shmulevich 2003; Ivanov and Dougherty 2004; Ivanov et al. 2007) consider deleting genes to reduce the state space, we focus on deleting states by changing the regulatory rules and thereafter the transition probability matrix of the original network, in a way that does not interfere with the trajectories of the critical states in the network, for example, its attractors. We reduce the state space based on the structure of the basins of attraction (BOAs) in a network. As the BOAs before and after this state reduction procedure remain similar, the long-run dynamics, especially the proportion of stationary masses for critical states, also remains similar. Hence, we can design stationary control policies on the reduced network based on long-run dynamics similar to those in Qian et al. (2009) and then, from these, induce stationary policies on the original network. Our in silico experiments show that the induced control policies achieve substantial beneficial shift of stationary mass of the original network toward desirable phenotypes.

2 SYSTEMS AND METHODS

2.1 Background

We focus on binary PBNs in this article but our results directly extend to more finely quantized PBNs since the underlying models are always finite Markov chains. Following the standard definitions in Kauffman (1969) and Shmulevich et al. (2002), a PBN is a collection of context Boolean networks (BNs), whose network dynamics are determined by Boolean regulatory rules, represented by function truth tables. In a BN of n genes, each gene x_i ∈ {0, 1} at time t + 1 is determined by the values of a set V_i of predictor genes at t via a Boolean function f_i : {0, 1}^K_i ↦ {0, 1}, where K_i = |V_i| denotes the number of predictor genes in V_i and is called the input degree of x_i in the network. A truth table representing regulatory rules for one BN gives a network predictor function f = (f₁,…, f_n). The network evolves as a trajectory of gene expression states X_t ∈ {0, 1}ⁿ, which lie in the state space of size 2ⁿ. From any initial state, a BN will eventually reach a set of states, called an attractor cycle, through which it will cycle endlessly. Each state flows into a unique attractor cycle and the set of states leading to a specific attractor cycle is known as its basin of attraction (BOA). One type of attractors are singleton attractors, i.e. states x for which f(x) = x.

For PBNs with k context BNs, there are k network predictor functions, F = {f₁,…, f_k}. Perturbation is introduced with a probability p by which the current state of each gene in the network can be randomly flipped. At each updating time, a decision is made whether to maintain the current governing context or to switch the context (allowing the current context to be selected). There is a switching probability q and, given the decision to switch, selection probabilities c_j, 1 ≤ j ≤ k corresponding to the set of context BNs. Assuming perturbation, the simplest type of PBN is a BN with perturbation (BNp), which has only one context BN and k = 1. As described in Shmulevich and Dougherty (2010), we can derive transition probability matrices P = (p(x, y))_x,y of the underlying Markov chains for different types of PBNs based on the truth tables and the involved probabilistic parameters (Supplementary Materials), where p(x, y) is the probability of the chain undergoing the transition from the state x to the state y. Introduction of perturbation makes the corresponding Markov chains ergodic and irreducible. Hence, a PBN possesses a SSD, defined by π^T = π^TP, describing the long-run behavior, where T denotes transpose. Note that P can be decomposed into two parts, (1 − p)ⁿF and H (Supplementary Materials), where the rows of F are vectors determined by regulatory rules and H is the perturbation term determined by Hamming distances between the network states, and with p fixed, H is the same for all PBNs of n genes. A PBN inherits the attractor structures from its context BNs. With sufficiently small p, π will reflect the attractor structures within these BNs. To develop therapeutic interventions, we are especially interested in the proportion of time the network occupies an attractor when in its steady state. As has been hypothesized (Kauffman 1969; Li et al. 2004), attractors may capture cellular phenotypes and occupy a large proportion of the stationary mass.

2.2 State reduction strategies

We first present a reduction procedure motivated by the aggregation algorithms for computing SSDs for large Markov chains (Dayar and Stewart 1996; Kafeety et al. 1992). These algorithms are based on grouping the states so that the SSD can be approximated by solving small linear systems for groups of states. Since the SSD reflects the long-run behavior for a given PBN, we desire that the reduction preserves the original proportion of stationary masses for critical states as much as possible. The difference of the SSDs before and after reduction has been one measure used for different reduction mappings (Ivanov et al. 2007). At the same time, the SSD is determined by the properties of BOAs in the network. More specifically, it has been shown that the steady-state probabilities for attractors are dependent on the size and structure of BOAs (Brun et al. 2005). For a PBN, the underlying Markov chain is often sparse. There are many transient states with negligible stationary mass that are not observed in experiments. The attractors represent the essential long-run network behavior and their stationary masses are critical for both understanding and controlling the network. Biologically, attractors have been widely recognized to correspond to meaningful cellular states (Kauffman, 1969; Li et al., 2004). We consider them as the critical states in the network (it being straightforward to include more states as critical states if they are desirable from biologists, e.g. corresponding to important phenotypes). The goal of our state reduction procedure is to prune away the transient states so that we preserve the proportion of stationary masses of the critical states.

Assuming that there are m critical states if there are altogether m attractors in the given network, S = {x_i1,x_i2,…, x_im}, where m ≪ 2ⁿ, we want to preserve the proportion of π_S = [π_xi1, π_xi2,…, π_xim] with π_x as the steady-state probability of state x. One criterion is

(1)

where 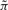is the SSD after reduction. Starting from the original network, we select a state u, which belongs to a set of states that are the most distant from the corresponding attractor cycles in all the BOAs, to delete so that the change of c in (1) is minimum. We delete u in the sense that we force u to transit to itself by setting f(u) = u. Since u will always be the most outside transient state in its corresponding BOA, setting f(u) = u isolates u to be a singleton attractor with its BOA size equal to 1, so that after ‘deletion’, it will not interfere with the trajectories of the other state transitions in the network. This greedy sequential procedure recursively selects the states having the least influence on the SSD according to c until the change c is beyond a given threshold c_th. As we discuss next, these iteratively deleted states are grouped as one ‘mega’ state in the reduced Markov chain.

Each step in this sequential procedure perturbs the transition probability matrix P of the original network to a new matrix 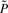, whose dimension equals to that of P. During this procedure, the major computational task is to compute c in (1). As we take only one state from one context network and make it transit to itself at each step, only two entries in one row of the transition matrix changes. Assuming f(u) = v in the original network, we set f(u) = u for state reduction. Let 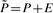, where the perturbation matrix E can be written as:

where e_u is a 2ⁿ-dimensional unit vector with the u-th element equal to 1 and

with ϵ changing for different types of PBNs according to their corresponding transition probabilities (Supplementary Materials). Therefore, we can implement the same analytic solution adapted from perturbation theory in Markov chains (Hunter, 2005; Qian and Dougherty, 2008; Schweitzer, 1968) to derive the exact perturbed SSD efficiently at each sequential step:

where z_u and z_v are two rows of the fundamental matrix Z (a generalized inverse of I − P) that correspond to the states u and v; and z_uu and z_vu are the u-th entries in the two rows. We emphasize that π and Z need to be updated as in Qian et al. (2009) during the recursive procedure.

At the end of the recursive procedure, we group all the ‘deleted’ states into one ‘mega’ state as they do not interfere with the remaining states. We want to construct a new transition probability matrix P^* with the dimension (m^′ + 1) × (m^′ + 1), where m^′ is the number of remaining states and m^′ ≥ m. We first re-order the states by groups of remaining states and deleted states. The re-ordered transition probability matrix 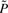has a special structure because the deleted states are singleton attractors (Supplementary Materials):

where F^* is determined by the regulatory rules in the original network as the reduction does not interfere with the state transitions for the remaining states. From 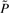, we obtain P^* using the following heuristic. We first add up the last 2ⁿ − m^′ columns of 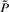, these corresponding to the deleted states. They are aggregated into one mega state. We then take the average of the last 2ⁿ − m^′ rows in 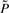as the transition probabilities from the mega state to the remaining states, since the mega state represents all the deleted states and these states are similar to each other with respect to state transitions to the remaining states. With P^*, we can compute the SSD, π^*, for this reduced Markov chain to approximate the original network dynamics with the complexity O(m^′) reduced from O(2ⁿ). The worst case for the sequential procedure is when m^′ = 2ⁿ, meaning there is no state that can be pruned away, and the best case is when m^′ = m, where all remaining states are critical.

2.2.1 BOA-based state reduction

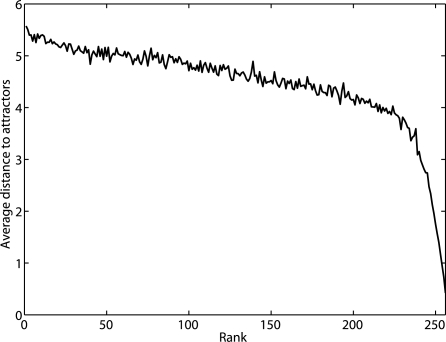
The state space of the underlying Markov chains grows exponentially so that computing SSDs becomes prohibitively expensive for large networks. Hence, the preceding reduction procedure becomes computationally infeasible because each iterative step requires for the computation of a perturbed SSD. Nevertheless, removing transient states far from their corresponding attractor cycles should intuitively have small effect on proportional change of stationary masses for critical states. To validate this heuristic, we ran simulations with 100 randomly generated BNps with n = 8. The parameters to generate random BNps are given in Section 3.1. For the simulation of each BNp, we perturb it by making every state transit to itself one at a time and rank the change to the SSD in an ascending order. At the same time, we compute the number of transitions for each state to reach its corresponding attractor cycle in the original BNp as our distance measure for each state. We plot the average distance for 100 random networks with respect to the rank in Figure 1. The plot shows that the states that are farthest from their corresponding attractors influence the SSD the least.

Fig. 1.

The average distance of ‘deleted’ states with respect to the rank of SSD change in an ascending order for 8-gene random BNps.

Based on this observation, we propose an aggressive reduction procedure to prune or ‘strip’ away the outmost transient states in a BOA. In this section, we assume that the complete information of the original PBN is available and we can compute the structure of BOAs for the network. Based on BOA structure, we can reduce the underlying Markov chain layer by layer. These pruned states are forced to transit to themselves by re-setting the corresponding regulatory functions as described above. They all become singleton attractors and grouped as a mega state after reduction. Since there is no guarantee of the bound for the proportional change of the critical states using this procedure, we study the effects of the reduction on the proportional change in silico in Section 3.

We note here that heuristics can be used to achieve better preservation of stationary masses for critical states based on BOA structure. Because attractor steady-state probabilities depend on the corresponding BOA sizes and structures (Brun et al., 2005), the reduction procedure can selectively delete the states by appropriately sampling the space of outmost transient states according to either their distances to the attractor cycles to which they belong, or the sizes of the corresponding BOAs. However, since our final goal of state reduction is to derive effective intervention strategies instead of approximating SSDs, we focus on this aggressive procedure for our experimental evaluation.

2.2.2 Transition probability-based state reduction

For a given PBN, we can compute the transition matrix P of its underlying Markov chain. The outmost transient states can be easily identified based on the transition probabilities in P. We first compute ∑_xp(x, y) for all the outmost transient states y. Because these states are at the outmost layers, there are no other states transiting to them based on the regulatory functions F. Based on the definitions of p(x, y) in Supplementary Materials, if ∑_xp(x, y) < min_jc_j(1 − p)ⁿ where c_j is again the network selection probability and c_j = 1 for BNps, then y has to be an outmost state and can be deleted for reduction. Thus, the reduction procedure described in Section 2.2.1 can be implemented based on the transition matrix without finding the BOAs.

2.2.3 Observation-based state reduction

If there is insufficient information about the state transitions of a PBN, we can still implement the same reduction procedure using only experimentally observed state transitions based on the above observation. The motivation is that the unobserved state transitions appear with very low probabilities in network dynamics. Hence, the observed state transitions can directly approximate the network dynamics and we can use the observed attractors as our critical states and prune away all the unobserved states, which have high probabilities of being transient states. In this case, the transition probabilities p(x, y) have to be inferred from experimental data, and accurate estimation is difficult to achieve, in particular, for transient states that are rarely observed experimentally. In fact, we can directly delete and group states that are not observed experimentally. The reduction procedure can then proceed by considering those states as forming their own singleton attractors and grouping them into one mega state, and the resulting reduced Markov chain can be used to find effective control policies.

Note that once the outmost states are identified, either based on the BOA structure, the transition probability matrix, or directly from experimental observations, the reduction procedure is similar: force these states to transit to themselves and form a mega state in the reduced Markov chain.

2.3 Stationary control policies after reduction

To mitigate the computational complexity inherent in dynamic programming, several greedy stationary control policies (Qian et al., 2009; Vahedi et al., 2008) have been introduced based on long-run network behavior; nonetheless, these policies still have exponential complexity with respect to the number of genes in a network. Here, we derive two control policies on the reduced network based on the principles introduced in Qian et al. (2009). When considering therapeutic interventions, the state space can be partitioned into the set of desirable states D and the set of undesirable states U according to the expression values of a given set of genes. For simplicity, we will assume that the gene expression of the leftmost gene x₁ in the network determines that the network state x is either desirable (x₁ = 1) or undesirable (x₁ = 0). Furthermore, without loss of generality, we focus on the control policies by flipping a single control gene g, which is typically different from x₁ as we discussed in Section 3. The principle of deriving effective control policies is based on the intuition that the control policy should reduce the likelihood of visiting undesirable states π_U = ∑_x1=0π_x (π_x is the steady-state probability for state x) either by directly shifting SSD or decreasing the time to reach D.

2.3.1 BOA control policy

First, we introduce the BOA control policy on the original network (Qian et al., 2009). For any state x, let A(x) be the set of attractors (the cycle) for the basin containing x. Let d_D(x) and d_U(x) be the minimal distances of state x to states in D and U, respectively. For a pair of undesirable states x and x_g (the state that differs from x only in the value of the control gene g), we first check whether A(x) or A(x_g) contains any desirable attractors. If only one of these sets contains desirable attractors, then we set the control actions for x and x_g to always flip to that state so that we increase the likelihood of entering into desirable attractors. If both A(x) and A(x_g), or neither one, has desirable attractors then, we compare d_D(x) and d_D(x_g): whichever is minimum, we apply control by flipping to that state so that the network can reach the desirable states D faster. We do not apply any control if d_D(x_g) = d_D(x). For a pair of desirable states x and x_g, we first check whether A(x) or A(x_g) contains any undesirable attractors. If only one of them contains undesirable attractors, then we apply control to flip away from that state so that we reduce the probability of getting into undesirable attractors. If the condition is satisfied for both of the states or neither of them, we then compare d_U(x) and d_U(x_g) to make the time to reach the undesirable states U longer. The computational complexity for finding this control policy in the original network is O(2ⁿ).

With state reduction, we delete states to reduce the state space by making them transit to themselves and the mega state, representing the group of these deleted states, forms a singleton attractor in the reduced network. When we design the control policy based on the BOA structure of the reduced network, we simply look at the remaining states. If either x or x_g remains in the reduced network, we derive the control policy in the exactly same way as in the original network, taking the advantage of knowing that a deleted state should be a singleton attractor; otherwise, we do not apply any control. Derivation of this control policy uses only the m^′ remaining states in the reduced network because they are the only ones remaining in the reduced Markov chain. Hence, the complexity of deriving the control policy reduces from O(2ⁿ) to O(m^′). The control policy based on the reduced network is induced back to the original network based on the fact that the reduction does not change state transitions for the remaining states and each state in the original network corresponds to a single state in the reduced network. For deleted states by reduction, we do not apply any control.

2.3.2 SSD control policy

It has been shown that SSD control policy performs better than BOA control policy on original networks (Qian et al. 2009) because it directly uses the shift of undesirable stationary mass as the criterion of applying control. A key issue for this algorithm is the efficient computation of the shifted stationary mass resulting from the intervention, which can be done by the same analytic solution as in Section 2.2 (Hunter, 2005; Qian and Dougherty, 2008; Schweitzer, 1968). The control action by flipping g at any given state x simply replaces the row in the original transition probability matrix P corresponding to the state x by the row corresponding to x_g. The perturbed SSD is given by:

(2)

where p_x and p_xg are the two rows corresponding to the states x and x_g in P, respectively, z^x is the column corresponding to the state x in Z, and 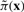denotes the SSD after we apply control. Following this analytic solution, we can quickly compute the total stationary mass, π_U, for the undesirable states and 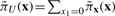. Once this is done for each state, we can derive a SSD control policy by comparing the total stationary mass of undesirable states after applying control to x and x_g: 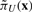and 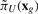. If both are larger than the original undesirable stationary mass π_U, then we do not apply any control; otherwise, we apply control to the state which leads to less stationary mass of the undesirable states. The computational complexity for finding this new control policy is again O(2ⁿ), while the complexity for each iteration in the algorithm increases from the BOA control policy by the vector-matrix multiplications involved in (2).

For the reduced network, we can design a similar SSD control policy. However, in the reduced network, we compute the approximate stationary masses for the remaining states to derive the control policy based on the new transition probability matrix P^* and its corresponding fundamental matrix Z^* with (2). We only check the remaining states after reduction. If both x and x_g remain in the reduced network, then we derive the control policy in exactly the same way as in the original network. If only one of these remains, then we compute the shift of undesirable stationary mass by considering the mega state as the corresponding flipped state. Otherwise, we do not apply any control. Since the reduction procedure leads to small proportional changes in stationary masses of the critical states, this control policy should capture well the actual shift of undesirable stationary mass in the original network. The derived control policy can be induced back to the original network with no control for the deleted states. The complexity also reduces from O(2ⁿ) to O(m^′), which makes it possible to derive the induced SSD control policy for large networks.

Clearly, it is more efficient to derive the BOA control policy than other policies, such as the mean-first-passage-time policy (Vahedi et al., 2008) and the SSD policy (Qian et al., 2009), which involve solving large linear systems and are often computationally infeasible to derive for large networks. Although the computational complexity of our state reduction procedure is O(2ⁿ), which is the same as that for deriving the BOA control policy directly on the original network, the state reduction procedure is more efficient because it does not utilize the complete structural properties of the BOAs. The complete procedure of deriving the state reduction, obtaining the BOA policy based on the reduced network, and inducing that back to the original network is more efficient than directly deriving the BOA policy based on the original network. In the case of a network for which it is computationally feasible to directly derive the BOA policy on the original network, its performance will be better because full knowledge of the model is utilized. However, when there is no sufficient information about the network, which is often the case, it is still feasible to derive a SSD control policy based either on transition probabilities between states or directly on experimental observations.

3 DISCUSSION

Using randomly generated networks as well as a larger, real-world network designed from a gastrointestinal cancer dataset (Price et al., 2007), we now study the effects of the proposed state reduction algorithm with respect to both the approximation of long-run dynamics and intervention performance.

3.1 Simulations with randomly generated networks

This section considers reduction effects based on a large number of randomly generated networks with similar properties. The two most important parameters for generating random BNs are the bias (p_b) and connectivity (K), where K is the maximum input degree of the Boolean functions in the network and p_b is the mean of the Bernoulli distribution to generate the truth table of one Boolean function. All simulation results are based on randomly generated networks with K = 3 and p_b = 0.5. We test the state reduction algorithm on random BNps and PBNs with two context BNs. We set the perturbation probability P = 0.001 and selection probabilities with c₁ uniformly distributed in (0, 1) and c₁ + c₂ = 1. In all experiments, the control gene is g = x_n. In practice, one might consider all genes (other than x₁) as potential targets for intervention and identify the best control gene with the largest beneficial impact as in Pal et al. (2006), Qian et al. (2009) and Vahedi et al. (2008).

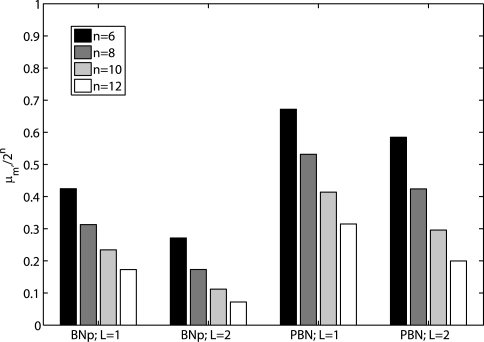
First, we study the effectiveness of the proposed state reduction procedure by running simulations of 1000 randomly generated networks with 6, 8, 10 and 12 genes.¹ The number of remaining states m^′ reflects the degree of the reduction and determines the computational complexity for finding control policies. In the experiments, one and two layers of states are stripped from the original networks (L = 1, 2). Figure 2 shows the ratio of the average number, μ_m^′, of final remaining states to the original number of states (N = 2ⁿ) in both BNps and PBNs with different numbers of genes. It shows that, with similar network properties, the number of transient states farthest away from the attractor cycles within the corresponding BOAs increases with the network size and the degree of the reduction increases with increasing number of genes in networks. PBNs have larger numbers of remaining states because we delete and group only the intersection set of outmost transient states in its context BNs. Details, including the average numbers of remaining states and their standard deviations, are given in Supplementary Materials.

Fig. 2.

The average ratio of the number of remaining states to the number of states of original networks for randomly generated BNps and instantaneously random PBNs with different numbers of genes.

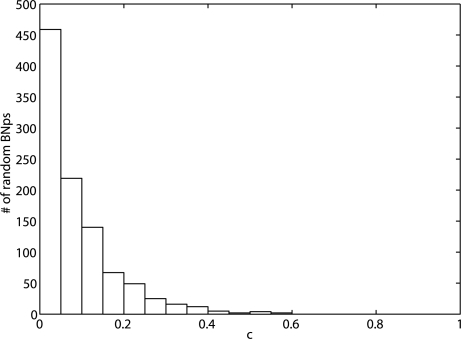
To investigate reduction effects on the long-run network behavior, we consider the proportional change of the stationary mass for the critical states in S in (1) by replacing 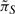with π_S^*, which is the steady-state vector corresponding to S for the final reduced Markov chain after grouping deleted states into the mega state. Using the same randomly generated networks from the experiments described above, we provide the average proportional changes of the stationary masses for the essential states and the respective standard deviations in Table 1. On average, with increasing L, the proportional change increases as we prune away more transient states. But the proportional changes are small and decrease with increasing number of genes for PBNs. The proportional changes of PBNs are much smaller than those of BNps, which is to be expected since the degree of reduction for PBNs is smaller as shown in Figure 2. These results indicate that the state reduction is promising because the previous experiments have shown that degree of reduction increases with the number of genes for both BNps and PBNs. We conjecture that with larger networks, one can reduce the state space greatly while preserving the long-run network behavior fairly well. Note the relatively large standard deviations in Table 1. To check whether the state reduction procedure performs well for most of the random networks, we plot the histogram of the actual proportional changes for essential stationary masses for 1000 random 10-gene BNps with L = 1 layers of transient states removed in Figure 3. More than 86% of the 1000 random BNps have <0.2 proportional change for the critical states' steady-state probabilities and the trend is similar with other random networks (Supplementary Materials). This demonstrates that in general, the reduction procedure preserves the network dynamics.

Table 1.

The average actual proportional changes for the stationary masses of critical states μ_c and their standard deviations σ_c after reduction for random BNps and PBNs with different numbers of genes n

		BNp				PBN
n		6	8	10	12	6	8	10	12
L = 1	μc	0.10	0.10	0.10	0.11	0.06	0.02	0.01	0.007
	σc	0.12	0.12	0.12	0.13	0.23	0.08	0.05	0.015
L = 2	μc	0.15	0.14	0.13	0.14	0.06	0.02	0.01	0.009
	σc	0.17	0.15	0.15	0.15	0.23	0.08	0.05	0.017

Fig. 3.

The histogram of actual proportional change for the stationary mass of critical states for randomly generated 10-gene BNps with L = 1 layer of transient states removed.

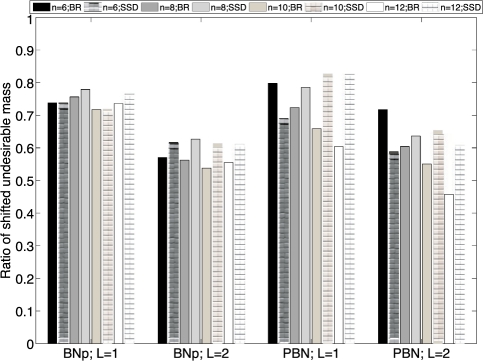
Since our ultimate goal is to apply intervention strategies to achieve therapeutic benefits, we study the effects of state reduction on the intervention performance with both BOA and SSD control policies for a fixed control gene x_n. In Table 2, we provide the average stationary mass of undesirable states π_U before control (ORG) and after applying the BOA control policy based on the original network (BOA), the BOA control policy induced from the reduced network with one layer of transient states grouped together (BR1), the BOA control policy induced from the reduced network with two layers of transient states grouped together (BR2), the induced SSD control policy from the reduced network with one layer of transient states grouped together (SSD1) and the induced SSD control policy from the reduced network with two layers of transient states grouped together (SSD2). All control policies reduce the undesirable stationary mass significantly on average and the performance for both the induced BOA and SSD control policies from the reduced networks is comparable with the performance for the BOA policy based on the original networks. The induced SSD control policy performs slightly better than the induced BOA policy. We show the performance degradation by plotting the ratio of shifted undesirable masses by the policies after reduction to the shifted masses by the BOA policy from the original networks in Figure 4. The degradation is stable with respect to similar amounts of reduction. Since the degree of reduction increases with the increasing number of genes, we believe that, for networks with large size, the reduction can still achieve significant beneficial results, the key point being that the reduction allows the development of control policies for networks that are too large for the policy to be derived directly.

Table 2.

The average undesirable stationary masses π_U before and after applying control for random BNps and PBNs

	BNp				PBN
n	6	8	10	12	6	8	10	12
ORG	0.49	0.50	0.49	0.49	0.50	0.50	0.50	0.49
BOA	0.27	0.30	0.33	0.34	0.35	0.38	0.40	0.41
BR1	0.33	0.35	0.37	0.38	0.38	0.41	0.43	0.44
BR2	0.37	0.39	0.40	0.41	0.39	0.43	0.44	0.45
SSD1	0.33	0.35	0.37	0.38	0.40	0.41	0.41	0.42
SSD2	0.36	0.38	0.39	0.40	0.41	0.42	0.43	0.44

Fig. 4.

The average ratio of the undesirable stationary mass shift for the induced control policies to that of the BOA control policy based on the original networks for randomly generated networks.

3.2 Gastrointestinal cancer network application

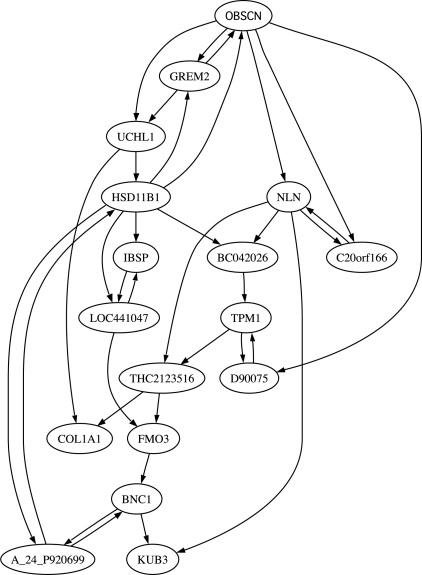
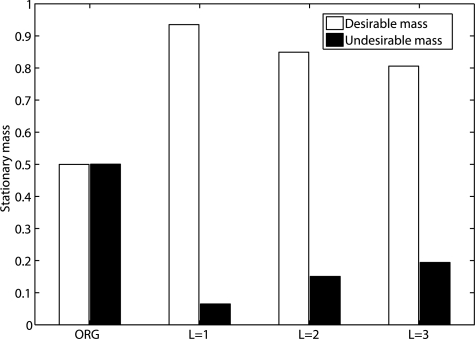
We have also applied state reduction to a 17-gene network designed from a gastrointestinal cancer dataset (Price et al. 2007). The same dataset has been used to test a gene reduction algorithm in Ghaffari et al. (2010). The microarray data have been normalized, filtered and binarized using the methods from Shmulevich and Zhang (2002). A BNp is inferred based on the coefficient of determination (CoD; Dougherty et al., 2000) using a modified network-growing algorithm (Hashimoto et al., 2004) with gene OBSCN as a seed. The inferred network has 17 genes: OBSCN, GREM2, HSD11B1, UCHL1, A_24_P920699, BNC1, FMO3, LOC441047, THC2123516, NLN, COL1A1, IBSP, C20orf166, KUB3, TPM1, D90075 and BC042026 (Fig. 5). For intervention, we partition the state space into a desirable set D and an undesirable set U based on the seed gene OBSCN (x₁) since OBSCN is one of two genes composing the best classifier in Price et al. (2007). Following Ghaffari et al. (2010), GREM2 is set as the control gene. Since it is infeasible to compute numerically the SSDs for the original network before and after applying control policies based on π^T = π^T P with 2¹⁷ states, we estimate the SSDs by running the underlying Markov chains for a long time and using the Kolmogorov–Smirnov test to decide if the network has reached its steady state. We strip away L = 1, 2, 3 layers of transient states and the number m^′ of remaining states in the final reduced models is 7808, 2016 and 1016, respectively. In this example, as the degree of reduction is very large with < 1% of states remaining after reduction when L = 3, there is not even one pair of x and x_g both remaining after reduction, and therefore, the induced BOA control policy, derived by comparing BOA structure for this pair of states, does not perform well as shown in Supplementary Materials. However, the reduction preserves long-term network dynamics and the proportional change of steady-state probabilities for the critical states with l_∞ norm is <0.015 for L = 1, 2, 3. As expected, our induced SSD control policy maintains the integrity of the control. Figure 6 shows the significant shifts in the SSD of the network toward desirable states by applying the induced SSD control policies. This further demonstrates that the proposed state reduction and control policies are potentially helpful for developing effective intervention strategies for future gene-based therapeutics.

Fig. 5.

An abstract diagram of the gastrointestinal cancer network inferred based on the CoD using a modified network-growing algorithm (Ghaffari et al., 2010; Hashimoto et al., 2004). Arrows show the predictor relationships among genes.

Fig. 6.

SSD shift toward the desirable states in gastrointestinal cancer network after applying the induced SSD control policy from the reduced network with L = 1, 2, 3.

3.3 Concluding remarks

In this article, we propose to reduce the state space of the underlying Markov chain of PBNs in order to reduce the computational complexity of searching for (sub-)optimal control policies. Through simulations, we have demonstrated that the proposed state reduction algorithm achieves good performance for both approximating the long-run network behavior and intervening for beneficial dynamics as both the reduction and intervention are directly tied to the long-run network dynamics reflected by the SSDs. The proposed algorithms are useful for designing effective intervention strategies based on the information about the critical states which represent important phenotypes, especially when a limited number of gene expression patterns are observed in microarray experiments. Similar research has a long history in system decompression in the absence of qualifying knowledge. More importantly, the induced control policies derived from the reduced networks yield substantial SSD shifts away from the undesirable network states, and that is our pragmatic goal. Future mathematical work will focus on deriving theoretical bounds on the effects of the state reduction strategy for both long-run behavior and intervention performance. In addition, we are interested in investigating the benefits of the reduction for both network inference and structural intervention.

Funding: National Science Foundation (CCF-0514644); National Cancer Institute (2 R25CA090301-06); the University of South Florida Internal Awards Program (grant No. 78068 to X.Q., in parts).

Conflict of Interest: none declared.